Structural Breaks, Inflation and Interest Rates: Evidence from the G7 Countries
Abstract
:1. Introduction
2. Fisher Effect with Non-Integrated Variables
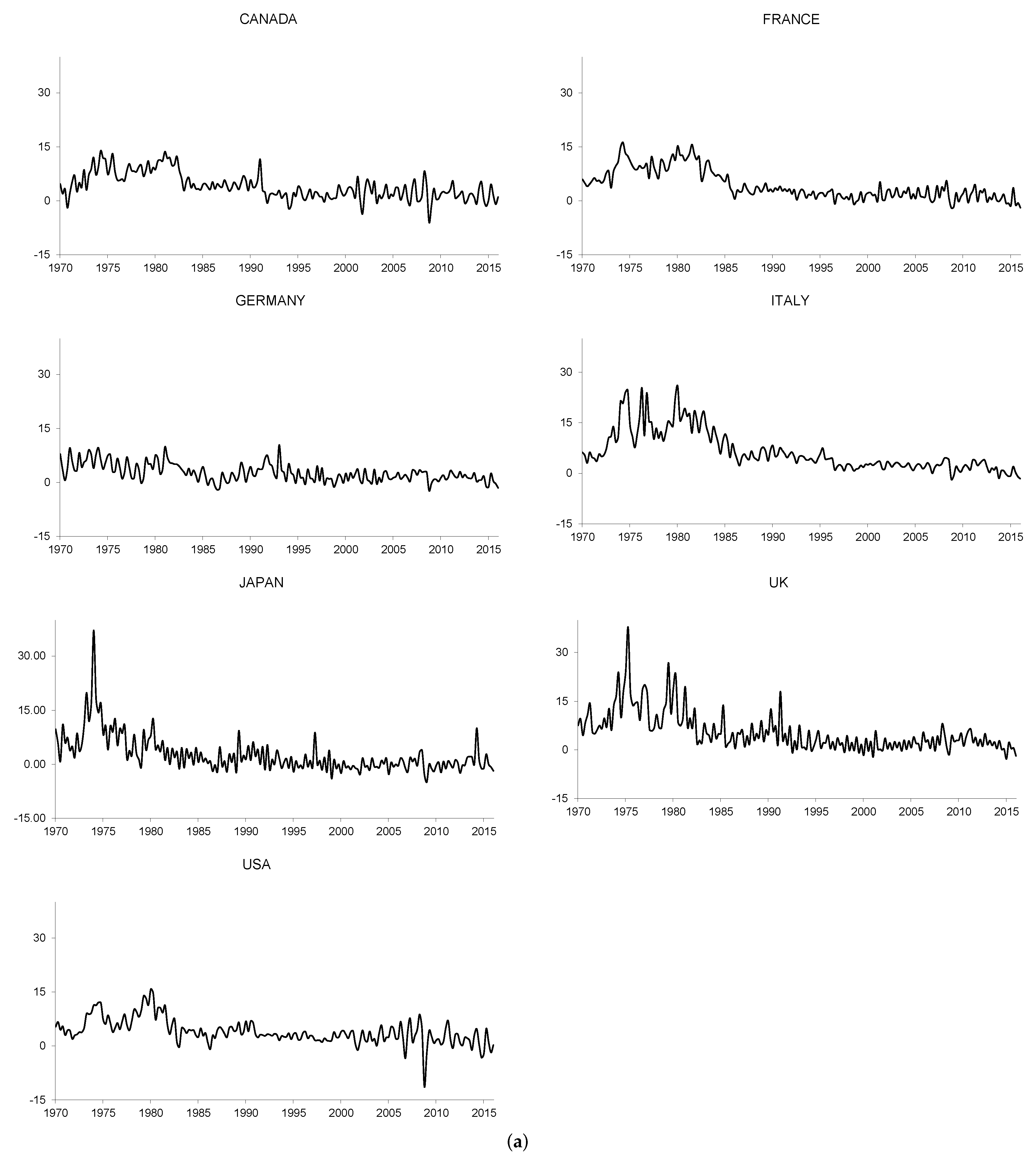
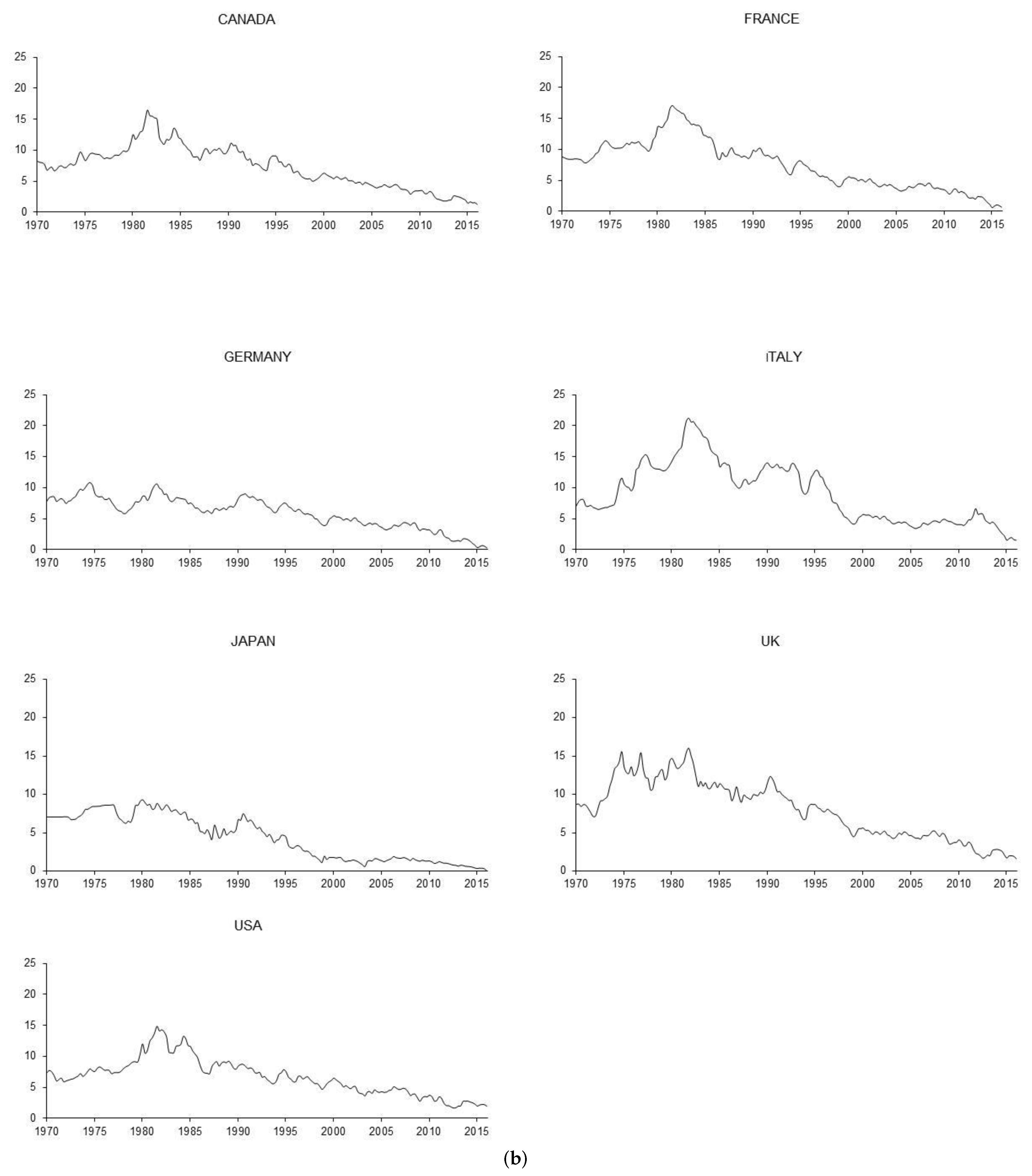
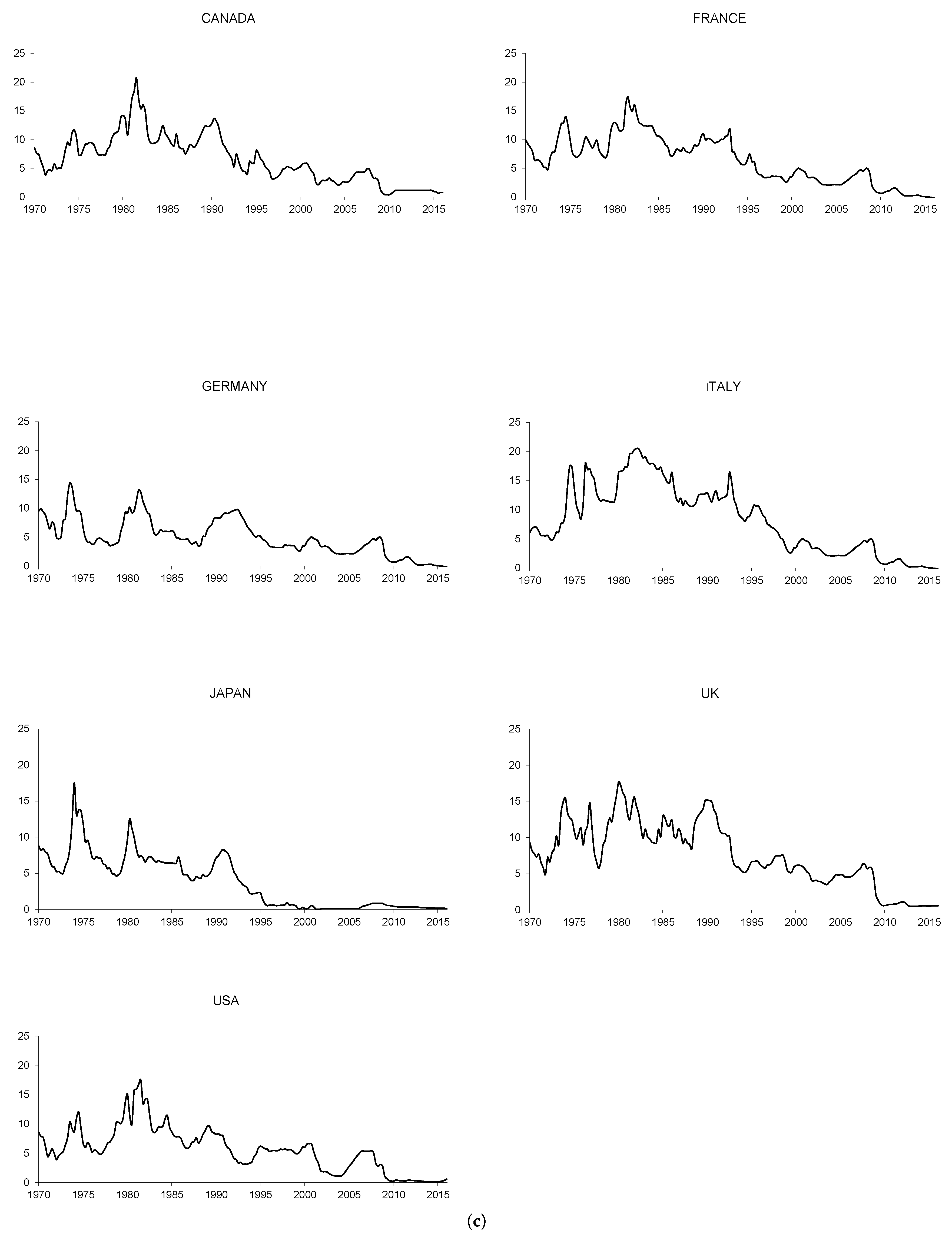
2.1. Analysis of the Time Properties of the Nominal Interest Rates and Inflation Rates
2.2. Empirical Evidence from the G7 Countries
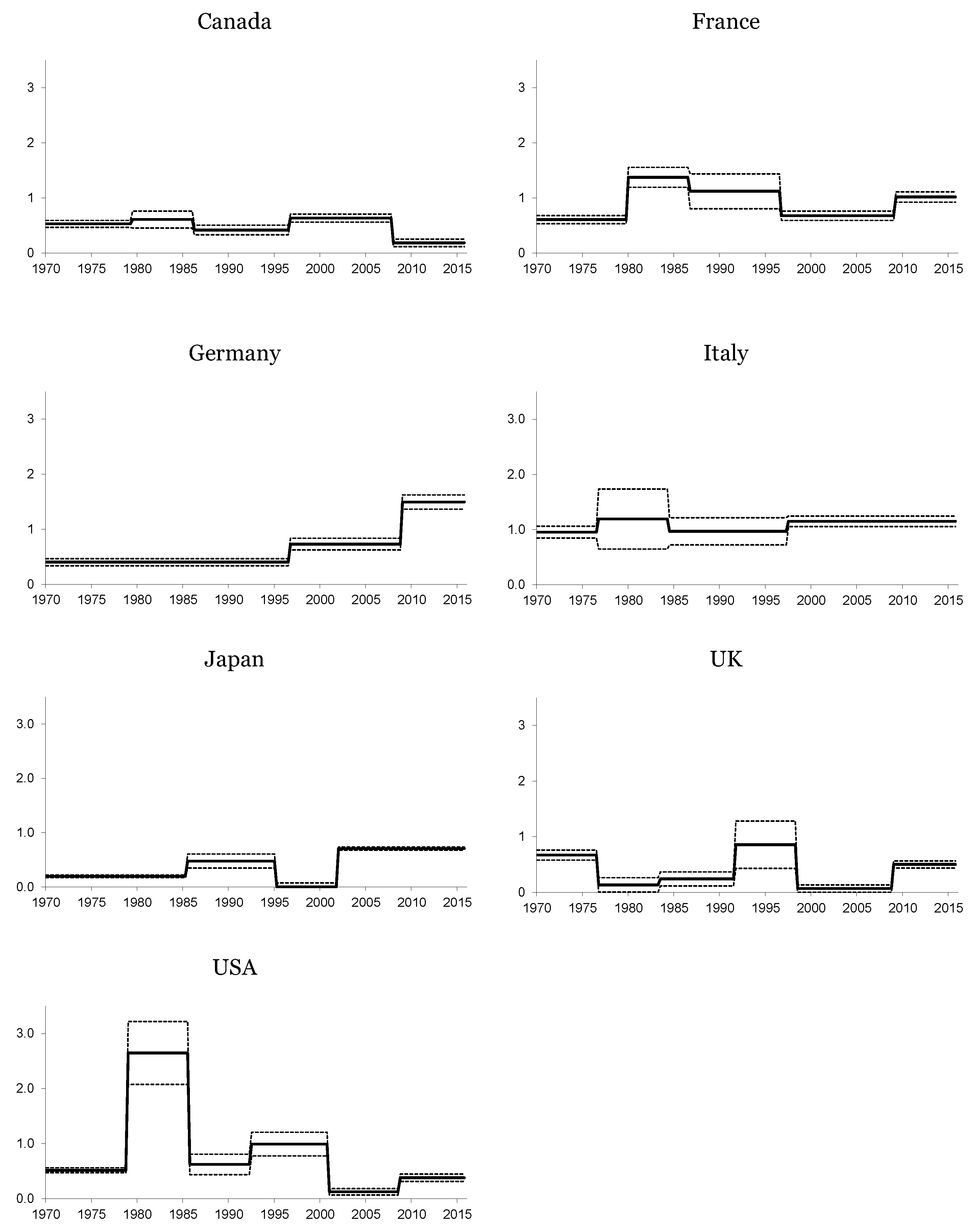
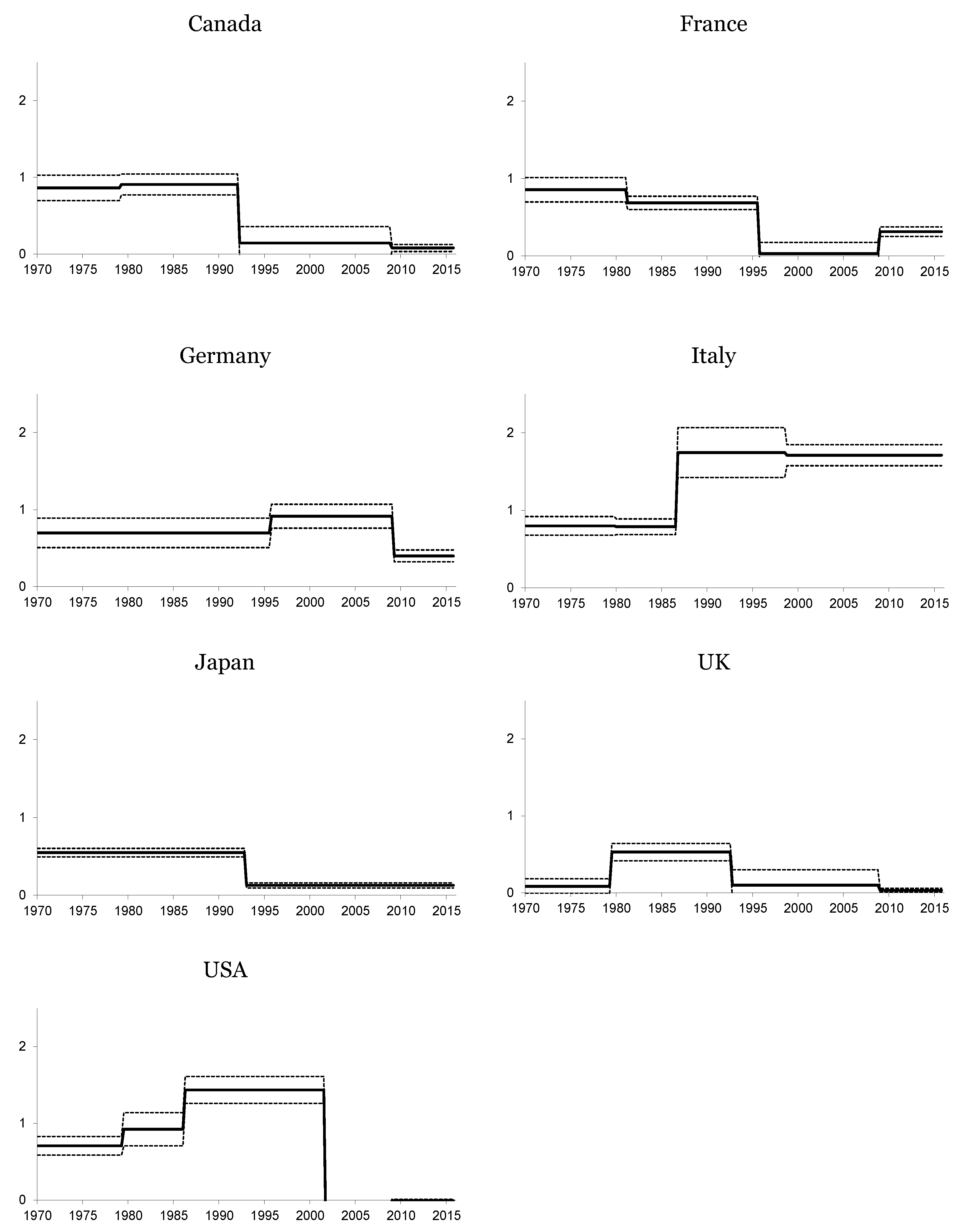
3. Structural Breaks and the Fisher Effect
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
- 2.In our present case, we only include an intercept in the model specification.
- 3.The Italian short-term interest rates for 1970:Q1–1970:Q4 were estimated using the evolution of Italy’s long-term interest rates.
- 4.See Pesaran (2012) [39] in this regard.
- 6.This hypothesis has recently been re-examined with optimizing agents in an overlapping generations context. See Rapach (2003) [59] for a comprehensive survey.
- 7.In order to analyze the robustness of the estimated periods, we have obtained the Bai–Perron statistics for the 1980:Q1–2015:Q4 and for the 1970:Q1–2007:Q4 samples. In this latter case, the estimated periods of breaks almost coincide with those of the full sample. In the former, the variations are a bit larger, especially for the short-run case. The total number of estimated breaks is 19, 15 being coincident with the full sample analysis. For the long-run model, the new total of estimated breaks is 23, 20 being coincident. In summary, given this high degree of coincidence in the results and taking into account that these new estimated breaks are a consequence of the decrease in the size of the lowest segment, we can conclude that the Bai–Perron procedure offers very robust results in this scenario.
References
- I. Fisher. The Theory of Interest. New York, NY, USA: MacMillan, 1930. [Google Scholar]
- G.M. Caporale, and N. Pittis. “Estimator Choice and Fisher’s Paradox: A Monte Carlo Study.” Econom. Rev. 23 (2004): 25–52. [Google Scholar] [CrossRef]
- E. Panopoulou. “A Resolution of the Fisher Effect Puzzle: A Comparison of Estimators.” IIIS Discussion Paper, 67. 2005. Available online: https://ssrn.com/abstract=680401 (accessed on 15 July 2016).
- A.K. Rose. “Is the Real Interest Rate Stable? ” J. Financ. 43 (1988): 1095–1112. [Google Scholar] [CrossRef]
- F. Mishkin. “Is the Fisher effect for real: A Reexamination of the Relationship between Inflation and Interest Rates.” J. Monetary Econ. 30 (1992): 195–215. [Google Scholar] [CrossRef]
- W.J. Crowder, and M.E. Wohar. “Are Tax Effects Important in the Long-Run Fisher Relationship? Evidence from the Municipal Bond Market.” J. Financ. 54 (1992): 307–317. [Google Scholar] [CrossRef]
- Z. Koustas, and A. Serletis. “On the Fisher Effect.” J. Monetary Econ. 44 (1999): 105–130. [Google Scholar] [CrossRef]
- D.E. Rapach. “The Log-run Relationship between Inflation and Real Stock Price.” J. Macroecon. 24 (2004): 331–351. [Google Scholar] [CrossRef]
- F. Laatsch, and D.P. Klein. “Nominal Interest Rate and Expected Inflation: Results from a Study of US Treasury Inflation-Protected Securities.” Q. Rev. Econ. Financ. 43 (2003): 3405–3417. [Google Scholar] [CrossRef]
- D.E. Rapach, and C. Weber. “Are Real Interest Rates Really Nonstationary? New Evidence from Tests with Good Size and Power.” J. Macroecon. 26 (2005): 409–430. [Google Scholar] [CrossRef]
- J. Westerlund. “Panel cointegration tests of the Fisher effect.” J. Appl. Econom. 23 (2008): 193–233. [Google Scholar] [CrossRef]
- B. Ozcan, and A. Ari. “Does the Fisher hypothesis hold for the G7? Evidence from the panel cointegration test.” Econ. Res.-Ekon. Istraz. 28 (2015): 271–283. [Google Scholar] [CrossRef]
- J.C. Cox, J.E. Ingersoll, and S.A. Ross. “A theory of the term structure of interest rates.” Econometrica 53 (1985): 385–407. [Google Scholar] [CrossRef]
- D. Malliaropulos. “A Note on Nonstationarity, Structural Breaks and the Fisher Effect.” J. Bank. Financ. 24 (2000): 695–707. [Google Scholar] [CrossRef]
- M. Lanne. “Near Unit Root and the Relationship between Inflation and Interest Rate: A Reexamination of the Fisher Effect.” Empir. Econ. 26 (2001): 357–366. [Google Scholar] [CrossRef]
- N. Olekalns. An Empirical Investigation of the Structural Breaks in the Ex Ante Fisher Effect. Research Paper Number 786; Melbourne, Australia: Department of Economics, University of Melbourne, 2001. [Google Scholar]
- L.A. Gil-Alaña. “A Mean Shift Break in the US Interest Rate.” Econ. Lett. 77 (2002): 357–363. [Google Scholar] [CrossRef]
- F.J. Atkins, and P.J. Coe. “An ARDL Bounds Test of the Long-term Fisher Effect in the United States and Canada.” J. Macroecon. 24 (2002): 255–266. [Google Scholar] [CrossRef]
- C.F. Baum, J.T. Barkoulas, and M. Caglayan. “Persistence in International Inflation Rates.” South Econ. J. 65 (1999): 900–913. [Google Scholar] [CrossRef]
- P. Phillips, and P. Perron. “Testing for a Unit Root in Time Series Regression.” Biometrika 75 (1988): 335–346. [Google Scholar] [CrossRef]
- W.J. Tsay. “The long memory story of the real interest rate.” Econ. Lett. 67 (2000): 325–330. [Google Scholar] [CrossRef]
- X. Sun, and P.C.B. Phillips. “Understanding the Fisher Equation.” J. Appl. Econom. 19 (2004): 869–896. [Google Scholar] [CrossRef]
- L.A. Gil-Alaña. “Estimation of the order of integration in the UK and the US interest rates using fractionally integrated semiparametric techniques.” Eur. Res. Stud. 7 (2004): 29–40. [Google Scholar]
- L.A. Gil-Alaña, and A. Moreno. “Fractional integration and structural breaks in U.S. macro dynamics.” Empir. Econ. 43 (2012): 427–446. [Google Scholar] [CrossRef]
- U. Hassler, and J. Wolters. “Long Memory in Inflation Rates: International Evidence.” J. Bus. Econ. Stat. 13 (1995): 37–45. [Google Scholar] [CrossRef]
- C.S. Bos, P.H. Franses, and M. Ooms. “Long Memory and Level Shifts: Reanalysing Inflation Rates.” Empir. Econ. 24 (1999): 427–449. [Google Scholar] [CrossRef]
- R.E. Lucas Jr. “Econometric Policy Evaluation: A Critique.” Carnegie-Rochester Conf. Ser. Public Policy 2 (1976): 19–46. [Google Scholar] [CrossRef]
- J.S. Chadha, and N.H. Dimsdale. “A Long Review of Real Rates.” Oxf. Rev. Econ. Policy 15 (1999): 17–45. [Google Scholar] [CrossRef]
- P. Söderlind. “Monetary Policy and the Fisher Effect.” J. Policy Model. 23 (2001): 491–495. [Google Scholar] [CrossRef]
- J. Bai, and P. Perron. “Estimating and Testing Linear Models with Multiple Structural Changes.” Econometrica 66 (1998): 47–78. [Google Scholar] [CrossRef]
- J. Bai, and P. Perron. “Computation and analysis of multiple structural-change models.” J. Appl. Econom. 18 (2003): 1–22. [Google Scholar] [CrossRef]
- C.R. Nelson, and C.I. Plosser. “Trends and Random Walks in Macroeconomic Time Series: Some Evidence and Implications.” J. Monetary Econ. 10 (1982): 139–162. [Google Scholar] [CrossRef]
- D. Dickey, and W. Fuller. “Distribution of the Estimators for Autoregressive Time Series with a Unit Root.” J. Am. Stat. Assoc. 74 (1979): 427–431. [Google Scholar] [CrossRef]
- S.E. Said, and D. Dickey. “Testing for Unit Roots in Autoregressive-Moving Average Models of Unknown Order.” Biometrika 71 (1984): 599–607. [Google Scholar] [CrossRef]
- S. Ng, and P. Perron. “Lag Length Selection and the Construction of Unit Root Tests With Good Size and Power.” Econometrica 69 (2001): 1519–1554. [Google Scholar] [CrossRef]
- G. Elliot, T.J. Rothenbert, and J.H. Stock. “Efficient tests for an autoregressive unit root.” Econometrica 64 (1996): 813–836. [Google Scholar] [CrossRef]
- M.H. Pesaran. “General Diagnostic Tests for Cross Section Dependence in Panels.” IZA Discussion Paper 1240. 2004. Available online: http://www.econ.cam.ac.uk/research/repec/cam/pdf/cwpe0435.pdf (accessed on 1 August 2016).
- M.H. Pesaran. “A simple panel unit root test in the presence of cross-section dependence.” J. Appl. Econom. 22 (2007): 265–312. [Google Scholar] [CrossRef]
- M.H. Pesaran. “Testing Weak Cross-Sectional Dependence in Large Panels.” IZA Discussion Paper 6432. 2012. Available online: http://ftp.iza.org/dp6432.pdf (accessed on 1 August 2016).
- M. Costantini, and C. Lupi. “An analysis of inflation and interest rates. New panel unit root results in the presence of structural breaks.” Econ. Lett. 95 (2007): 408–414. [Google Scholar] [CrossRef]
- C.C. Lee, and C.P. Chang. “Mean reversion of inflation rates in 19 OECD countries: Evidence from panel Lm unit root tests with structural breaks.” Econ. Bull. 3 (2007): 1–15. [Google Scholar]
- C.C. Lee, and C.P. Chang. “Trend stationary of inflation rates: Evidence from LM unit root testing with a long span of historical data.” Appl. Econ. 40 (2008): 2523–2536. [Google Scholar] [CrossRef]
- J. Lee, and M. Strazicich. “Minimum LM Unit Root Tests with Two Structural Breaks.” Rev. Econ. Stat. 40 (2003): 1082–1089. [Google Scholar] [CrossRef]
- J. Lee, and M. Strazicich. “Minimum LM Unit Root Test.” Econ. Bull. 33 (2013): 2483–2492. [Google Scholar]
- M.D. Gadea, A. Montañés, and M. Reyes. “The European Union Currencies and the US Dollar: From post-Bretton-Woods to the Euro.” J. Int. Money Financ. 23 (2004): 1109–1136. [Google Scholar] [CrossRef]
- F.J. Atkins, and M. Chan. “Trend breaks and the Fisher Hypothesis in Canada and the United States.” Appl. Econ. 36 (2004): 1907–1913. [Google Scholar] [CrossRef]
- R. Garcia, and P. Perron. “An Analysis of the Real Interest Rate under Regime Shifts.” Rev. Econ. Stat. 78 (1996): 111–125. [Google Scholar] [CrossRef]
- H.J. Bierens. “Nonparametric Nonlinear Co-Trending Analysis, with an Application to Inflation and Interest in the U.S.” J. Bus. Econ. Stat. 18 (2000): 323–337. [Google Scholar]
- M. Lanne. “Nonlinear dynamics of interest and inflation.” J. Appl. Econom. 21 (2006): 1157–1168. [Google Scholar] [CrossRef]
- E. Panopoulou, and T. Pantelidis. “The Fisher effect in the presence of time-varying coefficients.” Comp. Stat. Data Anal. 100 (2016): 495–511. [Google Scholar] [CrossRef]
- J. Bai. “Estimation of a Change Point in Multiple Regression Models.” Rev. Econ. Stat. 79 (1997): 551–563. [Google Scholar] [CrossRef]
- D.W.K. Andrews. “Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation.” Econometrica 59 (1991): 817–858. [Google Scholar] [CrossRef]
- E.F. Fama. “Term structure forecast of interest rates, inflation and real returns.” J. Monetary Econ. 25 (1990): 59–76. [Google Scholar] [CrossRef]
- Y.A.F. Fahmy, and M. Kandil. “The Fisher effect: New evidence and implications.” Int. Rev. Econ. Financ. 12 (2003): 451–465. [Google Scholar] [CrossRef]
- M. Evans, and K. Lewis. “Do expected shifts in inflation affect estimates of the long-run Fisher relation? ” J. Financ. 50 (1995): 225–253. [Google Scholar] [CrossRef]
- D.E. Rapach, and M.E. Wohar. “Regime Changes in International Real Interest Rates: Are They a Monetary Phenomenon? ” J. Money Credit Bank. 37 (2005): 887–906. [Google Scholar] [CrossRef]
- J. Tobin. “The interest-elasticity of transactions demand for cash.” Rev. Econ. Stat. 38 (1956): 241–247. [Google Scholar] [CrossRef]
- R. Mundell. “Inflation and Real Interest.” J. Polit. Econ. 71 (1963): 280–283. [Google Scholar] [CrossRef]
- D.E. Rapach. “International Evidence on the Long-run Impact of Inflation.” J. Money Credit Bank. 33 (2003): 23–48. [Google Scholar] [CrossRef]
- R. Clarida, J. Galí, and M. Gertler. “Monetary policy rules and macroeconomic stability evidence and some theory.” Q. J. Econ. 115 (2000): 147–180. [Google Scholar] [CrossRef]
| Long-Run Nominal Interest | Short-Run Nominal Interest | Inflation | |
|---|---|---|---|
| p = 0 | 29.25 * | 19.13 * | 20.06 * |
| p = 1 | 26.33 * | 15.39 * | 20.32 * |
| p = 2 | 25.85 * | 15.52 * | 19.27 * |
| p = 3 | 25.16 * | 15.32 * | 19.83 * |
| p = 4 | 24.76 * | 15.28 * | 18.78 * |
| Long-Run Nominal Interest | Short-Run Nominal Interest | Inflation | |
|---|---|---|---|
| p = 0 | −2.89 ** | −6.73** | −12.94 ** |
| p = 1 | −3.08 ** | −7.19** | −12.46 ** |
| p = 2 | −2.27 * | −6.14** | −10.79 ** |
| p = 3 | −2.38 ** | −5.67** | −7.52 ** |
| p = 4 | −2.36 ** | −5.87** | −7.50 ** |
| ψ1 | TB1 | ψ2 | TB2 | ψ3 | TB3 | ψ4 | TB4 | ψ5 | TB5 | ψ6 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel A: long-run nominal interest rates | ||||||||||||
| Canada | 616 | 0.53 | 79:2 | 0.61 | 86:1 | 0.42 | 96:3 | 0.63 | 07:4 | 0.18 | - | - |
| France | 258 | 0.61 | 79:4 | 1.37 | 86:3 | 1.11 $ | 96:3 | 0.68 | 09:1 | 1.02 | - | - |
| Germany | 178 | 0.40 | 96:3 | 0.73 | 08:4 | 1.50 | - | - | - | - | - | - |
| Italy | 218 | 0.95 | 76:3 | 1.27 $ | 84:2 | 1.52 | 97:2 | 1.15 | - | - | - | - |
| Japan | 1337 | 0.20 | 85:2 | 0.47 | 95:1 | 0.07 | 01:4 | 0.71 | - | - | - | - |
| UK | 495 | 0.67 | 76:3 | 0.13 | 83:2 | 0.24 | 91:3 | 0.86 | 98:2 | 0.07 | 08:4 | 0.50 |
| USA | 254 | 0.52 | 78:4 | 2.63 $ | 85:4 | 0.62 | 92:2 | 0.99 | 00:4 | 0.12 | 08:3 | 0.38 |
| Panel B: short-run nominal interest rates | ||||||||||||
| Canada | 642 | 0.86 | 79:1 | 0.89 | 92:1 | 0.15 | 08:4 | 0.08 | - | - | - | - |
| France | 375 | 0.86 $ | 81:1 | 0.68 | 95:3 | 0.03 | 08:4 | 0.31 | - | - | - | - |
| Germany | 185 | 0.70 | 95:3 | 0.92 | 09:1 | 0.40 | - | - | - | - | - | - |
| Italy | 586 | 0.80 | 79:4 | 0.79 | 86:3 | 1.75 | 98:3 | 1.71 | - | - | - | - |
| Japan | 266 | 0.55 | 92:4 | 0.13 | - | - | - | - | - | - | - | - |
| UK | 526 | 0.08 | 79:2 | 0.53 | 92:3 | 0.10 | 08:4 | 0.03 | - | - | - | - |
| USA | 500 | 0.71 | 79:2 | 0.92 | 86:1 | 1.43 | 01:3 | −0.70 | 08:4 | −0.01 | - | - |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clemente, J.; Gadea, M.D.; Montañés, A.; Reyes, M. Structural Breaks, Inflation and Interest Rates: Evidence from the G7 Countries. Econometrics 2017, 5, 11. https://doi.org/10.3390/econometrics5010011
Clemente J, Gadea MD, Montañés A, Reyes M. Structural Breaks, Inflation and Interest Rates: Evidence from the G7 Countries. Econometrics. 2017; 5(1):11. https://doi.org/10.3390/econometrics5010011
Chicago/Turabian StyleClemente, Jesús, María Dolores Gadea, Antonio Montañés, and Marcelo Reyes. 2017. "Structural Breaks, Inflation and Interest Rates: Evidence from the G7 Countries" Econometrics 5, no. 1: 11. https://doi.org/10.3390/econometrics5010011
APA StyleClemente, J., Gadea, M. D., Montañés, A., & Reyes, M. (2017). Structural Breaks, Inflation and Interest Rates: Evidence from the G7 Countries. Econometrics, 5(1), 11. https://doi.org/10.3390/econometrics5010011






