Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels
Abstract
:1. Introduction
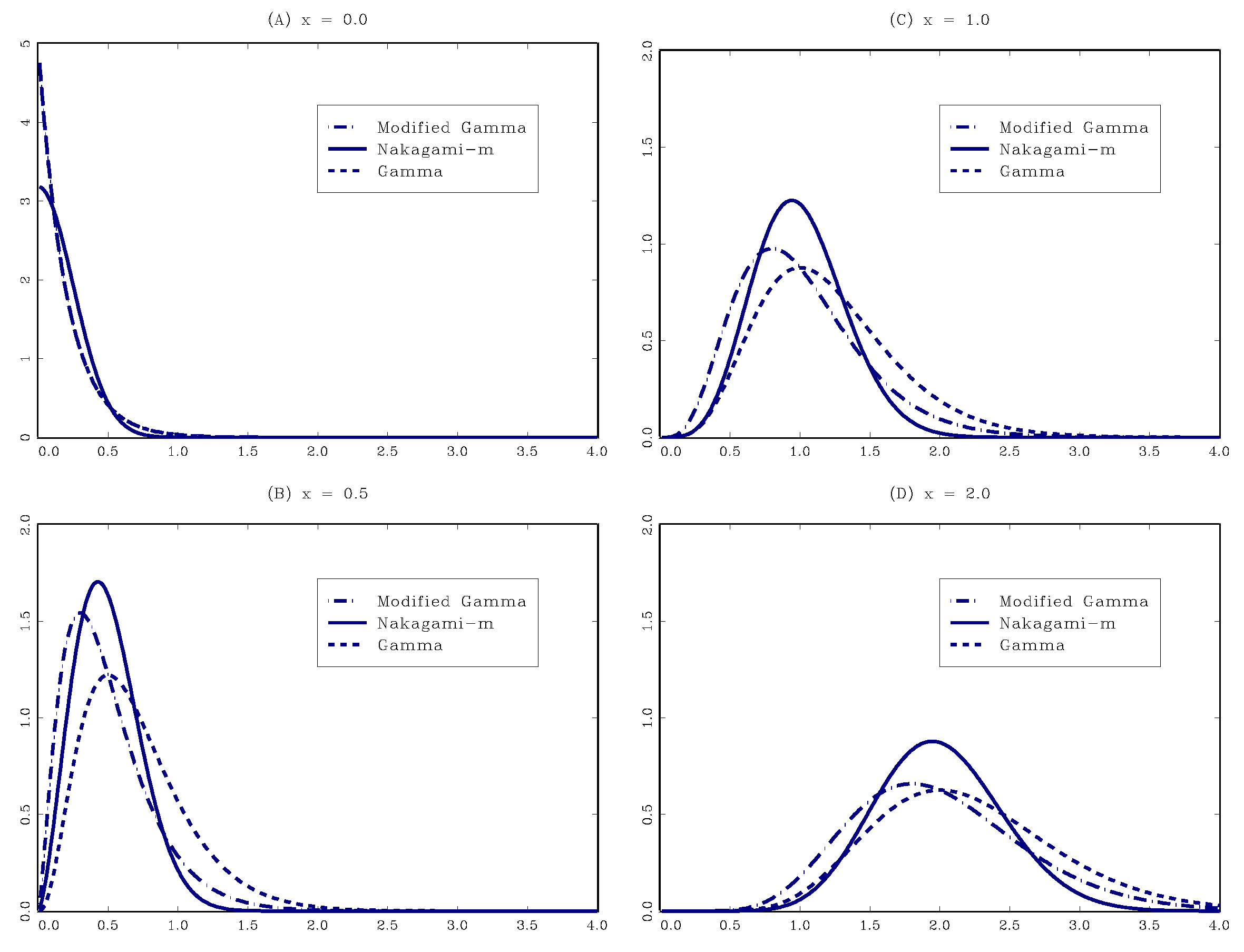
2. Family of the GG Kernels: A Brief Review
3. Tests for Symmetry and Conditional Symmetry Smoothed by the GG Kernels
3.1. SSST as a Special Case of Two-Sample Goodness-of-Fit Tests
- (a)
- ; and .
- (b)
- ;; ;and , where is a kernel-specific constant given in Condition 5 of Definition 1.
- (i)
- Under , as , wherewhich reduces to under , and is a kernel-specific constant given in Condition 5 of Definition 1.
- (ii)
- A consistent estimator of is given by
3.2. SSST When Two Sub-Samples Have Unequal Sample Sizes
- (i)
- Under , as , wherewhich reduces to under .
- (ii)
- A consistent estimator of is given by
3.3. Extension to a Test for Conditional Symmetry
4. Smoothing Parameter Selection
| Step 1: Choose some and specify . |
| Step 2: Make M sub-samples of sizes . |
| Step 3: Pick two constants and define . |
| Step 4: Set and find by a grid search. |
| Step 5: Obtain and calculate . |
5. Finite-Sample Performance
5.1. Setup
5.2. Simulation Results
6. Conclusions
Appendix A. Appendix
Appendix A.1. Proof of Lemma 1
- Stirling’s formula (“SF”):
- Legendre’s duplication formula (“LDF”):
| Step 1: approximating |
| Step 2: approximating |
Appendix A.2. Proof of Theorem 1
- (a)
- ; ;; and where is given in Condition 5 of Definition 1.
- (b)
- ; ;; and .
- (c)
- ; and .
- (d)
- ; ;; and .
Appendix A.2.1. Proof of Lemma A2
Appendix A.2.2. Proof of Lemma A3
Appendix A.2.3. Proof of Lemma A4
Appendix A.2.4. Proof of Theorem 1
Appendix A.3. Proof of Proposition 1
Appendix A.4. Proof of Theorem 3
Acknowledgments
Author Contributions
Conflicts of Interest
References
- R.W. Bacon. “Rockets and feathers: The asymmetric speed of adjustment of UK retail gasoline prices to cost changes.” Energy Econ. 13 (1991): 211–218. [Google Scholar] [CrossRef]
- J.Y. Campbell, and L. Hentschel. “No news is good news: An asymmetric model of changing volatility in stock returns.” J. Financ. Econ. 31 (1992): 281–318. [Google Scholar] [CrossRef]
- R. Clarida, and M. Gertler. “How the Bundesbank conducts monetary policy.” In Reducing Inflation: Motivation and Strategy. Edited by C.D. Romer and D.H. Romer. Chicago, IL, USA: University of Chicago Press, 1997, pp. 363–412. [Google Scholar]
- G. Chamberlain. “A characterization of the distributions that imply mean-variance utility functions.” J. Econ. Theory 29 (1983): 185–201. [Google Scholar] [CrossRef]
- J. Owen, and R. Rabinovitch. “On the class of elliptical distributions and their applications to the theory of portfolio choice.” J. Finance 38 (1983): 745–752. [Google Scholar] [CrossRef]
- J.E. Ingersoll Jr. Theory of Financial Decision Making. Savage, MD, USA: Rowman & Littlefield, 1987. [Google Scholar]
- P.J. Bickel. “On adaptive estimation.” Ann. Stat. 10 (1982): 647–671. [Google Scholar] [CrossRef]
- W.K. Newey. “Adaptive estimation of regression models via moment restrictions.” J. Econom. 38 (1988): 301–339. [Google Scholar] [CrossRef]
- R.J. Carroll, and A.H. Welsh. “A note on asymmetry and robustness in linear regression.” Am. Stat. 42 (1988): 285–287. [Google Scholar]
- M.-J. Lee. “Mode regression.” J. Econom. 42 (1989): 337–349. [Google Scholar] [CrossRef]
- M.-J. Lee. “Quadratic mode regression.” J. Econom. 57 (1993): 1–19. [Google Scholar] [CrossRef]
- V. Zinde-Walsh. “Asymptotic theory for some high breakdown point estimators.” Econom. Theory 18 (2002): 1172–1196. [Google Scholar] [CrossRef]
- H.D. Bondell, and L.A. Stefanski. “Efficient robust regression via two-stage generalized empirical likelihood.” J. Am. Stat. Assoc. 108 (2013): 644–655. [Google Scholar] [CrossRef] [PubMed]
- M. Baldauf, and J.M.C. Santos Silva. “On the use of robust regression in econometrics.” Econ. Lett. 114 (2012): 124–127. [Google Scholar] [CrossRef]
- Y. Fan, and R. Gencay. “A consistent nonparametric test of symmetry in linear regression models.” J. Am. Stat. Assoc. 90 (1995): 551–557. [Google Scholar] [CrossRef]
- I.A. Ahmad, and Q. Li. “Testing symmetry of unknown density functions by kernel method.” J. Nonparametr. Stat. 7 (1997): 279–293. [Google Scholar] [CrossRef]
- J.X. Zheng. “Consistent specification testing for conditional symmetry.” Econom. Theory 14 (1998): 139–149. [Google Scholar] [CrossRef]
- C. Diks, and H. Tong. “A test for symmetries of multivariate probability distributions.” Biometrika 86 (1999): 605–614. [Google Scholar] [CrossRef]
- Y. Fan, and A. Ullah. “On goodness-of-fit tests for weakly dependent processes using kernel method.” J. Nonparametr. Stat. 11 (1999): 337–360. [Google Scholar] [CrossRef]
- R.H. Randles, M.A. Fligner, G.E. Policello II, and D.A. Wolfe. “An asymptotically distribution-free test for symmetry versus asymmetry.” J. Am. Stat. Assoc. 75 (1980): 168–172. [Google Scholar] [CrossRef]
- L.G. Godfrey, and C.D. Orme. “Testing for skewness of regression disturbances.” Econ. Lett. 37 (1991): 31–34. [Google Scholar] [CrossRef]
- J. Bai, and S. Ng. “Tests for skewness, kurtosis, and normality for time series data.” J. Bus. Econ. Stat. 23 (2005): 49–58. [Google Scholar] [CrossRef]
- G. Premaratne, and A. Bera. “A test for symmetry with leptokurtic financial data.” J. Financ. Econom. 3 (2005): 169–187. [Google Scholar] [CrossRef]
- W.K. Newey, and J.L. Powell. “Asymmetric least squares estimation and testing.” Econometrica 55 (1987): 819–847. [Google Scholar] [CrossRef]
- J. Bai, and S. Ng. “A consistent test for conditional symmetry in time series models.” J. Econom. 103 (2001): 225–258. [Google Scholar] [CrossRef]
- M.A. Delgado, and J.C. Escanciano. “Nonparametric tests for conditional symmetry in dynamic models.” J. Econom. 141 (2007): 652–682. [Google Scholar] [CrossRef]
- T. Chen, and G. Tripathi. “Testing conditional symmetry without smoothing.” J. Nonparametr. Stat. 25 (2013): 273–313. [Google Scholar] [CrossRef]
- Y. Fang, Q. Li, X. Wu, and D. Zhang. “A data-driven test of symmetry.” J. Econom. 188 (2015): 490–501. [Google Scholar] [CrossRef]
- M. Fernandes, E.F. Mendes, and O. Scaillet. “Testing for symmetry and conditional symmetry using asymmetric kernels.” Ann. Inst. Stat. Math. 67 (2015): 649–671. [Google Scholar] [CrossRef]
- S.X. Chen. “Probability density function estimation using gamma kernels.” Ann. Inst. Stat. Math. 52 (2000): 471–480. [Google Scholar] [CrossRef]
- N. Gospodinov, and M. Hirukawa. “Nonparametric estimation of scalar diffusion models of interest rates using asymmetric kernels.” J. Empir. Finance 19 (2012): 595–609. [Google Scholar] [CrossRef]
- M. Hirukawa, and M. Sakudo. “Family of the generalised gamma kernels: A generator of asymmetric kernels for nonnegative data.” J. Nonparametr. Stat. 27 (2015): 41–63. [Google Scholar] [CrossRef]
- M. Fernandes, and J. Grammig. “Nonparametric specification tests for conditional duration models.” J. Econom. 127 (2005): 35–68. [Google Scholar] [CrossRef]
- K.B. Kulasekera, and J. Wang. “Smoothing parameter selection for power optimality in testing of regression curves.” J. Am. Stat. Assoc. 92 (1997): 500–511. [Google Scholar] [CrossRef]
- K.B. Kulasekera, and J. Wang. “Bandwidth selection for power optimality in a test of equality of regression curves.” Stat. Probab. Lett. 37 (1998): 287–293. [Google Scholar] [CrossRef]
- E.W. Stacy. “A generalization of the gamma distribution.” Ann. Math. Stat. 33 (1962): 1187–1192. [Google Scholar] [CrossRef]
- I.S. Abramson. “On bandwidth variation in kernel estimates—A square root law.” Ann. Stat. 10 (1982): 1217–1223. [Google Scholar] [CrossRef]
- C.J. Stone. “Optimal rates of convergence for nonparametric estimators.” Ann. Stat. 8 (1980): 1348–1360. [Google Scholar] [CrossRef]
- N.H. Anderson, P. Hall, and D.M. Titterington. “Two-sample test statistics for measuring discrepancies between two multivariate probability density functions using kernel-based density estimates.” J. Multivar. Anal. 50 (1994): 41–54. [Google Scholar] [CrossRef]
- P. Hall. “Central limit theorem for integrated square error of multivariate nonparametric density estimators.” J. Multivar. Anal. 14 (1984): 1–16. [Google Scholar] [CrossRef]
- V.S. Koroljuk, and Y.V. Borovskich. Theory of U-Statistics. Dordrecht, The Netherlands: Kluwer Academic Publishers, 1994. [Google Scholar]
- B.E. Hansen. “Uniform convergence rates for kernel estimation with dependent data.” Econom. Theory 24 (2008): 726–748. [Google Scholar] [CrossRef]
- B.W. Silverman. Density Estimation for Statistics and Data Analysis. London, UK: Chapman & Hall, 1986. [Google Scholar]
- J. Gao, and I. Gijbels. “Bandwidth selection in nonparametric kernel testing.” J. Am. Stat. Assoc. 103 (2008): 1584–1594. [Google Scholar] [CrossRef]
- J.S. Ramberg, and B.W. Schmeiser. “An approximate method for generating asymmetric random variables.” Commun. ACM 17 (1974): 78–82. [Google Scholar] [CrossRef]
- M. Fernandes, and P.K. Monteiro. “Central limit theorem for asymmetric kernel functionals.” Ann. Inst. Stat. Math. 57 (2005): 425–442. [Google Scholar] [CrossRef]
| Distribution | Skewness | Kurtosis | |
|---|---|---|---|
| S1 | |||
| S2 | |||
| S3 | or Standard Laplace | ||
| S4 | or GLD with | ||
| A1 | |||
| A2 | |||
| A3 | GLD with | ||
| A4 | GLD with |
| (A) Size | (%) | |||||||||||||
| N | Test | δ | Distribution | |||||||||||
| S1 | S2 | S3 | S4 | |||||||||||
| 5% | 10% | 5% | 10% | 5% | 10% | 5% | 10% | |||||||
| 50 | FMS-G-O | − | 4.8 | 9.4 | 4.9 | 9.5 | 6.0 | 10.8 | 7.4 | 12.6 | ||||
| FMS-G-AltVar | − | 4.7 | 9.3 | 4.4 | 8.9 | 5.8 | 10.9 | 6.9 | 12.6 | |||||
| -G | 0.3 | 3.5 | 7.5 | 3.1 | 7.0 | 4.5 | 8.7 | 5.2 | 9.6 | |||||
| 0.5 | 3.8 | 6.8 | 3.0 | 7.3 | 4.4 | 7.9 | 5.4 | 10.2 | ||||||
| 0.7 | 3.4 | 6.7 | 3.4 | 7.3 | 4.5 | 8.9 | 5.4 | 10.5 | ||||||
| -MG | 0.3 | 3.6 | 7.7 | 3.9 | 7.5 | 4.9 | 9.5 | 5.3 | 9.7 | |||||
| 0.5 | 4.0 | 7.2 | 3.7 | 7.2 | 4.9 | 8.7 | 5.4 | 10.2 | ||||||
| 0.7 | 3.3 | 6.8 | 3.8 | 7.3 | 4.7 | 9.1 | 5.3 | 10.7 | ||||||
| -NM | 0.3 | 3.4 | 7.3 | 3.1 | 6.7 | 4.3 | 8.3 | 5.2 | 9.3 | |||||
| 0.5 | 3.9 | 6.7 | 3.1 | 6.4 | 4.2 | 7.9 | 5.2 | 9.8 | ||||||
| 0.7 | 3.3 | 7.0 | 3.1 | 6.4 | 4.4 | 8.1 | 5.2 | 10.3 | ||||||
| 100 | FMS-G-O | − | 5.2 | 9.8 | 6.7 | 10.8 | 5.6 | 10.1 | 7.4 | 12.5 | ||||
| FMS-G-AltVar | − | 4.9 | 8.9 | 6.4 | 10.6 | 5.3 | 9.9 | 6.6 | 12.6 | |||||
| -G | 0.3 | 4.0 | 7.0 | 6.1 | 9.3 | 5.1 | 8.8 | 7.3 | 11.9 | |||||
| 0.5 | 3.6 | 7.3 | 5.8 | 9.1 | 5.2 | 8.9 | 7.1 | 11.4 | ||||||
| 0.7 | 3.8 | 7.6 | 5.9 | 9.5 | 4.8 | 9.3 | 6.6 | 11.8 | ||||||
| -MG | 0.3 | 4.5 | 7.4 | 6.2 | 9.5 | 5.8 | 9.6 | 7.3 | 12.1 | |||||
| 0.5 | 3.7 | 7.7 | 6.1 | 9.6 | 5.7 | 9.0 | 7.2 | 11.6 | ||||||
| 0.7 | 3.8 | 8.1 | 5.8 | 9.6 | 5.1 | 9.4 | 6.7 | 12.1 | ||||||
| -NM | 0.3 | 4.2 | 6.8 | 5.3 | 8.9 | 4.3 | 8.4 | 7.1 | 12.4 | |||||
| 0.5 | 4.0 | 6.6 | 5.3 | 8.7 | 4.9 | 8.7 | 7.2 | 11.6 | ||||||
| 0.7 | 4.2 | 6.8 | 5.3 | 8.8 | 4.9 | 8.4 | 7.3 | 11.7 | ||||||
| 200 | FMS-G-O | − | 4.1 | 7.3 | 6.0 | 9.3 | 5.8 | 8.9 | 8.9 | 14.1 | ||||
| FMS-G-AltVar | − | 4.1 | 7.0 | 6.1 | 8.9 | 5.4 | 9.3 | 8.7 | 15.1 | |||||
| -G | 0.3 | 3.3 | 6.3 | 4.9 | 8.0 | 4.9 | 8.7 | 8.9 | 12.9 | |||||
| 0.5 | 3.2 | 6.4 | 4.9 | 8.6 | 5.3 | 8.7 | 8.7 | 13.3 | ||||||
| 0.7 | 3.5 | 6.8 | 5.2 | 9.2 | 5.4 | 8.9 | 8.4 | 13.9 | ||||||
| -MG | 0.3 | 3.5 | 6.7 | 5.5 | 8.4 | 5.5 | 9.4 | 9.0 | 13.4 | |||||
| 0.5 | 3.5 | 6.8 | 5.2 | 9.0 | 5.7 | 8.8 | 8.7 | 13.6 | ||||||
| 0.7 | 3.5 | 7.0 | 5.5 | 9.8 | 5.7 | 9.1 | 8.6 | 13.7 | ||||||
| -NM | 0.3 | 3.5 | 6.0 | 4.0 | 7.5 | 4.4 | 8.5 | 8.7 | 13.3 | |||||
| 0.5 | 3.6 | 5.9 | 4.4 | 7.6 | 4.4 | 8.4 | 8.7 | 13.3 | ||||||
| 0.7 | 3.6 | 5.8 | 4.6 | 7.4 | 4.5 | 8.4 | 8.8 | 13.1 | ||||||
| (B) Power | (%) | |||||||||||||
| N | Test | δ | Distribution | |||||||||||
| A1 | A2 | A3 | A4 | |||||||||||
| 5% | 10% | 5% | 10% | 5% | 10% | 5% | 10% | |||||||
| 50 | FMS-G-O | − | 42.0 | 51.6 | 21.4 | 30.3 | 26.3 | 37.2 | 28.8 | 40.8 | ||||
| [43.7] | [52.4] | [22.7] | [31.0] | [27.6] | [38.1] | [30.5] | [42.0] | |||||||
| FMS-G-AltVar | − | 24.9 | 37.0 | 13.3 | 22.4 | 39.8 | 52.2 | 43.1 | 55.3 | |||||
| [27.5] | [39.0] | [13.9] | [24.1] | [41.5] | [53.6] | [44.9] | [57.4] | |||||||
| -G | 0.3 | 31.3 | 41.5 | 17.3 | 24.7 | 30.8 | 41.3 | 33.8 | 44.3 | |||||
| [35.4] | [46.6] | [20.8] | [29.5] | [35.1] | [46.3] | [38.7] | [50.8] | |||||||
| 0.5 | 29.5 | 39.7 | 16.0 | 23.8 | 29.4 | 39.1 | 31.4 | 42.9 | ||||||
| 0.7 | 27.8 | 38.7 | 14.5 | 22.6 | 28.0 | 36.8 | 30.2 | 40.6 | ||||||
| -MG | 0.3 | 32.1 | 42.2 | 17.9 | 25.8 | 31.6 | 41.8 | 35.5 | 45.5 | |||||
| [35.2] | [45.7] | [20.9] | [29.3] | [35.0] | [45.8] | [39.1] | [49.5] | |||||||
| 0.5 | 30.1 | 40.8 | 16.5 | 24.5 | 30.2 | 40.3 | 32.2 | 43.1 | ||||||
| 0.7 | 28.0 | 38.9 | 15.1 | 23.0 | 28.5 | 37.5 | 30.8 | 41.1 | ||||||
| -NM | 0.3 | 33.8 | 42.5 | 18.2 | 25.2 | 32.9 | 42.5 | 35.2 | 46.5 | |||||
| [36.6] | [48.8] | [20.7] | [30.4] | [36.8] | [48.5] | [39.2] | [53.5] | |||||||
| 0.5 | 33.5 | 42.2 | 17.7 | 24.9 | 32.4 | 42.2 | 34.6 | 45.8 | ||||||
| 0.7 | 33.0 | 41.4 | 17.4 | 24.2 | 32.2 | 41.6 | 34.5 | 45.7 | ||||||
| 100 | FMS-G-O | − | 73.0 | 81.5 | 41.4 | 51.4 | 59.1 | 71.2 | 64.2 | 74.6 | ||||
| [72.7] | [81.8] | [40.7] | [52.3] | [58.7] | [71.8] | [63.8] | [74.6] | |||||||
| FMS-G-AltVar | − | 56.4 | 70.2 | 30.3 | 43.4 | 73.7 | 80.7 | 77.2 | 83.7 | |||||
| [58.1] | [71.6] | [32.2] | [44.4] | [74.4] | [81.8] | [78.1] | [84.4] | |||||||
| -G | 0.3 | 72.3 | 80.5 | 37.9 | 48.6 | 70.3 | 78.4 | 74.1 | 80.5 | |||||
| [75.4] | [84.4] | [40.2] | [54.9] | [72.8] | [82.3] | [76.1] | [84.1] | |||||||
| 0.5 | 67.1 | 77.2 | 33.9 | 45.0 | 65.2 | 75.7 | 69.5 | 78.2 | ||||||
| 0.7 | 62.9 | 73.6 | 31.9 | 42.5 | 61.7 | 72.3 | 65.2 | 75.8 | ||||||
| -MG | 0.3 | 73.1 | 80.2 | 38.3 | 49.3 | 70.5 | 78.3 | 73.6 | 81.0 | |||||
| [74.8] | [83.6] | [40.9] | [53.5] | [72.4] | [80.7] | [75.4] | [83.3] | |||||||
| 0.5 | 67.4 | 77.5 | 34.6 | 45.4 | 65.6 | 75.4 | 69.5 | 77.9 | ||||||
| 0.7 | 62.9 | 73.5 | 32.0 | 42.3 | 62.2 | 72.5 | 65.3 | 75.2 | ||||||
| -NM | 0.3 | 76.8 | 84.0 | 41.7 | 51.9 | 75.5 | 82.1 | 76.8 | 84.0 | |||||
| [79.6] | [87.2] | [44.8] | [58.0] | [77.6] | [85.0] | [79.7] | [86.9] | |||||||
| 0.5 | 77.0 | 84.0 | 40.1 | 51.0 | 75.1 | 82.0 | 75.7 | 83.0 | ||||||
| 0.7 | 76.4 | 83.7 | 39.6 | 50.1 | 74.9 | 81.9 | 75.6 | 82.9 | ||||||
| 200 | FMS-G-O | − | 97.4 | 98.3 | 71.5 | 80.7 | 95.6 | 98.1 | 97.1 | 97.8 | ||||
| [97.8] | [98.6] | [75.0] | [84.2] | [96.9] | [98.6] | [97.4] | [98.4] | |||||||
| FMS-G-AltVar | − | 93.4 | 96.3 | 60.4 | 72.8 | 98.7 | 99.0 | 98.4 | 99.1 | |||||
| [95.2] | [97.5] | [69.1] | [78.5] | [98.8] | [99.2] | [99.0] | [99.2] | |||||||
| -G | 0.3 | 97.7 | 99.1 | 77.0 | 84.8 | 98.6 | 99.1 | 98.6 | 99.2 | |||||
| [98.7] | [99.4] | [82.7] | [90.3] | [98.8] | [99.4] | [98.9] | [99.2] | |||||||
| 0.5 | 97.2 | 98.1 | 71.3 | 80.9 | 97.7 | 98.9 | 97.9 | 98.7 | ||||||
| 0.7 | 96.4 | 97.6 | 65.4 | 75.8 | 96.7 | 98.8 | 97.2 | 98.3 | ||||||
| -MG | 0.3 | 97.9 | 99.1 | 76.2 | 85.3 | 98.6 | 99.1 | 98.5 | 99.1 | |||||
| [98.6] | [99.4] | [81.8] | [89.8] | [98.7] | [99.4] | [98.7] | [99.2] | |||||||
| 0.5 | 97.3 | 98.1 | 71.4 | 80.3 | 97.6 | 98.9 | 97.9 | 98.6 | ||||||
| 0.7 | 96.5 | 97.6 | 65.5 | 75.9 | 96.7 | 98.7 | 97.2 | 98.3 | ||||||
| -NM | 0.3 | 98.9 | 99.0 | 84.8 | 91.1 | 98.8 | 99.2 | 98.6 | 98.9 | |||||
| [99.0] | [99.2] | [91.1] | [95.8] | [99.4] | [99.7] | [99.5] | [99.7] | |||||||
| 0.5 | 96.8 | 97.0 | 81.2 | 88.2 | 98.3 | 98.6 | 98.4 | 98.6 | ||||||
| 0.7 | 95.6 | 95.7 | 80.9 | 88.3 | 98.3 | 98.6 | 98.4 | 98.6 | ||||||
- 1Hirukawa and Sakudo [32] present the Weibull kernel as yet another special case. However, it is not confirmed that this kernel satisfies Lemma 1 below, and thus the kernel is not investigated throughout.
- 2It is possible to use different asymmetric kernels and/or different smoothing parameters to estimate f and g. For convenience, however, we choose to employ the same asymmetric kernel function and a single smoothing parameter.
- 3Although the GLDs corresponding to A3 and A4 are used in Zheng [17] and FMS, they are found to have non-zero means. Therefore, we adjust the values of and with skewness and kurtosis maintained so that the resulting distributions have means of zero.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirukawa, M.; Sakudo, M. Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels. Econometrics 2016, 4, 28. https://doi.org/10.3390/econometrics4020028
Hirukawa M, Sakudo M. Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels. Econometrics. 2016; 4(2):28. https://doi.org/10.3390/econometrics4020028
Chicago/Turabian StyleHirukawa, Masayuki, and Mari Sakudo. 2016. "Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels" Econometrics 4, no. 2: 28. https://doi.org/10.3390/econometrics4020028
APA StyleHirukawa, M., & Sakudo, M. (2016). Testing Symmetry of Unknown Densities via Smoothing with the Generalized Gamma Kernels. Econometrics, 4(2), 28. https://doi.org/10.3390/econometrics4020028





