A Note on the Asymptotic Normality of the Kernel Deconvolution Density Estimator with Logarithmic Chi-Square Noise
Abstract
:1. Introduction
2. Logarithmic Chi-Square Distribution
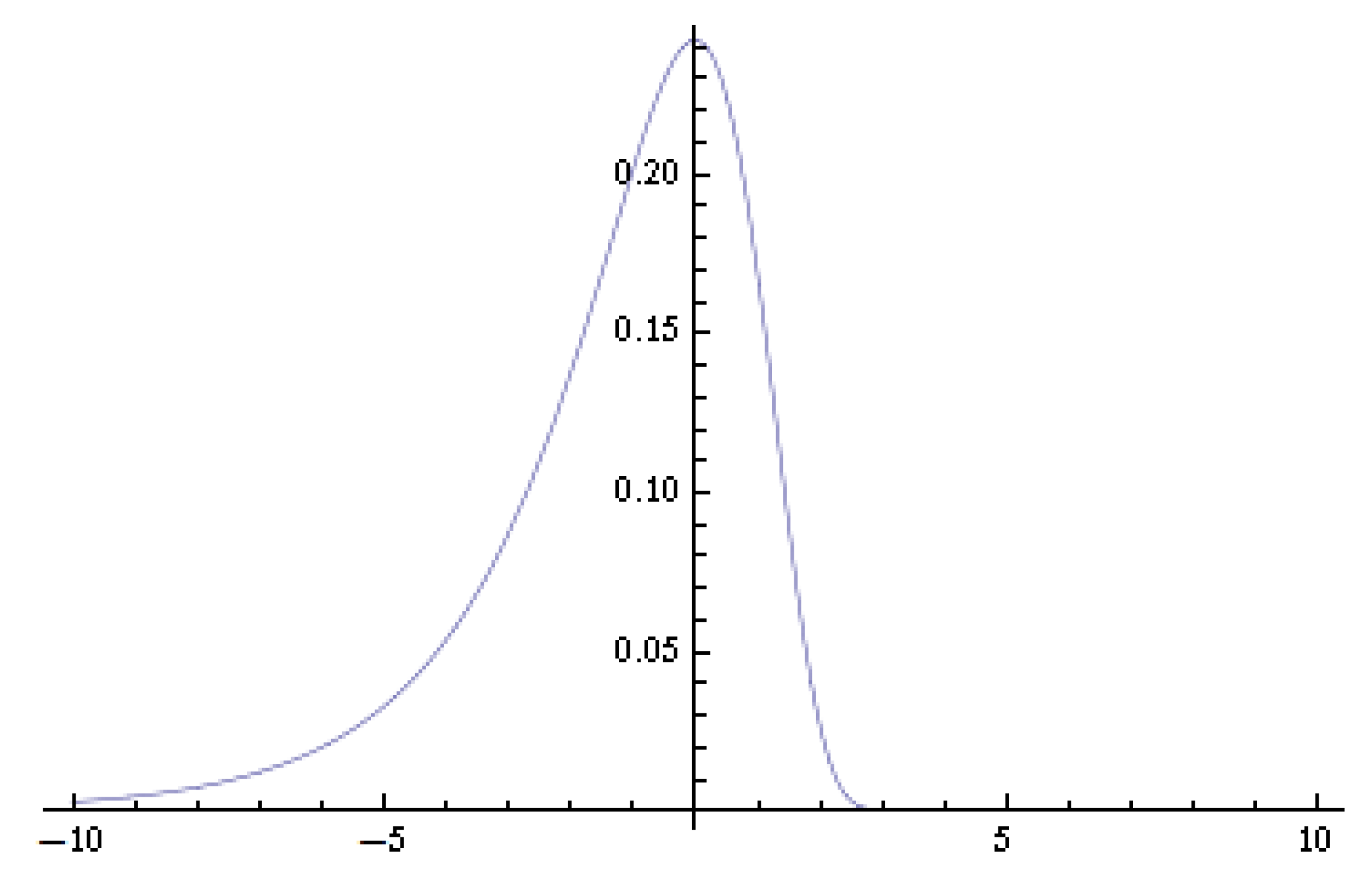
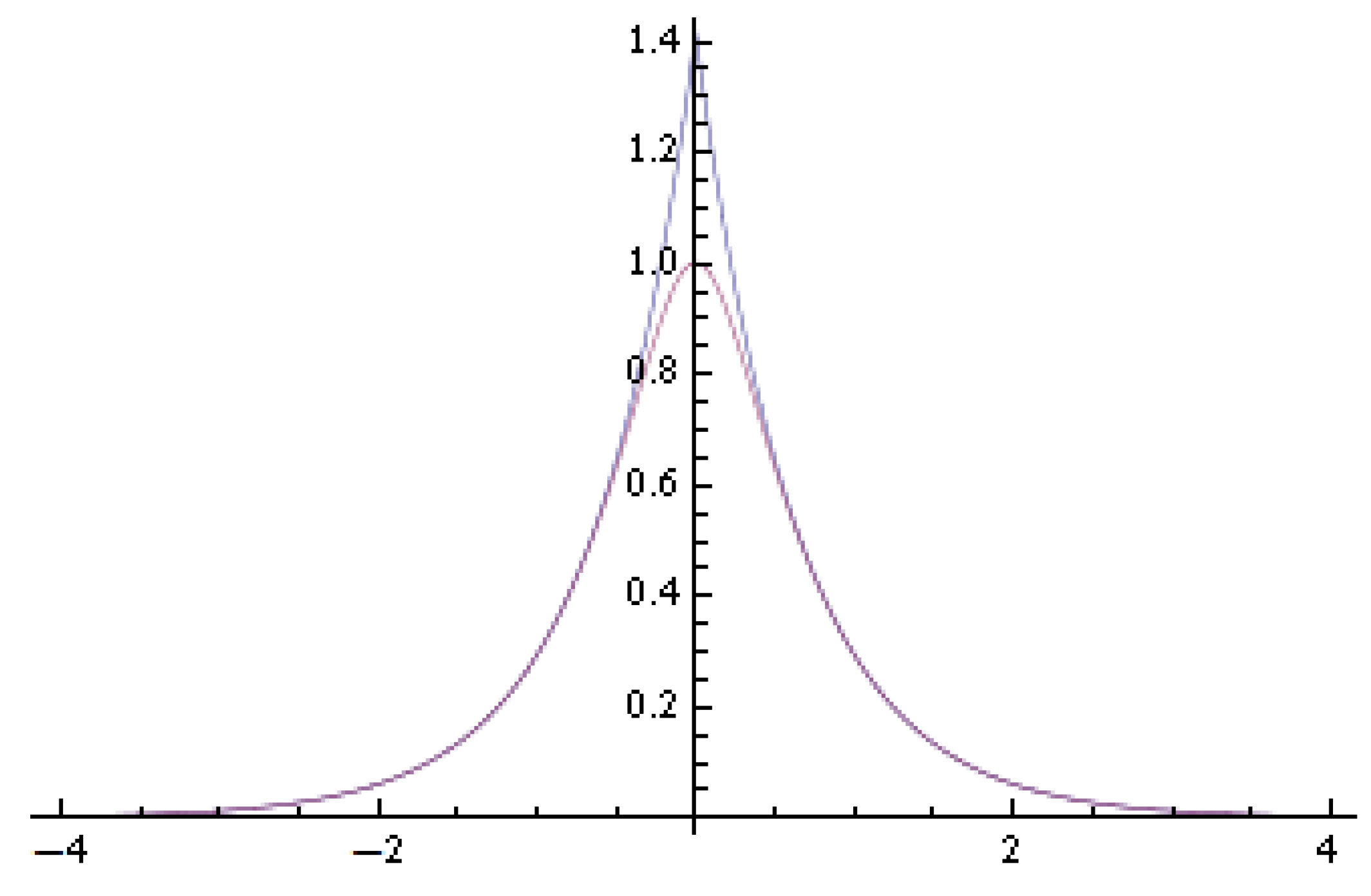
3. Asymptotic Normality
3.1. i.i.d. Observations
3.2. Strong Mixing Observations
4. Application to Density Estimation in the Stochastic Volatility Model
5. Conclusions
Acknowledgements
Conflicts of Interest
References
- R. Carroll, and P. Hall. “Optimal rates of convergence for deconvolving a density.” J. Am. Stat. Assoc. 83 (1988): 1184–1186. [Google Scholar] [CrossRef]
- L. Stefanski, and R. Carroll. “Deconvoluting kernel density estimators.” Statistics 21 (1990): 169–184. [Google Scholar] [CrossRef]
- J. Fan. “Asymptotic normality for deconvolution kernel density estimators.” Sankhya Indian J. Stat. A 53 (1991): 97–110. [Google Scholar]
- Y. Fan, and Y. Liu. “A note on asymptotic normality for deconvolution kernel density estimators.” Sankhya Indian J. Stat. A 59 (1997): 138–141. [Google Scholar]
- B. Van Es, and H. Uh. “Asymptotic normality of nonparametric kernel type deconvolution density estimators: Crossing the Cauchy boundary.” J. Nonparametr. Stat. 16 (2004): 261–277. [Google Scholar] [CrossRef]
- B. Van Es, and H. Uh. “Asymptotic normality of kernel-type deconvolution estimators.” Scand. J. Stat. 32 (2005): 467–483. [Google Scholar]
- E. Masry. “Asymptotic normality for deconvolution estimators of multivariate densities of stationary processes.” J. Multivar. Anal. 44 (1993): 47–68. [Google Scholar] [CrossRef]
- R. Kulik. “Nonparametric deconvolution problem for dependent sequences.” Electron. J. Stat. 2 (2008): 722–740. [Google Scholar] [CrossRef]
- B. Van Es, P. Spreij, and H. van Zanten. “Nonparametric volatility density estimation.” Bernoulli 9 (2003): 451–465. [Google Scholar] [CrossRef]
- B. Van Es, P. Spreij, and H. van Zanten. “Nonparametric volatility density estimation for discrete time models.” Nonparametr. Stat. 17 (2005): 237–251. [Google Scholar] [CrossRef]
- F. Comte, and V. Genon-Catalot. “Penalized projection estimator for volatility density.” Scand. J. Stat. 33 (2006): 875–893. [Google Scholar] [CrossRef]
- V. Todorov, and G. Tauchen. “Inverse realized laplace transforms for nonparametric volatility density estimation in jump-diffusions.” J. Am. Stat. Assoc. 107 (2012): 622–635. [Google Scholar] [CrossRef]
- J. Fan. “On the optimal rates of convergence for nonparametric deconvolution problems.” Ann. Stat. 19 (1991): 1257–1272. [Google Scholar] [CrossRef]
- A. Delaigle, and I. Gijbels. “Practical bandwidth selection in deconvolution kernel density estimation.” Comput. Stat. Data Anal. 45 (2004): 249–267. [Google Scholar] [CrossRef]
- C. Butucea. “Asymptotic normality of the integrated square error of a density estimator in the convolution model.” Sort 28 (2004): 9–26. [Google Scholar]
- E. Masry. “Multivariate probability density deconvolution for stationary random processes.” IEEE Trans. Inf. Theory 37 (1991): 1105–1115. [Google Scholar] [CrossRef]
- J. Fan, and Q. Yao. Nonlinear Time Series. Berlin, Germany: Springer, 2002, Volume 2. [Google Scholar]
- S.J. Taylor. “Financial returns modelled by the product of two stochastic processes-a study of the daily sugar prices 1961–1975.” Time Ser. Anal. Theory Pract. 1 (1982): 203–226. [Google Scholar]
- N. Shephard, ed. Stochastic Volatility: Selected Readings. Oxford, UK: Oxford University Press, 2005.
- N. Shephard, and T.G. Andersen. “Stochastic volatility: Origins and overview.” In Handbook of Financial Time Series. Edited by T.G. Andersen, R.A. Davis, J.P. Kreiß and T. Mikosch. Berlin, Germany: Springer, 2009, pp. 233–254. [Google Scholar]
- T.G. Andersen, T. Bollerslev, F.X. Diebold, and P. Labys. “Parametric and nonparametric volatility measurement.” Handb. Financ. Econom. 1 (2009): 67–138. [Google Scholar]
- 1The characteristic function of a random variable with density f is defined as .
- 2In this paper, I follow the convention to define the Fourier transform of a function f to be
- 3Usually, for practical implementations, the following kernels:with Fourier transform:are used because they have better numerical properties; see Delaigle and Gijbels [14] for the discussions.
- 4This is easy to see by noticing for .
- 5Here, again, the splitting integral argument as in proving (7) is used; I omit the details for the ease of exposition.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zu, Y. A Note on the Asymptotic Normality of the Kernel Deconvolution Density Estimator with Logarithmic Chi-Square Noise. Econometrics 2015, 3, 561-576. https://doi.org/10.3390/econometrics3030561
Zu Y. A Note on the Asymptotic Normality of the Kernel Deconvolution Density Estimator with Logarithmic Chi-Square Noise. Econometrics. 2015; 3(3):561-576. https://doi.org/10.3390/econometrics3030561
Chicago/Turabian StyleZu, Yang. 2015. "A Note on the Asymptotic Normality of the Kernel Deconvolution Density Estimator with Logarithmic Chi-Square Noise" Econometrics 3, no. 3: 561-576. https://doi.org/10.3390/econometrics3030561
APA StyleZu, Y. (2015). A Note on the Asymptotic Normality of the Kernel Deconvolution Density Estimator with Logarithmic Chi-Square Noise. Econometrics, 3(3), 561-576. https://doi.org/10.3390/econometrics3030561




