3.2. A Re-Examination of Bell and Bockstael (2000)
An article often cited to justify the myth is Bell and Bockstell [
7], who explicitly argue that estimates and inference are sensitive to small changes in the weight matrix. They use this line of argument to further contend that the generalized moments method of estimation from Kelejian and Prucha [
9] allow flexible weight structures to be more easily implemented than maximum likelihood estimation methods. In an application involving land parcels, they explore three (row-normalized) contiguity-based weight matrices that assign values of 0 or 1 to neighboring observations that are within 200, 400 and 600 m distances of each observation. These three matrices are compared to a fourth (row-normalized) matrix where inverse distance-based weights were assigned to each neighboring observation within 600 m. They rely on a spatial error model (SEM) shown in equation Equation (
28) and compare estimates from least-squares, maximum likelihood and generalized moments, with the latter two sets of estimates constructed using the four different types of spatial weight matrices.
They conclude:
What emerges from the example is that our results are more sensitive to the specification of the spatial weight matrix than to estimation technique. Compared to the variation across estimation methods, the results across spatial weight matrices are much less stable.
Where qualitative results change, they are almost universally associated with changes in the spatial weight matrix and not with changes in the estimation method. For three of the estimated coefficients, one spatial weight matrix produces results qualitatively different from the others, and, for three more of the estimated coefficients, two spatial weight matrices produce results qualitatively different from the other two. There is no particular pattern to these reversals, nor is there a pattern when comparing the spatial correlation-corrected results to the OLS results.
To put the work of Bell and Bockstell [
7] into perspective, consider that for a
correctly specified SEM model, the only difference between least-squares (OLS) and SEM model estimates should be in the measures of dispersion, not the coefficient estimates for
β. This is because coefficient estimates for
β from OLS are unbiased under the null hypothesis of an SEM specification (Anselin [
10], p. 59). This follows because spatial dependence in the disturbances leads to an efficiency problem for OLS, but no bias in the estimates for
β. Changes in the weight matrix should lead to changes in the
statistics that we observe from OLS versus SEM model estimates, but not in the coefficient estimates for
β. Pace and LeSage [
11] use this idea to develop a Hausman specification test for significant differences between OLS and SEM estimates for
β. Intuitively, significant differences in OLS and SEM estimates for
β point to model misspecification that should lead us to reject the SEM model as an appropriate choice.
In Bell and Bockstell [
7] the sample size used was 1000 observations, so we would expect no small sample issues that would lead to differences between OLS and SEM estimates for the parameters
β. As noted above, this should be true irrespective of the spatial weight matrix employed. Changes in the spatial weight specification could lead to changes in measures of dispersion (e.g.,
statistics), but not significant differences in the coefficients
β. The discussion (quoted above) by Bell and Bockstell [
7] appropriately focused on differences in significance or inference that arise in response to the four alternative weight matrices used to estimate their model. However, they neglect to note that five of the ten coefficients
β from OLS estimation versus maximum likelihood estimation of the SEM model differ by more than 1.67 standard deviations, suggesting model misspecification.
7 Table 2 presents their OLS and maximum likelihood SEM estimates, along with standard errors and a
test for significant differences between these.
8There is one coefficient where the SEM estimate is 2.8 standard deviations away from the OLS, two cases where the two estimates are 1.99 standard deviations apart and two more that are different using the 90% level of significance. Of the ten coefficients five are likely to be significantly different, suggesting the SEM model represents a misspecification.
The sensitivity of estimates and inferences to changes in the weight matrix noted in Bell and Bockstell [
7] was likely due to misspecification in their SEM model. For example, following the argument of LeSage and Pace [
1], if their SEM model omitted variables that were correlated with included variables, this would lead to biased and inconsistent estimates for the parameters
β. This meshes with their observation that “There is no particular pattern to these reversals, nor is there a pattern when comparing the spatial correlation-corrected results to the OLS results.” In general, sensitivity to changes in the weight matrix may be indicative of model misspecification.
Table 2.
Bell and Bockstell(2000) OLS and maximum likelihood SEM estimates.
Table 2.
Bell and Bockstell(2000) OLS and maximum likelihood SEM estimates.
| | OLS | ML | t–Statistic (t–Probability) |
|---|
| | () | () | |
|---|
| Intercept | 4.7332 (0.2047) | 5.1725 (0.2204) | 1.9932 (0.0465) |
| LIV | 0.6926 (0.0124) | 0.6537 (0.0135) | 2.8815 (0.0040) |
| LLT | 0.0079 (0.0052) | 0.0002 (0.0052) | 1.4808 (0.1390) |
| LDC | −0.1494 (0.0195) | −0.1774 (0.0245) | 1.1429 (0.2534) |
| LBA | −0.0453 (0.0114) | −0.0169 (0.0156) | 1.8205 (0.0690) |
| POPN | −0.0493 (0.0408) | −0.0149 (0.0414) | 0.8309 (0.4062) |
| PNAT | 0.0799 (0.0177) | 0.0586 (0.0212) | 1.0047 (0.3153) |
| PDEV | 0.0677 (0.0180) | 0.0253 (0.0253) | 1.6759 (0.0941) |
| PLOW | −0.0166 (0.0194) | −0.0374 (0.0224) | 0.9286 (0.3533) |
| PSEW | −0.1187 (0.0173) | −0.0828 (0.0180) | 1.9944 (0.0464) |
3.3. A Re-Examination of Kostov (2010)
Another factor contributing to the myth arises in the case of models that include spatial lags of the dependent variable. There are different types of spatial regression specifications that include spatial lags of the dependent variable, but LeSage and Pace [
1] argue that one specification, the spatial Durbin model (SDM) stands out as superior in a wide number of applied situations. The SDM shown in Equation (
30) includes a spatial lag of the dependent variable (
) as well as explanatory variables (
):
In the case of OLS where observations are independent, changes in
can only influence
, so we use the coefficient estimates for the
rth explanatory variable (
) to summarize the average (across the sample) impact of changing the
rth explanatory variable on the dependent variable vector
y. LeSage and Pace [
1] point out that this is not the case when the dependent variable observation
exhibits dependence on other observations. They rewrite the model in Equation (
30) as in Equation (
31), which is useful for examining the partial derivatives of
y with respect to a change in the
rth variable
from
X, which is shown in Equation (
32).
The partial derivatives are an
matrix rather than the typical scalar expression
from OLS. The matrix arises because a change in a single observation
can influence all observations of the vector
. Considering changes in each of the
observations and the associated
vectors of
responses gives rise to the
matrix of partial derivatives. The own-region or
direct response is captured by the own-partial derivative
which are elements on the diagonal of the matrix in Equation (
32). The cross-partial derivatives
reflect
indirect or spillover responses, and these are located on the off-diagonal elements of the matrix in Equation (
32).
Changes in coefficient estimates for β and ρ observed by practitioners who try alternative weight matrix specifications may have contributed to formulation of the myth. This is because practitioners who incorrectly believe that coefficient estimates β measure partial derivative responses in the dependent variable to changes in the independent variables would infer sensitivity of estimates and inferences arising from changes in W. As noted earlier, this focus on how changes in the matrix W impact coefficient estimates for ρ and β, is misplaced, since the focus should be on changes in the true partial derivatives, the direct and indirect effects estimates described above. In fact, changes in estimates for ρ and β may arise systematically as a response to changes in the matrix W, because these are required to maintain relatively stable partial derivatives in the face of changing W. Past misinterpretation of estimates from spatial regression models containing lags of the dependent variable may have contributed to the myth that estimates and inferences are sensitive to the choice of W. Ironically, these changes might be occurring in an effort to ensure a well-conditioned model where the true partial derivative responses remain relatively constant in the face of changing W.
We re-examine the model from Kostov [
6], who used the data set from Harrison and Rubinfeld [
12]. This data set containing 506 Boston census tract observations was augmented to have latitude-longitude coordinates from Gilley and Pace [
13]. The 10 explanatory variables used in the model are shown in
Table 3.
Table 3.
Variables and definitions.
Table 3.
Variables and definitions.
| Variable | Description |
|---|
| CRIME | per capita crime rate by town |
| CHARLES | Charles River dummy variable (=1 if tract bounds river; 0 otherwise) |
| NOX | nitric oxides concentration (parts per 10 million) |
| ROOMS | average number of rooms per dwelling |
| DISTANCE | weighted distances to five Boston employment centers |
| RADIAL | index of accessibility to radial highways |
| TAX | full-value property-tax rate per $10,000 |
| PTRATIO | pupil-teacher ratio by town |
| B | 1000(Bk - 0.63) where Bk is the proportion of blacks by town |
| LSTATUS | % lower status of the population |
The parameterized weight structure used by Kostov [
6] takes the form:
where
denotes the distance between the
m nearest neighboring observations
j to observation
i and
is a decay parameter. Other values for
for neighbors
are set to zero. The model used is the SAR:
.
Rather than estimate the parameter
γ, Kostov [
6] considers a “boosting” type of model search/comparison procedure that is applied to a discrete set of models based on a 0.1 grid of values for
γ in the interval
and a range of
. His approach identifies models based on
γ values in the range
to 1, and
as representing the “best” weight structure for the SAR model and sample data.
Bayesian model comparison methods can be used to compare this discrete set of models. Specifically Hepple [
14] shows that the log-marginal likelihood for the SAR model takes the form in Equation (
34):
9
where we use
to denote model
i based on spatial weight matrix
, and
D to denote the interval defined by the minimum and maximum eigenvalues of the matrix
.
10Table 4 presents posterior model probabilities for a discrete set of models based on a grid of values for the parameter
γ in the interval
based on increments of 0.1, and three values
of nearest neighbors that we considered. Of course, we chose these values based on the results from Kostov [
6].
Table 4.
Posterior model probabilities .
Table 4.
Posterior model probabilities .
| γ | | | |
|---|
| 0 | 0.0001 | 0.0095 | 0.0007 |
| 0.1 | 0.0004 | 0.0288 | 0.0025 |
| 0.2 | 0.0013 | 0.0726 | 0.0083 |
| 0.3 | 0.0028 | 0.1381 | 0.0207 |
| 0.4 | 0.0041 | 0.1835 | 0.0368 |
| 0.5 | 0.0041 | 0.1672 | 0.0445 |
| 0.6 | 0.0029 | 0.1080 | 0.0376 |
| 0.7 | 0.0015 | 0.0525 | 0.0234 |
| 0.8 | 0.0007 | 0.0203 | 0.0114 |
| 0.9 | 0.0002 | 0.0065 | 0.0045 |
| 1 | 0.0001 | 0.0018 | 0.0015 |
| 1.1 | 0.0000 | 0.0004 | 0.0004 |
| 1.2 | 0.0000 | 0.0001 | 0.0001 |
| 1.3 | 0.0000 | 0.0000 | 0.0000 |
| 1.4 | 0.0000 | 0.0000 | 0.0000 |
| 1.5 | 0.0000 | 0.0000 | 0.0000 |
| 1.6 | 0.0000 | 0.0000 | 0.0000 |
| 1.7 | 0.0000 | 0.0000 | 0.0000 |
| 1.8 | 0.0000 | 0.0000 | 0.0000 |
| 1.9 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 0.0000 | 0.0000 | 0.0000 |
From the table we see the highest posterior model probability associated with
, a result consistent with those reported by Kostov [
6] based on his alternative “boosting” type of model search/comparison procedure.
An interesting question is—do these fine-tuning adjustments of the spatial weight matrix make a difference in terms of the estimates and inferences?
To explore this issue we produce estimates for models based on values of
γ ranging from 0.2 to 1, in 0.2 increments and for
and
.
11 We note that
Table 4 indicates there is virtually no posterior probability support for models based on
, so one might expect estimates based on
to differ greatly from those based on
. The lack of posterior probability support is also evident in the table for models with weight matrices based on values of
γ equal to 0, 0.9 and 1.0, when
. One would typically not want to use weight structures having such low support from the sample data, but we use these here to make the point that estimates and inferences will not differ greatly even for these weight matrices.
Table 5 and
Table 6 show (posterior median) direct effects estimates for the ten variables constructed using a set of 2000 retained draws from Bayesian Markov Chain Monte Carlo estimation of the model (see LeSage and Pace [
1], Chapter 6).
12 These are equivalent to median direct effects values constructed using simulated draws based on the maximum likelihood estimates and variance-covariance matrix. Estimates for both
and
are presented along with lower and upper 95% confidence intervals based on plus or minus two standard deviations. (The standard deviations are from the
model.)
From the tables, we see very little change in the (median) direct effects as values of the decay parameter vary from 0 to 1, despite the fact that there is little posterior probability support for models based on values of
and
(see
Table 4). The direct effects estimates for models based on
and
are also remarkably similar, given there is virtually no support for models based on
(see
Table 4). The estimates are within the lower and upper 95% confidence intervals for the model based on
, which has the highest posterior model probability. This suggests no substantive changes in inference would arise from use of any of these weight matrix structures.
In the case of the Charles River dummy variable which is not significantly different from zero, we see a relatively dramatic change in the direct effects as we change weight matrices from to . However, none of these effects magnitudes are different from zero given the lower and upper limits reported in the table.
Table 5.
Direct effects estimates, varying γ and m.
Table 5.
Direct effects estimates, varying γ and m.
| | Direct Effects CRIME |
| Decay | −2 | | | +2 |
| 0.2 | −0.0100 | −0.0079 | −0.0079 | −0.0058 |
| 0.4 | −0.0101 | −0.0079 | −0.0080 | −0.0058 |
| 0.6 | −0.0102 | −0.0080 | −0.0080 | −0.0059 |
| 0.8 | −0.0102 | −0.0081 | −0.0082 | −0.0060 |
| 1 | −0.0104 | −0.0082 | −0.0083 | −0.0061 |
| | Direct Effects CHARLES |
| Decay | −2 | | | +2 |
| 0.2 | −0.0374 | 0.0189 | 0.0263 | 0.0753 |
| 0.4 | −0.0358 | 0.0198 | 0.0279 | 0.0754 |
| 0.6 | −0.0336 | 0.0228 | 0.0286 | 0.0792 |
| 0.8 | −0.0308 | 0.0263 | 0.0308 | 0.0835 |
| 1 | −0.0271 | 0.0299 | 0.0342 | 0.0869 |
| | Direct Effects NOX |
| Decay | −2 | | | +2 |
| 0.2 | −0.4767 | −0.2889 | −0.2879 | −0.1010 |
| 0.4 | −0.4908 | −0.2966 | −0.2927 | −0.1023 |
| 0.6 | −0.4951 | −0.3085 | −0.3147 | −0.1219 |
| 0.8 | −0.5136 | −0.3190 | −0.3252 | −0.1245 |
| 1 | −0.5184 | −0.3267 | −0.3365 | −0.1350 |
| | Direct Effects ROOMS |
| Decay | −2 | | | +2 |
| 0.2 | 0.0051 | 0.0073 | 0.0074 | 0.0095 |
| 0.4 | 0.0052 | 0.0073 | 0.0074 | 0.0093 |
| 0.6 | 0.0052 | 0.0073 | 0.0074 | 0.0094 |
| 0.8 | 0.0052 | 0.0073 | 0.0074 | 0.0095 |
| 1 | 0.0053 | 0.0074 | 0.0074 | 0.0095 |
| | Direct Effects DISTANCE |
| Decay | −2 | | | +2 |
| 0.2 | −0.1976 | −0.1521 | −0.1481 | −0.1066 |
| 0.4 | −0.1949 | −0.1506 | −0.1468 | −0.1062 |
| 0.6 | −0.1922 | −0.1486 | −0.1461 | −0.1050 |
| 0.8 | −0.1920 | −0.1468 | −0.1448 | −0.1016 |
| 1 | −0.1924 | −0.1466 | −0.1443 | −0.1007 |
Table 6.
Direct effects estimates, varying γ and m (continued).
Table 6.
Direct effects estimates, varying γ and m (continued).
| | Direct Effects RAD |
|---|
| Decay | −2 | | | +2 |
| 0.2 | 0.0467 | 0.0766 | 0.0760 | 0.1065 |
| 0.4 | 0.0460 | 0.0769 | 0.0769 | 0.1078 |
| 0.6 | 0.0468 | 0.0776 | 0.0773 | 0.1083 |
| 0.8 | 0.0478 | 0.0783 | 0.0781 | 0.1088 |
| 1 | 0.0473 | 0.0791 | 0.0777 | 0.1109 |
| | Direct Effects TAX |
| Decay | −2 | | | +2 |
| 0.2 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.4 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.6 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.8 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 1 | −0.0005 | −0.0003 | −0.0003 | −0.0002 |
| | Direct Effects PTRATIO |
| Decay | −2 | | | +2 |
| 0.2 | −0.0203 | −0.0120 | −0.0117 | −0.0038 |
| 0.4 | −0.0209 | −0.0125 | −0.0123 | −0.0040 |
| 0.6 | −0.0215 | −0.0133 | −0.0130 | −0.0050 |
| 0.8 | −0.0223 | −0.0137 | −0.0139 | −0.0052 |
| 1 | −0.0229 | −0.0145 | −0.0148 | −0.0061 |
| | Direct Effects B |
| Decay | −2 | | | +2 |
| 0.2 | 0.0001 | 0.0003 | 0.0003 | 0.0005 |
| 0.4 | 0.0001 | 0.0003 | 0.0003 | 0.0005 |
| 0.6 | 0.0001 | 0.0003 | 0.0003 | 0.0005 |
| 0.8 | 0.0001 | 0.0003 | 0.0003 | 0.0005 |
| 1 | 0.0001 | 0.0003 | 0.0003 | 0.0005 |
| | Direct Effects LSTATUS |
| Decay | −2 | | | +2 |
| 0.2 | −0.3059 | −0.2641 | −0.2619 | −0.2223 |
| 0.4 | −0.3019 | −0.2603 | −0.2592 | −0.2186 |
| 0.6 | −0.3015 | −0.2594 | −0.2578 | −0.2173 |
| 0.8 | −0.3000 | −0.2581 | −0.2571 | −0.2161 |
| 1 | −0.3002 | −0.2574 | −0.2584 | −0.2146 |
Indirect effects are presented in
Table 7 and
Table 8 in the same format used for the direct effects. We might expect to see indirect effects estimates that are slightly smaller (in absolute value terms) for models based on
neighbors weight matrices. This is because the scalar summary measures of the indirect effects reflect an average of spatial spillovers cumulated over all neighbors. Since
results in fewer neighbors, this should have some impact on the cumulative indirect effects estimates. From the table, we see this is the case, but the differences are quite small.
Table 7.
Indirect effects estimates, varying γ and m.
Table 7.
Indirect effects estimates, varying γ and m.
| | Indirect Effects CRIME |
|---|
| Decay | −2 | | | +2 |
| 0.2 | −0.0094 | −0.0073 | −0.0068 | −0.0052 |
| 0.4 | −0.0094 | −0.0073 | −0.0067 | −0.0052 |
| 0.6 | −0.0091 | −0.0069 | −0.0065 | −0.0048 |
| 0.8 | −0.0088 | −0.0067 | −0.0063 | −0.0046 |
| 1 | −0.0086 | −0.0064 | −0.0060 | −0.0042 |
| | Indirect Effects CHARLES |
| Decay | −2 | | | +2 |
| 0.2 | −0.0393 | 0.0171 | 0.0226 | 0.0734 |
| 0.4 | −0.0375 | 0.0181 | 0.0239 | 0.0737 |
| 0.6 | −0.0369 | 0.0195 | 0.0230 | 0.0759 |
| 0.8 | −0.0359 | 0.0212 | 0.0233 | 0.0784 |
| 1 | −0.0341 | 0.0229 | 0.0245 | 0.0799 |
| | Indirect Effects NOX |
| Decay | −2 | | | +2 |
| 0.2 | −0.4553 | −0.2675 | −0.2481 | −0.0796 |
| 0.4 | −0.4652 | −0.2710 | −0.2481 | −0.0768 |
| 0.6 | −0.4537 | −0.2672 | −0.2532 | −0.0806 |
| 0.8 | −0.4575 | −0.2630 | −0.2456 | −0.0684 |
| 1 | −0.4462 | −0.2545 | −0.2428 | −0.0629 |
| | Indirect Effects ROOMS |
| Decay | −2 | | | +2 |
| 0.2 | 0.0046 | 0.0067 | 0.0064 | 0.0087 |
| 0.4 | 0.0046 | 0.0067 | 0.0063 | 0.0088 |
| 0.6 | 0.0042 | 0.0063 | 0.0060 | 0.0085 |
| 0.8 | 0.0040 | 0.0061 | 0.0057 | 0.0082 |
| 1 | 0.0036 | 0.0057 | 0.0054 | 0.0079 |
| | Indirect Effects DISTANCE |
| Decay | −2 | | | +2 |
| 0.2 | −0.1855 | −0.1406 | −0.1275 | −0.0957 |
| 0.4 | −0.1823 | −0.1366 | −0.1249 | −0.0909 |
| 0.6 | −0.1745 | −0.1290 | −0.1182 | −0.0834 |
| 0.8 | −0.1664 | −0.1209 | −0.1111 | −0.0754 |
| 1 | −0.1582 | −0.1130 | −0.1036 | −0.0679 |
Table 8.
Indirect effects estimates, varying γ and m (continued).
Table 8.
Indirect effects estimates, varying γ and m (continued).
| | Indirect Effects RAD |
|---|
| Decay | −2 | | | +2 |
| 0.2 | 0.0401 | 0.0708 | 0.0651 | 0.1016 |
| 0.4 | 0.0395 | 0.0701 | 0.0650 | 0.1007 |
| 0.6 | 0.0366 | 0.0674 | 0.0621 | 0.0983 |
| 0.8 | 0.0318 | 0.0636 | 0.0597 | 0.0955 |
| 1 | 0.0298 | 0.0612 | 0.0567 | 0.0926 |
| | Indirect Effects TAX |
| Decay | −2 | | | +2 |
| 0.2 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.4 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.6 | −0.0005 | −0.0003 | −0.0003 | −0.0001 |
| 0.8 | −0.0004 | −0.0003 | −0.0003 | −0.0001 |
| 1 | −0.0004 | −0.0003 | −0.0002 | −0.0001 |
| | Indirect Effects PTRATIO |
| Decay | −2 | | | +2 |
| 0.2 | −0.0193 | −0.0111 | −0.0100 | −0.0029 |
| 0.4 | −0.0198 | −0.0113 | −0.0103 | −0.0029 |
| 0.6 | −0.0197 | −0.0115 | −0.0106 | −0.0033 |
| 0.8 | −0.0198 | −0.0112 | −0.0106 | −0.0027 |
| 1 | −0.0197 | −0.0113 | −0.0107 | −0.0029 |
| | Indirect Effects B |
| Decay | −2 | | | +2 |
| 0.2 | 0.0001 | 0.0003 | 0.0003 | 0.0004 |
| 0.4 | 0.0001 | 0.0003 | 0.0003 | 0.0004 |
| 0.6 | 0.0001 | 0.0002 | 0.0002 | 0.0004 |
| 0.8 | 0.0001 | 0.0002 | 0.0002 | 0.0004 |
| 1 | 0.0000 | 0.0002 | 0.0002 | 0.0004 |
| | Indirect Effects LSTATUS |
| Decay | −2 | | | +2 |
| 0.2 | −0.2876 | −0.2458 | −0.2283 | −0.2039 |
| 0.4 | −0.2804 | −0.2388 | −0.2215 | −0.1971 |
| 0.6 | −0.2668 | −0.2247 | −0.2097 | −0.1827 |
| 0.8 | −0.2545 | −0.2126 | −0.1976 | −0.1706 |
| 1 | −0.2416 | −0.1988 | −0.1870 | −0.1560 |
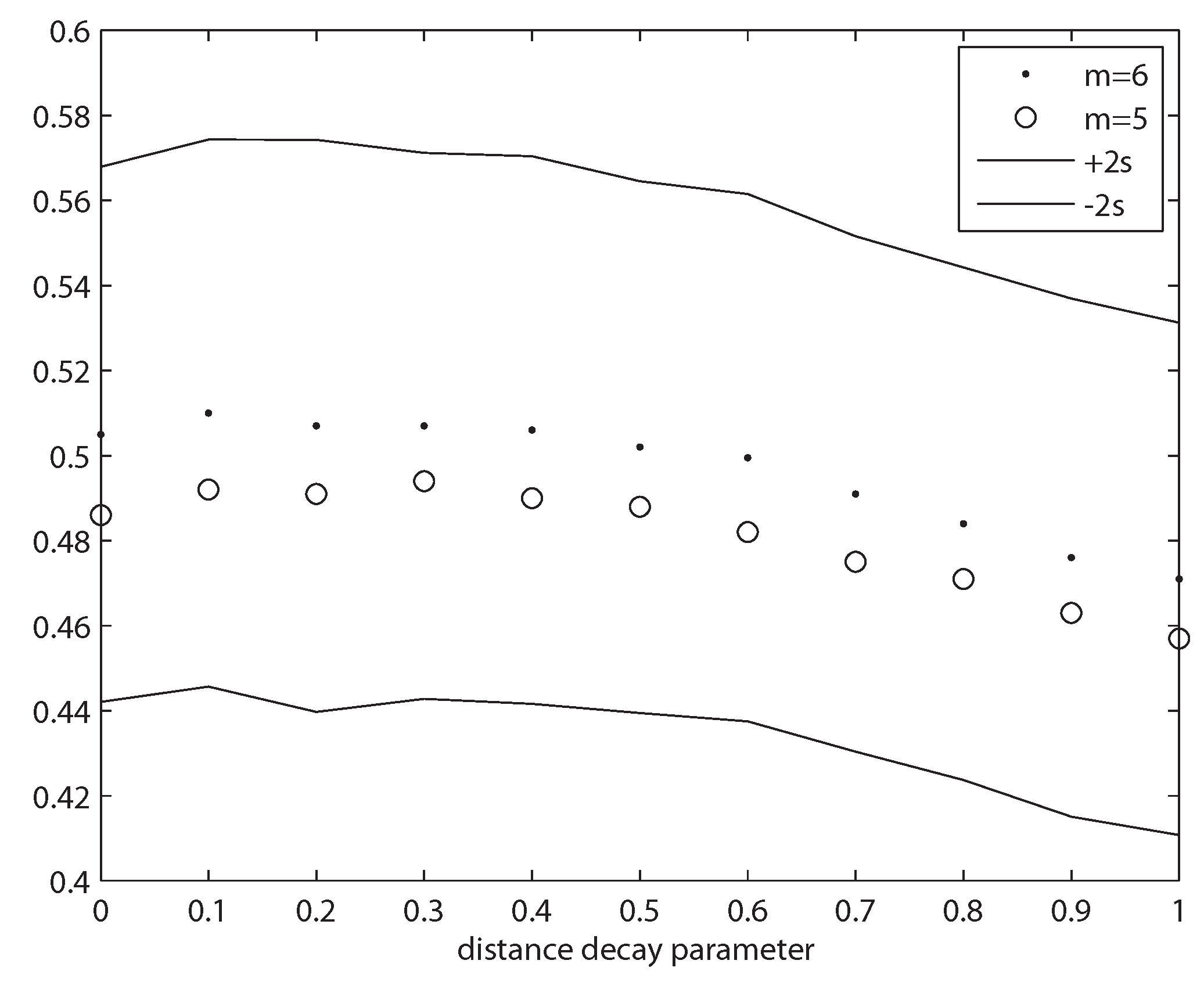
As noted, the parameters
β and
ρ change in response to changes in the spatial weight matrix in an effort to produce consistent effects estimates (partial derivatives). To illustrate this point, we present a plot of the posterior median values for
ρ for the 22 models based on
m equal to 5 and 6 and
γ ranging from 0 to 1 in
Figure 1, where one should note the scale of the vertical axis ranges between 0.4 and 0.6 making the (small) changes appear large.
Figure 1.
Variation in estimates for ρ over γ and m values.
Figure 1.
Variation in estimates for ρ over γ and m values.
From the figure, we see fairly large variation in values for the spatial dependence parameter ρ in response to changes in the decay parameter γ and in the number of neighbors m used. The effects estimates remain relatively more stable as a result of changes in the coefficients β that offset the changes shown for the parameter ρ in the figure. This of course has lead practitioners to perceive sensitivity of estimates and inferences to the choice of weight matrix. However, as already noted this reflects an incorrect interpretation of the model estimates. For purposes of inference regarding response of the dependent variable to changes in the independent variables, the effects estimates are what is relevant, not the coefficients β and ρ.
In conclusion, our answer to the question—do the fine-tuning adjustments of the spatial weight matrix advocated by Kostov [
6] make a difference in terms of the estimates and inferences?—is no. In the context of the research question addressed by Harrison and Rubinfeld [
12] who constructed the data set, a much better question to ask is whether the spatial spillovers from NOX
pollution represent a situation that is more appropriately modeled using a
global or
local spillover specification. LeSage and Pace [
17] motivate that distinguishing between these two types of situations that arise in applied modeling situations has a great deal of influence on how one interprets estimates and inferences.
In the case of NOX pollution, it seems likely that the appropriate specification is a local spillover model which implies contextual effects rather than endogenous interaction between economic agents. The SAR specification represents a global spillover scenario and is likely inappropriate here.
3.4. A Diagnostic Example
For an illustration of how one might proceed in applied practice to explore the issue of sensitivity of estimates and inferences to the weight matrix specification, we use the voter turnout data set from Gilley and Pace [
13]. The data set contains observations on 3107 US counties for the 1980 presidential election, where the dependent variable is votes cast as a proportion of population over age 19 eligible to vote. The explanatory variables are:
educ, population with college degrees as proportion of population over age 19 eligible to vote,
homeownership, homeownership as proportion of population over age 19 eligible to vote, and
income, income per capita of population over age 19 eligible to vote. All variables were transformed using logs, so the effects estimates can be interpreted as approximate elasticities.
Table 9 shows posterior model probabilities for a number of alternative spatial weight matrices, including a contiguity-based matrix and (equally weighted) nearest neighbors ranging from 3 to 20.
13 Both SAR and SDM models were examined and they both produced probabilities that provide very strong evidence in favor of models based on 15 nearest neighbors.
Table 9.
Posterior model probabilities
Table 9.
Posterior model probabilities
| Model | SAR Model | SDM Model |
|---|
| Posterior Probability | Posterior Probability |
|---|
| W-contiguity | 0.0000 | 0.0000 |
| neighbors = 3 | 0.0000 | 0.0000 |
| neighbors = 4 | 0.0000 | 0.0000 |
| neighbors = 5 | 0.0000 | 0.0000 |
| neighbors = 6 | 0.0000 | 0.0000 |
| neighbors = 7 | 0.0000 | 0.0000 |
| neighbors = 8 | 0.0000 | 0.0000 |
| neighbors = 9 | 0.0000 | 0.0000 |
| neighbors = 10 | 0.0000 | 0.0000 |
| neighbors = 11 | 0.0000 | 0.0000 |
| neighbors = 12 | 0.0000 | 0.0000 |
| neighbors = 13 | 0.0000 | 0.0000 |
| neighbors = 14 | 0.0093 | 0.0030 |
| neighbors = 15 | 0.9905 | 0.9940 |
| neighbors = 16 | 0.0003 | 0.0030 |
| neighbors = 17 | 0.0000 | 0.0000 |
| neighbors = 18 | 0.0000 | 0.0000 |
| neighbors = 19 | 0.0000 | 0.0000 |
| neighbors = 20 | 0.0000 | 0.0000 |
One might suppose that given such strong data evidence in favor of a 15 nearest neighbor weight matrix, estimates and inferences would be sensitive to an incorrect choice of neighbors.
Figure 2 shows a plot of the direct effects estimates for both SAR and SDM models for models based on 10 to 20 nearest neighbors. In addition to the direct effects for the three explanatory variables
educ, homeowners, income, a lower and upper three standard deviation confidence interval is shown in the figure.
Figure 3 shows a similarly formatted plot for the indirect effects estimates.
Figure 2.
Direct effects.
Figure 2.
Direct effects.
Figure 3.
Indirect effects.
Figure 3.
Indirect effects.
From the plots, we see that despite the very strong preference of the sample data for models based on 15 nearest neighbors, the direct effects estimates are relatively constant across the different models. In addition, the direct effects magnitudes for both the SAR and SDM models are similar. It appears that the SDM model consistently produces effects that are more stable as the number of neighbors used to construct
W vary. LeSage and Pace [
1] provide an extensive development documenting the robustness and desirable statistical properties of the SDM model in applied modeling situations.
The indirect effects estimates in
Figure 3 are also relatively constant across models with varying numbers of nearest neighbors, but we see some increase in the indirect effects for models based on 19 and 20 neighbors. Elhorst [
18] provides a detailed discussion and simple illustration of important differences in the relative flexibility and sophistication of indirect effects for the SAR versus SDM models.
An interesting point is that differences between indirect effects arising from varying the number of neighbors is much smaller than the difference between the SAR and SDM indirect effects magnitudes. For example, the elasticity of voter turnout with respect to educ is around twice as large for the SDM as the SAR model. The homeowner variable has a large positive indirect effect (near unity) in the SAR model, but is not different from zero in the SDM model (based on the three standard deviation intervals). Finally, the (negative) SDM indirect effects for the income variable are around three times those of the SAR model.