I(2) Cointegration in Macroeconometric Modelling: Tourism Price and Inflation Dynamics

Abstract

This study enhances macroeconometric modelling by utilising an I(2) cointegration framework to analyse the dynamic link between tourism prices and inflation in Slovenia and the Eurozone. Using monthly data from 2000 to 2017, we estimate cointegrated VAR models that capture long-run equilibria, short-run adjustments, and persistent deviations inherent in I(2) processes. The results reveal strong spillover effects from Slovenian tourism and input prices to Eurozone inflation and hospitality prices in the short run, while Eurozone-wide shocks dominate the long-run dynamics. By explicitly accounting for nonstationarity, structural breaks, and seasonal patterns, the I(2) model provides a more reliable framework than traditional I(1)-based approaches, which are often prone to misspecification when higher-order integration and persistent deviations are ignored. The findings contribute to macroeconometric theory by demonstrating the value of I(2) cointegration in modelling complex price systems and offer policy insights into inflation management and competitiveness in tourism-dependent economies.

1. Introduction

This paper draws inspiration from the work of Juselius (2021) regarding the cointegration method and its variations within econometrics. Understanding the temporal behaviour of economic factors is essential for both theoretical and applied research. The objectives of this study are twofold: firstly, to develop a robust econometric model for tourism-related inflation based on price dynamics and secondly, to apply and expand upon the methodological insights presented by Ross (2021). Furthermore, this study contributes to the ongoing discussions surrounding methodology in economics that heavily depend on data obtained from secondary sources (Couix, 2021).

The primary objective is to advance time series analysis in macroeconometric research by building on the foundations of Haldrup (1998); Cubadda (1999); Busetti (2006); Fisher et al. (2015); Rahul et al. (2018); Ross (2021); Gil-Alana et al. (2021) and others. In the context of tourism price dynamics, the methodological contributions of Juselius have been applied and critically assessed by Archontakis and Mosconi (2021). Building on this line of work, we focus on the role of seasonal effects, higher-order integration, and misspecification patterns in shaping tourism inflation (Braun et al., 2013). The analysis concentrates on the Eurozone, using Slovenia as a case study, and applies an I(2) cointegration framework to model long- and short-run interactions between tourism prices and inflation. Section 3 outlines the methodological framework and data and presents the empirical I(2) model.

Although the research gap has been acknowledged in the literature, most contributions remain theoretical, with relatively fewer applied case studies. We address this gap by demonstrating the importance of higher-order integrated variables in the dynamics of aggregate prices. While the GDP growth rate is typically treated as I(0) and inflation as I(1), prices are often I(2), requiring more sophisticated econometric treatment.

The novelty and contribution of this study lie in the application of an I(2) cointegration framework to estimate the long- and short-run dynamics of tourism-related prices. Econometric methods are used to allow price spreads and seasonal effects to vary in response to shocks or to remain persistent during exceptional shocks (Alghalith, 2007). A key contribution is the extension of theory and applied computational economics by explicitly modelling spillovers and persistent deviations in integrated markets.

The analysis focuses on the Eurozone, with a case study of Slovenia using monthly statistical time series data. Special attention is given to two sets of shocks: (i) Slovenia’s accession to the European Union in 2004 and adoption of the euro in 2007 and (ii) episodes of high food prices, economic crises, and subsequent recovery. The hospitality sector, as the most significant part of the tourism industry, provides the empirical setting.

The article’s broader goal is to examine how financial and price volatilities can be treated in econometrics beyond conventional misspecification tests. The motivation stems from ex-ante econometric modelling aimed at predicting future events that may have potentially adverse effects on economies and societies (Gričar et al., 2021). The remainder of the paper is structured as follows: Section 2 reviews the literature and develops the research questions; Section 3 outlines the methods and data; Section 4 presents the empirical results; and Section 5 discusses the findings and concludes this paper.

2. Literature Review

The dynamics of tourism price inflation can be examined as a further development of the work by Archontakis and Mosconi (2021), who applied the I(2) cointegration framework—a methodology available since the early 1990s but still underutilised in empirical applications (Juselius, 2006; Kongsted, 2005). As Juselius (2006) notes, cointegration provides a systematic process for capturing interactions among nonstationary variables, and the framework developed by Johansen & Juselius has become one of the most influential in modern econometrics. This research builds on that foundation by providing a step-by-step procedure for implementing I(2) modelling in applied contexts, thereby establishing a robust statistical framework for predictive macroeconometrics.

At the same time, several studies have highlighted persistent misspecification problems in econometric time series (Gjelsvik et al., 2020; Harvey et al., 2012), including unreliable inference (Trafimow, 2019), the treatment of shocks (Pollock, 2020), and incorrect variable selection (Błażejowski et al., 2020). Addressing these issues is crucial in tourism economics, where prices play a critical role in determining both industrial performance and financial stability. The application of an I(2) procedure to tourism price dynamics thus offers a methodological advance with strong practical relevance.

Distinct forces shape tourism price behaviour. First, the sector has been among the most severely affected by various crises (Plzáková & Smeral, 2021), which have generated short-term ex-post inflationary pressures, echoing earlier findings on price volatility in the hospitality sector (Gričar & Bojnec, 2013). Second, tourism is one of the most dynamic global industries (Gričar & Bojnec, 2013), yet predictions in this field often lack robustness (Teixeira & Fernandes, 2014). This underscores the importance of using advanced econometric tools to isolate variables and model persistent deviations. Building on earlier work (Gričar & Bojnec, 2013; Pacifico, 2021), we apply a vector autoregressive model with I(2) integration, following the theoretical developments of Franchi and Paruolo (2021).

In addition, this study addresses often neglected econometric features. For instanc, normality in residuals has mainly been overlooked in applied time series (Juselius, 2021), yet its treatment is crucial for reliable inference (Braione & Scholtes, 2016; Chen et al., 2021; Desgagné & Lafaye de Micheaux, 2018). Similarly, recent advances in stationarity testing (Hudecová et al., 2021) and autocorrelation procedures (Vougas, 2021) provide complementary tools that strengthen the empirical framework.

Against this backdrop, our study extends the application of I(2) cointegration to tourism and inflation in the Eurozone, with Slovenia as a case study. This approach not only integrates methodological rigour but also responds to rising concerns about inflation risk in the Eurozone (Hein, 2017; Ruth, 2021). By incorporating past shocks—such as EU accession, euro adoption, and food price surges—into the econometric framework, we aim to demonstrate how I(2) cointegration improves predictive performance.

Building on earlier cointegration research in tourism (Kulendran, 1996; Dritsakis, 2004), this paper models both general consumer price indices (CPIs) and tourism-related input price indices (hospitality and food and beverages). These time series exhibit long and persistent deviations from linear trends, which the I(2) framework captures more effectively than fractional alternatives. This enables us to evaluate the homogeneity of price behaviour between Slovenia and the wider Eurozone (Gričar & Bojnec, 2018), offering new insights into market integration.

Building on these theoretical advances, the main research question is: How much does using an I(2) cointegration model enhance our understanding of the long- and short-term relationships between tourism prices and inflation in small open economies like Slovenia within the Eurozone?

3. Materials and Methods

This section introduces a theoretical framework on tourism and prices, presents the cointegrating model, and the data used.

3.1. Tourism and Prices—Theoretical Framework

Gričar and Bojnec (2013) analyse inflation and price trends in the hospitality sector through time series models. Given that tourism has a significant impact on the Eurozone economy and that prices are crucial for determining income and profitability for firms, our goal is to examine the roles of prices and inflation in time series data projections. Notably, to date, no study has addressed this issue in advanced time series models for Eurozone countries. Several studies deal with prices and demand or prices and exchange rates or prices and oil shocks (Ahumada & Cornejo, 2021; Gričar & Bojnec, 2018; Katircioglu et al., 2018; Meo et al., 2018), but no study deals with prices in the context of $I\left(2\right)$ cointegration and exclusively with price treatments and inflation. We first review the existing empirical studies on price spillovers in tourism and then apply $I\left(2\right)$ cointegration in modelling time series in tourism to enrich the high quality of quantitative analyses in tourism. This can provide valuable in-depth evidence on price as an essential management tool for firms, as it is the primary determinant of income (Gričar & Bojnec, 2018). Therefore, it is essential to accurately explore input and output prices as inflation, as an external variable, determines firms’ input costs and output prices (Cranage, 2003).

Juselius (2006) has recognised that inflation in the economy is an essential variable in the empirical work and data vector. Therefore, the model must be built with this aspect in mind. Following the idea of Gričar and Bojnec (2013), the econometric explanation of prices can be expressed as a data vector consistent with the framework of Castle et al. (2021), where each variable maintains the integration of the chosen order I(d). Building on this foundation, the econometric framework applies the I(2) cointegrated (C) vector autoregressive (VAR) approach, extending the conventional I(1) model to variables whose second differences are stationary. This structure enables a coherent analysis of long-run equilibria among price indices with persistent trends while accounting for short-run adjustments. It distinguishes between permanent and transitory components of inflation and tourism-related prices, ensuring both are adequately represented in the model. Deterministic elements, such as constants and linear trends, capture gradual structural shifts, whereas stochastic shocks describe short-term fluctuations. This framework provides the theoretical basis for the empirical specification developed in Section 3.2.

3.2. The I(2) Cointegration Model

Building on the preceding theoretical framework, the empirical model applies Johansen’s (1992, 1995) representation of the I(2) CVAR system. This formulation extends the conventional I(1) model by allowing variables whose second differences are stationary, thereby capturing both I(1) and I(2) components within the same structure. The model separates long-run equilibrium relations among price levels from the short-run dynamics of their changes, enabling analysis of how persistent price trends and transitory shocks interact. Deterministic terms, such as constants and linear trends, account for gradual structural shifts, while the stochastic error structure represents short-term fluctuations around equilibrium. This I(2) framework is particularly suitable for modelling the joint evolution of tourism-related and consumer prices in Slovenia and the Eurozone, where sustained nominal growth and cross-market spillovers create higher-order stochastic trends. It thus provides the theoretical foundation for the empirical estimation that follows.

Recent uses of the I(2) model include studies by Kivedal (2023) on CO₂ emissions; Juselius and Stillwagon (2018), focusing on interest rate dynamics for the UK and US; Juselius and Assenmacher (2017), analysing PPP between Switzerland and the US; and Juselius (2017), studying Germany and the US. Hetland and Hetland (2017) applied the I(2) model to the Danish housing market, while Juselius and Dimelis (2019) investigated the Greek crisis. The explanation of the I(2) model below closely follows these references. More details are available in Juselius (2006, Chapter 17), Johansen (1995, Chapter 9), and Franchi and Paruolo (2021).

A VAR model incorporating $k$ lags can be expressed as:

$$X_t={\Pi }_1{X}_{t-1}+\dots {\Pi }_k{X}_{t-k}+\Phi D_t+{\epsilon }_t,$$

(1)

where $X_t$ contains a vector of variables for period t, $D_t$ is a vector of dummy variables that may be included and ${\epsilon }_t$ is an error term. It can be reformulated to a vector equilibrium correction model, such as:

$$\Delta X_t={\Gamma }_1\Delta X_{t-1}+\dots +{\Gamma }_{k-1}\Delta X_{t-k+1}+\alpha {\tilde{\beta }}^{\prime }{\tilde{X}}_{t-1}+\Phi D_t+{\mu }_0+{\mu }_{1}t+{\epsilon }_t,$$

(2)

where ${\tilde{\beta }}^{\prime }=\left[\beta ,{\beta }_0,{\beta }_1\right]$, ${\tilde{X}}_{t-1}={\left[X_{t-1},1,t\right]}^{\prime }$, ${\epsilon }_t\sim N_p\left(0,\Omega \right)$ (p is the number of variables in the data vector) for $t=1,\dots ,T$, and $X_{-1},X_0$ is given. $D_t$ is a vector of dummy variables (if included), and ${\mu }_0$ and ${\mu }_1$ are constants. The trend is restricted to lie within the cointegrating space to avoid quadratic trends (i.e., ${\beta }_1\ne 0$ and ${\mu }_1=0$). To simplify this, the trend is restricted to ${\beta }^{\prime }{X}_{t-1}$, and the notation ${\tilde{\beta }}^{\prime }$ is omitted. Additionally, the Vector Error Correction Model (VECM) described in (2) can be expressed in terms of acceleration rates, changes, and levels. For a lag length of $k=2$, this yields

$${\Delta }^2{X}_t=\Pi X_{t-1}+\Gamma \Delta X_{t-1}+\Phi D_t+{\mu }_0+{\mu }_{1}t+{\epsilon }_t.$$

(3)

This can be written using the maximum likelihood parameterisation (see Johansen (1992)), yielding

$${\Delta }^2{X}_t=\alpha \left({\beta }^{\prime }{X}_{t-1}+d^{\prime }\Delta X_{t-1}\right)+\zeta {\tau }^{\prime }\Delta X_{t-1}+\Phi D_t+{\mu }_0+{\mu }_{1}t+{\epsilon }_t,$$

(4)

where $\alpha$ contains the adjustment coefficients, whilst $\beta$ represents the parameters related to the long-run relationships among the $p$ variables in the system. If the lag length is k = 3, we also have to add the term ${\Gamma }_1{\Delta }^2{X}_{t-1}$ to (3) and (4) with a negative sign, where $\Gamma =-\left(I-{\Gamma }_1\right)$. This term will then represent short-run effects; see Johansen (1995). Following Rahbek et al. (1999) to avoid quadratic trends, the trend is restricted to be in ${\beta }^{\prime }{X}_{t-1}$ and the constant to be in $d^{\prime }\Delta X_{t-1}$. See, e.g., Juselius (2006, Chapter 17) for a more detailed description of the I(2) cointegrated VAR model.

Johansen’s (1992, 1995) representation of the I(2) model extends the VECM to systems where some variables are integrated of order two. In such settings, the second-differenced vector ${∆}^2{X}_t$ can be expressed as

$${\Delta }^2{X}_t=\alpha {\beta }^{\prime }{∆X}_{t-1}+{\alpha }_2{\beta }_2^{\prime }{∆X}_{t-2}+{\Gamma \Delta }^2{X}_{t-1}+{\epsilon }_t,$$

(5)

where ${\beta }^{\prime }{∆X}_{t-1}$ captures the I(1) cointegration relationships, and ${\beta }_2^{\prime }{∆y}_{t-2}$ represents the long-run I(2) relations. The matrices $\alpha$ and ${\alpha }_2$ contain the adjustment coefficients that link deviations from equilibrium to short-run dynamics. This formulation enables the decomposition of the system into transient and permanent components, distinguishing between stationary relations in the first and second differences. The representation, therefore, generalises the standard I(1) VECM to handle higher-order stochastic trends in non-stationary macroeconomic and price processes.

3.3. Data

We utilise six monthly price variables, unadjusted for seasonality, covering the period from January 2000 to December 2017. These are: the input costs for the hospitality industry include Slovenian prices (${IPHI}_t$), prices in the Eurozone’s hospitality sector (${IPHIEA}_t$), Slovenian consumer prices (${CPI}_t$), consumer prices across the Eurozone (${CPIEA}_t$), Slovenian food and beverages prices (${IFB}_t$), and food and beverage prices in the rest of the Eurozone (${IFBEA}_t$) as input costs for the hospitality industry. The original VAR method is used. Data are sourced from the Statistical Office of the Republic of Slovenia (SORS, 2021) and Eurostat (2021). Figure 1 displays the with base-10 indices, with January 2000 set as the baseline at 100.

Figure 1 shows the evolution of six-monthly price indices from 2000 to 2017, covering hospitality, consumer, and food and beverage prices for Slovenia and the Eurozone. All indices demonstrated clear upward trends, aligning with the long-term nominal price growth seen in both economies. The Slovenian indices (IPHI, CPI, IFB) experienced slightly stronger cumulative increases compared to the Eurozone indices, reflecting faster price convergence and domestic service-sector dynamics. Conversely, the Eurozone indices (IPHIEA, CPIEA, IFBEA) followed more stable paths, consistent with the larger and more diverse structure of the overall market. Despite some short-term fluctuations, all series showed significant persistence and co-movement, indicating a high level of integration between national and regional price systems. The combined movements of these indices supported using the I(2) cointegration framework to analyse long- and short-term adjustments in tourism-related and consumer prices across both economies.

4. Results

4.1. Estimating the Unrestricted I(2) Model

By estimating a VAR(4) model, we obtain a model that is sufficiently well specified. The misspecification tests are shown in

Table 1. Misspecification tests for the unrestricted VAR(4) and VECM.

Univariate Tests
	LIPHI	LIPHIEA	LCPI	LCPIEA	LIFB	LIFBEA
No ARCH	$\underset{\left[1.00\right]}{0.002}$	$\underset{\left[0.99\right]}{0.053}$	$\underset{\left[0.56\right]}{1.16}$	$\underset{\left[0.05\right] *}{5.95}$	$\underset{\left[0.04\right]}{6.43}$	$\underset{\left[0.00\right]}{12.21}$
Skewness	$-4.88$	$-0.21$	$0.20$	$-0.004$	$0.005$	$0.55$
Excess kurtosis	$72.18$	$3.84$	$3.36$	$3.65$	$4.07$	$4.64$
Normality	$\underset{\left[0.00\right] **}{181.8}$	$\underset{\left[0.03\right] *}{7.41}$	$\underset{\left[0.24\right]}{2.82}$	$\underset{\left[0.08\right]}{5.18}$	$\underset{\left[0.00\right] **}{11.05}$	$\underset{\left[0.00\right] **}{16.37}$
Multivariate tests
No autocorrelation	LM(1)	${\chi }^2\left(36\right)=49.777$				$\left[0.063\right]$
	LM(2)	${\chi }^2\left(36\right)=40.025$				$\left[0.296\right]$
Normality		${\chi }^2\left(12\right)=223.63$				${\left[0.00\right] }^{**}$
No ARCH	LM(1)	${\chi }^2\left(441\right)=595.57$				${\left[0.00\right]}^{ **}$
	LM(2)	${\chi }^2\left(882\right)=960.40$				${\left[0.034\right] }^{*}$

Note: The multivariate tests for autocorrelation and autoregressive conditional heteroscedasticity (ARCH) model effects are those from Godfrey (1988). The univariate and multivariate normality tests are from J. A. Doornik and Hansen (1994). See Figure 1 for the meaning of the abbreviations for the variables—p-values in the brackets; ** for significance at the 1% level and * for significance at the 5% level.

.

As shown in Table 1, residual diagnostics revealed minor deviations from normality and some evidence of ARCH effects. Additional analysis using residual plots, recursive estimates, and difference-of-log transformations in OxMetrics 8 (J. Doornik & Juselius, 2017). suggested that these issues were primarily due to a few mild outliers around the 2008–2009 financial crisis and 2020, rather than structural breaks. Incorporating level-shift dummies and re-estimating the model produced nearly identical cointegration ranks and short-run dynamics. These results confirm that the minor non-normality and weak ARCH effects did not significantly impact the robustness of the findings.

There is no residual autocorrelation of orders 1 and 2 in the VAR(4) model, but some variables show ARCH effects and non-normality. Statistical inference is robust to moderate ARCH effects (Rahbek et al., 2002), but non-normality may lead to problems. However, the non-normality appears to be primarily caused by kurtosis, rather than skewness. This is less of a concern for inference (Juselius, 2006, Chapter 4.3), such that the non-normality we find in the residuals here is not sufficient to conclude that our model is not well specified. Including various dummy variables to control for events that may occur outside the model did not correct the non-normality caused by kurtosis or the ARCH effects; therefore, we proceed with the VAR(4) model without dummy variables.

As seen in

Table 2. Rank test statistics.

p-r	r	${\mathit{s}}_2=6$	${\mathit{s}}_2=5$	${\mathit{s}}_2=4$	${\mathit{s}}_2=3$	${\mathit{s}}_2=2$	${\mathit{s}}_2=1$	${\mathit{s}}_2=0$
$6$	$0$	$502.2$	$394.8$	$324.2$	$265.7$	$218.5$	$172.8$	$154.2$
		$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.001\right]$	$\left[0.000\right]$
$5$	$1$		$314.3$	$243.$9	$187.7$	$137.5$	$111.2$	$100.2$
			$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.000\right]$	$\left[0.004\right]$	$\left[0.014\right]$	$\left[0.005\right]$
$4$	$2$			$171.7$	$120.3$	$92.3$	$71.2$	$61.5$
				$\left[0.024\right]$	$\left[0.024\right]$	$\left[0.069\right]$	$\left[0.129\right]$	$\left[0.076\right]$
$3$	$3$				$91.2$	$58.6$	$37.2$	$27.7$
					$\left[0.033\right]$	$\left[0.292\right]$	$\left[0.635\right]$	$\left[0.644\right]$
$2$	$4$					$30.9$	$19.2$	$12.1$
						$\left[0.758\right]$	$\left[0.793\right]$	$\left[0.806\right]$
$1$	$5$						$11.9$	$2.9$
							$\left[0.471\right]$	$\left[0.875\right]$

Note: The first column shows the p-r number of stochastic trends, and the second column shows the number of long-run relations r. The following columns show the $s_2$ number of I(2) trends—p-values in the brackets.

, the rank test suggests a rank of r = 2 and $s_2=2$ I(2) trends when starting with the model in the top left corner of the table and going to the right before going to the next line. The first model being significant (having a p-value above 0.05), is the model with a rank of r = 2 and $s_2=2$ I(2) trends. We can thereby simplify the model since we find that there are two long-run multicointegrating relationships in the data, and two I(2) trends, such that the model has reduced rank. Hence, we use this model in the analysis by reducing the rank to 2 and incorporating 2 I(2) trends.

4.2. The I(2) Model with Reduced Rank and Over-Identifying Restrictions

When estimating the reduced-rank model, we impose restrictions to obtain the identified long-run structure in $\beta$. First, we imposed restrictions that resulted in one beta vector for Slovenia and one for the rest of the Eurozone. However, these restrictions could not be accepted at a significance level higher than 3.3%, suggesting spillovers between Slovenia and the rest of the Eurozone By including the hospitality price index in the Eurozone for the long-run relationship related to Slovenia, we have restrictions that cannot be rejected (at the highest level of significance compared to including other variables in one of the two beta vectors). The identifying restrictions involves removing euro area CPI and food and beverage prices from the first cointegrating relationship and removing all Slovenian variables from the second cointegrating relationship. The first relationship can thus be interpreted as a relationship between Slovenian variables, which also includes euro area hospitality prices, while the second relationship can be interpreted as a relationship specific to the euro area. Since the euro area hospitality prices are significant in the first relationship, this indicates that long-run relationship exists between prices in Slovenia and the Eurozone. The identified structure suggests that hospitality prices in the rest of the Eurozone are important for hospitality prices in Slovenia in the long run. Estimates are shown in

Table 3. An estimated reduced rank model with identified $\beta$.

	LIPHI	LIPHIEA	LCPI	LCPIEA	LIFB	LIFBEA	Det
${\beta }_1^{\prime }$	$\underset{\left[\right]}{1.00}$	$\underset{\left[-18.2\right]}{-25.5}$	$\underset{\left[2.1\right]}{1.51}$	$\underset{\left[\right]}{0.00}$	$\underset{\left[8.9\right]}{4.8}$	$\underset{\left[\right]}{0.00}$	$\underset{\left[9.9\right]}{0.024}$
$d_1^{\prime }$		$\underset{\left[-6.5\right]}{-19.1}$	$-\underset{\left[-5.9\right]}{183}$	$\underset{\left[-5.2\right]}{-64.1}$	$-\underset{\left[-5.2\right]}{45.4}$	$\underset{\left[-6.7\right]}{-39.6}$	$\underset{\left[17.0\right]}{85.9}$
${\alpha }_1^{\prime }$	$\underset{\left[-4.3\right]}{-0.030}$		$\underset{\left[3.1\right]}{0.008}$	$\underset{\left[5.8\right]}{0.008}$	$\underset{\left[-2.0\right]}{-0.009}$	$\underset{\left[3.3\right]}{0.006}$
${\beta }_2^{\prime }$	$\underset{\left[\right]}{0.00}$	$\underset{\left[\right]}{1.00}$	$\underset{\left[\right]}{0.00}$	$\underset{\left[2.8\right]}{0.223}$	$\underset{\left[\right]}{0.00}$	$-\underset{\left[-10.9\right]}{0.843}$	$-\underset{\left[-4.8\right]}{0.0006}$
$d_2^{\prime }$		$\underset{\left[6.4\right]}{1.03}$	$\underset{\left[4.9\right]}{8.21}$	$\underset{\left[4.0\right]}{2.7}$	$\underset{\left[5.6\right]}{2.67}$	$\underset{\left[6.1\right]}{1.93}$	$-\underset{\left[-5.0\right]}{1.85}$
${\alpha }_2^{\prime }$	$-\underset{\left[-4.6\right]}{0.618}$			$\underset{\left[5.0\right]}{0.131}$	$\underset{\left[-2.2\right]}{-0.181}$	$\underset{\left[3.0\right]}{0.010}$

Note: t-values in the brackets. The rightmost column shows the deterministic term, implying the trend for the $\beta$ vector and a constant for the $d$ vector. An asterisk implies that there is no significant effect (given |t-value| < 1.6 following, e.g., Juselius and Assenmacher (2017)), and boldfaced font indicates that the variable in the corresponding column is error increasing. “Det” denotes a deterministic term that is a constant in $d^{\prime }$ and a trend in ${\beta }^{\prime }$. See Figure 1 for the other variable abbreviations.

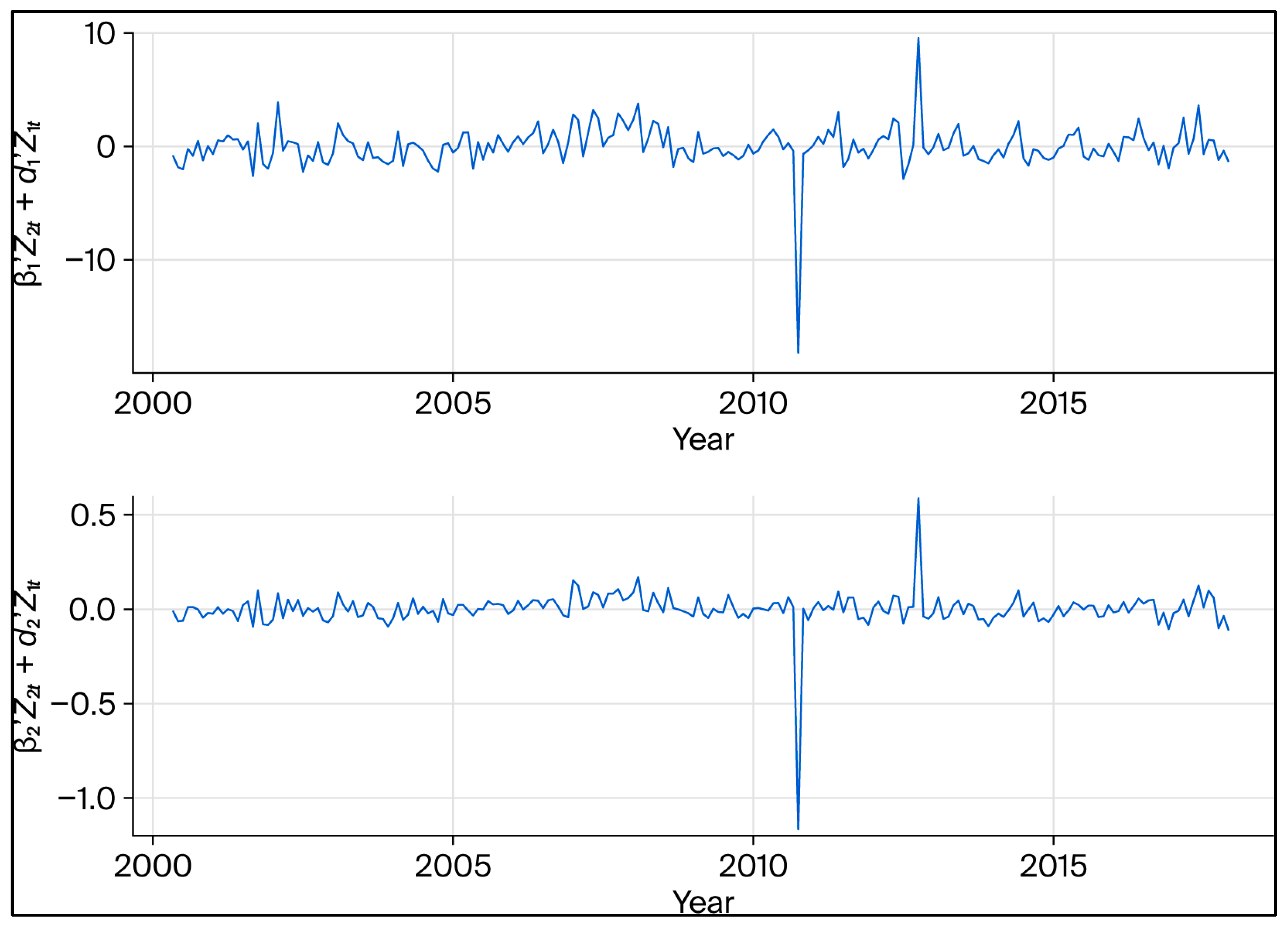
. These restrictions cannot be rejected at a p-value of 0.37. The two cointegrating relationships (with identifying restrictions applied) are also shown in Figure 2, where we observe stationary relationships with some outliers.

To further investigate the pushing and pulling forces of the variables in our system and understand how Slovenia and the rest of the Eurozone interact with each other in the long, medium, and short term, we examine the estimated parameters.

Suppose we label the first long-run relationship as the Slovenian and the second as the relationship for the rest of the Eurozone. In that case, we can look at whether the estimated products of ${\alpha }_{ij}{\beta }_{ij}$ < 0 and/or ${\alpha }_{ij}{d}_{ij}<0$ for error correction in the long run and $d_{ij}{\beta }_{ij}>0$ for error-correcting in the medium run are given significant $\alpha$ (or error increasing behaviour for the opposite inequality signs) to see which variables are error increasing or error-correcting the system, respectively.

For the Slovenian relationship (the first cointegrating relationship), we observe an error-increasing behaviour related to Slovenian CPI since ${\alpha }_{ij}{\beta }_{ij}>$ 0 for this, while the Eurozone CPI is error increasing in the Eurozone relationship. Slovenian CPI and food and beverage prices are also error increasing in the medium run for the Slovenian relationship since $d_{ij}{\beta }_{ij}<0$ for these, and food and beverage prices in the Eurozone are increasing error in the medium run for the Eurozone relationship for the same reason. Hence, Slovenian prices do not seem to influence the rest of the Eurozone, or vice versa, in the long or medium run related to the long-run relationships.

The stationary dynamic long-run relations ${\beta }_i^{\prime }{X}_t+d_i^{\prime }\Delta X_t$ then become

$$\begin{array}{c}LPIH{I}_t+\underset{\left[2.1\right]}{1.51}LCP{I}_t-\underset{\left[-18.2\right]}{25.5}LPIHIE{A}_t+\underset{\left[8.9\right]}{4.8}LIF{B}_t+\underset{\left[9.9\right]}{0.024}t-\underset{\left[-6.5\right]}{19.1}\Delta LPIHIE{A}_t+\underset{\left[3.1\right]}{0.008}\Delta LCP{I}_t\\ +\underset{\left[5.8\right]}{0.008}\Delta LCPIE{A}_t-\underset{\left[-2.0\right]}{0.009}\Delta LIF{B}_t+\underset{\left[3.3\right]}{0.006}\Delta LIFBEA+\underset{\left[17.0\right]}{85.9},\end{array}$$

(6)

for the Slovenian relationship and

$$\begin{array}{c}PPIH{IEA}_t+\underset{\left[2.8\right]}{0.223}LCP{IEA}_t-\underset{\left[-10.9\right]}{0.843}LIF{BEA}_t-\underset{\left[-4.8\right]}{0.0006} t+\underset{\left[6.4\right]}{1.03}\Delta LPIH{IEA}_t+\underset{\left[4.9\right]}{8.21}\Delta LCP{I}_t+\underset{\left[4.0\right]}{2.7}\Delta LCPIE{A}_t\\ +\underset{\left[5.6\right]}{2.67}\Delta LIF{B}_t+\underset{\left[6.1\right]}{1.93}\Delta LIFBE{A}_t-\underset{\left[-5.0\right]}{1.85},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(7)

for the rest of the Eurozone.

Equations (6) and (7) present the estimated stationary long-run relations obtained from the cointegrated I(2) system. The coefficients describe how hospitality prices in Slovenia and the Eurozone adjust to long-term equilibrium levels in response to movements in consumer and food-and-beverage prices, both domestically and regionally. The significant parameters confirm the existence of two stable cointegration relationships linking national and Eurozone price dynamics. The inclusion of deterministic terms and first-difference variables captures gradual structural shifts and short-run adjustments within the system. Overall, the estimated β-relations suggest a strong interdependence between the Slovenian and Eurozone price indices, consistent with the hypothesis of price convergence in integrated tourism and consumer markets.

4.3. Moving Average Representation

We can estimate the common trends and their loadings. They are shown in

Table 4. Common trends and their loadings.

	LIPHI	LIPHIEA	LCPI	LCPIEA	LIFB	LIFBEA
${\tilde{\beta }}_{\perp \mathrm{2,1}}$	0.01	0.01	0.06	0.03	0.06	0.03
${\tilde{\beta }}_{\perp \mathrm{2,2}}$	0.21	0.02	–0.14	–0.13	−0.11	–0.04
${\alpha }_{\perp \mathrm{2,1}}$		$\underset{\left[1.9\right]}{0.92}$	$-\underset{\left[-2.3\right]}{0.61}$	$\underset{\left[2.2\right]}{0.58}$	$1$	$0$
${\alpha }_{\perp \mathrm{2,2}}$		$\underset{\left[-1.9\right]}{-0.38}$		$\underset{\left[-6.3\right]}{-0.72}$	$0$	$1$

Note: Refer to Figure 1 for the definitions of the abbreviations used for the variables, as well as the t-test values in brackets. Non-significant variables (t-value smaller than 1.6 in absolute value) are removed.

.

From the common trends and their loadings in Table 4, we observe from the alphas that the first I(2) trend is generated from cumulated shocks to food and beverage prices, Euro Area hospitality prices and CPI both in Slovenia and the Eurozone and thereby represents an I(2) trend related to general price levels in the entire Eurozone. However, this trend primarily affects Slovenian food and beverage prices and CPI, since these are the estimated beta coefficients with the highest loadings at 0.06. The second I(2) trend is generated from all Euro area price indices and primarily affects Slovenian hospitality prices, as well as CPI in Slovenia and the Eurozone and Slovenian food and beverage prices to a lesser extent. This suggests that hospitality, as well as food and beverage prices in the Eurozone, may impact Slovenian hospitality prices in the long run through twice-cumulated shocks.

4.4. Short-Run Effects

While there are few long-run effects between Slovenia and the rest of the Eurozone, there are more short-run effects, especially effects from Slovenia on the Eurozone. There are short-term effects on the Eurozone and the Slovenian CPI from the changes in Slovenian hospitality prices. The Eurozone’s food and beverage price index is affected by both Slovenian hospitality prices and Slovenian food and beverage prices in the short run. The estimated one-period effects on the acceleration rates are shown in

Table 5. Short-run effects.

	${\mathbf{\Delta }}^2\mathit{L}\mathit{I}\mathit{P}\mathit{H}{\mathit{I}}_{\mathit{t}}$	${\mathbf{\Delta }}^2\mathit{L}\mathit{I}\mathit{P}\mathit{H}\mathit{I}\mathit{E}{\mathit{A}}_{\mathit{t}}$	${\mathbf{\Delta }}^2\mathit{L}\mathit{C}\mathit{P}{\mathit{I}}_{\mathit{t}}$	${\mathbf{\Delta }}^2\mathit{L}\mathit{C}\mathit{P}\mathit{I}\mathit{E}{\mathit{A}}_{\mathit{t}}$	${\mathbf{\Delta }}^2\mathit{L}\mathit{I}\mathit{F}{\mathit{B}}_{\mathit{t}}$	${\mathbf{\Delta }}^2\mathit{L}\mathit{I}\mathit{F}\mathit{B}\mathit{E}{\mathit{A}}_{\mathit{t}}$
${\Delta }^{2}LIPH{I}_{t-1}$	−0.0921	−0.0139	−0.00781	0.00121	−0.0221	0.00212
	[−0.9]	[−0.8]	[−0.2]	[0.1]	[−0.4]	[0.1]
${\Delta }^{2}LIPHIE{A}_{t-1}$	−1.3	−0.0369	−0.228	−0.0942	−0.775	−0.309
	[−2.3]	[−0.4]	[−1.2]	[−0.9]	[−2.3]	[−2.3]
${\Delta }^{2}LCP{I}_{t-1}$	0.1	−0.0101	0.234	0.0878	0.0542	−0.108
	[0.2]	[−0.1]	[1.7]	[1.1]	[0.2]	[−1.1]
${\Delta }^{2}LCPIE{A}_{t-1}$	0.0663	0.00277	−0.0743	0.0146	−0.0812	0.343
	[0.1]	[0.0]	[−0.3]	[0.1]	[−0.2]	[2.0]
${\Delta }^{2}LIF{B}_{t-1}$	0.425	−0.057	0.187	0.0988	0.00962	−0.024
	[2.0]	[−1.5]	[2.6]	[2.4]	[0.1]	[−0.5]
${\Delta }^{2}LIFBE{A}_{t-1}$	−0.676	0.0314	−0.432	−0.189	−0.477	−0.208
	[−1.4]	[0.4]	[−2.7]	[−2.1]	[−1.7]	[−1.8]
${\Delta }^{2}LIPH{I}_{t-2}$	−0.0506	−0.00385	−0.0089	0.00291	−0.0614	−0.00248
	[−0.7]	[−0.3]	[−0.4]	[0.2]	[−1.5]	[−0.1]
${\Delta }^{2}LIPHIE{A}_{t-2}$	−0.422	0.148	−0.0504	0.0477	−0.521	−0.265
	[−1.1]	[2.0]	[−0.4]	[0.6]	[−2.2]	[−2.8]
${\Delta }^{2}LCP{I}_{t-2}$	0.14	−0.0046	−0.0121	0.0323	−0.108	−0.0869
	[0.5]	[−0.1]	[−0.1]	[0.6]	[−0.7]	[−1.4]
${\Delta }^{2}LCPIE{A}_{t-2}$	0.213	−0.0708	0.154	−0.119	0.433	0.293
	[0.5]	[−0.8]	[1.0]	[−1.3]	[1.5]	[2.6]
${\Delta }^{2}LIF{B}_{t-2}$	0.307	−0.0547	0.104	0.0449	−0.0891	−0.0322
	[2.1]	[−2.1]	[2.1]	[1.6]	[−1.0]	[−0.9]
${\Delta }^{2}LIFBE{A}_{t-2}$	−0.782	0.0501	−0.297	−0.0225	−0.285	−0.107
	[−2.4]	[0.8]	[−2.7]	[−0.4]	[−1.4]	[−1.4]

Note: ${\Delta }^2$ is the second difference in the variable, i.e., ${\Delta }^2{X}_t=\Delta X_t-\Delta X_{t-1}$. See Figure 1 for the meaning of the abbreviations for the variables, t-test values in the brackets.

.

From Table 5, we see significant short-run effects on Slovenian hospitality prices from hospitality prices in the rest of the Eurozone and Slovenian food and beverage prices, as well as food and beverage prices in the Eurozone from two months earlier. Food and beverage prices in the Eurozone impact Slovenian CPI and hospitality prices, while Slovenian food and beverage prices influence the Eurozone CPI. Hence Slovenian prices have a short-term impact on the rest of the Eurozone. This contrasts with the long- and medium-term effects, where Slovenia did not have a significant impact on the rest of the Eurozone, but rather, we observed effects from the Eurozone on Slovenia. There are thus significant short-term effects on prices in the rest of the Eurozone from the Slovenian restaurant industry. This may suggest a spillover effect of the Slovenian sector on the Eurozone, by Slovenian tourism demand having a cost-push effect on Eurozone prices.

5. Discussion

The study explores how using the I(2) cointegration framework can enhance the modelling of tourism prices and inflation dynamics between Slovenia and the broader Eurozone. By examining both long- and short-term relationships, it shows that the I(2) method effectively detects persistent deviations, spillover effects, and asymmetric adjustments across economies of different sizes and structures. This approach enables more precise identification of equilibrium relationships and short-term shocks that traditional I(1) methods might miss. As a result, the findings suggest that accounting for higher-order integration offers a better understanding of inflation transmission in tourism-dependent economies, directly addressing the research question and highlighting the relevance of the I(2) approach both methodologically and practically.

This study’s empirical findings offer fresh insights into the behaviour of tourism prices and inflation trends in Slovenia and the Eurozone, emphasising the significance of employing an I(2) cointegration framework. Although much of the existing tourism price research relies on I(1) methods, our results show that ignoring I(2) processes can conceal long-term equilibrium relationships and distort short-term spillover effects. The I(2) model effectively captures persistent deviations, shared trends, and seasonal shock interactions, providing a more comprehensive and dependable econometric foundation for assessing inflation risks in interconnected markets.

A key finding is the asymmetry between long-term and short-term impacts. Over the long run, Slovenian hospitality and input prices are primarily affected by Eurozone-wide shocks, reinforcing the significant influence of the larger integrated market. This supports the theoretical view that small, open economies adapt to macroeconomic conditions driven by their larger trading partners. Conversely, the short-term analysis shows that Slovenian prices have a tangible spillover effect on Eurozone consumer and hospitality prices. These results highlight the dual nature of small economies. Although they generally accept prices as given in the long run, they can temporarily induce shocks that spread through the regional system. In practice, price changes in Slovenian tourism sectors, particularly in food and beverages, can impact regional inflation, serving as a cost-push factor in both domestic and European markets.

This duality highlights the importance of differentiating between short-term and long-term effects when formulating policy. For Slovenian policymakers, the findings suggest that managing domestic tourism and hospitality prices cannot be performed in isolation from broader Eurozone conditions, as structural shocks from larger economies impact long-term price trends. Conversely, Slovenian authorities should also acknowledge that domestic tourism demand and pricing strategies can have a spillover effect, temporarily influencing Eurozone-wide inflation expectations. These results align with broader macroeconomic discussions about the relationship between small open economies and larger integrated systems, particularly within monetary unions where exchange rate adjustments are no longer possible.

The importance of this study extends beyond its methodological contributions. For Eastern European nations like Slovenia, empirical research on the factors influencing tourism prices remains scarce, despite the sector’s growing role in inflation patterns. The results presented here offer a valuable contribution, especially amid the 2022–2023 inflation spike, driven primarily by rising service and hospitality costs across Europe. By illustrating the link between tourism prices and overall price movements in the Eurozone, the study shows how cost increases in small, tourism-dependent economies can spread into broader inflation trends. Therefore, the I(2) framework enhances econometric analysis and provides a valuable basis for understanding recent inflation trends driven by the service sector.

In comparison to earlier research (Cró & Martins, 2024; Singh & Alam, 2024; Xie et al., 2025; Pérez-Rodríguez et al., 2024), this study presents several new contributions to the existing knowledge base. It is among the few empirical studies applying the I(2) cointegration model to tourism price trends, illustrating its usefulness for analysing higher-order integration in service sectors. Additionally, it emphasises the crucial role of food and beverage prices as channels transmitting inflationary pressures in tourism-reliant economies, thereby broadening the understanding of sector-specific price interactions. Furthermore, it adds to hospitality management and competitiveness research by demonstrating how price changes in small open economies can affect regional inflation trends. Overall, these findings combine methodological innovation with practical policy implications, offering fresh insights into price movements within integrated European markets.

Although the I(2) cointegration framework used in this study provides a strong foundation for analysing long- and short-term dynamics, several methodological extensions could further enhance future research. In particular, expanding the model to include tourism or consumer prices from other Mediterranean countries, such as Italy, Greece, or Spain, would enable a more accurate identification of regional spillover channels and could test whether the observed short-term causality from Slovenian to Eurozone food and beverage prices reflects a broader pattern in Southern Europe. Additionally, future work could analyse impulse–response functions within ±2 standard deviation bands and perform variance decomposition of residuals to assess the size and longevity of short-term shocks. Incorporating controls for wage dynamics could also improve the explanation of price adjustments, as labour costs influence both service inflation and tourism demand. Finally, sensitivity analyses with longer lag lengths or quarterly data could verify the stability of the VAR estimates and account for possible quadratic trends linked to seasonality in tourism prices (Lozano et al., 2021).

6. Conclusions

The study’s conclusions align with the empirical evidence from I(2) cointegration and VAR analysis, directly answering the main research question about the interaction between tourism prices and inflation in the Eurozone.

This study employs an I(2) cointegration framework to analyse the dynamics of tourism and inflation in Slovenia and the Eurozone. It shows that higher-order integration is crucial for capturing persistent deviations and complex price interactions. The findings indicate that, in the long run, Eurozone-wide shocks are dominant, but Slovenian hospitality and input prices have significant short-term spillover effects on regional inflation. Neglecting I(2) structures could lead to model misspecification and misinterpretation of these dynamics.

The contributions are threefold: scientifically, this study offers a rare empirical application of I(2) cointegration in tourism economics, combining methodological innovation with practical evidence; for policy, it emphasises food and beverage prices as channels for inflationary pressures, highlighting the need for coordinated Eurozone responses; and practically, it guides hospitality price management and competitiveness, showing that pricing strategies must consider domestic shocks and market integration.

This study’s main methodological contribution is in showing how the I(2) cointegration framework improves econometric analysis, especially in settings with persistent deviations and multiple stochastic trends. Unlike traditional I(1) models, the I(2) approach captures more complex nonstationarity and structural changes, leading to more accurate long-term equilibria and short-term adjustments in interconnected markets. This allows us to analyse long-run, medium-run, and short-term effects in the same model framework. We may also use the nominal data directly, rather than transforming these variables by deflating or detrending them, which is often performed in empirical analysis. Hence, all of the information in the data is contained within the empirical framework. By explicitly modelling higher-order integration and spillover effects, it enhances macroeconometric theory and extends the use of cointegration to price system analysis. This advancement not only enhances predictive accuracy but also bridges the gap between theoretical econometrics and practical policy analysis. The framework provided can be adopted by other small, open economies or sectors with complex price interactions, making the findings more broadly applicable and improving the understanding of dynamic relationships in tourism and inflation research. The robust checks further confirmed that minor deviations from normality and weak ARCH effects had no material impact on the validity or stability of the estimated relationships.

Future research should expand to comparative analysis with other small Eurozone economies, explicitly model structural breaks such as EU accession and the adoption of the euro, and incorporate recent shocks, including COVID-19 and the inflation surge of the 2020s.

Overall, the study emphasises the methodological and practical importance of I(2) cointegration for understanding tourism prices and inflation. By integrating theory, empirical findings, and policy implications, it reinforces the value of advanced macroeconometric models in explaining the dynamics of tourism-dependent economies within the monetary union.