Complexity-Aware Vector-Valued Machine Learning of State-Level Bond Returns: Evidence on South African Trade Spillovers Under SALT and OBBBA

Abstract

This study examines the impact of international trade shocks from South Africa and recent U.S. federal tax reforms on state-level municipal bond returns within the United States. Employing a unique transaction-level dataset comprising more than 50 million municipal bond trades from 2020 to 2024, the empirical approach integrates machine learning estimators with econometric volatility models to examine daily nonlinear spillovers and structural complexity across twenty U.S. states. The study introduces and extends the application of a vector radial basis function neural network framework, leveraging its universal approximation capacity to jointly model multiple state-level outcomes and uncover complex response patterns The empirical results reveal substantial cross-state heterogeneity in bond-return resilience, influenced by variation in state tax regimes, economic complexity, and differential exposure to external financial forces. States exhibiting higher economic adaptability demonstrate faster recovery and weaker shock amplification, whereas structurally rigid states experience persistent volatility and slower mean reversion. These findings demonstrate that complexity-aware predictive modeling, when combined with granular fiscal and trade-linkage data, provides valuable insight into the pathways through which global and domestic shocks propagate into U.S. municipal bond markets and shape subnational financial stability.

1. Introduction

A municipal bond (muni) is a debt security issued by a state, municipality, or county to finance public projects, such as schools or infrastructure, and offers tax-advantaged returns to investors. The 2025 One Big Beautiful Bill Act (OBBBA) significantly impacts the muni market by raising the state and local tax (SALT) deduction cap from $10,000 to $40,000, effective for tax years 2025 through 2029, before reverting to $10,000 in 2030. This change alters the federal deductibility of property taxes, especially benefiting high-revenue states, and creates an exogenous shift in state tax treatment and fiscal incentives following the expiration of the 2017 Tax Cuts and Jobs Act provisions. The increased SALT cap provides short-term relief to taxpayers in high-tax jurisdictions, potentially increasing investor demand and influencing municipal bond yields and credit conditions.

The OBBBA’s expansion of SALT deductibility provides a quasi-experimental setting for analyzing how federal tax changes affect fiscal capacity, investor demand, and municipal bond yields. Cross-sectional variation in post-reform tax treatment generates heterogeneity in after-tax incomes, property tax revenues, and credit conditions—key determinants of yield spreads and return dynamics (Schwert & Testa, 2020; Bartha et al., 2023). These variations support a robust empirical strategy for identifying the fiscal transmission of federal policy into municipal bond markets.

As fiscal systems become increasingly integrated with global capital and trade networks, external developments generate shocks that propagate through domestic credit markets via correlated risk premia, trade exposure, and shared investor bases (Simon, 1962). Policy shifts such as the expiration of the African Growth and Opportunity Act (AGOA) can influence U.S. municipal bond returns through macroeconomic linkages with South Africa (Lamprecht & Tolmay, 2017; Tadesse, 2024). Yet, empirical research on how global linkages shape state-level municipal bond performance under heterogeneous tax regimes remains limited.

This study develops an econometric framework to quantify the impact of international macro-financial linkages on U.S. municipal bond returns, incorporating state-level variation in SALT policy and underlying economic complexity. Drawing on the literature connecting production diversity to shock resilience (Ghosh et al., 2023; Hartmann et al., 2017; Hidalgo & Hausmann, 2009; Mealy et al., 2019; Pugliese et al., 2019; Vu, 2020), we integrate cross-country metrics of productive sophistication, including metals, manufacturing, and advanced export capacity. A more integrated approach to these structural dimensions enables a more precise evaluation of how the composition of production, particularly in sectors such as metals and mineral processing, oil and gas, and agriculture, influences the transmission of global economic shocks into U.S. subnational bond markets.

Recent advances in spillover modeling underscore the mutual dependence of returns, volatility, and macroeconomic conditions across financial markets, with shocks originating in one market often propagating to others through measurable spillover effects. Foundational econometric frameworks such as the ARCH model by Engle (1982), the GARCH extension by Bollerslev (1986), and the EGARCH specification by Nelson (1991) formalized the modeling of time-varying volatility and asymmetry in financial data, profoundly influencing modern financial econometrics. Later extensions, including the Diebold–Yilmaz framework (Diebold & Yilmaz, 2012), formalized the quantification of directional spillovers. Nonetheless, the inherent linearity of these models limits their ability to capture the nonlinear dependencies and structural complexities increasingly observable in global financial networks.

Contemporary research addresses these shortcomings by fusing traditional econometric techniques with machine learning methodologies. For example, new spillover models are being adapted to leverage deep learning architectures (Tang et al., 2024), and hybrid approaches, such as GARCH-based neural networks, have been recommended in the recent literature (Mohammed, 2024; Roszyk & Ślepaczuk, 2024; Y. Zhou & Yan, 2020). Empirical evidence now suggests that Gated Recurrent Unit (GRU) networks can outperform conventional Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) models in detecting early warning signals related to financial market spillovers (Del Nero & Giudici, 2025).

Despite these innovations, deep learning architectures often exhibit degraded performance when faced with structural breaks or limited data relative to complexity unless specifically augmented with localized feature engineering or hybrid noise filtering (Lemus, 2018; Li et al., 2025; Mahfooz et al., 2022; Naufal & Wibowo, 2023). In contrast, the robustness and predictive accuracy of radial basis function networks (RBFNs) in financial applications have been empirically documented by multiple researchers (Bayoumi et al., 1995; Buendía-Carrillo et al., 2025; Edwards, 2018; Poterba & Rueben, 2001). Furthermore, enhancements in RBFN variants have been shown to improve yield curve estimation and sharpen the identification of liquidity-driven volatility, thereby strengthening predictions and contagion analysis in interconnected financial settings (Benbya & McKelvey, 2006; Gu et al., 2020; Kelly et al., 2023). Support for the efficacy of shallow learning models is also evident in the work by H. Zhou et al. (2023), who demonstrate that RBFNs can outperform deep learning models in scenarios characterized by regime shifts or data scarcity. A schematic comparison of the RBFN and LSTM architectures is provided in Appendix A.

This study advances the literature by introducing a hybrid EGARCH and a Bayesian-enhanced regularized Vector Radial Basis Function Neural Network (VRBFN) framework. The EGARCH-VRBFN framework integrates econometric volatility modeling and machine learning to jointly estimate temporal volatility and nonlinear cross-state dependencies in municipal bond returns. Building on the foundations of traditional GARCH models, the proposed model captures high-dimensional and time-varying spillover effects that conventional approaches cannot fully represent (Dash et al., 2023; Prathiba et al., 2016).

The analysis draws on transaction-level data from the Municipal Securities Rulemaking Board (MSRB), comprising more than 50 million municipal bond trades across 48 U.S. states from 2020 to 2024. These data are aggregated to a daily frequency, yielding 1269 observations per state for 20 representative states to examine spillover behavior in municipal bond markets. The results reveal complex and nonlinear transmission dynamics between external financial shocks and domestic fiscal regimes. Building on these findings, the hybrid EGARCH VRBFN platform offers a unified and adaptive framework for quantifying volatility transmission and state-level financial interdependence. The key contributions of this paper are as follows:

• Methodological Contribution: This study advances hybrid spillover modeling by extending EGARCH–machine learning frameworks to a multi-target architecture. We integrate EGARCH volatility dynamics with the nonlinear cross-sectional predictive capabilities of the VRBFN, utilizing Haykin’s fixed-width kernel tuning (Haykin, 1994) to optimize learning and capture complex, asymmetric spillover effects across multiple financial series.
• Complexity-Aware Predictive Modeling: Our study develops a predictive framework for daily state-level municipal bond returns, where measures of Gaussian and SVM-based complexity take precedence in explaining how fiscal and financial structures influence market behavior. South African trade exposure, the U.S. tax structure, and a global commodity pricing proxy are additional factors that help reveal how complexity conditions the absorption and transmission of external shocks.
• Evaluation of State-level Resiliency: The study introduces a novel state-level resiliency score that measures each municipal bond market’s capacity to absorb and recover from internal disruptions and external shocks. This standardized metric enables a comparative analysis of fiscal stability and shock response across states, providing policymakers and investors with actionable insights.

The remainder of the paper is organized as follows. Figure 1 presents a roadmap of the research design, tracing the sequence from data collection and model construction to policy interpretation. Section 2 describes the data sources and variable definitions. Section 3 outlines the hybrid EGARCH–VRBFN modeling framework. Section 4 reports the model estimation results and performance evaluation. Section 5 discusses the policy implications for fiscal resilience and market stability in the post-reform U.S. municipal bond environment, and Section 6 provides a conclusion.

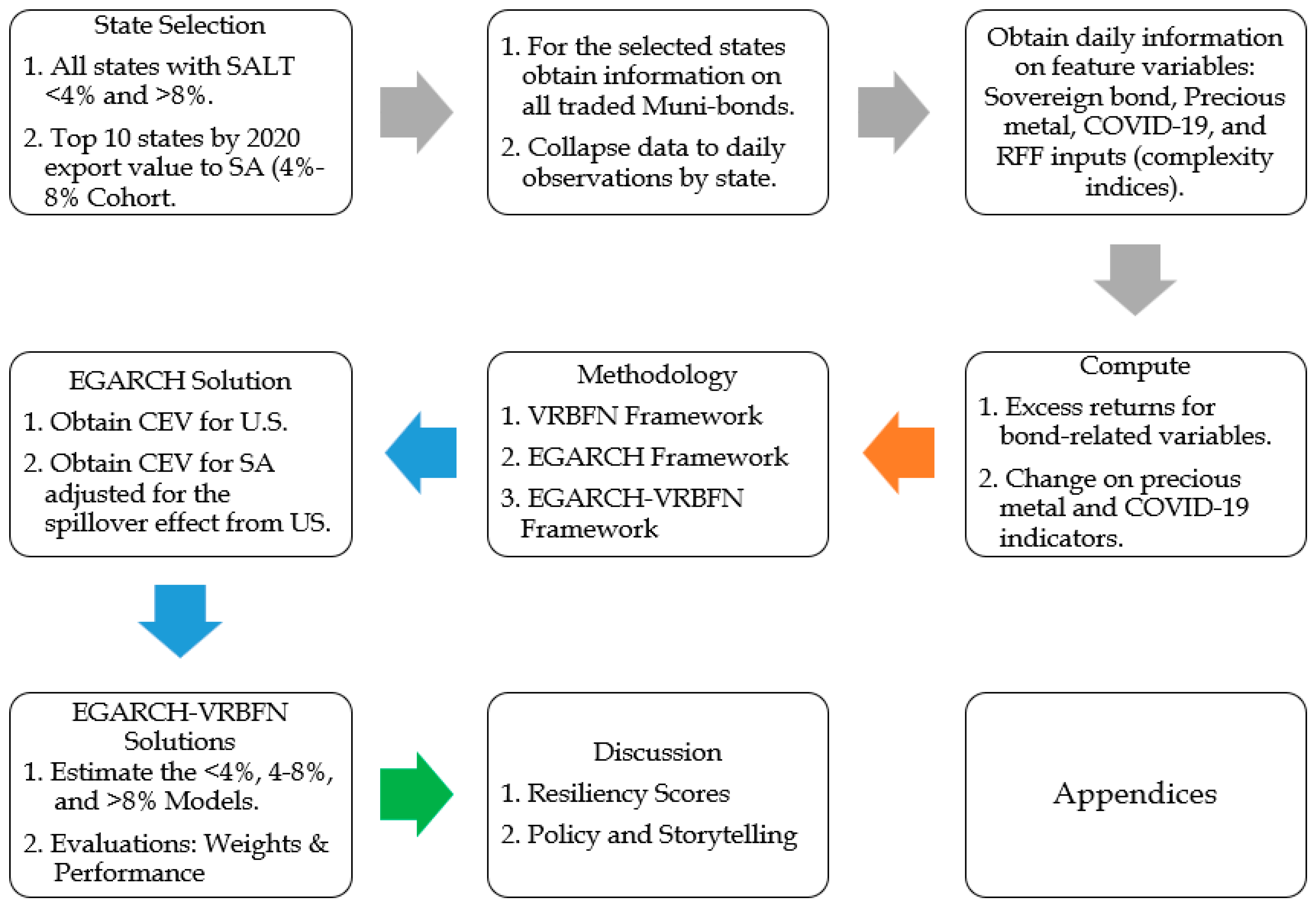
2. Data

2.1. TCJA and SALT State Selection

International trade and its interaction with the TCJA are crucial to the economies of most U.S. states. Following Sammartino et al. (2018) and Dash et al. (2023), states are classified into three SALT categories based on the TCJA’s impact: (1) six states with tax increases above 8%, (2) six states with increases below 4%, and (3) remaining states with increases between 4% and 8%. Excluding territories, this study’s sample includes the 12 states in the first two categories and the top 10 states with the highest dollar-reported 2020 exports to South Africa. Except for California and New York, which were already in the >8% category, the remaining exporting states fall within the 4–8% SALT range, yielding a final sample of 20 states for analysis (see Figure 2).

High-SALT states (>8%) are shown in dark green, concentrated along the East and West coasts. Medium-SALT states (4–8%) appear in medium green, primarily located in the Southern region. Low-SALT states (<4%) are shown in blue-green and are predominantly located in the northern U.S.

2.2. Data and Pricing of Municipal Bond Transactions

Building on the restricted sample period in Dash et al. (2023), the primary dataset comprises transaction-level records of municipal bond trades, sourced from the Municipal Securities Rulemaking Board (MSRB) trade tape, spanning January 2020 to December 2024. The sample includes 50,823,385 observations covering the forty-eight contiguous U.S. states and territories. For empirical estimation, the retained variables are defined as follows: trade size (par value exchanged), trade price (transaction price), yield to maturity (implied annualized return), coupon schedule (periodic interest payment structure), and issuing state (jurisdiction of origin). Standard data cleaning procedures are implemented to address outliers, missing values, and inconsistent entries before analysis.

To ensure data comparability across markets, the sample was refined using the following criteria: (i) inclusion of trades only from the 20 states identified in the SALT state selection process; (ii) retention of investment-grade bonds, based on the lower of the two ratings assigned by Moody’s Investor Service and Standard & Poor’s; and exclusion of (iii) bonds priced to put, (iv) taxable bonds, (v) zero-coupon bonds, (vi) pre-refunded issues, and (vii) bonds with a remaining maturity shorter than one year or longer than thirty years. To comply with provider confidentiality requirements, trades valued at US$1 million or more were standardized and recorded as transactions of US$1 million or more in value.

Following these filters, the final dataset comprises 21,338,423 intraday bond trades across the 20 selected states, forming a robust basis for modeling state-level return dynamics and volatility transmission. Figure 3 presents the distribution of municipal bond trades by credit rating across these states. The dotted line depicts the total number of COVID-19 cases reported by the Centers for Disease Control and Prevention (CDC) during the sample period, while green circles indicate the top ten exporting states to South Africa in 2020, as reported by the North American Industry Classification System (NAICS). Of these, California (CA) and New York (NY) are shown as dark green circles and belong to the >8% SALT category, whereas the remaining eight states fall within the 4–8% SALT category.

To address the pervasive illiquidity in the municipal bond market, which results in a limited number of trade observations for many securities, we follow previously cited literature (Dash et al., 2023) and treat bonds as homogeneous entities when constructing pooled statewide price measures. This treatment enables the aggregation of trade data to produce representative market prices at the state level. Furthermore, to account for interest rate sensitivity and potential heterogeneity in trading frequency, each transaction price is normalized by the bond’s reported duration, consistent with established procedures in the literature (see van Binbergen et al. (2025) for applications in the corporate bond market and Livingston & Zhou (2005) for duration-based predictive methodologies across varying yield environments). This normalization facilitates the comparison of bond prices across instruments and trading dates, ensuring that duration-driven price variation is explicitly modeled as part of the empirical analysis.

Specifically, the weighted average price of bond i in state k on day t is calculated as follows.

$${WgDPrice}_{k,i,t}=\left[{\displaystyle \frac{P_{i,t}\ast S_{i,t}}{D_{i,t}}}\right]÷1000$$

(1)

where P_i,t is the trade price for bond i on day t, D_i,t is the duration for bond i on day t, and S_i,t is the trade size of bond i on day t; S = 1 M for any trade size > 1 M.

Given that multiple bonds may be traded within a state on any given day, the average bond transaction price for state k on day t is calculated as follows,

$${WgDPrice}_{k,t}={\displaystyle \frac{1}{Q_{k,t}}}{\sum }_{i=1}^{Q_{k,t}}{WgDPrice}_{k,i,t}$$

(2)

In Equation (2) $Q_{k,t}$ is the number of traded bonds for a state (k) on a given day (t). For the period from 1 January 2020, through 31 December 2024, the pooling results in a sample size of 1269 daily observations across 20 states.

2.3. Global Financial and Macroeconomic Feature Variables

In recent years, rising global uncertainty—driven by financial crises, political polarization, trade conflicts, and the pandemic—has become a central economic concern. However, capturing and comparing uncertainty across time and countries remains challenging, as it reflects a complex and intangible mix of macroeconomic, firm-level, and geopolitical factors (Ahir et al., 2022). Our empirical framework incorporates a multidimensional set of indicators that capture both global and domestic forces influencing U.S. municipal bond returns. In this section, we focus on (i) sovereign bond indices, (ii) precious metals, and (iii) a COVID-19 indicator. Sovereign bond indices represent long-term interest rate dynamics and international capital flows, while precious metal ratios serve as a proxy for investor sentiment and macro-financial linkages. A COVID-19 severity index captures the evolving impact of health-related systemic shocks. Together, these variables provide a comprehensive foundation for assessing how external and domestic disturbances propagate through state-level fiscal and financial networks.

2.3.1. Sovereign Bond Indices

Long-term U.S. Treasury exposure is proxied by the iShares 20+ Year Treasury Bond ETF (TLT), which tracks U.S. government securities with maturities exceeding twenty years. South African sovereign exposure is captured via the 20-Year Bond Yield (20YrSA), as reported by Investing.com. For risk-free benchmarks, the analysis employs the PIMCO 25+ Year Zero Coupon U.S. Treasury Index ETF (ZROZ) and the South African 3-Month Bond Yield (3MthSA).

2.3.2. Precious Metal Indicators

Gold and platinum are pivotal to global and South African financial markets, with gold constituting a significant share of South Africa’s exports and platinum serving as a complementary benchmark. Previous studies link precious metal prices to macroeconomic, monetary, and equity variables (Batten et al., 2008; Dash et al., 2023; Erling, 2016; Vuyyuri & Mani, 2005). Recent research has highlighted asymmetric relationships and preference shocks among metals and financial assets (Huang & Kilic, 2019; Urom et al., 2019). Futures contract data for gold and platinum corresponding to the study period form the pricing ratio (GP) for estimation objectives. The ratio is employed as a proxy for investor sentiment, with gold typically outperforming platinum during periods of uncertainty.

2.3.3. COVID-19 Indicator

For the selected states in the study, the pandemic’s daily severity is captured by the ratio of new deaths to new confirmed cases as calculated by the World Health Organization (WHO) (Daily frequency reporting of new COVID-19 cases and deaths by date reported to WHO, 2024). This COVID-19 severity index provides a time-sensitive proxy for case fatality, facilitating daily alignment with market data during the study period.

2.4. Structural and Complexity Features

In machine learning prediction, data noise and model complexity are closely linked: noise often drives the need for complex architectures to capture hidden structure (Raubitzek & Neubauer, 2022). Rather than expanding feature sets or introducing artificial noise (Zheng et al., 2021), this study employs controlled model complexity with strong regularization to approximate the latent return-generating process and improve out-of-sample accuracy. Conceptually, complexity is treated as an epistemic strength rather than noise, consistent with the Virtue of Complexity (VoC) (Kelly et al., 2023), and the economic complexity framework proposed by Hidalgo and Hausmann (2009). Both perspectives emphasize systemic interdependence and emergent structure as essential to understanding real-world economic behavior.

In this study, we model these nonlinear dynamics by using Random Fourier Features (RFFs) to project high-dimensional interactions into a lower-dimensional representation (Rahimi & Recht, 2007). Gaussian-kernel RFFs capture cyclical and asymmetric fluctuations in local economic activity, approximating sectoral comovement structures (Hidalgo, 2023). These features also enable long-range extrapolation and support assessments of structural stability (Bahrami et al., 2022). In the South African context, we postulate that the SVM-kernel RFFs proxy provincial productive capabilities by capturing latent diversification capacity and embedded sectoral knowledge (Benbya & McKelvey, 2006). Unlike the Gaussian complexity measure, the SVM complexity index does not have a fixed directional interpretation (Haldane & May, 2011). Instead, it reflects the intensity of predictive nonlinearity: positive values indicate greater adaptive flexibility, while negative values signal increased structural fragility to South African market dynamics.

Together, the Gaussian and SVM RFFs yield a compact representation of the national economic structure. The Gaussian component models nonlinear dependencies embedded in municipal bond returns. In contrast, the SVM component captures structural rigidity and the persistence underlying societal and production dynamics typical of a developing economy. South Africa, widely recognized as a developing nation, boasts a highly diversified and industrialized economy, yet it remains challenged by persistent poverty, severe inequality, infrastructure constraints, and limited job creation.

For each period (t), we compute five Gaussian (RFF_G) and five SVM (RFF_SVM) Random Fourier features using Python 3.10 and the Rfflearn library. These features are averaged to construct two average composite complexity indices (see Equations (3) and (4)).

$${Complexity}_{G,t}={\displaystyle \frac{\sum _{i=1}^5{RFF}_{G,i}}{5}}$$

(3)

$${Complexity}_{SVM,t}={\displaystyle \frac{\sum _{i=1}^5{RFF}_{SVM,t}}{5}}$$

(4)

Following the methodology outlined by Gladston et al. (2022), we validate ${Complexity}_G$ as a proxy for U.S. macroeconomic dynamics and ${Complexity}_{SVM}$ as a proxy for South African dynamics. Regression benchmarking implementation details are provided in Appendix B.

2.5. Market and Commodity Returns

Traded bond prices are obtained from the MSRB trade tape. Subsequently, we transformed the raw prices using Equation (2). Excess daily returns for both target and feature variables are then computed. As shown in Equation (5), for each state k on day t, the excess return for each traded bond is calculated as the weighted bond price return minus the risk-free benchmark (ZROZ).

$$R_{k,t}=\left[{Ln(WgDPrice}_{k,t})-Ln\left({WgDPrice}_{k,t-1}\right)\right]-\left[{Ln(P}_{ZROZ,t})-Ln\left(P_{ZROZ,t-1}\right)\right]$$

(5)

U.S. and South African sovereign excess returns are defined analogously. For U.S. municipal bonds, the aggregate excess return shown in Equation (6) is computed as the difference between the iShares 20+ Year Treasury Bond ETF (TLT) and the PIMCO 25+ Year Zero Coupon U.S. Treasury Index ETF (ZROZ). The TLT fund tracks Treasuries with maturities over 20 years, resulting in a portfolio duration of roughly 17–18 years. ZROZ, composed of zero-coupon bonds and STRIPS, is selected for its pronounced rate sensitivity. For cross-border comparisons (Equation (7)), the excess return for South Africa is defined as the spread between the 20-year sovereign yield (20YrSA) and the 3-month sovereign yield (3MthSA).

$$R_{US,t}=\left[{Ln(P}_{TLT,t})-Ln\left(P_{TLT,t-1}\right)\right]-\left[{Ln(P}_{ZROZ,t})-Ln\left(P_{ZROZ,t-1}\right)\right]$$

(6)

$$R_{SA,t}=\left[{(r}_{20YrSA,t})-\left(r_{3MthSA,t}\right)\right]$$

(7)

Finally, the return for the GP ratio (a proxy for commodity) is computed as,

$$R_{GP,t}=\left[{Ln(GP}_t)-Ln\left({GP}_{t-1}\right)\right]$$

(8)

2.6. Average State Returns

We define $\overline{R}$, the trade-weighted average municipal bond return across states, partitioned by SALT category. The set of states is divided into three cohorts, $N_1$, $N_2$, and $N_3$, corresponding respectively to <4%, 4–8%, and >8% SALT classifications. For each $N_j$, the weighted average municipal bond return at time t, denoted ${\overline{R}}_{N_j,t}$, is computed as follows:

$${\overline{R}}_{N_j,t}={\sum }_{i\in N_j}\left({\displaystyle \frac{B_{i,t}}{{\sum }_{k\in N_j}{B}_{k,t}}}\right)R_{i,t},$$

(9)

where $R_{i,t}$, denotes the municipal bond return for state i at time t, $B_{i,t}$ represents the number of trades executed in state i at time t, and ${\sum }_{k\in N_j}{B}_{k,t}$ is the total number of trades across all states within the category $N_j$. Accordingly, ${\overline{R}}_{N_j,t}$ represents the trade-weighted average return for the SALT category $N_j.$ This weighting scheme ensures that states with a larger share of transactions contribute proportionally more to the aggregate return within their respective category. This approach enables the model to capture representative return dynamics within each state grouping while accounting for cross-sectional heterogeneity in trading intensity. Each SALT cohort is analyzed separately to isolate category-specific market behavior.

3. Methodology

In this section, we detail the modeling framework based on the VRBFN, EGARCH, and their hybrid extension, the VRBFN-EGARCH. We first outline recent VRBFN enhancements and describe the implementation approach used for multi-target financial prediction. The section concludes by stating the testable hypothesis guiding this empirical analysis.

3.1. The VRBFN Framework

Formally, a VRBFN expresses the input-output relationship as $Y=f\left(X\right)+\mathrm{є}$, where Y ∈ ℝⁿ represents the matrix of q target or output variables, X ∈ ℝⁿ is the matrix of p input features, and ε the disturbance term. Each hidden unit j = 1, …, m applies a radial basis activation σ(r), with the output computed as yₖ(x) = Σⱼ wⱼₖhⱼ(x), where hⱼ(x) = σ(||x − cⱼ||/rⱼ), cⱼ is the center, and rⱼ the width of neuron j. Figure 4 illustrates this three-layer VRBFN architecture.

3.1.1. Regularization and Width Specification

This study employs the VRBFN, an extension of the K4-RBFN framework originally introduced by Kajiji (2001) and implemented in WinORS-2023 (2023) The K4-RBFN advanced the classical RBFN of Broomhead and Lowe (1988) by incorporating linear optimization with Tikhonov regularization (Tikhonov & Arsenin, 1977), as proposed by Orr (1995). By adopting the Bayesian unbiased ridge estimator proposed by Crouse et al. (1995), the K4-RBFN eliminates the need for iterative tuning of the regularization parameter, thereby ensuring a global minimum of the mean squared error, improving computational efficiency in high-dimensional settings. The regularization parameter governs the balance between model complexity and empirical fit.

The VRBFN applies the same regularization principle to the multi-output setting. For each target output yₖ(x), the regularized cost function is defined as:

$$\frac{\mathrm{argmin}}{\omega }(\sum _{t=1}^T(y_t-f(x_t){)}^2+\sum _{j=1}^m{\omega }_j{x}_j^2)$$

(10)

where T is the number of observations, m is the number of hidden nodes, w is the weight vector, f(x_t) is the model’s prediction given w, and ω is the regularization parameter.

VRBFN’s solution generates a weight matrix: Ŵ = Inv(H’H + ΩI) H’Y, where H is the hidden-layer activation matrix, I is the identity matrix, and Ω is the vector of regularization parameters, ω, that control bias-variance trade-offs. The VRBFN preserves the universal approximation property of the single-target RBFN. Owing to its linear-in-parameters architecture, the VRBFN can approximate any continuous multivariate mapping $f:{\mathbb{R}}^n⟶{\mathbb{R}}^m$ to an arbitrary accuracy, given sufficient basis functions and appropriately estimated coefficients (León-Delgado et al., 2018; Wu et al., 2012).

Model calibration focuses on selecting hyperparameters that enhance the stability of estimation and generalization. Following Benoudjit and Verleysen (2003), improper width selection can materially reduce model performance. To address this, the constant width parameter is determined by implementing Haykin’s distance-based estimator: $r=d_{max}$/$\sqrt{2m}$, where dₘₐₓ is the maximum Euclidean distance between any two centers, c, and m is the number of hidden neurons (Haykin, 1994). This data-driven approach balances model smoothness to local variations, ensuring stable convergence and consistent predictive behavior across state-level bond return estimations.

3.1.2. Implementation

Because RBFNs compute activations using Euclidean distance, inputs were standardized to prevent scale dominance. The VRBFN was trained on partitioned data, with neuron centers initialized via regularized orthogonal least squares and widths refined using Haykin’s distance-based estimator. Gaussian activations were applied at hidden units, and output weights were estimated through closed-form Bayesian ridge regression. The generalized cross-validation (GCV) criterion with Tikhonov regularization replaced backpropagation to ensure global optimality and robustness (Bradshaw et al., 2023; Craven & Wahba, 1979; Poggio & Girosi, 1990; Tikhonov & Arsenin, 1977). Robustness was verified by comparing training and validation errors (Appendix C) and by cross-validation and sample-size perturbations, which confirmed the stability of model weights and spillover estimates (Zhang et al., 2024).

Model performance will be evaluated using three complementary criteria: mean squared error (MSE) to assess predictive accuracy, the Akaike information criterion (AIC) to balance goodness of fit and parsimony for cross-model comparison, and Wilks’ Lambda to quantify unexplained multivariate variation in target returns (Everitt & Dunn, 1991). Directional accuracy, as measured by the Modified Direction (M.Dir) metric, is defined as the sum of correctly predicted upward and downward movements minus one, averaged across targets in multi-output settings. Together, these metrics provide a comprehensive evaluation of predictive accuracy, stability, and explanatory power.

3.2. EGARCH Framework

Considering the EGARCH specification as a starting point, we construct our hybrid modeling approach as follows:

$$R_{US,t}=b_0+b_1{R}_{US,t-1}+{\epsilon }_{US,t},{\epsilon }_{US,t}~N\left(0,h_t\right),$$

(11)

where $R_{US,t}$ denotes the bond return at time t, $b_0$ is a constant, $b_1$ captures autoregressive dependence, and $h_t$ is the conditional variance.

The conditional variance dynamics follow an EGARCH(1,1) process:

$$ln\left(h_t\right)=\tau +\beta \left(h_{t-1}\right)+{\gamma }_{us}{\displaystyle \frac{{\epsilon }_{t-1}}{\sqrt{h_{t-1}}}}+\alpha \left(\left|{\displaystyle \frac{{\epsilon }_{t-1}}{\sqrt{h_{t-1}}}}\right|\right)-\mathsf{{\rm E}}\left(\left|{\displaystyle \frac{{\epsilon }_{t-1}}{\sqrt{h_{t-1}}}}\right|\right),$$

(12)

where τ is a constant, β captures persistence, ${\gamma }_{us}$ measures asymmetry in the response to shocks, and $\mathsf{\alpha }$ governs the magnitude effect. Unlike standard GARCH, the logarithmic form guarantees positivity of $h_t$ without imposing parameter restrictions. The model accommodates auto-regressive (AR) mean dynamics, GARCH-type volatility clustering, and asymmetry, allowing positive and negative shocks to predict differential responses of conditional volatility.

Recognizing the long-standing trade and investment linkages between the United States and South Africa, return and volatility spillovers are modeled using an AR(1)–EGARCH(1,1) specification to account for both persistence and asymmetric transmission effects. The conditional excess return for the South African 20-Year Bond Yield is given by Equation (13),

$$R_{SA,t}=b_0+b_1{R}_{SA,t-1}+b_2{R}_{US,t-1}+b_3{\sigma }_{US,t-1}^2+a_{SA,t}$$

(13)

where $R_{US,t-1}$ and ${\sigma }_{US,t-1}^2$ capture predictive spillover relationships from U.S. returns and volatility, and $a_{SA,t}={\sigma }_{SA,t}{\epsilon }_{SA,t}$.

The conditional variance for SA follows an EGARCH(1,1) process as shown in Equation (14).

$$\ln \left({\sigma }_{SA,t}^2\right)={\alpha }_{0,SA}+{\alpha }_{1,SA}{\displaystyle \frac{\left|a_{SA,t-1}\right|+{\gamma }_{SA}{a}_{SA,t-1}}{{\sigma }_{SA,t-1}}}+{\beta }_{SA}ln\left({\sigma }_{SA,t-1}^2\right).$$

(14)

Equation (14) allows volatility dynamics to respond asymmetrically to positive and negative shocks, while preserving stationarity and scale-invariance. Together, Equations (13) and (14) form a mean–variance system that links return dynamics with volatility spillovers.

3.3. EGARCH-VRBFN Framework

The hybrid EGARCH–VRBFN spillover models are stated in Equations (15)–(17). Equation (15) specifies the responsiveness of the state-level municipal bond returns in the <4% cohort at time t to changes in the feature variables. In comparison, Equations (16) and (17) were applied to the 4–8% and >8% cohorts using the same framework. After computing the lagged feature variables and the EGARCH spillover variables, the total number of observations for the analysis is T = 1267.

As a nonparametric mathematical inference method, the estimated weights of the shallow network, ($b_i$), are analogous to nonlinear least-squares regression parameters,

$$\begin{gathered} {\left(R_{1,t}\dots R_{N_1,t}\right)}^{<4\%}=b_1{\overline{R}}_{N_1,t-1}+b_2{R}_{US,t-1}+b_3{R}_{SA,t-1}+{b_{4}COVID}_{t-1}+ \\ {b_{5}GP}_{t-1}+b_6{\sigma }_{SA,t-1}^2+{b_{7}Complexity}_{G,t-1}+{b_{8}Complexity}_{SVM,t-1}+E_{N_1,t} \end{gathered}$$

(15)

$$\begin{gathered} {\left(R_{1,t}\dots R_{N_2,t}\right)}^{4\%-8\%}=b_1{\overline{R}}_{N_2,t-1}+b_2{R}_{US,t-1}+b_3{R}_{SA,t-1}+{b_{4}COVID}_{t-1}+ \\ {b_{5}GP}_{t-1}+b_6{\sigma }_{SA,t-1}^2+{b_{7}Complexity}_{G,t-1}+{b_{8}Complexity}_{SVM,t-1}+E_{N_2,t} \end{gathered}$$

(16)

$$\begin{gathered} {\left(R_{1,t}\dots R_{N_3,t}\right)}^{>8\%}=b_1{\overline{R}}_{N_3,t-1}+b_2{R}_{US,t-1}+b_3{R}_{SA,t-1}+{b_{4}COVID}_{t-1}+ \\ {b_{5}GP}_{t-1}+b_6{\sigma }_{SA,t-1}^2+{b_{7}Complexity}_{G,t-1}+{b_{8}Complexity}_{SVM,t-1}+E_{N_3,t} \end{gathered}$$

(17)

where $\overline{R}$ is as previously defined. Additionally, the predictive model system expresses the lagged effects for excess returns for the U.S. ($R_{US}$) and South Africa ($R_{SA}$), the COVID-19 severity index (COVID), the precious metals index (GP), and the EGARCH term measuring SA spillover idiosyncratic shock $\left({\sigma }_{SA,t-1}^2\right)$. Lastly, the model incorporates proxies for the VoC. The variables Complexity_G and Complexity_SVM are specified to capture the extent to which the system embraces uncertainty and diversity. Due to the multiple target specification of the model, the error matrices $E_{N_1}$, $E_{N_2}$, and $E_{N_3}$ are dimensioned $T\times N_1$, $T\times N_2$, and $T\times N_3$, respectively.

3.4. Study Hypotheses

Grounded in this conceptual and empirical framework, we formally test four hypotheses, categorized as External spillover channels (H₁ and H₂) and Domestic fiscal asymmetries (H₃ and H₄):

H₁. 

Trade Spillover Hypothesis: States with greater exposure to South African long-term yields and yield volatility exhibit lower resilience in municipal bond returns, indicating stronger transmission of external trade-linked shocks into state-level borrowing costs.

H₂. 

Commodity Contagion Hypothesis: Shocks to U.S. state municipal bond returns are transmitted through South African commodity spillovers, proxied by changes in the gold–platinum price ratio, with lower-resilience states exhibiting stronger transmission effects.

H₃. 

Tax Asymmetry Hypothesis: High-SALT states exhibit greater sensitivity of municipal bond returns to long-term U.S. Treasury excess returns, unless institutional employment density or financial sector income smoothing offsets these effects.

H₄. 

Complexity Hypothesis: Municipal bond markets in states with higher Gaussian Complexity exhibit stronger resilience to South African shock transmission, while states with lower (or negative) SVM Complexity display greater vulnerability and more persistent return distortions.

These hypotheses encompass both international and domestic transmission mechanisms, aiming to identify the key structural features that govern state-level resilience in the U.S. municipal bond market.

4. Empirical Results

4.1. EGARCH Model Results

The EGARCH(1,1) analysis was conducted in SAS-V9.4 (2013). Before solving Equations (13) and (14), the variables $R_{US}$ and $R_{SA}$ were tested for stationarity using the Augmented Dickey–Fuller (ADF) test. For both variables, we reject the null hypothesis of a unit root (i.e., for $R_{US}$ τ = 36.67; and for $R_{SA}$ τ = 59.87) at the 95% level and conclude that the series are stationary.

Table 1. EGARCH Results for the South African Daily Excess Yields.

Parameter Estimates
Variable	DF	Estimate	Standard Error	t Value	Approx Pr > |t|
Intercept ($b_0$)	1	−0.0046	0.0023	−1.99	0.0460
USAEGCev ($b_3$)	1	205.5383	78.8551	2.61	0.0091
EARCH0 (${\alpha }_{0,SA}$)	1	−3.7188	0.0420	−88.64	0.0001
EARCH1 $({\alpha }_{1,SA}$)	1	1.4696	0.0391	37.59	0.0001
EGARCH1 ${(\beta }_{SA}$)	1	0.0738	0.0061	12.07	0.0001
THETA (${\gamma }_{SA}$)	1	−0.3233	0.0154	−20.99	0.0001

presents the results of the EGARCH(1,1) analysis. The results indicate that all parameter estimates are significant at the 95% level.

The constant term in the mean equation (−0.0046) is slightly negative, indicating a minimal drift component in the return series. The covariate coefficient (205.5383) suggests that U.S. conditional volatility (USAEGCev) exerts a strong positive influence on South African bond returns, with a one-unit increase associated with an approximate 205-unit rise. In the variance equation, the negative constant (EARCH0 = −3.7188) aligns with the EGARCH specification, which models conditional variance in a logarithmic form. The persistence coefficient (EGARCH1 = 0.0738) confirms volatility clustering, while the magnitude of the combined coefficients implies sustained shock persistence. The leverage parameter (THETA = −0.3233) indicates asymmetric effects, whereby negative shocks increase volatility more sharply than positive shocks.

4.2. EGARCH-VRBFN Model Performance

Across all SALT categories, four performance metrics are reported: MSE, AIC, Wilks’ Lambda, and the average Modified Direction (M.Dir). MSE values remained below 0.0018 across cohorts, differing by only 0.0016, reflecting high predictive precision. The <4% cohort produced the weakest fit (AIC = −7946.00; MSE = 0.00185; Wilks’ Λ = 0.0001; F(48, 1243) = 258,367.67; p < 0.001) relative to the 4–8% (AIC = −10,757.47; MSE = 0.00020; Wilks’ Λ = 0.0001; F(64, 1234) = 192,522.42; p < 0.001) and >8% (AIC = −10,462.17; MSE = 0.00025; Wilks’ Λ = 0.0001; F(48, 1243) = 258,367.67; p < 0.001) cohorts. Despite minor differences in fit quality, overall performance remained robust. The average M.Dir exceeded 97% across all groups, confirming strong directional accuracy and validating the model’s reliability in capturing state-level return dynamics.

4.3. EGARCH-VRBFN Feature Weights and Network Map

Estimated weights (W) derived from the EGARCH–VRBFN model capture the directional spillover dynamics within the U.S. municipal bond market.

Table A2. VRBFN Weights for Each State by Cohort.

Cohort	State	Intercept	Lagged States $\left(\overline{\mathit{R}}\right)$	Lagged USA $\left({\mathit{R}}_{\mathit{U}\mathit{S}}\right)$	Lagged SA $\left({\mathit{R}}_{\mathit{S}\mathit{A}}\right)$	Lagged COVID $\left(\mathit{C}\mathit{o}\mathit{v}\mathit{i}\mathit{d}\right)$	Lagged GP $\left(\mathit{G}\mathit{P}\right)$	Lagged SA Vol $\left({\mathit{\sigma }}_{\mathit{S}\mathit{A}}^2\right)$	Gaussian Complexity (ComplexityG)	SVM Complexity (ComplexitySVM)
Less than 4%	AK	−0.0437	−0.2314	−0.2829	−0.0467	0.3632	−0.1404	0.0239	−0.1588	−0.1571
	IN	0.1198	−0.0519	−0.0138	0.0429	0.0286	−0.0373	0.0951	−0.0761	−0.0753
	ND	−0.0021	−0.2707	−0.1716	0.1593	0.5819	−0.2140	0.1257	−0.3397	−0.2551
	SD	−0.0721	−0.1720	−0.2878	0.1296	0.1304	−0.1961	−0.1576	−0.0351	−0.1448
	WV	0.1139	0.0122	0.0257	0.1460	0.0721	−0.0488	0.0422	−0.0449	0.0632
	WY	0.1781	−0.2386	−0.1752	0.2731	0.1797	−0.1355	−0.0241	−0.1775	−0.0398
	Avg.	0.0490	−0.1587	−0.1509	0.1174	0.2260	−0.1287	0.0175	−0.1387	−0.1015
	AIC = −7946.00		Errors: Training = 0.0007; Validation = 0.0012; MSE = 0.0019					M. Dir = 97.4% r = 1.54; 40% Training
4 to 8%	AL	0.0044	0.0541	0.0258	0.0436	−0.0378	0.0549	0.0093	0.0184	0.0078
	GA	−0.0659	−0.0442	−0.0567	−0.0118	−0.1204	−0.0309	−0.1068	−0.0953	−0.0337
	IL	−0.0193	0.0059	−0.0169	0.0220	−0.0633	−0.0380	−0.0027	0.0237	−0.0350
	MI	−0.0938	−0.0979	−0.1050	−0.0693	−0.0846	−0.0591	−0.0859	−0.0455	−0.1085
	OK	−0.0819	−0.1498	−0.1785	−0.1379	−0.0788	−0.1197	−0.1381	−0.0848	−0.1894
	SC	−0.0471	−0.1080	−0.1045	−0.0703	−0.0093	−0.0664	−0.0520	0.0055	−0.0941
	TN	−0.0276	−0.0776	−0.0720	−0.0241	−0.0962	−0.0467	−0.0861	−0.0688	−0.0425
	TX	0.0030	−0.0305	−0.0551	−0.0177	−0.0843	−0.0459	−0.0754	−0.0412	−0.0524
	Avg.	−0.0410	−0.0560	−0.0704	−0.0332	−0.0718	−0.0440	−0.0672	−0.0360	−0.0685
	AIC = −10757.47		Errors: Training = 0.0002; Validation = 0.0003; MSE = 0.0002					M. Dir = 98.4% r = 1.15; 60% Training
Greater than 8%	CA	0.0821	−0.0528	0.0416	0.0013	−0.1672	0.0474	−0.1154	0.0209	0.0054
	CT	0.0480	−0.0937	−0.2031	0.0948	0.0379	−0.1349	−0.2081	0.1103	−0.1227
	DC	0.1523	0.0655	−0.0296	0.1317	0.0584	0.0459	−0.0893	0.3947	−0.0143
	MD	−0.0706	0.0716	0.0324	0.0213	−0.0803	0.1277	0.1067	0.0926	−0.1094
	NJ	0.0292	−0.1193	−0.0474	0.0167	0.0132	−0.1779	−0.1246	0.2476	−0.1234
	NY	−0.1569	−0.1507	−0.0718	−0.0718	−0.1131	−0.0884	−0.0691	0.0526	−0.0965
	Avg.	0.0140	−0.0466	−0.0463	0.0323	−0.0419	−0.0300	−0.0833	0.1532	−0.0768
	AIC = −10462.17		Errors: Training = 0.0002; Validation = 0.0003; MSE = 0.0003					M. Dir = 98.3% r = 1.17; 70% Training

The performance measures—AIC, Errors (Training, Validation, and MSE), and M. Dir (Modified Direction)—are reported as averages. The width parameter r is computed by Haykin’s method. The training size was determined through simulation.

(Appendix D) reports feature weights by SALT category (<4%, 4–8%, >8%), where positive coefficients denote direct transmission effects and negative coefficients indicate inverse relationships. Figure A2, Figure A3 and Figure A4 visualize these feature interactions and directional linkages, with green representing positive and red indicating negative spillovers.

Table 2. VRBFN signed weights of the top 10 states with the highest number of trades (Rank Muni) against the export rank position (Trade Rank).

States	Intercept	Lagged States	Lagged USA	Lagged SA	Lagged COVID	Lagged GP	Lagged SA Vol	Gaussian Complexity	SVM Complexity	Rank Muni Trades	Trade Rank	Cohort
CA	+	–	+	+	–	+	–	+	+	1	4	>8%
NY	−	−	−	−	−	−	−	+	−	2	7	>8%
TX	+	−	−	−	−	−	−	−	−	3	1	4%–8%
NJ	+	−	−	+	+	−	−	+	−	4	>10	>8%
IL	−	+	−	+	−	−	−	−	−	5	2	4%–8%
MI	−	−	−	−	−	−	−	−	−	6	6	4%–8%
GA	−	−	−	−	−	−	−	−	−	7	9	4%–8%
MD	−	+	+	+	−	+	+	+	−	8	>10	>8%
CT	+	−	−	+	+	−	−	+	−	9	>10	>8%
IN	+	−	−	+	+	−	+	−	−	10	>10	<4%

summarizes the results as a heatmap of the ten states with the highest municipal trading volumes. Notably, five of the six states in the >8% SALT cohort appear among the most active trading jurisdictions, reflecting their elevated market depth. Within this group, New York and New Jersey exhibit predominantly negative weights, whereas Maryland, Connecticut, and California display mixed positive and negative linkages. By contrast, the 4–8% SALT cohort shows predominantly negative coefficients, suggesting lower resilience and stronger inverse responses to external shocks.

5. Discussion

Municipal bond market resilience—defined as the capacity to absorb and recover from external shocks—is quantified by aggregating VRBFN-derived weights across nine dimensions (Table 2) to generate a composite state-level resilience score. Figure 5 displays normalized scores ranging from −1 (most vulnerable) to +1 (most resilient), indicating that eight of the twenty states exhibit measurable resilience. The distribution reveals four regimes: High-Resilience (DC, WV), Transitional (MD–WY), Low-Resilience (NJ–MI), and Structurally Fragile (AK, NY, SD, OK). High-resilience states demonstrate strong fiscal adaptability, whereas structurally fragile economies exhibit policy rigidities and narrow production bases that amplify their exposure to external shocks. Each of these resiliency groups is discussed in Section 5.1, Section 5.2, Section 5.3 and Section 5.4 below. As shown in Appendix E, our results align with and extend the complexity-based fragility dynamics documented in Li et al. (2025) and Mena (2022).

5.1. High-Resilience States (Resilience ≥ 0.40)

The high-resilience cohort comprises the District of Columbia (DC) and West Virginia (WV), two jurisdictions that differ markedly in their tax structures and industrial compositions, yet share a strong capacity to absorb external shocks. DC maintains a high SALT share (>8%) and a service-oriented, institutionally dense economy, while WV operates with a narrower tax base (<4%) centered on resource-linked production. Their joint placement in this cohort suggests that resilience depends less on tax base size or diversification and more on how states mediate external financial signals through institutional and sectoral channels.

For DC, resilience is anchored in institutional adaptability and network density. Its strong positive association with Lagged SA (0.1317) reflects its role as a hub of policy coordination and global governance (Hidalgo, 2023; Mealy et al., 2019). A high Gaussian complexity score (0.3947) supports this interpretation, indicating dense inter-organizational linkages that facilitate rapid adjustment to global shifts. The modest positive effect of Lagged States (0.0655) implies limited regional spillovers. At the same time, the negative coefficients on Lagged USA (−0.0296) and Lagged SA Vol (−0.0893) suggest insulation from national safe-asset cycles but sensitivity to disruptions in international policy or financial stability (Bayoumi et al., 1995; Kelly et al., 2023).

In contrast, WV’s resilience stems from sectoral specialization rather than institutional adaptability. Its strong sensitivity to Lagged SA (0.1460) underscores commodity-based linkages, particularly in metallurgical coal and platinum-group metals (Bao, 2020). The positive coefficient on Lagged USA (0.0257) suggests partial support from shifts in U.S. Treasury asset demand, while the positive coefficient on Lagged SA Vol (0.0422) indicates resilience to global price fluctuations. Conversely, the negative GP coefficient (−0.0488) signals vulnerability to downturns in global manufacturing demand. WV’s mixed complexity scores (Gaussian = −0.0449; SVM = 0.0632) suggest that local bond market resilience weakens with U.S.-based structural complexity but improves when South African complexity factors are taken into account.

Together, DC and WV exemplify two distinct pathways of resilience. As pathways, institutional coordination and trade specialization demonstrate how state-level resilience emerges from adaptive mechanisms that mediate and transmit global economic signals.

H₁ and H₂ are not strongly supported, as these states absorb South African shocks without sustained deterioration in bond returns; H₄, with DC’s high Gaussian complexity and WV’s adaptive SA-linked structure, reinforces resilience; H₃ is not supported, since neither state exhibits the high-SALT revenue sensitivity associated with procyclical fiscal stress.

5.2. Moderate-Resilience States (0.40 > Resilience ≥ −0.20)

The moderate-resilience cohort comprises Maryland (MD), Alabama (AL), Indiana (IN), Illinois (IL), California (CA), and Wyoming (WY). The cohort records resilience scores ranging from 0.19 to −0.16. Although grouped within a similar resilience band, these states differ markedly in industrial composition, exposure to global commodity chains, and fiscal stabilization capacity. Consequently, their responses to external shocks, particularly those transmitted through South African sovereign yields, volatility cycles, and industrial metal pricing, reflect distinct adjustment mechanisms rather than a uniform resilience profile.

A consistent feature across this group is the positive coefficient on Lagged SA, indicating that movements in South African long-term yields function as external financial signals influencing state-level credit conditions. The magnitude aligns with the sectoral structure: Alabama (0.0436) and Indiana (0.0429) display the strongest responsiveness due to their automotive and advanced materials industries, which heavily depend on platinum-linked inputs (MacDonald et al., 2025). Maryland (0.0213) and Illinois (0.0220) exhibit weaker sensitivity, consistent with diversified service-based economies. In contrast, California’s near-zero coefficient (0.0013) suggests internal absorption within a broad production base. Wyoming (0.2731) exhibits the most significant dependence, reflecting an extractive economy that is highly exposed to global commodity cycles.

Volatility transmission, captured by Lagged SA Vol, further differentiates adjustment patterns. Maryland (0.1067) and Indiana (0.0951) show positive volatility transmission, indicating that external uncertainty prompts reallocative rather than contractionary responses—consistent with dynamic adjustment in capital and supply networks (Bollerslev, 1986). Alabama’s near-zero effect (0.0093) suggests stability in continuous-process sectors, while Illinois (−0.0027), California (−0.1154), and Wyoming (−0.0241) exhibit contractionary responses consistent with investment pullbacks during global uncertainty (Bastourre et al., 2010; Deng et al., 2023).

Differences in Lagged GP distinguish financial safe-haven shifts from industrial demand cycles. Maryland, Alabama, and California exhibit positive coefficients, indicating that rising gold-to-platinum ratios are associated with portfolio adjustments rather than real-sector slowdowns. In contrast, Indiana, Illinois, and Wyoming exhibit negative coefficients, indicating that flight-to-safety episodes narrow margins in metals-linked industries (Chen & Mo, 2025; Huang & Kilic, 2019; Lahiani et al., 2021; Urom et al., 2019).

Domestic comovement reinforces these distinctions. Maryland and Alabama have positive Lagged States coefficients, consistent with integrated fiscal systems and diversified capital flows, while Indiana, California, and Wyoming exhibit negative comovement, signaling higher sensitivity to liquidity tightening elsewhere in the U.S. The negative Lagged USA coefficients in Indiana, Illinois, and Wyoming indicate crowding-out effects as capital shifts toward U.S. Treasuries during flight-to-safety periods, especially from agricultural states (Oppedahl, 2017; Rey, 2013).

Complexity scores reveal differences in bond market resilience across the moderate-resilience cohort. West Virginia shows mixed results (Gaussian = −0.0449; SVM = 0.0632), with resilience improving under South African complexity but weakening with U.S. structural complexity. Maryland benefits from increasing U.S. complexity, while higher South African complexity dampens returns. Alabama’s near-zero scores indicate indifference to both domestic and external factors. Indiana and Wyoming exhibit negative values, reflecting structural rigidity, whereas California and Illinois show diversified but uneven adaptability.

Overall, moderate resilience arises not solely from diversification but from the interaction of sectoral specialization, commodity exposure, and fiscal capacity to absorb macroeconomic shocks.

H₁ and H₂ are partially supported, with measurable but not uniformly contractionary responses; H₄ results are mixed, depending on whether Gaussian complexity outweighs negative SVM rigidity. Support for H₃ is also mixed. It is supported for CA and MD, and weakly supported for the other states in this group.

5.3. Low-Resilience States (−0.20 > Resilience ≥ −0.60)

This cohort includes New Jersey (NJ), North Dakota (ND), Texas (TX), Connecticut (CT), Tennessee (TN), South Carolina (SC), Georgia (GA), and Michigan (MI). These states exhibit consistently negative resilience scores (−0.29 to −0.61), indicating limited adaptive capacity to shocks linked to South African sovereign yields, commodity cycles, and global financial volatility. Their economic structures are characterized by concentrated production bases, path-dependent industrial specialization, and constrained fiscal buffers that limit their ability to absorb shocks transmitted through trade and financial channels.

Negative weights on Lagged States and Lagged USA confirm that national financial tightening amplifies local municipal bond stress. Connecticut (−0.2031), North Dakota (−0.1716), and South Carolina (−0.1045) exhibit a flight-to-safety dynamic, where reallocations toward U.S. Treasuries lead to reduced local liquidity and fiscal capacity (Abrahams et al., 2022; Rey, 2013).

Lagged SA coefficients identify distinct exposure channels. North Dakota (0.1593) exhibits sensitivity through its global commodity markets, which are tied to oil and mineral extraction (Abrahams et al., 2022). Connecticut (0.0948) reflects a financial intermediation channel driven by insurance and wealth management portfolio rebalancing in response to South African yield differentials and bond-price volatility (Abrahams et al., 2022; Stulz, 2005). Tennessee, South Carolina, Georgia, and Michigan exhibit weaker or negative responses (−0.0177 to 0.0693), consistent with manufacturing-intensive economies, where capital rigidity and supply-chain configurations slow down adjustments (Hausmann & Hidalgo, 2011).

Volatility transmission also varies. CT, GA, TN, and MI exhibit negative spillover effects from Lagged SA Vol, indicating that external bond market uncertainty depresses state-level returns. ND (0.1257) shows the opposite pattern, where volatility of fixed-income assets in SA triggers positive changes in local bond returns.

Negative Lagged GP coefficients (ND: −0.2140; CT: −0.1349; MI: −0.0591) indicate contractionary effects from increases in the gold-to-platinum ratio. These effects reflect declining industrial margins in platinum-linked manufacturing and reduced reinvestment capacity across Midwestern and Southern industrial corridors, amplifying fiscal stress (Lahiani et al., 2021; MacDonald et al., 2025).

Complexity weights reinforce structural rigidity. Gaussian complexity is modestly positive in NJ (0.2476) and CT (0.1103), but SVM complexity is negative across all states, with particularly low adaptability in MI (−0.1085) and SC (−0.0941), indicating limited capacity for endogenous structural reconfiguration (Martin & Sunley, 2006). Financial rigidity from the improvement of the South African debt market is particularly felt in NJ and CT (Adesina, 2025).

Overall, vulnerability in this cohort stems from constrained flexibility in reallocating production, capital, and fiscal resources. These structural limitations heighten exposure to global trade and SA yield volatility and increase the persistence of downside risk in state municipal bond markets.

This group supports H₁, H₂, and H₄, with strong transmission of South African yield and commodity shocks, and consistently negative SVM complexity, indicating structural rigidity. H₃ is strongly supported for NJ and CT, where high-SALT exposure amplifies procyclical revenue stress. Support is weaker for the remaining states, primarily due to narrower tax bases and shallower fiscal buffers.

5.4. Structurally Fragile States (Resilience Score < −0.60)

The lowest resilience cohort, comprising Alaska (AK), New York (NY), South Dakota (SD), and Oklahoma (OK), records resilience scores between −0.67 and −1.16, indicating structural fragility rather than cyclical weakness. These states exhibit consistent directional responses to external shocks, reflecting path-dependent economic systems in which production structures, fiscal anchors, and market linkages amplify rather than absorb disturbances (Martin & Sunley, 2006).

A defining feature is the strong negative response to national macro financial conditions (Lagged USA). Alaska (−0.2829), South Dakota (−0.2878), and Oklahoma (−0.1785) experience amplified downturns during U.S. contractions, owing to their narrow specialization in extractive and large-scale agricultural sectors that remain highly sensitive to global commodity cycles (Kilian, 2009; Oppedahl, 2017; Rickman & Wang, 2020). New York (−0.0718) also exhibits a negative coefficient, transmitted primarily through financial channels, as liquidity and risk repricing directly influence employment and revenue in creative class and finance-intensive service industries (Florida, 2014). SALT-related tax exposure reinforces systemic fragility in this group.

Differences emerge in exposure to South African yields (Lagged SA). South Dakota (0.1296) co-moves with global industrial and storage-related commodity demand, while Oklahoma (−0.1379) and Alaska (−0.0467) exhibit contractionary responses consistent with tighter global discount rates that deter long-horizon energy and extraction investment (Kilian, 2009; Rickman & Wang, 2020). New York’s (−0.0718) response reflects financial risk transmission rather than commodity exposure (Florida, 2014).

Volatility transmission further reinforces state-level credit market fragility. South Dakota (−0.1576), Oklahoma (−0.1381), and New York (−0.0691) exhibit negative responses to rising South African sovereign volatility, indicating cross-market contagion (Diebold & Yılmaz, 2014). Alaska’s slight positive (0.0239) suggests a limited direct financial linkage, although it remains exposed through commodity price channels.

Uniformly negative Gold–Platinum (GP) coefficients (−0.0884 to −0.1961) indicate heightened sensitivity to declines in global precious metal demand, as platinum-linked components are embedded in machinery, refining, and heavy manufacturing (Chen & Mo, 2025; MacDonald et al., 2025).

Complexity indicators corroborate these structural weaknesses: both Gaussian and SVM complexity values are negative across Oklahoma, South Dakota, and Alaska, exhibiting the weakest capacity for structural reconfiguration. In New York, a positive Gaussian complexity (0.0526) and an inverse SVM complexity (−0.0965) indicate limited adaptive flexibility in response to the improving South African fiscal consolidation efforts on debt (Adesina, 2025; Kelly et al., 2023; Martin & Sunley, 2006).

Taken together, these states are not only exposed to external shocks but structurally positioned to amplify them. Narrow industrial specialization, limited diversification pathways, and low adaptive capacity generate persistent vulnerability that extends beyond the shock period, weakening fiscal and market resilience.

H₁, H₂, and H₄ are strongly supported, with pronounced shock amplification and almost uniformly negative Gaussian and SVM complexity, indicating systemic fragility. H₃ is strongly supported for NY, where high SALT exposure compounds fiscal stress. Support for the H₃ is consistent in AK, SD, and OK based on their SALT grouping.

6. Conclusions

This study demonstrates that U.S. state-level municipal bond returns exhibit heterogeneous sensitivities to global financial spillovers, domestic tax asymmetries, and underlying economic complexity. External shocks, including those originating from SA sovereign yields and commodity price volatility, interact with local fiscal architecture and industrial composition, ultimately shaping the cross-sectional distribution of return resilience and fragility. States characterized by higher economic complexity and institutional adaptability (e.g., DC, WV) exhibit greater resistance to both international and domestic shocks. In contrast, states with narrow sectoral specialization (e.g., AK, NY, SD, OK) tend to amplify and propagate volatility. The proposed hybrid EGARCH VRBFN framework integrates econometric and machine learning techniques to accommodate these nonlinear dependencies, yielding stable and interpretable predictions that remain stable under regime shifts. Gaussian complexity is identified as a salient indicator of adaptive fiscal capacity, whereas negative SVM complexity signals structural rigidity and heightened systemic vulnerability. Tax asymmetry further conditions these dynamics, with particularly pronounced effects in high SALT states, where institutional and sectoral structures drive divergent outcome patterns.

Future research should extend this framework to support more robust causal inference and enhanced model interpretability, incorporating higher-frequency data and cross-country comparisons. Including ESG factors, climate-related variables, and biodiversity dimensions may further strengthen the analysis of structural resilience and credit risk in subnational markets. In aggregate, these results underscore the crucial role of fiscal and structural complexity in mediating the transmission of global shocks into subnational bond markets, and support the case for adopting a complexity-oriented approach in machine learning within financial econometrics.