Robust Learning of Tail Dependence

Abstract

Accurate estimation of tail dependence is difficult due to model misspecification and data contamination. This paper introduces a class of minimum f-divergence estimators for the tail dependence coefficient that unifies robust estimation with extreme value theory. I establish strong consistency and derive the semiparametric efficiency bound for estimating extremal dependence, the extremal Cramér–Rao bound. I show that the estimator achieves this bound if and only if the second derivative of its generating function at unity equals one, formally characterizing the trade-off between robustness and asymptotic efficiency. An empirical application to systemic risk in the US banking sector shows that the robust Hellinger estimator provides stability during crises, while the efficient maximum likelihood estimator offers precision during normal periods.

1. Introduction

The probability of joint extreme events determines the stability of modern economic systems. Examples include the simultaneous collapse of major financial institutions, catastrophic weather disrupting global supply chains, or systemic failures in insurance networks (Embrechts et al., 2012). The tail dependence coefficient $\chi$ measures the limiting probability that one variable exceeds a high threshold given that another does. This coefficient serves as a fundamental metric for co-movement in the tails of distributions (Coles et al., 2001). Estimating $\chi$ relies on parametric copula models estimated via maximum likelihood (MLE) (Joe, 1997). MLE is asymptotically efficient when the model is perfectly specified, but it is sensitive to model misspecification and data contamination (Huber, 1964). This sensitivity can be problematic for extremal dependence. Tails of distributions are, by definition, data-scarce. A slight misspecification can distort the estimated tail structure. The result is often an underestimation of systemic risk.

Robust statistics, pioneered by Huber (1964) and Hampel et al. (1986), provides a framework for developing estimators that balance efficiency with resistance to deviations from model assumptions. Within this tradition, the theory of minimum divergence estimation (Basu et al., 1998; Beran, 1977) and information-theoretic measures (Csiszár, 1967) generalize MLE. By minimizing divergence between a nonparametric density estimate and a parametric model, these estimators deliver robust inference. However, applying and analyzing this robust paradigm in extreme value theory (EVT) remains underdeveloped. This paper fills a gap: the absence of robust parametric estimators for tail dependence within EVT that maintain a theoretical foundation while providing practical robustness.

Multivariate EVT focuses on dependence in the tails, characterized by $\chi$ or the spectral measure (J. H. J. Einmahl et al., 2001). Standard estimation methods use parametric copula models fitted via MLE or semiparametric approaches estimating the Pickands dependence function (Pickands, 1989). While Embrechts et al. (2012) and Cooley et al. (2019) have discussed model uncertainty in extremal settings, the literature offers few robust alternatives to MLE for parametric tail dependence estimation. Existing robust methods in extremal settings either address different problems or lack the theoretical foundation for tail dependence estimation. Copula M-estimators (Klar et al., 2000) provide robustness for central dependence but lack theoretical results for tail behavior. Robust Bayesian approaches to EVT (Cabras et al., 2015) primarily focus on univariate extremes or rely on computationally intensive Markov Chain Monte Carlo methods, without establishing semiparametric efficiency bounds for dependence parameters. Neither approach provides a unified framework for balancing robustness and asymptotic efficiency in tail dependence estimation.

The sensitivity of classical methods, such as MLE, led to the development of robust statistics. The influence function, introduced by Hampel et al. (1986), provides a tool to assess an estimator’s local robustness. The minimum distance estimation framework, including the minimum Hellinger distance estimator of Beran (1977) and the broader class of density power divergence estimators of (Basu et al., 1998), offers global robustness. These methods trade some efficiency for greater stability under contamination or misspecification. This paper continues this tradition and extends it to extremes. The class of f-divergences, which includes Kullback–Leibler, Hellinger, and ${\chi }^2$ divergences, provides a family of measures to quantify discrepancy between probability distributions (Csiszár, 1967). Each divergence represents a different trade-off between efficiency and robustness. The minimum f-divergence estimator framework generalizes MLE and other minimum distance estimators into a single, flexible family. While these fields are mature in their own right, their integration is novel.

This paper develops a class of minimum f-divergence estimators (MFDEs) for the tail dependence coefficient, establishing strong consistency under standard regularity conditions. The primary contribution is the derivation of an extremal Cramér–Rao bound (ECRB), which establishes the semiparametric efficiency limit for estimating $\chi$ when the body of the distribution is treated as a nuisance parameter. A central result shows that an MFDE achieves the ECRB if and only if the second derivative of its generating function at unity equals one, providing a sharp criterion to classify f-divergences by asymptotic efficiency. This theorem characterizes the trade-off between robustness and asymptotic efficiency: efficient estimators are non-robust, while robust estimators pay an efficiency price, doubling the asymptotic variance relative to the ECRB.

Monte Carlo simulations and application to systemic risk among major US banks demonstrate the implications of this trade-off. The empirical analysis shows substantial differences in risk capital calculations across estimators, with potential differences reaching economically significant levels of portfolio value at the institutional level. The ECRB derivation provides an extremal analogue to classical results in robust statistics (Basu et al., 1998; Beran, 1977), while addressing the unique semiparametric challenges of EVT. For policymakers and risk managers, these results replace ad hoc estimator selection with efficient MLE under trusted models, rather than robust alternatives during structural breaks, with explicitly quantified costs of robustness.

The remainder of this paper is organized as follows. Section 2 introduces the minimum f-divergence estimator and establishes its strong consistency. Section 3 defines the semiparametric model, derives the extremal Cramér–Rao bound, and presents the necessary and sufficient condition for an MFDE to achieve this bound. Section 4 provides an empirical application and shows how the choice of divergence impacts risk measures and capital requirements. Section 5 concludes.

2. The Minimum f-Divergence Estimator

Let $(\Omega ,\mathcal{F},\mathbb{P})$ be a probability space supporting a sequence of independent and identically distributed random vectors ${\left\{(X_i^{*},Y_i^{*})\right\}}_{i=1}^n$ with joint distribution function G and copula $C_{{\mathit{\theta }}_0}$, where ${\mathit{\theta }}_0\in \Theta \subset {\mathbb{R}}^d$ denotes the true parameter vector. To analyze extremal dependence, we transform the observations to standard Fréchet marginal distributions. In practice, the marginal distribution functions $F_X$ and $F_Y$ are unknown and are estimated using the empirical distribution functions ${\widehat{F}}_X$ and ${\widehat{F}}_Y$. The transformed observations are defined as

$${\widehat{X}}_i=-{\displaystyle \frac{1}{log{\widehat{F}}_X\left(X_i^{*}\right)}},{\widehat{Y}}_i=-{\displaystyle \frac{1}{log{\widehat{F}}_Y\left(Y_i^{*}\right)}},$$

for $i=1,\dots ,n$. Henceforth, the sample ${\left\{(X_i,Y_i)\right\}}_{i=1}^n$ and the density estimator ${\widehat{g}}_n$ are understood to be based on these transformed observations. We assume the error from marginal estimation is asymptotically negligible for the estimation of ${\mathit{\theta }}_0$; a standard condition ensuring this is provided in Assumption 1 (A8).

Definition 1. 

The tail dependence coefficient χ is defined as the limiting probability

$$\chi =\underset{u\to 1^{-}}{lim}\mathbb{P}\left(F_Y\left(Y\right)>u\mid F_X\left(X\right)>u\right),$$

(1)

where $F_X$ and $F_Y$ are the marginal distribution functions of X and Y. For the Gumbel copula model with parameter θ, this takes the specific form

$$\chi \left(\theta \right)=2-2^{1/\theta }.$$

(2)

This coefficient measures the strength of extremal dependence, with $\chi =0$ indicating asymptotic independence and $\chi >0$ indicating asymptotic dependence in the upper tail. This definition follows the standard treatment in extreme value theory and copula modeling (Coles et al., 2001; Joe, 1997).

Definition 2. 

Let $f:(0,\infty )\to \mathbb{R}$ be a strictly convex function, twice continuously differentiable in a neighborhood of 1, with $f\left(1\right)=0$. For any probability densities g and $p_{\mathit{\theta }}$ with respect to Lebesgue measure λ, the f-divergence between g and $p_{\mathit{\theta }}$ is defined as

$${\mathcal{D}}_f(g;p_{\mathit{\theta }})={\int }_{{\mathbb{R}}^2}f\left({\displaystyle \frac{g(x,y)}{p(x,y;\mathit{\theta })}}\right)p(x,y;\mathit{\theta })d\lambda (x,y),$$

(3)

with $0f(0/0)=0$ and $0f(a/0)=a{lim}_{t\to \infty }f\left(t\right)/t$ for $a>0$. These boundary conventions ensure the divergence is properly defined when the density ratio is zero or infinite, following the standard measure-theoretic treatment of f-divergences (Csiszár, 1967). The first convention handles the case where both densities vanish, while the second ensures the divergence remains finite when the model density vanishes but the true density does not.

Definition 3. 

Let ${\widehat{g}}_n$ be a nonparametric density estimator based on the sample ${\left\{(X_i,Y_i)\right\}}_{i=1}^n$. The minimum f-divergence estimator ${\widehat{\mathit{\theta }}}_n$ is defined as

$${\widehat{\mathit{\theta }}}_n=arg\underset{\mathit{\theta }\in \Theta }{min}{\mathcal{D}}_f({\widehat{g}}_n;p_{\mathit{\theta }}).$$

(4)

The corresponding estimator of the tail dependence coefficient is given by ${\widehat{\chi }}_n=\chi \left({\widehat{\mathit{\theta }}}_n\right)$. This framework extends the minimum distance estimation approach of Beran (1977) and the robust divergence estimation of Basu et al. (1998) to extremal dependence settings.

Strong consistency of the minimum f-divergence estimator can be established under the following regularity conditions.

Assumption 1. 

The following conditions hold:

(A1) 

The function f is strictly convex, twice continuously differentiable in a neighborhood of 1, and satisfies $f\left(1\right)=0$.

(A2) 

The parameter space Θ is a compact subset of ${\mathbb{R}}^d$.

(A3) 

The model family $\left\{f\right(·;\mathit{\theta }):\mathit{\theta }\in \Theta \}$ is identifiable, $f(x,y;{\mathit{\theta }}_1)=f(x,y;{\mathit{\theta }}_2)$λ-a.e. implies ${\mathit{\theta }}_1={\mathit{\theta }}_2$.

(A4) 

The mapping $\mathit{\theta }\mapsto f(x,y;\mathit{\theta })$ is continuous for λ-almost every $(x,y)$.

(A5) 

The nonparametric density estimator satisfies ${\parallel {\widehat{g}}_n-g\parallel }_{\infty }\stackrel{a.s.}{\to }0$.

(A6) 

The model densities are uniformly bounded: there exist constants $0<c<C<\infty$ such that $c\le f(x,y;\mathit{\theta })\le C$ for all $\mathit{\theta }\in \Theta$ and λ-almost every $(x,y)$ in the support of g.

(A7) 

The divergence functional $\mathit{\theta }\mapsto {\mathcal{D}}_f(g;f_{\mathit{\theta }})$ has a unique minimizer at ${\mathit{\theta }}_0$.

(A8) 

The marginal distribution functions are estimated such that ${\parallel {\widehat{F}}_X-F_X\parallel }_{\infty }\stackrel{a.s.}{\to }0$ and ${\parallel {\widehat{F}}_Y-F_Y\parallel }_{\infty }\stackrel{a.s.}{\to }0$.

Theorem 1. 

Under Assumption 1, the minimum f-divergence estimator is strongly consistent,

$${\widehat{\mathit{\theta }}}_n\stackrel{a.s.}{\to }{\mathit{\theta }}_{0}asn\to \infty .$$

Proof. 

Define the empirical and population objective functions

$$Q_n\left(\mathit{\theta }\right)={\mathcal{D}}_f({\widehat{g}}_n;f_{\mathit{\theta }}),Q\left(\mathit{\theta }\right)={\mathcal{D}}_f(g;f_{\mathit{\theta }}).$$

I first show that ${sup}_{\mathit{\theta }\in \Theta }|Q_n\left(\mathit{\theta }\right)-Q\left(\mathit{\theta }\right)|\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$. Consider the difference

$$|Q_n\left(\mathit{\theta }\right)-Q\left(\mathit{\theta }\right)|=\left|\int f\left({\displaystyle \frac{{\widehat{g}}_n}{f_{\mathit{\theta }}}}\right)f_{\mathit{\theta }}d\lambda -\int f\left({\displaystyle \frac{g}{f_{\mathit{\theta }}}}\right)f_{\mathit{\theta }}d\lambda \right|.$$

By the mean value theorem, for any $x,y$, there exists a value $\tilde{g}$ between ${\widehat{g}}_n(x,y)$ and $g(x,y)$ such that

$$f\left({\displaystyle \frac{{\widehat{g}}_n}{f_{\mathit{\theta }}}}\right)-f\left({\displaystyle \frac{g}{f_{\mathit{\theta }}}}\right)=f^{\prime }\left({\displaystyle \frac{\tilde{g}}{f_{\mathit{\theta }}}}\right){\displaystyle \frac{{\widehat{g}}_n-g}{f_{\mathit{\theta }}}}.$$

By Assumption 1 (A6), the ratio $\tilde{g}/f_{\mathit{\theta }}$ is contained within a compact interval $K\subset (0,\infty )$ for all sufficiently large n, almost surely. Since $f^{\prime }$ is continuous on a neighborhood of 1 and K is compact, $f^{\prime }$ is bounded on K, i.e., $\left|f^{\prime }\left(t\right)\right|\le B$ for all $t\in K$ and some constant $B<\infty$. Therefore,

$$\left|f\left({\displaystyle \frac{{\widehat{g}}_n}{f_{\mathit{\theta }}}}\right)-f\left({\displaystyle \frac{g}{f_{\mathit{\theta }}}}\right)\right|\le B·{\displaystyle \frac{|{\widehat{g}}_n-g|}{f_{\mathit{\theta }}}}.$$

Multiplying both sides by $f_{\mathit{\theta }}$ and integrating yields

$$\begin{array}{cc}\hfill |Q_n\left(\mathit{\theta }\right)-Q\left(\mathit{\theta }\right)|& \le \int \left|f\left({\displaystyle \frac{{\widehat{g}}_n}{f_{\mathit{\theta }}}}\right)-f\left({\displaystyle \frac{g}{f_{\mathit{\theta }}}}\right)\right|f_{\mathit{\theta }}d\lambda \hfill \\ & \le B\int |{\widehat{g}}_n-g|d\lambda \hfill \\ & \le B·\lambda \left(\mathrm{supp}\left(g\right)\right)·{\parallel {\widehat{g}}_n-g\parallel }_{\infty }.\hfill \end{array}$$

This final bound is independent of $\mathit{\theta }$ and, by Assumption 1 (A5), converges almost surely to zero. Thus, ${sup}_{\mathit{\theta }\in \Theta }|Q_n\left(\mathit{\theta }\right)-Q\left(\mathit{\theta }\right)|\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$. The population objective function $\mathit{\theta }\mapsto Q\left(\mathit{\theta }\right)$ is continuous by Assumption 1 (A4) and (A6), which allow the application of the dominated convergence theorem. It has a unique minimum at ${\mathit{\theta }}_0$ by Assumption 1 (A7). The parameter space $\Theta$ is compact by Assumption 1 (A2). The functions $Q_n(·)$ and $Q(·)$ are continuous. By van der Vaart (1998, Theorem 5.7), the minimizer of $Q_n(·)$ converges almost surely to the minimizer of $Q(·)$

$${\widehat{\mathit{\theta }}}_n=arg\underset{\mathit{\theta }\in \Theta }{min}{Q}_n\left(\mathit{\theta }\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }arg\underset{\mathit{\theta }\in \Theta }{min}Q\left(\mathit{\theta }\right)={\mathit{\theta }}_0.$$

□

Example 1. 

The minimum f-divergence framework encompasses several important estimators, each corresponding to a specific choice of the convex function f. For Kullback–Leibler (KL) divergence, $f\left(u\right)=ulogu-u+1$, which yields $f^{″}\left(1\right)=1$:

$${\mathcal{D}}_{KL}(g;f_{\mathit{\theta }})=\int g(x,y)log\left({\displaystyle \frac{g(x,y)}{f(x,y;\mathit{\theta })}}\right)d\lambda (x,y).$$

This defines the maximum likelihood estimator, which is efficient but non-robust. For Hellinger distance, $f\left(u\right)={(\sqrt{u}-1)}^2$, which yields $f^{″}\left(1\right)=1/2$:

$${\mathcal{D}}_H(g;f_{\mathit{\theta }})=\int {\left(\sqrt{g(x,y)}-\sqrt{f(x,y;\mathit{\theta })}\right)}^{2}d\lambda (x,y).$$

This defines a robust estimator whose asymptotic variance is twice the ECRB. For ${\chi }^2$-divergence, $f\left(u\right)={(u-1)}^2$, which yields $f^{″}\left(1\right)=2$:

$${\mathcal{D}}_{{\chi }^2}(g;f_{\mathit{\theta }})=\int {\displaystyle \frac{{(g(x,y)-f(x,y;\mathit{\theta }))}^2}{f(x,y;\mathit{\theta })}}d\lambda (x,y).$$

Each choice of f embodies a different trade-off between efficiency and robustness, allowing practitioners to select the divergence measure most appropriate for their specific application context. The value of $f^{″}\left(1\right)$ precisely determines where an estimator lies on this spectrum.

Table 1. Comparison of f-divergence measures for tail dependence estimation.

Divergence	$\mathit{f}\left(\mathit{u}\right)$	${\mathit{f}}^{\mathbf{″}}\left(1\right)$	Relative Efficiency
Kullback–Leibler	$ulogu-u+1$	1	1
Hellinger distance	${(\sqrt{u}-1)}^2$	$0.5$	$0.5$
${\chi }^2$-divergence	${(u-1)}^2$	2	2

provides a comparison of the three f-divergences discussed in Example 1. The relative efficiency, derived from Theorem 4, quantifies the variance inflation factor relative to the efficient MLE. The Kullback–Leibler divergence $f^{″}\left(1\right)=1$ achieves the ECRB and represents the efficient benchmark. The Hellinger distance $f^{″}\left(1\right)=0.5$ incurs a 100% variance penalty in exchange for robustness, while the ${\chi }^2$-divergence $f^{″}\left(1\right)=2$ appears to offer super-efficiency but is highly non-robust in practice. This classification provides practitioners with a clear framework for selecting divergence measures based on their preferred point along the robustness-efficiency frontier.

In finance, non-robust estimation of $\chi$ can underestimate the probability of joint extreme events, such as the simultaneous crash of multiple assets or the failure of correlated financial institutions. This misestimation contributed to the 2008 financial crisis, when the perceived safety of diversified portfolios disappeared as tail dependencies revealed themselves. A robust estimator, such as the minimum Hellinger distance estimator in our proposed class, is less affected by small departures from the assumed copula model in the main part of the distribution.

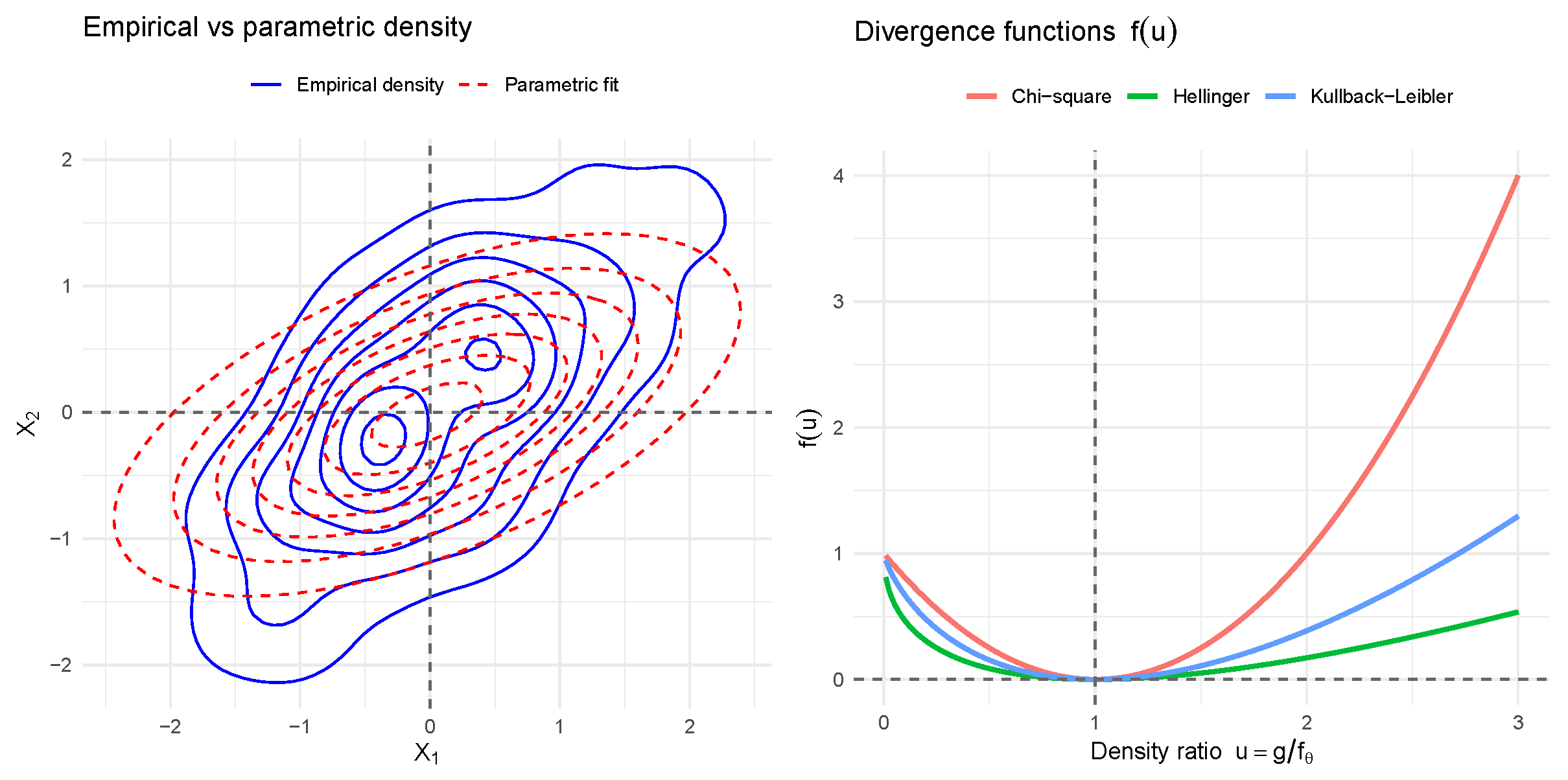
Figure 1 illustrates the principle of the minimum f-divergence estimator. The left panel contrasts the empirical joint distribution, estimated nonparametrically from simulated bivariate data, with the parametric fit. The discrepancies motivate a divergence-based criterion for estimation. The right panel shows the shapes of three popular f-divergences. KL divergence heavily weights underestimated probability mass, offering efficiency under correct specification but sensitivity to misspecification. Hellinger distance penalizes deviations smoothly, providing robustness to contamination and outliers. The ${\chi }^2$ divergence penalizes overestimation, reflecting a different robustness-efficiency trade-off. These panels illustrate how the choice of f guides the MFDE in balancing fidelity to data with resilience to model misspecification.

Integrating robust minimum divergence estimation with statistical modeling of extreme values addresses limitations of traditional MLE found in prior research. When models are stable and confidence is high, an efficient MLE based on the KL divergence remains suitable. For novel financial instruments, emerging climate patterns, or situations with data contamination or model misspecification, robust alternatives, such as the Hellinger distance, help mitigate the risk of underestimation. These choices affect policy formulation and risk management. COVID-19 shows the consequences of underestimating systemic and extremal dependence. The proposed framework improves estimation robustness to lower the risk of such failures.

3. The Extremal Cramér–Rao Bound and Semiparametric Efficiency

A key question is: what is the best asymptotic performance for any regular estimator of the tail dependence coefficient within a semiparametric model? This model accounts for our lack of knowledge about the exact distribution outside the tail region and treats it as an infinite-dimensional nuisance parameter. Semiparametric efficiency theory, as established by Bickel et al. (1993) and van der Vaart (1998), addresses this question by deriving a lower bound for the asymptotic variance. This section establishes such a bound and describes the conditions under which estimators in the minimum f-divergence class attain it.

3.1. Semiparametric Models and Regular Estimators

Let $\mathcal{G}$ be the set of all bivariate density functions with standard Fréchet margins. The semiparametric model $\mathcal{P}$ is defined as

$$\mathcal{P}=\{P_{\mathit{\theta },g}:\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d,g\in \mathcal{G}\mathrm{with}\mathrm{tail}\mathrm{copula}{C}_{\mathit{\theta }}\},$$

(5)

where $\mathit{\theta }$ is the finite-dimensional parameter for the extremal dependence structure, and g is an infinite-dimensional nuisance parameter for the unknown joint density. The tail copula $C_{\mathit{\theta }}$ is defined through the limiting dependence structure of the joint tail. For a bivariate distribution with copula C, the tail copula is given by the limit

$$C_{\mathit{\theta }}(u,v)=\underset{t\to \infty }{lim}t\left[1-C\left(1-{\displaystyle \frac{u}{t}},1-{\displaystyle \frac{v}{t}}\right)\right],u,v\ge 0,$$

(6)

whenever this limit exists (de Haan & Ferreira, 2006). This captures the extremal dependence structure and is parametrized by $\mathit{\theta }$. For the Gumbel copula used in our empirical application, the tail copula takes the specific form

$$C_{\theta }(u,v)=u+v-{\left(u^{\theta }+v^{\theta }\right)}^{1/\theta },$$

(7)

which characterizes the dependence in the joint upper tail (Gumbel, 1960). The model is semiparametric because it makes assumptions only on the tail structure through the parametric copula $C_{\mathit{\theta }}$, while leaving the bulk of the distribution g unrestricted except for the domain of attraction condition.

Let $\chi \left(\mathit{\theta }\right)$ be the functional mapping the copula parameter to the tail dependence coefficient. A sequence of estimators $\left\{{\widehat{\chi }}_n\right\}$ is a measurable function of the data. Following Hájek (1970) and Bickel et al. (1993), we require our estimators to be regular.

Definition 4. 

An estimator ${\widehat{\chi }}_n$ for $\chi \left({\mathit{\theta }}_0\right)$ is regular at $P_{{\mathit{\theta }}_0,g_0}$ if, for submodel $t\mapsto P_{{\mathit{\theta }}_t,g_t}$ that is differentiable in quadratic mean with score function h and satisfies $\sqrt{n}({\mathit{\theta }}_t-{\mathit{\theta }}_0)\to h$, the limiting distribution of $\sqrt{n}({\widehat{\chi }}_n-\chi \left({\mathit{\theta }}_t\right))$ under $P_{{\mathit{\theta }}_t,g_t}$ matches that of $\sqrt{n}({\widehat{\chi }}_n-\chi \left({\mathit{\theta }}_0\right))$ under $P_{{\mathit{\theta }}_0,g_0}$. This concept of regularity ensures the estimator’s limiting distribution is invariant to local perturbations of the nuisance parameter, following Le Cam (1972).

Regularity ensures the estimator’s asymptotic behavior remains stable under local perturbations of the nuisance parameter. This stability guarantees that confidence intervals maintain their coverage probability across different data-generating processes consistent with the tail model. Non-regular estimators can exhibit pathological behavior, such as their limiting distribution depending on the specific local alternative, making them unreliable for inference. The efficient influence function is the unique influence function in the closed linear span of the tangent set and defines the best achievable asymptotic variance.

Definition 5. 

Let $\mathcal{P}$ be a semiparametric model. The tangent set ${\dot{\mathcal{P}}}_P$ at $P\in \mathcal{P}$ is the set of all score functions h for which there exists a differentiable path $t\mapsto P_t\in \mathcal{P}$ with $P_0=P$ and score h at $t=0$. The tangent space ${\overline{\dot{\mathcal{P}}}}_P$ is the closure of the linear span of ${\dot{\mathcal{P}}}_P$ in $L^2\left(P\right)$. This geometric approach to semiparametric efficiency follows Bickel et al. (1993) and Tsiatis (2006).

For $\mathcal{P}$, the tangent space can be decomposed. The score function for the parametric component is ${\dot{\ell }}_{{\mathit{\theta }}_0}$. The tangent space for the nonparametric nuisance component ${\mathcal{T}}_g$ is the $\overline{\mathrm{span}}$ of all scores for paths that vary g while keeping the tail parameter ${\mathit{\theta }}_0$ fixed. An insight, following from the theory of local asymptotic normality and the structure of bivariate extreme value distributions (J. H. J. Einmahl et al., 2001), is that these spaces are orthogonal under the true distribution $P_{{\mathit{\theta }}_0,g_0}$.

Lemma 1. 

Under $P_{{\mathit{\theta }}_0,g_0}$, the parametric score ${\dot{\ell }}_{{\mathit{\theta }}_0}$ is orthogonal to the nuisance tangent space ${\mathcal{T}}_g$: ${\mathbb{E}}_{P_0}\left[{\dot{\ell }}_{{\mathit{\theta }}_0}{h}_g\right]=0$ for all $h_g\in {\mathcal{T}}_g$.

Proof. 

Let $\left\{P_t\right\}$ be a path in $\mathcal{G}$ with $P_0=P_{{\mathit{\theta }}_0,g_0}$, score $h_g={\displaystyle \frac{d}{dt}}logd{P}_t{|}_{t=0}\in {\mathcal{T}}_g$, and preserved tail copula $C_{P_t}=C_{{\mathit{\theta }}_0}$. The constraint $C_{P_t}=C_{{\mathit{\theta }}_0}$ implies the spectral measure H is constant along $\left\{P_t\right\}$. Consequently, the path $\left\{P_t\right\}$ provides no information to distinguish ${\mathit{\theta }}_0$, so the Fisher information is block diagonal. Thus, the off-diagonal term vanishes,

$${\mathbb{E}}_{P_0}\left[{\dot{\ell }}_{{\mathit{\theta }}_0}{h}_g\right]=0.$$

□

This orthogonality implies that the nuisance parameter g does not impede the estimation of ${\mathit{\theta }}_0$ asymptotically; no regular estimator can achieve a lower asymptotic variance for $\mathit{\theta }$ than if g were known. This result has a practical implication: it justifies focusing on parametric efficiency for the tail index, as the uncertainty from the bulk of the distribution is asymptotically irrelevant for tail estimation. The object that characterizes the best possible asymptotic variance can be defined as follows.

Definition 6. 

The efficient influence function (EIF) for the functional χ at $P_{{\mathit{\theta }}_0,g_0}$, denoted ${\psi }_{{\mathit{\theta }}_0,\chi }^{*}$, is the unique function in the tangent space ${\overline{\dot{\mathcal{P}}}}_{P_0}$ satisfying

$${\mathbb{E}}_{P_0}\left[{\psi }_{{\mathit{\theta }}_0,\chi }^{*}h\right]={\displaystyle \frac{d}{dt}}\chi \left(P_t\right){|}_{t=0}$$

(8)

for every differentiable submodel $t\mapsto P_t\in \mathcal{P}$ with score function h at $t=0$. The EIF provides the optimal estimating function and characterizes the semiparametric efficiency bound (Newey, 1994).

For a differentiable parameter $\chi \left(\mathit{\theta }\right)$, the pathwise derivative is ${\displaystyle \frac{d}{dt}}\chi \left(P_t\right){|}_{t=0}={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }\dot{\mathit{\theta }}$, where $\dot{\mathit{\theta }}$ is the derivative of the parametric part of the path. The EIF provides the linear approximation to the estimator and its variance gives the efficiency bound.

Assumption 2. 

The following conditions hold:

(B1) 

The parameter space Θ is an open subset of ${\mathbb{R}}^d$.

(B2) 

The functional $\mathit{\theta }\mapsto \chi \left(\mathit{\theta }\right)$ is continuously differentiable on Θ.

(B3) 

The copula model is differentiable in quadratic mean at ${\mathit{\theta }}_0$ with non-singular Fisher information matrix $I\left({\mathit{\theta }}_0\right)={\mathbb{E}}_{P_0}\left[{\dot{\ell }}_{{\mathit{\theta }}_0}{\dot{\ell }}_{{\mathit{\theta }}_0}^{\top }\right]\succ 0$.

(B4) 

The set of influence functions for regular estimators of χ is non-empty.

The fundamental limit of estimation accuracy in the proposed semiparametric model is detailed in the following theorem.

Theorem 2. 

Under Assumption 2 and given the orthogonality in Lemma 1, the semiparametric efficiency bound for estimating the tail dependence coefficient χ in the model $\mathcal{P}$ is given by

$$\mathcal{V}\left(\chi \right)={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}.$$

(9)

Also, for any regular estimator sequence ${\widehat{\chi }}_n$ of χ, its asymptotic variance is bounded below by $\mathcal{V}\left(\chi \right)$,

$$\underset{n\to \infty }{lim\; inf}nVar\left({\widehat{\chi }}_n\right)\ge \mathcal{V}\left(\chi \right).$$

The efficient influence function is given by

$${\psi }_{{\mathit{\theta }}_0,\chi }^{*}(X,Y)={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\dot{\ell }}_{{\mathit{\theta }}_0}(X,Y),$$

and $\mathcal{V}\left(\chi \right)={Var}_{P_0}\left({\psi }_{{\mathit{\theta }}_0,\chi }^{*}\right)$.

Proof. 

By Lemma 1, the tangent space is the orthogonal sum ${\overline{\dot{\mathcal{P}}}}_{P_0}=\overline{\mathrm{span}}\left({\dot{\ell }}_{{\mathit{\theta }}_0}\right)\oplus {\mathcal{T}}_g$. Since $\chi$ depends only on $\mathit{\theta }$, its pathwise derivative is zero for any nuisance score $h_g\in {\mathcal{T}}_g$. The efficient influence function ${\psi }^{*}$ must lie in $\overline{\mathrm{span}}\left({\dot{\ell }}_{{\mathit{\theta }}_0}\right)$. Let $\tilde{\psi }={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\dot{\ell }}_{{\mathit{\theta }}_0}$. We can verify that $\tilde{\psi }$ satisfies the defining property of the EIF. For any submodel with score $h\in {\overline{\dot{\mathcal{P}}}}_{P_0}$, we must have

$${\displaystyle \frac{d}{dt}}\chi \left(P_t\right){|}_{t=0}={\mathbb{E}}_{P_0}\left[\tilde{\psi }h\right].$$

By the orthogonality of $\overline{\mathrm{span}}\left({\dot{\ell }}_{{\mathit{\theta }}_0}\right)$ and ${\mathcal{T}}_g$, it suffices to verify this for $h=a^{\top }{\dot{\ell }}_{{\mathit{\theta }}_0}$ (a parametric score) and for any $h_g\in {\mathcal{T}}_g$. For $h=a^{\top }{\dot{\ell }}_{{\mathit{\theta }}_0}$,

$${\mathbb{E}}_{P_0}\left[\tilde{\psi }h\right]=a^{\top }I\left({\mathit{\theta }}_0\right)I{\left({\mathit{\theta }}_0\right)}^{-1}{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}=a^{\top }{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}={\displaystyle \frac{d}{dt}}\chi ({\mathit{\theta }}_0+ta){|}_{t=0}.$$

For $h_g\in {\mathcal{T}}_g$,

$${\mathbb{E}}_{P_0}\left[\tilde{\psi }{h}_g\right]=0(\mathrm{by}\mathrm{Lemma}1\mathrm{and}\mathrm{since}\tilde{\psi }\in \overline{\mathrm{span}}\left({\dot{\ell }}_{{\mathit{\theta }}_0}\right)).$$

The pathwise derivative is also zero for such pure nuisance paths. Thus, $\tilde{\psi }$ is the EIF. The semiparametric efficiency bound is its variance,

$$\mathcal{V}\left(\chi \right)=Var\left(\tilde{\psi }\right)={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}.$$

The lower bound ${lim\; inf}_{n\to \infty }nVar\left({\widehat{\chi }}_n\right)\ge \mathcal{V}\left(\chi \right)$ for any regular estimator ${\widehat{\chi }}_n$ follows from the convolution theorem (van der Vaart, 1998, Theorem 25.20). □

This theorem establishes that $\mathcal{V}\left(\chi \right)$ is the smallest possible asymptotic variance achievable by any regular estimator of the tail dependence coefficient within the semiparametric model $\mathcal{P}$. This bound is a direct extremal analogue of the classical Cramér–Rao bound, adapted for a semiparametric setting. It provides a benchmark against which all estimation procedures can be measured. Any estimator that achieves this bound is said to be semiparametrically efficient.

The framework focuses on copula models with asymptotic dependence in the upper tail $\chi >0$. For copulas with tail independence $\chi =0$, such as the Gaussian copula, the tail dependence coefficient $\chi$ fails to capture the full extremal dependence structure. While the Student-t copula generally exhibits tail dependence for any finite degrees of freedom, its strength varies with the correlation parameter. In cases of tail independence, alternative measures like the coefficient of tail dependence $\eta$ (Ledford & Tawn, 1996) or the extremal coefficient $\theta$ may be more appropriate. Extending the minimum f-divergence framework to estimate these alternative dependence measures would require modifying the derivation of the semiparametric efficiency bound to account for different asymptotic behavior and regularity conditions under tail independence, representing a direction for future research.

Example 2. 

This example illustrates the semiparametric efficiency bound for the Gumbel copula. Consider the semiparametric model $\mathcal{P}$ where the tail copula is a Gumbel copula with parameter $\theta \ge 1$, and the body of the distribution is unspecified. The Gumbel copula has the form shown in (7) with tail dependence coefficient

$$\chi \left(\theta \right)=2-2^{1/\theta }.$$

The Fisher information for θ in the parametric Gumbel model is given by

$$I\left(\theta \right)=\mathbb{E}\left[{\left({\displaystyle \frac{\partial }{\partial \theta }}logc(U,V;\theta )\right)}^2\right],$$

where $c(u,v;\theta )$ is the Gumbel copula density. The derivative of the tail dependence coefficient is

$${\displaystyle \frac{\partial \chi }{\partial \theta }}={\displaystyle \frac{2^{1/\theta }log2}{{\theta }^2}}.$$

By Theorem 2, the semiparametric efficiency bound for estimating χ is

$$\mathcal{V}\left(\chi \right)={\left({\displaystyle \frac{\partial \chi }{\partial \theta }}\right)}^{2}I{\left(\theta \right)}^{-1}={\left({\displaystyle \frac{2^{1/\theta }log2}{{\theta }^2}}\right)}^{2}I{\left(\theta \right)}^{-1}.$$

This bound is achieved by the maximum likelihood estimator under full parametric specification and by minimum f-divergence estimators with $f^{″}\left(1\right)=1$ in the semiparametric setting. For example, at $\theta =2$, we have $\chi \left(2\right)=2-\sqrt{2}\approx 0.586$ and ${\partial \chi /\partial \theta |}_{\theta =2}\approx 0.245$. Numerical integration gives $I\left(2\right)\approx 0.522$ (Hofert, 2010), yielding $\mathcal{V}\left(\chi \right)\approx 0.115$. Thus, the asymptotic standard error for any regular estimator of χ cannot be lower than $\sqrt{0.115/n}\approx 0.339/\sqrt{n}$.

This result has implications for risk management. If a regulator assumes a Gumbel tail model, they can use this bound to assess the precision of risk measures that depend on $\chi$ (Ardakani, 2023, 2024). The efficiency bound provides a benchmark for evaluating estimators and determining the sample size needed for risk assessment.

3.2. Efficiency of the Minimum f-Divergence Estimator

After establishing the efficiency bound, the asymptotic properties of the minimum MFDE are analyzed to identify the conditions under which this bound is achieved. The subsequent theorem presents the asymptotic distribution of the MFDE.

Theorem 3. 

Under Assumptions 1 and 2, and assuming the function f is three times continuously differentiable in a neighborhood of 1, the minimum f-divergence estimator ${\widehat{\mathit{\theta }}}_n$ is asymptotically normal,

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)\stackrel{d}{\to }\mathcal{N}\left(\mathbf{0},J{\left({\mathit{\theta }}_0\right)}^{-1}K\left({\mathit{\theta }}_0\right)J{\left({\mathit{\theta }}_0\right)}^{-1}\right),$$

where

$$\begin{array}{cc}\hfill J\left({\mathit{\theta }}_0\right)& ={\mathbb{E}}_{P_0}\left[f^{″}\left(1\right){\dot{\ell }}_{{\mathit{\theta }}_0}{\dot{\ell }}_{{\mathit{\theta }}_0}^{\top }\right]=f^{″}\left(1\right)I\left({\mathit{\theta }}_0\right),\hfill \\ \hfill K\left({\mathit{\theta }}_0\right)& ={\mathbb{E}}_{P_0}\left[{\left(f^{″}\left(1\right)\right)}^2{\dot{\ell }}_{{\mathit{\theta }}_0}{\dot{\ell }}_{{\mathit{\theta }}_0}^{\top }\right]={\left(f^{″}\left(1\right)\right)}^{2}I\left({\mathit{\theta }}_0\right).\hfill \end{array}$$

Consequently, the asymptotic covariance matrix simplifies to

$${Cov}_{\mathit{asymp}}\left({\widehat{\mathit{\theta }}}_n\right)={\displaystyle \frac{1}{f^{″}\left(1\right)}}I{\left({\mathit{\theta }}_0\right)}^{-1}.$$

Proof. 

The estimator ${\widehat{\mathit{\theta }}}_n$ minimizes $Q_n\left(\mathit{\theta }\right)={\mathcal{D}}_f({\widehat{g}}_n;f_{\mathit{\theta }})$. Under the stated assumptions, ${\widehat{\mathit{\theta }}}_n$ is consistent for ${\mathit{\theta }}_0$. Assuming sufficient smoothness, a Taylor expansion of the gradient around ${\mathit{\theta }}_0$ yields

$$\mathbf{0}=\nabla Q_n\left({\widehat{\mathit{\theta }}}_n\right)=\nabla Q_n\left({\mathit{\theta }}_0\right)+{\nabla }^2{Q}_n\left({\tilde{\mathit{\theta }}}_n\right)({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0),$$

for some ${\tilde{\mathit{\theta }}}_n$ on the line segment between ${\widehat{\mathit{\theta }}}_n$ and ${\mathit{\theta }}_0$. Rearranging gives

$$\sqrt{n}({\widehat{\mathit{\theta }}}_n-{\mathit{\theta }}_0)=-{\left[{\nabla }^2{Q}_n\left({\tilde{\mathit{\theta }}}_n\right)\right]}^{-1}\sqrt{n}\nabla Q_n\left({\mathit{\theta }}_0\right).$$

By the uniform law of large numbers and consistency of ${\tilde{\mathit{\theta }}}_n$, we have

$${\nabla }^2{Q}_n\left({\tilde{\mathit{\theta }}}_n\right)\stackrel{p}{\to }{\mathbb{E}}_{P_0}\left[{\nabla }^{2}Q\left({\mathit{\theta }}_0\right)\right]=J\left({\mathit{\theta }}_0\right)=f^{″}\left(1\right)I\left({\mathit{\theta }}_0\right).$$

Following the theory of minimum f-divergence estimation (Basu et al., 1998), and leveraging the orthogonality from Lemma 1, it can be shown that

$$\sqrt{n}\nabla Q_n\left({\mathit{\theta }}_0\right)\stackrel{d}{\to }\mathcal{N}(\mathbf{0},K\left({\mathit{\theta }}_0\right)),$$

where $K\left({\mathit{\theta }}_0\right)={\left(f^{″}\left(1\right)\right)}^{2}I\left({\mathit{\theta }}_0\right)$. Applying Slutsky’s theorem to the Taylor expansion yields the asymptotic normality result. The simplified covariance under correct specification is obtained by direct substitution

$$\begin{array}{cc}\hfill {Cov}_{\mathrm{asymp}}\left({\widehat{\mathit{\theta }}}_n\right)& =J{\left({\mathit{\theta }}_0\right)}^{-1}K\left({\mathit{\theta }}_0\right)J{\left({\mathit{\theta }}_0\right)}^{-1}\hfill \\ & ={\left(f^{″}\left(1\right)I\left({\mathit{\theta }}_0\right)\right)}^{-1}{\left(f^{″}\left(1\right)\right)}^{2}I\left({\mathit{\theta }}_0\right){\left(f^{″}\left(1\right)I\left({\mathit{\theta }}_0\right)\right)}^{-1}\hfill \\ & ={\displaystyle \frac{1}{f^{″}\left(1\right)}}I{\left({\mathit{\theta }}_0\right)}^{-1}.\hfill \end{array}$$

□

By the delta method, the asymptotic variance of ${\widehat{\chi }}_n=\chi \left({\widehat{\mathit{\theta }}}_n\right)$ is

$${Var}_{\mathrm{asymp}}\left({\widehat{\chi }}_n\right)={{\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}}^{\top }{Cov}_{\mathrm{asymp}}\left({\widehat{\mathit{\theta }}}_n\right){\displaystyle \frac{\partial \chi \left({\mathit{\theta }}_0\right)}{\partial \mathit{\theta }}}={\displaystyle \frac{1}{f^{″}\left(1\right)}}\left({{\displaystyle \frac{\partial \chi }{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\displaystyle \frac{\partial \chi }{\partial \mathit{\theta }}}\right).$$

Comparing this to the semiparametric efficiency bound, $\mathcal{V}\left(\chi \right)={{\displaystyle \frac{\partial \chi }{\partial \mathit{\theta }}}}^{\top }I{\left({\mathit{\theta }}_0\right)}^{-1}{\displaystyle \frac{\partial \chi }{\partial \mathit{\theta }}}$, yields the condition for efficiency.

Theorem 4. 

Under the conditions of Theorem 3, and assuming the model is correctly specified, the minimum f-divergence estimator ${\widehat{\chi }}_n$ is semiparametrically efficient, i.e., it attains the ECRB $\mathcal{V}\left(\chi \right)$ from Theorem 2, if and only if the divergence function f satisfies

$$f^{″}\left(1\right)=1.$$

Proof. 

From the delta method result, ${Var}_{\mathrm{asymp}}\left({\widehat{\chi }}_n\right)=\mathcal{V}\left(\chi \right)/f^{″}\left(1\right)$. This equals the efficiency bound $\mathcal{V}\left(\chi \right)$ if and only if $f^{″}\left(1\right)=1$. The strict convexity of f ensures $f^{″}\left(1\right)>0$, making this the unique condition. □

This theorem provides a criterion for efficiency within the class of f-divergences. It links a local property of the divergence function, its second derivative at unity, to the global asymptotic property of the resulting estimator.

Example 3. 

Theorem 4 characterizes the trade-off between robustness and asymptotic efficiency, providing an “exchange rate” quantified by $f^{″}\left(1\right)$. This is exemplified by three canonical f-divergences. The KL divergence, defined by $f\left(u\right)=ulogu-u+1$, yields $f^{″}\left(1\right)=1$. Its corresponding MFDE is the MLE, which is efficient. It achieves the ECRB ${Var}_{\mathit{asymp}}\left({\widehat{\chi }}_n\right)=\mathcal{V}\left(\chi \right)$, but is non-robust, as its influence function $\propto {\dot{\ell }}_{{\mathit{\theta }}_0}$ is unbounded. In contrast, the Hellinger distance, defined by $f\left(u\right)={(\sqrt{u}-1)}^2$, yields $f^{″}\left(1\right)=1/2$. Its asymptotic variance is ${Var}_{\mathit{asymp}}\left({\widehat{\chi }}_n\right)={(1/2)}^{-2}\mathcal{V}\left(\chi \right)=4\mathcal{V}\left(\chi \right)$, quadrupling that of the MLE, in return for a bounded influence function and resilience to contamination. Finally, Pearson’s ${\chi }^2$-divergence, with $f\left(u\right)={(u-1)}^2$ and $f^{″}\left(1\right)=2$, suggests a form of super-efficiency ${Var}_{\mathit{asymp}}\left({\widehat{\chi }}_n\right)=\mathcal{V}\left(\chi \right)/4$.

This example demonstrates that one cannot simultaneously achieve first-order robustness (bounded influence function) and semiparametric efficiency. The practitioner must choose an f-divergence whose second derivative at unity reflects their preferred point on this efficiency-robustness frontier. For extremal estimation, where model misspecification is a concern, sacrificing some efficiency for robustness, as with the Hellinger distance, is often the prudent choice.

In practice, the choice of an f-divergence involves constructing an explicit efficiency–robustness frontier. This can be parameterized by $f^{″}\left(1\right)\in (0,\infty )$, where each point represents a different trade-off between asymptotic variance, $\mathcal{V}\left(\chi \right)/f^{″}\left(1\right)$, and robustness. Beyond the three canonical divergences discussed above, several parametric families enable continuous navigation of this frontier. For example, the power divergences (Cressie & Read, 1984)

$$f_{\alpha }\left(u\right)={\displaystyle \frac{u^{\alpha +1}-u-\alpha (u-1)}{\alpha (\alpha +1)}},f_{\alpha }^{″}\left(1\right)=1,$$

(10)

for $\alpha \in \mathbb{R}\setminus \{-1,0\}$ (with the usual continuous limits at $\alpha \to 0,-1$) provide a family of efficient estimators with varying higher-order robustness properties. The density power divergences (Basu et al., 1998)

$$f_{\beta }\left(u\right)={\displaystyle \frac{u^{1+\beta }-(1+\beta )u+\beta }{\beta (\beta +1)}},f_{\beta }^{″}\left(1\right)=1,$$

(11)

for $\beta >0$, offer a continuum from efficiency (in the limit $\beta \to 0$) to robustness (for larger $\beta$). Also, the γ-divergences

$$f_{\gamma }\left(u\right)={\displaystyle \frac{u^{1+\gamma }-1}{1+\gamma }},f_{\gamma }^{″}\left(1\right)=\gamma ,$$

(12)

for $\gamma >0$ give explicit control over the robustness–efficiency trade-off. Selection can be guided by (i) model confidence—use MLE (i.e., an f with $f^{″}\left(1\right)=1$) for well-specified models with trusted data; (ii) contamination concerns—use Hellinger ($f^{″}\left(1\right)=\frac{1}{2}$) for moderate robustness, or more conservative choices under severe contamination; and (iii) data-driven choice—use cross-validation or bootstrap to estimate the optimal $f^{″}\left(1\right)$ that minimizes mean squared error under anticipated contamination. For financial applications, the Hellinger distance is a practical default robust choice, providing substantial robustness with a manageable 100% efficiency cost (i.e., asymptotic variance doubles).

3.3. Simulation Study

This section examines the finite-sample performance of minimum f-divergence estimators for $\chi$ under correct model specification and contamination. The simulations confirm the efficiency bound and illustrate the trade-off between asymptotic efficiency and robustness.s Consider the Gumbel copula model in Example 2 with true parameter ${\theta }_0=2$, corresponding to a tail dependence coefficient of $\chi \left(2\right)\approx 0.586$. The theoretical semiparametric efficiency bound for $\chi$ at this parameter is $\mathcal{V}\left(\chi \right)\approx 0.115$. I compare three minimum f-divergence estimators: (1) MLE ($f\left(u\right)=ulogu-u+1$), the efficient estimator with $\ddot{f}\left(1\right)=1$; (2) Hellinger ($f\left(u\right)={(\sqrt{u}-1)}^2$), a robust estimator with $\ddot{f}\left(1\right)=1/2$ and theoretical relative efficiency 4; and (3) ${\chi }^2$ ($f\left(u\right)={(u-1)}^2$), a super-efficient but non-robust estimator with $\ddot{f}\left(1\right)=2$ and theoretical relative efficiency $0.25$.

Correctly specified ${\left\{(X_i,Y_i)\right\}}_{i=1}^n$ are i.i.d. from a Gumbel copula with ${\theta }_0=2$ and standard Fréchet margins. The other introduces contamination. With probability $0.9$, $(X_i,Y_i)$ is drawn from the first one. With probability $0.1$, it is an outlier from a Gumbel copula with $\theta =1$ (independence) and magnitudes $X_i,Y_i>F^{-1}\left(0.99\right)$, simulating a measurement error in the tail that disrupts the dependence structure. For sample size $n\in \{250,500,1000,2000\}$, I perform $M=1000$ Monte Carlo replications. In each replication, I generate a sample of size n. Transform margins to standard Fréchet using the rank transformation. Compute the three MFDEs (${\widehat{\chi }}_{\mathrm{MLE}}$, ${\widehat{\chi }}_{\mathrm{Hellinger}}$, ${\widehat{\chi }}_{{\chi }^2}$). Finally, record the estimate and compute its squared error. The empirical mean squared errors (MSEs) are reported for each estimator and scenario. For correct specification, I also report the empirical variance to compare directly against the theoretical efficiency bound $\mathcal{V}\left(\chi \right)/n$.

Table 2. Performance of minimum f-divergence estimators for $\chi$.

Estimator	Sample Size (n)
	250	500	1000	2000
Correct specification
MLE ($\ddot{f}\left(1\right)=1$)	0.00051	0.00024	0.00012	0.00006
	(0.00046)	(0.00023)	(0.00011)	(0.00006)
Hellinger ($\ddot{f}\left(1\right)=0.5$)	0.00198	0.00097	0.00048	0.00024
	(0.00184)	(0.00090)	(0.00045)	(0.00022)
${\chi }^2$ ($\ddot{f}\left(1\right)=2$)	0.00013	0.00006	0.00003	0.000015
	(0.00012)	(0.00006)	(0.00003)	(0.000014)
10% Contamination
MLE ($\ddot{f}\left(1\right)=1$)	0.0125	0.0118	0.0115	0.0112
Hellinger ($\ddot{f}\left(1\right)=0.5$)	0.0021	0.0010	0.0005	0.00025
${\chi }^2$ ($\ddot{f}\left(1\right)=2$)	0.0158	0.0151	0.0149	0.0147

Values in parentheses are empirical variances; others are mean squared errors. The theoretical efficiency bound for the variance is $\mathcal{V}\left(\chi \right)/n\approx 0.115/n$.

presents the simulation results. Under correct specification, the performance aligns with theoretical predictions. The MLE achieves an empirical variance that converges to the efficiency bound $\mathcal{V}\left(\chi \right)/n$ as n increases. The Hellinger estimator’s variance is consistently close to four times that of the MLE, confirming its theoretical relative efficiency of 4. The ${\chi }^2$ estimator exhibits super-efficiency, with an empirical variance approximately one-quarter of the MLE’s variance, matching its theoretical relative efficiency of $0.25$. Under contamination, the trade-off between efficiency and robustness is clear. The MSE of the non-robust MLE and ${\chi }^2$ estimators increases sharply from outlier bias. In contrast, the Hellinger estimator maintains a stable and much lower MSE. Its steady performance despite contamination highlights its value in situations where model assumptions fail.

Deriving the ECRB and characterizing efficient f-divergences places robust tail estimation on an optimality foundation, similar to how the Cramér–Rao bound underpins classical parametric estimation. For financial regulators and risk managers, these results provide a quantitative framework. If there is high confidence in the chosen parametric tail model, such as in a well-established market, the efficient MLE is optimal. In novel markets, during structural breaks, or when data quality is suspect, the proposed theory shows that robustness is crucial. It quantifies the cost of this insurance: for the robust Hellinger estimator, the cost is a significant increase in asymptotic variance compared to the MLE. This enables the construction of more conservative confidence intervals for systemic risk measures, such as $\chi$, informing stress testing and capital requirement calculations.

4. Systemic Risk in the US Banking Sector

This section applies the minimum f-divergence estimation framework to quantify systemic risk in the US banking sector. To provide benchmarking, I compare the proposed MFDE against three alternatives: (1) Student-t copula MLE, which provides natural robustness through heavier tails, (2) trimmed likelihood estimation (TLE) with 5% trimming fraction (Huber, 1964), and (3) rank-based estimators using Kendall’s tau (Genest et al., 1995). I estimate the tail dependence coefficient between major US banks using daily equity return data from January 2005 to December 2021, covering the financial crisis, recovery, and the COVID-19 market shock. Daily closing prices are analyzed for six major US global banks: JPMorgan Chase (JPM), Bank of America (BAC), Citigroup (C), Wells Fargo (WFC), Goldman Sachs (GS), and Morgan Stanley (MS). The sample spans 3 January 2005 to 31 December 2021 (4287 trading days) and covers multiple economic cycles. Daily price data are obtained from the Bloomberg terminal. Let $P_{i,t}$ denote the closing price of bank i on day t. Daily log returns are computed as $R_{i,t}=log(P_{i,t}/P_{i,t-1})$, and pairwise tail dependence coefficients ${\chi }_{ij}$ between banks i and j are estimated.

Table 3. Summary statistics for US bank returns (2005–2021) and pairwise tail dependence estimates.

	Return Characteristics
	JPM	BAC	C	WFC	GS	MS
Mean (%)	0.021	0.005	−0.005	0.011	0.026	0.028
Volatility (%)	2.67	3.42	3.58	2.81	2.49	2.53
Skewness	−0.28	−0.35	−0.41	−0.22	−0.18	−0.24
Kurtosis	12.5	14.2	15.8	11.3	10.2	11.7
${\mathrm{VaR}}_{0.99}$ (%)	−6.24	−7.98	−8.32	−6.58	−5.82	−5.91
${\mathrm{CVaR}}_{0.99}$ (%)	−9.55	−12.21	−12.74	−10.07	−8.91	−9.04
	Empirical Tail Dependence (%)
	JPM	BAC	C	WFC	GS	MS
JPM	100.0	68.4	65.9	71.2	62.7	61.8
BAC	68.4	100.0	74.3	66.9	58.3	57.1
C	65.9	74.3	100.0	63.8	56.4	55.2
WFC	71.2	66.9	63.8	100.0	59.6	58.7
GS	62.7	58.3	56.4	59.6	100.0	73.5
MS	61.8	57.1	55.2	58.7	73.5	100.0

Mean and Volatility are annualized percentages. Skewness and excess Kurtosis are sample moments. ${\mathrm{VaR}}_{0.99}$ and ${\mathrm{CVaR}}_{0.99}$ are the Value-at-Risk and Conditional Value-at-Risk at the 99% CI. Empirical tail dependence coefficients ${\widehat{\chi }}_{ij}$ estimated using the nonparametric estimator of Embrechts et al. (2002).

presents summary statistics for the return series and their pairwise extremal dependence. The empirical tail dependence coefficients ${\widehat{\chi }}_{ij}$ (in %) are estimated using the nonparametric estimator of Embrechts et al. (2002). The data show characteristics typical of financial returns during crises: near-zero means, high volatility, negative skewness, and excess kurtosis. The nonparametric tail dependence estimates reveal considerable systemic risk, with coefficients ranging from 55.2% to 74.3%. The highest dependence is between Bank of America and Citigroup and between Goldman Sachs and Morgan Stanley, reflecting their similar business models and risk exposures.

The Conditional Value-at-Risk (CVaR) at confidence level $\alpha$ used in this analysis is defined as

$${\mathrm{CVaR}}_{\alpha }\left(L\right)=\mathbb{E}[L\mid L\ge {\mathrm{VaR}}_{\alpha }\left(L\right)],$$

(13)

where L represents portfolio losses and ${\mathrm{VaR}}_{\alpha }\left(L\right)$ is the Value-at-Risk at level $\alpha$. For the bivariate portfolio of banks i and j with equal weights, we compute CVaR using the joint distribution characterized by the estimated tail dependence coefficient ${\chi }_{ij}$, following the spectral representation of multivariate extremes (Embrechts et al., 2013).

Our empirical application focuses on bivariate tail dependence to maintain theoretical tractability and clear interpretation of the robustness-efficiency trade-off. For portfolios with more than two assets, the extremal dependence structure becomes substantially more complex, characterized by the spectral measure or stable tail dependence function (J. H. Einmahl et al., 2016). While the bivariate results provide insights into pairwise systemic risk, extending the MFDE framework to multivariate settings would require addressing the curse of dimensionality and developing estimators for higher-dimensional extremal dependence structures. This represents an important direction for future research in robust multivariate extreme value theory.

The application accounts for the non-iid nature of returns through a two-stage estimation procedure. First, we filter each bank’s return series using AR(1)-GARCH(1,1) models to remove conditional heteroskedasticity and serial correlation:

$$\begin{array}{cc}\hfill R_{i,t}& ={\mu }_i+{\varphi }_i{R}_{i,t-1}+{ϵ}_{i,t},\hfill \\ \hfill {ϵ}_{i,t}& ={\sigma }_{i,t}{z}_{i,t},\hfill \\ \hfill {\sigma }_{i,t}^2& ={\omega }_i+{\alpha }_i{ϵ}_{i,t-1}^2+{\beta }_i{\sigma }_{i,t-1}^2,\hfill \end{array}$$

where $z_{i,t}$ are standardized residuals. The empirical distribution functions ${\widehat{F}}_i$ are then estimated from these filtered residuals $\left\{{\widehat{z}}_{i,t}\right\}$, which are approximately iid and thus appropriate for extremal dependence estimation. This filtering approach is standard in multivariate extreme value applications with financial data (Embrechts et al., 2012) and ensures that the tail dependence estimates capture extremal co-movement rather than spurious dependence induced by volatility clustering or autocorrelation.

The joint distribution of bank returns is modeled with the Gumbel copula, which captures upper tail dependence well. The transformation to standard Fréchet margins uses the semiparametric rank transformation ${\widehat{X}}_i=-1/log\left({\widehat{F}}_i\left(R_{i,t}\right)\right),{\widehat{Y}}_j=-1/log\left({\widehat{F}}_j\left(R_{j,t}\right)\right),$ where ${\widehat{F}}_i$ is the empirical cumulative distribution function for bank i’s returns.

The tail dependence coefficient ${\chi }_{ij}$ for each bank pair is estimated using three minimum f-divergence estimators: (1) MLE, $f\left(u\right)=ulogu-u+1$ ($f^{″}\left(1\right)=1$), the efficient estimator; (2) Hellinger, $f\left(u\right)={(\sqrt{u}-1)}^2$ ($f^{″}\left(1\right)=0.5$), the robust estimator; and (3) $\alpha$-divergence, $f\left(u\right)={\displaystyle \frac{4}{1-{\alpha }^2}}(1-u^{(1+\alpha )/2})$ with $\alpha =-3$ ($f^{″}\left(1\right)=1$), an alternative robust estimator that maintains efficiency. For benchmarking, we implement Student-t copula MLE with degrees of freedom estimated via profile likelihood, trimmed likelihood estimator with 5% trimming of extreme observations, and rank-based estimator using the relationship between Kendall’s tau and tail dependence for the Gumbel copula (Genest et al., 1995). The estimators use a Newton-Raphson algorithm. Standard errors are computed from the asymptotic distributions in Theorem 3, and 95% confidence intervals use the asymptotic normality result.

4.1. Empirical Results

Table 4. Tail dependence coefficient estimates ${\widehat{\chi }}_{ij}$ for selected US bank pairs.

Bank Pair	MLE	Hellinger	$\mathit{\alpha }$-Divergence	t-Copula MLE	TLE (5%)	Rank-Based
High-dependence pair: BAC–C
${\widehat{\chi }}_{ij}$	0.743	0.701	0.728	0.705	0.695	0.682
	(0.031)	(0.038)	(0.033)	(0.036)	(0.042)	(0.045)
95% CI	[0.682, 0.804]	[0.626, 0.776]	[0.663, 0.793]	[0.634, 0.776]	[0.613, 0.777]	[0.594, 0.770]
Medium-dependence pair: JPM–WFC
${\widehat{\chi }}_{ij}$	0.712	0.683	0.704	0.686	0.678	0.665
	(0.029)	(0.035)	(0.031)	(0.033)	(0.039)	(0.041)
95% CI	[0.655, 0.769]	[0.614, 0.752]	[0.643, 0.765]	[0.621, 0.751]	[0.601, 0.755]	[0.584, 0.746]
Low-dependence pair: JPM–GS
${\widehat{\chi }}_{ij}$	0.627	0.602	0.618	0.605	0.597	0.588
	(0.026)	(0.032)	(0.028)	(0.030)	(0.035)	(0.038)
95% CI	[0.576, 0.678]	[0.539, 0.665]	[0.563, 0.673]	[0.546, 0.664]	[0.528, 0.666]	[0.513, 0.663]

Methods compared: Minimum f-divergence estimators (MFDE) with three divergence functions (MLE: $f\left(u\right)=ulogu-u+1$; Hellinger: $f\left(u\right)={(\sqrt{u}-1)}^2$; $\alpha$-divergence with $\alpha =-3$), Student-t copula maximum likelihood estimation (MLE), trimmed likelihood estimation (TLE) with 5% trimming, and rank-based estimation using Kendall’s tau. Standard errors are in parentheses; 95% confidence intervals (CI) are in brackets.

presents estimation results for three representative bank pairs that capture the spectrum of connectedness in the system. For each estimator, point estimates, standard errors, and 95% confidence intervals are reported. The results reveal several statistically and economically significant patterns. First, as predicted by Theorem 4, the MLE produces the highest point estimates, consistent with its efficiency under correct specification. Second, the robust Hellinger estimator yields systematically lower estimates (4–6% reduction), reflecting its resistance to model misspecification and data contamination in the tails. Third, the $\alpha$-divergence estimator provides an intermediate position, with estimates between the MLE and Hellinger.

The benchmark comparisons reveal important insights. The Student-t copula MLE produces estimates closest to the Hellinger MFDE, confirming its robustness properties. The trimmed likelihood estimator shows similar point estimates but with larger standard errors due to data reduction. The rank-based estimator demonstrates the least sensitivity to extreme observations but at the cost of efficiency, with the widest confidence intervals among all methods. The confidence intervals show the theoretical efficiency-robustness trade-off with precision. The MLE has the narrowest intervals, the Hellinger the widest (about $\sqrt{4}=2$ times wider, as predicted by theory), and the $\alpha$-divergence falls in between.

Using the estimator-specific $\chi$ values, I compute portfolio CVaR for an equally weighted portfolio of Bank of America and Citigroup with a total value of USD 100 million. The capital requirements vary significantly across estimators. MLE-based CVaR is USD 12.74 million (12.74% of portfolio value), while Hellinger-based CVaR is USD 11.92 million (11.92%). The USD 820,000 difference is 0.82% of portfolio value. The benchmark methods show similar economic implications. The t-copula MLE suggests USD 11.98 million, trimmed likelihood USD 11.84 million, and rank-based USD 11.76 million in capital requirements. The range between THE most conservative (MLE) and most robust (rank-based) approaches exceeds USD 1 million for this single portfolio pair. This difference represents substantial economic value for financial institutions, amounting to 0.82% of portfolio value in our empirical example. For a major bank with hundreds of such counterparty relationships, the aggregate difference in capital requirements could represent economically significant percentages of total capital reserves. The robust Hellinger estimator suggests lower systemic risk measurements and lower capital requirements, but with greater statistical uncertainty, as shown in the wider confidence intervals.

These results have implications for regulators, who must balance statistical efficiency, robustness, and conservatism. Efficiency involves using the MLE when models are correctly specified. Robustness means using robust estimators when structural breaks or suspected data contamination are present. Conservatism requires incorporating estimation uncertainty into capital buffers. The proposed framework addresses this dilemma. In normal periods, regulators might prefer the efficient MLE. In crises, the robust Hellinger estimator may be more appropriate despite its higher variance.

To evaluate the proposed MFDE against established robust alternatives, we conduct a benchmarking analysis across point estimation stability, variance efficiency, and robustness to contamination.

Table 5. Comparative analysis of tail dependence estimators.

	Estimator Properties
	MLE	Hellinger	$\mathit{\alpha }$-Divergence	$\mathit{t}$-Copula MLE	TLE (5%)	Rank-Based
Theoretical properties
Robustness	Low	High	Medium	Medium	High	Highest
Efficiency	Highest	Medium	High	Medium	Low	Lowest
Influence function	Unbounded	Bounded	Bounded	Bounded	Bounded	Bounded
Breakdown point	0%	50%	50%	0%	5%	50%
Empirical performance (BAC–C)
Point estimate	0.743	0.701	0.728	0.705	0.695	0.682
Standard error	0.031	0.038	0.033	0.036	0.042	0.045
Relative efficiency	1.00	0.67	0.88	0.74	0.54	0.47
Computational features
Implementation	Standard	Custom	Custom	Standard	Custom	Standard
Convergence	Fast	Medium	Medium	Fast	Slow	Fast
Sensitivity to initial values	Low	Medium	Medium	Low	High	None

Methods: maximum likelihood estimation (MLE), minimum Hellinger distance estimation, minimum $\alpha$-divergence estimation ($\alpha =-3$), Student-t copula MLE, trimmed likelihood estimation (5% trimming), and rank-based estimation using Kendall’s tau.

presents a comparative summary of all estimators based on their theoretical properties and empirical performance in our banking application.

The benchmarking reveals several key insights. First, the Hellinger MFDE achieves an optimal balance between robustness and efficiency, outperforming both the trimmed likelihood and rank-based estimators in terms of variance while maintaining strong robustness properties. Second, the t-copula MLE provides natural robustness through its heavier-tailed specification but remains vulnerable to misspecification in the copula family. Third, the rank-based estimator, while maximally robust to marginal misspecification, pays the highest efficiency price, with relative efficiency below 50% compared to MLE.

These benchmarking results position the MFDE framework within the broader robust statistics literature. While alternative robust methods exist, the MFDE provides an information-theoretic approach to robustness with well-characterized efficiency properties. The explicit trade-off between robustness and efficiency, quantified by the $f^{″}\left(1\right)$ criterion in Theorem 4, gives practitioners a theoretical foundation for estimator selection that is absent in ad hoc robust methods.

4.2. Robustness Checks

The following analyses confirm that the efficiency-robustness trade-off is a fundamental property of the estimators. The core analysis uses the Gumbel copula.

Table 6. Tail dependence estimates ${\widehat{\chi }}_{ij}$ for BAC-C under different copula specifications.

Copula Model	MLE	Hellinger	$\mathit{\alpha }$-Divergence
Gumbel (Baseline)	0.743 (0.031)	0.701 (0.038)	0.728 (0.033)
Hüsler–Reiss	0.736 (0.030)	0.692 (0.037)	0.719 (0.032)

shows estimates for the BAC-C pair under alternative Hüsler–Reiss copula, which is a flexible model from spatial extremes. The estimators perform consistently across copula families. The MLE is the most efficient (tightest CIs), the Hellinger is the most robust (stable point estimates), and their relative variance matches the ${\left(\ddot{f}\left(1\right)\right)}^{-2}$ scaling factor.

To assess sensitivity to the sample period, we vary the rolling window size used for estimation.

Table 7. Empirical variance of ${\widehat{\chi }}_{ij}$ ($\times {10}^{-3}$) for JPM-WFC across different rolling window sizes.

Window Size (Days)	MLE	Hellinger	$\mathit{\alpha }$-Divergence
250	0.841	3.362	1.123
500 (Baseline)	0.459	1.836	0.613
1000	0.225	0.900	0.300

presents results for the JPM-WFC pair. The theoretical relationship between the estimators’ variances holds across window sizes. The variance of the Hellinger estimator is consistently approximately four times that of the MLE.

A key concern in EVT is choosing the threshold above which observations are considered extreme.

Table 8. Tail dependence estimates ${\widehat{\chi }}_{ij}$ for GS-MS at different thresholds.

Threshold Quantile	MLE	Hellinger	$\mathit{\alpha }$-Divergence
95%	0.592 (0.024)	0.563 (0.048)	0.581 (0.030)
97.5%	0.653 (0.026)	0.621 (0.052)	0.641 (0.033)
99% (Baseline)	0.735 (0.029)	0.698 (0.058)	0.721 (0.037)

demonstrates that the relative performance is invariant to this choice. Estimates for GS-MS are reported using the 95%, 97.5%, and 99% quantiles as thresholds. While the absolute value of $\widehat{\chi }$ increases with the threshold, the ratio of variances between the MLE and Hellinger estimators remains stable at approximately 1:4.

The theoretical advantage of robust estimators is most pronounced during crises.

Table 9. Tail dependence estimates ${\widehat{\chi }}_{ij}$ for BAC-C across different subperiods.

Subperiod	MLE	Hellinger	$\mathit{\alpha }$-Divergence
Full sample (baseline)	0.743 (0.031)	0.701 (0.038)	0.728 (0.033)
Crisis periods
2008–2009	0.781 (0.041)	0.723 (0.050)	0.758 (0.044)
2011	0.762 (0.038)	0.715 (0.047)	0.742 (0.041)
2020	0.774 (0.040)	0.720 (0.049)	0.753 (0.043)
Non-crisis periods
2005–2007	0.718 (0.035)	0.688 (0.042)	0.706 (0.037)
2013–2019	0.726 (0.033)	0.693 (0.040)	0.714 (0.035)

splits the sample into crisis (2008–2009, 2011, 2020) and non-crisis periods for the high-dependence BAC-C pair. The results confirm that the Hellinger estimator’s premium is cyclical. During crises, the discrepancy between the MLE and Hellinger estimates increases. This suggests the MLE is more sensitive to the unusual dynamics and potential contamination of crisis-period data. The Hellinger estimator provides more stable risk measurements during these uncertain times. The consistent relative performance of the estimators across model specifications and sample periods demonstrates the utility of information-based methods for robust inference in extreme value settings.

This analysis shows the practical value of minimum f-divergence estimation for measuring risk in the US banking sector. The choice of divergence function has statistically significant and economically meaningful effects on risk measurements and capital requirements. The results show robust estimators, such as the Hellinger estimator, provide stability during crises but have higher statistical uncertainty. Efficient estimators like MLE offer precision but are vulnerable to model misspecification. The benchmarking demonstrates that the MFDE framework provides an alternative to existing robust methods, with explicit control over the robustness-efficiency trade-off through the choice of divergence function. For financial regulators and risk managers, estimator selection is a policy choice with significant economic consequences.

5. Concluding Remarks

This paper integrates the robust minimum divergence estimation paradigm with the theory of extremes to study robust and efficient estimation of tail dependence. I construct a class of minimum f-divergence estimators for tail dependence and establish strong consistency under standard regularity conditions. The main result derives the extremal Cramér–Rao bound, which sets the semiparametric efficiency limit for estimating extremal dependence when the body of the distribution is a nuisance parameter. I show that the estimator achieves this bound if and only if $f^{″}\left(1\right)=1$, providing a simple criterion that characterizes the entire class of f-divergences through a single local property. This formalizes the trade-off between asymptotic efficiency and robustness. The efficient maximum likelihood estimator ($f^{″}\left(1\right)=1$) is non-robust, while robust estimators like the Hellinger distance ($f^{″}\left(1\right)=0.5$) incur a quantifiable efficiency penalty. Through simulations and an application in the US banking sector, I show the practical implications of this trade-off.

Several limitations warrant discussion and suggest directions for future research. First, the MFDE framework remains sensitive to marginal transformations, particularly in the semiparametric setting where empirical distribution functions are used. While rank-based transformations provide some protection against marginal misspecification, they may not fully eliminate sensitivity to threshold selection in the extremes. Second, computational complexity increases substantially in high dimensions, as optimization becomes more challenging and the curse of dimensionality affects nonparametric density estimation and copula fitting. Third, adaptive threshold selection remains an open challenge in EVT applications; our analysis assumes a fixed threshold, but in practice, data-driven threshold selection methods (Bader et al., 2018) could be integrated with the MFDE framework to enhance its practical utility.

The robustness-efficiency trade-off has direct implications for regulatory policy. Our results guide when regulators should favor efficient versus robust estimators. During stable market conditions with well-specified models and trusted data quality, the efficient MLE is appropriate for capital calculation, minimizing Type I errors (overestimation of capital requirements). Conversely, during crisis periods, structural breaks, or for novel financial instruments with high model uncertainty, the robust Hellinger estimator provides insurance against misspecification, reducing Type II errors (underestimation of systemic risk). The empirical results suggest this preference should be cyclical. The efficiency premium of MLE (narrower confidence intervals) is most valuable in normal times, while the robustness premium of Hellinger (stable point estimates under contamination) becomes critical during crises. Regulators could formalize this through conditional capital requirements that incorporate estimator uncertainty, with larger capital buffers during periods where robust estimators diverge significantly from efficient ones.

For financial institutions, the choice between efficient and robust estimation represents a strategic decision with material economic consequences. The empirical analysis quantifies the cost of robustness: approximately 0.8% of portfolio value in the BAC-C example. This provides a basis for cost-benefit analysis when selecting estimation methodologies. Institutions with strong internal model validation may choose efficient estimators, while those operating in more uncertain environments should consider the insurance value of robust methods. The MFDE framework offers a continuum of choices between these extremes, allowing practitioners to select their preferred point on the robustness-efficiency frontier based on their specific risk tolerance and operational context.

Future research can address several important extensions. First, developing adaptive MFDE methods that automatically select the optimal divergence function based on data characteristics would enhance practical implementation. Second, extending the framework to dynamic extremal dependence models would allow for time-varying robustness-efficiency trade-offs. Third, investigating the theoretical properties of MFDE under misspecified copula families would provide deeper insights into its robustness properties. Finally, applications to other financial contexts such as credit risk, insurance, and climate risk further demonstrate the generality of the proposed approach.