Forecasting of GDP Growth in the South Caucasian Countries Using Hybrid Ensemble Models
Abstract
1. Introduction
2. Literature Review
3. Methods
3.1. Forecasting Models
3.2. Cross-Validation
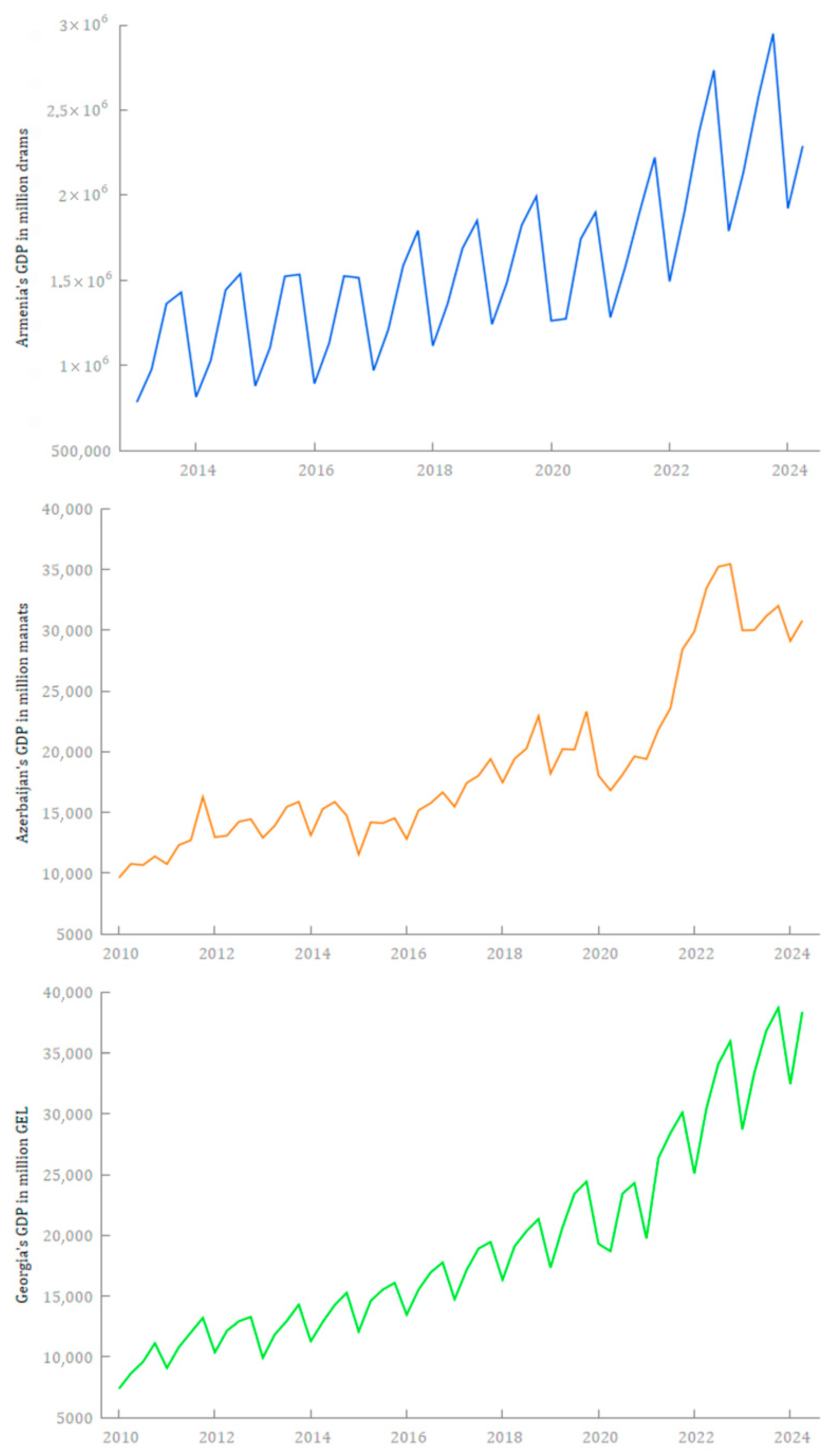
4. Data
- ➢
- the quarterly GDP of Armenia at average prices of the previous year, expressed in million drams, from Q1-2013 to Q2-2024 (The Statistical Committee of the Republic of Armenia, 2025);
- ➢
- the quarterly GDP of Azerbaijan at 2015 prices, expressed in million manats, from Q1-2010 to Q2-2024 (The State Statistical Committee of the Republic of Azerbaijan, 2025);
- ➢
- and the quarterly GDP of Georgiaby current (market) prices, expressed in million Georgian laris (GEL), from Q1-2020 to Q2-2024 (National Statistics Office of Georgia, 2025).
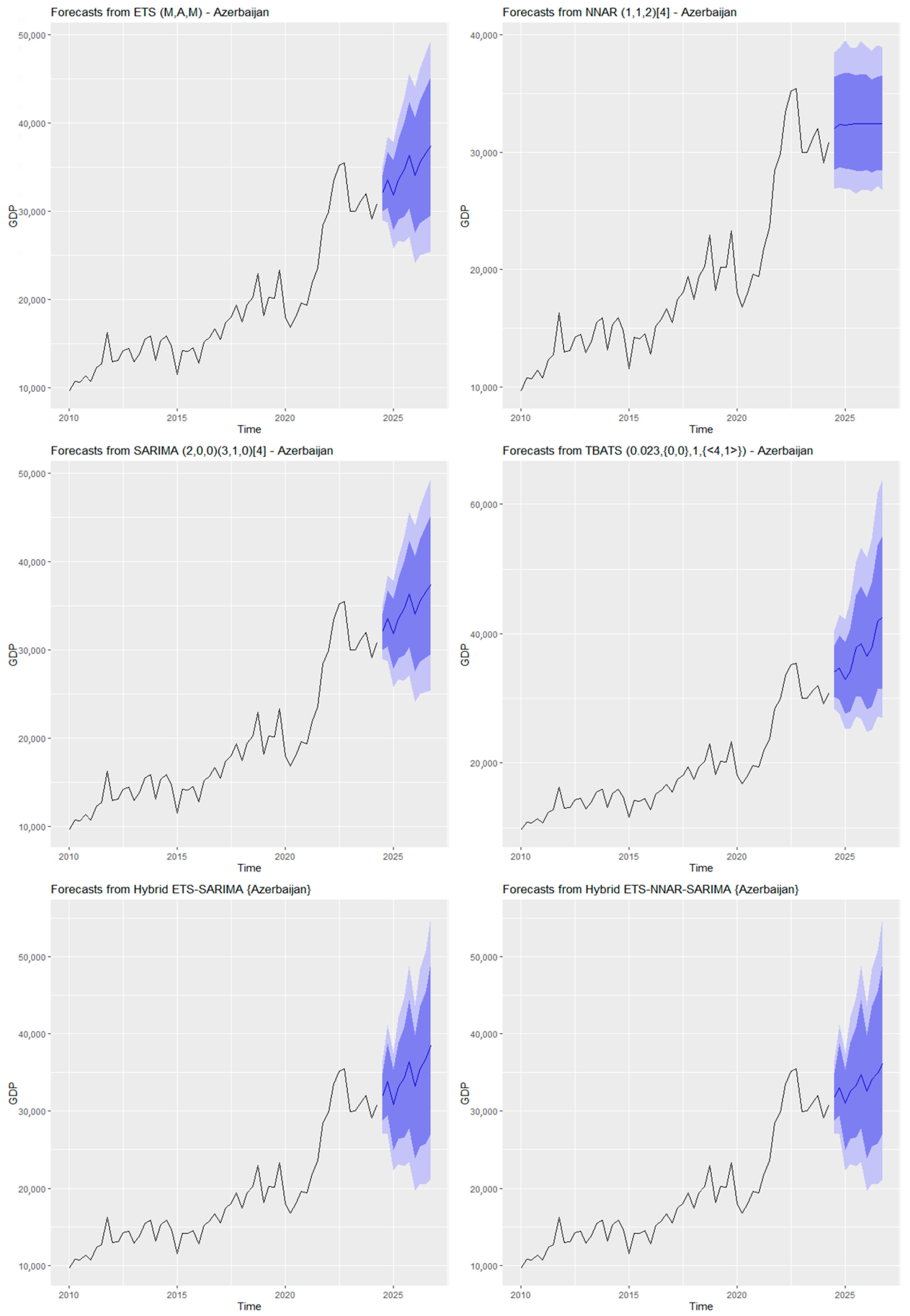
5. Results
5.1. Forecast Accuracy
5.2. Out-of-Sample Cross-Validation

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | It should be noted that hybrid models are built using equal weights across components. This choice yields lower forecast errors compared to alternative weighting schemes and is consistent with the literature, which highlights the robustness of equal-weight combinations and their role as a natural benchmark in forecasting, particularly when sample sizes are limited, as in this case (Timmermann, 2006; Claeskens et al., 2016). |
| 2 | In addition, Figure 5 offers a visual representation of the forecast versus actual values for the last eight quarters, allowing for an intuitive assessment of model performance and predictive alignment over the recent time. |
References
- Abdić, A., Resić, E., Abdić, A., & Rovčanin, A. (2020). Nowcasting GDP of Bosnia and Herzegovina: A comparison of forecast accuracy models. The South East European Journal of Economics and Business, 15(2), 1–14. [Google Scholar] [CrossRef]
- Alaminos, D., Salas, M. B., & Fernández-Gámez, M. A. (2022). Quantum computing and deep learning methods for GDP growth forecasting. Computer Economics, 59, 803–829. [Google Scholar] [CrossRef]
- Allgaier, J., & Pryss, R. (2024). Cross-validation visualized: A narrative guide to advanced methods. Machine Learning and Knowledge Extraction, 6(2), 1378–1388. [Google Scholar] [CrossRef]
- Almarashi, A. M., Daniyal, M., & Jamal, F. (2024). Modelling the GDP of KSA using linear and non-linear NNAR and hybrid stochastic time series models. PLoS ONE, 19(2), e0297180. [Google Scholar] [CrossRef]
- Atif, D. (2024). Enhancing long-term GDP forecasting with advanced hybrid models: A comparative study of ARIMA-LSTM and ARIMA-TCN with dense regression. Computational Economics, 65, 3447–3473. [Google Scholar] [CrossRef]
- Babii, A., Ghysels, E., & Striaukas, J. (2024). Econometrics of machine learning methods in economic forecasting. In M. P. Clements, & A. B. Galvão (Eds.), Handbook of research methods and applications in macroeconomic forecasting (pp. 246–273). Chapter 10. Edward Elgar Publishing. [Google Scholar]
- Ballarin, G., Dellaportas, P., Grigoryeva, L., Hirt, M., Van Huellen, S., & Ortega, J. (2024). Reservoir computing for macroeconomic forecasting with mixed-frequency data. International Journal of Forecasting, 40(3), 1206–1237. [Google Scholar] [CrossRef]
- Botha, B., Reid, G., Olds, T., Steenkamp, D., & van Jaarsveld, R. (2021). Nowcasting South African gross domestic product using a suite of statistical models. South African Journal of Economics, 89(4), 526–554. [Google Scholar] [CrossRef]
- Bragoli, D., & Fosten, J. (2018). Nowcasting Indian GDP. Oxford Bulletin of Economics and Statistics, 80(2), 259–282. [Google Scholar] [CrossRef]
- Cepni, O., Guney, I. E., & Swanson, N. R. (2019). Forecasting and nowcasting emerging market GDP growth rates: The role of latent global economic policy uncertainty and macroeconomic data surprise factors. Journal of Forecasting, 39(1), 18–36. [Google Scholar] [CrossRef]
- Cerqueira, V., Torgo, L., & Mozetič, I. (2020). Evaluating time series forecasting models: An empirical study on performance estimation methods. Machine Learning, 109(11), 1997–2028. [Google Scholar] [CrossRef]
- Chernis, T., & Sekkel, R. (2017). A dynamic factor model for nowcasting Canadian GDP growth. Empirical Economics, 53, 217–234. [Google Scholar] [CrossRef]
- Cicceri, G., Inserra, G., & Limosani, M. (2020). A machine learning approach to forecast economic recessions—An Italian case study. Mathematics, 8(2), 241. [Google Scholar] [CrossRef]
- Claeskens, G., Magnus, J. R., Vasnev, A. L., & Wang, W. (2016). The forecast combination puzzle: A simple theoretical explanation. International Journal of Forecasting, 32(3), 754–762. [Google Scholar] [CrossRef]
- Claudio, J. C., Heinisch, K., & Holtemöller, O. (2020). Nowcasting East German GDP growth: A MIDAS approach. Empirical Economics, 58(1), 29–54. [Google Scholar] [CrossRef]
- Darvas, Z. (2011). Beyond the crisis: Prospects for emerging Europe. Comparative Economic Studies, 53, 261–290. [Google Scholar] [CrossRef]
- De Livera, A. M., Hyndman, R. J., & Snyder, R. D. (2011). Forecasting time series with complex seasonal patterns using exponential smoothing. Journal of the American Statistical Association, 106(496), 1513–1527. [Google Scholar] [CrossRef]
- Domit, S., Monti, F., & Sokol, A. (2019). Forecasting the UK economy with a medium-scale Bayesian VAR. International Journal of Forecasting, 35(4), 1669–1678. [Google Scholar] [CrossRef]
- Dritsaki, M., & Dritsaki, C. (2023). Modelling and forecasting GDP of Greece with a modified exponential smoothing state-space framework. In Advances in empirical economic research (pp. 89–110). Springer. [Google Scholar]
- Elbatal, I., Sarwar, M., Jamal, F., Daniyal, M., Hussain, Z., & Ben Ghorbal, A. (2025). Modelling on gross domestic product Annual growth rate data by using time series, machine learning, and probability models. Journal of Radiation Research and Applied Sciences, 18(2), 101481. [Google Scholar] [CrossRef]
- Fan, L. (2024, April 19–21). Long-term forecast of regional economy based on least squares support vector machine. 2024 International Academic Conference on Edge Computing, Parallel and Distributed Computing (ECPDC 2024), Xi’an, China. [Google Scholar] [CrossRef]
- Gerasimov, A. N., Gromov, Y. I., & Gulay, T. A. (2015). Forecasting the indicators of socioeconomic development of the North Caucasus Federal District. Stavropol State Agrarian University. [Google Scholar]
- Gu, Y., Shao, Z., Huang, X., & Cai, B. (2022). GDP forecasting model for China’s provinces using nighttime light remote sensing data. Remote Sensing, 14(15), 3671. [Google Scholar] [CrossRef]
- Habib, M. M., Mileva, E., & Stracca, L. (2017). The real exchange rate and economic growth: Revisiting the case using external instruments. Journal of International Money and Finance, 73, 386–398. [Google Scholar] [CrossRef]
- Hewamalage, H., Ackermann, K., & Bergmeir, C. (2023). Forecast evaluation for data scientists: Common pitfalls and best practices. Data Mining and Knowledge Discovery, 37(2), 788–832. [Google Scholar] [CrossRef]
- Higgins, P., Zha, T., & Zhong, W. (2016). Forecasting China’s economic growth and inflation. China Economic Review, 41, 46–61. [Google Scholar] [CrossRef]
- Hyndman, R., Koehler, A., Ord, K., & Snyder, R. (2008). Forecasting with exponential smoothing: The state space approach. Springer. [Google Scholar]
- Hyndman, R. J., & Athanasopoulos, G. (2021). Forecasting: Principles and practice (3rd ed.). OTexts. Available online: https://otexts.com/fpp3/ (accessed on 17 May 2025).
- Hyndman, R. J., & Khandakar, Y. (2008). Automatic time series forecasting: The forecast Package for R. Journal of Statistical Software, 27(3), 1–22. [Google Scholar] [CrossRef]
- Hyndman, R. J., & Koehler, A. B. (2006). Another look at measures of forecast accuracy. International Journal of Forecasting, 22(4), 679–688. [Google Scholar] [CrossRef]
- International Monetary Fund. (2025). World economic outlook database: April 2025. Available online: https://www.imf.org/en/Publications/WEO/weo-database/2025/April (accessed on 28 June 2025).
- Jallow, H., Mwangi, R. W., Gibba, A., & Imboga, H. (2025). Transfer learning for predicting of gross domestic product growth based on remittance inflows using RNN-LSTM hybrid model: A case study of The Gambia. Frontiers in Artificial Intelligence, 8, 1510341. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y., Guo, Y., & Zhang, Y. (2017). Forecasting China’s GDP growth using dynamic factors and mixed-frequency data. Economic Modelling, 66, 132–138. [Google Scholar] [CrossRef]
- Jibuti, M. (2020). Convergence and growth—Conflicting goals of economics policy—A case study of Georgia. Environmental & Socio-Economic Studies, 8(1), 1–8. [Google Scholar] [CrossRef]
- Kant, D., Pick, A., & Winter, J. d. (2025). Nowcasting GDP using machine learning methods. AStA Advances in Statistical Analysis, 109, 1–24. [Google Scholar] [CrossRef]
- Krkoska, L., & Teksoz, U. (2007). Accuracy of GDP growth forecasts for transition countries: Ten years of forecasting assessed. International Journal of Forecasting, 23(1), 29–45. [Google Scholar] [CrossRef]
- Kumar, B., & Yadav, N. (2023). A novel hybrid model combining βSARMA and LSTM for time series forecasting. Applied Soft Computing, 134, 110019. [Google Scholar] [CrossRef]
- Longo, L., Riccaboni, M., & Rungi, A. (2022). A neural network ensemble approach for GDP forecasting. Journal of Economic Dynamics and Control, 134, 104278. [Google Scholar] [CrossRef]
- Maccarrone, G., Morelli, G., & Spadaccini, S. (2021). GDP Forecasting: Machine learning, linear or autoregression? Frontiers in Artificial Intelligence, 4, 757864. [Google Scholar] [CrossRef] [PubMed]
- Madhou, A., Sewak, T., Moosa, I., & Ramiah, V. (2020). Forecasting the GDP of a small open developing economy: An application of FAVAR models. Applied Economics, 52(17), 1845–1856. [Google Scholar] [CrossRef]
- Makridakis, S., & Wheelwright, S. (1998). Forecasting: Methods and applications (3rd ed.). John Wiley & Sons. [Google Scholar]
- Mariano, R. S., & Ozmucur, S. (2021). Predictive performance of mixed-frequency nowcasting and forecasting models (with application to Philippine inflation and GDP growth). Journal of Quantitative Economics, 19(Suppl. S1), 383–400. [Google Scholar] [CrossRef]
- Mohamed, A. O. (2022). Modeling and forecasting Somali economic growth using ARIMA models. Forecasting, 4(4), 1038–1050. [Google Scholar] [CrossRef]
- National Statistics Office of Georgia. (2025). GEOSTAT. Available online: https://www.geostat.ge/en (accessed on 10 February 2025).
- Perone, G. (2021). Comparison of ARIMA, ETS, NNAR, TBATS and hybrid models for forecasting COVID-19 cases. Journal of Forecasting, 40(6), 1009–1022. [Google Scholar] [CrossRef]
- Perone, G. (2022). Using the SARIMA model to forecast the fourth global wave of cumulative deaths from COVID-19: Evidence from 12 hard-hit big countries. Econometrics, 10(2), 18. [Google Scholar] [CrossRef]
- Perone, G. (2024). A novel hybrid forecasting model for Georgian GDP. International School of Economics at TSU, Policy Paper No. 2024/03. Available online: https://iset-pi.ge/storage/media/other/2024-04-11/d630bf30-f80f-11ee-8485-056f0b7dde49.pdf (accessed on 20 May 2025).
- Pkhaladze, T. (2025). Navigating geopolitical realities: The EU’s strategic positioning in the South Caucasus and Central Asia. European Centre for International Political Economy (ECIPE). Available online: https://ecipe.org/publications/eu-strategic-positioning-in-the-south-caucasus-central-asia/ (accessed on 30 August 2025).
- Poghosyan, K., & Poghosyan, R. (2020). On the applicability of dynamic factor models for forecasting real GDP growth in Armenia. Applied Econometrics, 61, 28–46. [Google Scholar] [CrossRef]
- Puttanapong, N., Prasertsoong, N., & Peechapat, W. (2023). Predicting provincial gross domestic product using satellite data and machine learning methods: A case study of Thailand. Asian Development Review, 40(2), 39–85. [Google Scholar] [CrossRef]
- Richardson, A., Van Florenstein Mulder, T., & Vehbi, T. (2021). Nowcasting GDP using machine-learning algorithms: A real-time assessment. International Journal of Forecasting, 37(2), 941–948. [Google Scholar] [CrossRef]
- Rodrik, D. (2008). The Real exchange rate and economic growth. Brookings Papers on Economic Activity, 2008(2), 365–412. [Google Scholar] [CrossRef]
- Rostan, P., Rostan, A., & Wall, J. (2024). Measuring the resilience to the COVID-19 pandemic of Eurozone economies with their 2050 forecasts. Computational Economics, 63(3), 1137–1157. [Google Scholar] [CrossRef]
- Rusnák, M. (2016). Nowcasting Czech GDP in real time. Economic Modelling, 54, 26–39. [Google Scholar] [CrossRef]
- Sabri, R., Tabash, M. I., Rahrouh, M., Alnaimat, B. H., Ayubi, S., & AsadUllah, M. (2023). Prediction of macroeconomic variables of Pakistan: Combining classic and artificial network smoothing methods. Journal of Open Innovation: Technology, Market, and Complexity, 9(2), 100079. [Google Scholar] [CrossRef]
- Schorfheide, F., & Song, D. (2021). Real-time forecasting with a (standard) mixed-frequency VAR during a pandemic (No. w29535). National Bureau of Economic Research. [CrossRef]
- Sein, P., & Sah, A. N. (2025). Export dynamics, exchange rate volatility, and economic stability: Evidence from Asia-Pacific economies. Humanities and Social Sciences Communications, 12, 808. [Google Scholar] [CrossRef]
- Şen Doğan, B., & Midiliç, M. (2019). Forecasting Turkish real GDP growth in a data-rich environment. Empirical Economics, 56, 367–395. [Google Scholar] [CrossRef]
- Shams, M. Y., Tarek, Z., El-kenawy, E. S. M., Eid, M. M., & Elshewey, A. M. (2024). Predicting Gross Domestic Product (GDP) using a PC-LSTM-RNN model in urban profiling areas. Computational Urban Science, 4, 3. [Google Scholar] [CrossRef]
- Shaub, D., & Ellis, P. (2020). Package ‘forecastHybrid’. Available online: https://cran.r-project.org/web/packages/forecastHybrid/forecastHybrid.pdf (accessed on 10 January 2025).
- Staněk, F. (2023). Optimal out-of-sample forecast evaluation under stationarity. Journal of Forecasting, 42(8), 2249–2279. [Google Scholar] [CrossRef]
- Tashman, L. J. (2000). Out-of-sample tests of forecasting accuracy: An analysis and review. International Journal of Forecasting, 16(4), 437–450. [Google Scholar] [CrossRef]
- The State Statistical Committee of the Republic of Azerbaijan. (2025). System of national accounts and balance of payments. Available online: https://www.stat.gov.az/source/system_nat_accounts/?lang=en (accessed on 2 March 2025).
- The Statistical Committee of the Republic of Armenia. (2025). Economic and financial data for the Republic of Armenia. Available online: https://armstat.am/nsdp/ (accessed on 5 February 2025).
- Timmermann, A. (2006). Chapter 4: Forecast combinations. In G. Elliott, C. W. J. Granger, & A. Timmermann (Eds.), Handbook of economic forecasting (Vol. 1, pp. 135–196). Elsevier. [Google Scholar] [CrossRef]
- Tsuchiya, Y. (2023). Assessing the World Bank’s growth forecasts. Economic Analysis and Policy, 77, 64–84. [Google Scholar] [CrossRef]
- Tsuchiya, Y. (2024). Conservatism and information rigidity of the European Bank for Reconstruction and Development’s growth forecast: Quarter-century assessment. Journal of Forecasting, 43, 1399–1421. [Google Scholar] [CrossRef]
- Tümer, A. E., & Akkuş, A. (2018). Forecasting gross domestic product per capita using artificial neural networks with non-economical parameters. Physica A: Statistical Mechanics and Its Applications, 512, 468–473. [Google Scholar] [CrossRef]
- Yang, Y., Zhang, J., & Wang, L. (2022). A novel general-purpose hybrid model for time series forecasting. Applied Intelligence, 52(2), 2212–2223. [Google Scholar] [CrossRef] [PubMed]
- Yenilmez, İ., & Mugenzi, F. (2023). Estimation of conventional and innovative models for GDP per capita: A comparative analysis of artificial neural networks and Box–Jenkins methodologies. Scientific African, 22, e01902. [Google Scholar] [CrossRef]
- Yoon, J. (2021). Forecasting of real GDP growth using machine learning models: Gradient boosting and random forest approach. Computational Economics, 57, 247–265. [Google Scholar] [CrossRef]
- Zhang, S., Li, Z., Jing, L., & Li, X. (2025). Nowcasting monthly Chinese GDP with mixed frequency data: A model averaging approach. Computational Economics, 1–19. [Google Scholar] [CrossRef]


| Authors | Data Used | Methodology | Investigated Area |
|---|---|---|---|
| Krkoska and Teksoz (2007) | 1994–2004 | Bias and efficiency evaluation | 25 transition countries in Eastern Europe and former Soviet Union |
| Darvas (2011) | Up to 2010 | Cross-country growth regressions | Central and Eastern Europe, Caucasus, and Central Asia |
| Gerasimov et al. (2015) | Not specified | Socioeconomic forecasting scenarios | North Caucasus Federal District, Russia |
| Higgins et al. (2016) | 2000–2015 | BVAR | China |
| Rusnák (2016) | 2005–2012 | DFM | Czech Republic |
| Chernis and Sekkel (2017) | 1999–2016 | DFM, MIDAS, bridge regressions | Canada |
| Jiang et al. (2017) | 2000–2016 | DFM, MIDAS | China |
| Bragoli and Fosten (2018) | 1996–2015 | AR, BR, DFM | India |
| Tümer and Akkuş (2018) | 1996–2015 | ANN with FFBP | 13 countries |
| Cepni et al. (2019) | 2003–2018 | DFM, LASSO | Brazil, Indonesia, Mexico, South Africa, Turkey |
| Şen Doğan and Midiliç (2019) | 2000–2016 | ADL, FADL, MIDAS, and hybrid models | Turkey |
| Domit et al. (2019) | 1987–2015 | BVAR | UK |
| Abdić et al. (2020) | 2006–2016 | ARIMA, BM, FM | |
| Cicceri et al. (2020) | 1995–2019 | AR, BT, KNN, NAR, NARX, OLS, SVR | Italy |
| Claudio et al. (2020) | 1991–2018 | MIDAS | East German |
| Jibuti (2020) | Last 5–10 years | Logarithmic growth models | Georgia |
| Madhou et al. (2020) | 2003–2016 | BVAR, FVAR | Mauritius |
| Poghosyan and Poghosyan (2020) | 1996–2019 | Factor-augmented models (FAAR, FAVAR, Bayesian FAVAR) | Armenia |
| Maccarrone et al. (2021) | 1976–2020 | ARX, KNN, LR, SARIMAX | US |
| Mariano and Ozmucur (2021) | 1999–2019 | DLFM, MIDAS | Philippines |
| Richardson et al. (2021) | 2009–2019 | AR, DFM, EN, GB, LASSO, NN, Ridge, SVM, | New Zealand |
| Yoon (2021) | 2001–2018 | GB, RF | Japan |
| Alaminos et al. (2022) | 1980–2018 | DSVR, DNDT, DRCNN, SVRQBA, QBM, QNN | 70 countries |
| Gu et al. (2022) | 1992–2016 | ARIMA, ARIMAX, SARIMA, LR | Chinese provinces |
| Longo et al. (2022) | 1970–2021 | RNN, DFM-GAS | US |
| Mohamed (2022) | 1960–2022 | ARIMA | Somalia |
| Dritsaki and Dritsaki (2023) | 1995–2022 | ARIMA, ETS | Greece |
| Puttanapong et al. (2023) | 2000–2019 | GLS, NN, RF, SVR | Thai provinces |
| Sabri et al. (2023) | 1980–2022 | ANN, ETS | Pakistan |
| Tsuchiya (2023) | 1999–2019 | World Bank growth forecast evaluation | 130 countries and 6 global regions |
| Yenilmez and Mugenzi (2023) | 1960–2021 | ARIMA, GRNN, MLP, LSTM | Rwanda |
| Almarashi et al. (2024) | 1969–2021 | ARIMA, ETS, NNAR, TBATS and hybrid models | Saudi Arabia |
| Fan (2024) | Not specified | LSSVM | Specific region in China |
| Rostan et al. (2024) | 1994–2022 | ARIMA, ETS, LR, MCS, PM, Wavelet | 17 countries of the Eurozone |
| Shams et al. (2024) | 1961–2021 | PC-LSTM-RNN | India |
| Tsuchiya (2024) | 1994–2019 | Forecast evaluation and asymmetric loss | 38 countries covered by EBRD |
| Kant et al. (2025) | 1992–2018 | DFM, LASSO, MIDAS, RF, RSR | Netherlands |
| Zhang et al. (2025) | 2011–2022 | DFM, EN, JMA, LASSO, MIDAS, Ridge | China |
| Models | Armenia | Azerbaijan | Georgia |
|---|---|---|---|
| ETS | (M,M,M) | (M,A,M) | (M,A,M) |
| NNAR | (1,1,2)4 | (1,1,2)4 | (1,1,2)4 |
| SARIMA | (0,1,0)(0,1,1)4 | (2,0,0)(3,1,0)4 with drift | (0,1,1)(2,1,0)4 |
| TBATS | (0.502,{4,0},-,{<4,1>}) | (0.023,{0,0},1,{<4,1>}) | (0.077,{0,0},1,{<4,1>}) |
| Models | RMSE | MAE | MAPE | MASE | ACF1 |
|---|---|---|---|---|---|
| Armenia | |||||
| ETS | 76,053.37 | 52,243.16 | 3.3663 | 0.3661 | 0.0809 |
| NNAR | 95,504.71 | 66,465.49 | 4.145 | 0.4658 | 0.2469 |
| TBATS | 85,168.42 | 65,544.08 | 4.4943 | 0.1723 | −0.0457 |
| SARIMA | 92,389.99 | 61,973.81 | 3.9364 | 0.4343 | −0.224 |
| Hybrid ES | 78,038.76 | 53,243.5 | 3.3593 | 0.3712 | −0.1 |
| Hybrid EN | 80,657.43 | 54,524.17 | 3.405 | 0.3821 | 0.1825 |
| Hybrid ET | 76,038.35 | 55,285.48 | 3.6549 | 0.3874 | 0.0313 |
| Hybrid NS | 86,336.48 | 59,009.18 | 3.6777 | 0.4135 | −0.0254 |
| Hybrid NT [2] | 77,163.67 | 51,744.49 | 3.254 | 0.3626 | 0.1242 |
| Hybrid ST | 81,683.1 | 60,646.37 | 4.0117 | 0.425 | −0.1218 |
| Hybrid ENS | 79,747.4 | 54,399.15 | 3.383 | 0.3812 | 0.0092 |
| Hybrid ENT [1] | 75,387.76 | 51,574.67 | 3.2356 | 0.3614 | 0.1128 |
| Hybrid EST | 75,478.1 | 54,219.91 | 3.5218 | 0.38 | −0.0669 |
| Hybrid NST | 79,198.45 | 54,975.99 | 3.4615 | 0.3853 | −0.0209 |
| Hybrid SENT | 76,772.39 | 53,192.27 | 3.3249 | 0.3728 | 0.0049 |
| Azerbaijan | |||||
| ETS | 1388.3 | 1005.48 | 5.4094 | 0.3925 | 0.1837 |
| NNAR | 1464.66 | 1192.99 | 6.6422 | 0.4657 | 0.1111 |
| TBATS | 1799.59 | 1410.51 | 7.6692 | 0.8366 | 0.1108 |
| SARIMA | 1410.98 | 1081.68 | 5.7723 | 0.4222 | −0.0052 |
| Hybrid ES | 1346.01 | 997.26 | 5.3372 | 0.3893 | 0.1058 |
| Hybrid ET | 1496.58 | 1122.58 | 6.0807 | 0.4382 | 0.273 |
| Hybrid EN [2] | 1257.67 | 975.98 | 5.4047 | 0.381 | 0.2194 |
| Hybrid NS | 1290.13 | 1002.78 | 5.5279 | 0.3914 | 0.0772 |
| Hybrid NT | 1522.32 | 1190.72 | 6.4748 | 0.4648 | 0.0741 |
| Hybrid ST | 1472 | 1090.45 | 5.8955 | 0.4256 | 0.1485 |
| Hybrid ENS [1] | 1265.57 | 965.84 | 5.267 | 0.377 | 0.1469 |
| Hybrid ENT | 1394.78 | 1067.59 | 5.7895 | 0.4167 | 0.2105 |
| Hybrid EST | 1403.03 | 1023.8 | 5.5169 | 0.3996 | 0.2137 |
| Hybrid NST | 1393.46 | 1074.02 | 5.8408 | 0.4192 | 0.1128 |
| Hybrid ENST | 1353.01 | 1031.39 | 5.5819 | 0.4026 | 0.185 |
| Georgia | |||||
| ETS [2] | 885.64 | 520.89 | 2.7801 | 0.2441 | 0.0273 |
| NNAR | 1188.86 | 754.8 | 3.8325 | 0.3538 | 0.1521 |
| TBATS | 1399.75 | 1112.8 | 6.0662 | 0.4436 | −0.2318 |
| SARIMA | 1058.86 | 611.5227 | 3.0789 | 0.2866 | −0.0071 |
| Hybrid ES [1] | 930.03 | 510.45 | 2.6585 | 0.2393 | 0.0449 |
| Hybrid ET | 1005.25 | 696.45 | 3.8176 | 0.3264 | 0.0192 |
| Hybrid EN | 965.19 | 583.8 | 2.9778 | 0.2736 | 0.0786 |
| Hybrid NS | 1073.58 | 643.08 | 3.2586 | 0.3014 | 0.0358 |
| Hybrid NT | 1195.02 | 836.95 | 4.2162 | 0.3923 | 0.0087 |
| Hybrid ENS | 977.12 | 566.95 | 2.8921 | 0.2657 | 0.0458 |
| Hybrid ENT | 1020.98 | 655.52 | 3.3411 | 0.3072 | 0.072 |
| Hybrid EST | 983.59 | 636.95 | 3.3741 | 0.2985 | 0.0195 |
| Hybrid NST | 1107.87 | 722.97 | 3.6261 | 0.3389 | −0.0047 |
| Hybrid ENST | 1011.97 | 633.12 | 3.2011 | 0.2967 | 0.0443 |
| Models | Armenia | Azerbaijan | Georgia | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ENT | NT | Actual | ENS | EN | Actual | ES | E | Actual | |
| 1Q-2020 | 1,365,750 | 1,382,919 | 1,263,058.8 | 19,377.7 | 19,254 | 18,043.6 | 20,405.7 | 20,012.1 | 19,305.5 |
| 2Q-2020 | 1,574,390 | 1,596,964 | 1,274,458.7 | 20,671.7 | 20,599 | 16,813.2 | 22,484.4 | 22,517.9 | 18,694.2 |
| 3Q-2020 | 1,771,272 | 1,773,823 | 1,743,630.8 | 17,581.8 | 17,544.1 | 18,103.1 | 19,938.7 | 20,174.4 | 23,428. |
| 4Q-2020 | 1,880,519 | 1,895,748 | 1,900,754.3 | 19,956.1 | 19,028.9 | 19,618.2 | 24,962.6 | 24,076.1 | 24,301.8 |
| 1Q-2021 | 1,278,545 | 1,295,823 | 1,282,290.1 | 17,490.1 | 18,640.9 | 19,393.4 | 19,551 | 19,329.4 | 19,739.9 |
| 2Q-2021 | 1,438,366 | 1,419,950 | 1,577,120.1 | 19,666.1 | 19,539.2 | 21,820.5 | 20,911.2 | 22,354.8 | 26,364.3 |
| 3Q-2021 | 1,890,049 | 1,872,546 | 1,909,558.9 | 21,370.7 | 21,127.4 | 23,571 | 27,429.8 | 27,264.1 | 28,413. |
| 4Q-2021 | 2,015,887 | 2,012,124 | 2,222,808.7 | 23,877.4 | 23,668 | 28,418.3 | 28,708.2 | 29,764.3 | 30,112.3 |
| 1Q-2022 | 1,441,316 | 1,407,310 | 1,493,436.3 | 23,861.5 | 23,411.6 | 29,881.5 | 24,652.6 | 24,078.1 | 25,089.6 |
| 2Q-2022 | 1,702,447 | 1,698,711 | 1,899,612.1 | 31,225.9 | 31,680.1 | 33,441.6 | 26,246.5 | 28,962.9 | 30,430.7 |
| 3Q-2022 | 2,139,738 | 2,105,522 | 2,373,227.4 | 34,523.4 | 34,644.9 | 35,212.3 | 33,251.2 | 33,100.8 | 34,120.3 |
| 4Q-2022 | 2,779,721 | 2,944,221 | 2,735,173.6 | 37,537.1 | 37,201.1 | 35,437.3 | 35,641.5 | 36,002.6 | 35,940.6 |
| 1Q-2023 | 2,032,655 | 2,043,999 | 1,789,887.9 | 34,249.3 | 33,197.2 | 29,977.3 | 30,004.6 | 29,029.7 | 28,720 |
| 2Q-2023 | 2,132,951 | 2,153,862 | 2,138,726.2 | 31,790.1 | 31,896.4 | 30,005.1 | 32,606.8 | 33,823.1 | 33,389.5 |
| 3Q-2023 | 2,581,360 | 2,572,687 | 2,575,328.7 | 28,262.9 | 27,395.1 | 31,152.3 | 36,846.9 | 36,862.3 | 36,807.9 |
| 4Q-2023 | 2,944,673 | 2,946,939 | 2,949,232.2 | 32,750.4 | 32,752 | 31,993.7 | 38,644.5 | 39,022.8 | 38,688.5 |
| 1Q-2024 | 2,016,150 | 2,075,621 | 1,922,772.8 | 29,041 | 29,955.8 | 29,096.8 | 31,853.3 | 30,768.7 | 32,438.8 |
| 2Q-2024 | 2,310,898 | 2,317,256 | 2,289,276.2 | 30,631.7 | 31,206.2 | 30,786.3 | 37,915 | 37,748.4 | 38,356.5 |
| COVID-19 | 7.3% | 7.71% | - | 7.55% | 7.74% | - | 10.6% | 9.39% | - |
| Russia-Ukraine | 6.93% | 9.44% | - | 9.98% | 9.89% | - | 5.29% | 3.13% | - |
| Last 8 quarters | 3.84% | 5.21% | - | 4.86% | 5.28% | - | 1.67% | 1.71% | - |
| Total | 5.35% | 6.39% | - | 8.44% | 8.54% | - | 6.05% | 4.77% | - |
| Models | ||||||
|---|---|---|---|---|---|---|
| ENT | NT | ENS | EN | ES | E | |
| COVID-19 | 1.95% | 1.32% | −0.89% | −0.8% | 4.55% | 4.62% |
| Russia-Ukraine | 1.58% | 3.05% | 1.54% | 1.35% | −0.76% | −1.64% |
| Last 8 quarters | −1.51% | −1.18% | −3.58% | −3.26% | −4.38% | −3.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perone, G.; Zambrano-Monserrate, M.A. Forecasting of GDP Growth in the South Caucasian Countries Using Hybrid Ensemble Models. Econometrics 2025, 13, 35. https://doi.org/10.3390/econometrics13030035
Perone G, Zambrano-Monserrate MA. Forecasting of GDP Growth in the South Caucasian Countries Using Hybrid Ensemble Models. Econometrics. 2025; 13(3):35. https://doi.org/10.3390/econometrics13030035
Chicago/Turabian StylePerone, Gaetano, and Manuel A. Zambrano-Monserrate. 2025. "Forecasting of GDP Growth in the South Caucasian Countries Using Hybrid Ensemble Models" Econometrics 13, no. 3: 35. https://doi.org/10.3390/econometrics13030035
APA StylePerone, G., & Zambrano-Monserrate, M. A. (2025). Forecasting of GDP Growth in the South Caucasian Countries Using Hybrid Ensemble Models. Econometrics, 13(3), 35. https://doi.org/10.3390/econometrics13030035







