Real Option Valuation of an Emerging Renewable Technology Design in Wave Energy Conversion
Abstract
1. Introduction
1.1. Motivation and Research Objectives
“If very large wave energy installations are to be privately financed then this will involve pension funds and other very large investment funds and these investors will compare wave energy to other investment opportunities outside the power generation sector. In this case NPV or IRR should be preferred over LCoE.”.
1.2. Summary of Related Work and Our New Contribution
2. Materials and Methods
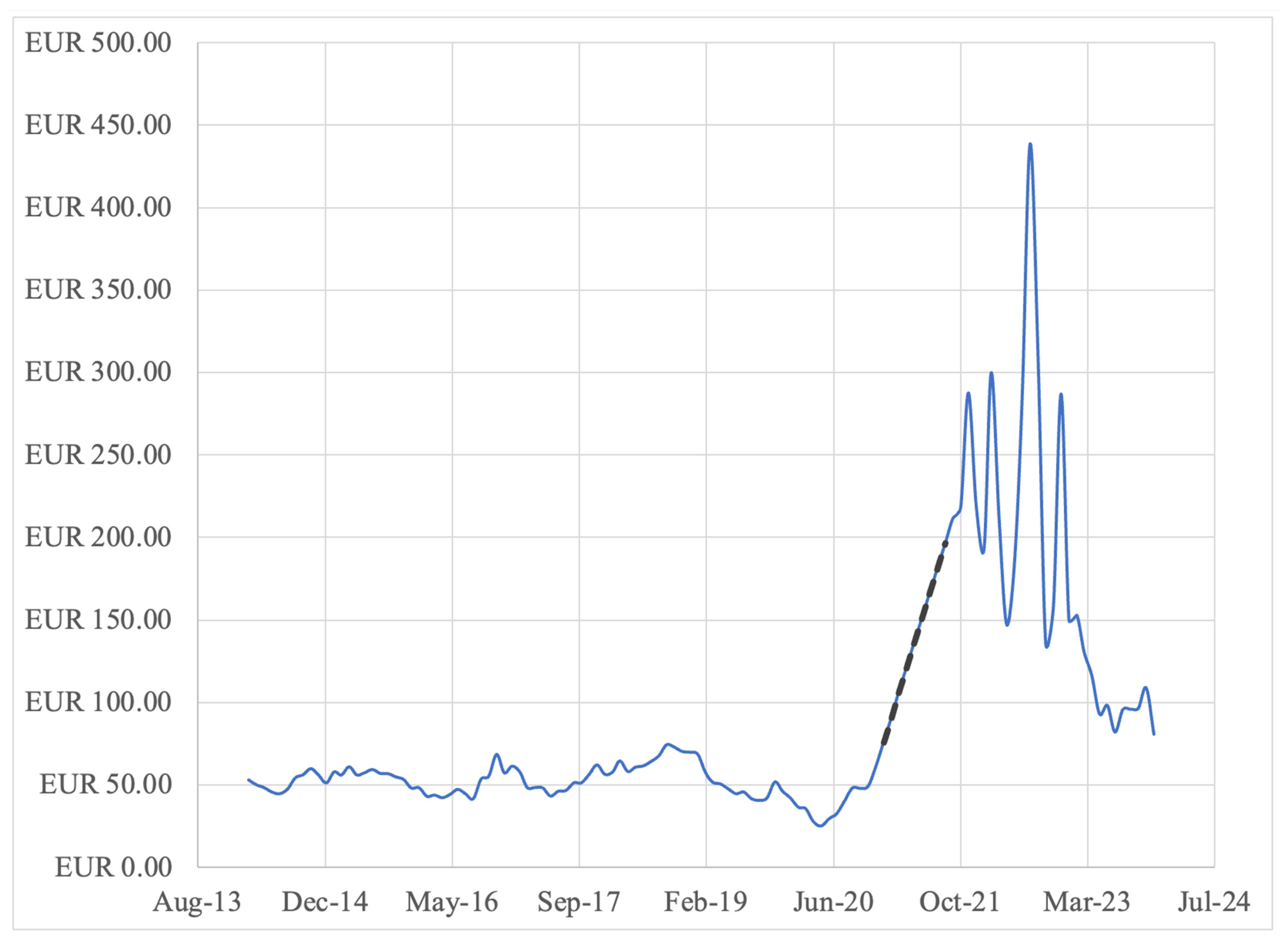
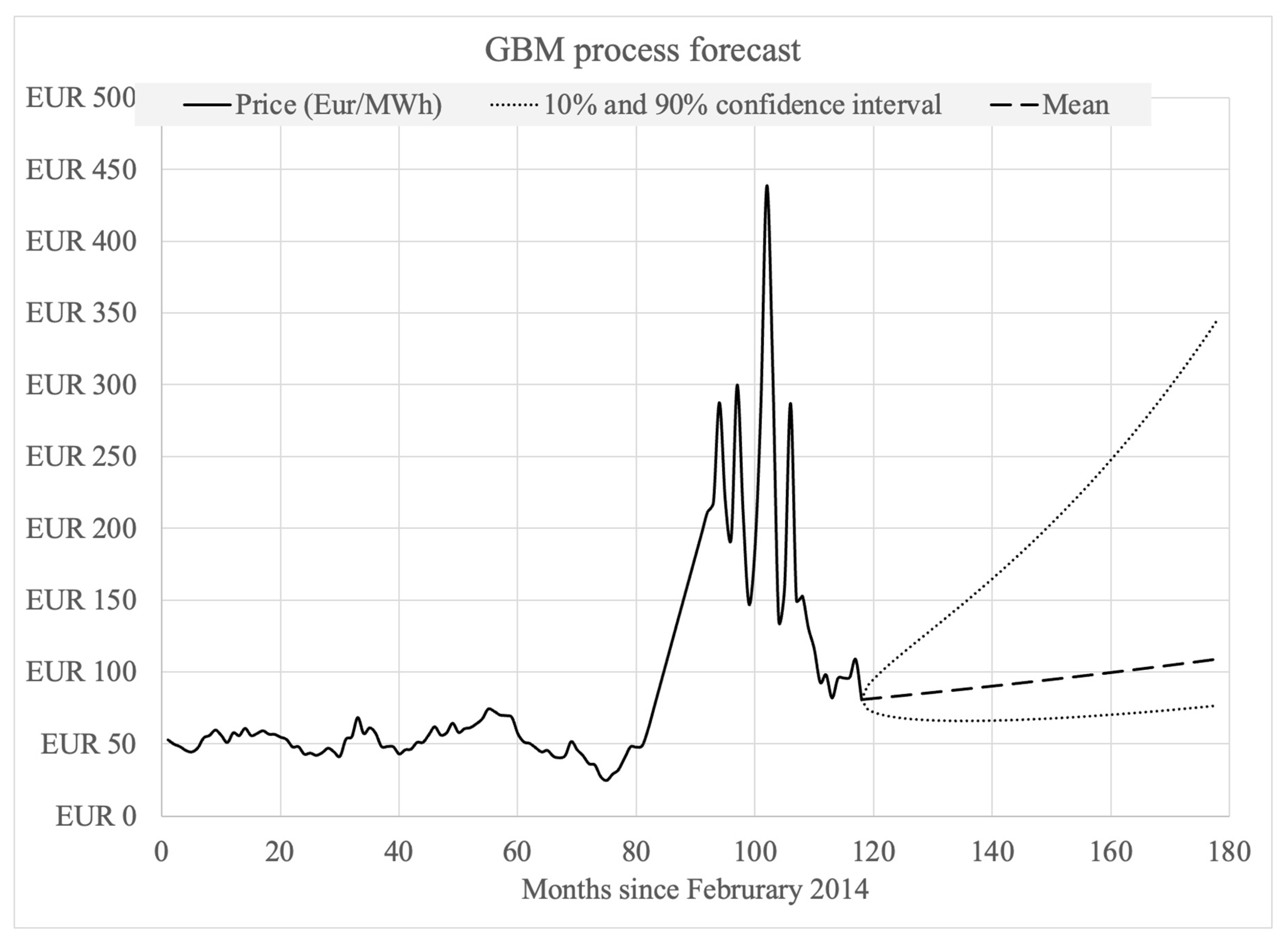
2.1. Energy Price Forecast with Uncertainty
2.2. Site Selection and Annual Energy Production
2.3. Reference Design of a WEC from a TALOS Design
2.4. Estimating Project Capacity
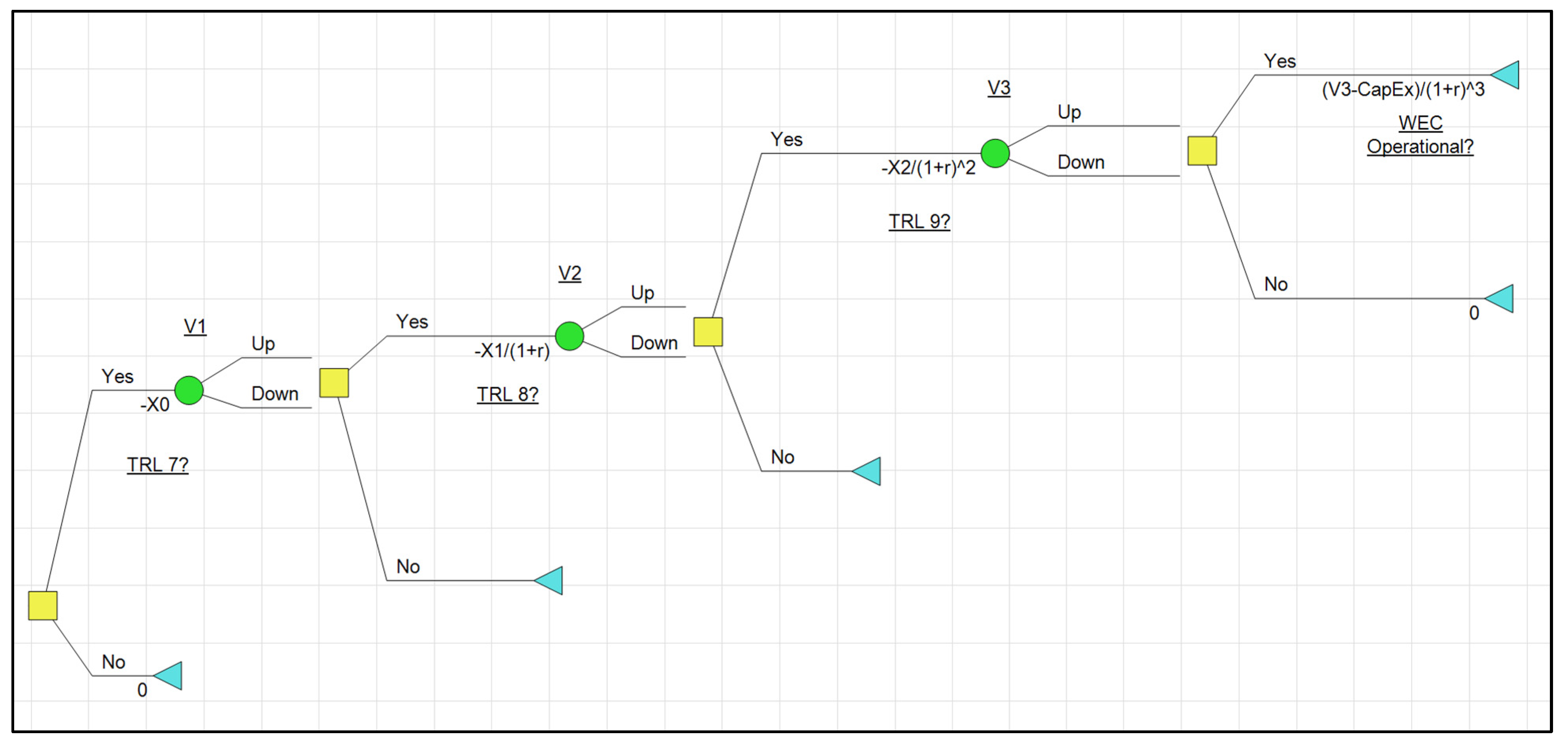
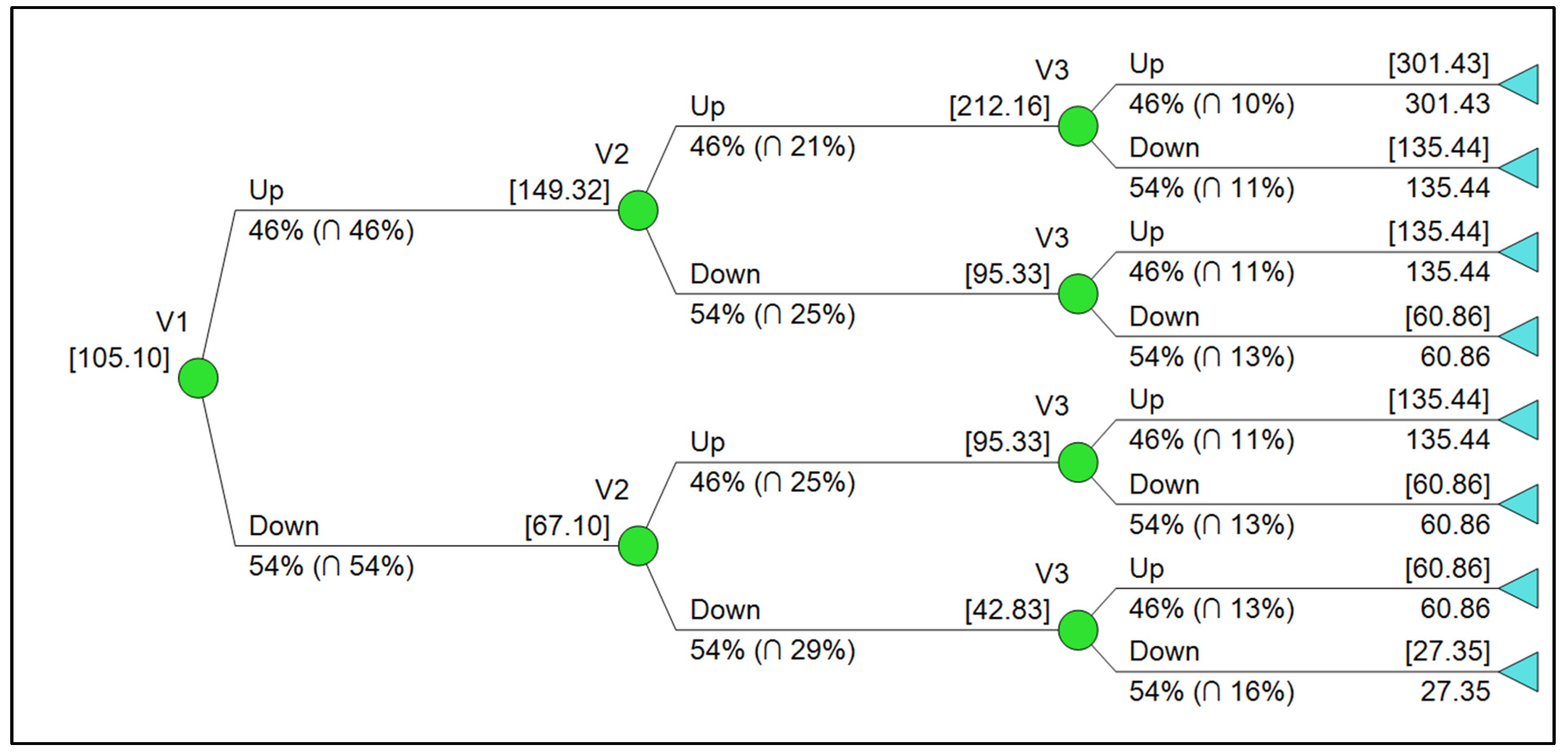
3. Cash Flow and Real Options Model
3.1. Underlying Model
3.2. Research, Development, CapEx, and OpEx Timelines
3.3. Sensitivity Analysis
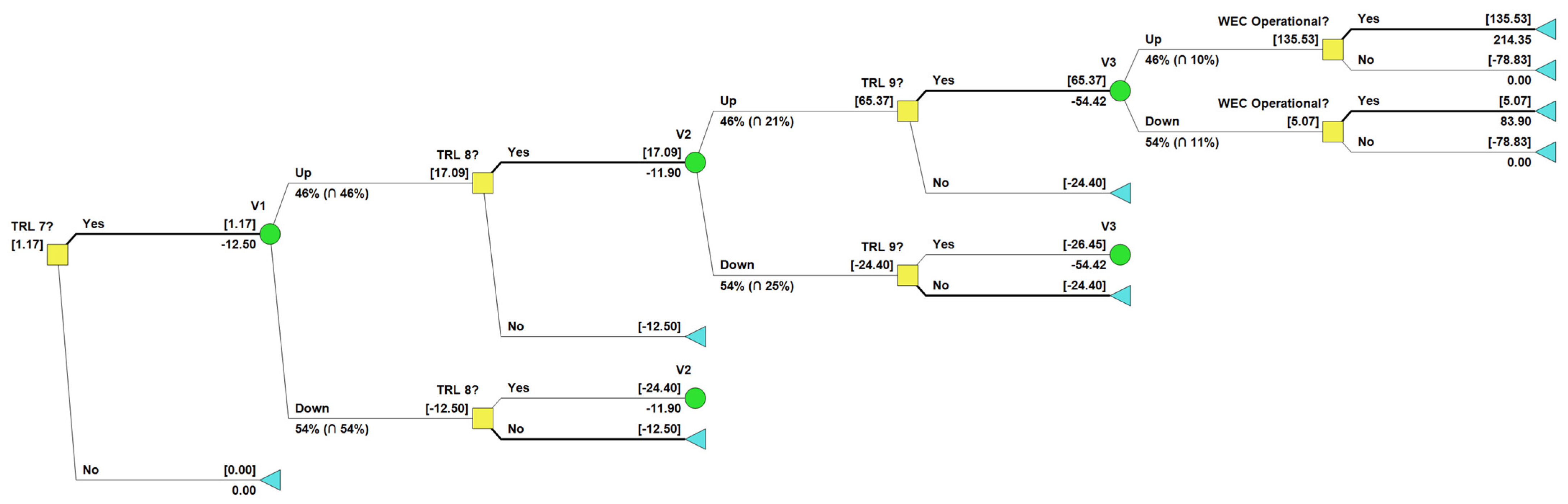
3.4. Risk-Neutral Valuation of the Option to Increase TRL and Operate the WEC System
4. Results and Discussion
Baseline Model Valuation with Option to Deploy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WEC | wave energy conversion |
| LCOE | levelized cost of energy |
| NPV | net present value |
| IRR | internal rate of return |
| TRL | technology readiness level |
| CapEx | capital expense |
| GBM | geometric Brownian motion |
| AEP | annual energy production |
| MEP | monthly energy production |
| CMEMS | Copernicus Marine Environment Monitoring Service |
| UK | United Kingdom |
| TALOS | Technologically Advanced Learning Ocean System |
| OpEx | operating expense |
| LACE | levelized avoided cost of energy |
| NHP | novel high power |
| EPSRC | engineering and physical sciences research council |
| 1 | https://data.marine.copernicus.eu/product/NWSHELF_ANALYSISFORECAST_WAV_004_014/description, accessed on 1 August 2023. |
| 2 | Product NORTH-WESTSHELF_ANALYSIS_FORECAST_WAV_004_014. |
References
- Aldersey-Williams, J., & Rubert, T. (2019). Levelised cost of energy—A theoretical justification and critical assessment. Energy Policy, 124, 169–179. [Google Scholar] [CrossRef]
- Babarit, A., Hals, J., Muliawan, M., Kurniawan, A., Moan, T., & Krokstad, J. (2012). Numerical benchmarking study of a selection of wave energy converters. Renewable Energy, 41, 44–63. [Google Scholar] [CrossRef]
- Beiter, P., Musial, W., Kilcher, L., Maness, M., & Smith, A. (2017). An assessment of the economic potential of offshore wind in the United States from 2015 to 2030 (National Renewable Energy Laboratory Technical Report NREL/TP-6A20-67675). National Renewable Energy Laboratory (NREL). [Google Scholar]
- Beji, S. (2013). Improved explicit approximation of linear dispersion relationship for gravity waves. Coastal Engineering, 73, 11–12. [Google Scholar] [CrossRef]
- Benninga, S. (2014). Financial modeling (4th ed.). MIT Press. [Google Scholar]
- Biyela, S., & Cronje, W. (2016). Techno-economic analysis framework for wave energy conversion schemes under South African conditions: Modeling and simulations. International Journal of Energy and Power Engineering, 10, 786–792. [Google Scholar]
- Black, F. (1976). The pricing of commodity contracts. Journal of Financial Economics, 3, 167–179. [Google Scholar] [CrossRef]
- Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654. [Google Scholar] [CrossRef]
- Chandrasekaran, S., & Sricharan, V. V. S. (2021). Numerical study of bean-float wave energy converter with float number parametrization using WEC-Sim in regular waves with the Levelized Cost of Electricity assessment for Indian sea states. Ocean Engineering, 237, 109591. [Google Scholar] [CrossRef]
- Chang, G., Jones, C. A., Roberts, J. D., & Neary, V. S. (2018). A comprehensive evaluation of factors affecting the levelized cost of wave energy conversion projects. Renewable Energy, 127, 344–354. [Google Scholar] [CrossRef]
- Chen, W. B. (2024). Analysing seven decades of global wave power trends: The impact of prolonged ocean warming. Applied Energy, 356, 122440. [Google Scholar] [CrossRef]
- Copeland, T. E., & Antikarov, V. (2003). Real options, revised edition: A practitioners guide. Texere. [Google Scholar]
- Copeland, T. E., & Tufano, P. (2004). A real-world way to manage real options. Harvard Business Review. [Google Scholar]
- Cox, J., Ross, S., & Rubinstein, M. (1979). Option pricing: A simplified approach. Journal of Financial Economics, 7(3), 229–263. [Google Scholar] [CrossRef]
- Dalbem, M., Brandao, L., & Gomes, L. (2014). Can the regulated market help foster a free market for wind energy in Brazil? Energy Policy, 66, 303–311. [Google Scholar] [CrossRef]
- de Andrés, A., Maillet, J., Todalshaug, J., Möller, P., Bould, D., & Jeffrey, H. (2016). Techno-economic related metrics for a wave energy converters feasibility assessment. Sustainability, 8, 1109. [Google Scholar] [CrossRef]
- de Andrés, A., Medina-Lopez, E., Crooks, D., Roberts, O., & Jeffrey, H. (2017). On the reversed LCOE calculation: Design constraints for wave energy commercialization. International Journal of Marine Energy, 18, 88–108. [Google Scholar] [CrossRef]
- DiLellio, J. (2022). Real option modeling and valuation: A decision analysis approach using DPL and Excel (3rd ed.). Amazon. [Google Scholar]
- Dixit, K., & Pindyck, R. (1994). Investment under uncertainty. Princeton University Press. [Google Scholar]
- Fama, E. (1965). The behavior of stock-market prices. Journal of Business, 64, 34–105. [Google Scholar] [CrossRef]
- Gray, A., Dickens, B., Bruce, T., Ashton, I., & Johanning, L. (2017). Reliability and O&M sensitivity analysis as a consequence of site specific characteristics for wave energy converters. Ocean Engineering, 141, 493–511. [Google Scholar]
- Guanche, R., de Andrés, A., Simal, P., Vidal, C., & Losada, I. (2014). Uncertainty analysis of wave energy farms financial indicators. Renewable Energy, 68, 570–580. [Google Scholar] [CrossRef]
- Guillou, N., Lavidas, G., & Chapalain, G. (2020). Wave energy resource assessment for exploitation—A review. Journal of Marine Science and Engineering, 8, 705. [Google Scholar] [CrossRef]
- Guo, C., Shen, W., De Silva, D., & Aggidis, G. (2023). A review of the levelized cost of wave energy based on a techno-economic model. Energies, 16(5), 2144. [Google Scholar] [CrossRef]
- Hahn, W., DiLellio, J., & Dyer, J. (2014). What do market-calibrated stochastic processes indicate about the long-term price of crude oil? Energy Economics, 44, 212–221. [Google Scholar] [CrossRef]
- Hahn, W., DiLellio, J., & Dyer, J. (2018). Risk premia in commodity price forecasts and their impact on valuation. Energy Economics, 72, 393–403. [Google Scholar] [CrossRef]
- Hahn, W., & Dyer, J. (2008). Discrete time modeling of mean-reverting stochastic processes for real option valuation. European Journal of Operational Research, 184, 534–548. [Google Scholar] [CrossRef]
- Lavidas, G., & Blok, K. (2021). Shifting wave energy perceptions: The case for wave energy converter (WEC) feasibility at milder resources. Renewable Energy, 170, 1143–1155. [Google Scholar] [CrossRef]
- Liang, B., Shao, Z., Wu, G., Shao, M., & Sun, J. (2017). New equations of wave energy assessment accounting for the water depth. Applied Energy, 188, 130–139. [Google Scholar] [CrossRef]
- Liu, J., Li, R., Li, S., Meucci, A., & Young, I. R. (2024). Increasing wave power due to global climate change and intensification of Antarctic Oscillation. Applied Energy, 358, 122572. [Google Scholar] [CrossRef]
- Longstaff, F. A., & Schwartz, E. S. (2001). Valuing American options by simulation: A simple least-squares approach. Review of Financial Studies, 14(1), 113–147. [Google Scholar] [CrossRef]
- Loth, E., Qin, C., Simpson, J. G., & Dykes, K. (2022). Why we must move beyond LCOE for renewable energy design. Advances in Applied Energy, 8, 100112. [Google Scholar] [CrossRef]
- Lu, S., Coutts, K., & Gudgin, G. (2024). Energy shocks and inflation episodes in the UK. Energy Economics, 129, 107208. [Google Scholar] [CrossRef]
- Nordpool Group. (2024). Day ahead auction average prices. Nordpool Group. [Google Scholar]
- Ocean Energy in the European Union. (2022). Status report on technology development, trends, value chains and markets. European Commission Joint Research Centre. [Google Scholar]
- Ocean Energy Systems. (2015). International levelised cost of energy for ocean energy technology. IEA Technology Collaboration Programme for Ocean Energy Systems (OES). [Google Scholar]
- O’Connell, R., & Furlong, R. (2021, September 16–17). An assessment of newly available Copernicus sea surface wave products for mapping wave energy in Irish and UK waters. Proceedings of the 14th CoastGIS International Symposium, Raseborg, Finland. [Google Scholar]
- Pecher, A., & Kofoed, J. P. (2016). Handbook of ocean wave energy. Springer. [Google Scholar]
- Rizaev, I. G., Dorrell, R. M., Oikonomou, C. L., Tapoglou, E., Hall, C., Aggidis, G. A., & Parsons, D. R. (2023). Wave power resource dynamics for the period 1980–2021 in Atlantic Europe’s Northwest Seas. In ISOPE international ocean and polar engineering conference (p. ISOPE-I). ISOPE. [Google Scholar]
- Saulter, A. (2021). North West European shelf Production Centre NWSHELF_REANALYSIS_WAV_004_015 (Issue 1.1). Copernicus Marine Environment Monitoring Service Quality Information Document. Copernicus Marine Service. [Google Scholar]
- Schwartz, E., & Smith, J. (2000). Short-term variations and long-term dynamics in commodity prices. Management Science, 46(7), 893–911. [Google Scholar] [CrossRef]
- Sheng, W., & Aggidis, G. (2023, June 18–23). Hydrodynamic comparisons of TALOS wave energy converter using panel methods. Proceedings of the 33rd International Ocean and Polar Engineering Conference, ISOPE-2023, Ottawa, ON, Canada. [Google Scholar]
- Sheng, W., & Aggidis, G. (2024, June 16–21). Optimizations for improving energy absorption of TALOS WEC. Proceedings of the 34th International Ocean and Polar Engineering Conference, ISOPE-2024, Rhodes, Greece. [Google Scholar]
- Stansby, P., Moreno, E., & Stallard, T. (2017). Large capacity multi-float configurations for the wave energy converter M4 using a time-domain linear diffraction model. Applied Ocean Research, 68, 53–64. [Google Scholar] [CrossRef]
- Tan, J., Polinder, H., Laguna, A., Wellens, P., & Miedema, S. (2021). The influence of sizing of wave energy converters on the techno-economic performance. Journal of Marine Science and Engineering, 9, 52. [Google Scholar] [CrossRef]
- Têtu, A., & Fernandez Chozas, J. (2021). A proposed guidance for the economic assessment of wave energy converters at early development stages. Energies, 14, 4699. [Google Scholar] [CrossRef]
- Winston, W. (2008). Financial models using simulation and optimization II: Investment valuation, options pricing, real options, & product pricing models. Palisade Corporation. [Google Scholar]
- Ziel, F., & Steinert, R. (2018). Probabilistic mid- and long-term electricity price forecasting. Renewable and Sustainable Energy Reviews, 94, 251–266. [Google Scholar] [CrossRef]


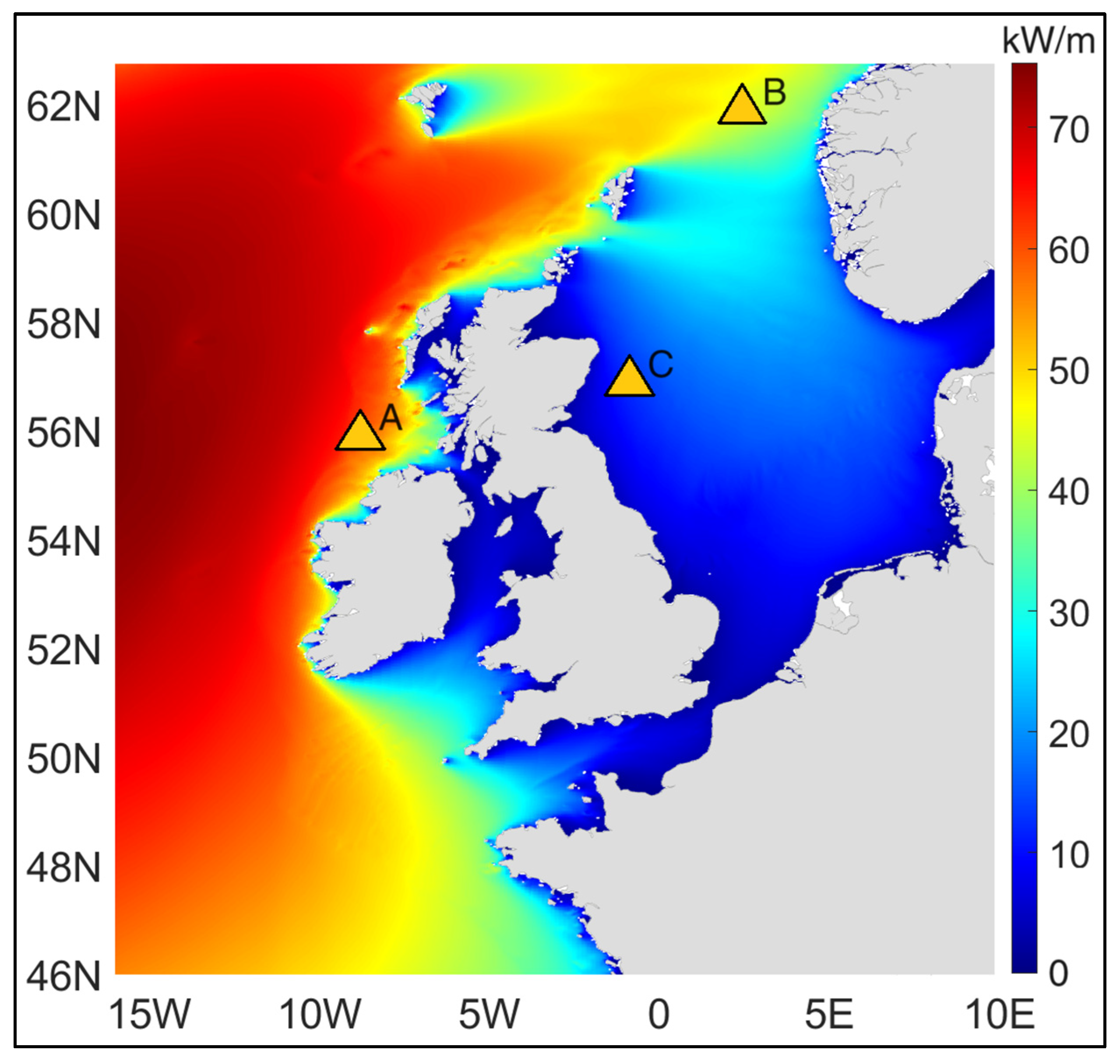


| Site | Winter (December, January, February) | Spring (March, April, May) | Summer (June, July, August) | Autumn (September, October, November) | |
|---|---|---|---|---|---|
(kW/m) | A | 109.634 | 48.3112 | 17.7887 | 55.9195 |
| B | 84.3359 | 38.7219 | 12.5485 | 46.5122 | |
| C | 18.8204 | 10.389 | 4.5571 | 13.5729 |
| Design Parameter | Value |
|---|---|
| 30 m | |
| 0.2 | |
| [December, January, February, March, April, May, June, July, August, September., October, November] = [0.99, 0.99, 0.99, 0.95, 0.95. 0.95, 0.9, 0.9, 0.9, 0.95, 0.95, 0.95] | |
| 25 |
| Site | AEP (MWh/Year) | AEP per WEC (MWh/Year) |
|---|---|---|
| A | 73,005 | 2920 |
| B | 57,394 | 2296 |
| C | 14,869 | 595 |
| Cost Parameter | Values | Source |
|---|---|---|
| CapEx per AEP (EUR/KWh) | EUR 0.455/KWh | Guo et al. (2023, p. 24) |
| OpEx/MWh, Year 1 | 5 to 15% of CapEx | Guo et al. (2023, p. 15) |
| TRL 6 to 7 | EUR 10 to 15 M | Pecher and Kofoed (2016, p. 88) |
| TRL 7 to 8 | EUR 10 to 15 M | Pecher and Kofoed (2016, p. 88) |
| TRL 8 to 9 | EUR 20 to 100 M | Pecher and Kofoed (2016, p. 88) |
| Discount Rate | 8 to 10% | Guo et al. (2023, p. 18). |
| Operating Years | 20 to 50 | Guo et al. (2023, p. 18). |
| Site | NPV | |||
|---|---|---|---|---|
| A | 74.5 M | 33.2 M | 105.1 M | −25.7 M |
| B | 74.5 M | 26.1 M | 82.6 M | −36.1 M |
| C | 74.5 M | 6.77 M | 21.4 M | −64.5 M |
| Variable | Low | Baseline | High |
|---|---|---|---|
| P_wave factor | 0.5 | 1.0 | 1.5 |
| Expected growth rate of wholesale electricity prices | 3% | 6% | 7.5% |
| Discount rate | 8% | 9% | 10% |
| CapEx per AEP (EUR/KWh) | 0.2275 | 0.455 | 0.6825 |
| OpEx/MWh for Year 1 | 22.75 | 45.5 | 68.25 |
| OpEx growth rate | 2% | 4% | 6% |
| TRL 6 to 7 (M EUR) | 10 | 12.5 | 15 |
| TRL 7 to 8 (M EUR) | 10 | 12.5 | 15 |
| TRL 8 to 9 (M EUR) | 20 | 60 | 100 |
| Variable | NPV Low | NPV Baseline | NPV High |
|---|---|---|---|
| TRL 8 to 9 (M EUR) | 9 | −25.7 | −59.3 |
| Expected growth rate of wholesale electricity prices | −63 | −25.7 | 2.8 |
| CapEx per AEP (EUR/KWh) | 6.9 | −25.7 | −58.2 |
| P_wave factor | −50 | −25.7 | −1.3 |
| OpEx/MWh for Year 1 | −5.9 | −25.7 | −45.4 |
| Discount rate | −12 | −25.7 | −36.2 |
| OpEx growth rate | −17 | −25.7 | −38 |
| TRL 6 to 7 (M EUR) | −23 | −25.7 | −28.2 |
| TRL 7 to 8 (M EUR) | −23 | −25.7 | −28 |
| Site | Expected NPV |
|---|---|
| A | EUR 12.6 M |
| B | EUR 1.17 M |
| C | EUR 0.0 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
DiLellio, J.A.; Butler, J.C.; Rizaev, I.; Sheng, W.; Aggidis, G. Real Option Valuation of an Emerging Renewable Technology Design in Wave Energy Conversion. Econometrics 2025, 13, 11. https://doi.org/10.3390/econometrics13010011
DiLellio JA, Butler JC, Rizaev I, Sheng W, Aggidis G. Real Option Valuation of an Emerging Renewable Technology Design in Wave Energy Conversion. Econometrics. 2025; 13(1):11. https://doi.org/10.3390/econometrics13010011
Chicago/Turabian StyleDiLellio, James A., John C. Butler, Igor Rizaev, Wanan Sheng, and George Aggidis. 2025. "Real Option Valuation of an Emerging Renewable Technology Design in Wave Energy Conversion" Econometrics 13, no. 1: 11. https://doi.org/10.3390/econometrics13010011
APA StyleDiLellio, J. A., Butler, J. C., Rizaev, I., Sheng, W., & Aggidis, G. (2025). Real Option Valuation of an Emerging Renewable Technology Design in Wave Energy Conversion. Econometrics, 13(1), 11. https://doi.org/10.3390/econometrics13010011








