Abstract
In actuarial practice, the modeling of total losses tied to a certain policy is a nontrivial task due to complex distributional features. In the recent literature, the application of the Dirichlet process mixture for insurance loss has been proposed to eliminate the risk of model misspecification biases. However, the effect of covariates as well as missing covariates in the modeling framework is rarely studied. In this article, we propose novel connections among a covariate-dependent Dirichlet process mixture, log-normal convolution, and missing covariate imputation. As a generative approach, our framework models the joint of outcome and covariates, which allows us to impute missing covariates under the assumption of missingness at random. The performance is assessed by applying our model to several insurance datasets of varying size and data missingness from the literature, and the empirical results demonstrate the benefit of our model compared with the existing actuarial models, such as the Tweedie-based generalized linear model, generalized additive model, or multivariate adaptive regression spline.
1. Introduction
In short-term insurance contracts, predicting insurance claim amounts is essential for major actuarial decisions such as pricing or reserving. In particular, the development of a full predictive distribution of aggregate claims is fundamental to understanding potential risks. However, it is often not easy to develop the loss distribution properly due to its complex distributional features, such as high skewness, zero inflation, hump shape, and multi-modality. It is known that such complexity stems from the presence of diverse, interconnected unknown risk classes and uncertainty in loss events. Accordingly, there have been many attempts by actuaries to develop loss models, accommodating multiple risk classes and quantifying the uncertainty. This includes the parametric mixture modeling approaches based on log-normal, Weibull, Burr, Pareto, etc. distributions to capture the various aspects of the loss of data (see ). The parametric approaches have been popular because they are conceptually simple, relying on established statistical principles. However, the reality is that we never know how many true risk classes are associated with the loss of data we have. Therefore, it is not surprising that many parametric approaches are often met with model misspecification biases. With respect to this, a Bayesian nonparametric (BNP) approach has been gradually recognized to solve such distributional conundrums in insurance loss analysis. The major difference between the traditional parametric models and the BNP is that the parametric model is built upon a fixed number of risk classes imagined by actuaries, while the BNP does not allow the number of risk classes to be fixed but instead lets the data determine the number of risk classes. In other words, the BNP framework theoretically supports an infinite number of clusters or parameters until it finishes investigating every corner of the parameter space with the Monte Carlo simulation technique. Aligned with such conceptual appeal, there have been several BNP frameworks studied and applied in actuarial practice recently, such as the Gaussian process, Dirichlet process, and Pitman–Yor process. (e.g., ; ; ). Focusing on the Dirichlet process prior, () recently developed the Dirichlet process mixture (DPM) model as a BNP approach that maximizes the fitting flexibility of the loss distribution with the presence of unknown risk classes. In this paper, as an extension of their work, we attempt to go beyond the search for the maximized fitting flexibility, addressing the issues that arise from the presence of covariates, missing data, and aggregate losses (total amount of losses). The implication is that the predictive distribution for the expected aggregate claims developed under Hong and Martin’s Dirichlet process framework cannot obviate the chance of model misspecification bias with the incorporation of covariate effects and log-normal convolution. For example, as covariates add new information that differentiates the data points of the outcome variable, a new structure can be introduced into the data space, and this increases the within-cluster heterogeneity (see ). That aside, the incorporation of missing covariates may exacerbate the existing heterogeneity. Additionally, given that the outcome variable describes the aggregate losses, rather than individual claim amounts, it is difficult to compute the log-normal convolution as it does not have a closed-form solution. In this regard, our study extends their work by addressing the following research questions:
- RQ1. If an additional unobservable heterogeneity is introduced by the inclusion of covariates, then what is the best method to capture the within-cluster heterogeneity in modeling the total losses, comparing several conventional approaches?
- RQ2. If an additional estimation bias results from the use of the incomplete covariates under missing-at-random (MAR) conditions, then what is the best way to increase the imputation efficiency, comparing several conventional approaches?
- RQ3. If an individual loss is distributed with log-normal densities, then what is the best way to approximate the sum of the log-normal outcome variables, comparing several conventional approaches?
2. Discussion on the Research Questions and Related Work
Let be the independent claim amount (reported by each policyholder for a single policy) random variable, defined on a common probability space () from a certain loss distribution, such as a log-normal distribution. Let be a vector of the covariates and be the total claim count, denoting the number of individual claims for a single policy up to time t (policy period). The aggregate claim for a single policy h given time t can be expressed as a convolution, where (assuming that each policy h is a group policy referring to the insurance coverage provided to a group of individuals under a single policy). At the end of the policy period t, let be the total aggregate claim amounts from the total policies received by an insurer. Then, , in which H is the total number of independent policies in the entire portfolio. Note that both convolutions described so far are built upon the assumption that the summands— and —are mutually independent and identically distributed (to maintain the homogeneity of each loss).
The involvement of covariates and the lack of closed-form solutions for the log-normal sum bring about several challenges that violate the assumptions for an accurate estimation of the total aggregate losses . To begin with, the use of covariates gives rise to an additional within-cluster heterogeneity. () described a standard aggregate loss modeling principle, denoting that the expected aggregate claims are obtained by the product of the mean claim counts and severities, where . With the inclusion of covariates , however, a new unknown structure or heterogeneity is introduced into the data space of , and this means that within a single policy can still be independent but cannot be identically distributed. Therefore, , and the total aggregate losses becomes difficult to compute with the conventional collective risk modeling approach. In addition, assuming that the severity follows a log-normal distribution, the computation of becomes quite difficult, as its convolution is not known to have a closed form (see ). Another challenge is the missing covariates in . As shown by (), the missing covariates under the missing-at-random (MAR) assumption lead to biased parameter estimations because the uncertainty in the estimation results of the parameters describing the outcome Y is heavily affected by the quality of the covariates . Again, in this case, cannot be computed properly.
Compounding all this, we propose the Dirichlet process log skew-normal mixture to model . We aim to cope with the within-cluster heterogeneity as suggested by (); () while employing the log skew-normal approximation studied by () to compute each and the sum of log-normal random variables . When it comes to the problem of missing covariates, we exploit the generative capability of the Dirichlet process to capture the latent structure of data, which allows for a rigorous statistical treatment of MAR covariates.
2.1. Can the Dirichlet Process Capture the Heterogeneity and Bias? RQ1 and RQ2
Figure 1 illustrates the unpredictable and heterogeneous nature of the aggregate losses and how this can be addressed by the Dirichlet process. A series of independent, identically distributed developed by for each policy h can be observed and collected within a certain policy period t. However, the presence of unsettled amounts of losses incurred from unknown policyholders or other unobservable features of the policyholders often increase the heterogeneity of each aggregate loss as well as the total aggregate losses . This is because any policyholders in different risk classes can raise claims at any time over a fixed time horizon t, and their unsettled claim amounts (i.e., random ) will not be known in advance. In order to understand the aggregate losses properly, one might need to answer questions such as “How much is ?” and “By which policy or risk class is incurred?”
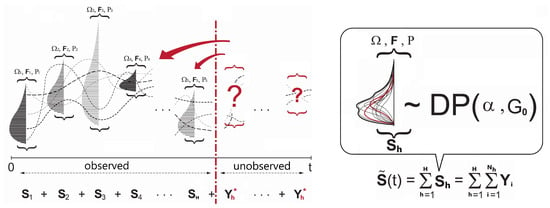
Figure 1.
A series of independent and identically distributed aggregate losses for each policy h and the emergence of unsettled losses tied to unknown policyholders that increases the heterogeneity of (left). The DPM as a mixture model to accommodate the inherent heterogeneity of (right).
With respect to this, () presented a DPM framework that takes into account such sources of heterogeneity via the extensive simulation of and the investigation of multiple mixture scenarios of . By associating each unobservable loss with every possible risk-clustering scenario built upon an infinite dimensional parametric structure, their DPM optimizes the prediction values for the future amount of . () also carried out a useful study of the DPM in insurance practice to capture unobservable heterogeneity in the loss data, such as intracorrelation between claim amounts in the different risk classes. In short, no matter how complex the distribution of the loss is, the DPM is capable of accommodating any distributional properties—multi-modes, skewness, heavy tails, etc.—resulting from unobservable heterogeneity and therefore dramatically minimizes model misspecification biases.
Having said that, however, if considering covariates to better understand the different risk classes, then one might introduce an additional source of heterogeneity into the scene, which prevents each cluster from being identically distributed. In regard to this, () pointed out that the covariate effect can be incorporated into the DPM framework by considering the weight of the mixture component to be covariate-dependent rather than constant. This allows the mixture model to keep each risk class homogeneous while identifying the unique loss patterns (relationship between the loss amount and the risk factors) of different types of policyholders. The research on covariate-dependent weights includes a series of stick-breaking method studies on regression, time series, loss distribution fitting problems, etc. in insurance. () presented the general stick-breaking framework to construct a prior distribution over an infinite number of mixture components, ensuring that the mixing weights are probabilities and their distribution is discrete with a probability of one. (, ) studied the order-based stick-breaking method that allows the mixing weights to vary over the covariate effect. They ordered the mixing weights according to a covariate-dependent ranking and associated risk classes for similar covariate values with similar orderings. () developed the probit stick-breaking process, aiming to diversify families of prior distributions while preserving computational simplicity. They suggest that the covariate effects can be integrated with the probit transformations of normal random variables to produce mixing weights, which is the replacement for the characteristic beta distribution in the stick formulation. The stick-breaking-based mixing weights can be used in determining the clustering structures in the time series or regression analysis. () and () studied applications of the stick-breaking process to hierarchical prior development for the coefficients of autoregressive time series models. () and () proposed combining the stick-breaking-based prior with the Gaussian density to build a regression model.
In this article, we use a generalized representation of the stick-breaking process developed by () to incorporate the covariate effects into the mixing weight. This is because, with the inclusion of the covariates subject to missingness, the advanced stick-breaking approaches listed above cannot be viable solutions. On the contrary, the DPM with Sethuraman’s stick-breaking formulation offers a useful bedrock (such as a multi-purpose joint distribution) for a MAR covariate treatment. As a generative modeling approach, the DPM framework coupled with Sethurman’s stick-breaking method models both the outcomes and covariates jointly to produce cluster memberships. This is used as key knowledge to identify the latent structure of the data and thus estimate the missing information (see ). For example, in the domain of medicine research, () developed a novel imputation strategy for the MAR covariate using the joint model of the BNP framework. A further survey of imputation methods based on the nonparametric Bayesian framework can be found in the work of () and the references therein.
2.2. Can a Log Skew-Normal Mixture Approximate the Log-Normal Convolution? RQ3
The log-normal distribution has been considered a suitable claim amount distribution due to its nonnegative support, right-skewed curve, and moderately heavy tail to accommodate some outliers. However, if one generalizes the individual claim amount by introducing a log-normal distribution, then the convolution computation for fails because the exact closed form for the log-normal sum is unknown.
() presented several existing methods for the log-normal sum approximation that have been studied in the literature. This includes the moment-matching approximation approaches such as minimax approximation, least squares approximation, log-shifted gamma approximation, and log skew-normal approximation. The distance minimization approaches—minimax approximation or least squares approximation—described by (); () are conceptually simple, but they require fitting the entire cumulative densities to the sum of the claim amounts, which can be computationally expensive and fail easily when the number of summands increases. The log-shifted gamma approximation suggested by () has less strict distributional assumptions, but it is not particularly accurate at the lower region of the distribution. In our study, special attention is paid to the possibility of the log skew-normal approximation method for the sake of simplicity. A skew-normal distribution as an extension of a normal distribution has a third parameter to naturally explain skewness apart from the other parameters (for a location and spread). () pointed out that one can exploit the third parameter of the skew-normal distribution to capture different skewness levels of each summand. By taking the log of the skew-normal densities, we can approximate , the sum of the log-normal . Using the log skew-normal as the underlying distribution for in the DPM framework, one can eliminate the need to compute the cumulative density curve, and its closed-form density and the optimal distribution parameters for can be easily obtained by the moment-matching technique. For further details, see () and the references contained within.
2.3. Our Contributions and Paper Outline
The contributions of this study are twofold. First, we propose a new method to efficiently model the sum of log-normal outcome variables representing the aggregate insurance losses . Using the log skew-normal model in the BNP framework, we cope with the (1) lack of a closed form for the log-normal convolution and (2) heterogeneity in the log-normal random variable at the same time. Second, we tackle the adverse impact triggered by the inclusion of covariates into the aggregate loss modeling framework. This encompasses the added heterogeneity across and the missing information fed by the MAR covariates . To our knowledge, there have been no previous attempts to estimate the log skew-normal mixture within the BNP framework or use the DPM to handle the MAR covariate in insurance loss modeling.
The rest of this paper is structured as follows. In Section 3, we describe the proposed modeling framework for , assuming a log-normal distributed and the inclusion of both continuous and discrete covariates . This section also presents our novel imputation approach for the MAR covariate within the DPM framework. Section 4 clarifies the final forms of the posterior and predictive densities accordingly. Section 5 presents our empirical results and validates our approach by fitting to two different datasets with different sample sizes drawn from the R package CASdatasets and the Wisconsin Local Government Property Insurance Fund (LGPIF). This is followed by a discussion in Section 6.
3. Model: DP Log Skew-Normal Mixture for
3.1. Background
Consider that there are multiple unknown risk classes (clusters) across the claim information within each policy, and then the individual aggregate claims for the policy h would have diverse characteristics that cannot be explained by fitting a single log skew-normal distribution. In order to approximate the distribution that captures such diverse characteristics in , we seek to investigate diverse clustering scenarios. To this end, as suggested by (), we exploit the infinite mixture of log skew-normal clusters and their complex dependencies by employing a Dirichlet process. The Dirichlet process produces a distribution over clustering scenarios (with clustering parameters):
where G denotes the clustering scenarios, and the important components of G are as follows:
- : the parameters of the outcome variable defined by cluster j.
- : the parameters of the covariates defined by cluster j.
G, as a single realization of the joint cluster probability vector sampled from the DPM model, takes independent partitions of the sample space of the support of . Through sufficient simulations of G, the Dirichlet process investigates all possible clustering scenarios rather than relying on a single best guess. The overall production of G is controlled with two parameters: the precision and a base measure . The precision controls a variance of sampling G in the sense that larger generates new clusters more often to account for the unknown risk classes. The base measure , as the mean of DP(), is a DP prior over the joint space of all parameters for the outcome model, covariate model, and the precision , as shown in ().
Note that the original research on DPM by () mainly focused on the random cluster weights that were not tied to the covariates . On the other hand, in our model, the covariate effects are incorporated into the development of the cluster weights . All calculations for the development of the DPM modeling components in this paper are based on the principles introduced by (); (), and ().
3.2. Model Formulation with Discrete and Continuous Clusters
If the goal of modeling is to perform prediction and uncertainty quantification with the presence of heterogeneity (resulting from previously unseen risk factors), then the DPM framework exploits the generative process to this end. This process provides all the necessary components to construct the predictive distribution, using the infinite clustering scenarios based on the joint distribution of observed outcomes, covariates, as well as hidden variables. Let the outcome be , denoting the H different aggregate claims (incurred by the H different policies). We assume that the covariate is binary and is Gaussian, and then our baseline DPM model can be expressed as follows:
where j is the risk class index, for the covariates, for parameters describing the outcome, and for parameters explaining the covariates. is modeled as a mixture of a point mass at 0 with positive values distributed with a log skew-normal density to address the complications of zero inflation in the loss data, while models the probability of the outcome being zero using a multivariate logistic regression. Variable Definitions has a brief description of all parameters used in this study.
When considering a Dirichlet process log skew-normal mixture to house the multiple unknown risk classes in , it is necessary to differentiate the forms of the mixture components, depending on the types of clusters they use: discrete and continuous. While keeping the inference of the cluster parameters data-dominated, the DPM first develops discrete clusters based on the given claim information and then extrapolates certain unobservable clusters of claims by examining the heterogeneity (or hidden risk classes) of each cluster. In this process, the DPM develops new continuous clusters additionally and assesses them with some probabilistic decision-making algorithms, rendering the parameter estimations computationally efficient and asymptotically consistent (see ).
The discrete mixture components (clusters) in the DPM framework have the standard form that is useful in accounting for the observed classes, such as policy information for aggregate losses (see ). In calculating the discrete cluster probabilities, we assume that the nonzero outcome and covariates are distributed with the densities denoted by
where and are standard normal probability and cumulative density functions for the log skew-normal density, respectively. To model the outcome data for the policy h, the DPM takes the general form of the mixture
where j is the cluster index, and are the outcome and covariate parameters to explain the risk clusters, respectively, and , for the functions of the covariates , represents the cluster component weights (mixing coefficient) satisfying . However, when the total number of mixture components is determined later from the data we have, the new continuous clusters can be introduced by (with its infinite-dimensional parametric structure) in order to tackle the additional unknown risk classes. This involvement of can address the within-class heterogeneity in by confronting the current discrete clustering result and investigating the homogeneity more closely. As the new clusters are considered countably infinite, their corresponding forms for the outcome and covariate models to obtain the continuous cluster are given by
They are also known as a “parameter-free outcome model” and a “parameter-free covariate model”, respectively, for developing the new continuous cluster mixture. Given a collection of outcome-covariate data pairs , the DPM puts together the current discrete clusters and new continuous clusters to update the mixture form in Equation (3), with help from the Monte Carlo Markov chain method (using sufficiently simulated samples of the major parameters ). Consequently, the sample G described in Equation (1) becomes , where denotes discrete clusters and the continuous cluster as a point mass distribution at the random locations sampled from . Aligned with such flexible cluster development, the form of the predictive distribution can be molded based on the knowledge extracted from G and the finite number of clusters J as follows:
The finalized cluster weights in Equation (5) are secured through computing the two submodels below for the discrete and continuous cluster weights, respectively, which reflect the properties of the clusters and relevant covariates:
where is the precision parameter to control the acceptance chances of the new clusters, is the number of observations in cluster j, is the parameter-free covariate model in Equations (4b) and (4c) to support the new continuous cluster, and is the covariate model to support the current discrete clusters. Note that Equation (5) is derived from the joint distribution of {} conditioned on the posterior samples. The mixture components— and —as a product comprise the joint distribution {}. The mixing weights are obtained by the covariate models of that explain and . This is based on a Polya Urn distribution suggested by (), which is aligned with the result from the generalized stick-breaking representation of the DPM presented by ().
3.3. Modeling with a Complete Case Covariate
The joint posterior update for the outcome and covariate parameters——in Equations (5) and (6) can be made through the DPM Gibbs sampler given in Algorithm A2 in Appendix B. In a nutshell, the DPM Gibbs sampler obtains draws from the analytically intractable posterior, alternating between two stages to ensure convergence: (1) updating the cluster membership for each observation and (2) updating the parameters given the cluster partitioning. By looping through this algorithm many times (e.g., M = 100,000 iterations), each iteration might give a slightly different selection of the new clusters based on the Polya Urn scheme (see ), but the log-likelihood calculated at the end of each iteration can help keep track of the convergence of the selections. A detailed description of these two stages in Algorithm A2 is given below.
- Stage 1.
- Cluster membership update:
- Step I.
- Let the cluster-index for the observation h be . First, the cluster membership j is initialized by some clustering methods such as hierarchical or k-means clustering. This provides an initial clustering of the data ( as well as the initial number of clusters.
- Step II.
- Next, with the parameters sampled from the DPM prior described in Section 4.1 and the conditional probability term on lines 6 and 9 in Algorithm A2 for the observation assignment, the ultimate probabilities of the selected observation h being in the current discrete clusters and the proposed continuous cluster are computed, respectively. (The use of such a nonparametric prior to the development of a new continuous cluster allows the shape of the cluster to be driven by the data). Note that the term is known as the Chinese Restaurant process (see ) probability given bywhere c is a scaling constant to ensure that the probabilities add up to one and is the collection of cluster indices assigned to every observation without the cluster index of the observation h. A larger results in a higher chance of developing the new continuous cluster and adding to the collection of the existing discrete clusters. Since the number of clusters is not fixed, and the sequence of cluster assignment to observation cannot be ordered, one might be concerned about the sampling variance or convergence problem in the Gibbs sampler. In this regard, we expect that Equation (7) can carry out stable simulations with the Gibbs sampler. () pointed out that from the example of Escobar’s algorithm, the sequence in which the observation h arrives in the cluster is exchangeable under this conditional probability distribution described in Equation (7). This means that the ultimate joint distribution to update the cluster memberships from lines 4 to 10 in Algorithm A2 does not depend on the order of the sequence in which the observations arrive.
- Step III.
- Lastly, the new cluster membership is determined and updated by the Polya Urn scheme using a multinomial distribution based on the resulting cluster probabilities. This is briefly illustrated in Figure 2. Please note how the development of the cluster weighting components in Equations (6a) and (6b) is made in Figure 2.
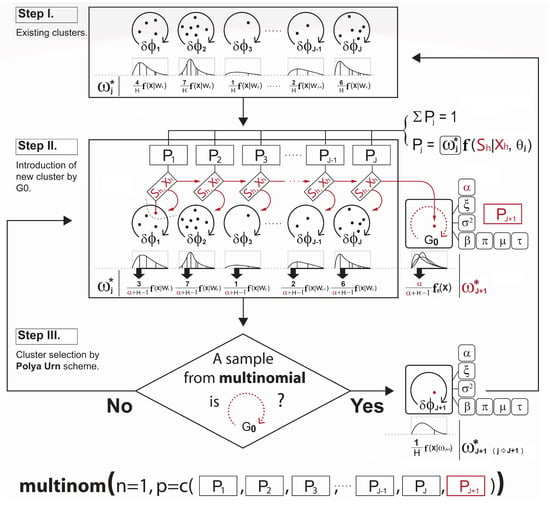 Figure 2. A schematic of the cluster membership update process in Stage 1. In Step I, the algorithm initializes the cluster memberships and parameters including . In Step II, the cluster probabilities of the selected observation h are computed. In Step III, the new cluster membership is determined by the Polya Urn scheme, and the new clustering weight component is created.
Figure 2. A schematic of the cluster membership update process in Stage 1. In Step I, the algorithm initializes the cluster memberships and parameters including . In Step II, the cluster probabilities of the selected observation h are computed. In Step III, the new cluster membership is determined by the Polya Urn scheme, and the new clustering weight component is created.
- Stage 2.
- Parameter update:
- Once all observations have been assigned to particular clusters at a given iteration in the Gibbs sampling, the parameters of our interest— and —for each cluster are updated, given the new cluster membership. This is accomplished using the posterior densities denoted by , and , in which represents all observations in cluster j. When it comes to the forms of the prior and posterior densities from lines 17 to 23 in Algorithm A2 that are used to simulate the parameters , we detail them in Appendix A.
The DPM model described here can be characterized by the investigation of the infinite number of clustering scenarios coupled with covariates. The simulated outcome model and its predictive model in Equation (5) show that although the DPM framework allows infinite-dimensional clustering, the dimension of the sampling output G is adaptive, as it is a mixture with at most finite components determined by the data themselves (its dimension cannot be greater than the total sample size H). This gives the model flexibility, and throughout such modeling flexibility, the clustering scenarios G accommodate all distributional properties of the given claims as well as the additional unknown claims. In this process, the DPM captures the within-class heterogeneity across the observations, and thus the resulting clusters can be kept as homogeneous as possible. As a result, the unobserved claim problem mentioned in Figure 1 can be addressed, which leads to a better prediction of the future value of .
3.4. Modeling with the MAR Covariate
The DPM model for complete case data was discussed in Section 3.3. In this Section, we present our novel imputation strategy for the MAR covariate in the DPM framework in which the missing values are explained by the observed data and the cluster membership. We focus on the missingness in the binary type covariate. With the model definition in Equation (1), suppose the binary covariate has missingness within it. To handle this MAR covariate, we suggest the following modifications (additional steps) to add to the DPM Gibbs sampler given in Algorithm A2:
- (a)
- Adding an imputation step in the parameter update stage:It is true that the missing covariate impacts on the parameter——update. For the parameters for the covariates , only the observations h without the missing covariate are used for updating. If the cluster does not have any observations with complete data for that covariate, then a draw from the prior distribution for would be used to update it. For the parameters for the outcome , however, we must first impute values for the missing covariates for all observations h within the cluster j. Since we already defined a full joint model——in Section 3.2, we can obtain draws for the MAR covariate from the imputation model, such asat each iteration in the Gibbs sampling. Each imputation model is proportional to the joint distribution as a product of the outcome model and the covariate model that has missing data. The imputation process is illustrated in depth in Figure 3. Once all missing covariate values have been imputed, then the parameters of each cluster are recalculated and sampled from the posterior of . After this cycle is complete in the Gibbs sampling, the imputed data are discarded, and the same imputation steps are repeated for every iteration.
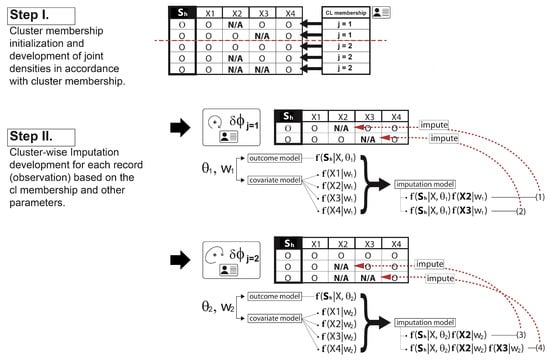 Figure 3. An example of the MAR imputation for the parameter update stage in the DPM Gibbs sampler for Step I and Step II. The imputations are made cluster membership-wise.
Figure 3. An example of the MAR imputation for the parameter update stage in the DPM Gibbs sampler for Step I and Step II. The imputations are made cluster membership-wise. - (b)
- Adding a reclustering step in the cluster membership update stage:To calculate each cluster probability after the parameter updates, the algorithm redefines the two main components: (1) the covariate model and (2) the outcome model. For the covariate model , we set this equal to the density functions of only those covariates with complete data for observation h. Assuming that , and the covariate is missing for observation h, then we drop and only use in the covariate model:This is the refined covariate model for the cluster j with the observation h, where the data in are not available. For the outcome model , the algorithm simply takes the imputation model in Equation (8) for the observation h and integrates it out of the covariates with missingness . This reduces the degrees of variance introduced by the imputations. In other words, as the covariate is missing for observation h, this missing covariate can be removed from the term that it is being conditioned on. Therefore, the refined outcome model isThe same process is performed for each observation with missing data and each combination of missing covariates. Hence, using Equations (9) and (10), the cluster probabilities and the predictive distribution can be obtained as illustrated in Step III in Figure 4.
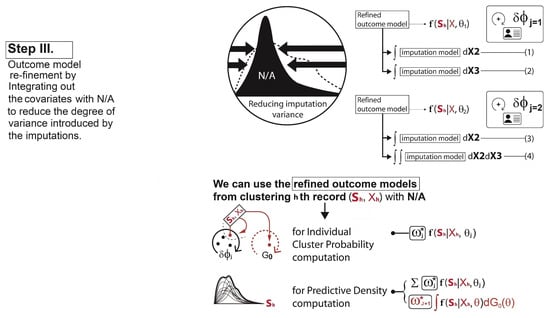 Figure 4. An example of the refined outcome model development for the cluster membership update stage in the DPM Gibbs sampler: Step III. Using these models, each cluster probability and the predictive density can be calculated.
Figure 4. An example of the refined outcome model development for the cluster membership update stage in the DPM Gibbs sampler: Step III. Using these models, each cluster probability and the predictive density can be calculated. - (c)
- Re-updating the parameters:The cluster probability computation is followed by the parameter reestimation for each cluster, which is illustrated via the diagram in Figure 5. This is the same idea as what we have discussed about the parameter () update in Section 3.3.
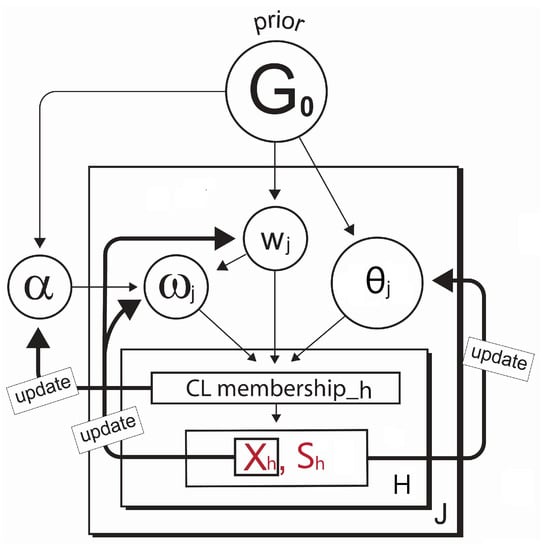 Figure 5. Parameter reestimation after the reclustering with imputation in the Gibbs sampler. This diagram articulates flows of the parameter updates using the acyclic graphical representation. The process cycles until achieving convergence.
Figure 5. Parameter reestimation after the reclustering with imputation in the Gibbs sampler. This diagram articulates flows of the parameter updates using the acyclic graphical representation. The process cycles until achieving convergence.
3.5. Gibbs Sampler Modification in Detail for the MAR Covariate
Now, we set out some modifications for the DPM Gibbs sampler in Algorithm A2 to address the MAR covariate . We aim to provide the details of the DPM implementation integrated with the MAR imputation strategy discussed in Section 3.4. The Gibbs sampler will alternate between imputing missing data and drawing parameters until it reaches convergence. We elaborate below on the modifications that fit into Algorithm A2 to update the clustering scenarios and the posterior cluster parameters properly:
- (a)
- (b)
- (c)
- In line 22, with the presence of a missing covariate , the imputation should be made before simulating the parameter as follows:The imputation model formulation above was discussed in Section 3.4.
Again, these modifications allow us to draw the missing covariate values from the conditional posterior density at each iteration using the Metropolis–Hastings algorithm with a random walk.
4. Bayesian Inference for with the MAR Covariate
In this section, we examine the parameter models and data models in depth to update the parameters of the DPM model given in Algorithm A2 under the assumption that the binary covariate is subject to missingness. The efficient simulation for the model parameters , and requires proper parameterization in the parameter models: the prior parameter model and posterior parameter model. The accurate estimations of cluster probabilities relies on the legitimate development of data models—the outcome model and covariate model—and the model parameter simulation results that govern the data model behaviors.
4.1. Parameter Models and the MAR Covariate
Our study is based on a three-level hierarchical structure. The first level regards data models such as the log skew-normal outcome model and the Bernoulli and Gaussian covariate models, the second level involves parameter models such as to explain the data, and the third level is developed from the generalized regression to explain the parameters or the related hyperparameters, such as and , to set a probabilistic distribution on the parameter vectors , . See Variable Definitions for further information on the variables. Given the model definition in Equation (1), we consider a set of conjugate parameter models due to its computational advantages (see ). For , , and , the prior models come in as
and their corresponding kernels chosen in this study are listed in Appendix A.1. Accordingly, the Dirichlet process prior (probability measure) in our case can be defined as . With a feed of the observed data inputs , the prior models for each cluster j described above will be updated into the following posterior models analytically apart from :
and their corresponding parameterizations are elaborated upon in Appendix A.2. Note that the value of the precision parameter relies on the total cluster number J and thus does not vary by the cluster membership j, and its derivation of the posterior parameterization is not subject to the Bayesian conjugacy. Hence, we instead adapt the form of the posterior density for the suggested by (), and its derivation is shown in Appendix C.1. As for , there are no conjugate priors available for the log skew-normal likelihood, but their posterior samples can be secured by the conventional Metropolis–Hastings algorithm described in Algorithm A1 in Appendix A.
Considering that has missing data, although the parameterizations of the posterior densities for the covariate parameter model of and the precision listed in Equation (11) are not affected, any outcome data of with missingness should be dropped. Therefore, and are defined with the only observations in cluster j that are not missing. This imputation example is provided in Appendix C.2. For the outcome parameter model of , the missing covariate must be imputed before its posterior computation shown in Algorithm A2. Once the parameters are updated with the imputation, the data models can be constructed as described in Equations (9) and (10).
4.2. Data Models and the MAR Covariate
Data models are the main components for the cluster probability computations depicted in Figure 2. As with the development of parameter models, the covariate data model of ignores the observations with missingness, while the outcome data model of requires completing the covariates beforehand. However, the formulation of their densities can be more complex due to the marginalization process with respect to the missing covariate. In addition, as discussed in Section 3.2, the data model development is bound by the types of clusters, such as discrete clusters and continuous clusters :
- (a)
- Covariate model for the discrete clusterFocusing on the scenario where is binary, is Gaussian, and the only covariate with missingness is , we simply drop the covariate to develop the covariate model for the discrete cluster. For instance, when computing the covariate probability term for the hth observation in cluster j, the covariate model simply becomes due to the missingness of . As we have , which is assumed to be normally distributed as defined in Equation (1), its probability term isinstead of
- (b)
- Covariate model for the continuous clusterIf the binary covariate is missing, then by the same logic, we drop the covariate for the continuous cluster. However, using Equation (4), the covariate model for the continuous cluster integrates out the relevant parameters simulated from the Dirichlet process prior as follows:instead ofThe derivation of the distributions above is provided in Appendix C.3.
- (c)
- Outcome model for the discrete clusterIn developing the outcome model, as with the parameter model case discussed in Section 4.1 and Appendix C.2, it should be ensured that the covariate is complete beforehand. With all missing data in imputed, the outcome model for the discrete cluster is obtained by marginalizing the joint out the MAR covariate , which is a log skew-normal mixture expressed as follows:instead of
- (d)
- Outcome model for the continuous clusterOnce a missing covariate is fully imputed, and the outcome model is marginalized out and conditioned to the MAR covariate , the outcome model for the continuous cluster can also be computed by integrating out the relevant parameters using Equation (4):However, it can be too complicated to compute its form analytically. Instead, we can integrate the joint model out of the parameters using Monte Carlo integration. For example, we can perform the following steps for each :
- (i)
- Sample from the DP prior densities specified previously;
- (ii)
- Plug these samples into ;
- (iii)
- Repeat the above steps many times, recording each output;
- (iv)
- Divide the sum of all output values by the number of Monte Carlo samples, which will be the approximate integral.
5. Empirical Study
5.1. Data
The performance of our DPM framework is assessed based on two insurance datasets. They highlight data difficulties such as unobservable heterogeneity in an outcome variable and MAR covariates. For simplicity, in each dataset, we only consider two covariates—one binary and one continuous—to explain its loss information (outcome variable). In this study, all computations on these two datasets are performed in the same data format:
The first dataset is PnCdemand, which is about the international property and liability insurance demand of 22 countries over 7 years from 1987 to 1993. Secondly, we use a dataset drawn from the Wisconsin Local Government Property Insurance Fund (LGPIF) with information about the insurance coverage for government building units in Wisconsin for the years from 2006 to 2010. The first one—PnCdemand—can be obtained from the R package CASdatasets. The dataset is relatively small as it has cases with an outcome variable GenLiab, the individual loss amount under the policies of general insurance for each case. As for the covariates, we consider one indicator variable of the statutory law system (LegalSyst: one or zero) and one continuous variable that measures a risk aversion rate (RiskAversion) for each area. For additional background on this dataset, see the work of (). In the LGPIF dataset, the insurance coverage samples for the government properties from policies are provided. The outcome variable is the sum of all types of losses (total losses) for each policy. Only the covariates—LnCoverage and Fire5—are considered in our study. Fire5 is a binary covariate that indicates fire protection levels, while LnCoverage is a continuous covariate that informs a total coverage amount in a logarithmic scale. For further details, see the work of ().
Histograms of the losses of the two datasets are exhibited in Figure 6. Due to the significant skewness, the loss data were log-transformed to attain Gaussianity. As shown in the histograms, each distribution displayed different characteristics in regard to skewness, modality, excess of zeros, etc. Note that the zero-inflated outcome variable in the LGPIF data (Figure 6(b1,b2)) required a two-part modeling technique that distinguished the probabilities of the outcome being zero and positive.
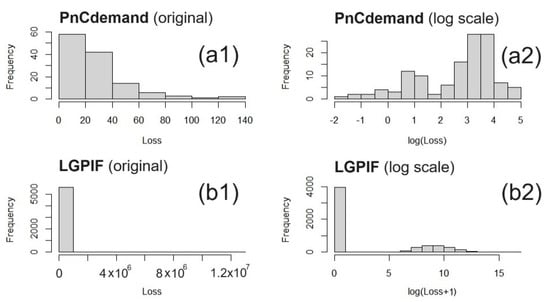
Figure 6.
Histograms of the outcomes and log-transformed outcomes for the two datasets: (a1,a2) PnCdemand and (b1,b2) LGPIF.
5.2. Three Competitor Models and Evaluation
Our DPM framework is compared to other commonly used actuarial models in practice. We employ three predictive models as benchmarks, namely a generalized linear mixture model (GLM), multivariate adaptive regression spline (MARS), and generalized additive model (GAM). In each dataset, we assume different distributions for the outcome variables, and thus the three benchmark models are built upon the different outcome data models. For example, the PnCdemand dataset (a1,a2) that appeared in Figure 6 had a high frequency of small losses without zero values, and hence it was safe to use a gamma mixture to explain the outcome data. As for the LGPIF data in Figure 6(b1,b2), we considered the outcome data model based on a Tweedie distribution to accommodate the zero-inflated loss data. The benchmark models were implemented in R with the mgcv, splines, and mice packages.
All four models were trained, and investigations were performed in terms of model fit, prediction accuracy, and the conditional tail expectation (CTE) of the predictive distribution. Note that the goodness of fit value for the DPM is not available. () argued that the goodness of fit evaluation for the DPM is unnecessary, as underfitting is mitigated by the unbounded complexity of the DPM while overfitting is alleviated by the approximation of the posterior densities over each parameter in the DPM. () pointed out that the posterior predictive check, which compares the simulated data under the fitted DPM to the observed data, can be useful for studying model adequacy, but its usage cannot be for model comparison. Therefore, the goodness of fit was only compared between the rival models.
For the evaluation of prediction performance, the sum of square prediction error (SSPE) and the sum of square absolute error (SAPE) were used in order to measure the differences between the predicted value and actual value . The SSPE penalizes large deviations much more than the SAPE. We preferred the SAPE over the SSPE because our data were heavily skewed, which could result in outliers occurring more often. In the distribution fitting problem, each data point had equal importance, and we did not need to penalize larger error values that could arise from the outliers.
5.3. Result with International General Insurance Liability Data
For this dataset, a training set of a response and covariate pair with n = 160 records and a test set of a response and covariate pair with m = 80 records were constructed. We implemented the following DPM:
A log-normal likelihood was chosen to accommodate the individual loss :GenLiab for a policy h. The covariate , RiskAversion, was subject to missingness and found to depend on (a MAR case). This was addressed by the internalized imputation process as discussed in Figure 3. The posterior parameters of were estimated with our DPM Gibbs sampler presented in Algorithm A2. The algorithm ran 10,000 iterations until convergence, and the resulting scenarios of the clustering mixture are shown in Figure 7. The plot reveals the overlays of predictive densities on the log scale from the last 100 iterations that were tied to convergence. Figure 8 lists the classical data imputation result using the multivariate imputation chained equation (MICE) and the predictive densities produced from our rival models: GLM, GAM, and MARS.
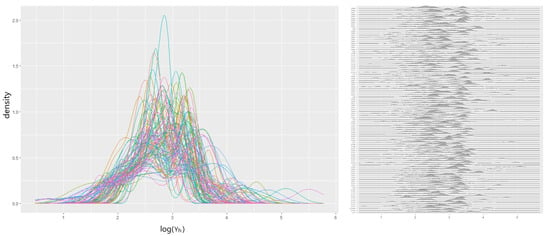
Figure 7.
LogN-DPM with the PnCdemand dataset, with the last 100 in-sample predictive densities (scenarios) overlaid together.
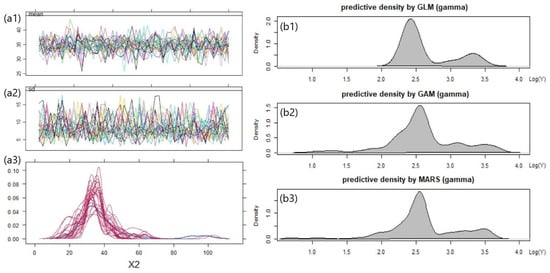
Figure 8.
MICE trace plots (a1,a2), the imputation comparison plot for the MAR covariate (a3), and in-sample predictive densities produced from GLM, GAM, and MARS (b1–b3) with the PnCdemand dataset.
The MICE runs multiple imputation chains and selects the imputation values from the final iteration. This process results in multiple candidate datasets. The trace plots (a1,a2) monitor the imputation mean and variance for the missing values in the dataset. In the covariate distribution plot (a3), the density of the observed covariate, shown in blue, is compared with the ones of the imputed covariate for each imputed dataset, shown in red. The parameter inferences for the rival models were performed based on the imputed datasets tied to convergence (see ). The gamma distribution was chosen to fit the rival models as was continuous and positively skewed with a constant coefficient of variation. The gamma-based predictive density plots (b1,b2,b3) estimated with GLM, GAM, and MARS look similar, showing unusual bumps near the right tail.
In Figure 9, a histogram of the outcome data in the test set is displayed. The posterior mean densities for the out-of-sample predictions produced with our DPM along with the rival models’ density estimates are overlaid on the histogram. Judging from the plot, one can say that our DPM model generated the best approximation. While the rival models generated smooth, mounded curves to make predictions, our DPM captured all possible peaks and bumps, which was closer to the actual situation.
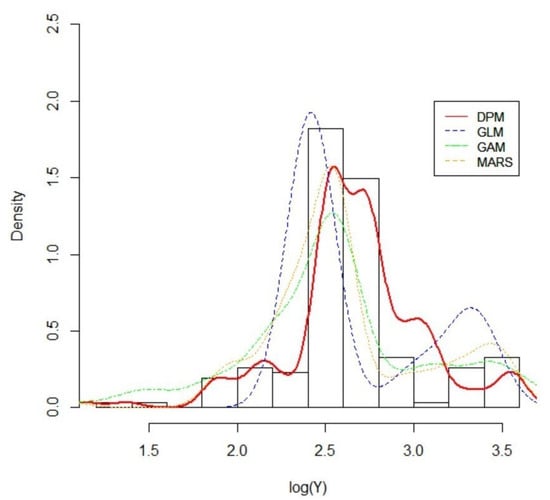
Figure 9.
A histogram of the observed loss on the log scale and the out-of-sample predictive densities for the typical class of a policy in the PnCdemand dataset.
According to Table 1, our DPM obtained the highest SSPE compared with other rival models. At first glance, our DPM might seem like a failure. However, upon closer inspection, it becomes evident that the presence of outliers greatly influenced its performance. Remarkably, our DPM excelled at capturing these outliers, leading to the highest SSPE. This is evidenced by the lowest SAPE of our DPM. In other words, as the SAPE weights all the individual differences equally, we can assume that the rival models tend to pay too much attention to the most probable data points and miss the majority of outliers. This can be mainly due to the insufficient sample size as well. However, our DPM had good performance under small sample sizes as long as there was sufficient prior knowledge available. From the perspective of CTE, Table 1 shows that our DPM proposed a heavier tail than other rival models, which reflects that our DPM captured more uncertainties given the small sample size.

Table 1.
The comparison of out-of-sample modeling results based on the dataset PnCdemand.
5.4. Result with LGPIF Data
For this dataset, a training set of a response and covariate pair with n = 4529 records and a test set of a response and covariate pair with m = 1110 records were constructed. We implemented the following DPM:
As the outcome , total losses, for a policy h in this dataset was considered to be distributed with the sum of the log-normal densities, a log skew-normal likelihood was chosen to approximate this convolution (see ). The covariate , Fire5, was subject to missingness under the MAR condition, and the internalized imputation process illustrated in Figure 3 resolved this issue without creating imputed datasets. As the outcome exhibited zero inflation, we employed a two-part model using a sigmoid and indicator function. Our DPM Gibbs sampler described in Algorithm A2 produced the posterior parameters of with 10,000 iterations until convergence. Figure 10 reveals the resulting scenarios of the clustering mixture. In the plot, there are 100 predictive densities suggested by our DPM, each of which stands for the convergence of the estimation results.
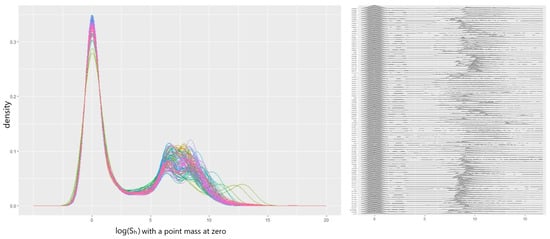
Figure 10.
LogSN-DPM with the LGPIF dataset, with the last 100 in-sample predictive densities (scenarios) overlaid together.
The output of the MICE and the resulting predictive densities from the rival models are displayed in Figure 11. The rival models were built upon a Tweedie distribution due to its ability to account for a large number of zero losses and the flexibility to capture the unique loss patterns of the different classes of policyholders. According to the plot, all three rival models reasonably captured zero inflation, but the GAM tended to suggest more bumps that indicated a need for further assessment of the prediction uncertainty.
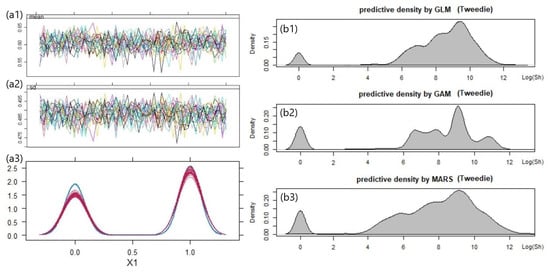
Figure 11.
MICE trace plots (a1,a2), the imputation comparison plot for the MAR covariate (a3), and in-sample predictive densities produced from GLM, GAM, and MARS (b1–b3) with the LGPIF dataset.
The overall out-of-sample prediction comparison is made in the histogram overlayed with predictive density curves generated from the four models in Figure 12. From the plot, it is apparent that the posterior predictive density proposed by our DPM best explained the new samples, while other rival models kept producing multiple peaks.
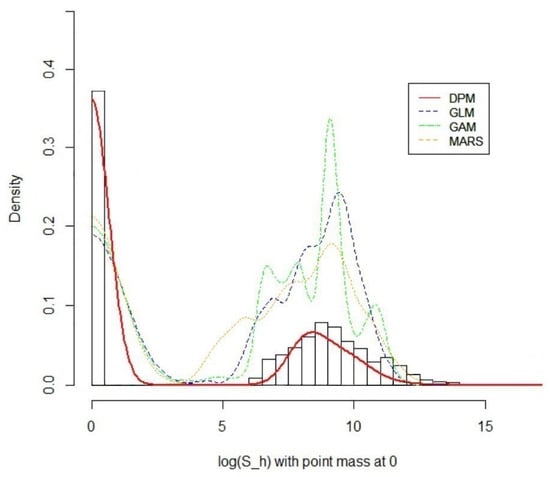
Figure 12.
A histogram of the observed total loss on the log scale and the out-of-sample predictive densities for the typical class of a policy in the LGPIF dataset.
The improved prediction performance of our DPM is confirmed by the smallest SAPE in Table 2. However, as for the SSPE, our DPM showed the second-highest performance, being slightly lower than that of the GAM. This is mainly due to the ability of our DPM to capture outliers more often, which is heavily penalized by the SSPE that squares the term. In terms of CTE, all three rival models suggested a similar level of tailedness, reflecting the knowledge obtained from the observed data. However, our DPM went beyond this and proposed a much heavier tail. This was because our DPM accommodated the presence of outliers and shaped the tail behavior based on the combined knowledge of the prior parameters and the observations available.

Table 2.
The comparison of out-of-sample modeling results based on the LGPIF dataset.
6. Discussion
This paper proposes a novel DPM framework for actuarial practice to model total losses with the incorporation of MAR covariates. Both the log-normal and log skew-normal DPM presented overall good empirical performances in capturing the shape of the distribution, out-of-sample prediction, and the estimation of the tailedness. This suggests that it is worth considering our DPM framework in order to avoid various model risks or biases in insurance claim analysis.
6.1. Research Questions
Regarding RQ1, we proposed a DPM framework to address the within-cluster heterogeneity emerging from the inclusion of covariates. By allowing for an infinite number of clustering scenarios determined by the observations as well as prior knowledge, our DPM outperformed the rival methods in drawing the lines for the cluster membership. This can be assessed by examining the homogeneity of the resulting clusters. In our case, we fit cluster-wise GLMs (based on gamma and Tweedie distributions) to the data points within each resulting cluster to compare the goodness-of-fit, and the consistent AICs across all clusters endorse the benefits of the DPM. Similarly, our rival methods, such as GAM or MARS, can capture heterogeneity by using customized smooth functions across different subsets of the data, but we observed some statistically insignificant smooth terms, indicating the presence of heterogeneity in the cluster.
In terms of RQ2, we suggest incorporating the imputation steps into the parameter and cluster membership update process in the DPM Gibbs sampler by leveraging the joint distribution of the observed outcomes and missing covariates. This approach allows the imputed values to be consistent with the observed data, preserving the correlation structure within the dataset. In order to make a comparison of our approach with an existing alternative, we additionally employed a chained equation technique. The multiple sets of imputed values simulated from both approaches were investigated, and the results show that our DPM Gibbs sampler did not represent a significant improvement over the chained equation because their average estimates of the imputed values were closer to each other. However, we feel that this result was mainly due to the relatively low dimensionality of the datasets we used and their simple data structure. The specific characteristics or dependencies in the data and the complexity of the missing patterns would give different results in practice.
As for RQ3, we fit a log skew-normal density to the aggregate loss outcomes. In order to assess its performance, one can consider minimax approximation, least squares approximation, log-shifted gamma approximation, etc. as the competitors. () provided a useful comparison between these competitors by overlaying the cumulative density curves for each technique, but the experiments were grounded in the simulated log-normal data with the predefined parameters and assumptions, which cannot be easily controlled in real-world scenarios. Therefore, we feel that the choice of the best approximation technique should be made based on the identification of the specific characteristics of the dataset. In our case, each summand in our dataset was significantly different from each other in magnitude (the minimax approach was inappropriate), and the LGPIF data had a large volume of data smaller than five (the log-shifted gamma was inappropriate). Therefore, we chose a log skew-normal density that was relatively simple while giving an accurate approximation at the lower region of the distribution.
6.2. Future Work
There are several concerns with our log skew-normal DPM framework:
- (a)
- Dimensionality: First, in our analysis, we only used two covariates (binary and continuous) for simplicity. Hence, more complex data should be considered. As the number of covariates grows, the likelihood components (covariate models) to describe the covariates grow, which results in the shrinking of the cluster weights. Therefore, using more covariates might enhance the level of sensitivity and accuracy in the creation of cluster memberships. However, it can also introduce more noise or hidden structures that render the resulting predictive distributions unstable. In this sense, further research on the problem of high dimensional covariates in the DPM framework would be worthwhile.
- (b)
- Measurement error: Second, although our focus in this article was the MAR covariate, mismeasured covariates is an equally significant challenge that impairs the proper model development in insurance practice. For example, () pointed out that “model risk” mainly arises due to missingness and measurement error in variables, leading to flawed risk assessments and decision making. Thus, further investigation is necessary to explore the specialized construction of the DPM Gibbs sampler for mismeasured covariates, aiming to prevent the issue of model risk.
- (c)
- Sum of the log skew-normal: Third, as an extension to the approximation of total losses (the sum of individual losses) for a policy, we recommend researching ways to approximate the sum of total losses across entire policies. In other words, we pose the following question: “How do we approximate the sum of log skew-normal random variables?” From the perspective of an executive or an entrepreneur whose concern is the total cash flow of the firm, nothing might be more important than the accurate estimation of the sum of total losses in order to identify the insolvency risk or to make important business decisions.
- (d)
- Scalability: Lastly, we suggest investigating the scalability of the posterior simulation with our DPM Gibbs sampler. As shown in our empirical study on the PnCdemand dataset, our DPM framework produced reliable estimates with relatively small sample sizes (). This was because our DPM framework actively utilized significant prior knowledge in posterior inference rather than heavily relying on the actual features of the data. In the result from the LGPIF dataset, our DPM exhibited stable performance at a sample size as well. However, a sample size of over 10,000 was not explored in this paper. With increasing amounts of data, our DPM framework raises the question of computational efficiency due to the growing demand for computational resources or degradation in performance (see ). This is an important consideration, especially in scenarios where the insurance loss information is expected to grow over time.
Author Contributions
All authors contributed substantially to this work. Conceptualization, M.K.; methodology, M.K., D.L., M.B. and M.C.; software, M.K. and D.L.; validation, M.K., M.B. and M.C.; formal analysis, M.K.; investigation, M.K., M.B. and M.C.; resources, M.K.; data curation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, M.K., M.B. and M.C.; visualization, M.K.; supervision, M.B. and M.C.; project administration, M.B. and M.C.; funding acquisition, M.C. All authors have read and agreed to the published version of this manuscript.
Funding
This research was conducted with financial support from the Science Foundation Ireland under Grant Agreement No.13/RC/2106 P2 at the ADAPT SFI Research Centre at DCU. ADAPT, the SFI Research Centre for AI-Driven Digital Content Technology, is funded by the Science Foundation Ireland through the SFI Research Centres Programme.
Data Availability Statement
Data and implementation details are available at https://github.com/mainkoon81/Paper2-Nonparametric-Bayesian-Approach01 (accessed on 25 May 2023).
Acknowledgments
We extend our appreciation to the Editor, Associate Editor, and anonymous referee for their thorough review of this paper and their valuable suggestions, which have greatly contributed to its enhancement.
Conflicts of Interest
The authors declare no conflict of interest.
Variable Definitions
The following variables and functions are used in this manuscript:
| Observation index i in a policy h | |
| Policy index h with a total policy number H | |
| Cluster index for J clusters | |
| Cluster index for observation h | |
| Number of observations in cluster j | |
| Number of observations in cluster j where observation h was removed from | |
| Individual loss i in a policy observation h | |
| Outcome variable which is in a policy observation h. | |
| Outcome variable which is across entire policies | |
| Vector of covariates (including ) for a policy observation h | |
| Vector of covariate (Fire5) | |
| Vector of covariate (Ln(coverage)) | |
| Individual value of covariate (Fire5) for a policy observation h | |
| Individual value of covariate (Ln(coverage)) for a policy observation h | |
| Parameter model (for prior) | |
| Parameter model (for posterior) | |
| Data model (for continuous cluster) | |
| Data model (for discrete cluster) | |
| Logistic sigmoid function—expit(·)—to allow for a positive probability of the zero outcome | |
| Set of parameters——associated with for cluster j | |
| Set of parameters——associated with for cluster j | |
| Cluster weights (mixing coefficient) for cluster j | |
| Vector of initial regression coefficients and variance-covariance matrix (i.e., ) obtained from the baseline multivariate gamma regression of | |
| Regression coefficient vector for a mean outcome estimation | |
| Cluster-wise variation value for the outcome | |
| Skewness parameter for log skew-normal outcome | |
| Vector of initial regression coefficients and variance-covariance matrix obtained from the baseline multivariate logistic regression of | |
| Regression coefficient vector for a logistic function to handle zero outcomes | |
| Proportion parameter for Bernoulli covariate | |
| Location and spread parameter for Gaussian covariate | |
| Precision parameter that controls the variance of the clustering simulation. For instance, a larger allows selecting more clusters. | |
| Prior joint distribution for all parameters in the DPM: , and . It allows all continuous, integrable distributions to be supported while retaining theoretical properties and computational tractability such as asymptotic consistency and efficient posterior estimation. | |
| Hyperparameters for inverse gamma density of | |
| Hyperparameters for Beta density of | |
| Hyperparameters for Student’s t density of | |
| Hyperparameters for Gaussian density of | |
| Hyperparameters for inverse gamma density of | |
| Hyperparameters for gamma density of | |
| Random probability value for gamma mixture density of the posterior on | |
| Mixing coefficient for gamma mixture density of the posterior on |
Appendix A. Parameter Knowledge
Appendix A.1. Prior Kernel for Distributions of Outcome, Covariates, and Precision
* gamma regression, logistic regression.
Appendix A.2. Posterior Inference for Outcome, Covariates, and Precision
| Algorithm A1 Posterior inference |
|
Appendix B. Baseline Inference Algorithm for the DPM
Once we obtain decent parameter samples from the posterior distributions, the posterior predictive density can be computed via the DPM Gipps sampling. The basic inference algorithm is described below. Note that the modification details for the missing data imputation are provided in Section 3.5. In every iteration, the algorithm updates the cluster memberships based on the parameter samples and observed data at hand, which leads to the recalculation of the cluster parameters. In the sampler, the state is the collection of membership indices and parameters , where refers to the parameter associated with cluster j.
| Algorithm A2 DPM Gibbs sampling for new cluster development |
|
Appendix C. Development of the Distributional Components for the DPM
Appendix C.1. Derivation of the Distribution of Precision α
In Section 4.1, the parameter model (posterior) of the precision term is defined as
To derive this, we first derive the distribution of the number of clusters given the precision parameter . Consider a trivial example where we want to determine the number of clusters that observations fall into. One possible arrangement would be that observations 1, 2, and 5 form new clusters, while observations 3 and 4 join an existing cluster (note that the order is important):
- Observation 1 forms a new cluster with a probability =
- Observation 2 forms a new cluster with a probability =
- Observation 3 enters into an existing cluster with a probability =
- Observation 4 enters into an existing cluster with a probability =
- Observation 5 forms a new cluster with a probability =
In this example, we have clusters. We want to find the probability of this arrangement. The probability is the following:
Hence, the probability of observing J clusters amongst a sample size of n is given by
This is also considered the likelihood function. The posterior on is proportional to the likelihood times the prior :
The beta function is defined as follows:
We can find the beta function of and n as follows:
Thus, the posterior simplifies to the following:
Now, under the prior for , by substituting with , then
Appendix C.2. Outcome Data Model of Sh Development with the MAR Covariate x1 for the Discrete Clusters
Prior to the outcome parameter estimation, the missing covariates should be imputed first to obtain the complete covariate model beforehand. In this study, if the binary covariate is the only covariate with missingness, then we develop the imputation model to impute the binary covariate by taking the steps below and then update based on the posterior sampling detailed in Algorithm A1 in Appendix A. The imputation model for is approximated by the joint values
where
which serves as the joint density that we can use to sample the imputation values. For example, we have
Then, we can impute with the values sampled from , where
Note that in R, the computation can be difficult when the numerator is too small. We suggest the following tricks:
Finally, the outcome model that is required to compute the parameter in the Metropolis–Hastings algorithm in Algorithm A1 is obtained by summing the joint values of and (marginalize) out of the MAR covariate , shown in Equation (10), as illustrated below:
Appendix C.3. Covariate Data Model of x2 Development with the MAR Covariate x1 for the Continuous Clusters
The parameter-free distributions and as data models for continuous clusters are needed to calculate the probabilities of cluster membership and for the post-processing calculations for prediction in the DPM. However, when MAR covariates are present, it gives extra complexity in specifying the distribution to integrate out the parameters. Recall that the integrals we are attempting to find are the following:
If the binary covariate is missing, then we will need to replace the distribution with the continuous distribution (Gaussian) of , which is . The derivation of the parameter-free distributions and for the continuous cluster is as shown below:
The first step is to integrate with respect to . First, we’ll simplify the exponent:
The integrand will have the kernel of a normal distribution for with a mean and variance :
The integrand is the kernel of an inverse gamma distribution with the shape parameter and scale parameter :
As shown above, a closed-form expression can be determined, but this is not always the case since it can be extremely complicated. To simplify, we instead might have to consider a Monte Carlo integral.
References
- Aggarwal, Ankur, Michael B. Beck, Matthew Cann, Tim Ford, Dan Georgescu, Nirav Morjaria, Andrew Smith, Yvonne Taylor, Andreas Tsanakas, Louise Witts, and et al. 2016. Model risk–daring to open up the black box. British Actuarial Journal 21: 229–96. [Google Scholar] [CrossRef]
- Antoniak, Charles E. 1974. Mixtures of dirichlet processes with applications to bayesian nonparametric problems. The Annals of Statistics 2: 1152–74. [Google Scholar] [CrossRef]
- Bassetti, Federico, Roberto Casarin, and Fabrizio Leisen. 2014. Beta-product dependent pitman–yor processes for bayesian inference. Journal of Econometrics 180: 49–72. [Google Scholar] [CrossRef]
- Beaulieu, Norman C., and Qiong Xie. 2003. Minimax approximation to lognormal sum distributions. Paper present at the 57th IEEE Semiannual Vehicular Technology Conference, VTC 2003-Spring, Jeju, Republic of Korea, April 22–25; Piscataway: IEEE, vol. 2, pp. 1061–65. [Google Scholar]
- Billio, Monica, Roberto Casarin, and Luca Rossini. 2019. Bayesian nonparametric sparse var models. Journal of Econometrics 212: 97–115. [Google Scholar]
- Blackwell, David, and James B. MacQueen. 1973. Ferguson distributions via pólya urn schemes. The Annals of Statistics 1: 353–55. [Google Scholar] [CrossRef]
- Blei, David M., and Peter I. Frazier. 2011. Distance dependent chinese restaurant processes. Journal of Machine Learning Research 12: 2461–88. [Google Scholar]
- Braun, Michael, Peter S. Fader, Eric T. Bradlow, and Howard Kunreuther. 2006. Modeling the “pseudodeductible” in insurance claims decisions. Management Science 52: 1258–72. [Google Scholar] [CrossRef]
- Browne, Mark J., JaeWook Chung, and Edward W. Frees. 2000. International property-liability insurance consumption. The Journal of Risk and Insurance 67: 73–90. [Google Scholar]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, and Marwa Khalaf-Allah. 2011. Bayesian stochastic mortality modelling for two populations. ASTIN Bulletin: The Journal of the IAA 41: 29–59. [Google Scholar]
- Diebolt, Jean, and Christian P. Robert. 1994. Estimation of finite mixture distributions through bayesian sampling. Journal of the Royal Statistical Society: Series B (Methodological) 56: 363–75. [Google Scholar] [CrossRef]
- Escobar, Michael D., and Mike West. 1995. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association 90: 577–88. [Google Scholar] [CrossRef]
- Ferguson, Thomas S. 1973. A bayesian analysis of some nonparametric problems. The Annals of Statistics 1: 209–30. [Google Scholar] [CrossRef]
- Furman, Edward, Daniel Hackmann, and Alexey Kuznetsov. 2020. On log-normal convolutions: An analytical–numerical method with applications to economic capital determination. Insurance: Mathematics and Economics 90: 120–34. [Google Scholar] [CrossRef]
- Gelman, Andrew, and Jennifer Hill. 2007. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge: Cambridge University Press. [Google Scholar]
- Gershman, Samuel J., and David M. Blei. 2012. A tutorial on bayesian nonparametric models. Journal of Mathematical Psychology 56: 1–12. [Google Scholar] [CrossRef]
- Ghosal, Subhashis. 2010. The dirichlet process, related priors and posterior asymptotics. Bayesian Nonparametrics 28: 35. [Google Scholar]
- Griffin, Jim, and Mark Steel. 2006. Order-based dependent dirichlet processes. Journal of the American statistical Association 101: 179–94. [Google Scholar] [CrossRef]
- Griffin, Jim, and Mark Steel. 2011. Stick-breaking autoregressive processes. Journal of Econometrics 162: 383–96. [Google Scholar] [CrossRef]
- Hannah, Lauren A., David M. Blei, and Warren B. Powell. 2011. Dirichlet process mixtures of generalized linear models. Journal of Machine Learning Research 12: 1923–53. [Google Scholar]
- Hogg, Robert V., and Stuart A. Klugman. 2009. Loss Distributions. Hoboken: John Wiley & Sons. [Google Scholar]
- Hong, Liang, and Ryan Martin. 2017. A flexible bayesian nonparametric model for predicting future insurance claims. North American Actuarial Journal 21: 228–41. [Google Scholar] [CrossRef]
- Hong, Liang, and Ryan Martin. 2018. Dirichlet process mixture models for insurance loss data. Scandinavian Actuarial Journal 2018: 545–54. [Google Scholar] [CrossRef]
- Huang, Yifan, and Shengwang Meng. 2020. A bayesian nonparametric model and its application in insurance loss prediction. Insurance: Mathematics and Economics 93: 84–94. [Google Scholar] [CrossRef]
- Kaas, Rob, Marc Goovaerts, Jan Dhaene, and Michel Denuit. 2008. Modern Actuarial Risk Theory: Using R. Berlin and Heidelberg: Springer Science & Business Media, vol. 128. [Google Scholar]
- Lam, Chong Lai Joshua, and Tho Le-Ngoc. 2007. Log-shifted gamma approximation to lognormal sum distributions. IEEE Transactions on Vehicular Technology 56: 2121–29. [Google Scholar] [CrossRef]
- Li, Xue. 2008. A Novel Accurate Approximation Method of Lognormal Sum Random Variables. Ph.D. thesis, Wright State University, Dayton, OH, USA. [Google Scholar]
- Neal, Radford M. 2000. Markov chain sampling methods for dirichlet process mixture models. Journal of Computational and Graphical Statistics 9: 249–65. [Google Scholar]
- Neuhaus, John M., and Charles E. McCulloch. 2006. Separating between-and within-cluster covariate effects by using conditional and partitioning methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68: 859–72. [Google Scholar] [CrossRef]
- Ni, Yang, Yuan Ji, and Peter Müller. 2020. Consensus monte carlo for random subsets using shared anchors. Journal of Computational and Graphical Statistics 29: 703–14. [Google Scholar] [CrossRef]
- Quan, Zhiyu, and Emiliano A. Valdez. 2018. Predictive analytics of insurance claims using multivariate decision trees. Dependence Modeling 6: 377–407. [Google Scholar] [CrossRef]
- Richardson, Robert, and Brian Hartman. 2018. Bayesian nonparametric regression models for modeling and predicting healthcare claims. Insurance: Mathematics and Economics 83: 1–8. [Google Scholar] [CrossRef]
- Rodriguez, Abel, and David B. Dunson. 2011. Nonparametric bayesian models through probit stick-breaking processes. Bayesian Analysis (Online) 6: 145–78. [Google Scholar]
- Roy, Jason, Kirsten J. Lum, Bret Zeldow, Jordan D. Dworkin, Vincent Lo Re III, and Michael J. Daniels. 2018. Bayesian nonparametric generative models for causal inference with missing at random covariates. Biometrics 74: 1193–202. [Google Scholar] [CrossRef]
- Sethuraman, Jayaram. 1994. A constructive definition of dirichlet priors. Statistica Sinica 4: 639–650. [Google Scholar]
- Shah, Anoop D., Jonathan W. Bartlett, James Carpenter, Owen Nicholas, and Harry Hemingway. 2014. Comparison of random forest and parametric imputation models for imputing missing data using mice: A caliber study. American Journal of Epidemiology 179: 764–74. [Google Scholar] [CrossRef] [PubMed]
- Shahbaba, Babak, and Radford Neal. 2009. Nonlinear models using dirichlet process mixtures. Journal of Machine Learning Research 10: 1829–50. [Google Scholar]
- Shams Esfand Abadi, Mostafa. 2022. Bayesian Nonparametric Regression Models for Insurance Claims Frequency and Severity. Ph.D. thesis, University of Nevada, Las Vegas, NV, USA. [Google Scholar]
- Si, Yajuan, and Jerome P. Reiter. 2013. Nonparametric bayesian multiple imputation for incomplete categorical variables in large-scale assessment surveys. Journal of Educational and Behavioral Statistics 38: 499–521. [Google Scholar] [CrossRef]
- Suwandani, Ria Novita, and Yogo Purwono. 2021. Implementation of gaussian process regression in estimating motor vehicle insurance claims reserves. Journal of Asian Multicultural Research for Economy and Management Study 2: 38–48. [Google Scholar] [CrossRef]
- Teh, Yee Whye. 2010. Dirichlet Process. In Encyclopedia of Machine Learning. Berlin and Heidelberg: Springer Science & Business Media, pp. 280–87. [Google Scholar]
- Ungolo, Francesco, Torsten Kleinow, and Angus S. Macdonald. 2020. A hierarchical model for the joint mortality analysis of pension scheme data with missing covariates. Insurance: Mathematics and Economics 91: 68–84. [Google Scholar] [CrossRef]
- Zhao, Lian, and Jiu Ding. 2007. Least squares approximations to lognormal sum distributions. IEEE Transactions on Vehicular Technology 56: 991–97. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).