Measuring Global Macroeconomic Uncertainty and Cross-Country Uncertainty Spillovers
Abstract
1. Introduction
2. The Econometric Framework
2.1. The GVAR Model
2.2. Time-Varying Uncertainty
- (i)
- The GVAR is repeatedly estimated over recursive and rolling sample windows. We first consider the recursive scheme, in which the shortest window goes from time 1 to time , then the sample is extended by one-quarter increments up to , where identifies the last observation in the dataset. To estimate the country-specific VECX* models on each window, window-specific foreign variables are constructed using trade data that were available in the final quarter of the window under consideration (Section 3 provides more details). In a generic window w ending in period , the maximum-likelihood estimate of the GVAR obtained using actual data is expressed as:where the symbol denotes estimates and .
- (ii)
- In each window, we perform a non-parametric bootstrap of the estimates, following the approach by Dées et al. (2007a, 2007b) First, we simulate alternative historical paths for all the variables in the global model within the sample window, using the maximum-likelihood GVAR (10) and the empirical distribution of residuals. Then, we re-estimate the model on the simulated time series.More specifically, in window w:
- (a)
- The window-specific maximum-likelihood GVAR estimate (10) produces a matrix of global residuals .
- (b)
- In the generic b-th bootstrap iteration, with , the columns of matrix are resampled. Then, we simulate time series for all the variables using model (10) and adding the resampled residuals as shocks. Denoting iteration b in window w with the superscript , let be the bootstrap shocks, generated by randomly drawing columns from (thereby preserving the cross-sectional covariances) with replacement. The simulated time series are given by:with and .Iteration-specific foreign variables are then constructed using the window-specific trade weight matrix for every i.
- (c)
- In each bootstrap iteration, all the VECX* models are re-estimated on the simulated data. Following Dées et al. (2007a, 2007b), the estimated model is:where is the vector of estimated error correction terms corresponding to the cointegrating relations found on actual data in window w.
As a result, we obtain B different estimates of the GVAR model for each quarter from to , denoted as: - (iii)
- Each of the B window-specific GVAR estimates is used to produce pseudo-out-of-sample forecasts for all the variables in the global economy (taking as starting values for each variable the last two actual values within the sample window). Let denote the h-step-ahead forecasts of the model estimated on window w in iteration b.
2.3. Spillovers of Uncertainty
3. The Empirical Implementation
3.1. Data
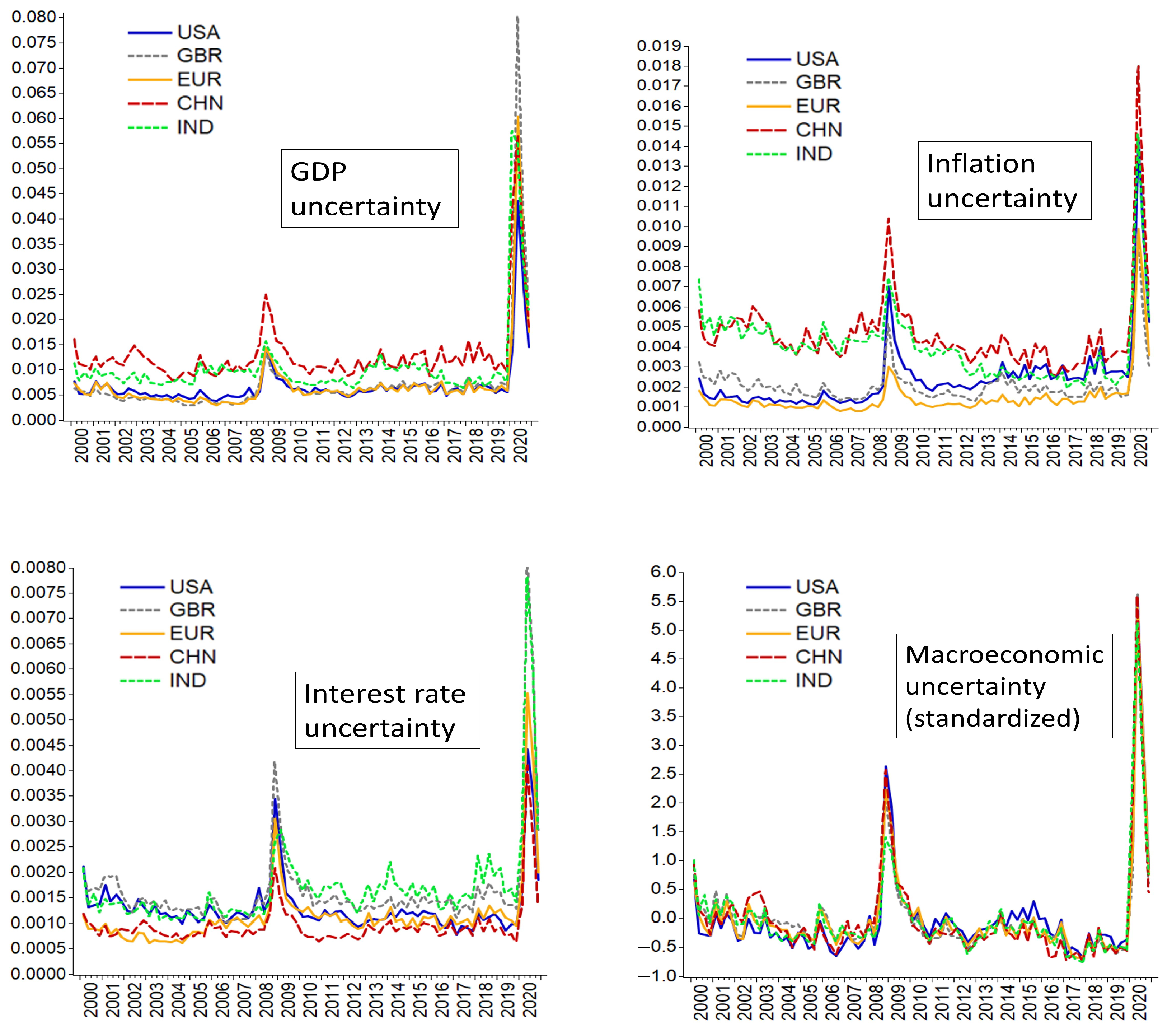
3.2. Results
3.2.1. Global Macroeconomic Uncertainty (GMU) Index
3.2.2. Global Spillovers of Uncertainty
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources for 2020Q1–2020Q4
Appendix B. Cointegration Relationships in the GVAR
| Coeff. | Variable | EUR | GBR | JAP | USA | ||
|---|---|---|---|---|---|---|---|
| rgdp | 1.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | |
| (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | ||
| infl | 6.37 | 0.00 | 1.00 | 0.00 | 1.00 | 16.2 | |
| (5.08) | (0.00) | (0.00) | (0.00) | (0.00) | (1.56) | ||
| eq | 0.41 | −0.07 | 0.02 | −0.07 | 0.00 | −0.09 | |
| (0.10) | (0.06) | (0.01) | (0.03) | (0.00) | (0.03) | ||
| fx | 0.84 | 0.10 | −0.01 | 0.22 | −0.00 | ||
| (0.16) | (0.05) | (0.01) | (0.05) | (0.00) | |||
| rshort | −47.8 | −10.5 | −0.11 | −14.1 | −0.77 | −5.23 | |
| (5.82) | (1.58) | (0.22) | (3.18) | (0.13) | (1.79) | ||
| rgdp * | −1.65 | −1.07 | −0.07 | −0.22 | −0.01 | −0.47 | |
| (0.62) | (0.23) | (0.03) | (0.32) | (0.01) | (0.28) | ||
| infl * | 8.80 | −0.91 | −0.25 | 4.689 | −0.01 | 0.91 | |
| (2.01) | (1.37) | (0.19) | (2.16) | (0.09) | (0.80) | ||
| eq * | −0.44 | 0.10 | −0.00 | 0.08 | −0.01 | ||
| (0.12) | (0.05) | (0.01) | (0.05) | (0.00) | |||
| fx * | −1.43 | −0.11 | 0.00 | −0.36 | 0.01 | 0.03 | |
| (0.310) | (0.05) | (0.01) | (0.11) | (0.00) | (0.09) | ||
| rshort * | 50.8 | 12.2 | 0.01 | −10.4 | −0.15 | ||
| (6.52) | (2.22) | (0.31) | (3.78) | (0.16) | |||
| rgdp | 0.04 | −0.01 | −0.14 | −0.09 | 0.43 | −0.03 | |
| (0.00) | (0.04) | (0.19) | (0.01) | (0.29) | (0.01) | ||
| infl | 0.00 | 0.01 | −0.48 | 0.03 | −1.06 | −0.04 | |
| (0.00) | (0.01) | (0.07) | (0.01) | (0.12) | (0.00) | ||
| eq | 0.02 | 0.11 | 0.64 | 0.03 | 0.39 | −0.15 | |
| (0.04) | (0.16) | (0.81) | (0.11) | (2.26) | (0.08) | ||
| fx | 0.01 | 0.05 | −1.71 | 0.06 | 2.40 | ||
| (0.02) | (0.12) | (0.60) | (0.07) | (1.57) | |||
| rshort | 0.00 | 0.03 | 0.07 | 0.00 | 0.06 | 0.00 | |
| (0.00) | (0.01) | (0.03) | (0.00) | (0.03) | (0.00) |
| Coeff. | Variable | AUS | CAN | CHE | CHN | IND | KOR | NOR | NZL | SEA | SWE | ZAF | LAM | MEX | SAU | TUR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rgdp | 1.00 | 1.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.00 | |
| (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | ||
| infl | −11.5 | −7.92 | −50.1 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 4.75 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 1.00 | 0.00 | 1.00 | −6.93 | 0.00 | 1.00 | 0.00 | 1.00 | |
| (1.13) | (0.77) | (6.29) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.85) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.00) | (0.94) | (0.00) | (0.00) | (0.00) | (0.00) | ||
| fx | 0.35 | 0.12 | 1.10 | 2.17 | −0.043 | 0.27 | 0.00 | −2.62 | 0.12 | −0.27 | 0.21 | −0.01 | 0.356 | −0.00 | 0.00 | 0.00 | 1.00 | −1.48 | −0.10 | −0.20 | −0.05 | 1.31 | 1.85 | 0.00 | −0.04 | −0.25 | |
| (0.07) | (0.03) | (0.33) | (0.30) | (0.01) | (0.03) | (0.01) | (0.82) | (0.04) | (0.10) | (0.09) | (0.01) | (0.09) | (0.01) | (0.00) | (0.00) | (0.00) | (1.00) | (0.05) | (0.05) | (0.01) | (0.24) | (0.32) | (0.00) | (0.05) | (0.04) | ||
| rshort | 7.31 | 2.46 | 10.8 | −86.5 | −0.11 | −1.11 | 0.37 | −129 | 4.43 | 4.29 | −9.41 | −1.12 | −17.6 | −0.68 | 165 | 15.0 | 190 | 116 | 5.92 | ||||||||
| (1.15) | (1.45) | (5.28) | (12.8) | (0.49) | (1.21) | (0.30) | (15.9) | (0.81) | (1.30) | (1.29) | (0.14) | (2.28) | (0.13) | (25.3) | (2.28) | (28.5) | (20.6) | (1.04) | |||||||||
| rgdp * | −0.48 | −1.02 | 0.14 | −6.12 | 0.11 | −0.65 | −0.01 | −8.57 | 0.25 | −1.00 | 0.68 | 0.04 | −1.67 | −0.03 | 0.99 | 0.12 | 1.48 | −8.65 | −0.50 | 1.26 | 0.25 | 1.78 | −1.24 | 0.01 | 0.62 | −1.06 | |
| (0.19) | (0.08) | (0.66) | (1.40) | (0.05) | (0.18) | (0.05) | (2.78) | (0.14) | (0.18) | (0.35) | (0.04) | (0.60) | (0.03) | (2.32) | (0.21) | (2.61) | (3.88) | (0.19) | (0.64) | (0.13) | (0.81) | (0.81) | (0.01) | (0.31) | (0.25) | ||
| infl * | 2.67 | 0.79 | 8.26 | −0.26 | −0.022 | −0.56 | −0.08 | −3.26 | 0.13 | 5.87 | 2.47 | −0.11 | −1.30 | −0.03 | −17.9 | −2.48 | −17.3 | −35.0 | −2.15 | −0.85 | −0.41 | 3.39 | −2.42 | 0.07 | 4.65 | 1.40 | |
| (1.24) | (0.94) | (6.33) | (5.08) | (0.19) | (0.87) | (0.22) | (16.2) | (0.83) | (1.35) | (2.62) | (0.28) | (4.50) | (0.26) | (28.7) | (2.59) | (32.2) | (35.7) | (1.81) | (0.76) | (0.16) | (6.13) | (3.70) | (0.06) | (2.35) | (1.86) | ||
| fx * | −0.62 | −0.26 | −0.90 | −2.72 | 0.05 | −0.11 | 0.03 | −2.07 | 0.06 | 0.20 | −0.04 | 0.04 | −0.81 | 0.02 | −0.24 | −0.02 | −1.29 | −1.52 | −0.06 | 0.88 | −0.02 | −0.60 | −0.86 | 0.00 | 0.27 | 0.32 | |
| (0.10) | (0.04) | (0.39) | (0.45) | (0.02) | (0.05) | (0.01) | (0.72) | (0.04) | (0.12) | (0.10) | (0.01) | (0.26) | (0.02) | (0.59) | (0.05) | (0.67) | (1.23) | (0.06) | (0.21) | (0.04) | (0.27) | (0.30) | (0.00) | (0.10) | (0.08) | ||
| rshort * | −6.01 | 1.17 | 16.8 | 6.27 | 1.02 | −9.48 | −0.81 | 138 | −5.13 | −0.96 | 9.88 | 0.93 | 30.4 | 0.65 | −169 | −15.8 | −211 | −115 | −6.68 | −22.0 | −8.00 | −2.97 | 12.6 | 0.00 | −8.61 | −0.20 | |
| (2.23) | (1.71) | (11.8) | (14.37) | (0.55) | (1.79) | (0.45) | (43.5) | (2.23) | (2.37) | (3.86) | (0.41) | (10.5) | (0.61) | (49.0) | (4.42) | (55.2) | (51.2) | (2.60) | (11.6) | (2.37) | (9.07) | (7.81) | (0.13) | (4.35) | (3.43) | ||
| rgdp | 0.00 | −0.04 | 0.00 | 0.018 | −0.24 | −0.51 | −0.43 | −0.00 | −0.30 | −0.13 | 0.06 | −0.22 | 0.03 | −0.06 | −0.05 | −0.12 | 0.05 | 0.02 | −0.55 | −0.02 | 0.08 | 0.03 | −0.01 | 0.28 | −0.23 | −0.04 | |
| (0.01) | (0.02) | (0.00) | (0.00) | (0.14) | (0.07) | (0.30) | (0.01) | (0.12) | (0.02) | (0.02) | (0.16) | (0.01) | (0.12) | (0.02) | (0.21) | (0.01) | (0.01) | (0.16) | (0.01) | (0.04) | (0.01) | (0.01) | (0.55) | (0.04) | (0.05) | ||
| infl | 0.09 | 0.10 | 0.01 | 0.00 | −0.22 | −0.00 | −0.80 | −0.00 | −0.11 | −0.06 | 0.06 | −0.59 | 0.02 | −0.61 | 0.05 | −0.78 | 0.02 | 0.04 | −0.76 | −0.12 | −0.47 | 0.06 | 0.04 | −0.84 | 0.11 | −0.25 | |
| (0.01) | (0.01) | (0.00) | (0.00) | (0.08) | (0.02) | (0.10) | (0.00) | (0.08) | (0.01) | (0.01) | (0.10) | (0.00) | (0.08) | (0.01) | (0.11) | (0.00) | (0.00) | (0.10) | (0.03) | (0.10) | (0.01) | (0.01) | (0.30) | (0.05) | (0.07) | ||
| fx | −0.19 | 0.03 | −0.02 | −0.05 | −0.85 | −0.02 | 0.10 | 0.02 | 0.48 | 0.10 | 0.06 | −0.96 | 0.02 | −4.52 | 0.16 | −0.82 | −0.08 | 0.04 | −0.87 | 0.23 | −0.52 | −0.04 | −0.04 | 0.21 | 0.22 | 0.45 | |
| (0.07) | (0.09) | (0.02) | (0.01) | (0.34) | (0.07) | (0.31) | (0.02) | (0.38) | (0.05) | (0.06) | (0.54) | (0.05) | (0.95) | (0.06) | (0.65) | (0.03) | (0.04) | (0.78) | (0.04) | (0.14) | (0.02) | (0.01) | (0.32) | (0.10) | (0.13) | ||
| rshort | −0.00 | −0.00 | −0.00 | 0.00 | 0.06 | −0.01 | 0.00 | 0.01 | 0.14 | −0.01 | 0.01 | 0.12 | 0.01 | −0.02 | 0.00 | −0.01 | −0.00 | 0.00 | −0.02 | ||||||||
| (0.00) | (0.00) | (0.00) | (0.0) | (0.01) | (0.00) | (0.02) | (0.00) | (0.02) | (0.01) | (0.00) | (0.03) | (0.00) | (0.05) | (0.00) | (0.05) | (0.00) | (0.00) | (0.03) |
Appendix C. SVAR Impulse Response Functions


| 1 | Moreover, as mentioned by Bhattarai et al. (2020), this kind of two-step estimation procedure is generally subject to the so-called generated regressor problem (Pagan 1984). |
| 2 | The estimates of uncertainty may be inflated by explosive roots in (13). For this reason, in each iteration we check whether the estimated models are dynamically stable, i.e., whether all the eigenvalues of the companion matrices are less than or equal to 1 in modulus. The stability check is performed both on the country-specific models and on the resulting global model. Unstable models are discarded, so that uncertainty is measured using stable models only. At the country level, each cointegration rank is determined by the Johansen trace test (at the 5% significance level), unless the resulting VARX* is unstable. In this case, we select the highest rank that makes the model stable. Since this does not ensure the stability of the global model, we also check the eigenvalues of the global companion matrix . If the global model is unstable, the bootstrap iteration is repeated until stability is achieved. To further mitigate the impact of extreme forecasts on the uncertainty measures, we also remove iteration-specific forecasts that are outliers with respect to U.S. GDP, chosen as a representative variable. In particular, global forecasts are discarded whenever the forecasts of U.S. GDP lie more than 3 standard deviations away from their average across iterations. |
| 3 | The forecast variance decomposition used to calculate uncertainty spillovers relies on a first-order Taylor series approximation of the variance. To get an intuition, consider that the variance of a nonlinear function of two random variables X and Y can be approximated as:
|
| 4 | Like Klößner and Sekkel (2014) and Rossi and Sekhposyan (2017), we do not give a causal interpretation to the uncertainty spillovers, as they are not based on structural (orthogonal) shocks. In this respect, we also follow the GVAR literature, which typically uses non-orthogonalized shocks to conduct impulse response analysis, in the form of generalized impulse response functions (GIRFs) and generalized forecast error variance decomposition (GFEVD) (see Pesaran et al. 2004 and Dées et al. 2007a, 2007b). |
| 5 | As in Cesa-Bianchi et al. (2014), real GDP, exchange rates and equity indices are transformed to logs, while each interest rate is transformed to , where is the rate expressed in percentage values on an annual basis. |
| 6 | All results are obtained using 1000 bootstrap iterations. |
| 7 | The two schemes provide highly correlated results for global uncertainty (the correlation coefficient is 0.75). In the quarters 2020Q2–2020Q4, the GVAR estimated by rolling windows on actual data is explosive for any choice of the cointegration ranks. In this case, to generate the bootstrap samples, we use the model estimates obtained on the window ending in 2019Q4. |
| 8 | To apply the methodology by Jurado et al. (2015), we transform the non-stationary variables used in the GVAR by first differencing. Once uncertainty is calculated for each variable, we first average variable-specific uncertainties within each country (with equal weights), then calculate global uncertainty as the PPP GDP-weighted average of uncertainty across countries. |
| 9 | The estimated spillovers from all countries to a given country do not exactly sum to 1, because the forecast variance decomposition is based on a linear approximation of a nonlinear function, as explained in endnote 3. However, the discrepancy is in general very small. The sum of the estimated spillovers is 0.98 on average and ranges between 0.93 and 1.04 across countries. In the results reported here, all spillovers are rescaled so that they exactly sum to 1 for each “uncertainty-importing” country. |
| 10 | We use the fast algorithm developed by Klößner and Wagner (2014). |
| 11 | Cointegration ranks in Table A1 and Table A2 are determined using the Johansen (1995) trace test at the 5% level of significance. Estimates are reported for all countries except Brazil, for which the Johansen (1995) test indicates no cointegration relationships. For the U.K. (GBR) and the Latin American aggregate area (LAM), Table A1 and Table A2 report results using the cointegration ranks determined over the pre-COVID-19 sample 1979Q4-2019Q4 (2 cointegration relationships for both), instead of the ranks estimated over the full sample 1979Q4-2020Q4 (1 and 3 cointegration relationships, respectively): this adjustment provides more reasonable long-run properties, while having almost no effect on our uncertainty measure (in particular, a rank of 1 for GBR would result in unrealistically large long-run coefficients linking GDP and inflation, while a rank of 3 for LAM would imply that all variables, including GDP, are trend-stationary). |
| 12 | Both types of uncertainty measures are highly correlated across countries, implying that the IRFs strongly depend on the specific Cholesky ordering. Still, the analysis is mainly intended to check if country-specific uncertainty shocks generate significant cross-border dynamic spillovers. |
References
- Ahir, Hites, Nicholas Bloom, and Davide Furceri. 2022. World Uncertainty Index. NBER Working Paper No. 29763. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Angelini, Giovanni, Mauro Costantini, and Joshy Easaw. 2018. Uncertainty and Spillover Effects across the Euro Area. Cardiff Economics Working Papers E2018/15. Cardiff: Cardiff University, Cardiff Business School. [Google Scholar]
- Bacchiocchi, Emanuele, and Catalin Dragomirescu-Gaina. 2022. Uncertainty Spill-Overs: When Policy and Financial Realms Overlap. Working Papers WP1174. Bologna: University of Bologna, Department of Economics. [Google Scholar]
- Bachmann, Rüdiger, Steffen Elstner, and Eric R. Sims. 2013. Uncertainty and economic activity: Evidence from business survey data. American Economic Journal: Macroeconomics 5: 217–49. [Google Scholar] [CrossRef]
- Baker, Scott R., Nicholas Bloom, and Steven J. Davis. 2016. Measuring economic policy uncertainty. The Quarterly Journal of Economics 131: 1593–636. [Google Scholar] [CrossRef]
- Benati, Luca. 2008. The “Great Moderation” in the United Kingdom. Journal of Money, Credit and Banking 40: 121–47. [Google Scholar] [CrossRef]
- Berger, Tino, Sibylle Grabert, and Bernd Kempa. 2016. Global and country-specific output growth uncertainty and macroeconomic performance. Oxford Bulletin of Economics and Statistics 78: 694–716. [Google Scholar] [CrossRef]
- Berger, Tino, Sibylle Grabert, and Bernd Kempa. 2017. Global macroeconomic uncertainty. Journal of Macroeconomics 53: 42–56. [Google Scholar] [CrossRef]
- Bhattarai, Saroj, Arpita Chatterjee, and Woong Yong Park. 2020. Global spillover effects of US uncertainty. Journal of Monetary Economics 114: 71–89. [Google Scholar] [CrossRef]
- Bloom, Nicholas. 2009. The impact of uncertainty shocks. Econometrica 77: 623–85. [Google Scholar]
- Bloom, Nicholas. 2014. Fluctuations in uncertainty. The Journal of Economic Perspectives 28: 153–75. [Google Scholar] [CrossRef]
- Bloom, Nicholas, Max Floetotto, Nir Jaimovich, Itay Saporta-Eksten, and Stephen J. Terry. 2012. Really uncertain business cycles. Econometrica 86: 1031–65. [Google Scholar] [CrossRef]
- Brainard, William. 1967. Uncertainty and the effectiveness of policy. American Economic Review 57: 411–25. [Google Scholar]
- Caggiano, Giovanni, and Efrem Castelnuovo. 2021. Global Uncertainty. Marco Fanno Working Papers 269. Padova: University of Padova. [Google Scholar]
- Caggiano, Giovanni, Efrem Castelnuovo, and Juan Manuel Figueres. 2020. Economic policy uncertainty spillovers in booms and busts. Oxford Bulletin of Economics and Statistics 82: 125–55. [Google Scholar] [CrossRef]
- Carriero, Andrea, Todd E. Clark, and Massimiliano Marcellino. 2017. Measuring Uncertainty and Its Impact on the Economy. Working Paper No. 16-22R. Cleveland: Federal Reserve Bank of Cleveland. [Google Scholar]
- Carriero, Andrea, Todd E. Clark, and Massimiliano Marcellino. 2020. Assessing international commonality in macroeconomic uncertainty and its effects. Journal of Applied Econometrics 35: 273–93. [Google Scholar] [CrossRef]
- Carrière-Swallow, Yan, and Luis Felipe Céspedes. 2013. The impact of uncertainty shocks in emerging economies. Journal of International Economics 90: 316–25. [Google Scholar] [CrossRef]
- Cesa-Bianchi, Ambrogio, M. Hashem Pesaran, and Alessandro Rebucci. 2014. Uncertainty and Economic Activity: A Global Perspective. CESifo Working Paper No. 4736. Munich: CESifo. [Google Scholar]
- Cesa-Bianchi, Ambrogio, M. Hashem Pesaran, and Alessandro Rebucci. 2020. Uncertainty and economic activity: A multicountry perspective. The Review of Financial Studies 33: 3393–445. [Google Scholar] [CrossRef]
- Chudik, Alexander, and M. Hashem Pesaran. 2016. Theory and practice of GVAR modelling. Journal of Economic Surveys 30: 165–97. [Google Scholar] [CrossRef]
- Clark, Todd E., and Michael W. McCracken. 2009. Improving forecast accuracy by combining recursive and rolling forecasts. International Economic Review 50: 363–95. [Google Scholar] [CrossRef]
- Clements, Michael P. 2017. Assessing macro uncertainty in real-time when data are subject to revision. Journal of Business & Economic Statistics 35: 420–33. [Google Scholar]
- Coibion, Olivier, Dimitris Georgarakos, Yuriy Gorodnichenko, Geoff Kenny, and Michael Weber. 2021. The Effect of Macroeconomic Uncertainty on Household Spending. ECB Working Paper 2557. Frankfurt: European Central Bank. [Google Scholar]
- Collin-Dufresne, Pierre, Michael Johannes, and Lars A. Lochstoer. 2016. Parameter learning in general equilibrium: The asset pricing implications. American Economic Review 106: 664–98. [Google Scholar] [CrossRef]
- Colombo, Valentina. 2013. Economic policy uncertainty in the US: Does it matter for the Euro area? Economics Letters 121: 39–42. [Google Scholar] [CrossRef]
- Crespo Cuaresma, Jesús, Florian Huber, and Luca Onorante. 2019. The Macroeconomic Effects of International Uncertainty. ECB Working Paper No. 2302. Frankfurt: European Central Bank. [Google Scholar]
- Davis, Steven J. 2016. An Index of Global Economic Policy Uncertainty. NBER Working Paper No. 22740. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Decker, Ryan A., Pablo N. D’Erasmo, and Hernan Moscoso Boedo. 2016. Market exposure and endogenous firm volatility over the business cycle. American Economic Journal: Macroeconomics 8: 148–98. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Drechsler, Itamar. 2013. Uncertainty, time-varying fear, and asset prices. The Journal of Finance 68: 1843–89. [Google Scholar] [CrossRef]
- Dées, Stephane, Filippo di Mauro, M. Hashem Pesaran, and L. Vanessa Smith. 2007a. Exploring the international linkages of the euro area: A global VAR analysis. Journal of Applied Econometrics 22: 1–38. [Google Scholar] [CrossRef]
- Dées, Stephane, Sean Holly, M. Hashem Pesaran, and L. Vanessa Smith. 2007b. Long run macroeconomic relations in the global economy. Economics - The Open-Access, Open-Assessment E-Journal 3: 1–20. [Google Scholar]
- ECB. 2009. Uncertainty and the economic prospects for the euro area. Monthly Bulletin 8: 58–61. [Google Scholar]
- ECB. 2016. The impact of uncertainty on activity in the euro area. Economic Bulletin 8: 55–74. [Google Scholar]
- ECB. 2017. Assessing the decoupling of economic policy uncertainty and financial conditions. Financial Stability Review 1: 135–43. [Google Scholar]
- Epstein, Larry G., and Tan Wang. 1994. Intertemporal asset pricing under Knightian uncertainty. Econometrica 62: 283–322. [Google Scholar] [CrossRef]
- Hansen, Lars Peter. 2007. Beliefs, doubts and learning: Valuing economic risk. American Economic Review: Papers & Proceedings 97: 1–30. [Google Scholar]
- Huber, Florian. 2016. Density forecasting using Bayesian global vector autoregressions with stochastic volatility. International Journal of Forecasting 32: 818–37. [Google Scholar] [CrossRef]
- IMF. 2012. World Economic Outlook: Coping with High Debt and Sluggish Growth. Washington, DC: International Monetary Fund. [Google Scholar]
- Johansen, Søren. 1995. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press. [Google Scholar]
- Jurado, Kyle, Sydney C. Ludvigson, and Serena Ng. 2015. Measuring uncertainty. The American Economic Review 105: 1177–216. [Google Scholar] [CrossRef]
- Klößner, Stefan, and Rodrigo Sekkel. 2014. International spillovers of policy uncertainty. Economic Letters 124: 508–12. [Google Scholar] [CrossRef]
- Klößner, Stefan, and Sven Wagner. 2014. Exploring all VAR orderings for calculating spillovers? Yes, we can!—A note on Diebold and Yilmaz (2009). Journal of Applied Econometrics 29: 172–79. [Google Scholar] [CrossRef]
- Kremer, Manfred, Marco Lo Duca, and Dániel Holló. 2012. CISS—A Composite Indicator of Systemic Stress in the Financial System. ECB Working Paper 1426. Frankfurt: European Central Bank. [Google Scholar]
- Lahiri, Kajal, and Xuguang Sheng. 2010. Measuring forecast uncertainty by disagreement: The missing link. Journal of Applied Econometrics 25: 514–38. [Google Scholar] [CrossRef]
- Londono, Juan M., Sai Ma, and Beth Anne Wilson. 2021. The Global Transmission of Real Economic Uncertainty. International Finance Discussion Papers 1317. Washington, DC: Board of Governors of the Federal Reserve System. [Google Scholar]
- Meinen, Philipp, and Oke Roehe. 2017. On measuring uncertainty and its impact on investment: Cross-country evidence from the euro area. European Economic Review 92: 161–79. [Google Scholar] [CrossRef]
- Mohaddes, Kamiar, and Mehdi Raissi. 2018. Compilation, Revision and Updating of the Global VAR (GVAR) Database, 1979Q2–2016Q4. Cambridge: University of Cambridge, Faculty of Economics (Mimeo). [Google Scholar]
- Mohaddes, Kamiar, and Mehdi Raissi. 2020. Compilation, Revision and Updating of the Global VAR (GVAR) Database, 1979Q2–2019Q4. Cambridge: University of Cambridge, Faculty of Economics (Mimeo). [Google Scholar]
- Mumtaz, Haroon. 2018. Measuring the Origins of Macroeconomic Uncertainty. Working Papers 864. London: Queen Mary University of London, School of Economics and Finance. [Google Scholar]
- Mumtaz, Haroon, and Alberto Musso. 2019. The evolving impact of global, region-specific, and country-specific uncertainty. Journal of Business & Economic Statistics 39: 466–81. [Google Scholar]
- Mumtaz, Haroon, and Konstantinos Theodoridis. 2017. Common and country specific economic uncertainty. Journal of International Economics 105: 205–16. [Google Scholar] [CrossRef]
- Orlik, Anna, and Laura Veldkamp. 2014. Understanding Uncertainty Shocks and the Role of Black Swans. NBER Working Paper No. 20445. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Orphanides, Athanasios, and John C. Williams. 2007. Robust monetary policy with imperfect knowledge. Journal of Monetary Economics 54: 1406–35. [Google Scholar] [CrossRef]
- Ozturk, Ezgi O., and Xuguang Simon Sheng. 2018. Measuring global and country-specific uncertainty. Journal of International Money and Finance 88: 276–95. [Google Scholar] [CrossRef]
- Pagan, Adrian. 1984. Econometric issues in the analysis of regressions with generated regressors. International Economic Review 25: 221–47. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Til Schuermann, and L. Vanessa Smith. 2009. Forecasting economic and financial variables with global VARs. International Journal of Forecasting 25: 642–75. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Til Schuermann, and Scott M. Weiner. 2004. Modeling regional interdependencies using a global error correcting macroeconometric model. Journal of Business and Economic Statistics 22: 129–62. [Google Scholar] [CrossRef]
- Pfarrhofer, Michael. 2022. Measuring international uncertainty using global vector autoregressions with drifting parameters. Macroeconomic Dynamics, 1–24. [Google Scholar] [CrossRef]
- Rossi, Barbara, and Tatevik Sekhposyan. 2015. Macroeconomic uncertainty indices based on nowcast and forecast error distributions. American Economic Review: Papers & Proceedings 105: 650–55. [Google Scholar]
- Rossi, Barbara, and Tatevik Sekhposyan. 2017. Macroeconomic uncertainty indices for the Euro Area and its individual member countries. Empirical Economics 53: 41–62. [Google Scholar] [CrossRef]
- Rossi, Barbara, Tatevik Sekhposyan, and Matthieu Soupre. 2018. Understanding the Sources of Macroeconomic Uncertainty. Economics Working Papers 1531. Barcelona: Universitat Pompeu Fabra. [Google Scholar]
- Scotti, Chiara. 2016. Surprise and uncertainty indexes: Real-time aggregation of real-activity macro-surprises. Journal of Monetary Economics 82: 1–19. [Google Scholar] [CrossRef]
- Söderström, Ulf. 2002. Monetary policy with uncertain parameters. The Scandinavian Journal of Economics 104: 125–45. [Google Scholar] [CrossRef]
- Stock, James H., and Mark Watson. 2012. Disentangling the channels of the 2007–2009 recession. Brookings Papers on Economic Activity 43: 81–135. [Google Scholar] [CrossRef]
- Van Nieuwerburgh, Stijn, and Laura Veldkamp. 2006. Learning asymmetries in real business cycles. Journal of Monetary Economics 53: 753–72. [Google Scholar] [CrossRef]
- Weitzman, Martin L. 2007. Subjective expectations and asset-return puzzles. American Economic Review 97: 1102–30. [Google Scholar] [CrossRef]
- Wieland, Volker. 2000. Monetary policy, parameter uncertainty and optimal learning. Journal of Monetary Economics 46: 199–228. [Google Scholar] [CrossRef]
- Xia, Yihong. 2001. Learning about predictability: The effects of parameter uncertainty on dynamic asset allocation. The Journal of Finance 56: 205–46. [Google Scholar] [CrossRef]
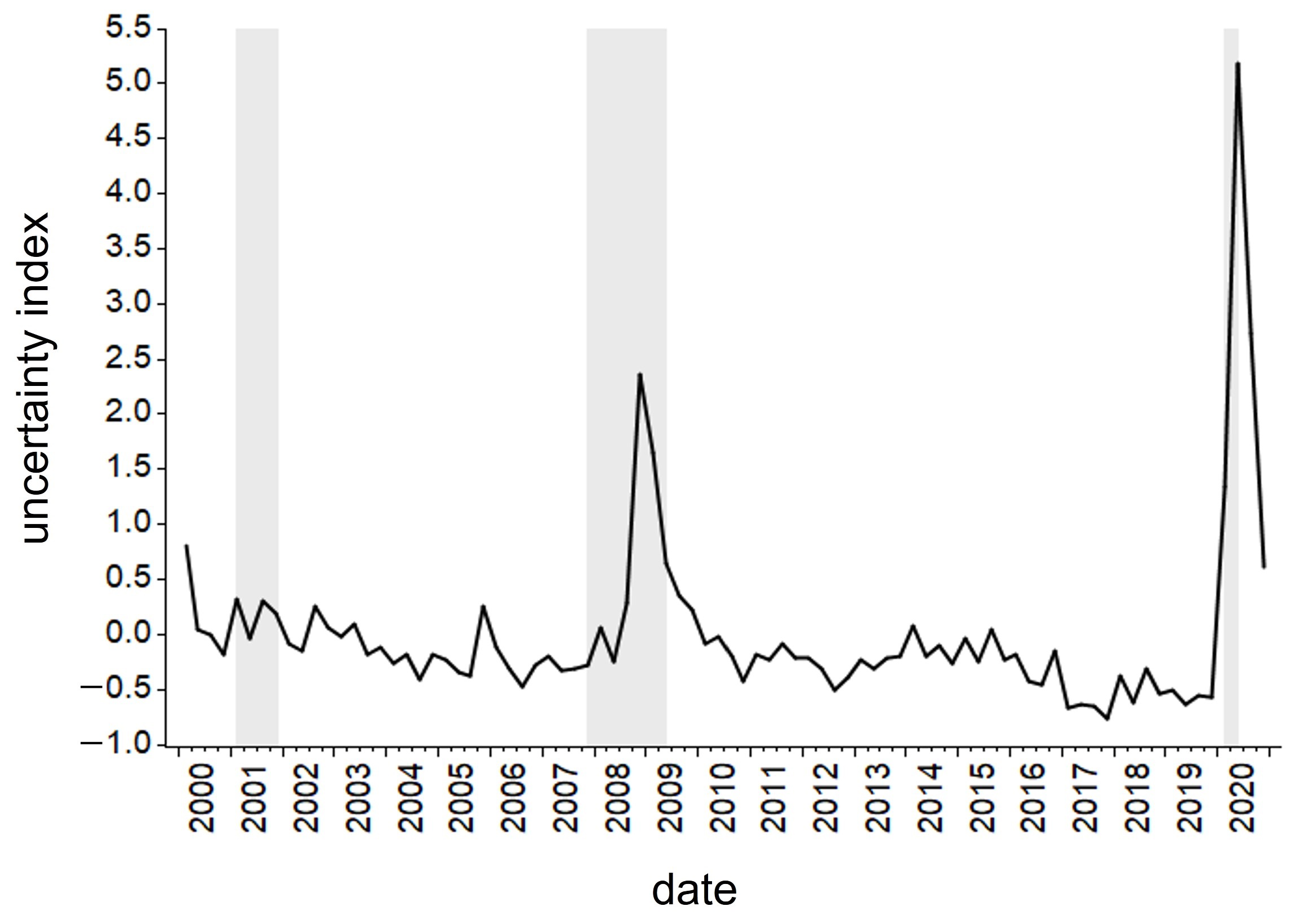
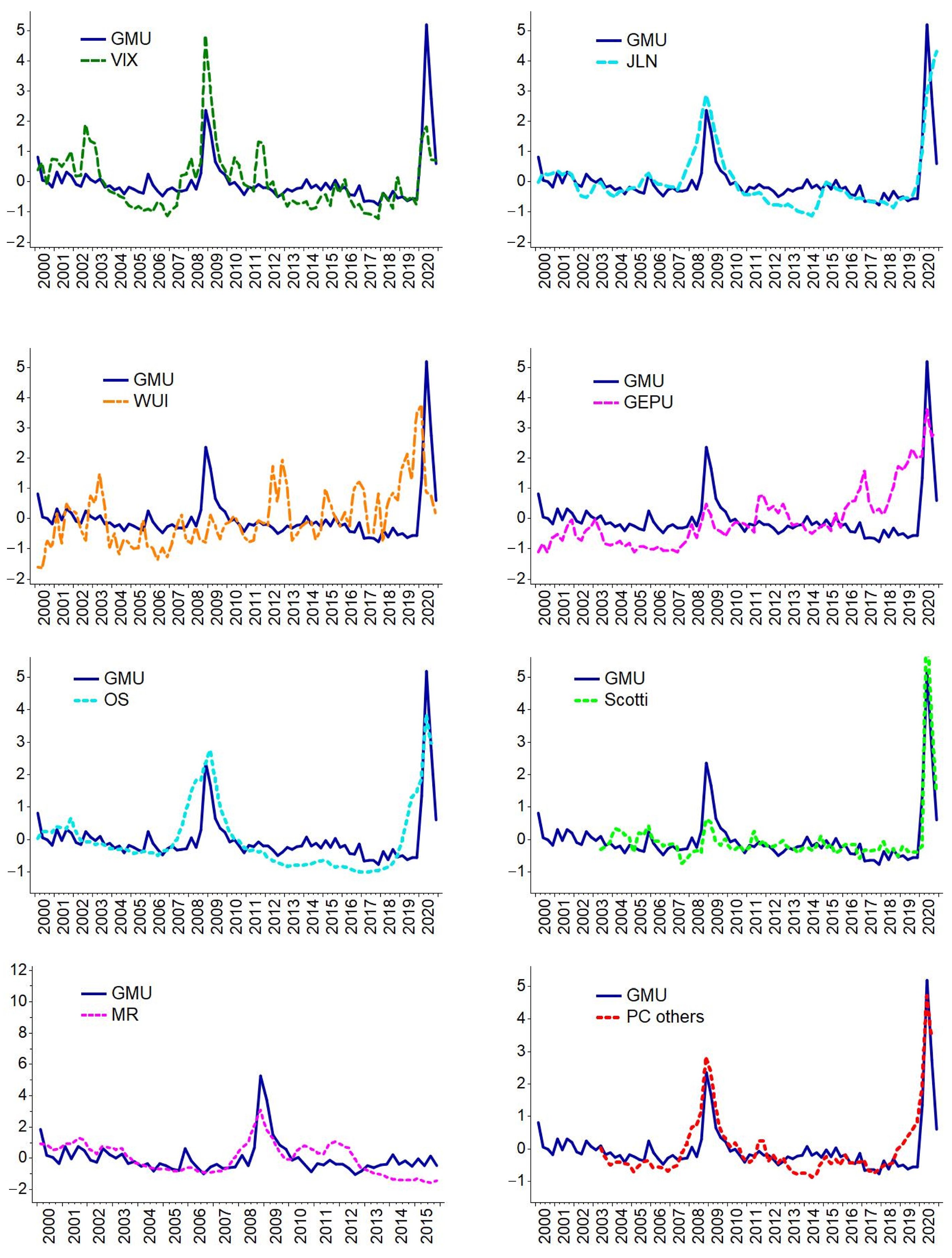

| VIX | JLN | WUI | GEPU | OS | Scotti | MR | GMU | |
|---|---|---|---|---|---|---|---|---|
| VIX | 1.00 | |||||||
| JLN | 0.62 | 1.00 | ||||||
| WUI | 0.01 | −0.02 | 1.00 | |||||
| GEPU | 0.19 | 0.33 | 0.67 | 1.00 | ||||
| OS | 0.67 | 0.89 | 0.14 | 0.35 | 1.00 | |||
| Scotti | 0.34 | 0.61 | 0.05 | 0.49 | 0.56 | 1.00 | ||
| MR | 0.83 | 0.65 | 0.01 | 0.32 | 0.75 | 0.22 | 1.00 | |
| GMU | 0.64 | 0.74 | 0.06 | 0.39 | 0.75 | 0.87 | 0.62 | 1.00 |
| AUS | BRA | CAN | CHE | CHN | EUR | GBR | IND | JAP | KOR | LAM | MEX | NOR | NZL | SAU | SEA | SWE | TUR | USA | ZAF | From | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUS | 66.9 | 2.6 | 0.1 | −0.1 | 14.2 | 1.8 | 0.5 | 0.8 | 3.1 | 1.3 | 1.0 | 0.5 | 0.2 | 0.6 | 0.8 | 3.6 | −0.4 | 0.1 | 2.4 | 0.3 | 33.1 |
| BRA | 0.4 | 80.8 | −0.2 | −0.3 | 5.7 | 3.0 | 0.1 | 0.4 | 1.9 | 0.8 | 2.4 | 1.0 | −0.1 | 0.1 | 0.1 | 1.0 | −0.5 | 0.2 | 3.0 | 0.1 | 19.2 |
| CAN | 1.5 | 6.0 | 25.8 | 0.2 | 14.9 | 7.1 | 2.1 | 1.5 | 4.1 | 1.8 | 0.8 | 4.8 | 0.1 | 0.3 | 1.4 | 3.2 | 0.0 | 0.2 | 23.7 | 0.5 | 74.2 |
| CHE | 0.9 | 12.2 | 0.1 | 41.7 | 10.7 | 13.6 | 3.6 | 0.6 | 3.3 | 0.3 | 0.9 | 1.8 | 0.0 | 0.2 | 0.8 | 1.0 | −0.5 | 0.3 | 8.2 | 0.3 | 58.3 |
| CHN | 0.0 | 6.7 | 0.0 | −0.1 | 84.7 | 1.4 | 0.8 | 0.0 | 2.0 | 0.3 | 0.3 | 0.1 | 0.0 | 0.0 | 0.4 | 2.8 | −0.3 | 0.0 | 0.8 | −0.1 | 15.3 |
| EUR | 0.9 | 9.7 | 0.1 | 0.2 | 11.8 | 46.8 | 3.7 | 0.9 | 3.1 | 1.3 | 1.1 | 2.2 | 0.1 | 0.2 | 1.0 | 2.2 | −0.5 | 0.6 | 14.8 | 0.0 | 53.2 |
| GBR | 0.7 | 6.0 | 0.0 | 0.2 | 10.3 | 14.8 | 41.1 | 1.0 | 2.5 | 1.3 | 1.0 | 2.0 | 0.0 | 0.2 | 1.2 | 2.1 | −0.2 | 0.5 | 15.3 | −0.1 | 58.9 |
| IND | 1.4 | 5.2 | 0.3 | 0.5 | 10.7 | 4.9 | 2.5 | 58.1 | 3.5 | 1.5 | 1.3 | 1.4 | 0.0 | 0.1 | 2.3 | 0.0 | −0.2 | 0.7 | 5.5 | 0.3 | 41.9 |
| JAP | 1.2 | 2.3 | 0.3 | −0.2 | 8.1 | 4.3 | 1.4 | 0.5 | 69.0 | 1.1 | 0.6 | 1.3 | -0.1 | 0.1 | 0.4 | 3.1 | −0.2 | 0.0 | 6.8 | 0.1 | 31.0 |
| KOR | 0.7 | 2.4 | 0.3 | 0.5 | 8.3 | 2.8 | 1.7 | 1.1 | 3.0 | 66.3 | 1.3 | 1.5 | 0.0 | 0.1 | 0.9 | 6.1 | 0.2 | 0.6 | 2.3 | 0.0 | 33.7 |
| LAM | −0.1 | 18.9 | −0.1 | −0.4 | 4.4 | 1.4 | −0.3 | 0.6 | 0.1 | −0.2 | 73.0 | 0.1 | 0.0 | 0.2 | 0.2 | −0.4 | −0.2 | −0.5 | 3.0 | 0.1 | 27.0 |
| MEX | 0.7 | 5.7 | 0.2 | 0.4 | 4.7 | 1.1 | 1.1 | 0.9 | 0.7 | 1.2 | 0.4 | 75.0 | 0.1 | 0.1 | 0.6 | −0.8 | 0.1 | −0.1 | 7.9 | −0.1 | 25.0 |
| NOR | 0.5 | 3.5 | 0.0 | 0.5 | 6.6 | 19.3 | 2.9 | 0.6 | 2.4 | 0.1 | 0.9 | 0.7 | 56.2 | 0.1 | 0.1 | 1.7 | 0.4 | 0.4 | 3.1 | 0.1 | 43.8 |
| NZL | 4.2 | 2.9 | 0.5 | 0.0 | 10.2 | 3.0 | 1.1 | 0.5 | 2.3 | 0.8 | 1.2 | 1.3 | 0.2 | 62.7 | 0.4 | 6.7 | −0.1 | 0.2 | 1.6 | 0.2 | 37.3 |
| SAU | 0.3 | 3.5 | 0.6 | 0.5 | 10.0 | 3.6 | 1.4 | 1.1 | 5.1 | 1.0 | 0.8 | 0.4 | 0.1 | 0.0 | 69.8 | −2.0 | −0.2 | 1.1 | 2.8 | 0.1 | 30.2 |
| SEA | 0.1 | 1.9 | 1.1 | −0.3 | 4.9 | 2.2 | 1.2 | 0.2 | 2.8 | 3.1 | 1.4 | 0.9 | 0.1 | 0.1 | 0.3 | 77.9 | −0.1 | 0.7 | 1.4 | 0.0 | 22.1 |
| SWE | 0.9 | 13.0 | 0.4 | 0.3 | 11.9 | 19.6 | 4.6 | 0.9 | 3.9 | 1.0 | 1.3 | 2.6 | 0.6 | 0.3 | 1.2 | 2.5 | 27.6 | 0.6 | 6.7 | 0.2 | 72.4 |
| TUR | 0.2 | 4.2 | −0.1 | 0.6 | 8.1 | 17.1 | 2.2 | 1.5 | 2.9 | 0.6 | 0.3 | 1.2 | −0.1 | 0.1 | 1.4 | 0.2 | 0.0 | 56.1 | 3.1 | 0.5 | 43.9 |
| USA | 1.4 | 2.1 | 0.9 | 0.1 | 8.9 | 4.2 | 1.7 | 1.3 | 1.5 | 1.9 | 0.9 | 6.2 | 0.1 | 0.3 | 0.9 | 3.0 | 0.0 | 0.2 | 64.3 | 0.1 | 35.7 |
| ZAF | 0.6 | 2.7 | 0.1 | 0.2 | 8.6 | 1.9 | 1.3 | 0.6 | 4.2 | 0.1 | 1.0 | 0.6 | 0.0 | 0.1 | 0.8 | 4.9 | −0.1 | 0.0 | 2.3 | 70.0 | 30.0 |
| To | 0.7 | 5.4 | 0.3 | 0.1 | 9.1 | 4.0 | 1.7 | 0.7 | 2.4 | 1.2 | 0.9 | 2.1 | 0.0 | 0.1 | 0.8 | 2.2 | −0.2 | 0.3 | 5.7 | 0.1 | 39.3 |
| AUS | BRA | CAN | CHE | CHN | EUR | GBR | IND | JAP | KOR | LAM | MEX | NOR | NZL | SEA | SWE | USA | From | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUS | 16.5 | 6.6 | 5.2 | 10.3 | 2.8 | 15.7 | 4.6 | 2.6 | 1.4 | 4.4 | 1.2 | 2.0 | 3.2 | 7.2 | 1.9 | 3.5 | 11.1 | 83.5 |
| BRA | 7.3 | 22.4 | 3.5 | 4.5 | 8.3 | 12.8 | 5.3 | 5.9 | 1.8 | 4.0 | 2.8 | 2.6 | 0.9 | 2.8 | 3.5 | 2.5 | 9.0 | 77.6 |
| CAN | 14.3 | 4.3 | 9.8 | 5.4 | 7.1 | 18.2 | 5.4 | 3.6 | 0.9 | 2.6 | 3.1 | 3.5 | 1.6 | 3.0 | 4.0 | 1.7 | 11.5 | 90.2 |
| CHE | 18.7 | 3.6 | 6.2 | 19.8 | 3.5 | 13.6 | 2.7 | 5.6 | 1.3 | 1.0 | 1.3 | 1.1 | 3.9 | 3.7 | 2.5 | 1.5 | 9.9 | 80.2 |
| CHN | 15.1 | 5.7 | 3.4 | 16.6 | 17.5 | 10.3 | 3.0 | 2.1 | 1.7 | 3.3 | 1.4 | 2.3 | 2.3 | 2.4 | 2.9 | 2.6 | 7.7 | 82.5 |
| EUR | 14.4 | 4.9 | 4.7 | 6.8 | 3.0 | 33.4 | 2.7 | 2.8 | 1.0 | 3.0 | 2.1 | 0.9 | 3.0 | 3.6 | 1.6 | 4.9 | 7.3 | 66.6 |
| GBR | 9.6 | 3.6 | 7.7 | 5.4 | 4.0 | 21.6 | 14.4 | 2.2 | 1.6 | 1.7 | 1.1 | 1.2 | 1.3 | 6.5 | 3.0 | 2.1 | 13.0 | 85.6 |
| IND | 7.5 | 8.6 | 2.7 | 11.2 | 4.0 | 6.5 | 2.0 | 37.5 | 3.8 | 2.9 | 0.6 | 0.7 | 1.8 | 1.9 | 2.9 | 2.6 | 2.9 | 62.5 |
| JAP | 5.1 | 6.5 | 2.9 | 9.3 | 2.3 | 10.8 | 2.3 | 5.3 | 18.4 | 3.9 | 0.9 | 1.8 | 3.3 | 3.2 | 2.5 | 2.1 | 19.5 | 81.6 |
| KOR | 9.4 | 3.9 | 2.6 | 15.0 | 3.5 | 8.1 | 2.4 | 3.1 | 6.0 | 14.0 | 0.6 | 2.2 | 2.5 | 6.8 | 2.2 | 5.2 | 12.3 | 85.9 |
| LAM | 10.5 | 10.9 | 1.3 | 1.5 | 1.4 | 9.8 | 2.0 | 1.3 | 1.0 | 1.2 | 32.2 | 9.2 | 4.5 | 0.9 | 1.4 | 1.3 | 9.6 | 67.8 |
| MEX | 8.4 | 4.1 | 3.3 | 5.2 | 9.5 | 19.8 | 3.3 | 4.8 | 2.6 | 3.1 | 5.8 | 13.4 | 1.3 | 2.2 | 2.9 | 2.0 | 8.3 | 86.6 |
| NOR | 5.7 | 4.3 | 1.7 | 16.0 | 1.4 | 7.6 | 4.5 | 7.4 | 4.5 | 1.3 | 1.4 | 1.4 | 28.2 | 3.6 | 1.0 | 7.7 | 2.4 | 71.8 |
| NZL | 8.7 | 2.1 | 7.6 | 8.8 | 2.6 | 11.1 | 5.0 | 6.0 | 5.0 | 4.6 | 0.7 | 1.6 | 2.0 | 13.9 | 2.6 | 2.4 | 15.1 | 86.1 |
| SEA | 11.1 | 6.0 | 7.1 | 8.9 | 6.0 | 18.2 | 3.1 | 3.7 | 1.4 | 5.0 | 1.8 | 2.5 | 1.8 | 3.0 | 10.2 | 2.3 | 7.8 | 89.8 |
| SWE | 7.2 | 1.4 | 2.9 | 18.2 | 0.9 | 14.5 | 2.1 | 7.3 | 5.2 | 1.4 | 1.2 | 3.0 | 5.6 | 8.5 | 3.1 | 13.9 | 3.6 | 86.1 |
| USA | 18.3 | 3.9 | 4.1 | 5.6 | 1.1 | 16.1 | 3.0 | 3.5 | 3.6 | 1.1 | 1.0 | 2.0 | 1.3 | 4.4 | 5.4 | 2.0 | 23.8 | 76.2 |
| To | 13.1 | 5.5 | 4.0 | 9.8 | 3.4 | 12.9 | 2.9 | 3.2 | 2.3 | 2.8 | 1.5 | 2.0 | 2.1 | 3.3 | 3.2 | 2.7 | 8.4 | 80.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moramarco, G. Measuring Global Macroeconomic Uncertainty and Cross-Country Uncertainty Spillovers. Econometrics 2023, 11, 2. https://doi.org/10.3390/econometrics11010002
Moramarco G. Measuring Global Macroeconomic Uncertainty and Cross-Country Uncertainty Spillovers. Econometrics. 2023; 11(1):2. https://doi.org/10.3390/econometrics11010002
Chicago/Turabian StyleMoramarco, Graziano. 2023. "Measuring Global Macroeconomic Uncertainty and Cross-Country Uncertainty Spillovers" Econometrics 11, no. 1: 2. https://doi.org/10.3390/econometrics11010002
APA StyleMoramarco, G. (2023). Measuring Global Macroeconomic Uncertainty and Cross-Country Uncertainty Spillovers. Econometrics, 11(1), 2. https://doi.org/10.3390/econometrics11010002







