Maximum Likelihood Inference for Asymmetric Stochastic Volatility Models
Abstract
:1. Introduction
2. Methods
2.1. Parameter Estimation
2.2. VaR Forecasting
- 1.
- Estimate the parameters for .
- 2.
- From the Kalman filter, calculate for and obtain the predicted volatilities , where .
- 3.
- Obtain the standardized residuals for and compute the -quantile of , which is called .
- 4.
- The %-VaR is then equal to
2.3. Implementation
2.4. The Stochvol Method
3. Monte Carlo Experiments
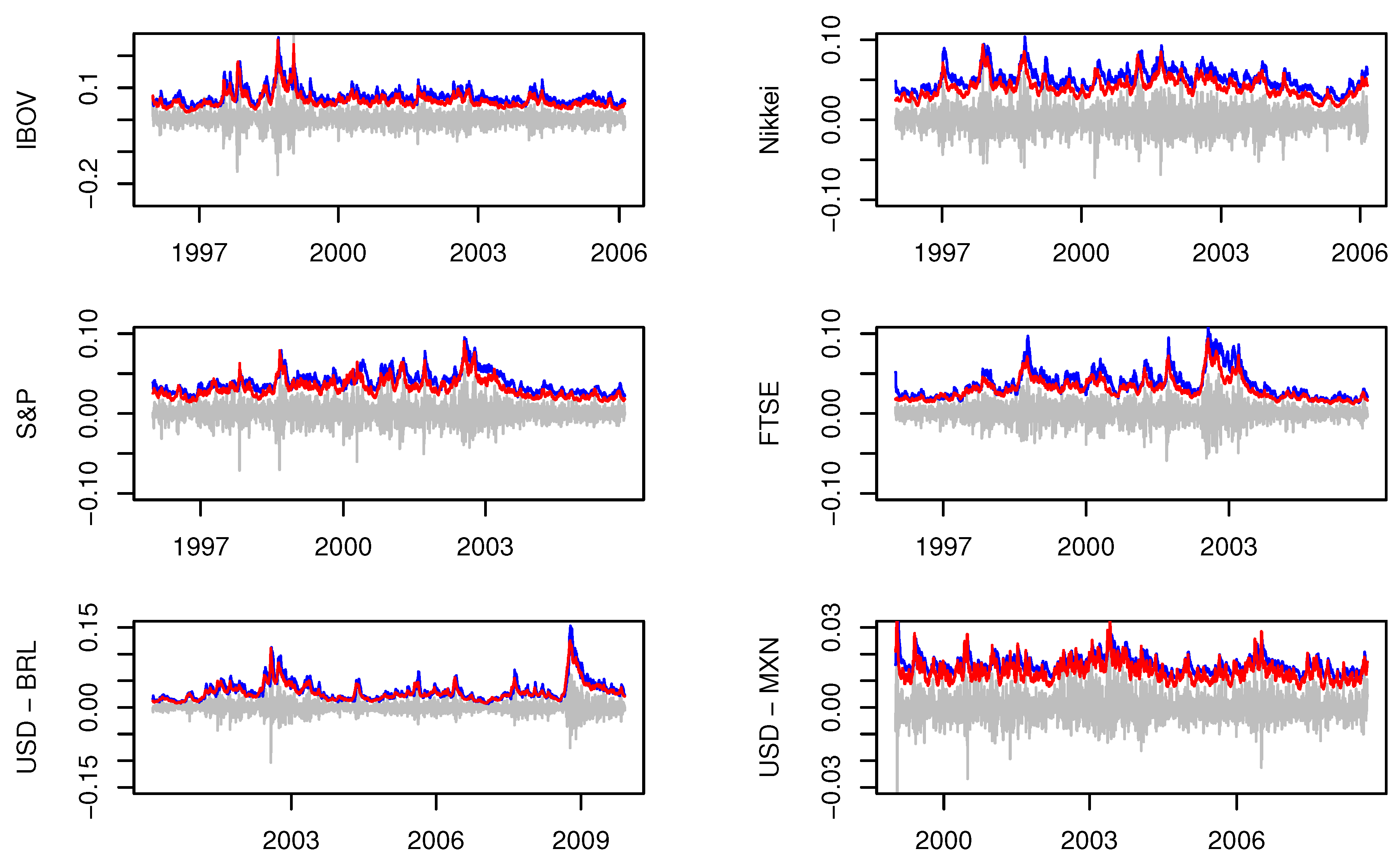
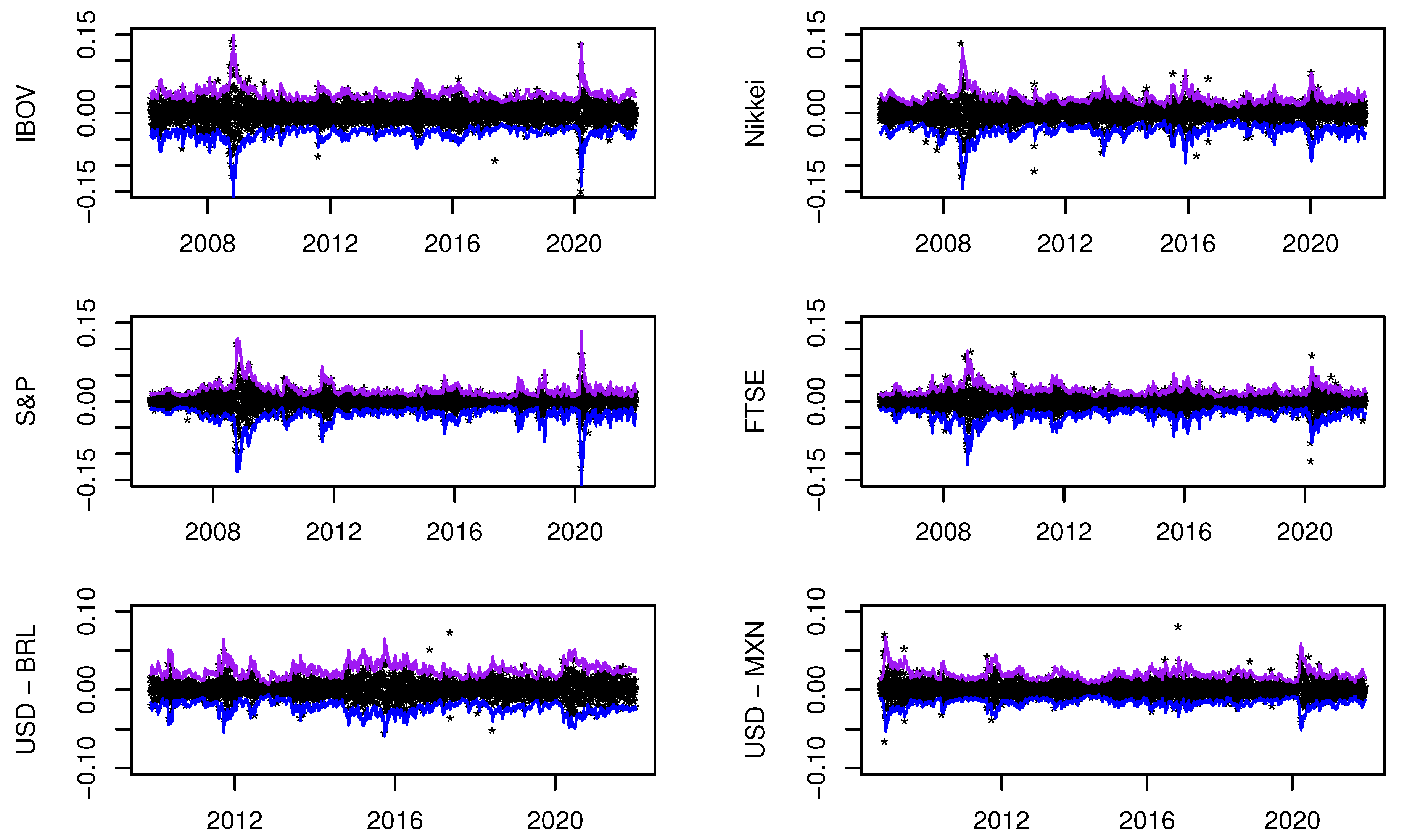
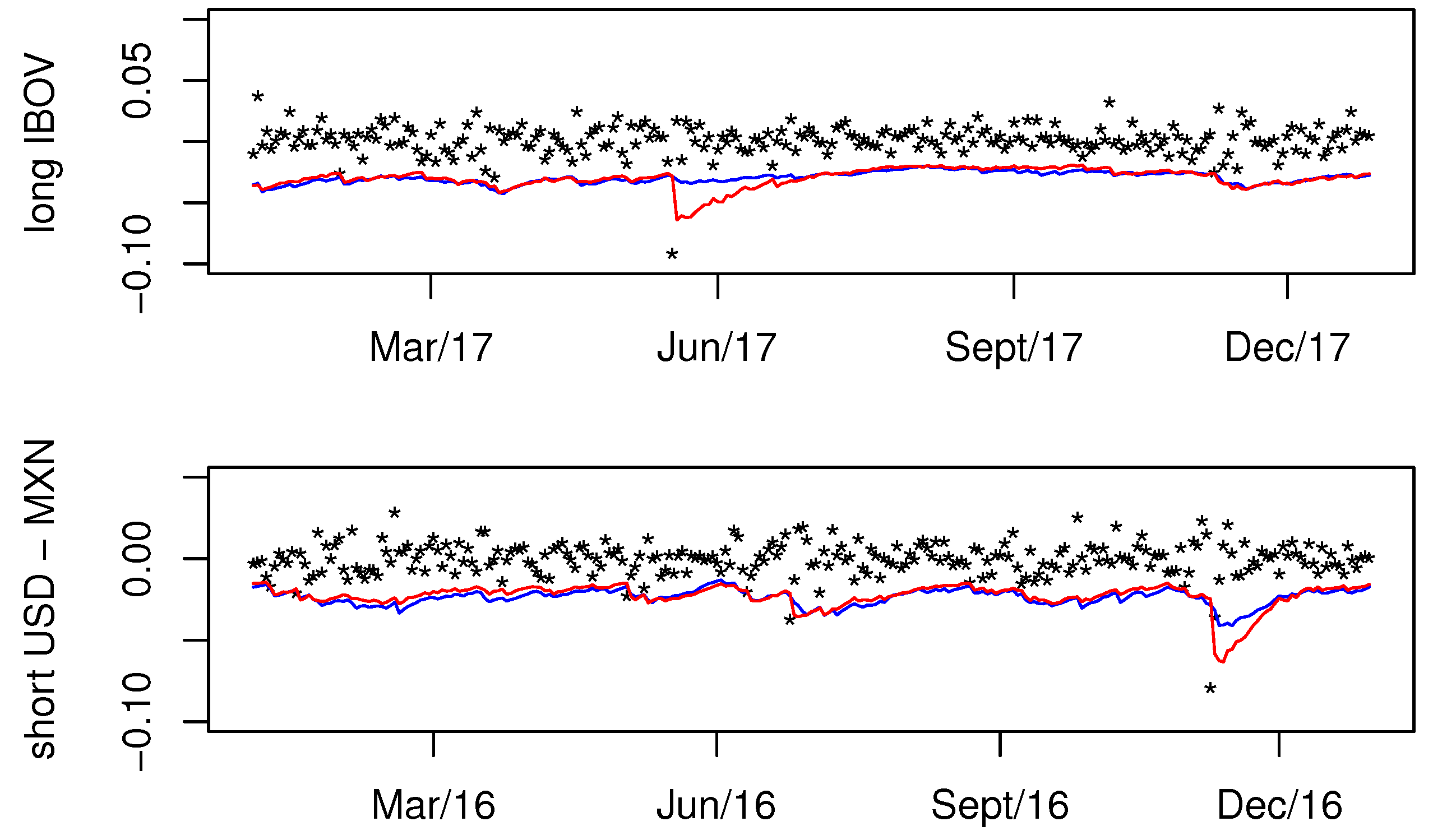
4. Empirical Illustrations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | In the ARCH/GARCH framework, models for accounting for the leverage effect include the EGARCH model of Nelson (1991) and the GJR model proposed by Glosten et al. (1993), among others. |
| 2 | The results for are qualitative similar and are available upon request |
| 3 | The total number of observations are as follows: 6419 for IBOV, 6543 for S&P 500, 6371 for Nikkei, 6565 for FTSE, 5533 for USD-BRL, and 5977 for USD-MXN. |
| 4 | We tested our method for both FX series in a different period compared to Asai and McAleer (2011). Since we did not obtain significant correlation parameter estimates even when using the stochvol method, the results are not reported here. |
| 5 | However, is significant using the stochvol method, and so we considered this time series in our analysis. |
| 6 | We tested the estimation when , but all degrees of freedom were higher than 30; thus, the results did not differ greatly from the Gaussian distribution. |
| 7 | As pointed out by a referee, the estimation process can be accelerated by using steady state expressions in the Kalman filter. This idea can be particularly fruitful for more complex models and deserves further investigation. |
References
- Abbara, Omar, and Mauricio Zevallos. 2019. A note on stochastic volatility model estimation. Brazilian Review of Finance 17: 22–32. [Google Scholar] [CrossRef] [Green Version]
- Abbara, Omar, and Mauricio Zevallos. 2022. Estimation and forecasting of long memory stochastic volatility models. Studies in Nonlinear Dynamics and Econometrics. [Google Scholar] [CrossRef]
- Asai, Manabu, and Michael McAleer. 2011. Alternative assymmetric stochastic volatility models. Econometric Reviews 30: 548–64. [Google Scholar] [CrossRef] [Green Version]
- Black, Fischer. 1976. Studies of stock price volatility changes. In Proceedings of the Business and Economics Section of the American Statistical Association. Washington, DC: American Statistical Association, pp. 177–81. [Google Scholar]
- Christoffersen, Peter. 1998. Evaluating interval forecasts. Symposium on Forecasting and Empirical Methods in Macroeconomics and Finance 39: 841–62. [Google Scholar] [CrossRef]
- Christoffersen, Peter, and Denis Pelletier. 2004. Backtesting value-at-risk: A duration-based approach. Journal of Financial Econometrics 2: 84–108. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of nominal excess return on stocks. Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Harvey, Andrew C., and Neil Shephard. 1996. Estimation of an asymmetric stochastic volatility model for asset returns. Journal of Business and Economic Statistics 14: 429–34. [Google Scholar]
- Hosszejni, Darjus, and Gregor Kastner. 2021. Modeling univariate and multivariate stochastic volatility in r with stochvol and factorstochvol. Journal of Statistical Software 100: 1–34. [Google Scholar] [CrossRef]
- Jacquier, Eric, Nicholas G. Polson, and Peter E. Rossi. 2004. Bayesian analysis of stochastic volatility models with fat-tails and correlated errors. Journal of Econometrics 122: 185–212. [Google Scholar] [CrossRef]
- Jensen, Mark J., and John M. Maheu. 2010. Bayesian semiparametric stochastic volatility modeling. Journal of Econometrics 157: 306–16. [Google Scholar] [CrossRef] [Green Version]
- Jensen, Mark J., and John M. Maheu. 2014. Estimating a semiparametric asymmetric stochastic volatility model with a dirichlet process mixture. Journal of Econometrics 178: 523–38. [Google Scholar] [CrossRef] [Green Version]
- Kupiec, Paul. 1995. Techniques for verifying the accuracy of risk management models. Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Mao, Xiuping, Veronika Czellar, Esther Ruiz, and Helena Veiga. 2020. Asymmetric stochastic volatility models: Properties and particle filter-based simulated maximum likelihood estimation. Econometrics and Statistics 13: 84–105. [Google Scholar] [CrossRef]
- McAleer, Michael. 2014. Asymmetry and leverage in conditional volatility models. Econometrics 2: 145–50. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, Jouchi, and Yasuhiro Omori. 2012. Stochastic volatility model with leverage and asymmetrically heavy-tailed error using gh skew student’s-t distribution. Computational Statistics and Data Analysis 56: 3690–704. [Google Scholar] [CrossRef]
- Nelson, Daniel. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Omori, Yasuhiro, Siddhartha Chib, Neil Shephard, and Jouchi Nakajima. 2007. Stochastic volatility with leverage: Fast and efficient likelihood inference. Journal of Econometrics 140: 425–49. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. 2020. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Schäfers, Torben, and Long Teng. 2022. Asymmetric stochastic volatility models with threshold and time-dependent correlations. Studies in Nonlinear Dynamics and Econometrics. [Google Scholar] [CrossRef]
- Selçuk, Faruk. 2005. Asymmetric stochastic volatility in emerging markets. Applied Financial Econometrics 15: 867–74. [Google Scholar] [CrossRef]
- Shumway, Robert H., and David S. Stoffer. 2006. Time Series Analysis and Its Applications. New York: Springer. [Google Scholar]
- Takahashi, Makoto, Toshiaki Watanabe, and Yasuhiro Omori. 2021. Forecasting daily volatility of stock price index using daily returns and realized volatility. Econometrics and Statistics. [Google Scholar] [CrossRef]
- Taylor, Stephen John. 1982. Financial returns modelled by the product of two stochastic processes—A study of daily sugar prices, 1961–79. In Time Series Analysis: Theory and Practice. Edited by Oliver Duncan Anderson. North-Holland and New York: Elsevier, vol. 1, pp. 203–26. [Google Scholar]
- Taylor, Stephen John. 1994. Modelling stochastic volatility: A review and comparative study. Mathematical Finance 4: 183–204. [Google Scholar] [CrossRef]
- Yu, Jun. 2005. On leverage in a stochastic volatility model. Journal of Econometrics 127: 165–78. [Google Scholar] [CrossRef]
| Proposal | Stochvol | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Bias | −0.005 | 0.008 | −0.141 | 0.120 | −0.006 | 0.026 | 0.382 | 0.096 | −0.012 | 0.017 | −0.002 | 0.090 | ||
| SD | 0.023 | 0.039 | 0.077 | 0.164 | 0.034 | 0.041 | 0.202 | 0.186 | 0.017 | 0.024 | 0.059 | 0.068 | |||
| RMSE | 0.024 | 0.039 | 0.160 | 0.203 | 0.034 | 0.049 | 0.432 | 0.210 | 0.021 | 0.030 | 0.059 | 0.113 | |||
| Case 2 | Bias | −0.004 | −0.005 | −0.145 | 0.121 | −0.004 | 0.022 | 0.359 | 0.114 | −0.013 | 0.020 | −0.005 | 0.150 | ||
| SD | 0.016 | 0.030 | 0.067 | 0.137 | 0.025 | 0.033 | 0.205 | 0.152 | 0.013 | 0.020 | 0.050 | 0.049 | |||
| RMSE | 0.016 | 0.030 | 0.160 | 0.183 | 0.025 | 0.039 | 0.413 | 0.189 | 0.018 | 0.029 | 0.050 | 0.158 | |||
| Case 3 | Bias | −0.002 | 0.023 | −0.148 | −0.134 | −0.002 | 0.055 | 0.399 | −0.108 | −0.005 | 0.009 | 0.002 | −0.045 | ||
| SD | 0.012 | 0.036 | 0.106 | 0.080 | 0.012 | 0.037 | 0.139 | 0.087 | 0.011 | 0.025 | 0.095 | 0.057 | |||
| RMSE | 0.013 | 0.043 | 0.182 | 0.156 | 0.012 | 0.066 | 0.423 | 0.138 | 0.012 | 0.026 | 0.095 | 0.072 | |||
| Case 4 | , | Bias | −0.008 | 0.006 | −0.523 | 0.153 | −0.008 | 0.021 | 0.037 | 0.110 | −0.030 | 0.041 | −0.020 | 0.135 | |
| SD | 0.026 | 0.046 | 0.081 | 0.145 | 0.032 | 0.048 | 0.169 | 0.167 | 0.045 | 0.045 | 0.074 | 0.079 | |||
| RMSE | 0.028 | 0.046 | 0.529 | 0.211 | 0.033 | 0.052 | 0.173 | 0.200 | 0.054 | 0.061 | 0.077 | 0.156 | |||
| Case 5 | Bias | −0.006 | −0.013 | −0.526 | 0.165 | −0.005 | 0.011 | 0.021 | 0.126 | −0.023 | 0.038 | −0.027 | 0.214 | ||
| SD | 0.019 | 0.038 | 0.076 | 0.176 | 0.019 | 0.038 | 0.137 | 0.149 | 0.027 | 0.032 | 0.066 | 0.060 | |||
| RMSE | 0.020 | 0.040 | 0.532 | 0.241 | 0.020 | 0.039 | 0.139 | 0.195 | 0.035 | 0.050 | 0.072 | 0.222 | |||
| Case 6 | , | Bias | −0.003 | 0.015 | −0.529 | −0.163 | −0.003 | 0.042 | 0.034 | −0.124 | −0.009 | 0.019 | −0.014 | −0.062 | |
| SD | 0.013 | 0.039 | 0.113 | 0.083 | 0.013 | 0.041 | 0.238 | 0.096 | 0.014 | 0.033 | 0.107 | 0.066 | |||
| RMSE | 0.014 | 0.042 | 0.541 | 0.183 | 0.013 | 0.058 | 0.240 | 0.157 | 0.016 | 0.039 | 0.108 | 0.091 | |||
| Proposal | Stochvol | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Bias | −0.002 | 0.022 | −0.119 | 0.149 | −0.002 | 0.052 | 0.402 | 0.133 | −0.002 | 0.007 | 0.007 | 0.078 | ||
| SD | 0.004 | 0.020 | 0.297 | 0.097 | 0.004 | 0.022 | 0.331 | 0.099 | 0.004 | 0.015 | 0.254 | 0.064 | |||
| RMSE | 0.004 | 0.030 | 0.320 | 0.178 | 0.004 | 0.056 | 0.521 | 0.166 | 0.004 | 0.017 | 0.254 | 0.100 | |||
| Case 2 | Bias | −0.001 | 0.007 | −0.150 | 0.174 | −0.001 | 0.043 | 0.327 | 0.175 | −0.002 | 0.008 | 0.024 | 0.123 | ||
| SD | 0.003 | 0.018 | 0.266 | 0.105 | 0.003 | 0.020 | 0.306 | 0.096 | 0.003 | 0.013 | 0.203 | 0.044 | |||
| RMSE | 0.004 | 0.020 | 0.305 | 0.204 | 0.004 | 0.047 | 0.448 | 0.200 | 0.004 | 0.015 | 0.204 | 0.131 | |||
| Case 3 | Bias | −0.001 | 0.043 | −0.065 | −0.151 | −0.001 | 0.087 | 0.419 | −0.137 | −0.002 | 0.005 | 0.025 | −0.040 | ||
| SD | 0.004 | 0.026 | 0.752 | 0.071 | 0.004 | 0.029 | 0.852 | 0.078 | 0.003 | 0.019 | 0.443 | 0.055 | |||
| RMSE | 0.004 | 0.051 | 0.755 | 0.167 | 0.004 | 0.092 | 0.949 | 0.157 | 0.004 | 0.020 | 0.444 | 0.068 | |||
| Case 4 | , | Bias | −0.002 | 0.014 | −0.522 | 0.190 | −0.002 | 0.039 | −0.001 | 0.158 | −0.003 | 0.010 | −0.007 | 0.105 | |
| SD | 0.004 | 0.022 | 0.275 | 0.102 | 0.004 | 0.025 | 0.370 | 0.111 | 0.004 | 0.018 | 0.260 | 0.072 | |||
| RMSE | 0.005 | 0.027 | 0.590 | 0.215 | 0.005 | 0.046 | 0.370 | 0.192 | 0.005 | 0.020 | 0.260 | 0.127 | |||
| Case 5 | Bias | −0.002 | −0.003 | −0.537 | 0.224 | −0.002 | 0.026 | −0.059 | 0.202 | −0.003 | 0.010 | −0.006 | 0.166 | ||
| SD | 0.004 | 0.022 | 0.252 | 0.125 | 0.004 | 0.024 | 0.364 | 0.119 | 0.004 | 0.016 | 0.216 | 0.050 | |||
| RMSE | 0.004 | 0.022 | 0.593 | 0.257 | 0.004 | 0.035 | 0.368 | 0.235 | 0.005 | 0.019 | 0.216 | 0.174 | |||
| Case 6 | , | Bias | −0.001 | 0.034 | −0.520 | −0.177 | −0.001 | 0.071 | 0.011 | −0.150 | −0.002 | 0.008 | −0.008 | −0.053 | |
| SD | 0.004 | 0.027 | 0.633 | 0.074 | 0.004 | 0.032 | 0.730 | 0.085 | 0.004 | 0.022 | 0.462 | 0.063 | |||
| RMSE | 0.004 | 0.043 | 0.819 | 0.191 | 0.004 | 0.078 | 0.730 | 0.172 | 0.004 | 0.023 | 0.462 | 0.083 | |||
| Proposal | Stochvol | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IBOV | Estimate | 0.975 | 0.168 | −7.950 | −0.386 | 0.968 | 0.224 | −7.431 | −0.413 | 0.956 | 0.214 | −7.850 | −0.471 |
| Std. error/Std. dev. | (0.010) | (0.034) | (0.172) | (0.118) | (0.011) | (0.041) | (0.165) | (0.113) | (0.010) | (0.025) | (0.095) | (0.058) | |
| Nikkei | Estimate | 0.982 | 0.136 | −8.811 | −0.345 | 0.984 | 0.157 | −8.254 | −0.380 | 0.971 | 0.165 | −8.727 | −0.463 |
| Std. error/Std. dev. | (0.008) | (0.029) | (0.191) | (0.155) | (0.007) | (0.032) | (0.206) | (0.162) | (0.007) | (0.020) | (0.111) | (0.063) | |
| S&P 500 | Estimate | 0.986 | 0.104 | −9.244 | −0.776 | 0.986 | 0.138 | −8.704 | −0.760 | 0.976 | 0.163 | −9.135 | −0.658 |
| Std. error/Std. dev. | (0.006) | (0.024) | (0.166) | (0.170) | (0.005) | (0.026) | (0.173) | (0.123) | (0.006) | (0.020) | (0.110) | (0.047) | |
| FTSE | Estimate | 0.987 | 0.137 | −9.222 | −0.728 | 0.986 | 0.178 | −8.744 | −0.752 | 0.987 | 0.135 | −9.265 | −0.627 |
| Std. error/Std. dev. | (0.004) | (0.022) | (0.219) | (0.136) | (0.004) | (0.025) | (0.208) | (0.105) | (0.003) | (0.015) | (0.174) | (0.058) | |
| USD-BRL | Estimate | 0.980 | 0.249 | −9.581 | 0.224 | 0.979 | 0.279 | −9.127 | 0.234 | 0.980 | 0.210 | −9.592 | 0.322 |
| Std. error/Std. dev. | (0.007) | (0.039) | (0.299) | (0.104) | (0.007) | (0.041) | (0.277) | (0.111) | (0.005) | (0.019) | (0.211) | (0.062) | |
| USD-MXN | Estimate | 0.968 | 0.143 | −11.037 | 0.163 | 0.967 | 0.164 | −10.463 | 0.118 | 0.862 | 0.354 | −10.926 | 0.363 |
| Std. error/Std. dev. | (0.018) | (0.046) | (0.135) | (0.170) | (0.018) | (0.052) | (0.155) | (0.191) | (0.038) | (0.059) | (0.060) | (0.054) | |
| Asset | Stat/Test | Long Position | Short Position | Long Position | Short Position | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IBOV | Proportion | 0.012 | 0.024 | 0.048 | 0.047 | 0.026 | 0.011 | 0.011 | 0.024 | 0.048 | 0.046 | 0.025 | 0.010 |
| Kupiec | 0.287 | 0.608 | 0.558 | 0.332 | 0.682 | 0.656 | 0.547 | 0.608 | 0.558 | 0.301 | 0.920 | 0.773 | |
| Christoffersen | 0.483 | 0.082 | 0.513 | 0.385 | 0.899 | 0.574 | 0.663 | 0.082 | 0.795 | 0.380 | 0.959 | 0.622 | |
| Christoffersen-Pelletier | 0.029 | 0.045 | 0.421 | 0.516 | 0.699 | 0.708 | 0.029 | 0.015 | 0.668 | 0.064 | 0.953 | 0.428 | |
| Nikkei | Proportion | 0.014 | 0.029 | 0.052 | 0.051 | 0.026 | 0.013 | 0.012 | 0.029 | 0.052 | 0.050 | 0.026 | 0.012 |
| Kupiec | 0.029 | 0.126 | 0.489 | 0.744 | 0.666 | 0.110 | 0.195 | 0.152 | 0.536 | 0.909 | 0.741 | 0.322 | |
| Christoffersen | 0.042 | 0.021 | 0.459 | 0.910 | 0.834 | 0.253 | 0.140 | 0.022 | 0.612 | 0.977 | 0.878 | 0.513 | |
| Christoffersen-Pelletier | 0.016 | 0.003 | 0.115 | 0.075 | 0.718 | 0.167 | 0.030 | 0.135 | 0.252 | 0.008 | 0.470 | 0.133 | |
| S&P 500 | Proportion | 0.017 | 0.034 | 0.056 | 0.052 | 0.026 | 0.013 | 0.016 | 0.032 | 0.055 | 0.050 | 0.025 | 0.011 |
| Kupiec | 0.000 | 0.000 | 0.105 | 0.481 | 0.769 | 0.080 | 0.000 | 0.009 | 0.180 | 0.894 | 0.994 | 0.389 | |
| Christoffersen | 0.000 | 0.002 | 0.266 | 0.029 | 0.868 | 0.201 | 0.000 | 0.022 | 0.407 | 0.065 | 0.956 | 0.406 | |
| Christoffersen-Pelletier | 0.001 | 0.047 | 0.099 | 0.010 | 0.914 | 0.432 | 0.001 | 0.113 | 0.083 | 0.000 | 0.329 | 0.247 | |
| FTSE | Proportion | 0.014 | 0.031 | 0.050 | 0.053 | 0.028 | 0.013 | 0.013 | 0.028 | 0.049 | 0.052 | 0.025 | 0.013 |
| Kupiec | 0.022 | 0.030 | 0.900 | 0.443 | 0.188 | 0.086 | 0.045 | 0.261 | 0.815 | 0.579 | 0.970 | 0.117 | |
| Christoffersen | 0.036 | 0.014 | 0.071 | 0.025 | 0.015 | 0.117 | 0.128 | 0.031 | 0.157 | 0.002 | 0.072 | 0.153 | |
| Christoffersen-Pelletier | 0.461 | 0.236 | 0.478 | 0.000 | 0.027 | 0.895 | 0.916 | 0.406 | 0.756 | 0.000 | 0.057 | 0.778 | |
| USD-BRL | Proportion | 0.012 | 0.026 | 0.054 | 0.048 | 0.023 | 0.010 | 0.011 | 0.025 | 0.054 | 0.049 | 0.023 | 0.010 |
| Kupiec | 0.405 | 0.801 | 0.310 | 0.697 | 0.420 | 0.952 | 0.511 | 0.923 | 0.272 | 0.760 | 0.493 | 0.903 | |
| Christoffersen | 0.470 | 0.773 | 0.230 | 0.927 | 0.639 | 0.740 | 0.548 | 0.990 | 0.326 | 0.549 | 0.686 | 0.721 | |
| Christoffersen-Pelletier | 0.679 | 0.094 | 0.038 | 0.956 | 0.482 | 0.553 | 0.661 | 0.230 | 0.013 | 0.686 | 0.451 | 0.492 | |
| USD-MXN | Proportion | 0.009 | 0.026 | 0.050 | 0.054 | 0.027 | 0.013 | 0.010 | 0.026 | 0.050 | 0.053 | 0.025 | 0.013 |
| Kupiec | 0.632 | 0.660 | 0.929 | 0.312 | 0.448 | 0.131 | 0.895 | 0.585 | 0.929 | 0.390 | 0.994 | 0.095 | |
| Christoffersen | 0.662 | 0.531 | 0.343 | 0.016 | 0.043 | 0.020 | 0.709 | 0.071 | 0.343 | 0.288 | 0.239 | 0.018 | |
| Christoffersen-Pelletier | 0.990 | 0.952 | 0.134 | 0.085 | 0.002 | 0.001 | 0.364 | 0.352 | 0.025 | 0.384 | 0.009 | 0.035 | |
| Asset | Stat/Test | Long Position | Short Position | ||||
|---|---|---|---|---|---|---|---|
| IBOV | Prop | 0.011 | 0.024 | 0.043 | 0.038 | 0.018 | 0.008 |
| Kupiec | 0.547 | 0.760 | 0.052 | 0.000 | 0.004 | 0.124 | |
| Christoffersen | 0.518 | 0.934 | 0.149 | 0.002 | 0.014 | 0.243 | |
| Christoffersen-Pelletier | 0.718 | 0.990 | 0.529 | 0.356 | 0.284 | 0.568 | |
| Nikkei | Prop | 0.014 | 0.032 | 0.051 | 0.043 | 0.016 | 0.005 |
| Kupiec | 0.009 | 0.013 | 0.800 | 0.045 | 0.000 | 0.000 | |
| Christoffersen | 0.017 | 0.044 | 0.968 | 0.134 | 0.001 | 0.000 | |
| Christoffersen-Pelletier | 0.648 | 0.950 | 0.476 | 0.687 | 0.027 | 0.261 | |
| S&P 500 | Prop | 0.019 | 0.037 | 0.060 | 0.044 | 0.017 | 0.005 |
| Kupiec | 0.000 | 0.000 | 0.003 | 0.089 | 0.001 | 0.001 | |
| Christoffersen | 0.000 | 0.000 | 0.005 | 0.120 | 0.001 | 0.005 | |
| Christoffersen-Pelletier | 0.660 | 0.878 | 0.061 | 0.274 | 0.468 | 0.786 | |
| FTSE | Prop | 0.016 | 0.035 | 0.057 | 0.040 | 0.017 | 0.006 |
| Kupiec | 0.000 | 0.000 | 0.059 | 0.002 | 0.001 | 0.008 | |
| Christoffersen | 0.000 | 0.000 | 0.162 | 0.000 | 0.001 | 0.025 | |
| Christoffersen-Pelletier | 0.053 | 0.148 | 0.123 | 0.005 | 0.944 | 0.282 | |
| USD-BRL | Prop | 0.009 | 0.017 | 0.044 | 0.054 | 0.026 | 0.010 |
| Kupiec | 0.536 | 0.005 | 0.134 | 0.310 | 0.630 | 0.952 | |
| Christoffersen | 0.415 | 0.004 | 0.009 | 0.571 | 0.888 | 0.740 | |
| Christoffersen-Pelletier | 0.412 | 0.905 | 0.479 | 0.394 | 0.749 | 0.412 | |
| USD-MXN | Prop | 0.008 | 0.020 | 0.043 | 0.067 | 0.034 | 0.018 |
| Kupiec | 0.311 | 0.033 | 0.069 | 0.000 | 0.001 | 0.001 | |
| Christoffersen | 0.469 | 0.026 | 0.102 | 0.001 | 0.002 | 0.001 | |
| Christoffersen-Pelletier | 0.899 | 0.281 | 0.194 | 0.018 | 0.529 | 0.091 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbara, O.; Zevallos, M. Maximum Likelihood Inference for Asymmetric Stochastic Volatility Models. Econometrics 2023, 11, 1. https://doi.org/10.3390/econometrics11010001
Abbara O, Zevallos M. Maximum Likelihood Inference for Asymmetric Stochastic Volatility Models. Econometrics. 2023; 11(1):1. https://doi.org/10.3390/econometrics11010001
Chicago/Turabian StyleAbbara, Omar, and Mauricio Zevallos. 2023. "Maximum Likelihood Inference for Asymmetric Stochastic Volatility Models" Econometrics 11, no. 1: 1. https://doi.org/10.3390/econometrics11010001
APA StyleAbbara, O., & Zevallos, M. (2023). Maximum Likelihood Inference for Asymmetric Stochastic Volatility Models. Econometrics, 11(1), 1. https://doi.org/10.3390/econometrics11010001






