Robust Estimation and Forecasting of Climate Change Using Score-Driven Ice-Age Models
Abstract
:1. Introduction
2. Climate Econometrics
2.1. Benchmark Ice-Age Model
2.2. Score-Driven Ice-Age Models
2.2.1. Score-Driven Homoskedastic Ice-Age Model
2.2.2. Score-Driven Heteroskedastic Ice-Age Model
3. Empirical Results
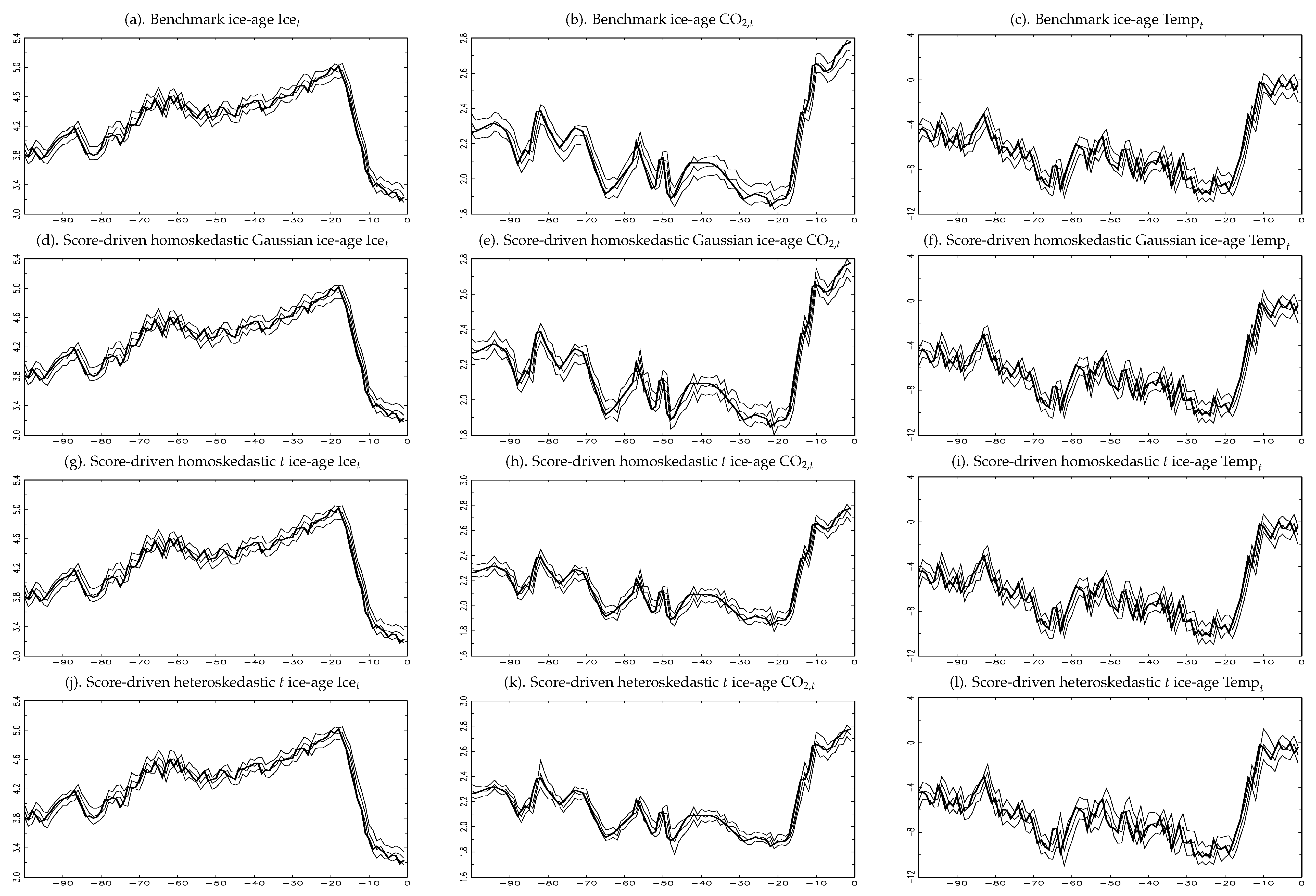
3.1. Data
3.2. Estimation Results
3.3. Forecasting Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Anet, Julien G., E. V. Rozanov, Stefan Muthers, T. Peter, Stefan Brönnimann, F. Arfeuille, J. Beer, A. I. Shapiro, C. C. Raible, F. Steinhilber, and et al. 2013. Impact of a potential 21st century “grand solar minimum” on surface temperatures and stratospheric ozone. Geophysical Research Letters 40: 4420–25. [Google Scholar] [CrossRef] [Green Version]
- Archer, David, Pamela Martin, Bruce Buffett, Victor Brovkin, Stefan Rahmstorf, and Andrey Ganopolski. 2004. The importance of ocean temperature to global biogeochemistry. Earth and Planetary Science Letters 222: 333–48. [Google Scholar] [CrossRef]
- Blasques, Francisco, Janneke van Brummelen, Siem Jan Koopman, and Andre Lucas. 2021. Maximum likelihood estimation for score-driven models. Journal of Econometrics. [Google Scholar] [CrossRef]
- Blasques, Francisco, Siem Jan Koopman, and Andre Lucas. 2015. Information-theoretic optimality of observation-driven time series models for continuous responses. Biometrika 102: 325–43. [Google Scholar] [CrossRef]
- Blazsek, Szabolcs, Alvaro Escribano, and Adrian Licht. 2020. Identification of seasonal effects in impulse responses using score-driven multivariate location models. Journal of Econometric Methods 10: 53–66. [Google Scholar] [CrossRef]
- Blazsek, Szabolcs, Alvaro Escribano, and Adrian Licht. 2021a. Co-integration with score-driven models: An application to US real GDP growth, US inflation rate, and effective federal funds rate. Macroeconomic Dynamics, 1–21. [Google Scholar] [CrossRef]
- Blazsek, Szabolcs, Alvaro Escribano, and Adrian Licht. 2021b. Multivariate Markov-switching score-driven models: An application to the global crude oil market. Studies in Nonlinear Dynamics & Econometrics. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef] [Green Version]
- Box, George E. P., and Gwilym M. Jenkins. 1970. Time Series Analysis, Forecasting and Control. San Francisco: Holden-Day. [Google Scholar]
- Bronselaer, Ben, Michael Winton, Stephen M. Griffies, William J. Hurlin, Keith B. Rodgers, Olga V. Sergienko, Roland J. Stouffer, and Joellen L. Russell. 2018. Change in future climate due to Antarctic meltwater. Nature 564: 53–58. [Google Scholar] [CrossRef]
- Castle, Jennifer, and David F. Hendry. 2020. Climate econometrics: An overview. Foundations and Trends in Econometrics 10: 145–322. [Google Scholar] [CrossRef]
- Cox, David R. 1981. Statistical analysis of time series: Some recent developments. Scandinavian Journal of Statistics 8: 93–115. [Google Scholar]
- Creal, Drew, Siem Jan Koopman, and Andre Lucas. 2008. A General Framework for Observation Driven Time-Varying Parameter Models. Tinbergen Institute Discussion Paper 08-108/4. Available online: https://www.tinbergen.nl/discussion-paper/2649/08-108-4-a-general-framework-for-observation-driven-timevarying-parameter-models (accessed on 25 December 2021).
- Creal, Drew, Siem Jan Koopman, and Andre Lucas. 2011. A dynamic multivariate heavy-tailed model for time-varying volatilities and correlations. Journal of Business & Economic Statistics 29: 552–63. [Google Scholar] [CrossRef] [Green Version]
- Creal, Drew, Siem Jan Koopman, and Andre Lucas. 2013. Generalized autoregressive score models with applications. Journal of Applied Econometrics 28: 777–95. [Google Scholar] [CrossRef] [Green Version]
- Engle, Robert. 2002. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–51. [Google Scholar] [CrossRef]
- Feulner, Georg, and Stefan Rahmstorf. 2010. On the effect of a new grand minimum of solar activity on the future climate on Earth. Geophysical Research Letters 37. [Google Scholar] [CrossRef] [Green Version]
- Harvey, Andrew C. 2013. Dynamic Models for Volatility and Heavy Tails: With Applications to Financial and Economic Time Series. Econometric Society Monographs. Cambridge: Cambridge University Press. [Google Scholar]
- Harvey, Andrew C., and Tirthankar Chakravarty. 2008. Beta-t-(E)GARCH. Cambridge Working Papers in Economics 0840. Cambridge: Faculty of Economics, University of Cambridge, Available online: http://www.econ.cam.ac.uk/research/repec/cam/pdf/cwpe0840.pdf (accessed on 25 December 2021).
- Ineson, Sarah, Amanda C. Maycock, Lesley J. Gray, Adam A. Scaife, Nick J. Dunstone, Jerald W. Harder, Jeff R. Knight, Mike Lockwood, James C. Manners, and Richard A. Wood. 2015. Regional climate impacts of a possible future grand solar minimum. Nature Communications 6: 443. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. 2021. Sixth Assessment Report. Available online: https://www.ipcc.ch/report/ar6/wg1/#SPM (accessed on 25 December 2021).
- Jones, Gareth S., Mike Lockwood, and Peter A. Stott. 2012. What influence will future solar activity changes over the 21st century have on projected global near-surface temperature changes? Journal of Geographical Research 117. [Google Scholar] [CrossRef]
- Jouzel, J., V. Masson-Delmotte, O. Cattani, G. Dreyfus, S. Falourd, and G. E. Hoffmann. 2007. Orbital and millennial Antarctic climate variability over the past 800,000 years. Science 317: 793–97. [Google Scholar] [CrossRef] [Green Version]
- Kibria, B. M. Golam, and Anwar H. Joarder. 2006. A short review of multivariate t-distribution. Journal of Statistical Research 40: 59–72. [Google Scholar]
- Kirchner, Ingo, Georgiy L. Stenchikov, Hans-F. Graf, Alan Robock, and Juan Carlos Antuna. 1999. Climate model simulation of winter warming and summer cooling following the 1991 Mount Pinatubo volcanic eruption. Journal of Geophysical Research 104: 19039–55. [Google Scholar] [CrossRef]
- Lisiecki, Lorraine E., and Maureen E. Raymo. 2005. A pliocene-pleistocene stack of 57 globally distributed Benthic δ18O records. Paleoceanography 20. [Google Scholar] [CrossRef] [Green Version]
- Ljung, Greta M., and George E. P. Box. 1978. On a measure of lack of fit in time-series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Lüthi, Dieter, Marthine Le Floch, Bernhard Bereiter, Thomas Blunier, Jean-Marc Barnola, Urs Steigenhaler, Dominique Raynaud, Jean Jouzel, Hubertus Fischer, Kenji Kawamura, and et al. 2008. High-resolution carbon dioxide concentration record 650,000–800,000 years before present. Nature 453. [Google Scholar] [CrossRef]
- Lütkepohl, Helmut. 2005. New Introduction to Multivariate Time Series Analysis. Berlin and Heidelberg: Springer. [Google Scholar]
- Maycock, A. C., S. Ineson, L. J. Gray, A. A. Scaife, J. A. Anstey, M. Lockwood, N. Butchart, S. C. Hardiman, D. M. Mitchell, and S. M. Osprey. 2015. Possible impacts of a future grand solar minimum on climate: Stratospheric and global circulation changes. JGR Atmospheres 120: 9043–58. [Google Scholar] [CrossRef] [Green Version]
- Meehl, Gerald A., Julie M. Arblaster, and Daniel R. Marsh. 2013. Could a future “Grand Solar Minimum” like the Maunder Minimum stop global warming? Geographical Research Letters 40: 1789–93. [Google Scholar] [CrossRef]
- NASA. 2021. Flip flop: Why Variations in Earth’s Magnetic Field Aren’t Causing Today’S Climate Change. Available online: https://climate.nasa.gov/ask-nasa-climate/3104/flip-flop-why-variations-in-earths-magnetic-field-arent-causing-todays-climate-change/ (accessed on 25 December 2021).
- Paillard, Didier, Laurent D. Labeyrie, and Pascal Yiou. 1996. Macintosh program performs time-series analysis. Eos Transactions AGU 77: 379–79. [Google Scholar] [CrossRef]
- Qin, Zhao, and Markus J. Buehler. 2012. Carbon dioxide enhances fragility of ice crystals. Journal of Physics D: Applied Physics 45. [Google Scholar] [CrossRef]
- Rubio-Ramirez, Juan F., Daniel Waggoner, and Tao Zha. 2010. Structural vector autoregressions: Theory for identification and algorithms for inference. Review of Economic Studies 77: 665–96. [Google Scholar] [CrossRef] [Green Version]
- Ruddiman, William. 2005. Plows, Plagues and Petroleum: How Humans Took Control of the Climate. Princeton: Princeton University Press. [Google Scholar]
- Steinhilber, F., J. A. Abreu, and J. Beer. 2008. Solar modulation during the Holocene. Astrophysics and Space Sciences Transactions 4: 1–6. [Google Scholar] [CrossRef] [Green Version]
- Stenchikov, Georgiy L., Ingo Kirchner, Alan Robock, Hans-F. Graf, Juan Carlos Antuna, R. G. Grainger, Alyn Lambert, and Larry Thomason. 1998. Radiative Forcing from the 1991 Mount Pinatubo volcanic eruption. Journal of Geophysical Research 103: 13837–57. [Google Scholar] [CrossRef] [Green Version]
- Tiao, George C., and Ruey S. Tsay. 1989. Model specification in multivariate time series. Journal of the Royal Statistical Society 51: 157–213. [Google Scholar] [CrossRef]
- Wadham, J. L., J. R. Hawkings, L. Tarasov, L. J. Gregoire, R. G. M. Spencer, M. Gutjahr, A. Ridgwell, and K. E. Kohfeld. 2019. Ice sheets matter for the global carbon cycle. Nature Communications 10: 3567. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- White, Halbert. 2001. Asymptotic Theory for Econometricians. revised edition. San Diego: Academic Press. [Google Scholar]






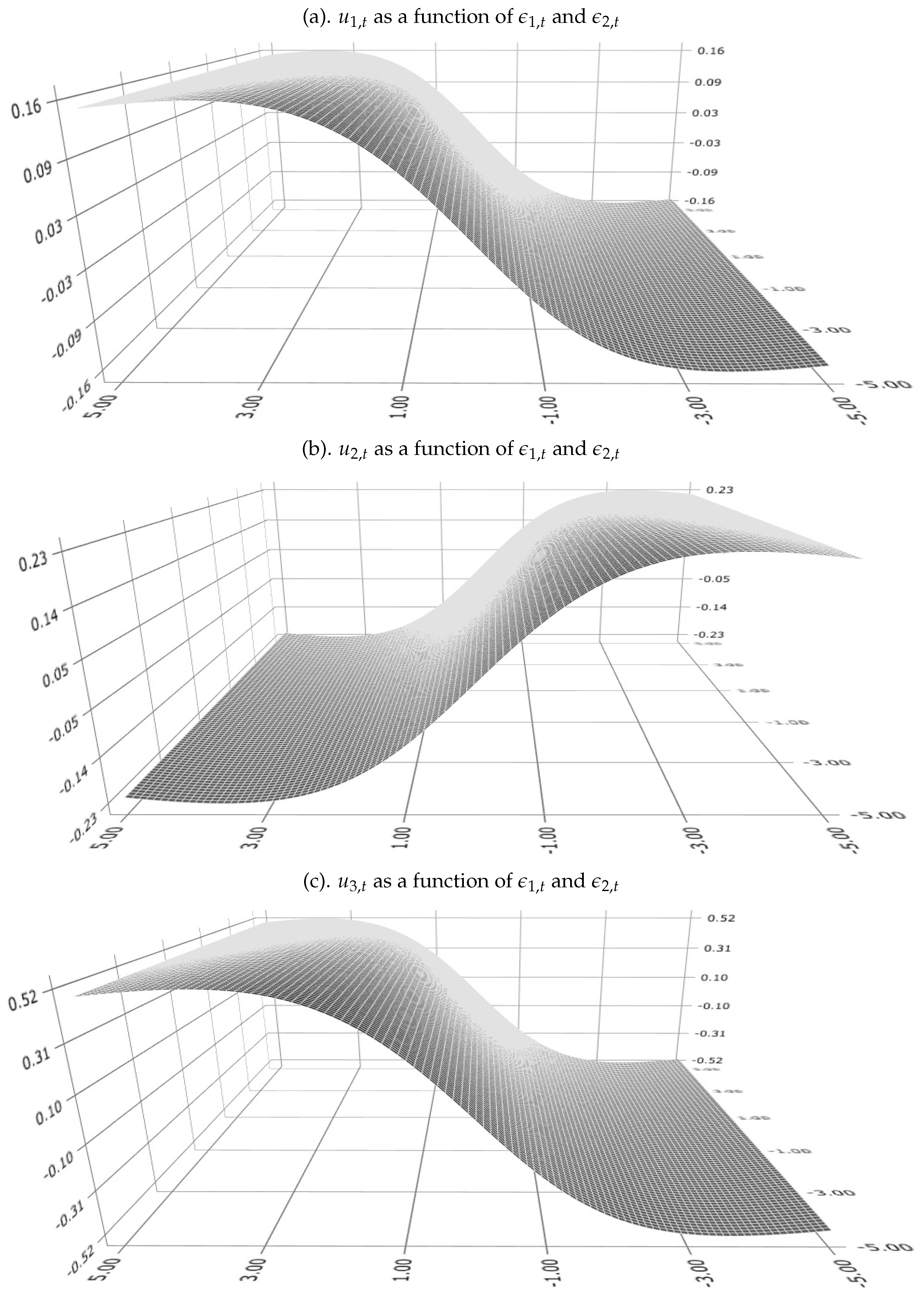


| Shock | Shock | Shock | |
|---|---|---|---|
| + | − | − | |
| − | + | + | |
| − | + | + |
| (a) Dependent Variables | |||
|---|---|---|---|
| Variable | Ice volume | Atmospheric | Antarctic-based land surface temperature |
| Start date | 798 thousand years ago | 798 thousand years ago | 798 thousand years ago |
| End date | 1 thousand years ago | 1 thousand years ago | 1 thousand years ago |
| Data frequency | 1 thousand years | 1 thousand years | 1 thousand years |
| Measurement | Based on the proxy | 1 unit = 780 gigatonnes of | 1 unit = 1 Celsius degree |
| Data source | Lisiecki and Raymo (2005) | Lüthi et al. (2008) | Jouzel et al. (2007) |
| Sample size | 798 | 798 | 798 |
| Minimum | |||
| Maximum | |||
| Mean | |||
| Standard deviation | |||
| (b) Explanatory Variables | |||
| Variable | Eccentricity of the Earth’s orbit | Obliquity | Precession of the equinox |
| Start date | 798 thousand years ago | 798 thousand years ago | 798 thousand years ago |
| End date | 1 thousand years ago | 1 thousand years ago | 1 thousand years ago |
| Data frequency | 1 thousand years | 1 thousand years | 1 thousand years |
| Measurement | Periodicity deriving from the | Periodicity deriving from the | Periodicity deriving from the |
| changing non-circularity of the Earth’s orbit | changes in the tilt of the Earth’s rotational axis | precession of the equinox | |
| (zero denotes circularity). | relative to the ecliptic (1 unit = 10 degrees). | (1 unit = 1 degree). | |
| Data source | Paillard et al. (1996) | Paillard et al. (1996) | Paillard et al. (1996) |
| Sample size | 798 | 798 | 798 |
| Minimum | |||
| Maximum | |||
| Mean | |||
| Standard deviation |
| Benchmark | Score-Driven Homoskedastic | Score-Driven Homoskedastic | Score-Driven Heteroskedastic | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ice-Age Model | Gaussian Ice-Age Model | t Ice-Age Model | t Ice-Age Model | ||||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | ||||||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | ||||||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | *** | |||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| ** | ** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| NA | *** | *** | *** | ||||||
| *** | *** | *** | NA | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | NA | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | *** | ||||||
| *** | *** | *** | NA | ||||||
| NA | NA | *** | *** | ||||||
| Benchmark | Score-Driven Homoskedastic | Score-Driven Homoskedastic | Score-Driven Heteroskedastic | |
|---|---|---|---|---|
| Ice-Age Model | Gaussian Ice-Age Model | t Ice-Age Model | t Ice-Age Model | |
| LL | ||||
| AIC | ||||
| BIC | ||||
| HQC | ||||
| NA | NA | NA | ||
| NA | NA | NA | ||
| NA | NA | NA | ||
| LB (p-value) | ||||
| LB (p-value) | *** | |||
| LB (p-value) | ** | |||
| LB (p-value) | ||||
| LB (p-value) | *** | |||
| LB (p-value) | ** | ** | ** | |
| LB (p-value) | NA | NA | ||
| LB (p-value) | NA | NA | ||
| LB (p-value) | NA | NA | ||
| LB (p-value) | NA | NA | NA | |
| LB (p-value) | NA | NA | NA | |
| LB (p-value) | NA | NA | NA |
| Score-Driven | Score-Driven | |||||||
|---|---|---|---|---|---|---|---|---|
| Homoskedastic | Score-Driven | Score-Driven | Homoskedastic | Score-Driven | Score-Driven | |||
| Benchmark | Gaussian | Homoskedastic | Heteroskedastic | Benchmark | Gaussian | Homoskedastic | Heteroskedastic | |
| Ice-Age Model | Ice-Age Model | t Ice-Age Model | t Ice-Age Model | Ice-Age Model | Ice-Age Model | t Ice-Age Model | t Ice-Age Model | |
| MSE | MSE | MSE | MSE | MAE | MAE | MAE | MAE | |
| last 100,000 years | ||||||||
| last 90,000 years | ||||||||
| last 80,000 years | ||||||||
| last 70,000 years | ||||||||
| last 60,000 years | ||||||||
| last 50,000 years | ||||||||
| last 40,000 years | ||||||||
| last 30,000 years | ||||||||
| last 20,000 years | ||||||||
| last 10,000 years | ||||||||
| MSE | MSE | MSE | MSE | MAE | MAE | MAE | MAE | |
| last 100,000 years | ||||||||
| last 90,000 years | ||||||||
| last 80,000 years | ||||||||
| last 70,000 years | ||||||||
| last 60,000 years | ||||||||
| last 50,000 years | ||||||||
| last 40,000 years | ||||||||
| last 30,000 years | ||||||||
| last 20,000 years | ||||||||
| last 10,000 years | ||||||||
| MSE | MSE | MSE | MSE | MAE | MAE | MAE | MAE | |
| last 100,000 years | ||||||||
| last 90,000 years | ||||||||
| last 80,000 years | ||||||||
| last 70,000 years | ||||||||
| last 60,000 years | ||||||||
| last 50,000 years | ||||||||
| last 40,000 years | ||||||||
| last 30,000 years | ||||||||
| last 20,000 years | ||||||||
| last 10,000 years |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blazsek, S.; Escribano, A. Robust Estimation and Forecasting of Climate Change Using Score-Driven Ice-Age Models. Econometrics 2022, 10, 9. https://doi.org/10.3390/econometrics10010009
Blazsek S, Escribano A. Robust Estimation and Forecasting of Climate Change Using Score-Driven Ice-Age Models. Econometrics. 2022; 10(1):9. https://doi.org/10.3390/econometrics10010009
Chicago/Turabian StyleBlazsek, Szabolcs, and Alvaro Escribano. 2022. "Robust Estimation and Forecasting of Climate Change Using Score-Driven Ice-Age Models" Econometrics 10, no. 1: 9. https://doi.org/10.3390/econometrics10010009
APA StyleBlazsek, S., & Escribano, A. (2022). Robust Estimation and Forecasting of Climate Change Using Score-Driven Ice-Age Models. Econometrics, 10(1), 9. https://doi.org/10.3390/econometrics10010009







