Green Bonds for the Transition to a Low-Carbon Economy
Abstract
:1. Introduction
2. Theoretical and Empirical Literature
2.1. Theoretical Literature
2.2. Empirical Literature
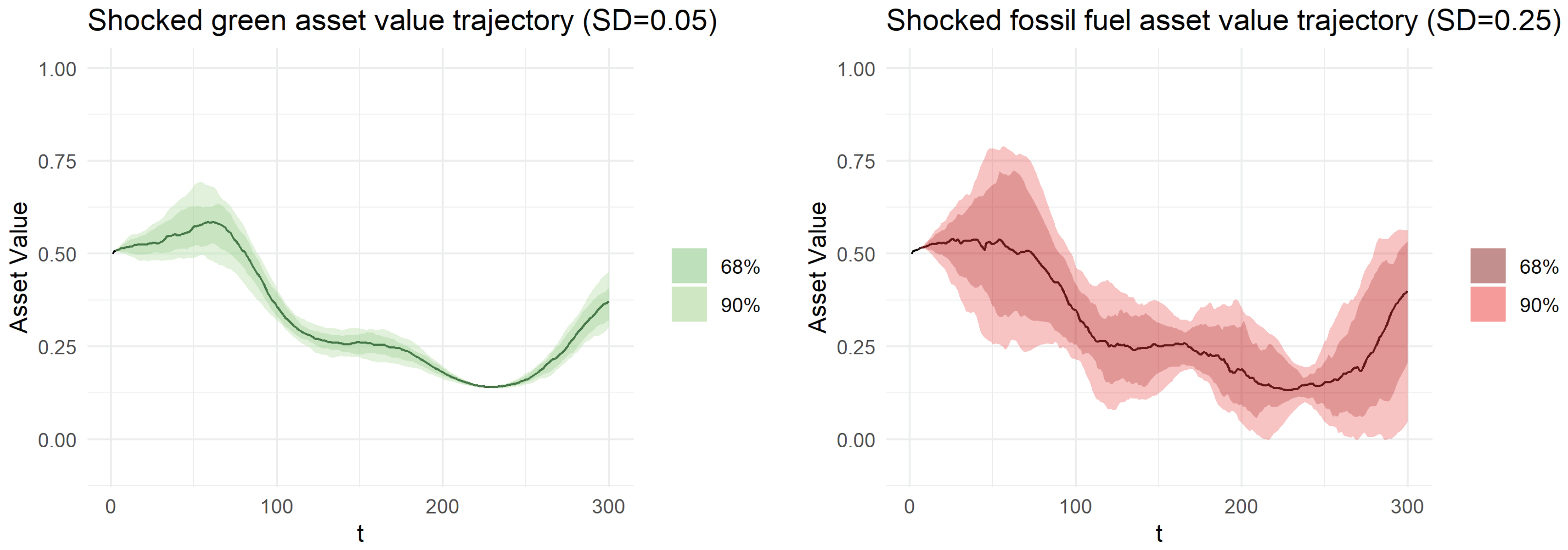
3. Setup and Results of the Dynamic Portfolio Model
3.1. Setup of the Dynamic Portfolio Model
3.2. Portfolio Modeling Results
4. Empirical Approach and Results
4.1. Testing for Underdiversification in the Time Series Data
4.2. Multivariate Regression on the Individual Bonds Data
4.3. Pairing Analysis
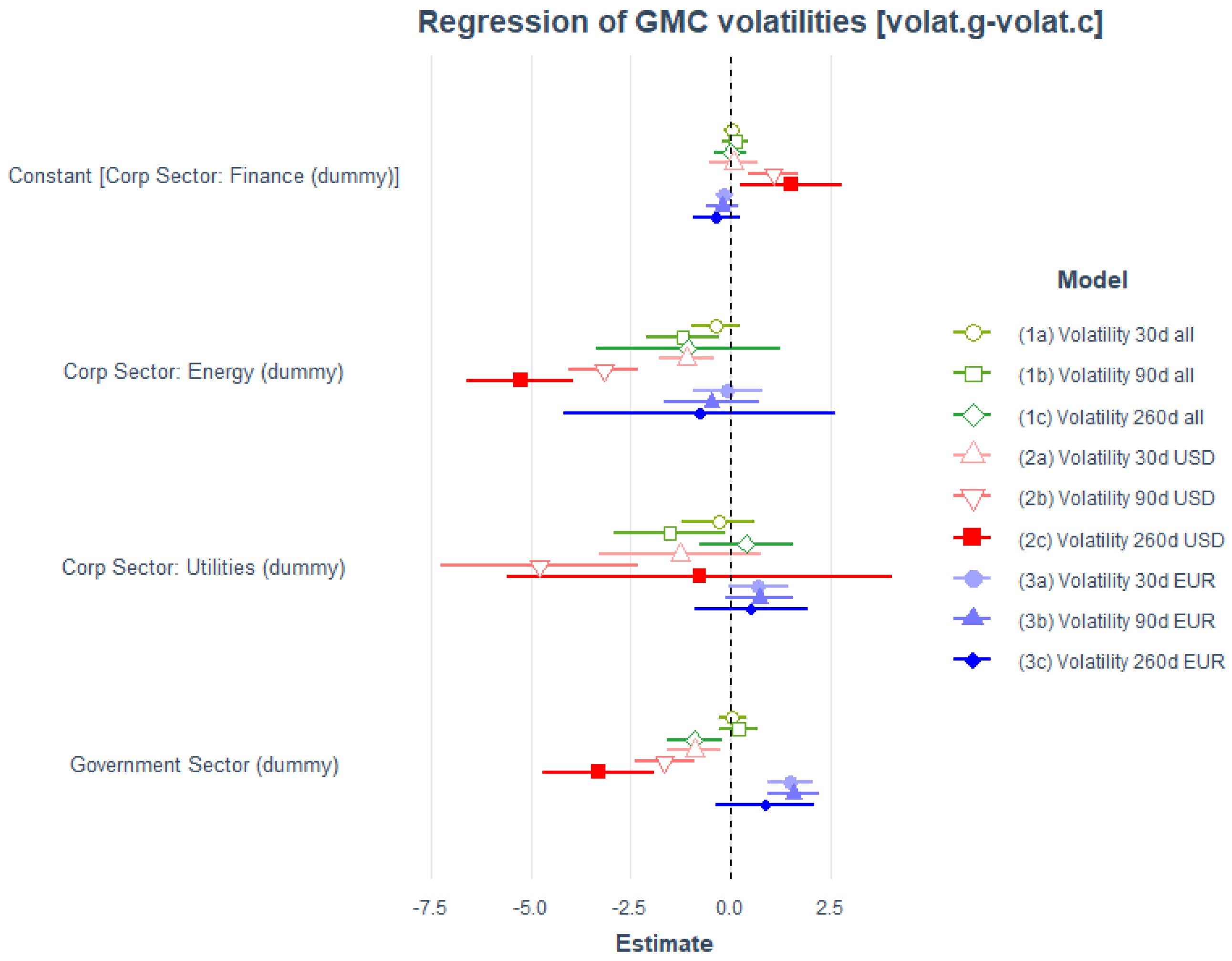
4.4. Volatility Analysis
4.5. Energy Sector Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
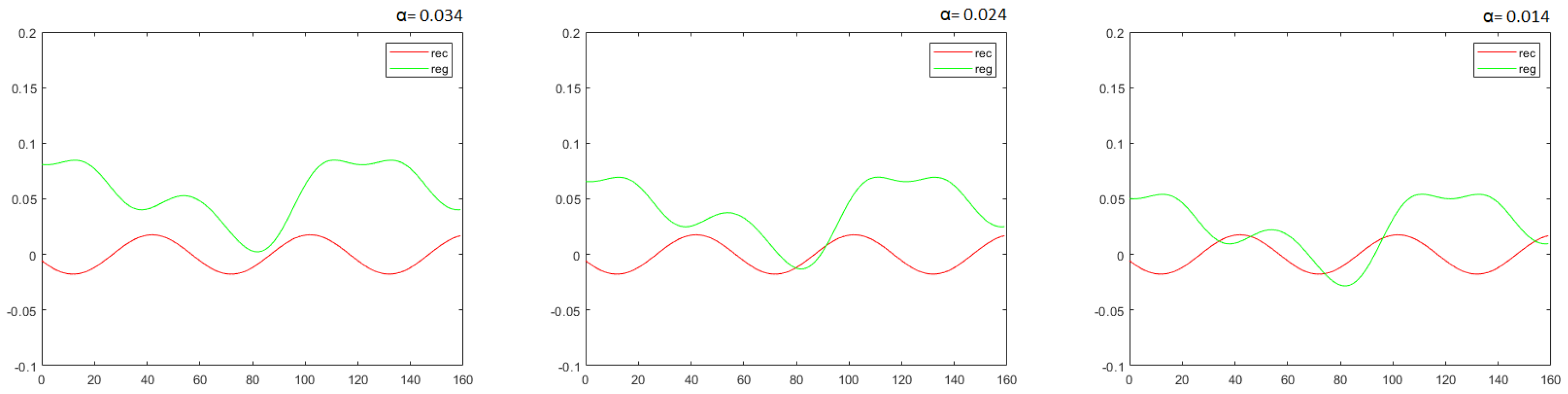
Appendix A. Fast Fourier Transform (FFT)
Appendix B. Outlook for a Stochasic Version of the Portfolio Model
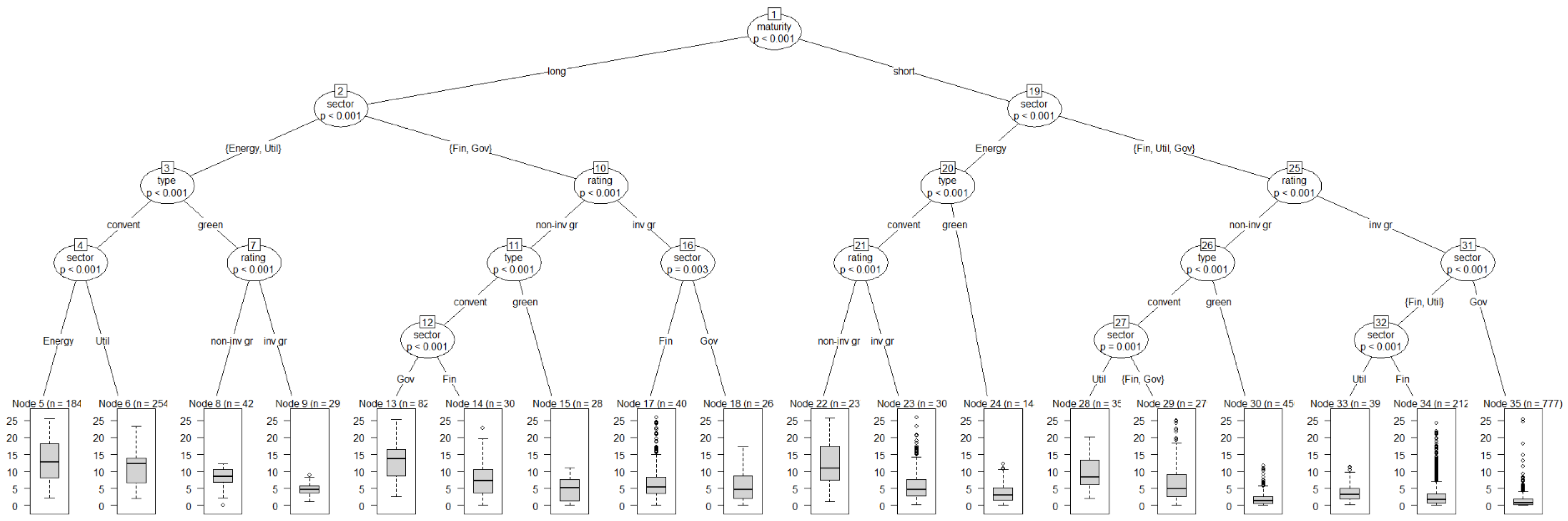
Appendix C. Further Empirical Analysis of the Individual Bonds Dataset
| Dependent Variable: Yield at Issue | ||||
|---|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | (4) EUR Model | |
| Intercept | *** | *** | *** | |
| Green bond (dummy) | *** | *** | *** | |
| Corp sector: energy (dummy) | ||||
| Corp sector: utilities (dummy) | *** | *** | ||
| Government sector (dummy) | *** | ** | ||
| R2 | ||||
| Adj. R2 | ||||
| Num. obs. | 2969 | 2969 | 1794 | 144 |
| Dependent Variable: YIELD to Maturity | ||||
|---|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | (4) EUR Model | |
| Intercept | *** | *** | *** | *** |
| Green bond (dummy) | * | ** | ** | |
| Volatility 90d | *** | *** | *** | * |
| Corp sector: energy (dummy) | *** | * | * | |
| Corp sector: utilities (dummy) | *** | *** | *** | |
| Government sector (dummy) | *** | *** | * | |
| R2 | ||||
| Adj. R2 | ||||
| Num. obs. | 4454 | 4454 | 2433 | 1739 |
| Dependent Variable: Yield at Issue | |||
|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | |
| Constant (green premium) | * | ||
| Government Sector (dummy) | |||
| R2 | |||
| Adj. R2 | |||
| Num. obs. | 115 | 50 | 47 |
| Dependent Variable: Yield to Maturity | ||||
|---|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | (4) EUR Model | |
| Constant (green premium) | *** | *** | ||
| GMC Volatility 90d | * | |||
| Corp Sector: Energy (dummy) | ** | *** | ||
| Corp Sector: Utilities (dummy) | *** | * | ** | |
| Government Sector (dummy) | *** | ** | *** | |
| R2 | ||||
| Adj. R2 | ||||
| Num. obs. | 304 | 304 | 116 | 176 |
| 1 | For example, short-termism in the financial market has been shown to be a roadblock; see Davies et al. (2014), Semmler et al. (2020). |
| 2 | For a survey, see Semmler et al. (2021). |
| 3 | However, one should note that there are still methodological challenges related to information asymmetry on the pricing externality effects of conventional and green financial assets (Berg et al. 2019; Candelon et al. 2021a). |
| 4 | In economics, harmonic estimations can capture the business cycle feature of prices, industrial production, employment, and asset returns. For the potential application of harmonic estimations, see Artis et al. (2007). |
| 5 | Respectively, the Bloomberg Barclays MSCI US Global Green Bond in USD (GBUSTRUU) and the Bloomberg Barclays US Corporate Energy in USD (I00388US). |
| 6 | The harmonic estimations are obtained using a FFT. As described in Appendix A, we first de-trend the time series for the real asset returns, and then we are able to apply the FFT in order to filter out short-term movements by estimating the coefficients for a linear combination of a sine–cosine function, based on the original data. The harmonic regression model is estimated for six different frequencies. We select the estimation with the lowest sum of squared errors. |
| 7 | Note that, in order to avoid additional state variables defining stocks of innovation capacity, we undertake a shortcut and let the respective innovations be driven by the respective fraction of wealth. Simulations could be undertaken with various fractions of . |
| 8 | We also want to note that the weights and ) of the two parts of the objective functions in Equations (3) and (5) can be varied, and some Pareto frontier can be computed to explore which weights are the realistic ones (see Kaya and Maurer 2014). |
| 9 | Risk aversion and discount rates have been explored in terms of their relevance to portfolio dynamics in chapters 4–5 in Chiarella et al. (2016). |
| 10 | See Davies et al. (2014) for a discussion of stranded assets. |
| 11 | For details, see (Cochrane et al. 2001, chp. 19), where the bond price is solved for solving the appropriate discount rate forward. In the portfolio context, see (Semmler 2011, chp. 17.5). |
| 12 | It might help to support green start-up firms, ensuring a minimum return if the business does not succeed but high returns if it does. If we think in terms of green treasury bonds, it can help to reduce sovereign debt due to debt to equity swaps. |
| 13 | Both indices were also used for the harmonic estimations and the portfolio model. |
| 14 | It would be ideal for the analyis of long-term bonds to work with a longer trajectory of data. However, the market of green bonds is still new and developing, and due to these market limitations, as well as to constraints in the data availability, we decided to work with data from the period of January 2017 to October 2020. |
| 15 | We abbreviate volatility measures for these 30-, 90-, and 260-day ranges by writing 30d, 90d, and 260d, respectively. |
| 16 | In our empirical analysis, we compared the bond-specific Sharpe ratio results with and without the risk-free rate for the two most frequent currencies (USD and EUR), and did not find a relevant change (differences in the size of the second or the third digit after the decimal). Hence, for simplicity, we do not consider the risk-free rate in our analysis when reporting results on the bond-specific Sharpe ratio SRb. |
| 17 | Even though the formal computation of the RSRL does not require computing the efficient frontier first, Candelon et al. (2021b) used efficient portfolio returns in the computation of the RSRL to connect their analysis to the real estate literature. |
| 18 | YAI values showed few outliers and only observations above the 99th percentile were truncated. In terms of YTM observations, values below the 2.5th percentile and above the 97.5th percentile were truncated. The SRb was calculated based on the filtered YTM and volatility values and outliers below the 2.5th percentile and above the 97.5th percentile were truncated. |
| 19 | e.g., the bond price volatility variable only appears in YTM regressions since YAI is the recorded bond yield at the time of bond issuance and its value is arguably not dependent on bond price changes of the more recent past, and SRb already includes information on bond volatility in its denominator. |
| 20 | In order to reduce the impact of outliers, bid-ask spread observations below the 1st and above the 99th percentile were truncated. |
| 21 | We define long-term bonds similar to Kapraun and Scheins (2019), who categorize them as bonds with a maturity structure of more than ten years (or, see https://www.thebalance.com/choosing-bond-fund-term-416948 (accessed on 18 September 2021)). Our non-long-term bonds include bonds with a maturity structure of 10 years or less and subsume short-term and intermediate-term bonds. In order to reduce the influence of outliers, we excluded observations with a maturity structure of more than 100 years. |
| 22 | In order to reduce the impact of outliers, coupon rate observations below the 1st and above the 99th percentile were truncated. |
| 23 | In order to reduce the impact of outliers, amount issued observations above the 97.5th percentile were truncated. |
| 24 | Since the subset of bonds for the energy sector offers less observations than our total sample, we reduced the date issued control from a year-quarter combination to a yearly dummy. |
| 25 | Our energy-specific subset of data did not have enough observations to run regressions with the YAI rate. |
| 26 | Of course, as Kapraun and Scheins (2019) also argue, once the bonds are traded, there might be a multiplicity of drivers of actual bond prices and yields; for example, relevant are the actual activities in portfolio management, monetary policy and interest rates, varying risk premia, and also for other assets, the varying Distance to Default, and more. |
| 27 | For a further discussion of the utility of convertible bonds, see Section 5.2 of the WB report of Semmler et al. (2021) |
| 28 | The new parameters are set as follows: = 0.9; ; . |
| 29 | We carried out all analyses with all three different volatility measures, but for the matter of simplicity (and unless specified, as in the case of analysis 4 on the energy sector), we only report regressions with the 90-day volatility measure. Results for the different volatility measures are similar and are available upon request. In order to reduce the impact of outliers, the 90d volatility observations above the 95th percentile were truncated. |
References
- Ardia, David, and Kris Boudt. 2015. Testing equality of modified Sharpe ratios. Finance Research Letters 13: 97–104. [Google Scholar] [CrossRef]
- Acemoglu, Daron, Philippe Aghion, Leonardo Bursztyn, and David Hemous. 2012. The environment and directed technical change. American Economic Review 102: 131–66. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Artis, Michael J., José G. Clavel, Mathias Hoffmann, and Dilip Nachane. 2007. Harmonic regression models: A comparative review with applications Working paper series. Institute for Empirical Research in Economics 2007: 333. [Google Scholar]
- Bachelet, Maria J., Leonardo Becchetti, and Stefano Manfredonia. 2019. The Green Bonds Premium Puzzle: The Role of Issuer Characteristics and Third-Party Verification. Sustainability 11: 1098. [Google Scholar] [CrossRef] [Green Version]
- Barro, Robert J., and Xavier I. Sala-i-Martin. 2004. Economic Growth. Cambridge and London: The MIT Press. [Google Scholar]
- Berg, Florian, Julian F. Koelbel, and Roberto Rigobon. 2019. Aggregate Confusion: The Divergence of ESG Ratings. Cambridge: MIT Sloan School of Management. [Google Scholar]
- Campbell, John Y., and Luis M. Viceira. 2002. Strategic Asset Allocation: Portfolio Choice for Long-Term Investors (Clarendon Lectures in Economics). Oxford: Oxford University Press. [Google Scholar]
- Candelon, Bertrand, Jean-Baptiste Hasse, and Quentin Lajaunie. 2021a. ESG-Washing in the Mutual Funds Industry? From Information Asymmetry to Regulation. Risks 9: 199. [Google Scholar] [CrossRef]
- Candelon, Bertrand, Franz Fuerst, and Jean-Baptiste Hasse. 2021b. Diversification potential in real estate portfolios. International Economics 166: 126–39. [Google Scholar] [CrossRef]
- Chiarella, Carl, Willi Semmler, Chih-Ying Hsiao, and Lebogang Mateane. 2016. Sustainable Asset Accumulation. and Dynamic Portfolio Decisions. Berlin/Heidelberg: Springer. [Google Scholar]
- Cochrane, John H. 2001. Asset Pricing. Princeton: Princeton University Press. [Google Scholar]
- Davies, Richard, Andrew G. Haldane, Mette Nielsen, and W. Silvia Pezzini. 2014. Measuring the costs of short-termism. Journal of Financial Stability 12: 25. [Google Scholar] [CrossRef]
- Ehlers, Torsten, and Frank Packer. 2017. Green bond finance and certification. BIS Quarterly Review 2017: 89–104. [Google Scholar]
- Engle, Robert F., Stefano Giglio, Bryan Kelly, Heebum Lee, and Johannes Stroebel. 2020. Hedging climate change news. The Review of Financial Studies 33: 1184–216. [Google Scholar] [CrossRef]
- Favre, Laurent, and José-Antonio Galeano. 2002. Mean-modified value-at-risk with hedge funds. The Journal of Alternative Investments 5: 21–25. [Google Scholar] [CrossRef]
- Flammer, Caroline. 2021. Corporate green bonds. Journal of Financial Economics 142: 499–516. [Google Scholar] [CrossRef]
- Gregoriou, Greg, and Jean-Pierre Gueyie. 2003. Risk-adjusted performance of funds of hedge funds using a modified Sharpe ratio. The Journal of Wealth Management 6: 77–83. [Google Scholar] [CrossRef]
- Gregory, Aidan. 2020. “Nascent” Green Convertible Bond Market Is Cause for Optimism. Global Capital. July 23. Available online: https://www.globalcapital.com/article/28mu9tpjsiu015prdxb7k/equity-linked/nascent-green-convertible-bond-market-is-cause-for-optimism (accessed on 20 September 2020).
- Greiner, Alfred, Willi Semmler, and Gang Gong. 2005. The Forces of Economic Growth. Princeton: Princeton University. [Google Scholar] [CrossRef] [Green Version]
- Gruene, Lars, Willi Semmler, and Marleen Stieler. 2015. Using nonlinear model predictive control for dynamic decision problems in economics. Journal of Economic Dynamics and Control 60: 112–33. [Google Scholar] [CrossRef] [Green Version]
- Hachenberg, Britta, and Dirk Schiereck. 2018. Are green bonds priced differently from conventional bonds? Journal of Asset Management 19: 371–83. [Google Scholar] [CrossRef]
- Hall, Bronwyn H., Jacques Mairesse, and Pierre Mohnen. 2010. Measuring the Returns to R&D. Handbook of the Economics of Innovation 2: 1033–82. [Google Scholar]
- Han, Yingwei, and Jie Li. 2022. Should investors include green bonds in their portfolios? Evidence for the USA and Europe. International Review of Financial Analysis 80: 1057–5219. [Google Scholar] [CrossRef]
- Hasse, Jean-Baptiste. 2021. DiversificationR: Econometric Tools to Measure Portfolio Diversification. R Package. Available online: https://cran.r-project.org/web/packages/DiversificationR/index.html (accessed on 15 January 2022).
- Hothorn, Torsten, Kurt Hornik, Carolin Strobl, and Achim Zeileis. 2021. Party: A Laboratory for Recursive Partytioning. R Package Version 1.3-7. Available online: https://CRAN.R-project.org/package=party (accessed on 8 May 2021).
- Huynh, Thanh, and Ying Xia. 2021. Climate change news risk and corporate bond returns. Journal of Financial and Quantitative Analysis 56: 1985–2009. [Google Scholar] [CrossRef]
- Immel, Moritz Immel, Britta Hachenberg, Florian Kiesel, and Dirk Schiereck. 2020. Green bonds: Shades of green and brown. Journal of Asset Management 22: 96–109. [Google Scholar] [CrossRef]
- Jones, Benjamin F., and Lawrence H. Summers. 2020. A Calculation of the Social Returns to Innovation. No w27863. National Bureau of Economic Research. Available online: https://www.nber.org/papers/w27863 (accessed on 8 May 2021).
- Kaya, C. Yalcin, and Helmut Maurer. 2014. A numerical method for nonconvex multi-objective optimal control problems. Computational Optimization and Applications 57: 685–702. [Google Scholar] [CrossRef]
- Kapraun, Julia, and Christopher Scheins. 2019. (In)-Credibly Green: Which Bonds Trade at a Green Bond Premium? SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Ledoit, Oliver, and Michael Wolf. 2008. Robust performance hypothesis testing with the Sharpe ratio. Journal of Empirical Finance 15: 850–9. [Google Scholar] [CrossRef] [Green Version]
- Leibowicz, Benjamin D. 2018. Welfare improvement windows for innovation policy. Research Policy 47: 390–98. [Google Scholar] [CrossRef]
- Lintner, John. 1965. Security prices, risk, and maximal gains from diversification. The Journal of Finance 20: 587–615. [Google Scholar]
- Löffler, Kristin Ulrike, Aleksandar Petreski, and Andreas Stephan. 2021. Drivers of green bond issuance and new evidence on the “greenium”. Eurasian Economic Review 11: 1–24. [Google Scholar] [CrossRef]
- MacAskill, Stefen, Eduardo Roca, Benjamin Liu, Rodney Anthony Stewart, and Oz Sahin. 2021. Is there a green premium in the green bond market? Systematic literature review revealing premium determinants. Journal of Cleaner Production 280: 124491. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. The utility of wealth. Journal of Political Economy 60: 151–58. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. An Intertemporal Capital Asset Pricing Model. Econometrica 41: 867887. [Google Scholar] [CrossRef]
- Munk, Claus. 2012. Dynamic Asset Allocation. Lecture Notes. Available online: https://sites.google.com/view/clausmunk/teaching (accessed on 6 June 2021).
- Nisbet, Robert, Gary Miner, and Ken Yale. 2018. Handbook of Statistical Analysis and Data Mining Applications. Amsterdam; Elsevier; Cambridge: Academic Press. [Google Scholar]
- Pham, Linh, and Canh Phuc Nguyen. 2021. How do stock, oil, and economic policy uncertainty influence the green bond market? Finance Research Letters 102128: 1544–6123. [Google Scholar] [CrossRef]
- Piñeiro-Chousa, Juan, M. Ange;es López-Cabarcos, Jerome Caby, and Aleksandar Šević. 2021. The influence of investor sentiment on the green bond market. Technological Forecasting and Social Change 162: 120351. [Google Scholar] [CrossRef]
- R Core Team. 2020. R: A Language and Environment for Statistical Computing. In R Foundation for Statistical Computing. Vienna, Austria: R Core Team, Available online: https://www.R-project.org/ (accessed on 30 October 2021).
- Romer, Paul M. 1986. Increasing returns and long-run growth. Journal of Political Economy 94: 1002–37. [Google Scholar] [CrossRef] [Green Version]
- Semmler, Willi. 2011. Asset Prices, Booms and Recessions: Financial Economics from a Dynamic Perspective. Berlin/Heidelberg: Springer Science & Business Media. [Google Scholar]
- Semmler, Willi, and Chih-Ying Hsiao. 2011. Dynamic Consumption and Portfolio Decisions with Estimated Low Frequency Movements of Asset Returns. The Journal of Wealth Management 14: 101–11. [Google Scholar] [CrossRef]
- Semmler, Willi, K. Lessman, and I. Tahri. 2020. Energy Transition, Asset Price Fluctuations, and Dynamic Portfolio Decisions. Available online: Https://ssrn.com/abstract=3688293 (accessed on 8 May 2021). [CrossRef]
- Semmler, Willi, Joao Paulo Braga, Andreas Lichtenberger, Marieme Toure, and Erin Haider. 2021. Fiscal Policies for a Low-Carbon Economy. Washington, DC: World Bank. [Google Scholar]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar]
- Sharpe, William F. 1994. The Sharpe ratio. Journal of Portfolio Management 21: 49–58. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Emmanuel Joel Aikins Abakah, David Gabauer, and Richard Adjei Dwumfour. 2022. Dynamic spillover effects among green bond, renewable energy stocks and carbon markets during COVID-19 pandemic: Implications for hedging and investments strategies. Global Finance Journal 51: 100692. [Google Scholar] [CrossRef]
- Tobin, James. 1958. Liquidity preference as behavior towards risk. The Review of Economic Studies 25: 65–86. [Google Scholar] [CrossRef]



| Categories | CB | GB |
|---|---|---|
| Sectors | ||
| Energy | 809 | 100 |
| Financials | 4822 | 739 |
| Government | 2367 | 271 |
| Utilities | 1028 | 419 |
| Ratings | ||
| A+:A− | 2656 | 118 |
| AAA:AA− | 3310 | 188 |
| B+:B− | 349 | 7 |
| BB+:BB− | 482 | 34 |
| BBB+:BBB− | 1964 | 147 |
| CCC+:D | 136 | 1 |
| Bond duration | ||
| long | 1916 | 266 |
| short | 7011 | 1237 |
| Currencies | ||
| AUD | 525 | 27 |
| BRL | 55 | 46 |
| CAD | 252 | 25 |
| CHF | 147 | 13 |
| CNY | 175 | 157 |
| EUR | 2354 | 355 |
| GBP | 376 | 26 |
| HKD | 210 | 32 |
| IDR | 54 | 5 |
| INR | 58 | 29 |
| Currencies | ||
| JPY | 278 | 70 |
| MXN | 69 | 7 |
| MYR | 1 | 108 |
| Currencies | ||
| NOK | 109 | 36 |
| NZD | 132 | 6 |
| SEK | 232 | 209 |
| TRY | 106 | 11 |
| USD | 3637 | 274 |
| ZAR | 78 | 14 |
| Other | 179 | 79 |
| Tests | Conventional | Green |
|---|---|---|
| RSRL | 0.7271399 *** | 0.6875913 *** |
| mRSRL | 0.5043868 *** | 0.501156 *** |
| Dependent Variable: Bond-Specific Sharpe Ratio (SRb) | ||||
|---|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | (4) EUR Model | |
| Intercept | 0.727 *** | 0.594 *** | 0.851 *** | |
| Green bond (dummy) | 0.603 ** | 0.535 ** | 1.189 * | |
| Corp sector: energy (dummy) | −0.132 *** | −0.165 *** | ||
| Corp sector: utilities (dummy) | −0.100 *** | −0.202 *** | *** | |
| Government sector (dummy) | *** | *** | *** | |
| R2 | ||||
| Adj. R2 | ||||
| Num. obs. | 4028 | 4028 | 2357 | 1532 |
| Dependent Variable: Bond-Specific Sharpe Ratio (SRb) | ||||
|---|---|---|---|---|
| (1) Base Model | (2) Sector Model | (3) USD Model | (4) EUR Model | |
| Constant (green premium) | *** | ** | * | |
| Corp Sector: Energy (dummy) | ** | ** | ||
| Corp Sector: Utilities (dummy) | ** | |||
| Government Sector (dummy) | *** | |||
| R2 | ||||
| Adj. R2 | ||||
| Num. obs. | 209 | 209 | 113 | 84 |
| Dependent Variable: Volatilities (30d, 90d, 260d) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (1a) | (1b) | (1c) | (2a) | (2b) | (2c) | (3a) | (3b) | (3c) | |
| 30d | 90d | 260d | USD.30d | USD.90d | USD.260d | EUR.90d | EUR.90d | EUR.260d | |
| Constant (Corp Sector: Finance) | *** | * | |||||||
| Corp Sector: Energy (dummy) | * | ** | *** | *** | |||||
| Corp Sector: Utilities (dummy) | * | *** | |||||||
| Gov Sector (dummy) | * | ** | *** | *** | *** | *** | |||
| R2 | |||||||||
| Adj. R2 | |||||||||
| Num. obs. | 413 | 312 | 265 | 125 | 117 | 77 | 190 | 183 | 132 |
| Dependent Variable: Yield to Maturity | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (1a) | (1b) | (1c) | (2a) | (2b) | (2c) | (3a) | (3b) | (3c) | |
| 30d | 90d | 260d | USD.30d | USD.90d | USD.260d | EUR.90d | EUR.90d | EUR.260d | |
| Intercept | *** | *** | *** | *** | *** | *** | *** | *** | *** |
| Green bond (dummy) | |||||||||
| Volatility 30d | *** | *** | |||||||
| Green × Volatility 30d | |||||||||
| Volatility 90d | *** | *** | |||||||
| Green × Volatility 90d | * | ||||||||
| Volatility 260d | *** | *** | |||||||
| Green × Volatility 260d | * | *** | |||||||
| R2 | |||||||||
| Adj. R2 | |||||||||
| Num. obs. | 653 | 640 | 534 | 485 | 503 | 386 | 77 | 76 | 70 |
| Dependent Variable: Bond-Specific Sharpe Ratio (SRb) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (1a) | (1b) | (1c) | (2a) | (2b) | (2c) | (3a) | (3b) | (3c) | |
| 30d | 90d | 260d | USD.30d | USD.90d | USD.260d | EUR.90d | EUR.90d | EUR.260d | |
| Intercept | *** | *** | * | *** | *** | *** | ** | ** | |
| Green bond (dummy) | * | * | * | ||||||
| R2 | |||||||||
| Adj. R2 | |||||||||
| Num. obs. | 650 | 637 | 528 | 485 | 503 | 386 | 75 | 73 | 67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lichtenberger, A.; Braga, J.P.; Semmler, W. Green Bonds for the Transition to a Low-Carbon Economy. Econometrics 2022, 10, 11. https://doi.org/10.3390/econometrics10010011
Lichtenberger A, Braga JP, Semmler W. Green Bonds for the Transition to a Low-Carbon Economy. Econometrics. 2022; 10(1):11. https://doi.org/10.3390/econometrics10010011
Chicago/Turabian StyleLichtenberger, Andreas, Joao Paulo Braga, and Willi Semmler. 2022. "Green Bonds for the Transition to a Low-Carbon Economy" Econometrics 10, no. 1: 11. https://doi.org/10.3390/econometrics10010011
APA StyleLichtenberger, A., Braga, J. P., & Semmler, W. (2022). Green Bonds for the Transition to a Low-Carbon Economy. Econometrics, 10(1), 11. https://doi.org/10.3390/econometrics10010011







