Bayesian Model-Updating Using Features of Modal Data: Application to the Metsovo Bridge
Abstract
1. Introduction
2. Bayesian Parameter Estimation Using Modal Data
2.1. Likelihood Formulation
2.1.1. Formulation Using Probabilistic Models for Mode Shape Vectors
2.1.2. Formulation Using Probabilistic Models for MAC Values
2.1.3. Likelihood Formulation Combining Modal Frequencies and Mode Shapes
2.2. Computational Tools
2.3. Outline of Procedure
3. Application to Metsovo Bridge
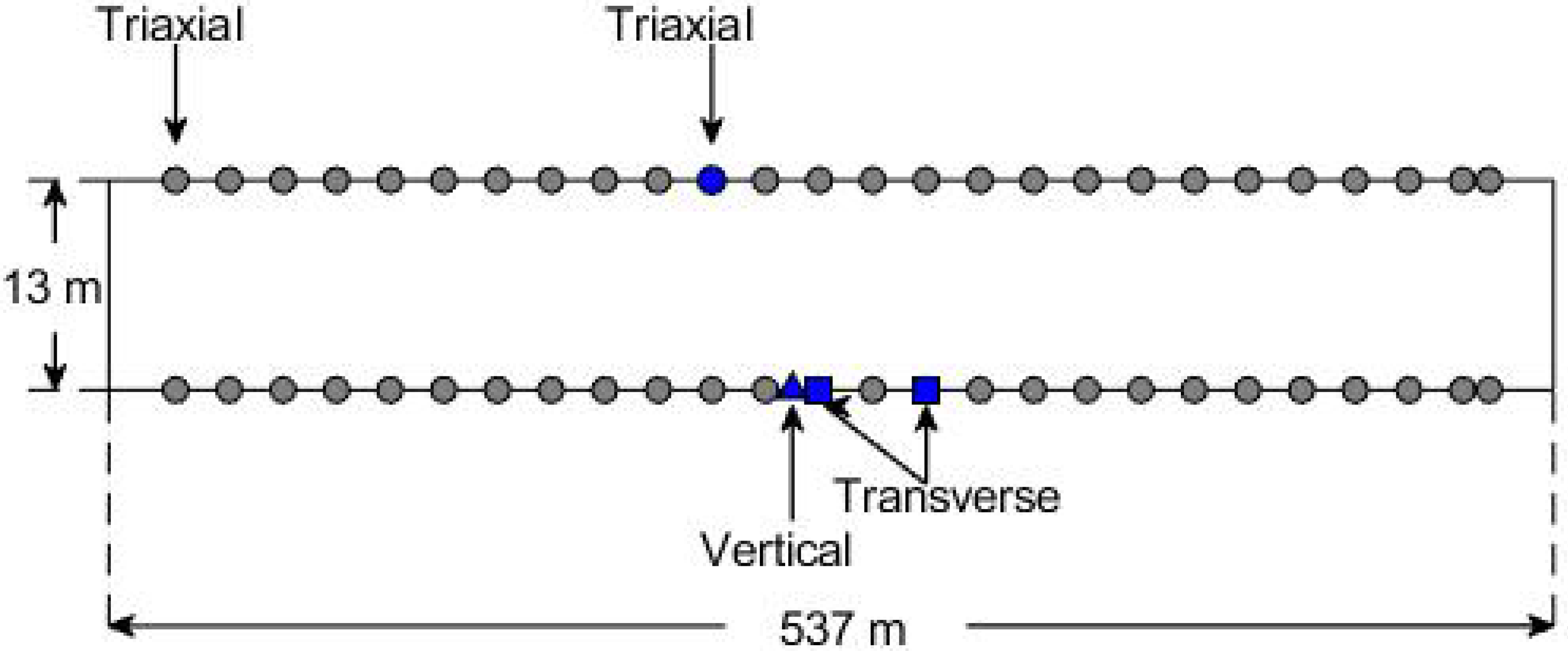
3.1. Description of Bridge
3.2. Finite Element Model of Bridge
3.3. Model Reduction Using CMS
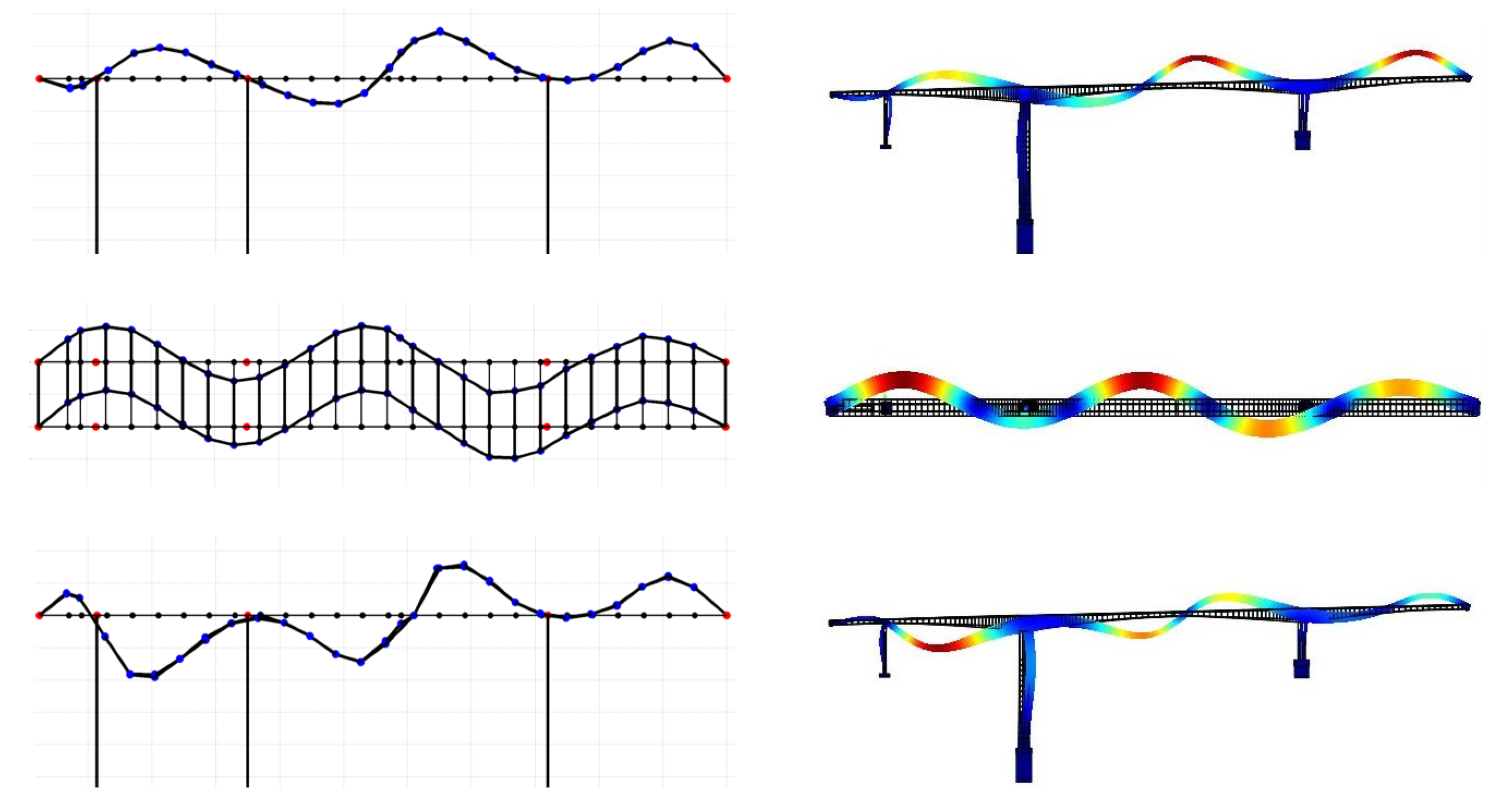
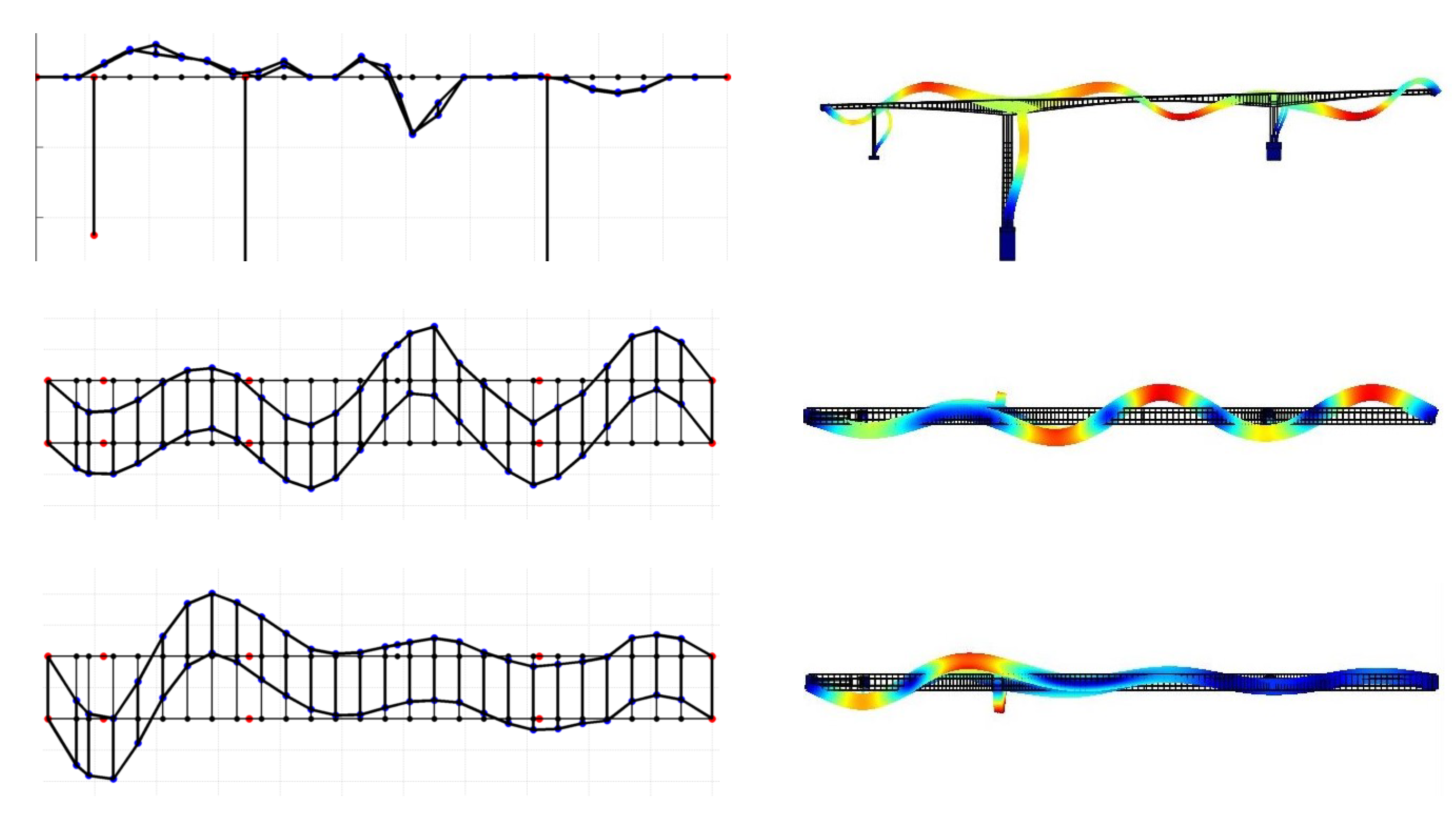
3.4. Experimental Modal Identification
4. Model Updating Results
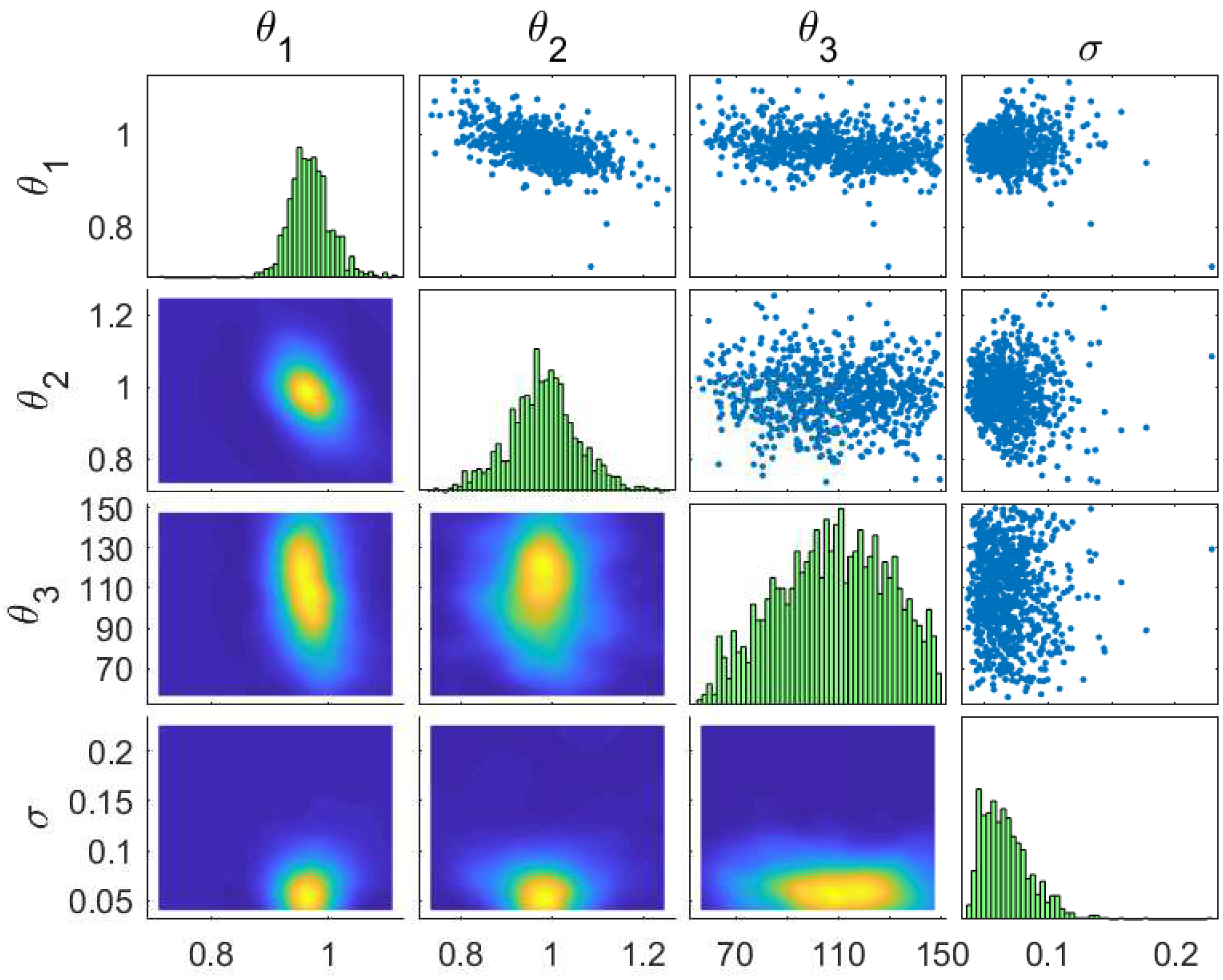
4.1. Model Updating Using Modal Frequencies Only
4.1.1. Flexible-Soil Model
4.1.2. Two-Parameter Stiff-Soil Model
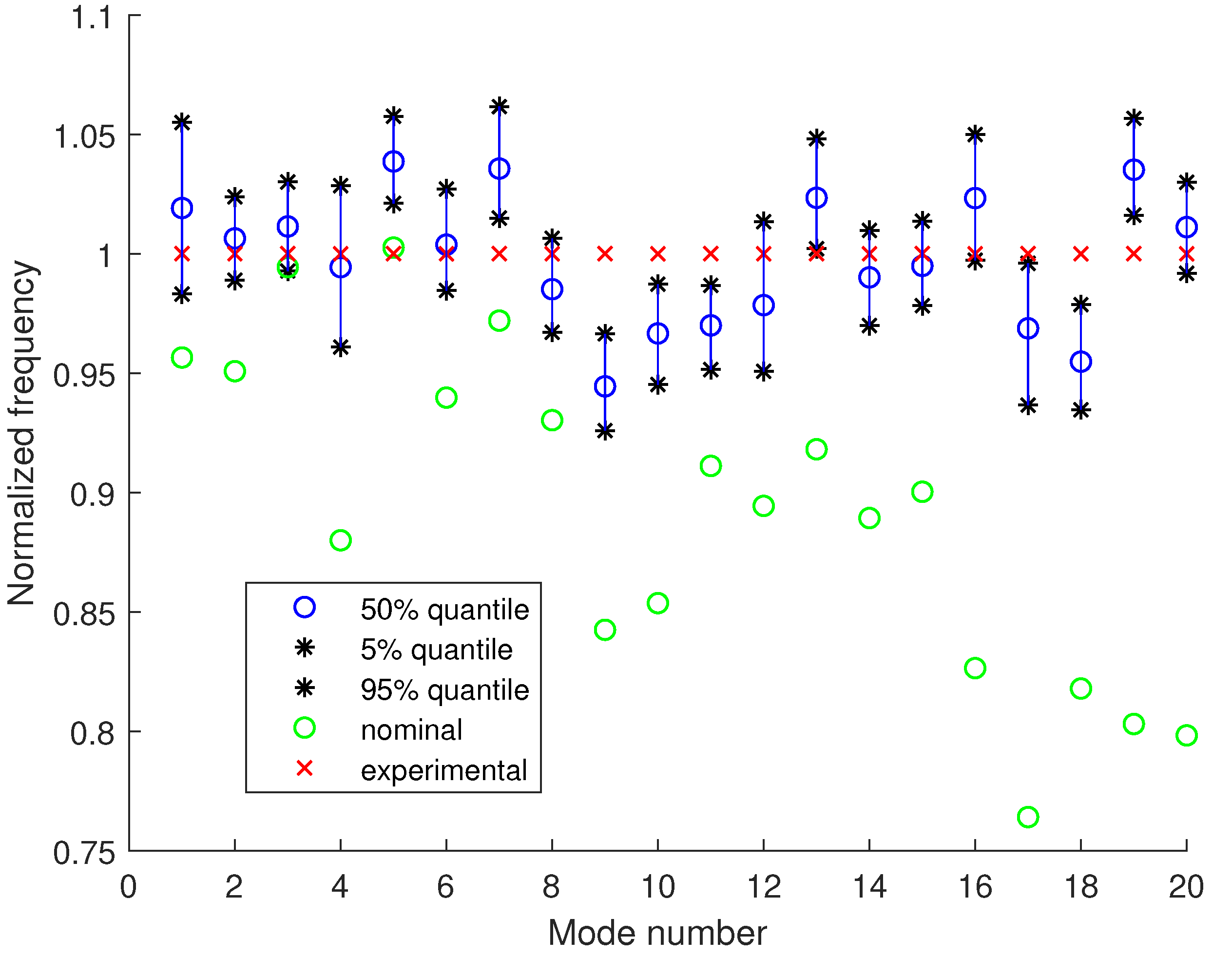
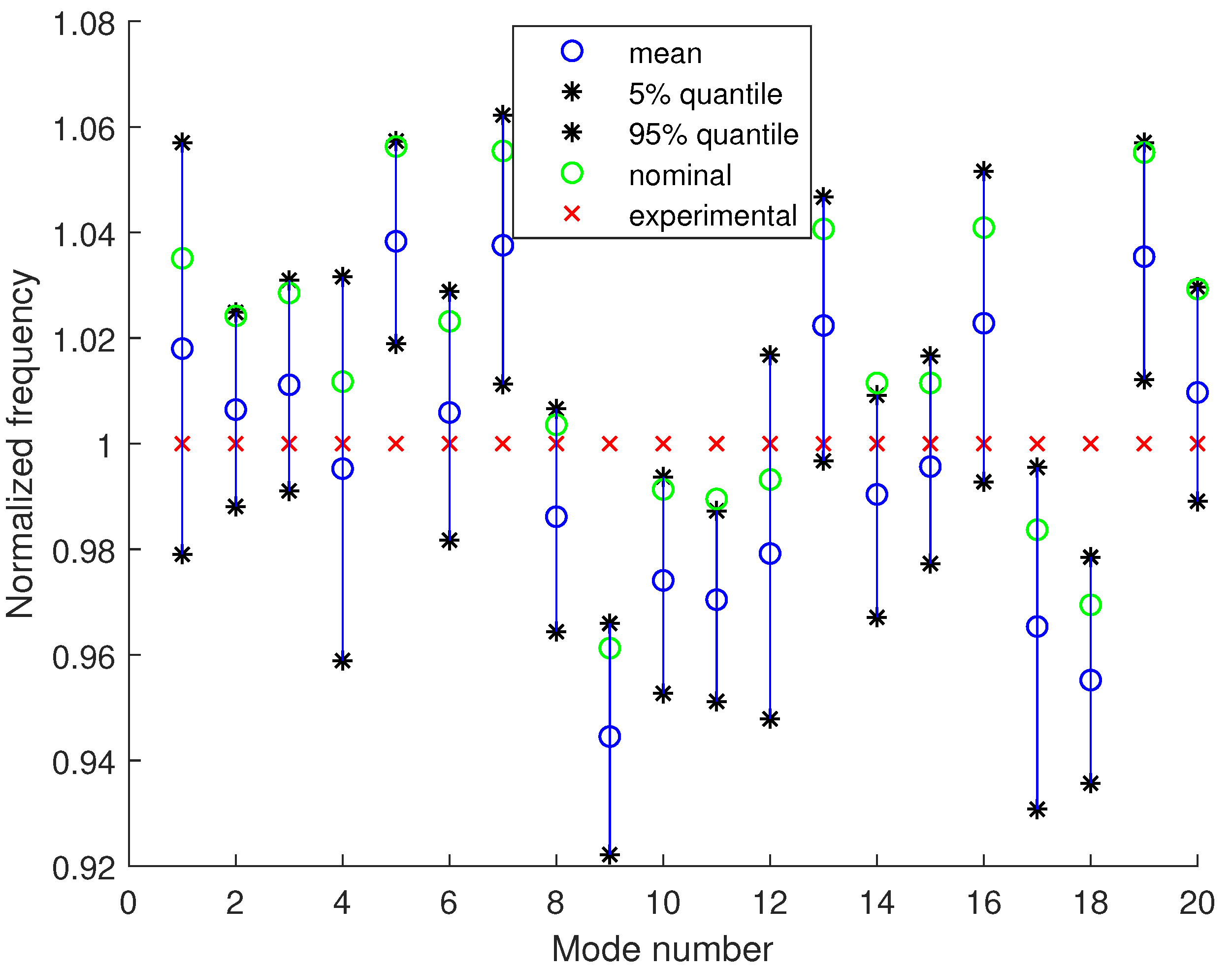
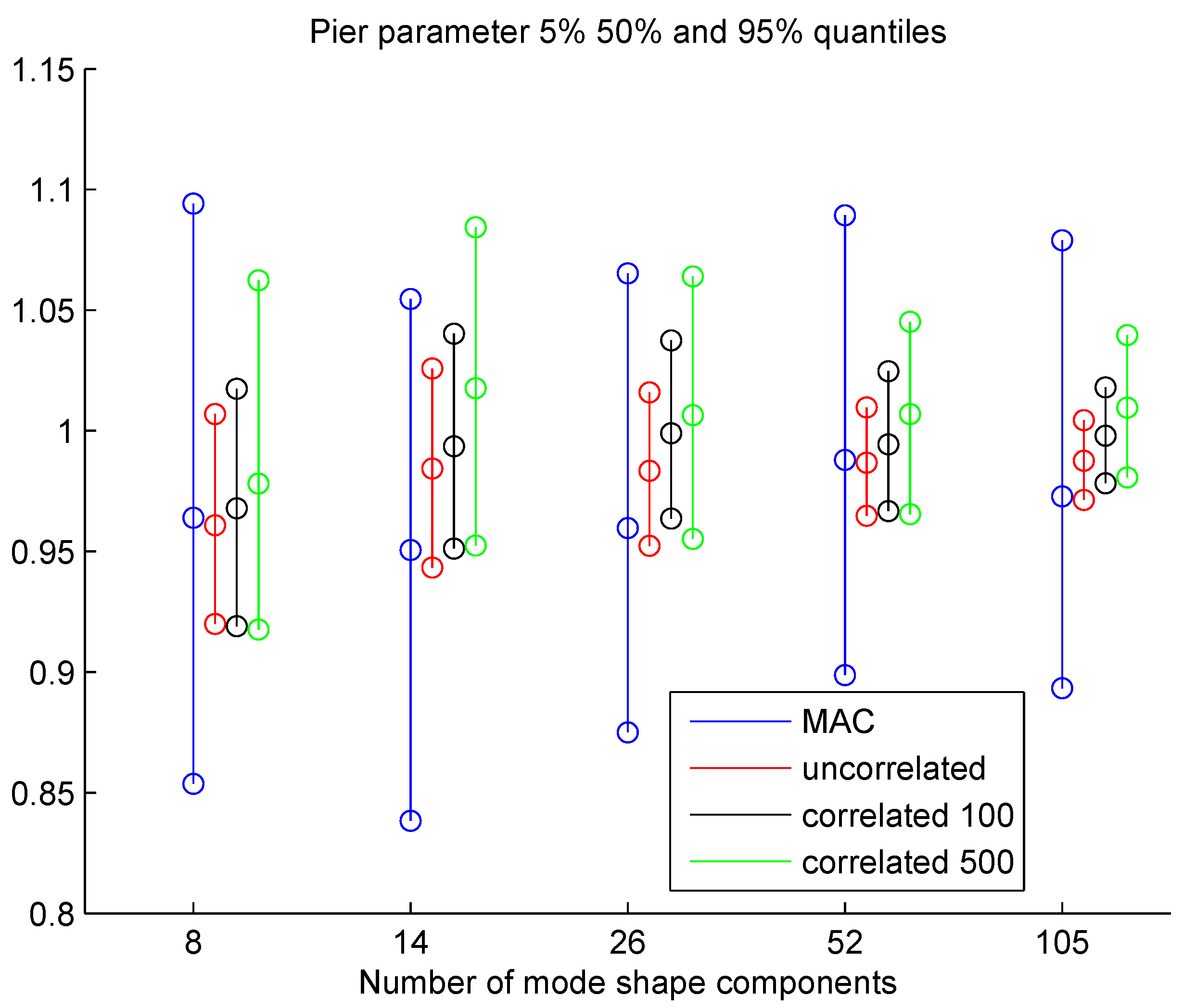
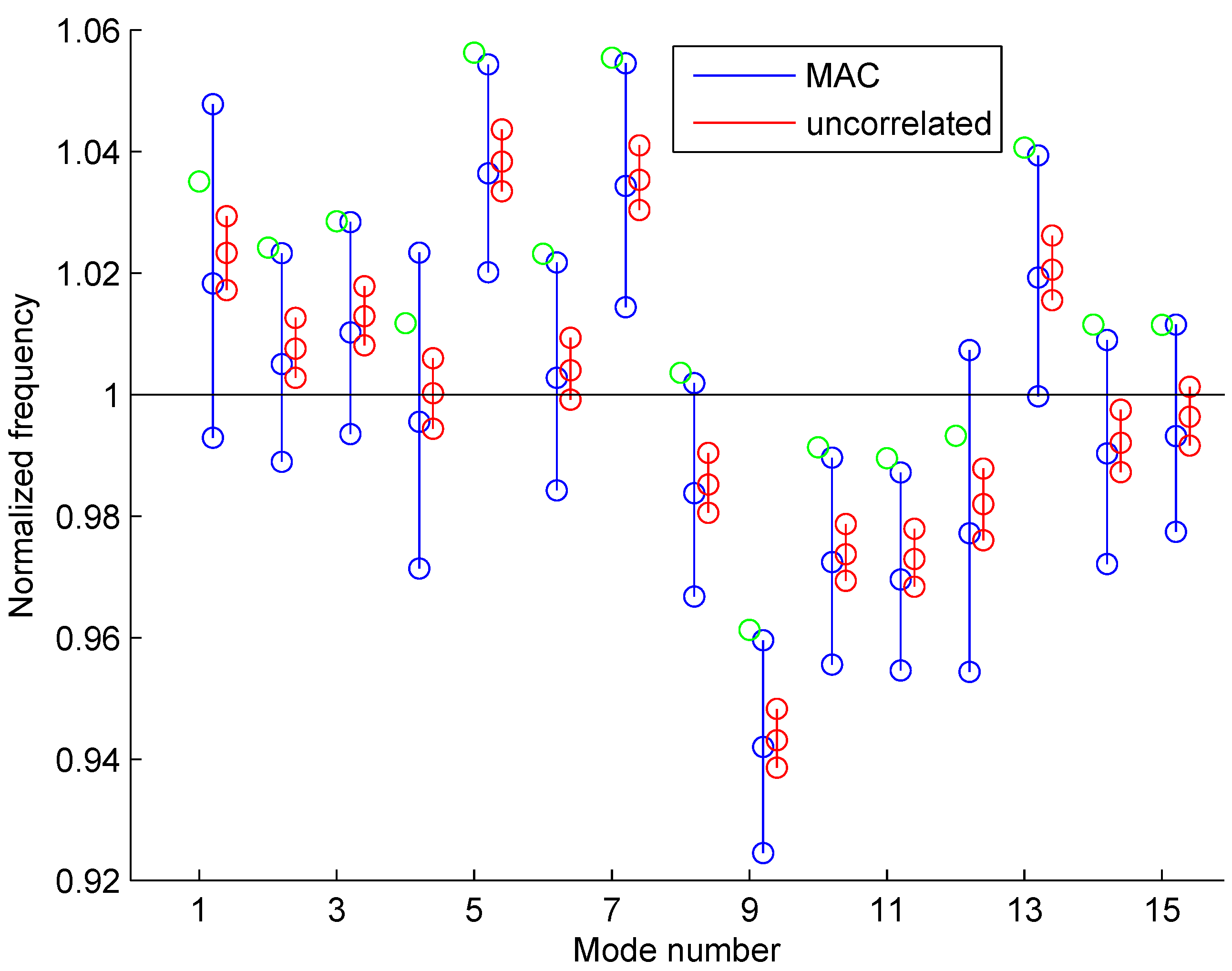
4.2. Model Updating Using Modal Frequencies and Mode Shapes
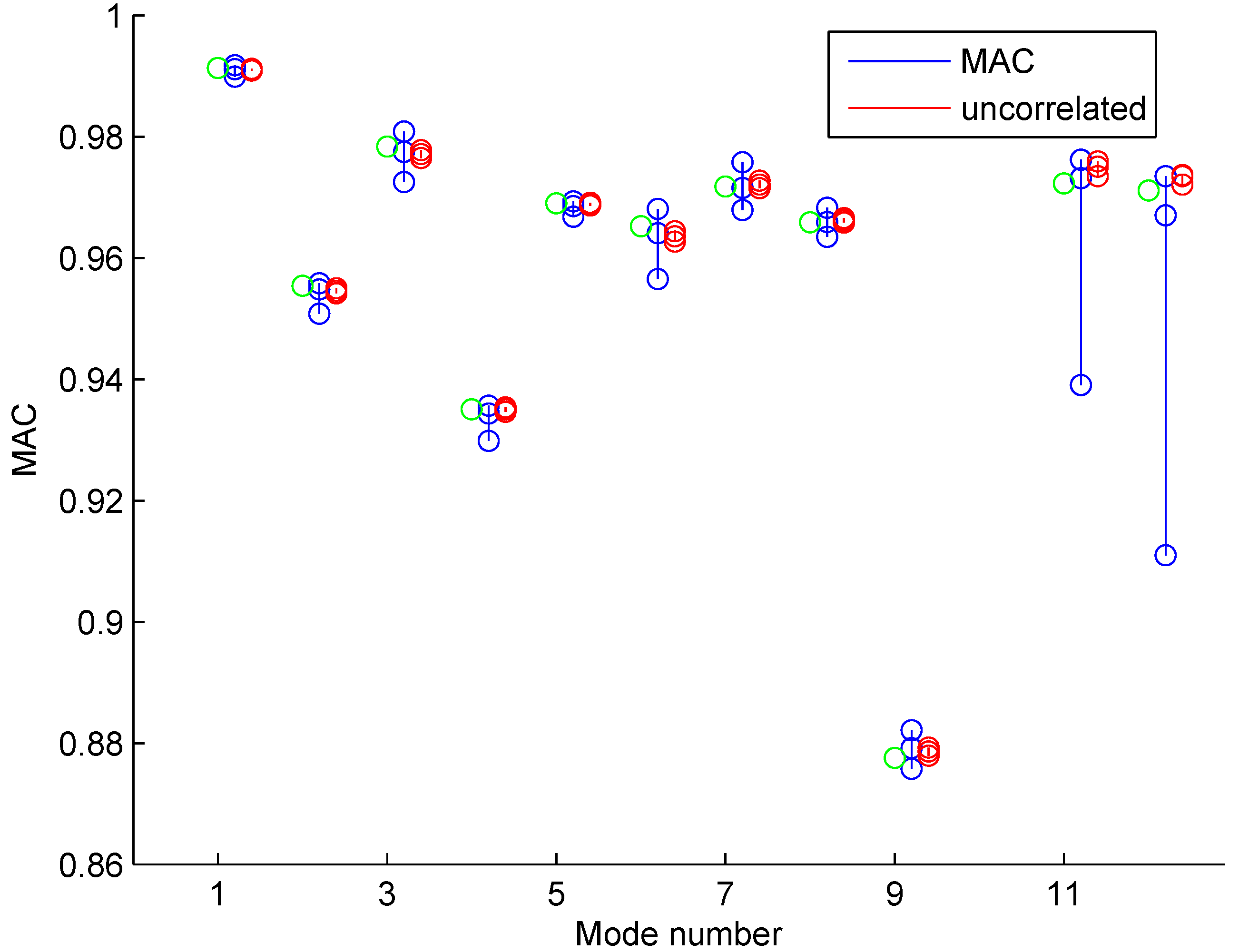
Uncertainty Propagation to Modal Frequencies and MAC Values
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Data


References
- Friswell, M.I.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer Science + Business Media Dordrecht: Berlin, Germany, 1995. [Google Scholar] [CrossRef]
- Sehgal, S.; Kumar, H. Structural Dynamic Model Updating Techniques: A State of the Art Review. Arch. Comput. Methods Eng. 2015. [Google Scholar] [CrossRef]
- Vanik, M.W.; Beck, J.L. A Bayesian probabilistic approach to structural health monitoring. Struct. Health Monit. 1998, 3243, 140–151. [Google Scholar] [CrossRef]
- Vanik, M.W.; Beck, J.L.; Au, S.K. Bayesian probabilistic approach to structural health monitoring. ASCE J. Eng. Mech. 2000, 126, 738–745. [Google Scholar] [CrossRef]
- Yuen, K.V. Bayesian Methods for Structural Dynamics and Civil Engineering; John Wiley & Sons: Singapore, 2010. [Google Scholar] [CrossRef]
- Yuen, K.V.; Beck, J.L.; Katafygiotis, L.S. Efficient model updating and health monitoring methodology using incomplete modal data without mode matching. Struct. Control Health Monit. 2006, 13, 91–107. [Google Scholar] [CrossRef]
- Mustafa, S.; Matsumoto, Y. Bayesian model updating and its limitations for detecting local damage of an existing truss bridge. J. Bridge Eng. 2017, 22, 04017019. [Google Scholar] [CrossRef]
- Yuen, K.V.; Beck, J.L.; Katafygiotis, L.S. Probabilistic approach for modal identification using non-stationary noisy response measurements only. Earthq. Eng. Struct. Dyn. 2002, 31, 1007–1023. [Google Scholar] [CrossRef]
- Au, S.K. Fast Bayesian ambient modal identification in the frequency domain, Part I: Posterior most probable value. Mech. Syst. Signal Process. 2012, 26, 60–75. [Google Scholar] [CrossRef]
- Au, S.K. Fast Bayesian ambient modal identification in the frequency domain, Part II: Posterior uncertainty. Mech. Syst. Signal Process. 2012, 26, 76–90. [Google Scholar] [CrossRef]
- Au, S.K.; Zhang, F.L.; To, P. Field observations on modal properties of two tall buildings under strong wind. J. Wind Eng. Ind. Aerodyn. 2012, 101, 12–23. [Google Scholar] [CrossRef]
- Au, S.K.; Zhang, F.L. Ambient modal identification of a primary–secondary structure by Fast Bayesian FFT method. Mech. Syst. Signal Process. 2012, 28, 280–296. [Google Scholar] [CrossRef]
- Au, S.K.; Zhang, F.L.; Ni, Y.C. Bayesian operational modal analysis: Theory, computation, practice. Comput. Struct. 2013, 126, 3–14. [Google Scholar] [CrossRef]
- Zhang, F.L.; Au, S.K. Fundamental two-stage formulation for Bayesian system identification, Part II: Application to ambient vibration data. Mech. Syst. Signal Process. 2016, 66, 43–61. [Google Scholar] [CrossRef]
- Zhang, F.L.; Ni, Y.C.; Au, S.K.; Lam, H.F. Fast Bayesian approach for modal identification using free vibration data, Part I–Most probable value. Mech. Syst. Signal Process. 2016, 70, 209–220. [Google Scholar] [CrossRef]
- Ni, Y.C.; Zhang, F.L.; Lam, H.F.; Au, S.K. Fast Bayesian approach for modal identification using free vibration data, Part II—Posterior uncertainty and application. Mech. Syst. Signal Process. 2016, 70, 221–244. [Google Scholar] [CrossRef]
- Kuok, S.; Yuen, K. Investigation of modal identification and modal identifiability of a cable-stayed bridge with Bayesian framework. Smart Struct. Syst. 2016, 17, 445–470. [Google Scholar] [CrossRef]
- Ni, Y.; Lu, X.; Lu, W. Operational modal analysis of a high-rise multi-function building with dampers by a Bayesian approach. Mech. Syst. Signal Process. 2017, 86, 286–307. [Google Scholar] [CrossRef]
- Beck, J.L.; Au, S.K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation. J. Eng. Mech. ASCE 2002, 128, 380–391. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Beck, J.L. Updating models and their uncertainties. II: Model identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Papadimitriou, C.; Lam, H.F. A probabilistic approach to structural model updating. Soil Dyn. Earthq. Eng. 1998, 17, 495–507. [Google Scholar] [CrossRef]
- Beck, J.L. Bayesian system identification based on probability logic. Struct. Control Health Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Yuen, K.V.; Beck, J.L.; Katafygiotis, L.S. Unified probabilistic approach for model updating and damage detection. J. Appl. Mech. Trans. ASME 2006, 73, 555–564. [Google Scholar] [CrossRef]
- Cheung, S.H.; Beck, J.L. Bayesian Model Updating Using Hybrid Monte Carlo Simulation with Application to Structural Dynamic Models with Many Uncertain Parameters. J. Eng. Mech. 2009, 135, 243–255. [Google Scholar] [CrossRef]
- Muto, M.; Beck, J.L. Bayesian updating and model class selection for hysteretic structural models using stochastic simulation. J. Vib. Control 2008, 14, 7–34. [Google Scholar] [CrossRef]
- Goller, B.; Schueller, G.I. Investigation of model uncertainties in Bayesian structural model updating. J. Sound Vib. 2011, 330, 6122–6136. [Google Scholar] [CrossRef] [PubMed]
- Yuen, K.V. Updating large models for mechanical systems using incomplete modal measurement. Mech. Syst. Signal Process. 2012, 28, 297–308. [Google Scholar] [CrossRef]
- Lam, H.F.; Yang, J.; Au, S.K. Bayesian model updating of a coupled-slab system using field test data utilizing an enhanced Markov chain Monte Carlo simulation algorithm. Eng. Struct. 2015, 102, 144–155. [Google Scholar] [CrossRef]
- Yan, W.J.; Katafygiotis, L.S. A novel Bayesian approach for structural model updating utilizing statistical modal information from multiple setups. Struct. Saf. 2015, 52, 260–271. [Google Scholar] [CrossRef]
- Asadollahi, P.; Huang, Y.; Li, J. Bayesian finite element model updating and assessment of cable-stayed bridges using wireless sensor data. Sensors 2018, 18, 3057. [Google Scholar] [CrossRef]
- Au, S.K. Assembling mode shapes by least squares. Mech. Syst. Signal Process. 2011, 25, 163–179. [Google Scholar] [CrossRef]
- Ching, J.; Chen, Y.C. Transitional Markov Chain Monte Carlo method for Bayesian model updating, model class selection and model averaging. J. Eng. Mech. 2007, 133, 816–832. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Papadioti, D.C. Component mode synthesis techniques for finite element model updating. Comput. Struct. 2013, 126, 15–28. [Google Scholar] [CrossRef]
- Jensen, H.A.; Millas, E.; Kusanovic, D.; Papadimitriou, C. Model-Reduction Techniques for Bayesian Finite Element Model Updating Using Dynamic Response Data. Comput. Struct. 2014, 279, 301–324. [Google Scholar] [CrossRef]
- Angelikopoulos, P.; Papadimitriou, C.; Koumoutsakos, P. Bayesian uncertainty quantification and propagation in molecular dynamics simulations: A high performance computing framework. J. Chem. Phys. 2012, 137, 103–144. [Google Scholar] [CrossRef]
- Hadjidoukas, P.; Angelikopoulos, P.; Papadimitriou, C.; Koumoutsakos, P. Π4U: A high performance computing framework for Bayesian uncertainty quantification of complex models. J. Comput. Phys. 2015, 284, 1–21. [Google Scholar] [CrossRef]
- Beck, J.L.; Yuen, K.V. Model selection using response measurements: Bayesian probabilistic approach. J. Eng. Mech. 2004, 130, 192–203. [Google Scholar] [CrossRef]
- Behmanesha, I.; Yousefianmoghadam, S.; Nozaric, A.; Moaveni, B.; Stavridis, A. Uncertainty quantification and propagation in dynamic modelsusing ambient vibration measurements, application to a10-story building. Mech. Syst. Signal Process. 2018, 107, 502–514. [Google Scholar] [CrossRef]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damageassessment: A review. Mech. Syst. Signal Process. 2015, 56–57, 123–149. [Google Scholar] [CrossRef]
- Simoen, E.; Papadimitriou, C.; Lombaert, G. On prediction error correlation in Bayesian model updating. J. Sound Vib. 2013, 332, 4136–4152. [Google Scholar] [CrossRef]
- Simoen, E.; Papadimitriou, C.; De Roeck, G.; Lombaert, G. Influence of the prediction error correlation model on Bayesian FE model updating results. In Proceedings of the Life-Cycle and Sustainability of Civil Infrastructure Systems—Proceedings of the 3rd International Symposium on Life-Cycle Civil Engineering (IALCCE 2012), Vienna, Austria, 3–6 October 2012. [Google Scholar]
- Papadimitriou, C.; Lombaert, G. The effect of prediction error correlation on optimal sensor placement in structural dynamics. Mech. Syst. Signal Process. 2012, 28, 105–127. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Ntotsios, E.; Giagopoulos, D.; Natsiavas, S. Variability of Updated Finite Element Models and their Predictions Consistent with Vibration Measurements. Struct. Control Health Monit. 2012, 19, 630–654. [Google Scholar] [CrossRef]
- Wu, S.; Angelikopoulos, P.; Papadimitriou, C.; Koumoutsakos, P. Bayesian annealed sequential importance sampling (BASIS): An unbiased version of transitional Markov chain Monte Carlo. ASCE ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2018, 4, 011008. [Google Scholar] [CrossRef]
- Craig, R., Jr.; Bampton, M. Coupling of substructures for dynamic analysis. AIAA J. 1965, 6, 678–685. [Google Scholar]
- Jensen, H.; Muñoz, A.; Papadimitriou, C. An enhanced substructure coupling technique for dynamic re-analyses: Application to simulation-based problems. Comput. Methods Appl. Mech. Eng. 2016, 307, 215–234. [Google Scholar] [CrossRef]
- Jensen, H.; Papadimitriou, C. Sub-Structure Coupling for Dynamic Analysis: Application to Complex Simulation-Based Problems Involving Uncertainty; Lecture Notes in Applied and Computational Mechanics 89; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Castanier, M.; Tan, Y.C.; Pierre, C. Characteristic constraint modes for component mode synthesis. AIAA J. 2001, 39, 1182–1187. [Google Scholar] [CrossRef]



| Mode | Experimental | Nominal Model | Mode Shape |
|---|---|---|---|
| Frequency (Hz) | Frequency (Hz) | MAC Value | |
| 1 | 0.306 | 0.293 | 0.991 |
| 2 | 0.603 | 0.574 | 0.955 |
| 3 | 0.623 | 0.619 | 0.978 |
| 4 | 0.965 | 0.849 | 0.935 |
| 5 | 1.047 | 1.050 | 0.969 |
| 6 | 1.139 | 1.070 | 0.965 |
| 7 | 1.428 | 1.388 | 0.972 |
| 8 | 1.697 | 1.578 | 0.966 |
| 9 | 2.005 | 1.690 | 0.878 |
| 10 | 2.303 | 1.966 | 0.85 |
| 11 | 2.367 | 2.156 | 0.972 |
| 12 | 2.590 | 2.317 | 0.971 |
| 13 | 2.723 | 2.500 | |
| 14 | 3.086 | 2.745 | |
| 15 | 3.127 | 2.815 | |
| 16 | 3.480 | 2.876 | |
| 17 | 3.861 | 2.950 | |
| 18 | 4.058 | 3.320 | |
| 19 | 4.210 | 3.381 | |
| 20 | 4.410 | 3.521 |
| Quantile | 0.919 | 0.844 | 70.428 | 0.044 |
| Quantile | 0.968 | 0.981 | 110.23 | 0.065 |
| Quantile | 1.029 | 1.115 | 150.20 | 0.105 |
| Quantile | 0.908 | 0.835 | 0.044 |
| Quantile | 0.965 | 0.966 | 0.065 |
| Quantile | 1.022 | 1.108 | 0.108 |
| NDOF | Uncorrelated | MAC | ||
|---|---|---|---|---|
| Deck | Pier | Deck | Pier | |
| 8 | 0.070 | 0.087 | 0.104 | 0.241 |
| 14 | 0.056 | 0.083 | 0.100 | 0.216 |
| 26 | 0.041 | 0.064 | 0.091 | 0.190 |
| 52 | 0.032 | 0.045 | 0.088 | 0.191 |
| 105 | 0.021 | 0.033 | 0.087 | 0.186 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyris, C.; Papadimitriou, C.; Panetsos, P.; Tsopelas, P. Bayesian Model-Updating Using Features of Modal Data: Application to the Metsovo Bridge. J. Sens. Actuator Netw. 2020, 9, 27. https://doi.org/10.3390/jsan9020027
Argyris C, Papadimitriou C, Panetsos P, Tsopelas P. Bayesian Model-Updating Using Features of Modal Data: Application to the Metsovo Bridge. Journal of Sensor and Actuator Networks. 2020; 9(2):27. https://doi.org/10.3390/jsan9020027
Chicago/Turabian StyleArgyris, Costas, Costas Papadimitriou, Panagiotis Panetsos, and Panos Tsopelas. 2020. "Bayesian Model-Updating Using Features of Modal Data: Application to the Metsovo Bridge" Journal of Sensor and Actuator Networks 9, no. 2: 27. https://doi.org/10.3390/jsan9020027
APA StyleArgyris, C., Papadimitriou, C., Panetsos, P., & Tsopelas, P. (2020). Bayesian Model-Updating Using Features of Modal Data: Application to the Metsovo Bridge. Journal of Sensor and Actuator Networks, 9(2), 27. https://doi.org/10.3390/jsan9020027





