1. Introduction
Determining the position of a receiver based on signal measurements from an array of spatially separated transmitters with well-known locations has been, and is still, an important issue in wireless sensor networks, mobile communications, radar, sonar, and global navigation satellite system (GNSS) applications. Position information is also the key enabler for a constantly increasing number of innovative services and applications. New applications increase the demand for positioning systems where the GNSS signals are denied, e.g., indoors. Current local positioning systems (LPSs) may fail to meet the requirements of certain applications such as indoor emergency operations, e.g., fire-fighting, security and military missions, due to the need for a pre-installed radio frequency (RF) infrastructure. The rapid deployment of a portable infrastructure for positioning during emergency operations may not allow us to carry out extensive calibrations and signal characterization in the target environment, in order to optimize positioning algorithms and increase their position solution accuracy.
RF-based LPSs use wireless technologies to estimate the position of the receiver in areas where no GNSS reception is available. Therefore, positioning based on wireless technologies is an active research area. The commonly used signal measurements for positioning, i.e., location-dependent parameters, include time measurements, i.e., time of arrival (ToA), time difference of arrival (TDoA), and round-trip time of flight (RToF), phase measurements, i.e., phase of arrival (PoA) and phase difference of arrival (PDoA), frequency-based measurements, i.e., signal Doppler frequency (SDF) and frequency difference of arrival (FDoA) (also called differential Doppler (DD)), received signal strength (RSS), and angle of arrival (AoA) of the transmitted signal in addition to hybrid signal measurements, e.g., ToA/RSS, ToA/AoA or TDoA/FDoA. Distance information or range between the receiver and the transmitters can be extracted from ToA, TDoA, RToF, PoA, PDoA, and RSS measurements. The nonlinear relationships of these measurements with the receiver’s position render positioning a nontrivial task.
ToA techniques use the signal propagation time to calculate the distance between the transmitter and the receiver, provided the signal propagation speed in the medium is known [
1]. Strict synchronization between transmitters and the receiver is required. The TDoA method exploits the difference in signals’ propagation times from different transmitters, measured at the receiver. Synchronization is required only between the transmitters. The positioning accuracy of ToA and TDoA approaches depends on the signal bandwidth and sampling rate at the receiver. The accuracy degrades in non-line-of-sight (NLoS) conditions. RToF measures the round-trip, i.e., transmitter–receiver–transmitter, signal propagation time to estimate the distance. Therefore, only moderate clock synchronization between the transmitters and the receiver is required. RToF estimation accuracy is also affected by the sampling rate and signal bandwidth, but even more severely due to the two-way signal propagation. Moreover, the response delay at the receiver further deteriorates the accuracy [
1].
Phase measurement approaches exploit the phase or phase difference of the carrier signal to estimate the distances between the transmitters and the receiver. The transmitted signals are commonly assumed to be purely sinusoidal, having the same frequency and zero phase offset [
2]. Line-of-sight (LoS) conditions are required for high positioning accuracy.
Techniques for radio source location based on the Doppler effect include SDF and FDoA approaches. SDF methods [
3] estimate the Doppler frequency shifts in received signals from radio sources and can be implemented by a single portable receiver. Spectrum analysis techniques enable the simultaneous localization of multiple radio sources [
4]. In FDoA methods [
5], the signal of a stationary radio source is intercepted by at least two moving receivers, and the frequency difference between the receivers is measured at several positions along their trajectories in order to determine the radio source location. For accurate FDoA estimates, the receivers’ frequencies have to be precisely synchronized.
The RSS-based approach is a simple, cost-efficient, and widely used method [
6]. The actual signal power strength received at the receiver is used to estimate the distance to the transmitter, where the higher the RSS value the smaller the distance. The positioning accuracy is generally poor due to multipath fading and especially in NLoS situations.
AoA-based approaches use antenna arrays [
7] at the receiver side. The TDoA at individual elements of the array are calculated to estimate the angle at which the transmitted signal impinges on the receiver. AoA-based positioning provides accurate estimation at small transmitter–receiver distances. With increasing distances and multipath effects, the accuracy deteriorates significantly.
Most positioning systems use the conventional suboptimal two-step approach, in which measurements, i.e., location-dependent parameters, are first extracted from the signals and then used for position determination. On the other hand, direct position determination (DPD) [
8,
9,
10] performs positioning in a single step and without first estimating the location-dependent parameters. However, the DPD often needs to minimize a nonconvex cost function in order to estimate the position, which demands high computational resources.
The focus in this article is on conventional hyperbolic positioning, i.e., TDoA-based positioning, where the position fix is computed from a set of intersecting hyperbolic curves generated by TDoA measurements. A summary of the most popular circular, i.e., ToA-based, and hyperbolic positioning algorithms is presented in ref. [
11]. When the positioning algorithm assumes an additive measurement error model, the available approaches include the maximum likelihood (ML) and the least squares (LS) approaches, which are implemented as iterative or non-iterative, i.e., closed-form (CF) algorithms. The nonlinear hyperbolic equations were linearized by using the Taylor series expansion and solved iteratively in [
12,
13] using the LS estimator (LSE). If the initial guess of the position estimate is not accurate enough, the convergence to the global solution cannot be guaranteed. Gradient-based techniques, such as the quasi-Newton technique [
14] and the Gauss–Newton-type Levenberg–Marquardt method [
15], have also been used in iterative algorithms. The ML solution to the hyperbolic equations [
16] is widely used due to the proven asymptotic consistency and efficiency of the ML estimator (MLE), which requires assumptions about the distribution of measurement errors. However, the iterative algorithm to find the solution is computationally intensive.
In this article, three CF LS algorithms, i.e., closed-form single set least squares (CFSSLS) [
17], closed-form extended single set least squares (CFExSSLS), which is based on the direct method (DM) algorithm in ref. [
18], and closed-form full set least squares (CFFSLS) [
19], are presented to estimate the 3-D position of a receiver using wireless signal TDoA measurements. Two algorithms, namely, CFSSLS and CFFSLS, estimate nuisance parameters. Therefore, both algorithms are extended, according to refs. [
19,
20], respectively, to benefit from the nuisance parameter information in refining, i.e., minimizing the error in, the vertical position estimates. Moreover, a design parameter is introduced to control the amount of nuisance parameter information to be used. The DM algorithm in ref. [
18], which requires exactly five transmitters, is extended to work with an arbitrary number of transmitters, i.e.,
, in order to obtain an LS position solution called the CFExSSLS algorithm. With coplanar transmitters, only 2-D position estimates can be obtained. To obtain 3-D position estimates, a height sensor might be required, or transmitters have to be placed at enough different heights to create the necessary good geometry for 3-D positioning. Simulations and experiments are carried out to confirm the capacity of the adapted algorithms to obtain 3-D position estimates with coplanar transmitters in challenging wireless signal conditions and without any extra sensors.
The rest of the article is organized as follows. Related work is discussed in
Section 2. In
Section 3, CF LS algorithms for TDoA-based 3-D positioning are developed. The utilization of nuisance parameters is introduced in order to refine the vertical position estimates when transmitters are placed in a coplanar arrangement. The setup and results of the simulation study and the conducted experiments are presented in
Section 4. The findings are then discussed in
Section 5 and conclusions are given in
Section 6.
2. Related Work
In the following, some useful material has been adopted from ref. [
19] and is indicated by citing at the end of the adoption. CF, i.e., analytical, methods were developed to overcome convergence problems, where a nuisance parameter, i.e., the range from the receiver to the master transmitter, is introduced to the set of the linearized equations. CF or analytical solutions are desirable because they usually have fewer computational loads than iterative methods or ML approaches [
19]. Moreover, CF algorithms achieve estimation accuracies at acceptable levels, are mathematically simple, robust, and easy to implement for practical real-time applications, where low computational time and memory storage requirements are of high priority to meet imposed power constraints. Another important class of techniques is the DMs, e.g., refs. [
21,
22,
23], which are algebraic, i.e., exact, solutions to the TDoA equations. However, their accuracy depends heavily on the accuracy of the measurements and works with a certain number of equations, i.e., they do not make use of the additional available measurements but the exactly required. Nevertheless, DMs may be desirable since they do not involve any matrix operations. DMs and CF LS algorithms still have two major advantages: They do not need an initial position estimate to run, and they do not require any probabilistic assumptions about the distribution of the measurement errors and therefore can be employed when the precise characterization of measurement errors cannot be determined.
The total number of TDoA measurements that can be generated with
N transmitters is
and is referred to as the full set (FS) measurements [
24]. If only measurements with respect to a single master transmitter are considered, they are referred to as the single set (SS) measurements, and their total number is
. Any transmitter can be considered as master, and thus, a number of
N SSs can be constructed [
19]. Any SS represents an independent set of measurements. The FS extends any SS by considering all possible linear combinations of the SS measurements. Thus, the FS also contains only
independent measurements, and the remaining ones (constructed by linear combinations) are dependent, i.e., redundant, measurements. When the SS and some extra measurements (less than the FS) are used for the position estimation, the set of measurements is referred to as the extended single set (ExSS).
CF unconstrained and constrained LS solutions using an SS of the TDoA measurements are well described in ref. [
17] and can be denoted as CFSSLS solutions. The CFSSLS algorithms developed in refs. [
25,
26] are called the spherical interpolation (SI) and the linear correction LS (LCLS), respectively. Both algorithms require range measurements which may not be available or may not be accurate enough due to clock synchronization errors, and are, respectively, equivalent to the unconstrained CFSSLS and constrained CFSSLS solutions in ref. [
17] that depend only on TDoA measurements, as correctly indicated in ref. [
27]. The constrained CFSSLS solution of ref. [
17] was repeated in ref. [
28] with corrections stated in ref. [
29]. The extension of the CFSSLS solution as suggested in ref. [
28] yielded an algorithm that utilizes two SSs of TDoA measurements made with respect to two reference transmitters, i.e., the total number of used measurements is
, where only
measurements are independent [
19]. The DM solution in ref. [
21] requires exactly four transmitters and uses an SS of the TDoA measurements, i.e., three independent measurements. The DM solution in ref. [
18] uses exactly
transmitters and depends on an ExSS, where the number of TDoA measurements used is
, i.e.,
independent and
dependent (redundant) measurements. Both DM solutions in refs. [
22,
23] require exactly four transmitters to work. The method in ref. [
22] uses four TDoA measurements; an SS, i.e., three independent measurements, in addition to one dependent measurement from the FS. The algorithm in ref. [
23] utilizes five TDoA measurements from two SSs, where one measurement is common to both SSs. The CF LS solution using an FS of the TDoA measurements is introduced in ref. [
19] and can be denoted as CFFSLS solution. This CFFSLS algorithm was used in ref. [
30] with a data-selective procedure to discard bad measurements.
3. Materials and Methods
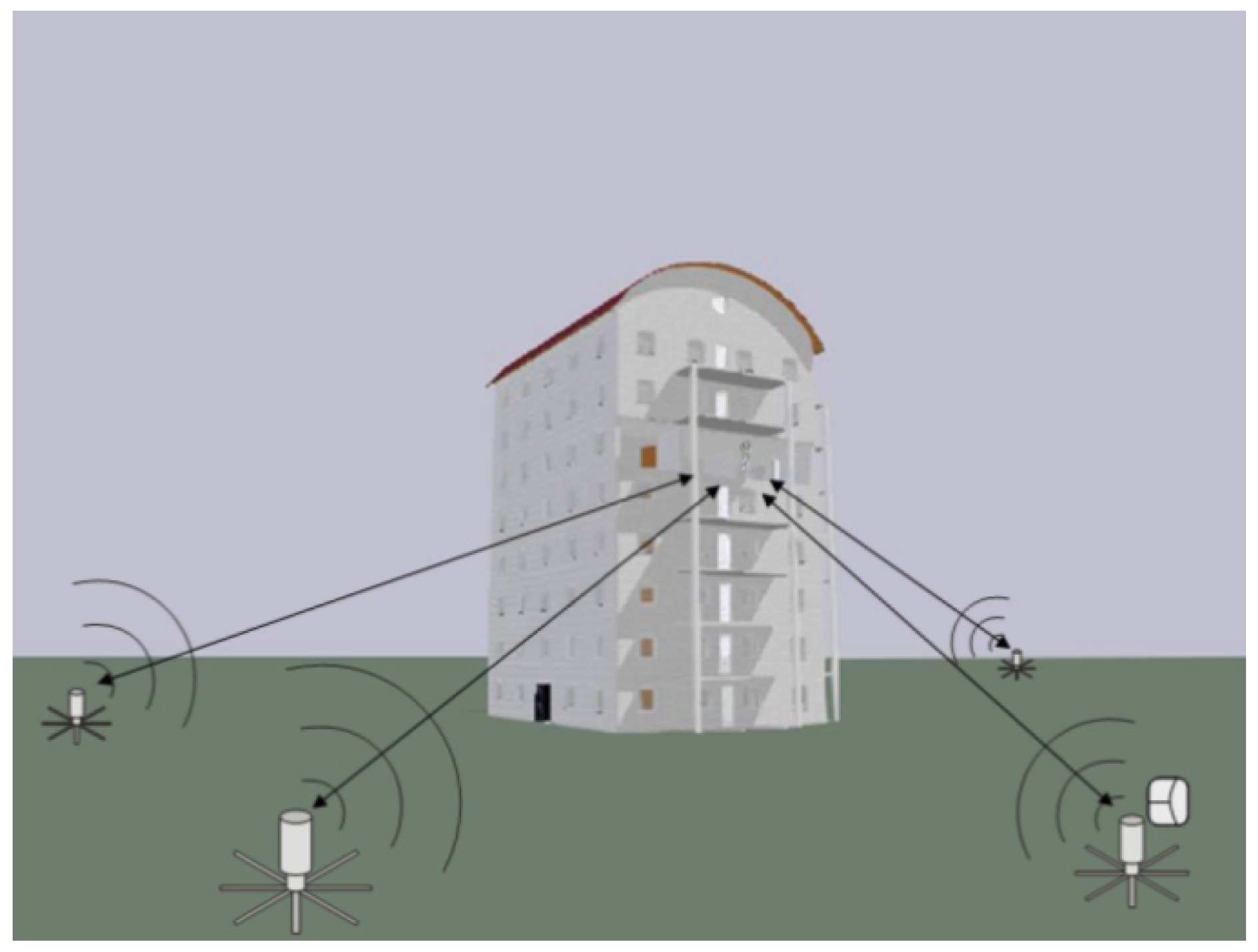
Simulations were conducted to investigate the performance of the proposed algorithms in order to better interpret the results of the real measurements. The performance of the algorithms was evaluated in terms of the root mean square error (RMSE) of the 3-D position estimates at a range of signal-to-noise ratio (SNR) levels. Details on the simulation setup and results are presented in
Section 4.1 and
Section 4.2, respectively. To obtain real-world measurements, a wireless transmitter system was utilized to estimate the position of an indoor passive receiver using TDoA measurements. The system consists of a set of transmitting stations (TSs) located around the target building, user terminals (UTs) or receivers inside the building, and a monitoring and control unit (MCU) for steering the TSs and for broadcasting information to the UTs. TSs broadcast multicarrier navigation signals at 420 with 40 MHz bandwidth. The signal design allows minimizing multipath effects in harsh indoor environments, such as massive multilevel buildings made of concrete, steel, and metal-shielded windows. System architecture, details, and measurement examples are given in ref. [
31] and references therein.
The following mathematical treatment is partially adopted from ref. [
19] for convenience and is indicated by a citation before the equation. Consider an array of
N transmitters located at known positions
, in a 3-D Cartesian coordinate system, where
i = 1, …,
N and
is the transpose operator, and a passive receiver, at an unknown position
, observing signals radiating from the transmitters. The receiver measures the TDoA of a pair of signals radiated by any pair of transmitters
i and
j, where
. The TDoA measurement,
, is related to the range difference,
, by the relation:
, where
c is the known propagation speed of the signal in the medium. Thus,
is expressed in the error-free case as [
19]:
where
i = 1, …,
N,
j = 1, …,
N,
, and
denotes the Euclidean vector norm. The problem, thus, is to estimate the vector
given a set of
, i.e.,
, noisy measurements and using the known vectors
, which in turn might contain uncertainties.
3.1. Closed-Form Single Set Least Squares Solution
LSE makes no assumptions about the statistical characteristics of the measurement errors and therefore is an attractive alternative if the statistics of measurement errors cannot be determined accurately. Moreover, a CF estimator would be advantageous for practical real-time applications. The LSE minimizes a squared error function called the cost function. In the absence of measurement errors and transmitter position uncertainties, the LSE minimization will yield a zero-cost function. From Equation (1), we can get [
19]:
With straightforward algebra, Equation (2) yields [
19]:
Without loss of generality, the first transmitter is considered as the master transmitter. Thus, Equation (3) is rewritten as [
19]:
Where
and
j = 2, …,
N. The LSE would minimize a cost function,
, which is expressed as [
19]:
Equation (4) can be expressed in matrix form as
, where [
19]:
and:
Note that
is a
matrix,
is a
column vector, and
is a
column state vector, where the range
to the master transmitter is a nuisance parameter. The cost function in Equation (5) can, thus, be rewritten using the matrix notation as
. The unconstrained CFSSLS solution of
reads [
19]:
and the corresponding estimate of
is given as [
19]:
We originally estimate the
state vector
. Therefore, we need at least four independent TDoA measurements with respect to a common master transmitter. That is, at least five transmitters are required in order to obtain a 3-D CF solution [
19].
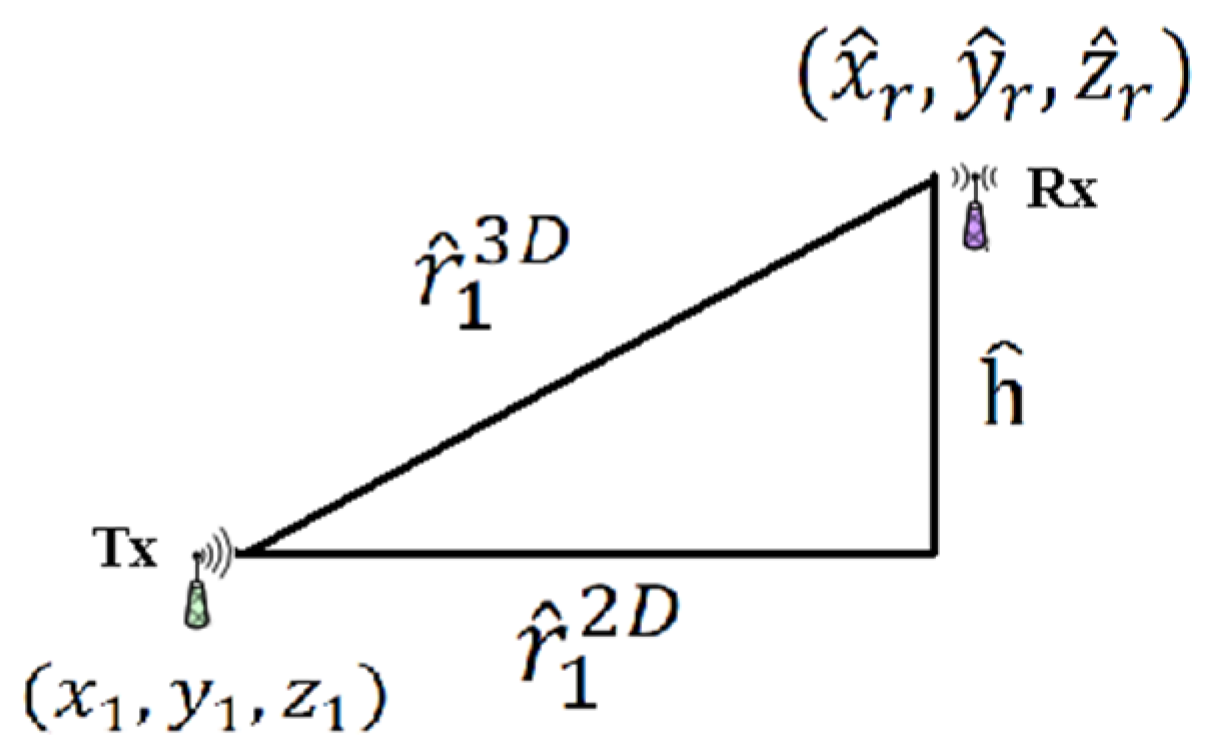
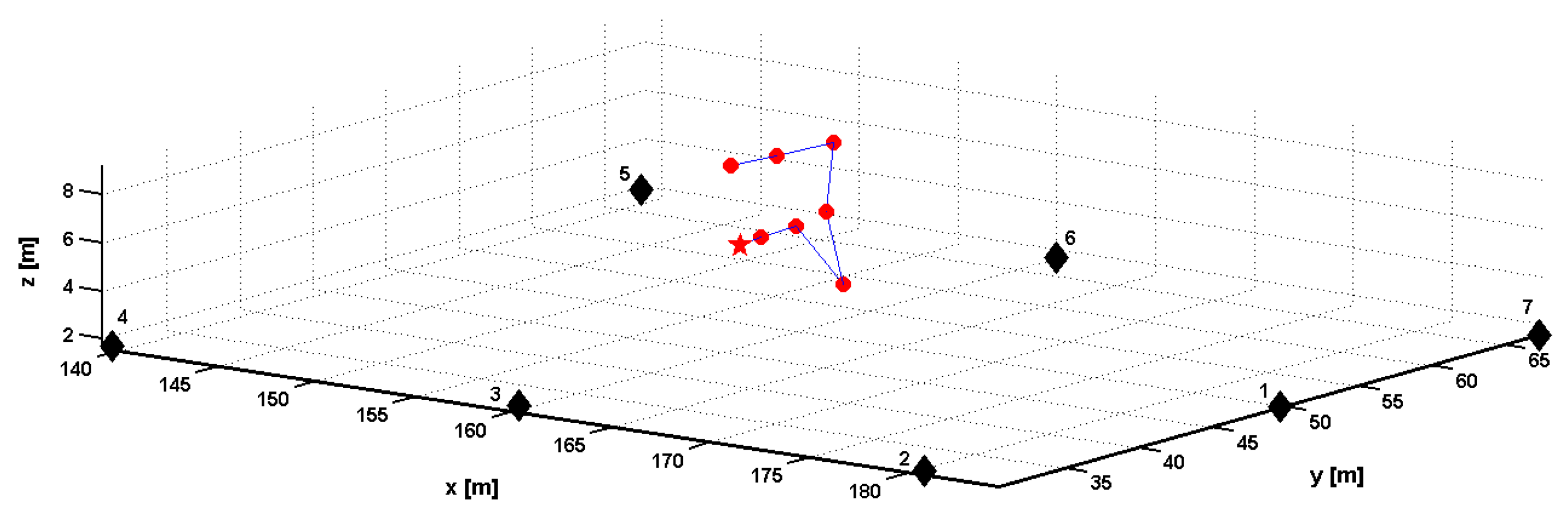
In a practical LPS, transmitters are often installed in coplanar or quasi-coplanar arrangements, see
Figure 1. Such an arrangement is a major challenge for accurate 3-D positioning, namely, the vertical component of the 3-D position estimate is of poor accuracy, and therefore, the LPS would be useless for applications requiring accurate 3-D position estimates. The problem can be fixed by utilizing the nuisance parameter of the CFSSLS solution [
20], which is the first element in the state vector,
, in Equation (8).
When coplanar or quasi-coplanar transmitters are used for TDoA measurements at the receiver, the CFSSLS solution of Equation (10) delivers acceptable accuracies for the 2-D, i.e., horizontal, position estimate,
, and poor estimates for the vertical position,
. Using the horizontal position estimate of the receiver,
, and the known horizontal coordinates of the first, i.e., master, transmitter,
, the horizontal range from the receiver to the first (master) transmitter,
, see
Figure 2, can be estimated with acceptable accuracy as:
The 3-D range from the receiver to the master transmitter,
, i.e., the nuisance parameter, which is the first element in the state vector,
, in Equation (8), is estimated by the CFSSLS algorithm as
and can be denoted as
, see
Figure 2. We can also see from
Figure 2 that the difference,
, between the vertical position of the receiver (Rx),
, and the vertical position of the master transmitter (Tx),
is estimated as:
Thus, the estimate of the receiver’s vertical position,
, can be refined by:
where
α is a design parameter value, set by the system user, to adjust the amount of information obtained via Equation (12), i.e., the amount of information obtained by the utilization of the nuisance parameter. Thus, full information is included when
. When
, the vertical position of the receiver is set at the height of the master transmitter, i.e., nuisance parameter information is not included. The steps of the CFSSLS algorithm and the utilization of the nuisance parameter are exhibited in Algorithm 1.
| Algorithm 1: The CFSSLS algorithm and refinement of the vertical position estimate. |
| 0. Input: The known transmitters’ coordinates, i.e., , and the SS range difference measurements, i.e., , as defined by Equation (4). |
| 1. Compute: The matrix and the vector as defined by Equations (6) and (7), respectively. |
| 2. Estimate: The state vector by LS estimation via Equation (9). |
| 3. CFSSLS Output: The receiver’s 3-D position estimate, i.e., , via Equation (10). |
| 4. Estimate: The horizontal range, i.e., , from the receiver to the master transmitter via Equation (11). |
| 5. Estimate: The difference, i.e., , between the vertical positions of the receiver and master transmitter via Equation (12). |
| 6. Refine: The vertical position estimate of the receiver via Equation (13). |
| 7. Output: The final 3-D position estimate of the receiver, i.e., , where were estimated in step 3 and was estimated in step 6. |
3.2. Closed-Form Extended Single Set Least Squares Solution
The CF algorithm presented in ref. [
18] is essentially based on transforming the hyperbolic equations into a set of vector equations by squaring the set of equations in Equation (1) and then differencing them. It requires a minimum of five transmitters, i.e.,
, and uses an SS of the TDoA measurements in addition to extra measurements made by the successive pairs of the rest transmitters, so that the following
measurements are used:
For an arbitrary number of transmitters, i.e.,
, the simultaneous equations are expressed in algebraic form, see ref. [
18] for detailed derivation, as
where:
The other constants in the set of equations in Expression (14) can be similarly written as in Expression (15). Expression (14) can be put in the matrix form
, where
and:
The dimension of the
matrix is
,
is a
column vector and
is a
column state vector. The matrix notation of the cost function to be minimized by the LSE is given by
. The unconstrained CF LS solution reads
This is referred to as the
CFExSSLS estimator. Note that only the unknown position vector of the receiver is estimated without any nuisance parameters. Therefore, this algorithm will deliver horizontal position estimates with acceptable accuracy and poor vertical position estimates if coplanar transmitters are used for 3-D positioning. The steps of the CFExSSLS solution are given in Algorithm 2.
| Algorithm 2: The CFSSExLS algorithm. |
| 0. Input: The known transmitters’ coordinates, i.e., , and the ExSS range difference measurements, i.e., |
| 1. Compute: The matrix and the vector as defined by Equations (16) and (17), respectively. |
| 2. CFExSSLS Output: The receiver’s 3-D position estimate, i.e., , by the LS estimation in Equation (19). |
3.3. Closed-Form Full Set Least Squares Solution
The set of measurement equations in the SS case is given in Equation (4). Accordingly, the set of measurement equations in the FS case can be straightforwardly written as [
19]:
where also without loss of generality, the first, second, … and (N − 1)th transmitters are considered in order as reference transmitters, and the corresponding range difference measurements
are considered only once. Expression (20) can also be written in the matrix form
, where [
19]:
and:
The
matrix has a dimension of
,
is a
column vector, and
is a
column state vector. The matrix notation of the cost function to be minimized by the LSE is given as
, and the unconstrained CFFSLS solution for
is written as:
Thus, the estimate of
reads:
Note that the number of nuisance parameters, i.e.,
, where
, in the
column state vector
given in Equation (23) increased to
nuisance parameters, which are 3-D range estimates to the transmitters that were considered as master transmitters in the
matrix given in Equation (21), i.e., all transmitters with the indices 1 to
[
19].
The nuisance parameters can also be exploited to refine the vertical position estimate of the receiver using the TDoA measurements from coplanar or quasi-coplanar transmitters in a similar way to the procedure explained in
Section 3.1 for the CFSSLS solution. Using the horizontal position estimate of the receiver,
, delivered by the CFFSLS solution, see Equations (24) and (25), and the known horizontal coordinates of the transmitters with the indices 1 to
, i.e.,
, where
, the horizontal ranges from the receiver to these transmitters,
can be estimated with acceptable accuracy as:
The 3-D ranges from the receiver to these transmitters,
, i.e., the nuisance parameters, which are the first
elements in the state vector,
, in Equation (23), are estimated by the CFFSLS algorithm as
,
and can be denoted as
. The differences,
, between the vertical position of the receiver,
, and the vertical position of the transmitters,
, are estimated as:
We can determine the minimum vertical difference estimate, denoted as
, from the difference estimates,
, according to:
Using
and the vertical position of the corresponding transmitter,
, the estimate of the receiver’s vertical position,
, can be refined as:
where
α is a design parameter value already defined. The steps of the CFFSLS algorithm and the utilization of the nuisance parameters are listed in Algorithm 3.
| Algorithm 3: The CFFSLS algorithm and refinement of the vertical position estimate. |
| 0. Input: The known transmitters’ coordinates, i.e., , and the FS range difference measurements, i.e., , as defined by the set of equations in (20). |
| 1. Compute: The matrix and the vector as defined by Equations (21) and (22), respectively. |
| 2. Estimate: The state vector by LS estimation via Equation (24). |
| 3. CFFSLS Output: The receiver’s 3-D position estimate, i.e., , via Equation (25). |
| 4. Estimate: The horizontal ranges, i.e., , from the receiver to the transmitters via Equation (26). |
| 5. Estimate: The differences, i.e., , between the vertical positions of the receiver and transmitters via Equation (27). |
| 6. Find: The minimum vertical difference estimate, i.e., , via Equation (28). |
| 7. Refine: The vertical position estimate of the receiver via Equation (29). |
| 8. Output: The final 3-D position estimate of the receiver, i.e., , where were estimate in step 3 and was estimated in step 7. |
5. Discussion
There are no positioning algorithms that best fit in all environments, situations, and wireless signal conditions. Positioning algorithms are usually developed for certain special cases because real environments are complex, and the geometries of receivers and transmitters are quite variable [
11]. Despite improvements in wireless, hardware, and software technologies, the development of low-cost and high-accuracy positioning systems is still a challenging task. Therefore, new positioning systems and approaches will be developed in the next few years since the current technology has not yet matured.
The experimental testing and evaluation of any indoor positioning system is a difficult task due to the need for a network deployment and for testing in several types of buildings [
33]. If a particular system is intended to be widely deployed, specific testing and evaluation in expected deployment environments may make sense. However, the repeatability of tests in the same environment is difficult to achieve because it is almost impossible to repeat the same environmental and signal conditions. Therefore, measures should be developed in order to create almost constant testing and evaluation conditions, in order to maximize repeatability and enable objective and fair performance comparisons. Repeatability can easily be achieved by simulations. However, simulation may not always be able to exactly resemble the varying conditions of the real world.
As previously indicated in ref. [
19], the TDoA-based positioning technique has increasing practical and theoretical importance in a wide range of applications. The TDoA measurements used in CF parametric estimation also depend on some nuisance parameters. The question of whether it is advantageous to exploit the knowledge about the nuisance parameters was addressed. Knowledge about the nuisance parameters is equivalent to having a more precise probabilistic model [
34] for the stochastic connection between the TDoA measurements and the receiver’s position. Thus, it contributes to uncertainty and estimation error reduction. The optimal exploitation of the knowledge about nuisance parameters or the contribution of this knowledge to theoretical lower bounds, e.g., the Cramer–Rao lower bound (CRLB), on the estimation errors are issues that still need further research efforts [
19]. The system designer often wants to know in advance the best an estimator can perform as a check against available designs in certain situations. The CRLB provides a benchmark for the best positioning accuracy for any unbiased estimator, e.g., the CFSSLS estimator. Both the CFExSSLS and CFFSLS are biased estimators since they use dependent TDoA measurements. If perfect knowledge of the real world is available, the CFSSLS estimator can deliver the best performance. However, an estimator designed to approach the CRLB is not robust if the estimator is not perfectly matched to the real world. The CRLB provides no indication of what to do to achieve the predicted performance in the presence of uncertainty. Therefore, the practical meaning of the CRLB is no other than to say that the designer must have perfect knowledge about the real world to obtain small estimation errors. Investigating the performance of estimators given some level of uncertainty yields the best an estimator can do. In this regard, a CRLB lacks a practical meaning, because it assumes that even smaller errors can be achieved, but without providing any indications of how to attain the predicted performance given the present level of uncertainty. Therefore, the CRLB might not always represent an objective to achieve when designing a practical estimator.
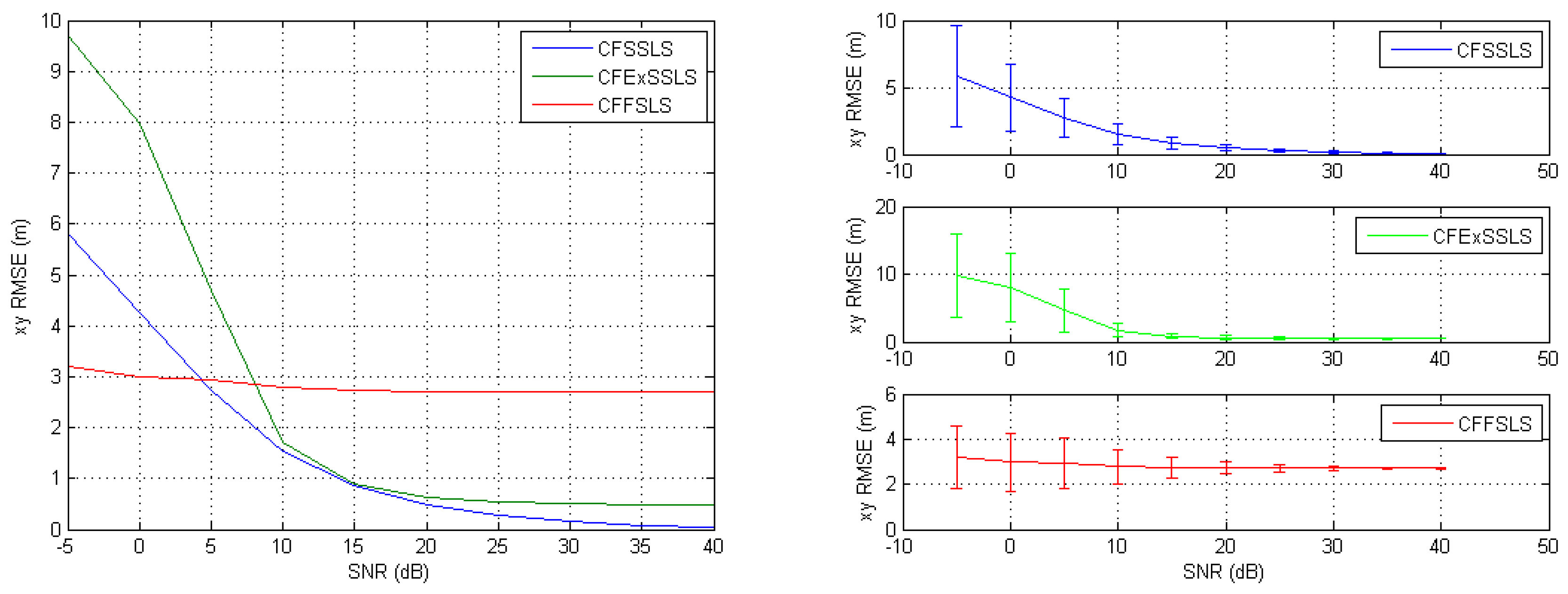
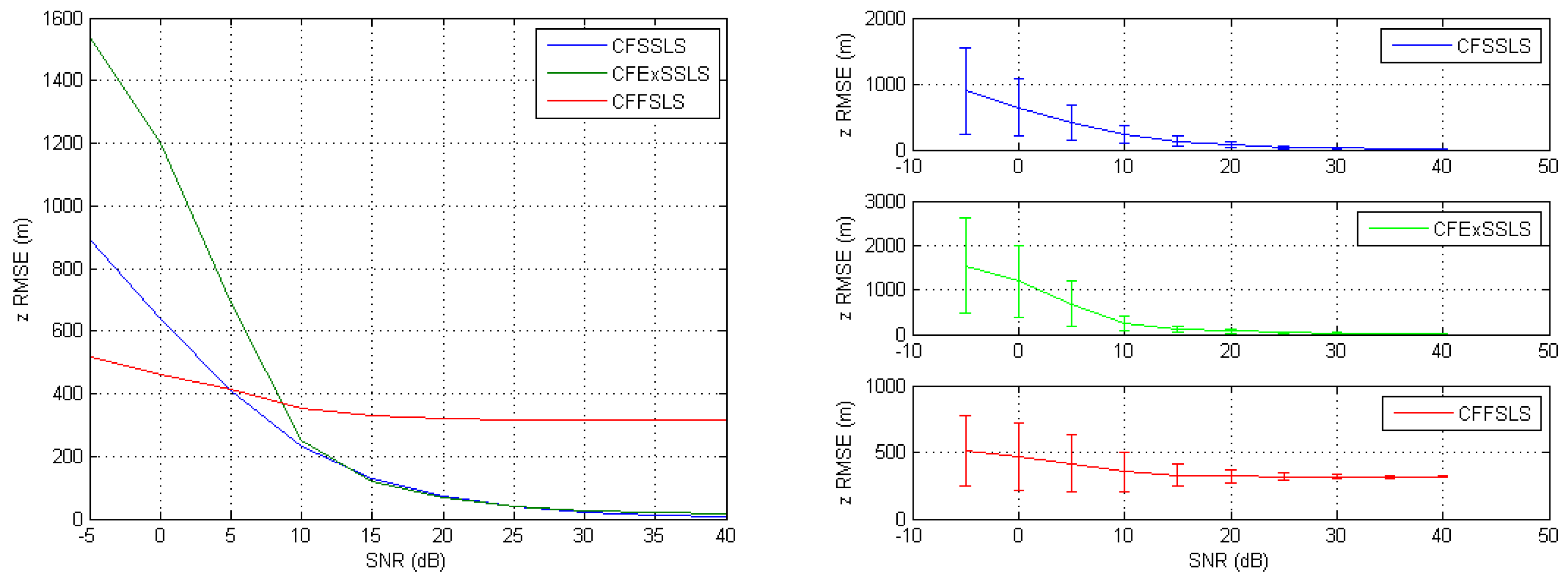
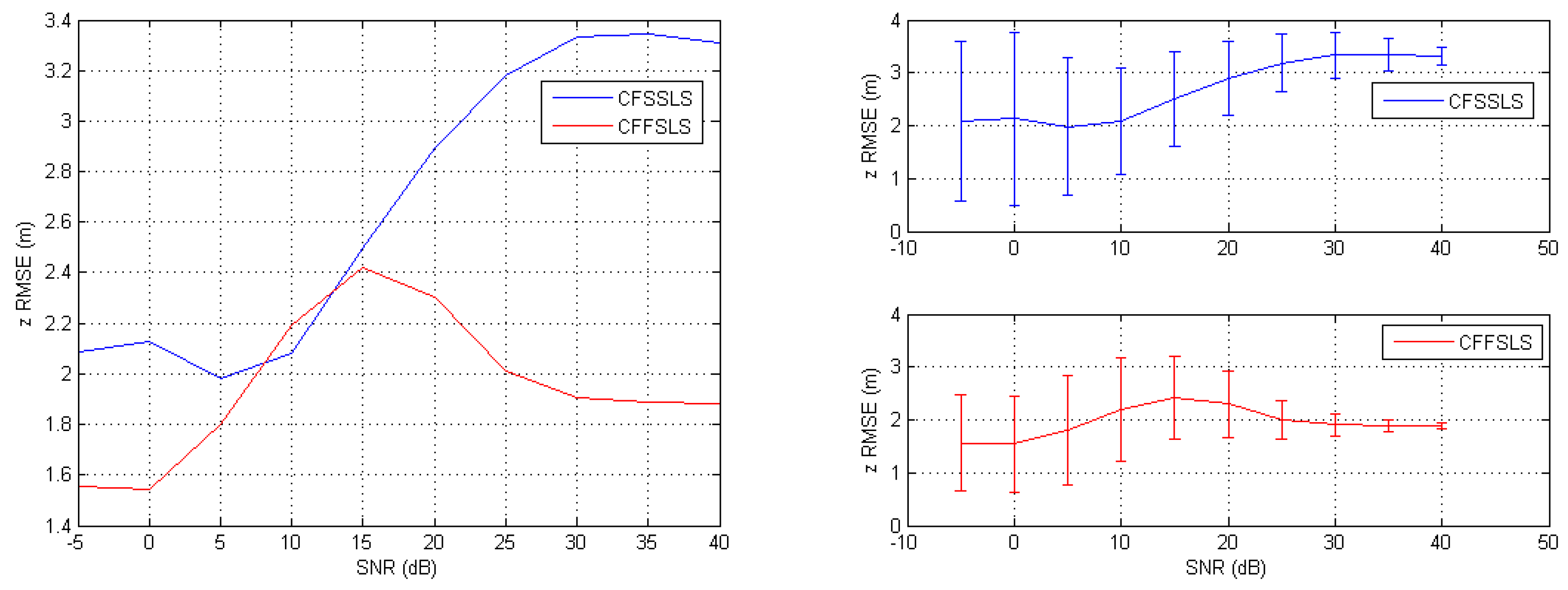
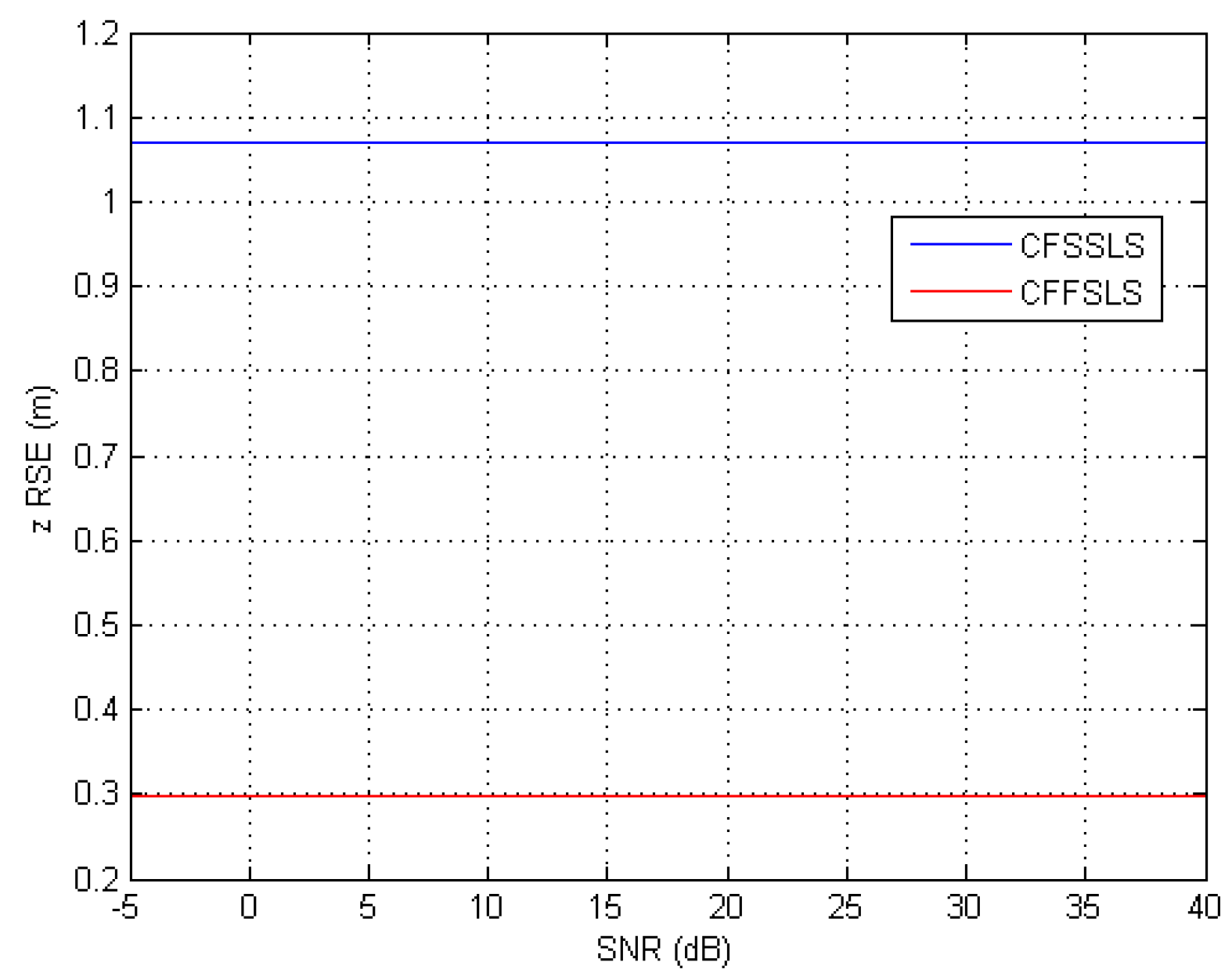
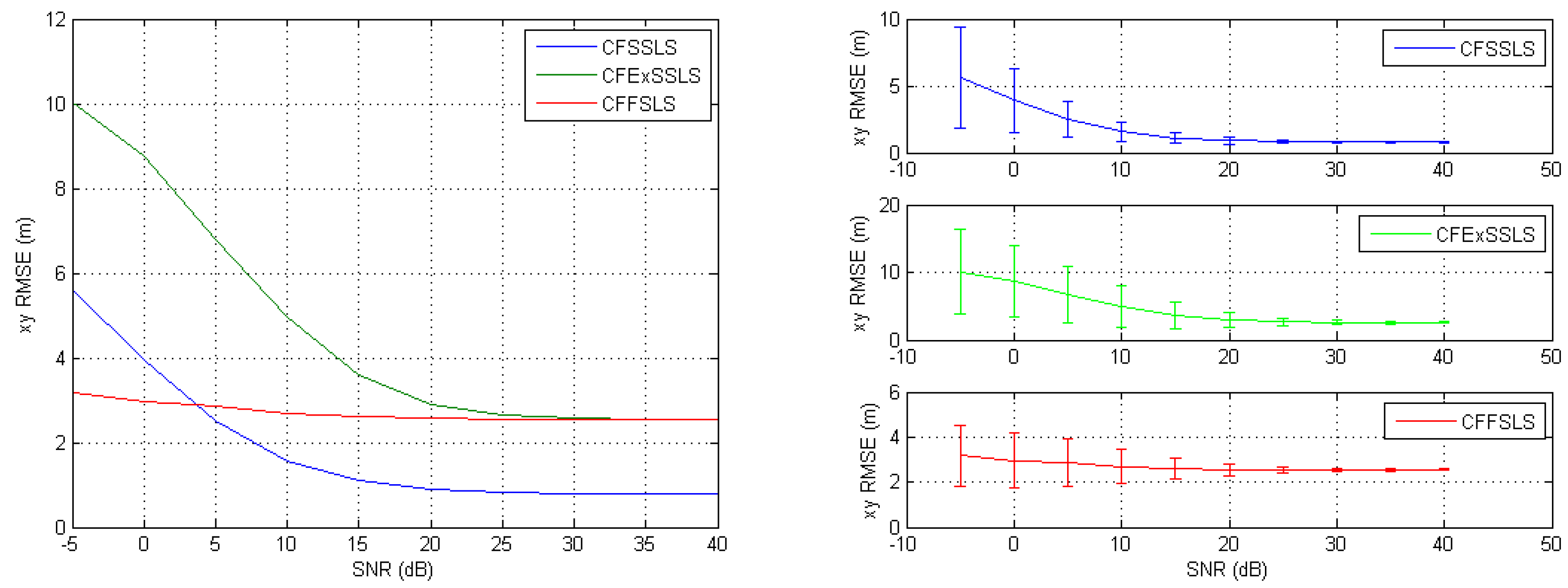
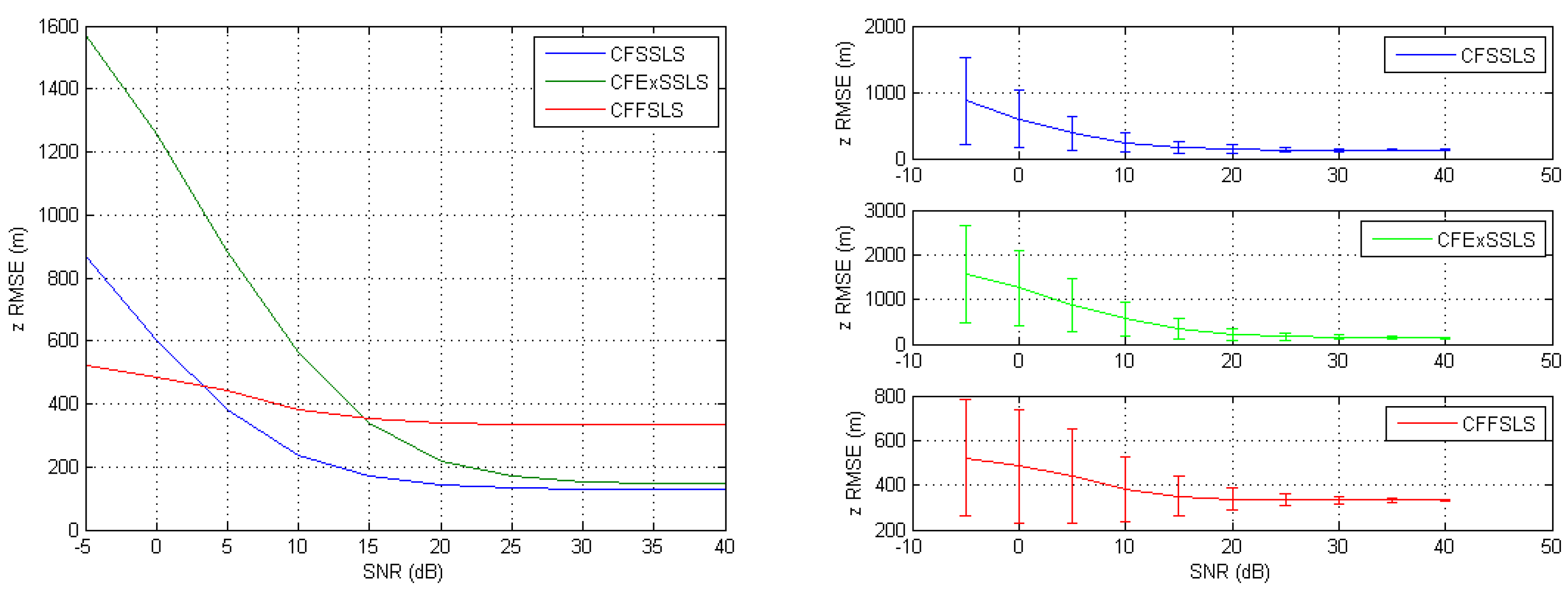
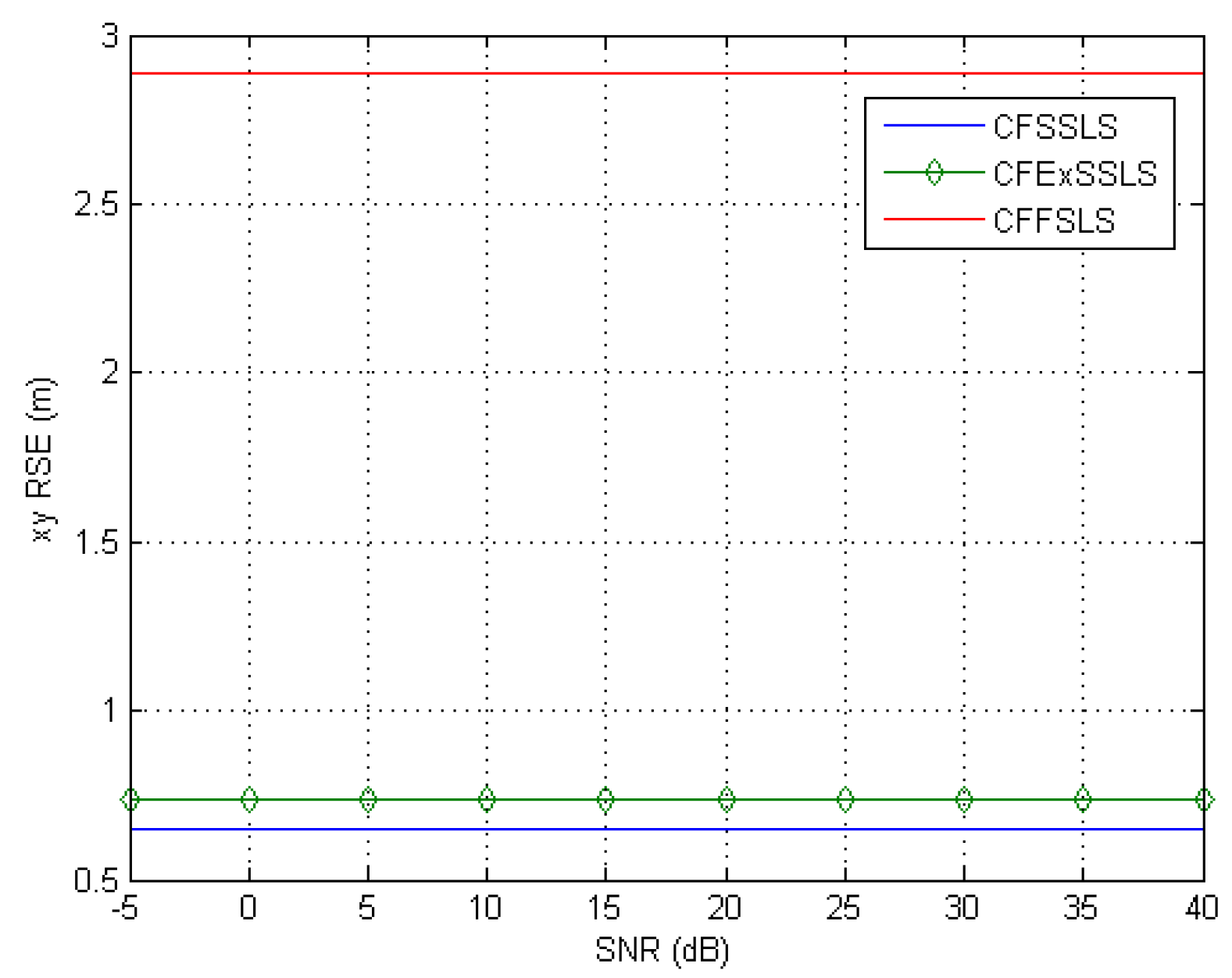
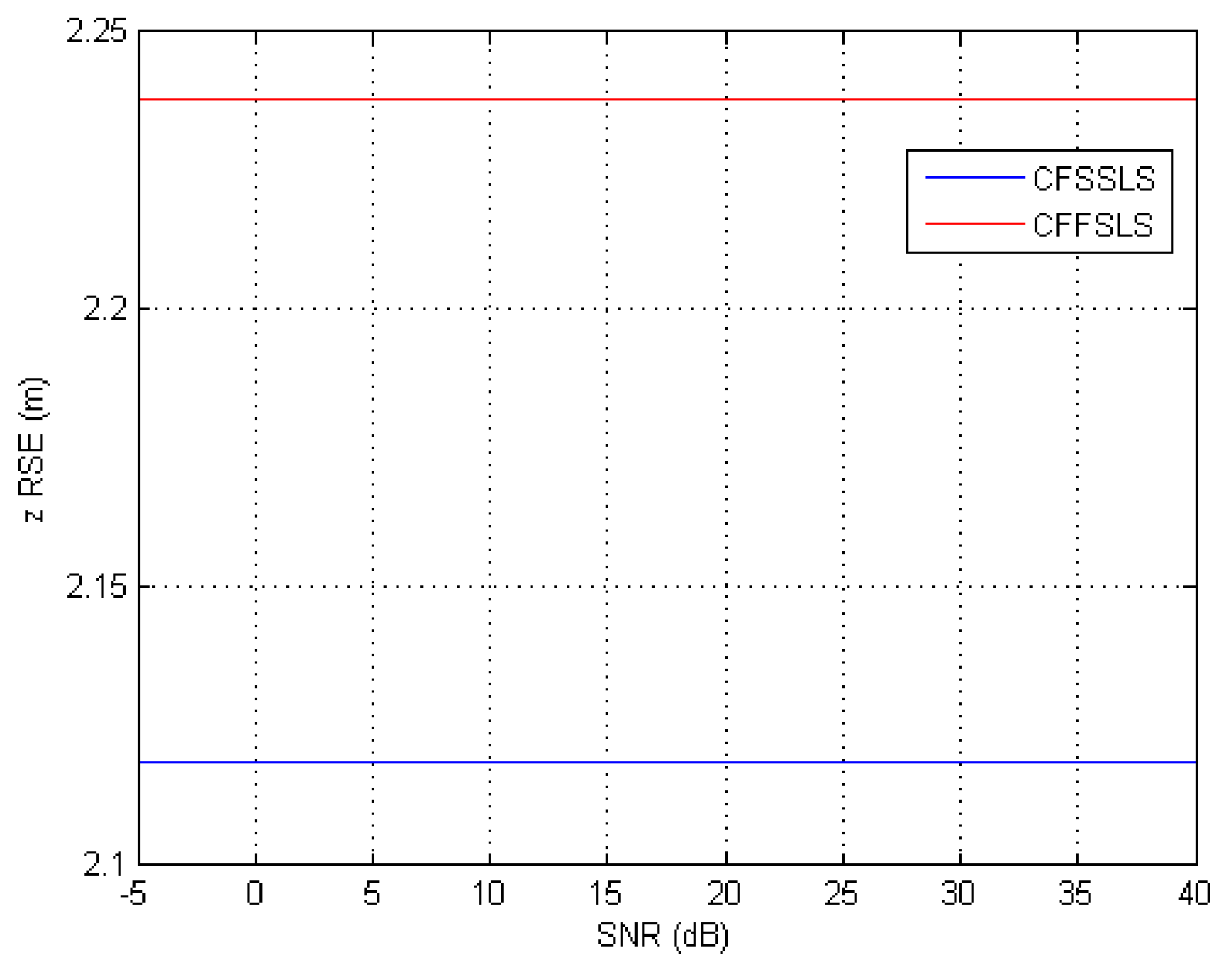
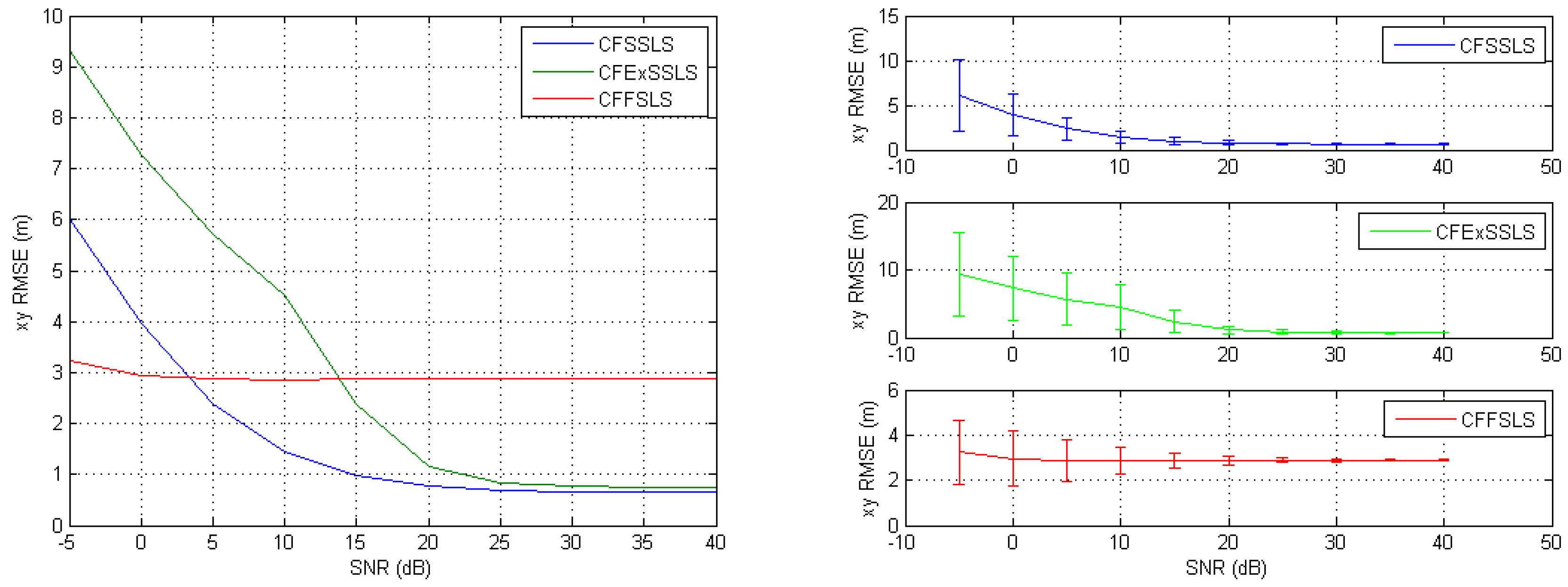
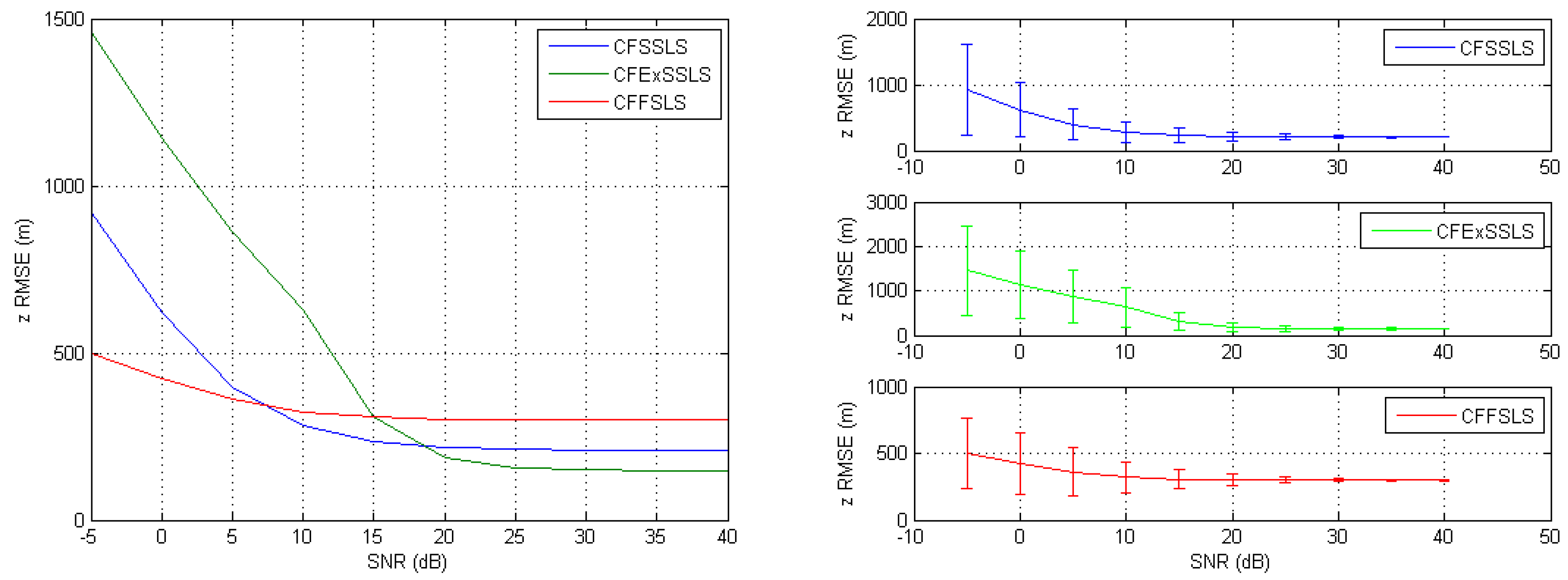
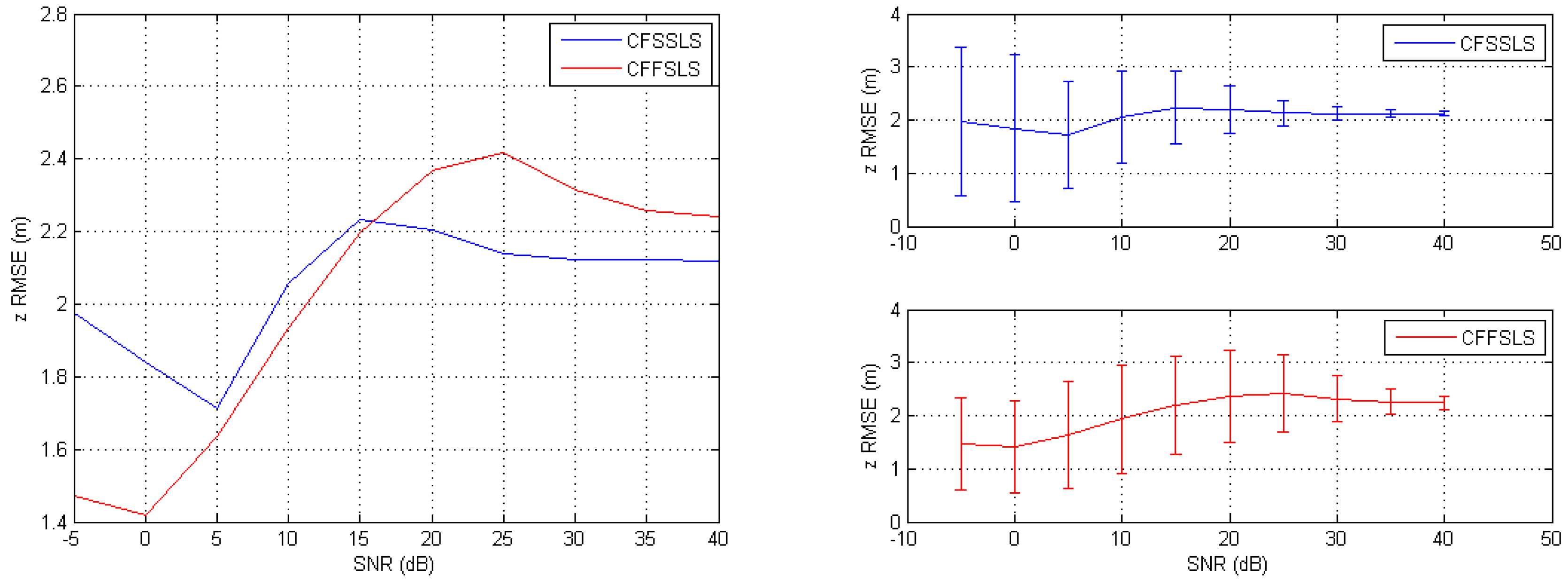
When simulated TDoA measurements were only corrupted by noise, the best position estimates were obtained by the CFSSLS, CFExSSLS, and CFFSLS solutions (ordered from best to worst), respectively, at moderate to high SNR levels. At low SNR levels, i.e., high noise levels, the CFFSLS algorithm delivers the best estimates. The CFFSLS algorithm is a biased solution, where noises contribute many times in different combinations leading to cancel-out effects, which are indicated by the constant accuracy, i.e., steady-state behavior, over the range of investigated SNR levels. The CFSSLS and CFFSLS algorithms can refine the vertical position estimate if they utilize the nuisance parameters. Generally, the CFFSLS solution delivers more accurate refined vertical position estimates as it utilizes more nuisance parameters, i.e., more information, than the CFSSLS solution.
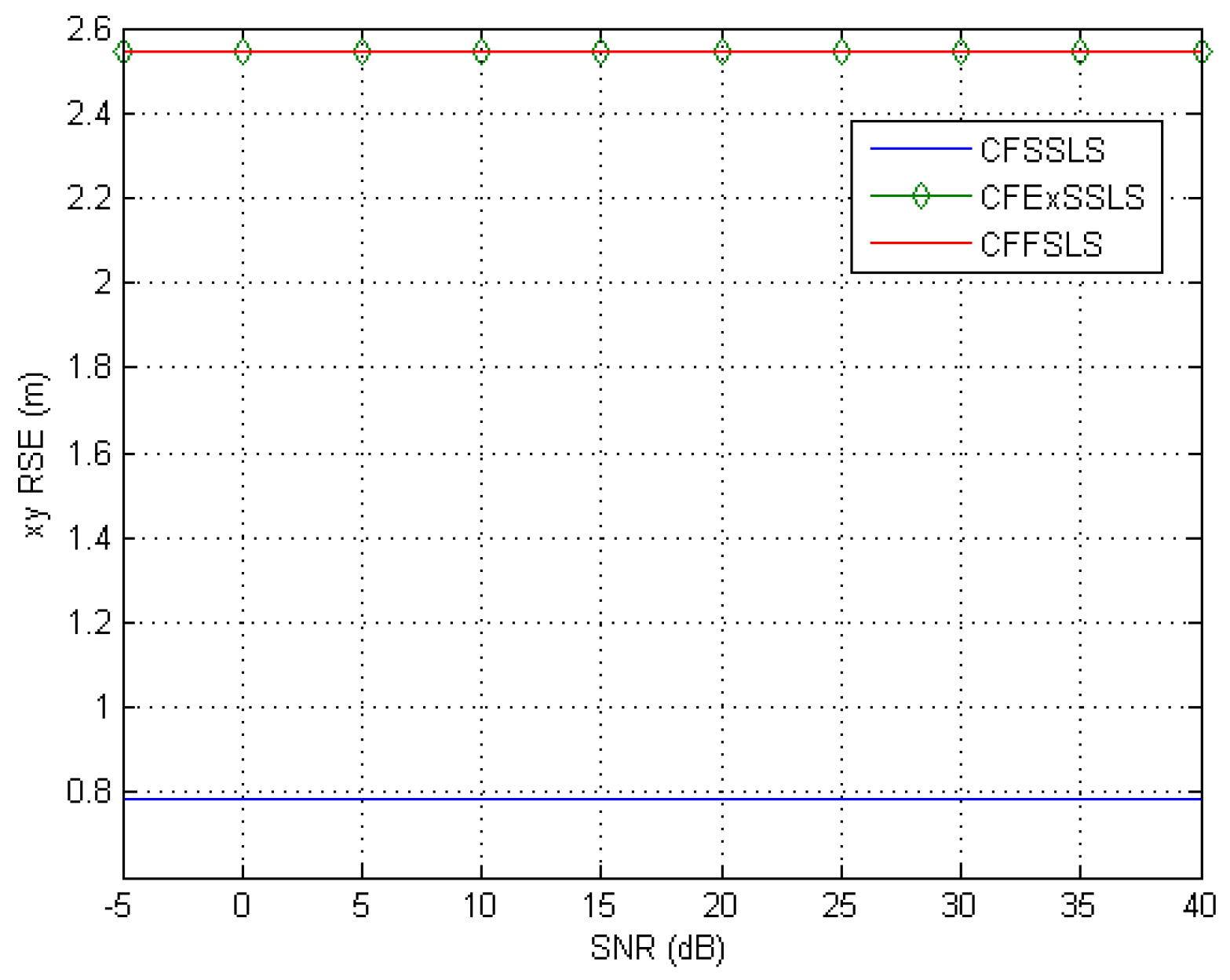
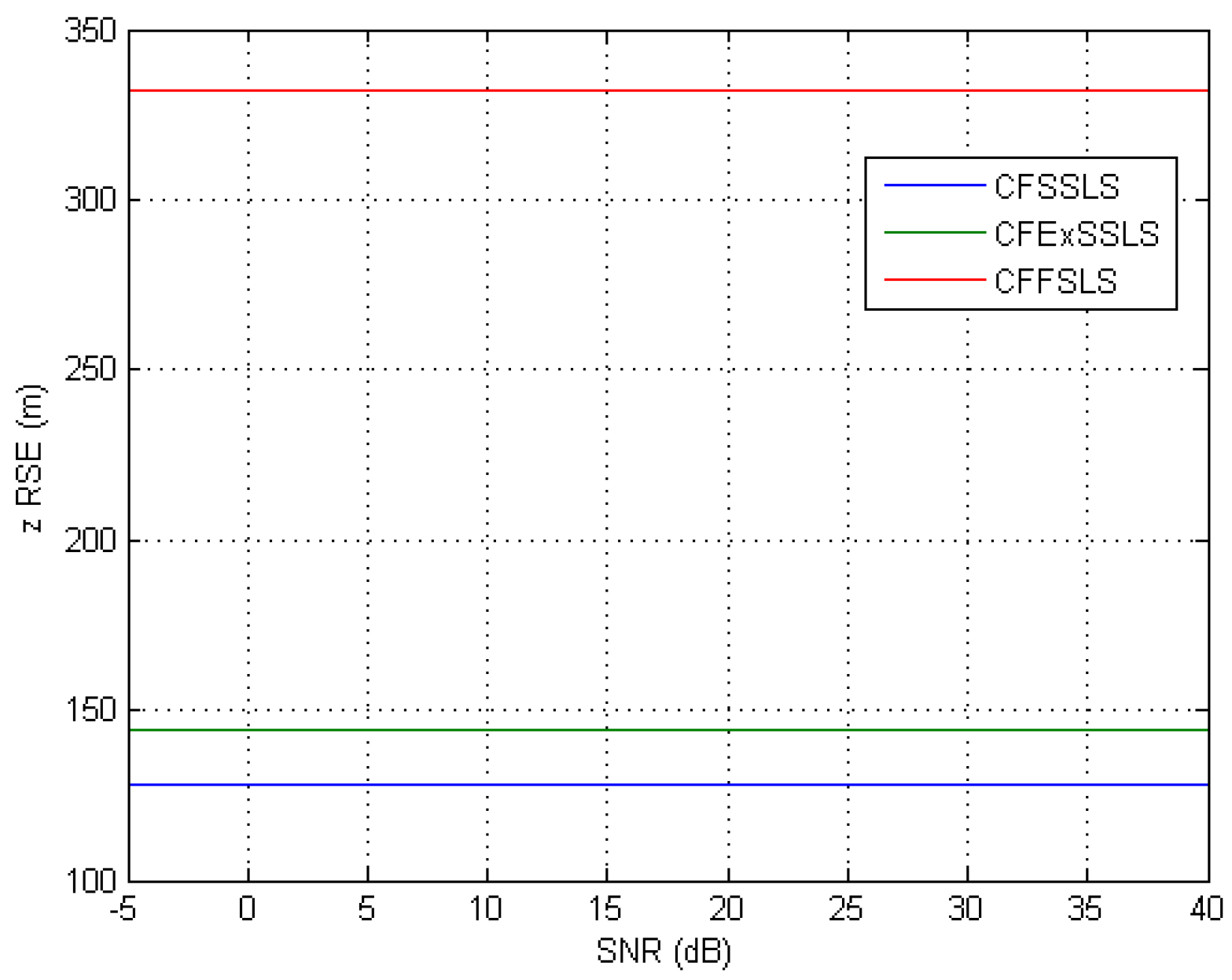
When only positive bias errors were present in the simulated TDoA measurements, the most accurate position estimates were obtained by the CFSSLS, CFExSSLS, and CFFSLS solutions (ordered from more to less accurate), respectively. In the horizontal space, using the FS TDoA measurements cancels out some bias effects and renders the CFExSSLS and CFFSLS solutions identical. The refined vertical position estimate of the CFFSLS algorithm is more accurate than that of the CFSSLS algorithm due to the utilization of more nuisance parameters.
The results of the two error input conditions, noise only and positive bias only, were consistently combined when simulated TDoA measurement errors were corrupted by noise and positive bias. The best performance is obtained by the CFSSLS algorithm followed by the CFExSSLS algorithm and then by the CFFSLS algorithm at moderate to high SNR levels. Both the CFExSSLS and CFFSLS horizontal position estimates are identical at high SNR levels. The CFFSLS solution is insensitive to the SNR level and, therefore, outperforms the other two solutions at low SNR, i.e., high noise, levels. The refined vertical position estimates of the CFFSLS solution is more accurate due to the utilization of more nuisance parameters.
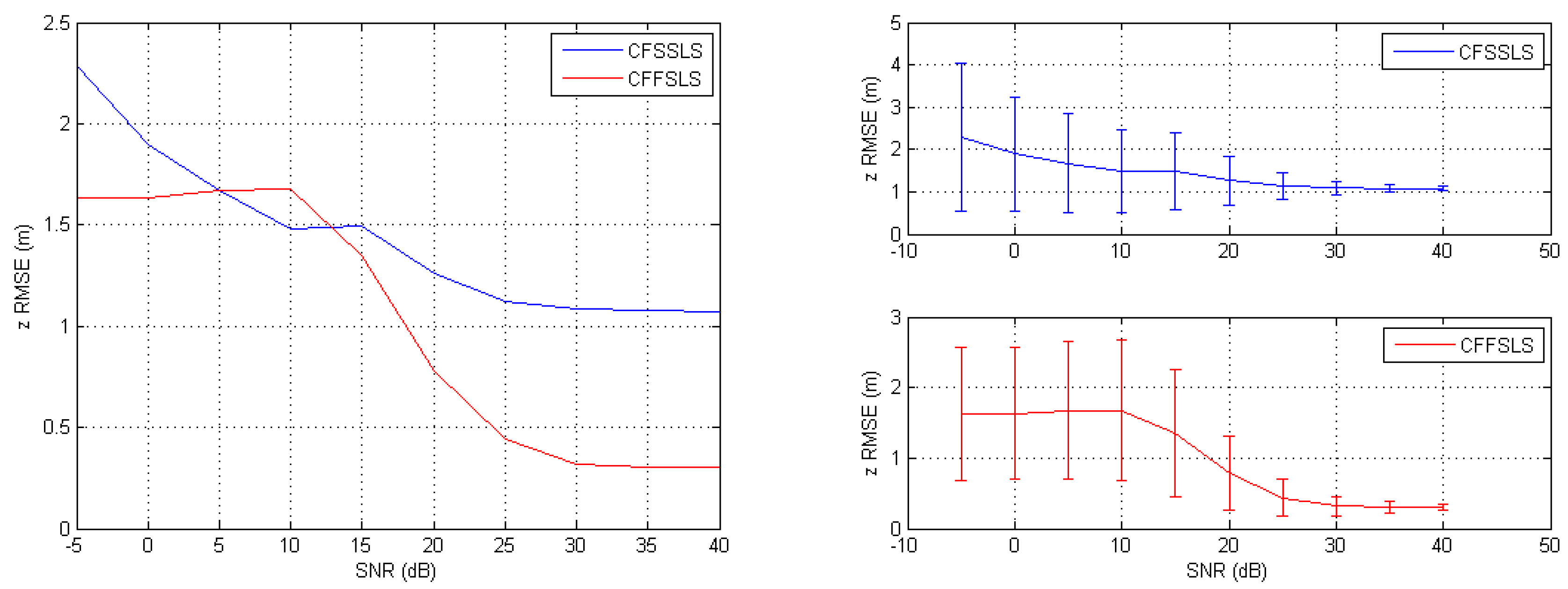
The simulations showed that negative bias only errors generally favored the CFExSSLS algorithm more than the other two solutions. In the horizontal space, the CFSSLS algorithm performed best and closely followed by the CFExSS solution. In the vertical space, the CFExSSLS algorithm was less affected than the other two algorithms. Negative biases also did not favor the utilization of more nuisance parameters for refining the vertical position estimation. The accuracy of the CFSSLS refined vertical position estimation is slightly better than that of the CFFSLS solution. Similar conclusions also apply when noise is added to negative bias errors.
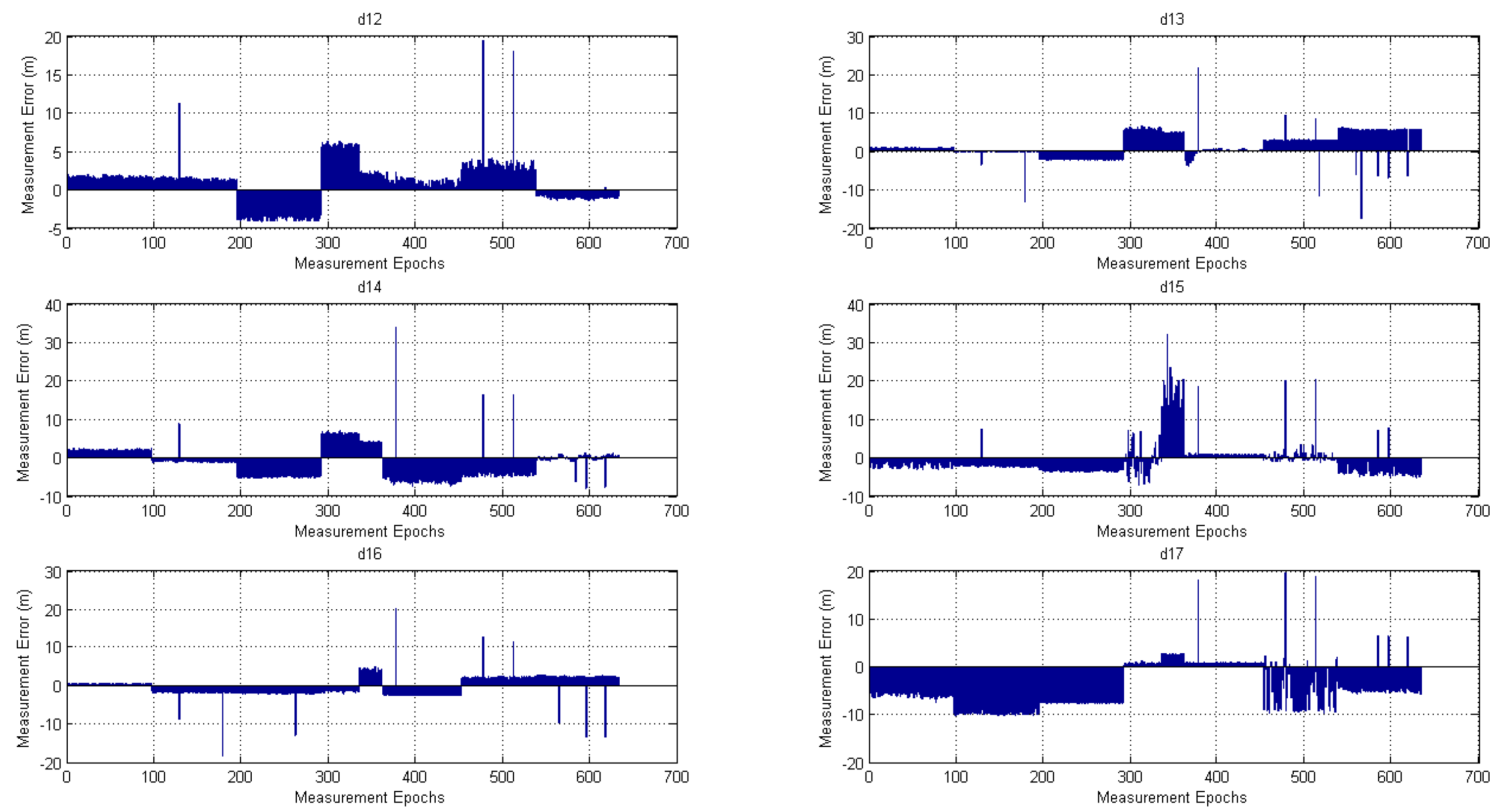
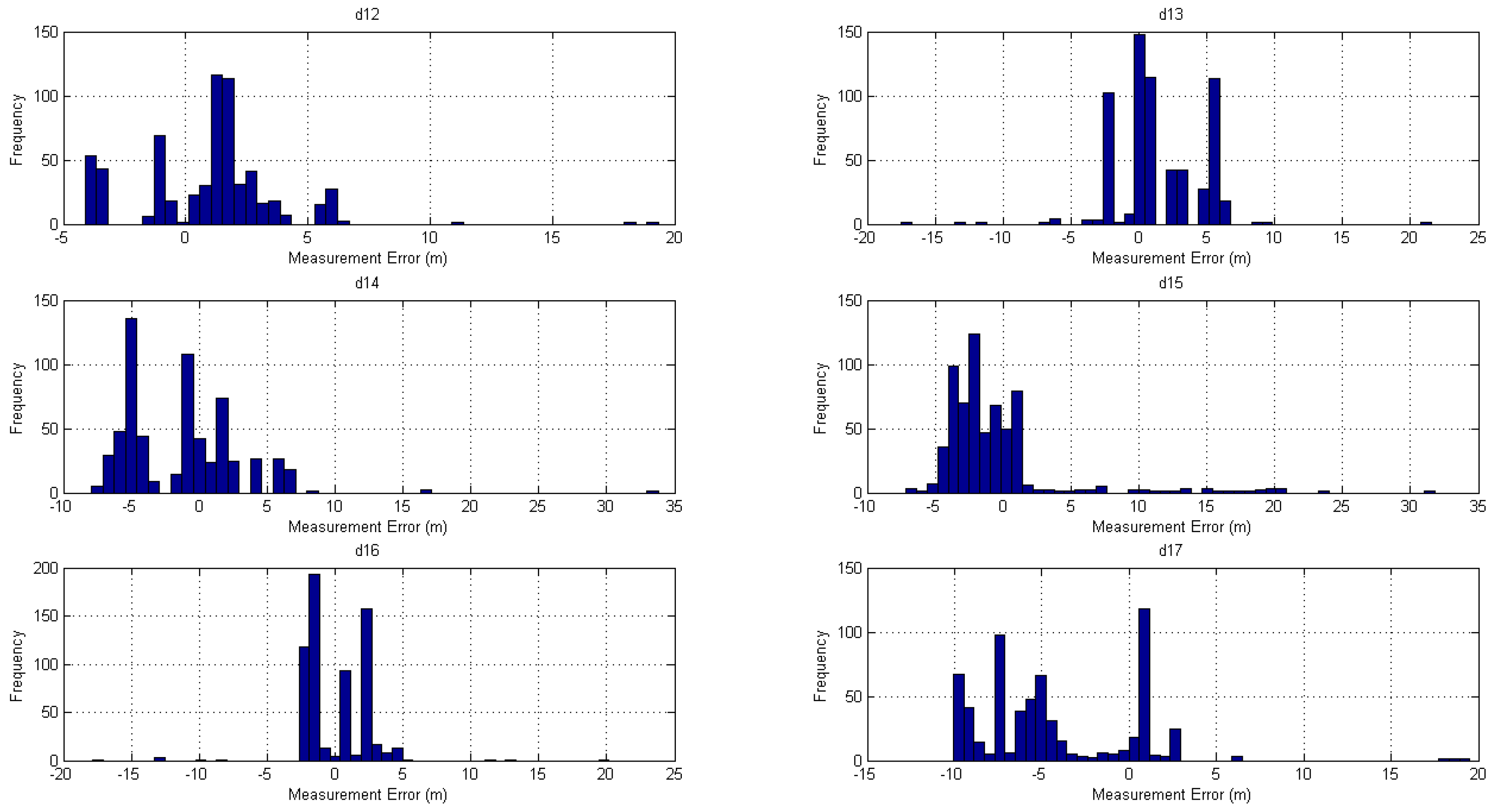
The experimental measurement errors contained a mix of the error conditions studied in the simulations. The CFFSLS algorithm had a better performance in the RMSE sense, since total NLoS conditions and non-uniform SNR levels prevailed during the experiments.
Thus, the concept of obtaining useful receiver’s vertical position estimates by the utilization of nuisance parameters in the coplanar transmitters’ setting was proved. However, a comprehensive evaluation of the approach is still needed, by repeating the experiments many times on different days and in several test buildings with different characteristics, in order to meet the recommendations provided in ref. [
33].