An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling
Abstract
:1. Introduction
2. Traffic Modeling
- Reviewing the existing research in road traffic flow modeling
- Defining the literature gaps for us to address within this work
2.1. Traffic Modeling and Its Benefits
2.2. Traffic Modeling Approaches
- Continuum models treat the traffic flows as fluid streams where vehicles can be represented through average values and the discrete nature of the system or its individual components can be discarded. This category of models began with the first order (time and space derivatives are the order of one) LWR model [14,15] and then extended into higher order models thereafter. The common equation for all these models is the fundamental law of conservation that governs the traffic flow, speed, and density relationship. The LWR model, which was developed by Lighthill and Whitham, and Richards independently, is a continuous macroscopic representation of traffic variables. The LWR model was derived from the fluid mathematical field and conservation law theory and provides a description of the traffic flow by using the fluid dynamic differential equation:where represents the numbers of lanes in position x; represents the density per lane per kilometer at location x and time t; q is the flow per hour at location x and time t. In the LWR model, the speed and/or flow rate are considered as a function of density, which consists of the following equations:where and are respectively the maximal speed and the maximal density of a road.There is a basic assumption made about the LWR model of the dependence of the velocity on density alone. The main drawback of this dependency is that the model assumed the vehicle’s velocity is always in equilibrium, i.e., given a particular density, mainly when density tends to zero, the velocity will tend to infinity. Therefore, the model cannot describe observed behavior in light traffic and non-equilibrium traffic such as stop and go. On the other hand, the model does not deal with external conditions such as road conditions or vehicle behavior in front.
- A cellular automaton (CA) [16] is a simple, but powerful discrete microscopic model that is able to simulate many complex systems. In CA-models, the road traffic flow systems require a discretization in both time and space; time is discretized into time steps of equal duration, and the road is discretized into cells of equal size that are chosen sufficiently large such that a vehicle can drive at a velocity equal to one move to the next downstream cell during one time step. Each cell can either be empty or contain a vehicle.The brake-light Nagel–Schreckenberg (BL-NaSch) model [17,18] was proposed to represent a more complete description of the empirical observed phenomena in highway traffic using the cellular automaton. The BL-NaSchmodel combines velocity anticipation and a slow-to-start rule into the Nagel–Schreckenberg (NaSh) model [19]. In addition, a dynamical long-range interaction was introduced: drivers react to the braking of the leading vehicle indicated by the brake light. Therefore, the BL-NaSch model is considered as an extension of cellular automaton where the velocity and position of every car depend on the cars ahead. However, an important drawback of the BL-NaSch model is the computational requirements and the related costs and complexities, especially for large-scale road networks.
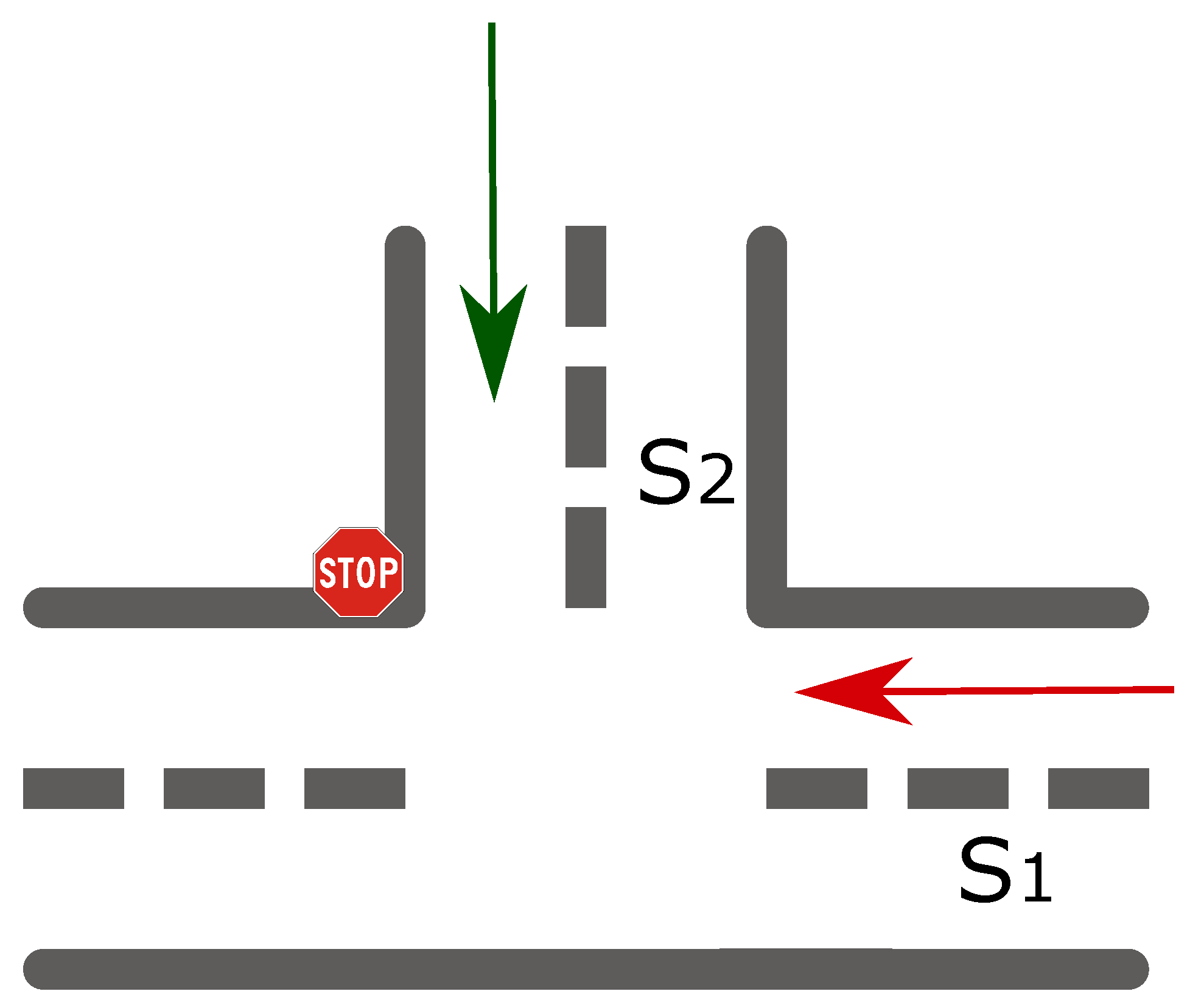
- The cell transmission model (CTM) was developed by Daganzo [20]. It was proposed for modeling the dynamic behavior of road traffic at the mesoscopic level. It adopts a discrete approach to predict traffic evolution in time and space. It consists of transforming the differential equations of the hydrodynamic model LWR [14,15] into simple differential equations. The CTMmodel divides the road network into small homogeneous and interconnected segments (called cells) and assumes piecewise linear relationships between flow and density in each cell. Hence, this model is able to describe and accurately capture the movement of propagation phenomena such as bottlenecks and the formation of shock waves in the traffic networks.Daganzo [20] showed that if the relationship between the traffic flow of vehicles (q) and the density (k) is of a triangular shape, then for a density k such that ( with the maximum density of a road), the flow is expressed as:where V,, W, and are constants designating, respectively, the free speed, maximum speed, the speed of propagation, and maximum density.CTM reveals several notable advantages at the mesoscopic level. The model is relatively simple and accurate enough to plan detailed analyses. Several studies have shown that the model enhances the realism in the representation of traffic for a variety of applications. However, several limitations of CTM must be overcome to meet the more complex needs of operational analysis.For example, the model in its original form requires the network to be divided into cells having a length corresponding to a clock tick (increment) of the simulation. This limitation may not be appropriate for large-scale networks because of possible geometric restrictions or inconsistencies with the division of network links in the cells and also the additional memory requirements by dividing the network into a large number of small cells. This limitation can lead to inefficient modeling of large-scale networks especially when combinations of small cells and various types of installations are used, such as highways and intersections of roads in the city.The original form of CTM [20,21] had a limited scope in the application to realistic networks, such as networks with traffic control devices (with traffic lights and intersections controlled, toll stations, etc.) that were either omitted or inadequately treated in the model.To our knowledge, most of the traffic models (including the aforementioned models) are performed with turning movement counts at intersections as a static input [22]. The fact is, however, that the real-time turning movement proportions are an important requirement for improving the road traffic modeling and increasing its relevance and efficiency. Turning movement counts are time-varying proportions that represent the intersection pattern during peak hours, morning middays and evenings, etc. Additionally, turning movement counts depend on the locations; at some locations, the traffic volume and then the turning movement may be higher than others, which leads to the guiding idea behind the contribution, in this article, which is that omitting modeling turning movement counts significantly decreases the validity of the real-world traffic modeling and its accuracy- and efficiency-related features.
3. Related Work
- Its inapplicability to medium and large scales as the error involving the random assignments will increase as the number of lanes increases;
- Its inability to be used in the cases where information of turning movement counts does not exist;
- The expensiveness of fully providing every intersection with sensors.
4. Our Traffic Prediction System
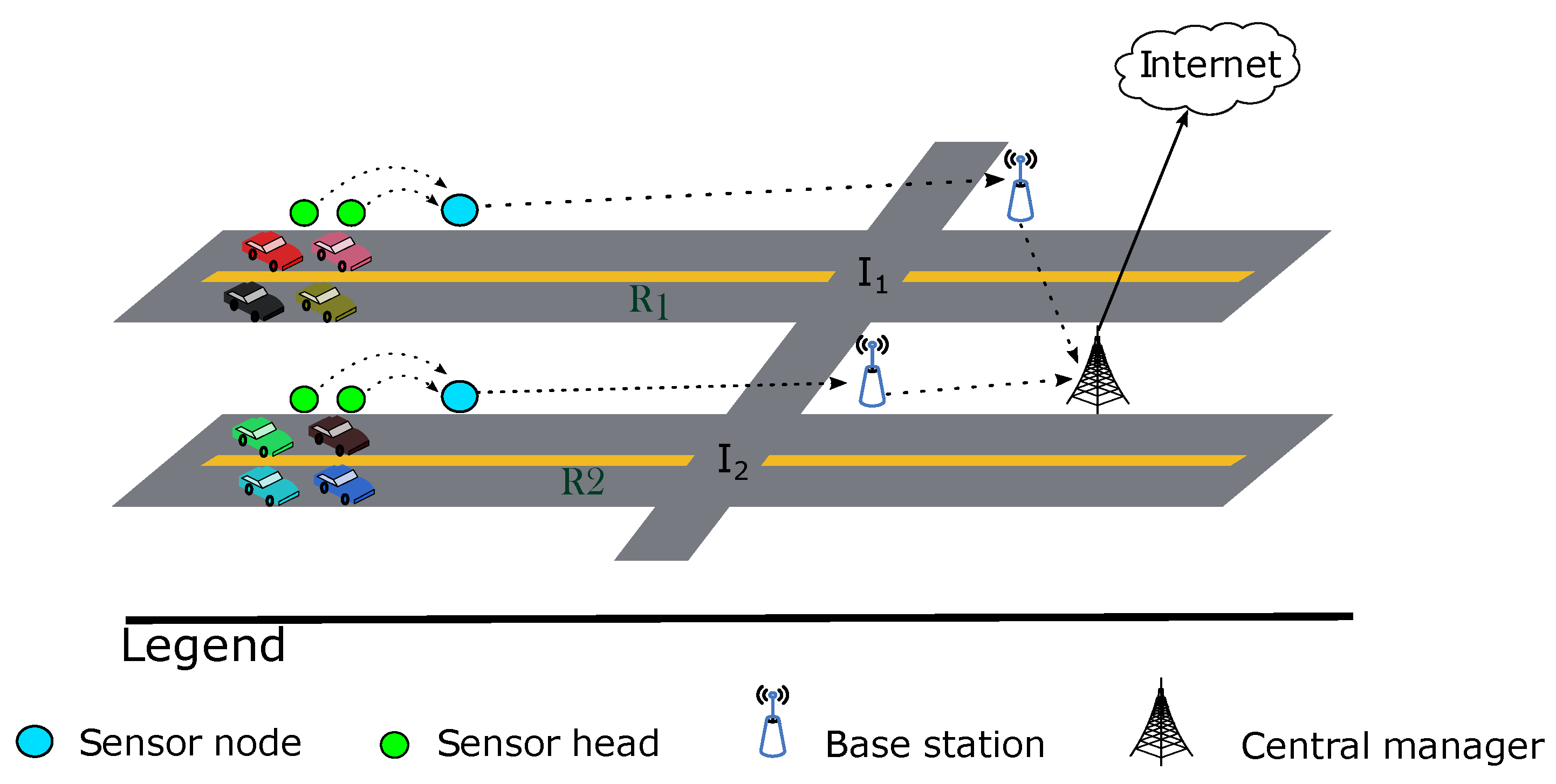
4.1. Overview
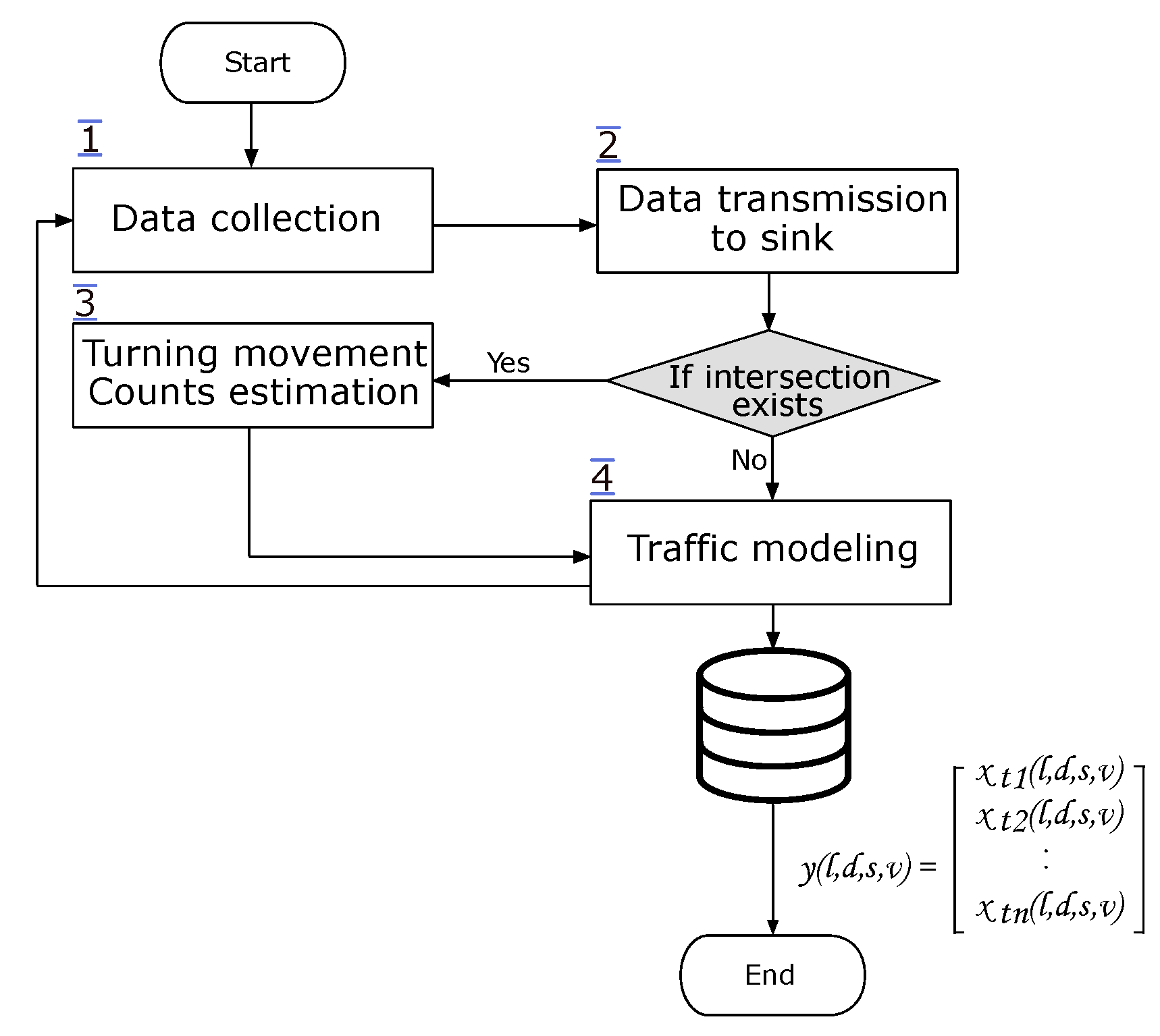
4.2. Detailed System Workflow
4.3. Generalized Nondeterministic Batch Petri Nets Modeling
- (1)
- The so-called untimed transitions. These non-deterministic time-based transitions are introduced in order to model operations that depend on external conditions (i.e., other places). Thus, uncontrollable events that are not by any means assigned to a fixed time interval can be included in our model (e.g., the case at intersections where the give way rule to vehicles of the immediate right has to be respected);
- (2)
- For every batch place, the total number of segments within it, as a new feature to its characteristic function. The purpose of adding this feature is to provide more precision about the geographical location where road traffic flow change takes places;
- (3)
- An estimation of the turning movement counts at intersections to make the model more relevant to the real behavior of vehicles.
- 1.
- P is a finite non-empty set of places
- 2.
- and are respectively the backward and forward incidence matrices.
- 3.
- T is a finite non-empty set of transitions that are divided into timed (), untimed (), and batch () transitions, .
- 4.
- C is a “characteristic function” that associates with every batch place a five-uplet () where , , , , and are respectively the speed, the maximum density, the length, the maximum flow, and the total number of segments of the batch place.
- 5.
- f: matches a non-negative number to every transition as follows:
- -
- if , then is expressed in time units and represents the firing delay associated with the timed transition;
- -
- if , then is expressed in entities/time units and denotes the maximal firing flow associated with the batch transition and can be estimated using statistical models in the case of multiple outputs.
- 6.
- identifies the priority of a transition according to the output flow of a place, . It is a function that determines the priority of transition t and applies only for transitions that are simultaneously active.
- 7.
- E is a set of events.
- : the length of the batch;
- : its density;
- : its head position;
- : its speed.
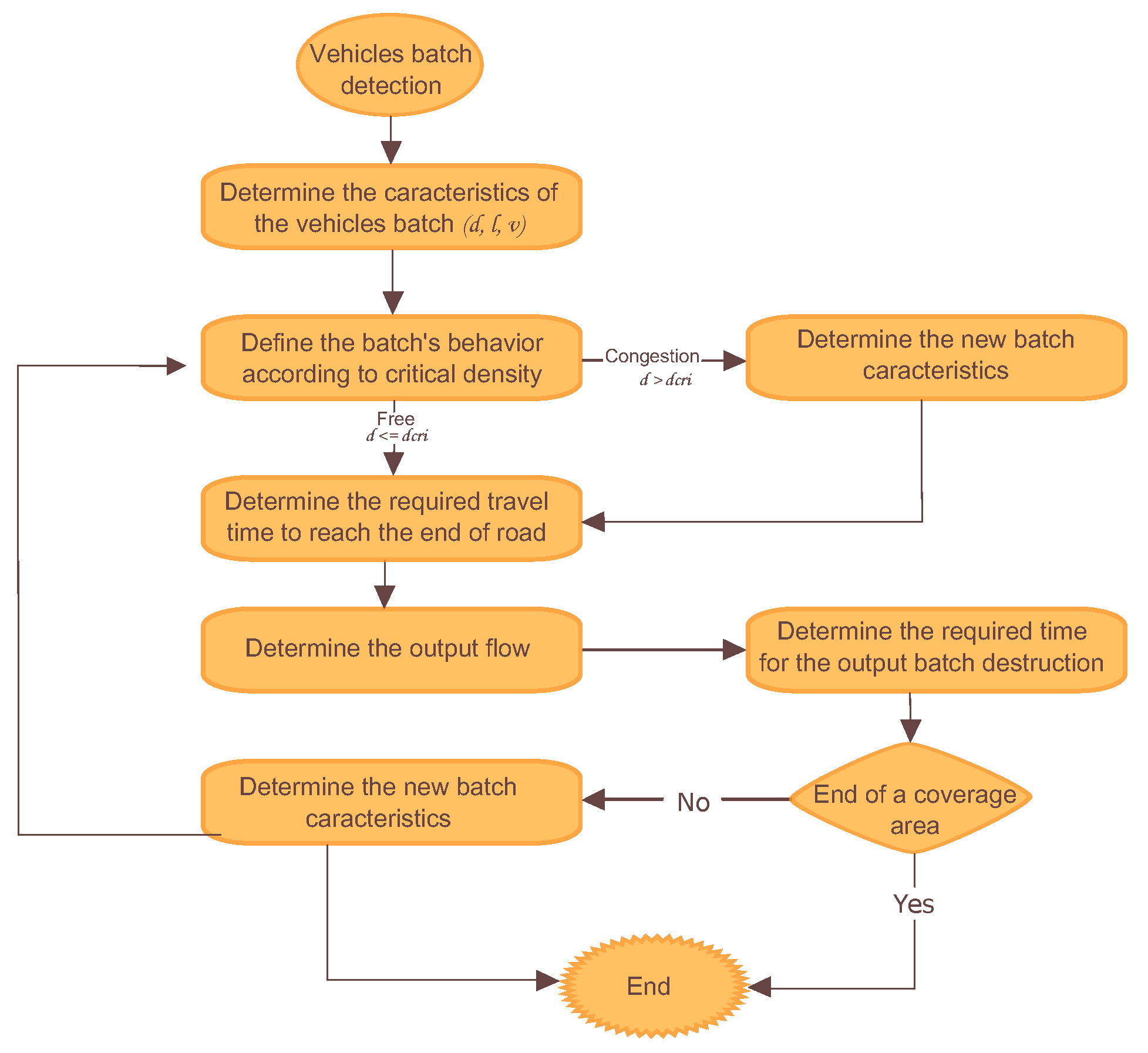
- Step 1:
- Determining the batch’s behavior according to the critical density.When the density of the vehicle batch is greater than the critical density of the road traveled, the controllable batch is congested. Whereas the opposite is also true; when the density of the vehicle batch is lower than the critical density of the road traveled, therefore, the controllable batch is free.
- Step 2:
- Determining the new batch’s characteristics.In the case of traffic congestion, the new characteristics of the batch have to be determined. The speed and density, in this case, vary according to the following:where is the propagation speed of congestion. In the free flow, the batch keeps performing the same behavior; therefore, its characteristics remain the same.
- Step 3:
- Determining the required travel time to reach the end of the road.To estimate the time required to traverse the road, we can divide the length of the road by the velocity of vehicle batch: .
- Step 4:
- Determining the output flow of the batch.Turning movement proportions at intersections is an essential parameter in our model since it allows estimating the output flow of the batch to different outgoing directions.According to the fundamental relation of traffic flow, the flow of a batch () is obtained as the product of the corresponding density (d) and its speed (v). .Taking into consideration the turning movement counts, we can write a dynamical equation describing the output flow of the batch as follows:where is the output flow of the batch from origin i to destination j, and are respectively the density and velocity of the batch at time t, and is the proportion of the traffic flow from origin i to destination j.
- Step 5:
- Determining the required time for the output batch destruction.To find the time, we need to divide the batch’s length by its velocity .
- Step 6:
- Determining the characteristics of the resulting batch.In case the resulting batches are within the coverage zone, we determine the new characteristics of each batch based on the output flow batch proportions, estimated in Step 4, and the characteristics of the associated road. We repeat Steps 1–6 until the coverage area is reached.
- 46 vehicles are turning left (40%).
- 34 vehicles are traveling straight ahead (30%).
- 34 vehicles are turning right (30%).
- 120 vehicles proceeding straight ahead (60%).
- 20 vehicles turning left (10%).
- 60 vehicles turning right (30%).
- .
4.4. Turning Movement Count Models
4.4.1. Random Forest
- Select bootstrap samples from the original dataset.
- Take each of the bootstrap samples, and grow an unpruned classification or regression trees, with the following steps: at each node, randomly select of the p predictors, and choose the best split from among those variables, rather than selecting the best split among all predictors. Bagging can be viewed as a special case of random forests if , the number of predictors.
- Each tree among the trees predicts the new data by aggregating the predictions either through averaging the values for regression or taking the majority votes for classification.
4.4.2. Neural Networks
5. Simulation
5.1. Data Preprocessing
5.2. Data Cleaning
5.3. Data Reorganization
- Time of day: this reflects how the traffic flow changes during the day and the night;
- Day of the week: traffic varies from day to day throughout the week;
- Week of the month: indicates the traffic flow changes from week to week during the month;
- Month of the year: refers to traffic flow changes from month to month throughout the year.
5.4. Missing Data Imputation
- Number of road segments: intersections have the same count of segments.
- Daily road traffic estimates: the estimated number of vehicles that drive through the intersection during 24 h.
- Rush hour and peak hour volume: intersections have the same period of the day during which the highest traffic volumes are observed, and they have mostly the same volumes.
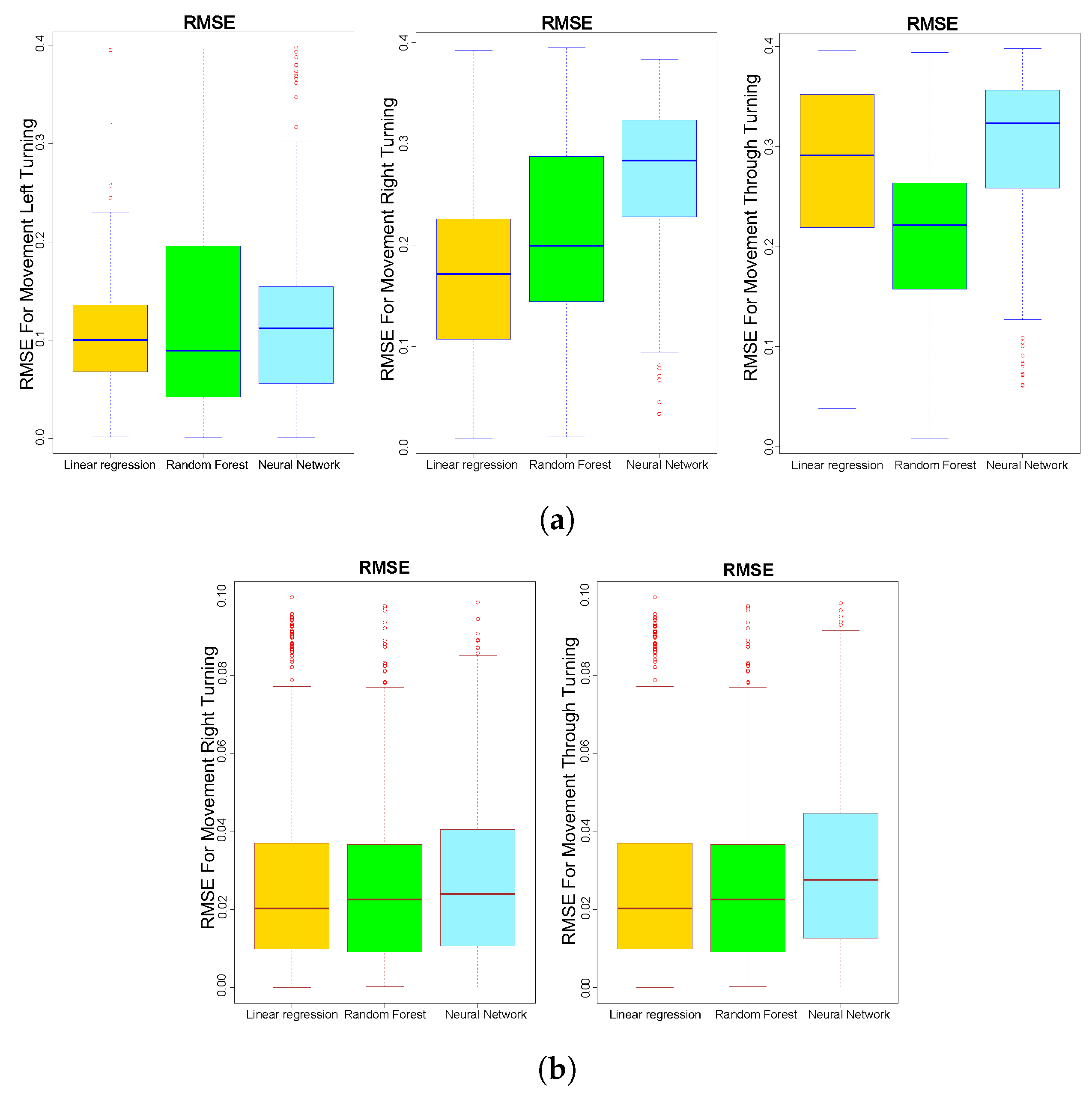
6. Results
- The training set was used for building the model;
- The test set was used for evaluating the model and testing its predictions.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WSN | wireless sensor network |
| RF | random forest |
| WTMS | WSN-based traffic management system |
| controllable batch |
References
- Nations, U. World Cities Report 2016 Urbanization and Development: Emerging Futures; World Cities Report; United Nations Publications: New York, NY, USA, 2016. [Google Scholar]
- Centre for Economics and Business Research (Cebr); INRIX. The Future Economic and Environmental Costs of Gridlock in 2030: An Assessment of the Direct and Indirect Economic and Environmental Costs of Idling in Road Traffic Congestion to Households in the UK, France, Germany and the USA; Cebr: London, UK, 2014; p. 67. [Google Scholar]
- Rad, T.G.; Sadeghi-Niaraki, A.; Abbasi, A.; Choi, S.M. A methodological framework for assessment of ubiquitous cities using ANP and DEMATEL methods. Sustain. Cities Soc. 2018, 37, 608–618. [Google Scholar] [CrossRef]
- Randhawa, A.; Kumar, A. Exploring sustainability of smart development initiatives in India. Int. J. Sustain. Built Environ. 2017, 6, 701–710. [Google Scholar] [CrossRef]
- Pardini, K.; Rodrigues, J.J.P.C.; Kozlov, S.A.; Kumar, N.; Furtado, V. IoT-Based Solid Waste Management Solutions: A Survey. J. Sens. Actuator Netw. 2019, 8, 5. [Google Scholar] [CrossRef]
- Wieringa, J.; Kannan, P.; Ma, X.; Reutterer, T.; Risselada, H.; Skiera, B. Data analytics in a privacy-concerned world. J. Bus. Res. 2019. [Google Scholar] [CrossRef]
- Goodman, M. Future Crimes: Inside The Digital Underground and the Battle For Our Connected World; Transworld: London, UK, 2015. [Google Scholar]
- Ballard, C.; Compert, C.; Jesionowski, T.; Milman, I.; Plants, B.; Rosen, B.; Smith, H.; Redbooks, I. Information Governance Principles and Practices for a Big Data Landscape; IBM Redbooks: Armonk, NY, USA, 2014. [Google Scholar]
- Haman, I.T.; Galland, S.; Claude, J. Towards an Multilevel Agent-based Model for Traffic Simulation Towards an Multilevel Agent-based Model for Traffic Simulation. Procedia Comput. Sci. 2017, 109, 887–892. [Google Scholar] [CrossRef]
- Ngoduy, D. Commun Nonlinear Sci Numer Simulat Instability of cooperative adaptive cruise control traffic flow: A macroscopic approach. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2838–2851. [Google Scholar] [CrossRef]
- Li, Y.; Sun, D. Microscopic car-following model for the traffic flow: The state of the art. J. Control. Theory Appl. 2012, 10, 133–143. [Google Scholar] [CrossRef]
- Li, K.; Ioannou, P. Modeling of Traffic Flow of Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2004, 5, 99–113. [Google Scholar] [CrossRef]
- Jamshidnejad, A.; Papamichail, I.; Papageorgiou, M.; Schutter, B.D. A mesoscopic integrated urban traffic flow-emission model. Transp. Res. Part C 2017, 75, 45–83. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On Kinematic Waves. II. A Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. A Math. Phys. Eng. Sci. 1955, 229, 317–345. [Google Scholar] [CrossRef]
- Richards, P.I. Shock Waves on the Highway; Technical Operations, Inc.: Arlington, MA, USA, 1956; pp. 42–51. [Google Scholar]
- Tonguz, O.K.; Viriyasitavat, W. Modeling Urban Traffic: A Cellular Automata Approach. IEEE Commun. Mag. 2009, 47, 142–150. [Google Scholar] [CrossRef]
- Knospe, W.; Santen, L.; Schadschneider, A.; Schreckenberg, M. Towards a realistic microscopic description of highway traffic. Int. J. Mod. Phys. C 2000, 21, 1311–1327. [Google Scholar] [CrossRef]
- Pascale, A.; Nicoli, M.; Deflorio, F.; Dalla Chiara, B.; Spagnolini, U. Wireless sensor networks for traffic management and road safety. IET Intell. Transp. Syst. 2012, 6, 67. [Google Scholar] [CrossRef]
- Nagel, K.; Schreckenberg, M. A cellular automaton model for freeway traffic. J. Phys. I 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model, part II: Network traffic. Transp. Res. Part B Methodol. 1995, 29, 79–93. [Google Scholar] [CrossRef]
- Wang, P.; Jones, L.S.; Yang, Q. A novel conditional cell transmission model for oversaturated arterials. J. Cent. South Univ. 2012, 19, 1466–1474. [Google Scholar] [CrossRef]
- Riouali, Y.; Benhlima, L.; Bah, S. Petri net extension for traffic road modelling. Int. J. Sci. Eng. Res. 2016, 7, 7–12. [Google Scholar]
- Ghods, A.H.; Fu, L. Real-time estimation of turning movement counts at signalized intersections using signal phase information. Transp. Res. Part C 2014, 47, 128–138. [Google Scholar] [CrossRef]
- Lan, C.J.; Davis, G.A. Real-time estimation of turning movement proportions from partial counts on urban networks. Transp. Res. Part C Emerg. Technol. 1999, 7, 305–327. [Google Scholar] [CrossRef]
- Turning, I.; Models, M. Estimation of Intersection Turning Movements from Approach Counts. ITE J. 1988, 58, 41–46. [Google Scholar]
- Chen, A.; Chootinan, P.; Ryu, S.; Lee, M.; Recker, W. An intersection turning movement estimation procedure based on path flow estimator. J. Adv. Transp. 2012, 46, 161–176. [Google Scholar] [CrossRef]
- Shirazi, M.S.; Morris, B.T. Vision-Based Turning Movement Monitoring: Count, Speed & Waiting Time Estimation. IEEE Intell. Transp. Syst. Mag. 2016, 8, 23–34. [Google Scholar]
- Razouki, S.S.; Yousif, S. A new turning movement algorithm for special road junctions. SCIREA J. Agric. 2016, 1, 35–49. [Google Scholar]
- Lee, S.; Wong, S.C.; Chun, C.; Pang, C.; Choi, K. Real-Time Estimation of Lane-to-Lane Turning Flows at Isolated Signalized Junctions. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1549–1558. [Google Scholar] [CrossRef]
- Jiao, P.; Liu, M.; Guo, J.; Sun, T. Bi-Bayesian Combined Model for Two-Step Prediction of Dynamic Turning Movement Proportions at Intersections. Adv. Mech. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Gaddouri, R.; Brenner, L.; Demongodin, I. Extension of Batches Petri Nets by Bi-parts batch places. In Proceedings of the 1st International Workshop on Petri Nets for Adaptive Discrete-Event Control Systems co-located with 35th International Conference on Application and Theory of Petri Nets and Concurrency (Petri Nets 2014), Tunis, Tunisia, 24 June 2014. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. Forest 2001, 23. [Google Scholar]
- Senthilkumar, M. 5 - Use of artificial neural networks (ANNs) in colour measurement. In Colour Measurement; Gulrajani, M., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Sawston, UK, 2010; pp. 125–146. [Google Scholar]
- Tutak, M.; Brodny, J. Predicting Methane Concentration in Longwall Regions Using Artificial Neural Networks. Int. J. Environ. Res. Public Health 2019, 16, 1406. [Google Scholar] [CrossRef]
- Abdi-Khanghah, M.; Bemani, A.; Naserzadeh, Z.; Zhang, Z. Prediction of solubility of N-alkanes in supercritical CO2 using RBF-ANN and MLP-ANN. J. CO2 Util. 2018, 25, 108–119. [Google Scholar] [CrossRef]
- Ebrahimpour, R.; Nikoo, H.; Masoudnia, S.; Yousefi, M.R.; Ghaemi, M.S. Mixture of MLP-experts for trend forecasting of time series: A case study of the Tehran stock exchange. Int. J. Forecast. 2011, 27, 804–816. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Neurocomputing: Foundations of Research; Chapter Learning R; MIT Press: Cambridge, MA, USA, 1988; pp. 696–699. [Google Scholar]
- Institute of Transportation Engineers; Wolshon, B.; Pande, A. Traffic Engineering Handbook; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Sivakumar, B.; Ghosn, M.; Moses, F. Protocols for Collecting and Using Traffic Data in Bridge Design; NCHRP Report; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar]
- Ishwaran, H.; Kogalur, U. randomForestSRC: Random Forests for Survival, Regression and Classification (RF-SRC). 2016. Available online: https://kogalur.github.io/randomForestSRC/theory.html (accessed on 26 August 2019).
- Matausek, M.R.; Miljkovic, D.M.; Jeftenic, B.I. Nonlinear multi-input-multi-output neural network control of DC motor drive with field weakening. IEEE Trans. Ind. Electron. 1998, 45, 185–187. [Google Scholar] [CrossRef]
- Günther, F.; Fritsch, S. Neuralnet: Training of Neural Networks. R J. 2010, 2, 30. [Google Scholar] [CrossRef]
- Kaya Uyanık, G.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef] [Green Version]
- Egoshin, V.; Ivanov, S.; Savvina, N.; Ermolaev, A.; Mamyrbekova, S.; Zhamaliyeva, L.; Grjibovski, A. Correlation and simple regression analysis using R. Hum. Ecol. 2018, 2018, 55–64. [Google Scholar] [CrossRef]
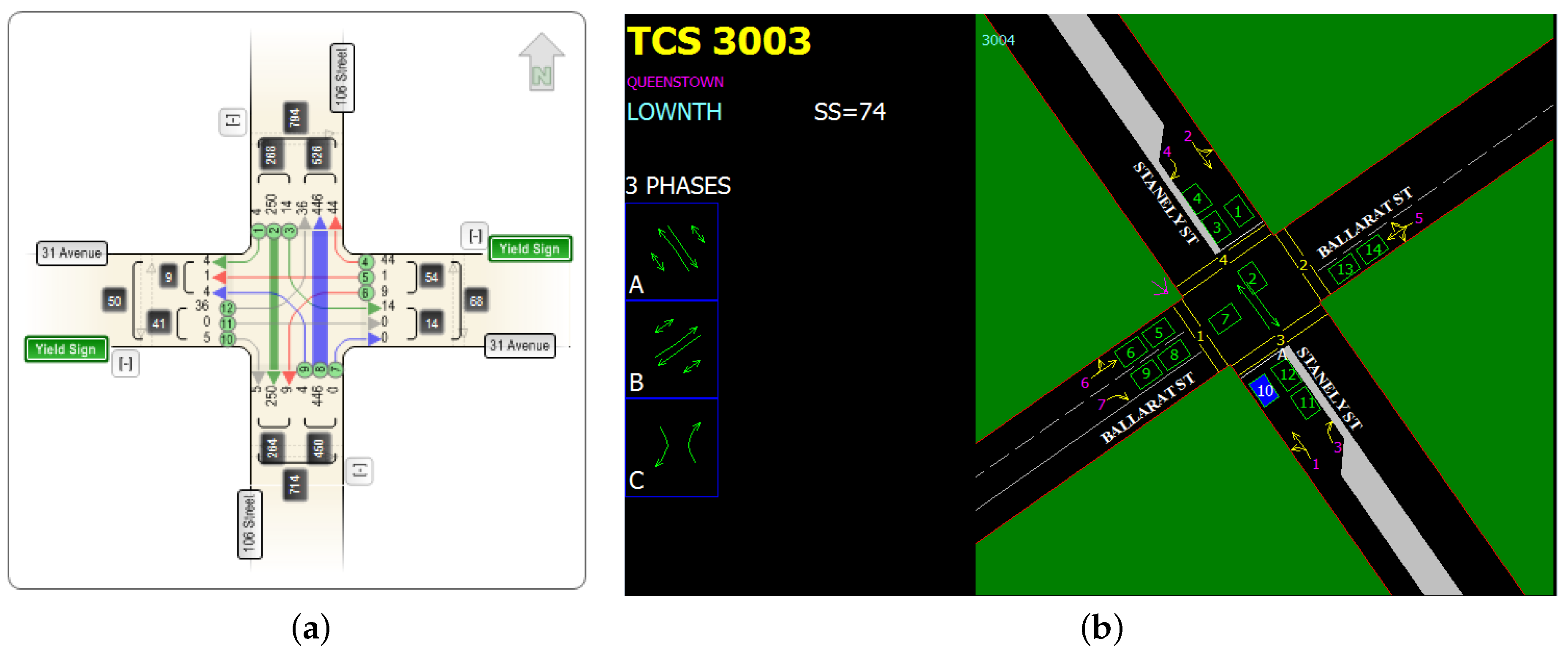
| Section | ||
|---|---|---|
| (km) | 6 | 5 |
| () | 40 | 80 |
| () | 200 | 100 |
| () | 2000 | 2000 |
| Day of Week | Week of Month | Month of Year | ms | ss | pmam | L | T | R | Sum |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 2 | 3 | 7 | 25 | 1 | 2 | 55 | 77 | 134 |
| Percentage Accuracy | Linear Regression | Random Forest | Neural Network |
|---|---|---|---|
| 81%–100% | 35 | 22.7 | 44.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riouali, Y.; Benhlima, L.; Bah, S. An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling. J. Sens. Actuator Netw. 2019, 8, 49. https://doi.org/10.3390/jsan8030049
Riouali Y, Benhlima L, Bah S. An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling. Journal of Sensor and Actuator Networks. 2019; 8(3):49. https://doi.org/10.3390/jsan8030049
Chicago/Turabian StyleRiouali, Youness, Laila Benhlima, and Slimane Bah. 2019. "An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling" Journal of Sensor and Actuator Networks 8, no. 3: 49. https://doi.org/10.3390/jsan8030049
APA StyleRiouali, Y., Benhlima, L., & Bah, S. (2019). An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling. Journal of Sensor and Actuator Networks, 8(3), 49. https://doi.org/10.3390/jsan8030049





