Theoretical Analysis of Interference Cancellation System Utilizing an Orthogonal Matched Filter and Adaptive Array Antenna for MANET
Abstract
:1. Introduction
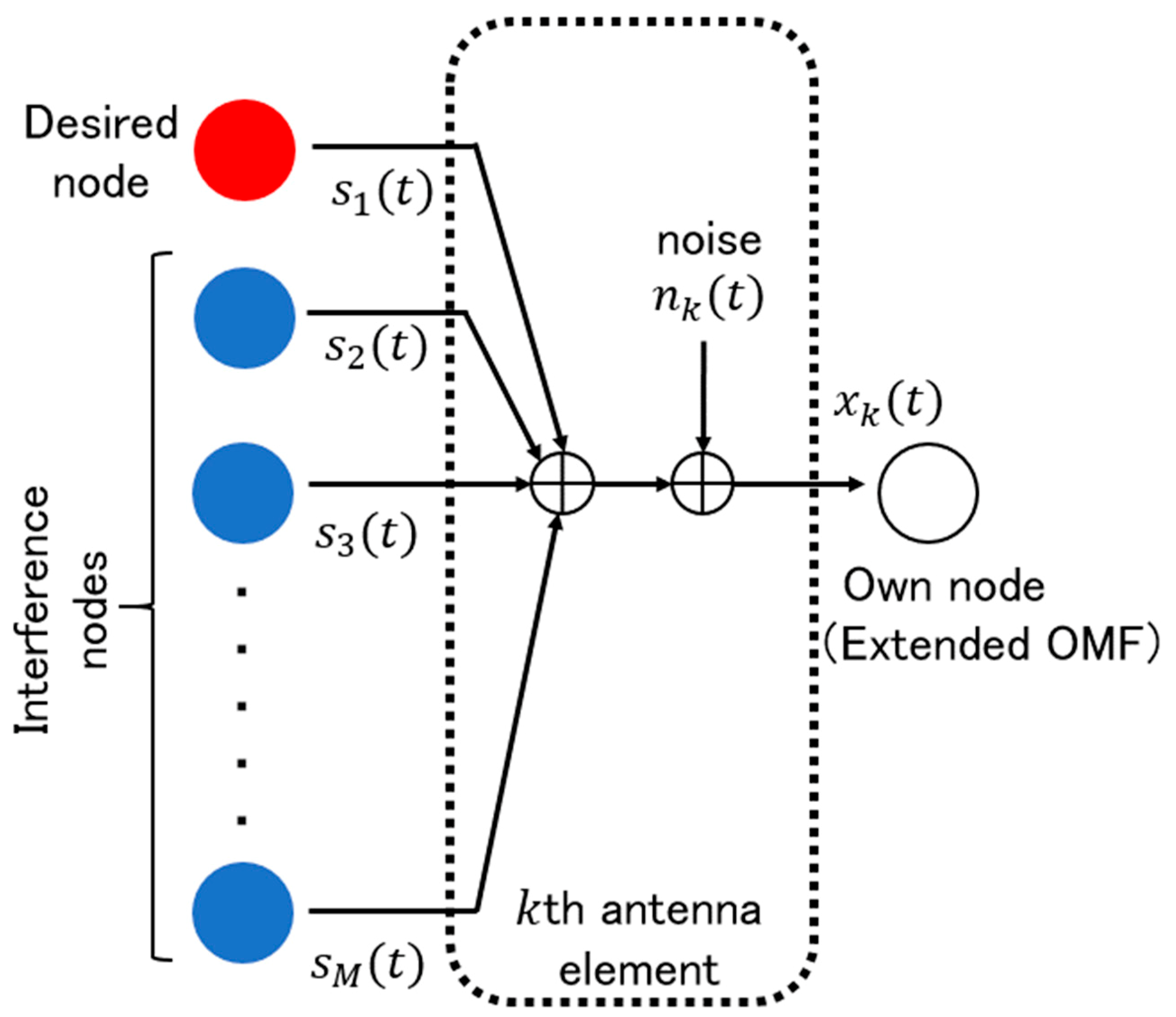
2. System Model
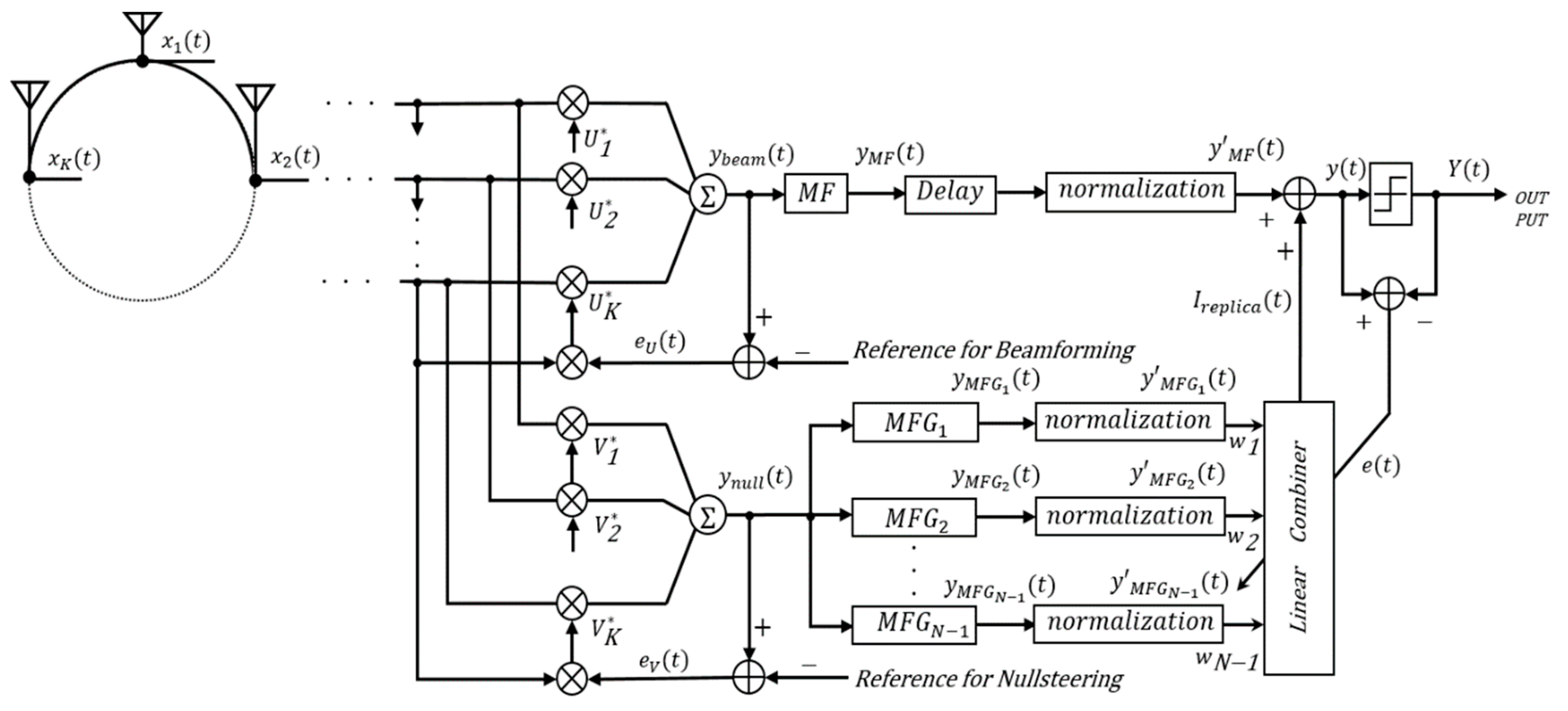
2.1. Structure of EOMF
2.2. Circular Array Antenna
2.3. OMF
2.4. EOMF
3. Theoretical Analysis
3.1. Noise Free and Interference Channel
3.2. Noisy Interference Channel
3.3. Residual Interference Due to Nonoptimal Weight Vector
3.4. Residual Noise Effect
3.5. Optimal Weight Vector in an Interference and AWGN Channel
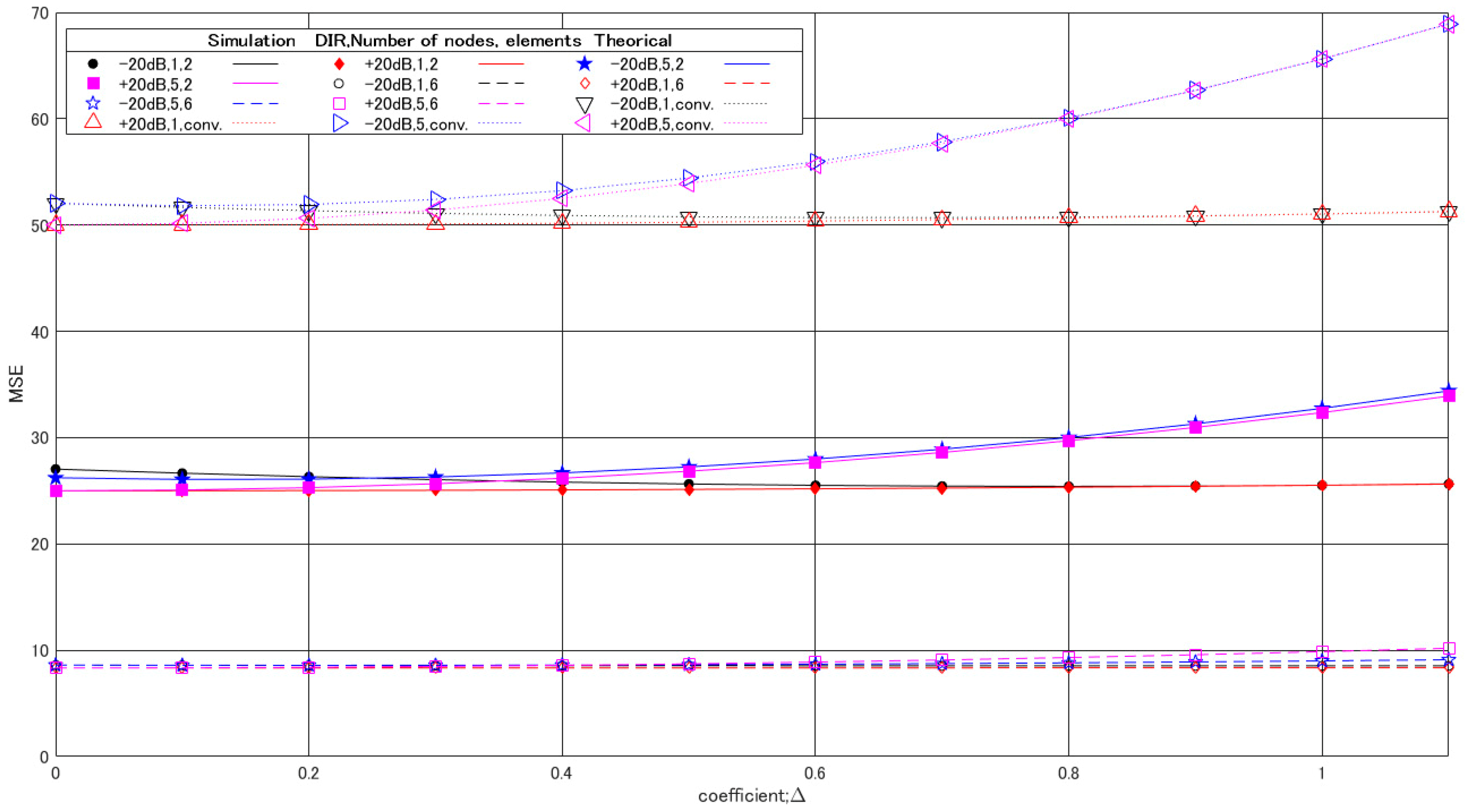
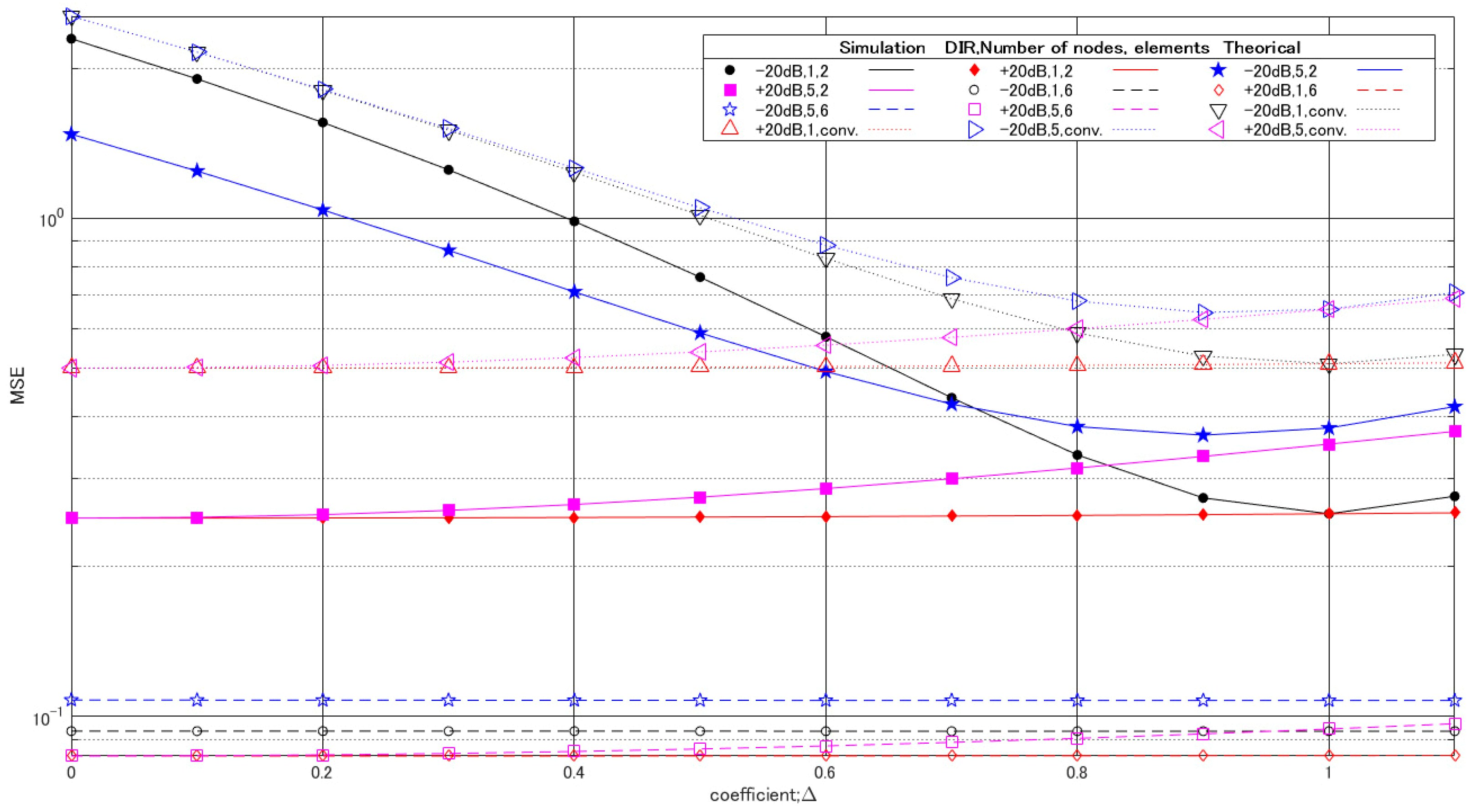
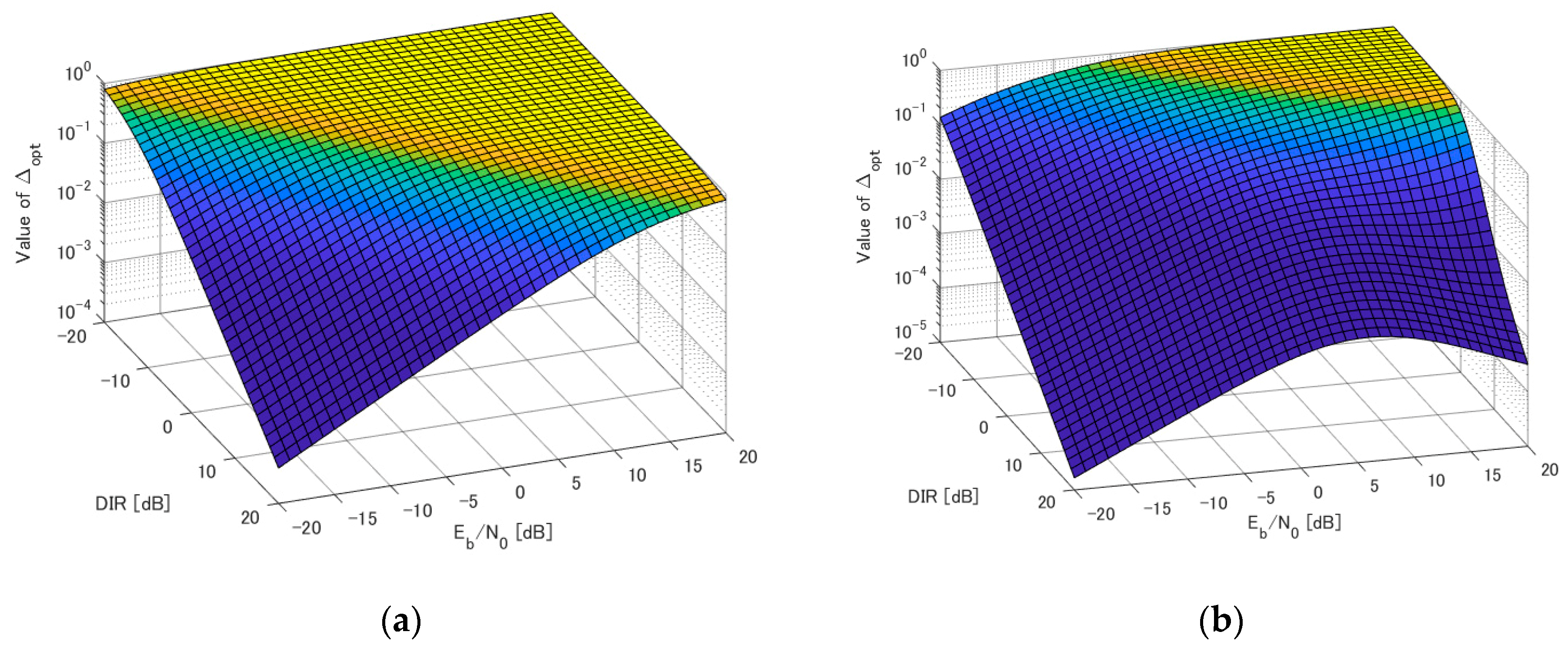
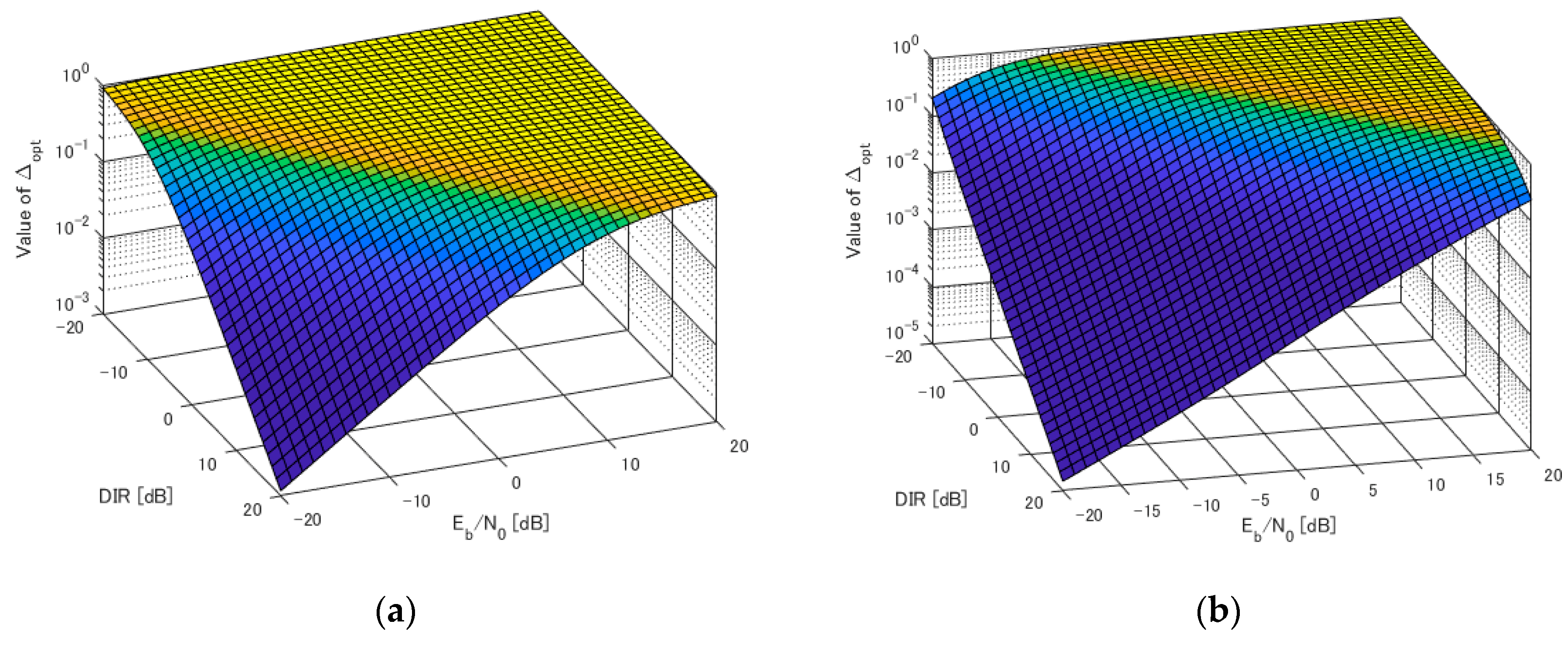
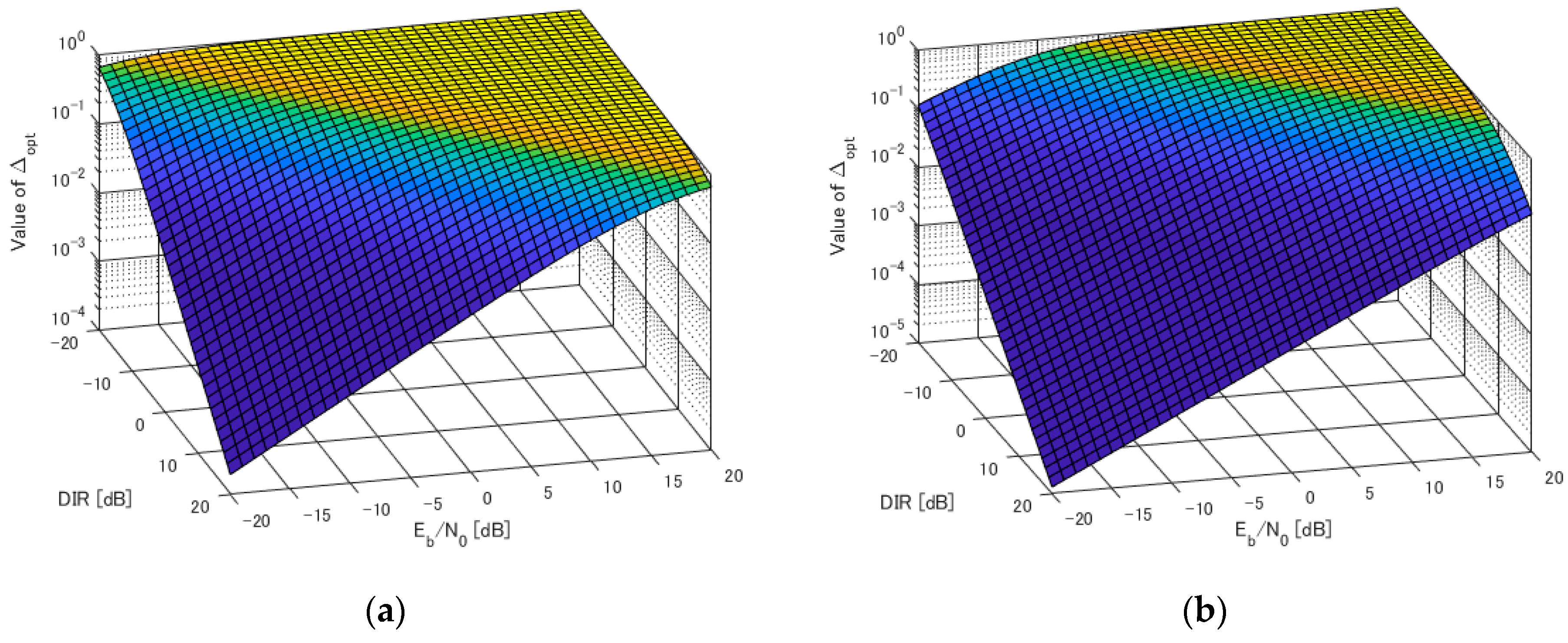
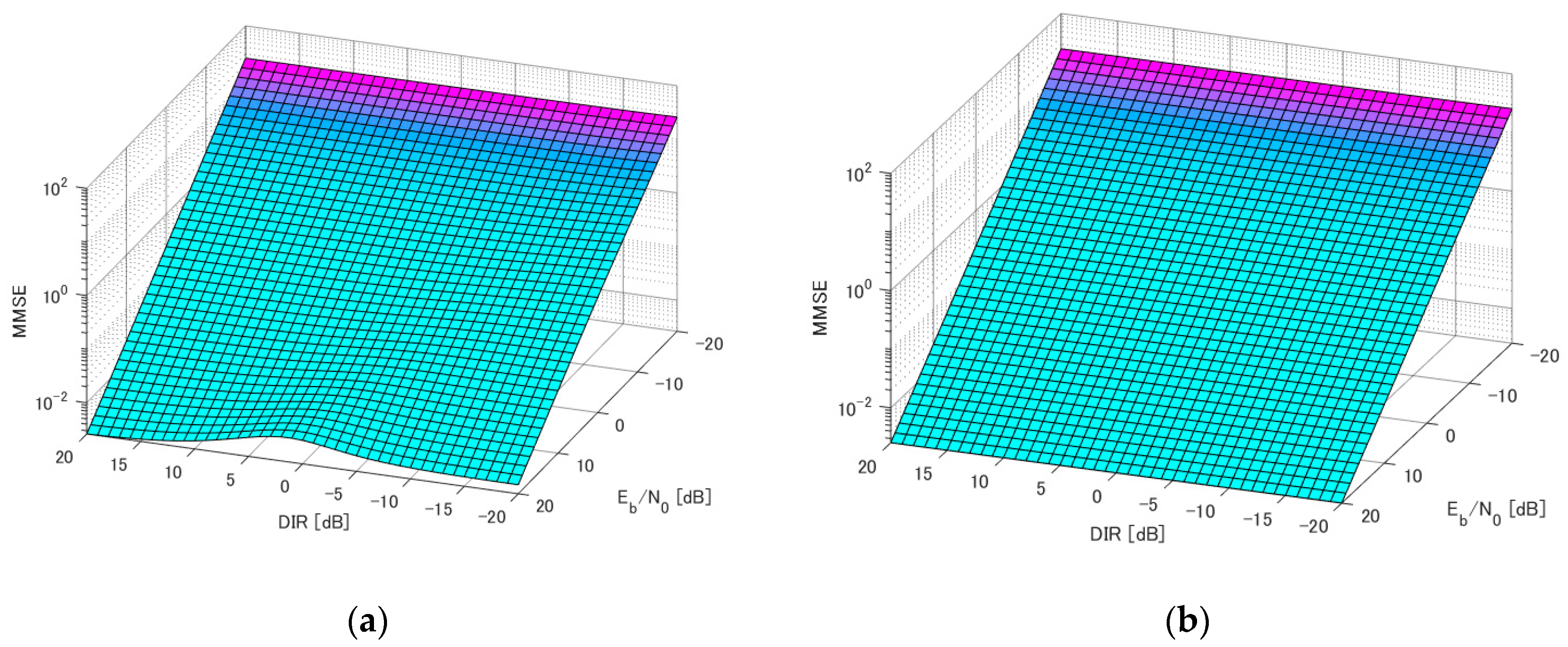
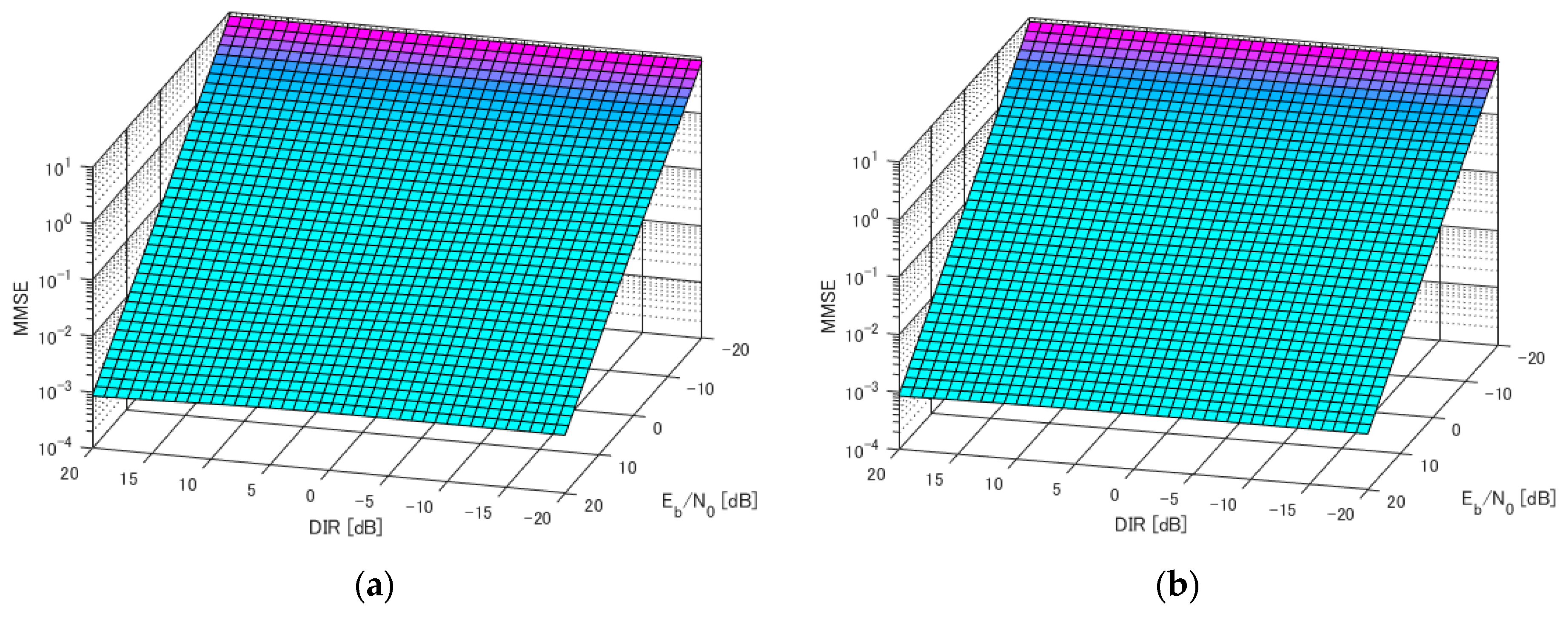
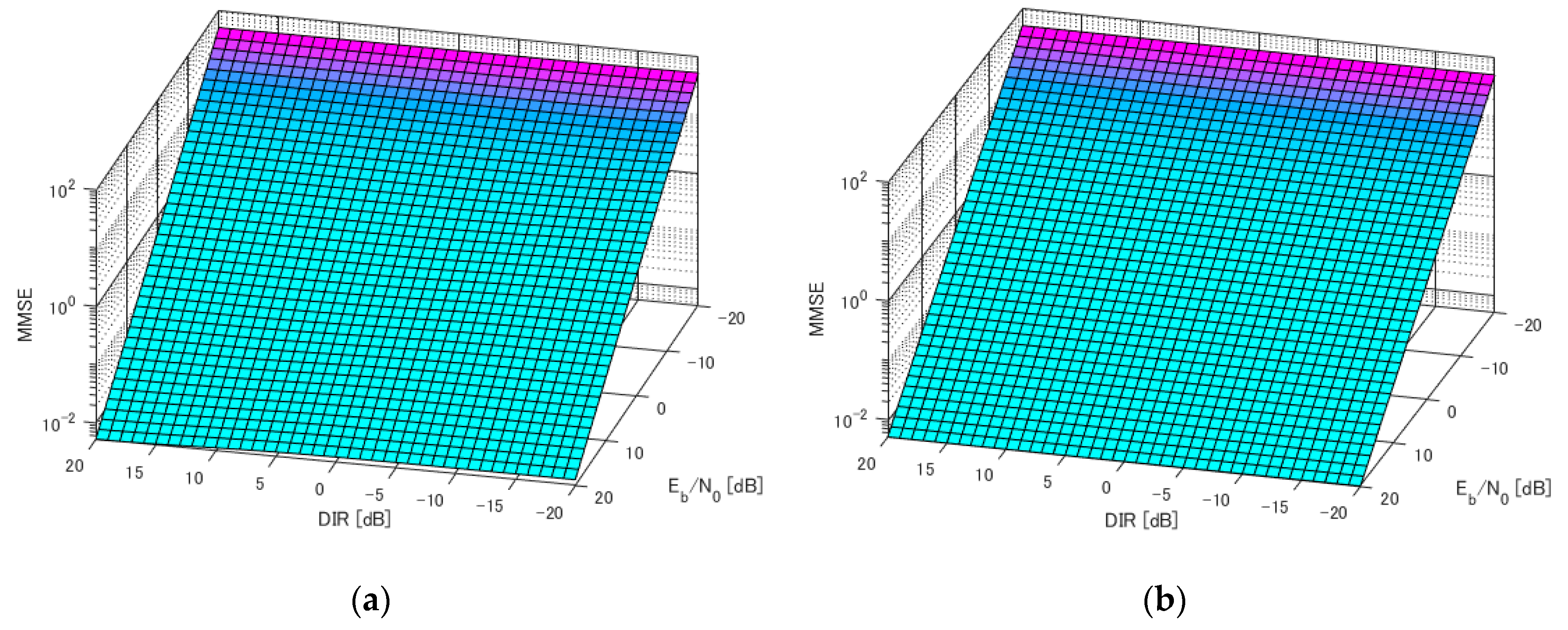
4. Numerical Results
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Alameri, I.A. MANETS and Internet of Things: The Development of a Data Routing Algorithm. Eng. Technol. Appl. Sci. Res. 2018, 8, 2604–2608. [Google Scholar]
- Reina, D.G.; Toral, S.L.; Barrero, F.; Bessis, N.; Asimakopoulou, E. The Role of Ad Hoc Networks in the Internet of Things: A Case Scenario for Smart Environments. In Internet of Things and Inter-Cooperative Computational Technologies for Collective Intelligence; Studies in Computational Intelligence; Bessis, N., Xhafa, F., Varvarigou, D., Hill, R., Li, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 460, pp. 89–113. [Google Scholar]
- Alnumay, W.; Ghosh, U.; Chatterjee, P.A. Trust-Based Predictive Model for Mobile Ad Hoc Network in Internet of Things. Sensors 2019, 19, 1467. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Zhuang, W. Token-Based Adaptive MAC for a Two-Hop Internet-of-Things Enabled MANET. IEEE Internet Things J. 2017, 4, 1739–1753. [Google Scholar] [CrossRef]
- Karlsson, J.; Dooley, L.S.; Pulkkis, G. Secure Routing for MANET Connected Internet of Things Systems. In Proceedings of the 2018 IEEE 6th International Conference on Future Internet of Things and Cloud (FiCloud), Barcelona, Spain, 6–8 August 2018. [Google Scholar]
- Park, J.; Huang, K.; Cho, S.; Kim, D. Mobility-aware spatial interference cancellation for mobile ad hoc networks. In Proceedings of the 2010 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea, 17–19 November 2010. [Google Scholar]
- Huang, K.; Andrews, J.G.; Guo, D.; Heath, R.W.; Berry, R.A. Spatial Interference Cancellation for Multiantenna Mobile Ad Hoc Networks. IEEE Trans. Inf. Theory 2012, 58, 1660–1676. [Google Scholar] [CrossRef] [Green Version]
- Mordachev, V.; Loyka, S. On node density—Outage probability tradeoff in wireless networks. IEEE J. Sel. Areas Commun. 2009, 27, 1120–1131. [Google Scholar] [CrossRef]
- Pinto, P.C.; Win, M.Z. Communication in a Poisson Field of Interferers--Part I: Interference Distribution and Error Probability. IEEE Trans. Wirel. Commun. 2010, 9, 2176–2186. [Google Scholar] [CrossRef]
- Zanella, A.; Zorzi, M. Theoretical Analysis of the Capture Probability in Wireless Systems with Multiple Packet Reception Capabilities. IEEE Trans. Commun. 2012, 60, 1058–1071. [Google Scholar] [CrossRef]
- Babich, F.; Comisso, M. Multi-Packet Communication in Heterogeneous Wireless Networks Adopting Spatial Reuse: Capture Analysis. IEEE Trans. Wirel. Commun. 2013, 12, 5346–5359. [Google Scholar] [CrossRef]
- Kim, C.; Cho, Y. Performance of a wireless MC-CDMA system with an antenna array in a fading channel: Reverse link. IEEE Trans. Commun. 2000, 48, 1257–1261. [Google Scholar]
- Sanada, Y.; Padilla, M.; Araki, K. Performance of adaptive array antenna with multicarrier DS/CDMA in a mobile fading environment. IEICE Trans. Commun. 1998, E81-B, 1392–1399. [Google Scholar]
- Ahn, C.J.; Sasase, I. Code Orthogonalizing Filter Based Adaptive Array Antenna Using Common Correlation Matrix of Time Domain Signals for Multicarrier DS/CDMA Systems. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2002, E85A, 1604–1611. [Google Scholar]
- Sakakibara, S.; Ohno, K.; Itami, M. Performance evaluation of DS-CDMA IVC scheme and CSMA/OFDM IVC scheme. In Proceedings of the 2013 13th International Conference on ITS Telecommunications (ITST), Tampere, Finland, 5–7 November 2013. [Google Scholar]
- Hachisuka, M. Interference Cancellation Using Layered Structure of Orthogonal Matched Filter for Inter-Vehicle Communication and Ranging. Master’s Thesis, Yokohama National University, Yokohama, Japan, 2014. [Google Scholar]
- Kobayashi, T.; Sugimoto, C.; Kohno, R. Interference Cancellation for Intra and Inter UWB Systems Using Modified Hermite Polynomials Based Orthogonal Matched Filter. IEICE Trans. Commun. 2016, E99.B, 569–577. [Google Scholar] [CrossRef]
- Kobayashi, T.; Suzuki, M.; Sugimoto, C.; Kohno, R. Space Temporal Interference Cancellation Using TDL Array Antenna and Waveform Based OMF for IR-UWB Systems. ICT Express 2015, 1, 71–75. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sugimoto, C.; Kohno, R. Theoretical analysis of interference canceler using modified hermite polynomials based orthogonal matched filter for IR-UWB systems in AWGN and interference channel. In Proceedings of the 2017 20th International Symposium on Wireless Personal Multimedia Communications (WPMC), Bali, Indonesia, 17–20 December 2017. [Google Scholar]
- Suzuki, M. Extended Orthogonal Matched Filter into Space and Time Domains for Cancelling Interference in Inter-Vehicle Communication and Radar. Master’s Thesis, Yokohama National University, Yokohama, Japan, 2016. [Google Scholar]
- Kikuma, N. Adaptive Signal Processing with Array Antenna; Science and Technology Publishing Company Inc.: Tokyo, Japan, 1998. (In Japanese) [Google Scholar]
- Masui, K.; Itami, M. Interference reduction in DS/SS inter-vehicle communication using circular array antenna. In Proceedings of the 2008 IEEE International Conference on Vehicular Electronics and Safety, Columbus, OH, USA, 22–24 September 2008. [Google Scholar]
| Parameter | Detail |
|---|---|
| Channel model | AWGN |
| Modulation | BPSK and DSSS |
| Spreading sequence | Gold sequence |
| Spreading factor | 7 |
| Carrier frequency | 760 [MHz] |
| Transmit power of desired node | 1 |
| Number of interference nodes | 1 or 5 |
| Number of antenna elements | 2 or 6 (EOMF case) 1 (Only conventional OMF case [16]) |
| Direction of arrival (desired node) | 0 [degree] |
| Information data length | 10,000 [bits] |
| Number of trials | 10,000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harada, S.; Takabayashi, K.; Kobayashi, T.; Sakakibara, K.; Kohno, R. Theoretical Analysis of Interference Cancellation System Utilizing an Orthogonal Matched Filter and Adaptive Array Antenna for MANET. J. Sens. Actuator Netw. 2019, 8, 48. https://doi.org/10.3390/jsan8030048
Harada S, Takabayashi K, Kobayashi T, Sakakibara K, Kohno R. Theoretical Analysis of Interference Cancellation System Utilizing an Orthogonal Matched Filter and Adaptive Array Antenna for MANET. Journal of Sensor and Actuator Networks. 2019; 8(3):48. https://doi.org/10.3390/jsan8030048
Chicago/Turabian StyleHarada, Shuhei, Kento Takabayashi, Takumi Kobayashi, Katsumi Sakakibara, and Ryuji Kohno. 2019. "Theoretical Analysis of Interference Cancellation System Utilizing an Orthogonal Matched Filter and Adaptive Array Antenna for MANET" Journal of Sensor and Actuator Networks 8, no. 3: 48. https://doi.org/10.3390/jsan8030048
APA StyleHarada, S., Takabayashi, K., Kobayashi, T., Sakakibara, K., & Kohno, R. (2019). Theoretical Analysis of Interference Cancellation System Utilizing an Orthogonal Matched Filter and Adaptive Array Antenna for MANET. Journal of Sensor and Actuator Networks, 8(3), 48. https://doi.org/10.3390/jsan8030048






