A Nonlinear Electromagnetic Energy Harvesting System for Self-Powered Wireless Sensor Nodes
Abstract
1. Introduction
2. Electromagnetic Energy Harvester and Nonlinear Model
2.1. Device Structure
2.2. Harvester Optimization
2.3. Modeling and Simulation
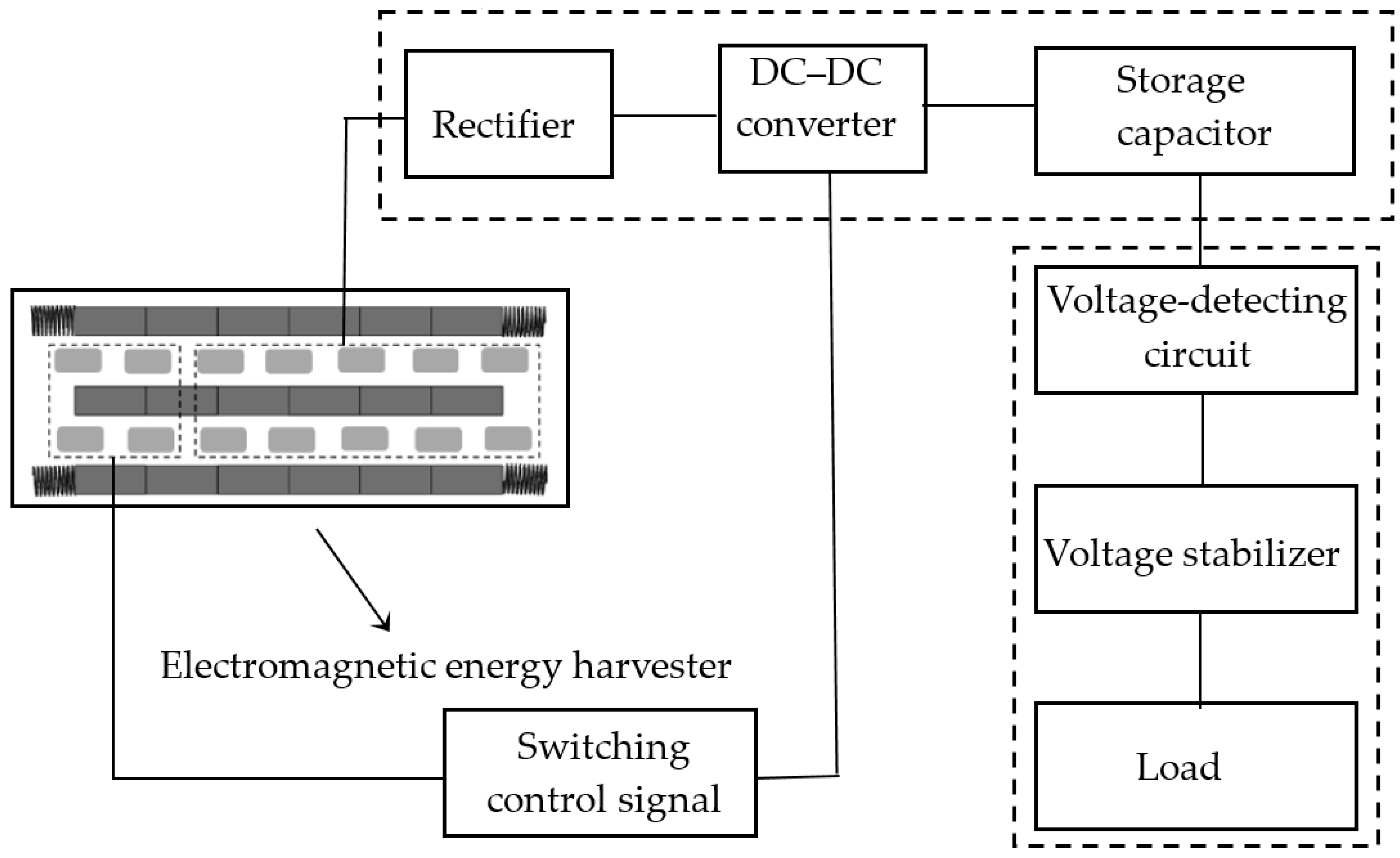
3. Energy Harvesting Circuit
3.1. A Standard Energy-Harvesting Circuit
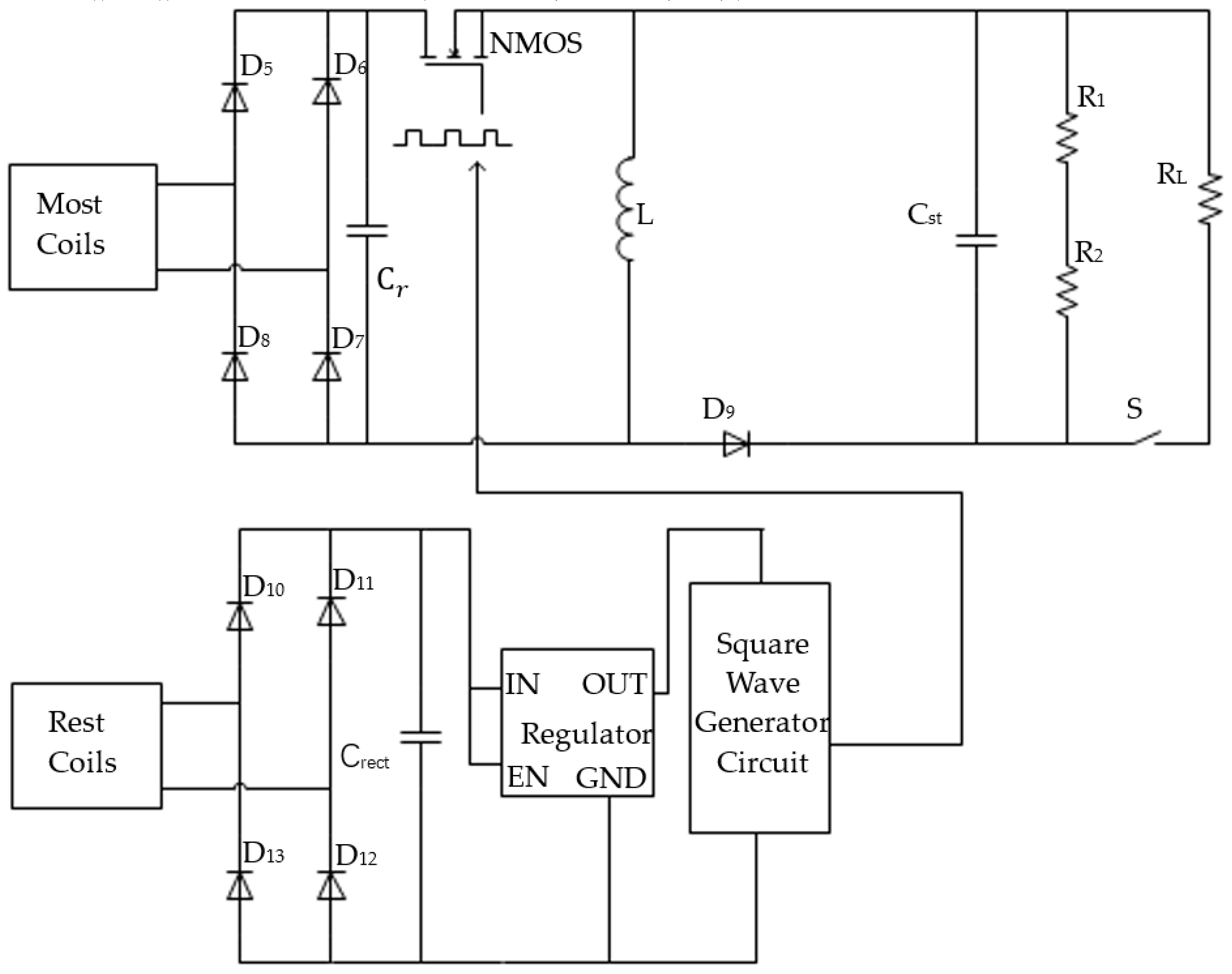
3.2. Proposed Power Management Circuit
3.3. Square-Wave-Generating Circuit
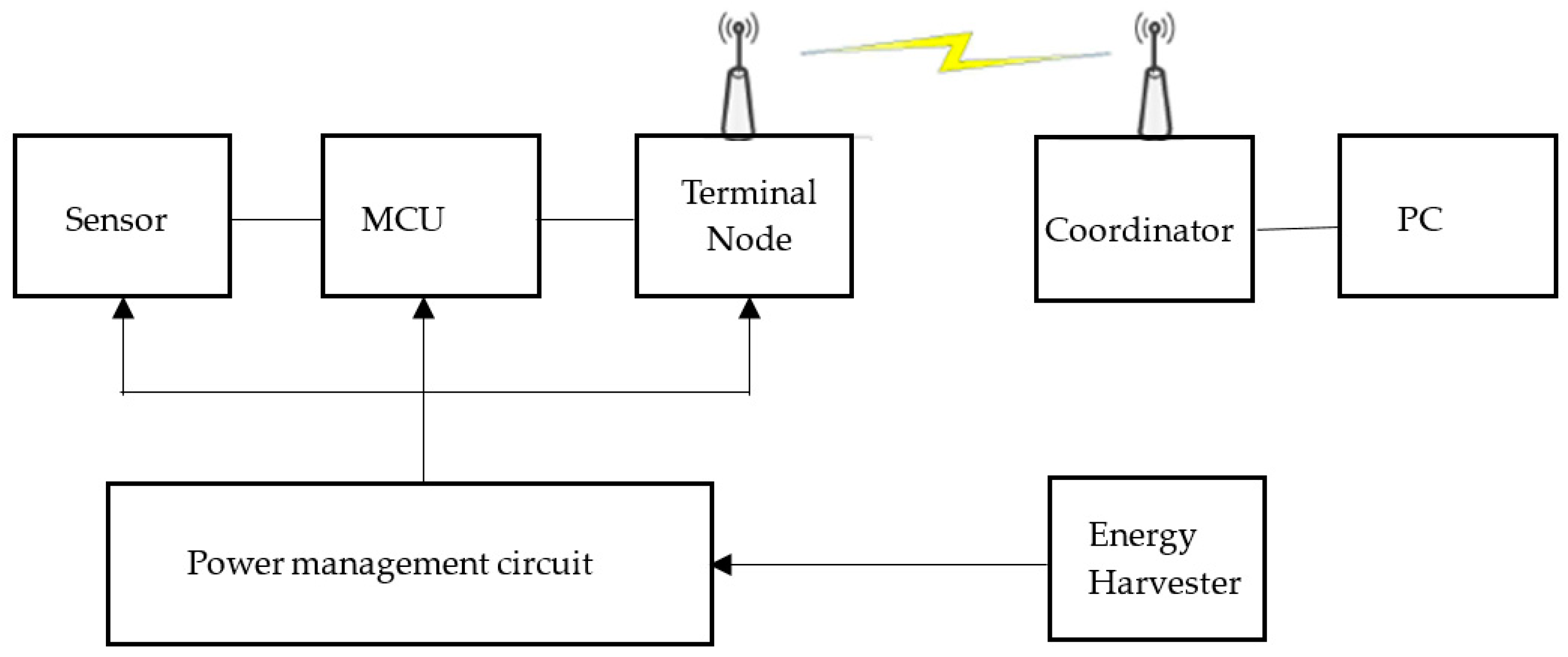
4. Wireless Sensor Node
5. Experimental Results and Discussions
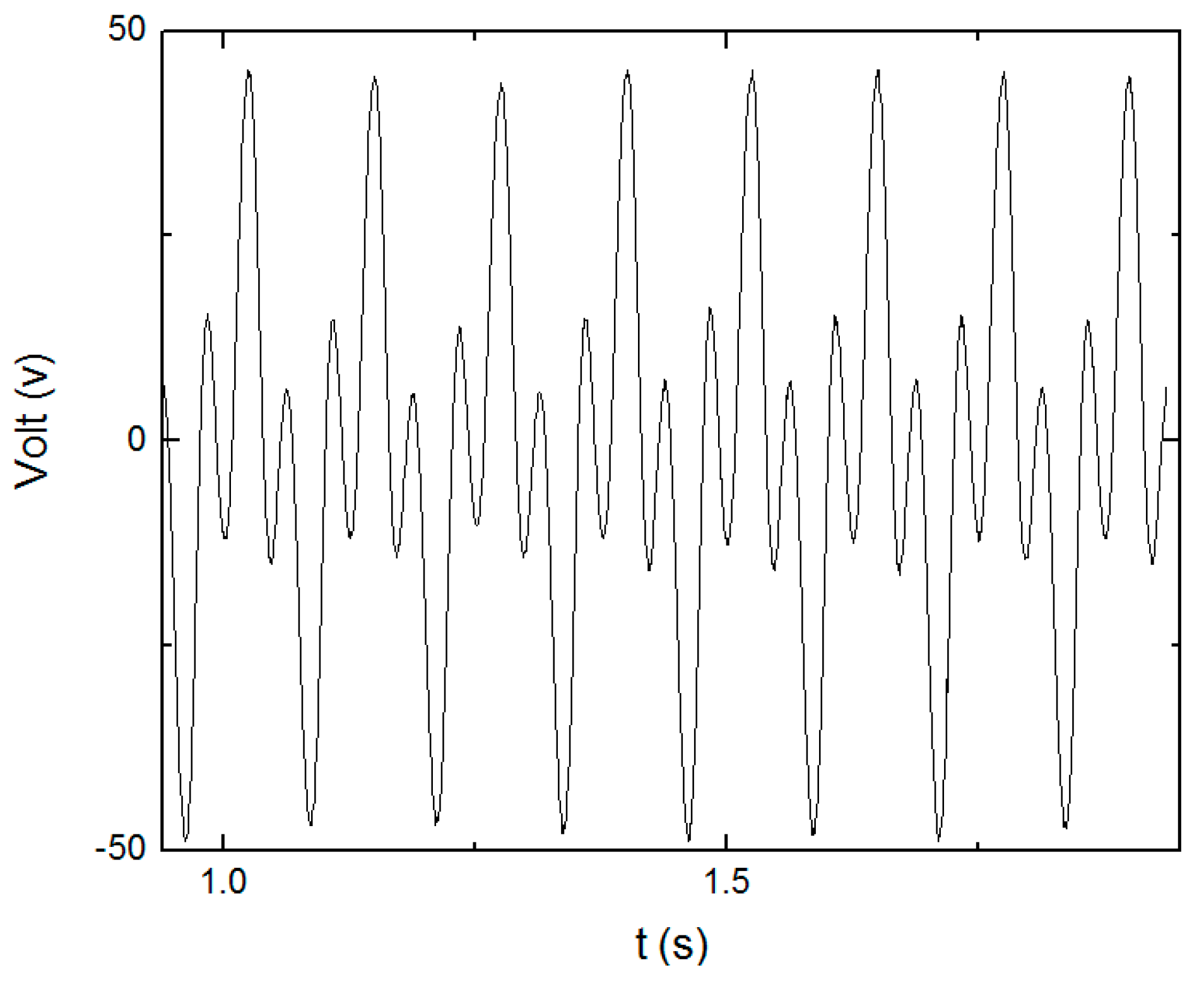
5.1. Experiments of the Harvester Prototype
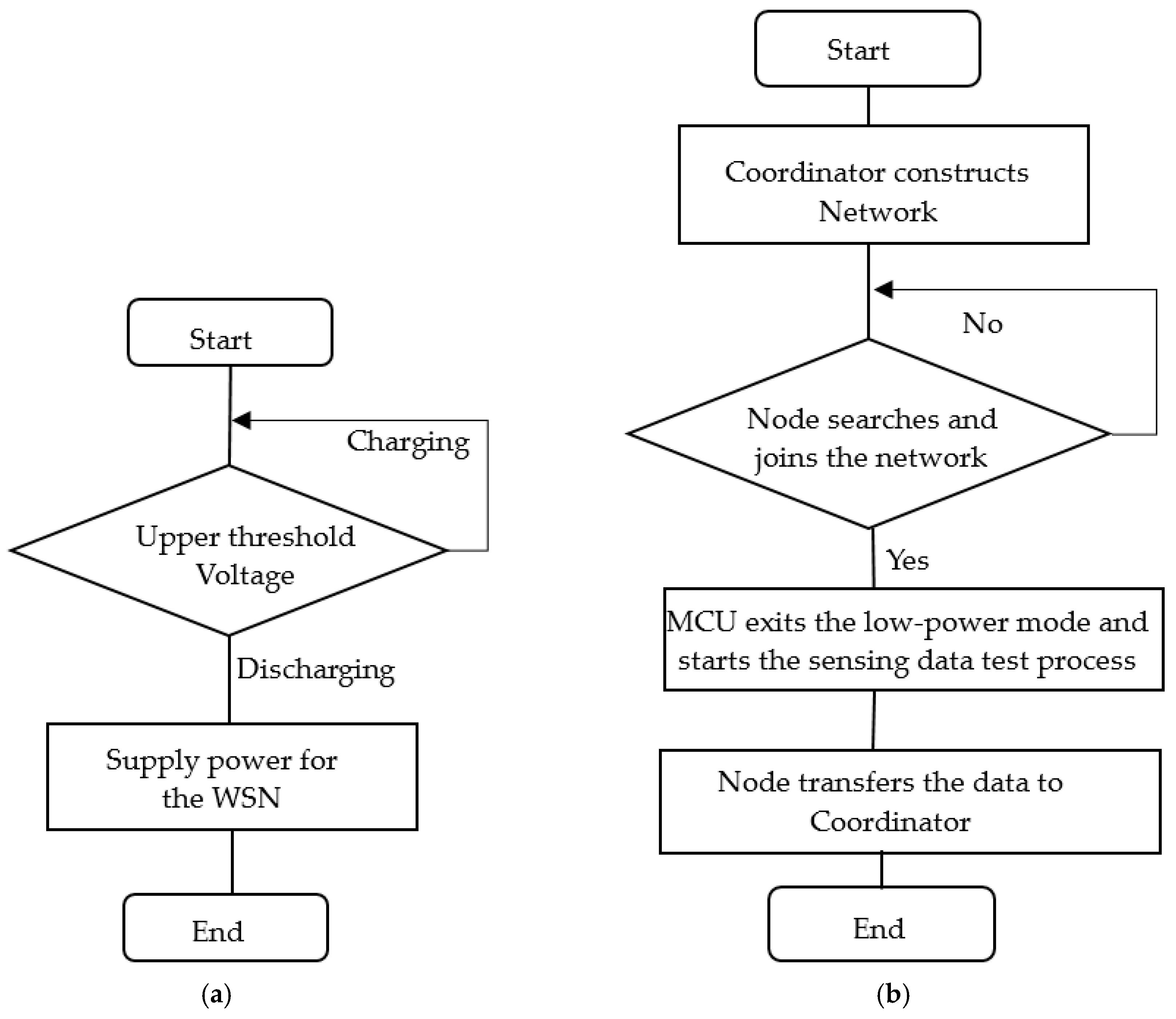
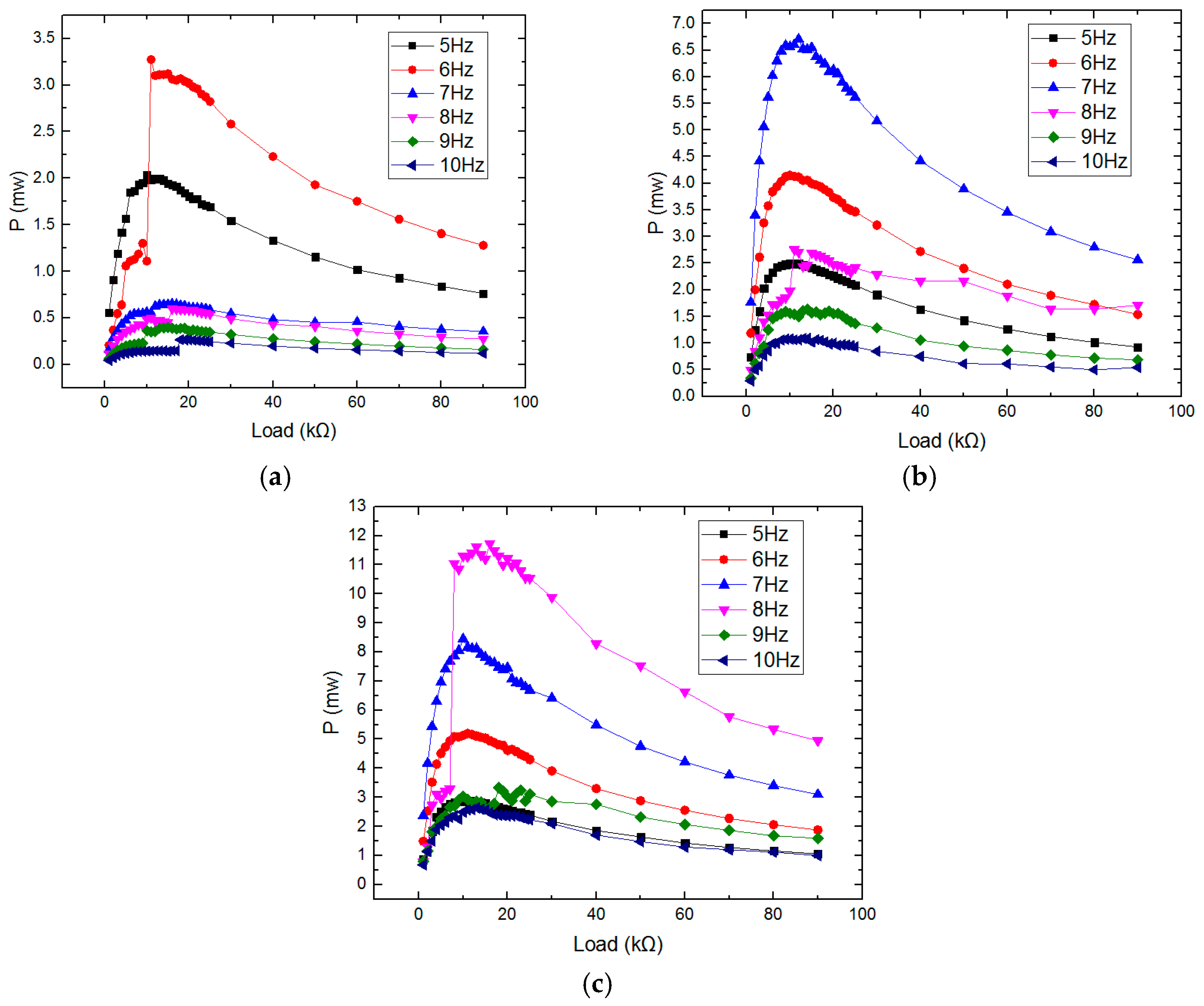
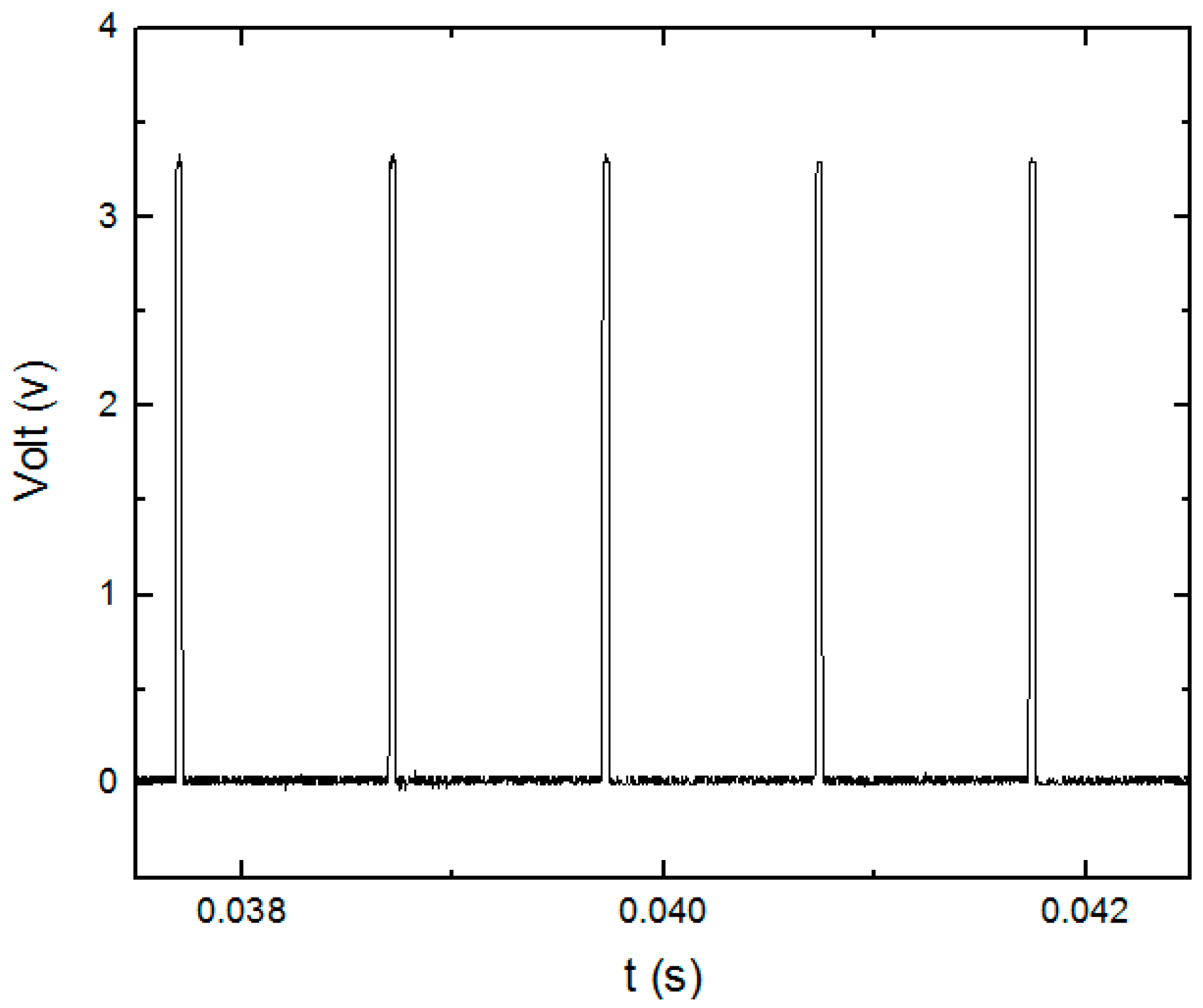
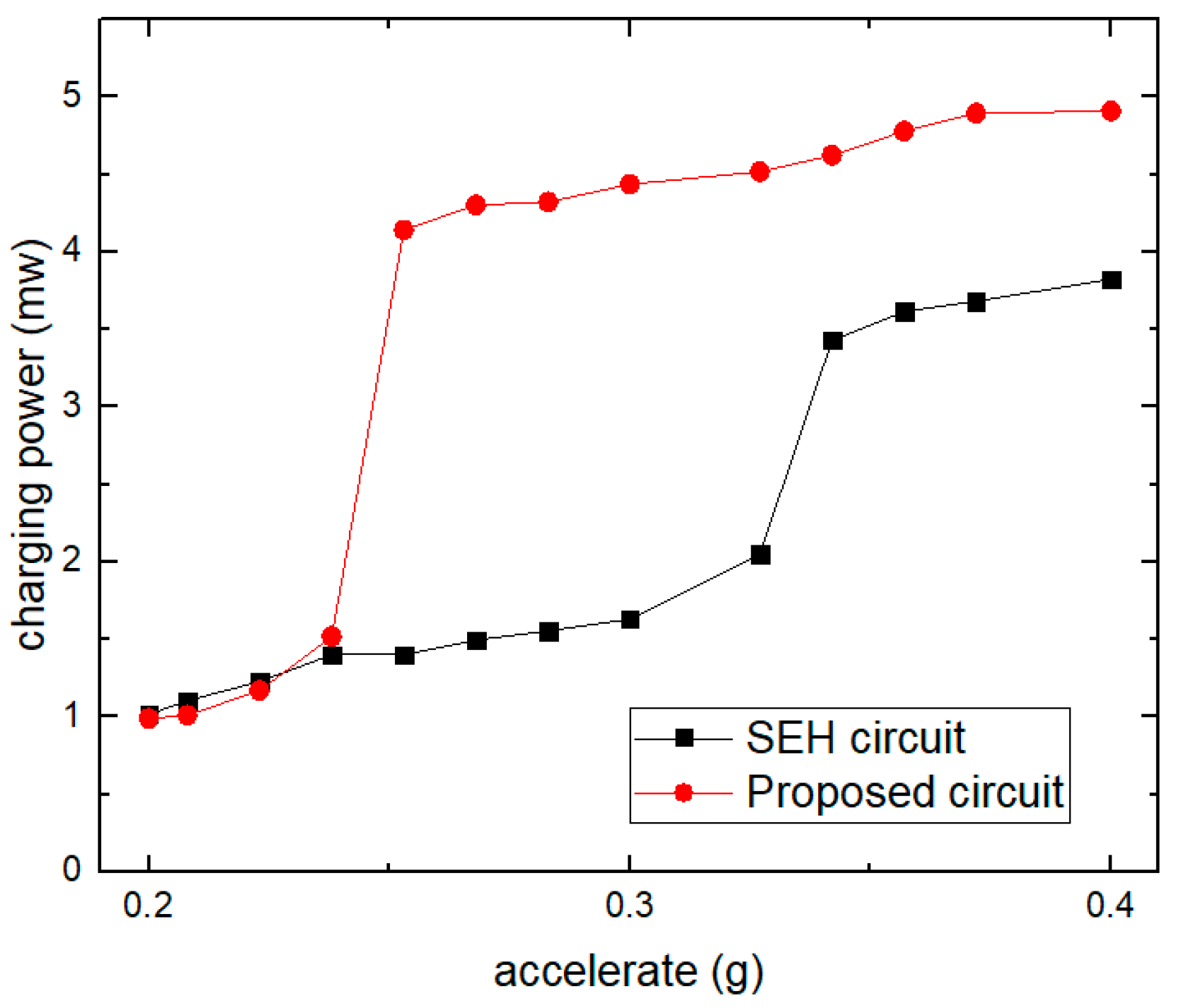
5.2. Experiments of the PMC and the Self-Powered Wireless Sensor Node
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Balato, M.; Costanzo, L.; Vitelli, M. MPPT in Wireless Sensor Nodes Supply Systems Based on Electromagnetic Vibration Harvesters for Freight Wagons Applications. IEEE Trans. Ind. Electron. 2016, 64, 3576–3586. [Google Scholar] [CrossRef]
- Ottman, G.K.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef]
- Sharma, H.; Haque, A.; Jaffery, Z.A. Modeling and Optimisation of a Solar Energy Harvesting System for Wireless Sensor Network Nodes. J. Sens. Actuator Netw. 2018, 7, 40. [Google Scholar] [CrossRef]
- Yan, B.; Zhang, S.; Zhang, X.; Wang, K.; Wu, C. Self-powered electromagnetic energy harvesting for the low power consumption electronics: Design and experiment. Int. J. Appl. Electromagn. Mech. 2017, 54, 165–175. [Google Scholar] [CrossRef]
- Xu, D.; Li, S.; Li, M.; Xie, D.; Dong, C.; Li, X. A high-efficiency self-powered wireless sensor node for monitoring concerning vibratory events. Smart Mater. Struct. 2017, 26, 095038. [Google Scholar] [CrossRef]
- Bendame, M.; Abdel-Rahman, E.; Soliman, M. Wideband, low-frequency springless vibration energy harvesters: Part I. J. Micromech. Microeng. 2016, 26, 115021. [Google Scholar] [CrossRef]
- Asharf, K.; Khir, M.H.; Dennis, J.O. Improved energy harvesting from low frequency vibrations by resonance amplification at multiple frequencies. Sens. Actuators A Phys. 2013, 195, 123–132. [Google Scholar] [CrossRef]
- Cao, X.; Chiang, W.J.; King, Y.C.; Lee, Y.K. Electromagnetic Energy Harvesting Circuit with Feedforward and Feedback DC–DC PWM Boost Converter for Vibration Power Generator System. IEEE Trans. Power Electron. 2007, 22, 679–685. [Google Scholar] [CrossRef]
- Li, P.; Wen, Y.; Liu, P.; Li, X.; Jia, C. A magnetoelectric energy harvester and management circuit for wireless sensor network. Sens. Actuators A Phys. 2010, 157, 100–106. [Google Scholar] [CrossRef]
- Szarka, G.D.; Burrow, S.G.; Proynov, P.P.; Stark, B.H. Maximum Power Transfer Tracking for Ultralow-Power Electromagnetic Energy Harvesters. IEEE Trans. Power Electron. 2013, 29, 201–212. [Google Scholar] [CrossRef]
- Bletsas, A.; Siachalou, S.; Sahalos, J.N. Anti-collision backscatter sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 5018–5029. [Google Scholar] [CrossRef]
- Hoang, D.T.; Niyato, D.; Wang, P.; Kim, D.I.; Le, L.B. Optimal data scheduling and admission control for backscatter sensor networks. IEEE Trans. Commun. 2017, 65, 2062–2077. [Google Scholar] [CrossRef]
- Assimonis, S.D.; Daskalakis, S.N.; Bletsas, A. Sensitive and efficient RF harvesting supply for batteryless backscatter sensor networks. IEEE Trans. Microw. Theory Tech. 2016, 64, 1327–1338. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Buonanno, A.; Urso, M.; Palmieri, F.A. Distributed classification of multiple moving targets with binary wireless sensor networks. In Proceeding of the FUSION—The 14th international Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011. [Google Scholar]
- Rossi, P.S.; Ciuonzo, D.; Kansanen, K.; Ekman, T. Performance analysis of energy detection for MIMO decision fusion in wireless sensor networks over arbitrary fading channels. IEEE Trans. Microw. Theory Tech. 2016, 15, 7794–7806. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S.; Dey, S. Massive MIMO channel-aware decision fusion. IEEE Trans. Signal Process. 2015, 63, 604–619. [Google Scholar] [CrossRef]
- Tarighati, A.; Gross, J.; Jalden, J. Decentralized hypothesis testing in energy harvesting wireless sensor networks. IEEE Trans. Signal Process. 2017, 65, 4862–4873. [Google Scholar] [CrossRef]
- Liang, J.; Liao, W. Improved Design and Analysis of Self-Powered Synchronized Switch Interface Circuit for Piezoelectric Energy Harvesting Systems. IEEE Trans. Ind. Electron. 2012, 59, 1950–1960. [Google Scholar] [CrossRef]
- Wang, X.; Liang, X.; Hao, Z.; Du, H.; Zhang, N.; Qian, M. Comparison of electromagnetic and piezoelectric vibration energy harvesters with different interface circuits. Mech. Syst. Signal Process. 2016, 72, 906–924. [Google Scholar] [CrossRef]
- Liang, J.; Liao, W. Impedance Modeling and Analysis for Piezoelectric Energy Harvesting Systems. IEEE/ASME Trans. Mech. 2012, 17, 1145–1157. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Badel, A.; Richard, C.; Guyomar, D. Piezoelectric Energy Harvesting Device Optimization by Synchronous Electric Charge Extraction. J. Intell. Mater. Syst. Struct. 2005, 16, 865–876. [Google Scholar] [CrossRef]
- Arroyo, E.; Badel, A. Electromagnetic vibration energy harvesting device optimization by synchronous energy extraction. Sens. Actuators A Phys. 2011, 171, 266–273. [Google Scholar] [CrossRef]
- Arroyo, E.; Badel, A.; Formosa, F.; Wu, Y.; Qiu, J. Comparison of electromagnetic and piezoelectric vibration energy harvesters: Model and experiments. Sens. Actuators A Phys. 2012, 183, 148–156. [Google Scholar] [CrossRef]
- Szarka, G.D.; Burrow, S.G.; Stark, B.H. Ultralow Power, Fully Autonomous Boost Rectifier for Electromagnetic Energy Harvesters. IEEE Trans. Power Electron. 2012, 28, 3353–3362. [Google Scholar] [CrossRef]
- Zhu, S.; Shen, W.; Xu, Y. Linear electromagnetic devices for vibration damping and energy harvesting: Modeling and testing. Eng. Struct. 2012, 34, 198–212. [Google Scholar] [CrossRef]
- Luo, Q.; He, X.; Jiang, S.; Wang, X. Impact-Based Electromagnetic Energy Harvester with High Output Voltage under Low-Level Excitations. Energies 2017, 10, 1848. [Google Scholar] [CrossRef]
- Zhang, H.; Lawrence, R.C.; Ma, T. Effects of electrical loads containing non-resistive components on electromagnetic vibration energy harvester performance. Mech. Syst. Signal Process. 2018, 101, 55–66. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Audigier, D.; Richard, C.; Guyomar, D. Buck-Boost Converter for Sensorless Power Optimization of Piezoelectric Energy Harvester. IEEE Trans. Power Electron. 2007, 22, 2018–2025. [Google Scholar] [CrossRef]
- Shen, W.; Zhu, S.; Zhu, H. Experimental study on using electromagnetic devices on bridge stay cables for simultaneous energy harvesting and vibration damping. Smart Mater. Struct. 2016, 25, 065011. [Google Scholar] [CrossRef]
- Kong, N.; Dong, S.; Erturk, A.; Daniel, J. Resistive Impedance Matching Circuit for Piezoelectric Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1293–1302. [Google Scholar] [CrossRef]
- Guo, T.; Lerley, R.; Ha, D.S. Development of a power conditioning circuit for railcar energy harvesting. In Proceeding of the MWSCAS—The 56th international Midwest Symposium on Circuits and Systems, Columbus, OH, USA, 4–7 August 2013; pp. 513–516. [Google Scholar]
- Chen, N.; Jung, H.J.; Jabbar, H.; Sung, T.H.; Wei, T. A Piezoelectric impact-induced vibration cantilever energy harvester from Speed Bump with a Low-power Power Management Circuit. Sens. Actuators A Phys. 2016, 254, 134–144. [Google Scholar] [CrossRef]
- Chen, N.; Wei, T.; Dong, H.; Jung, H.J.; Lee, S. Alternating Resistive Impedance Matching for an Impact-Type Micro Wind Piezoelectric Energy Harvester. IEEE Trans. Ind. Electron. 2018, 65, 7374–7382. [Google Scholar] [CrossRef]
- Xia, H.; Chen, R.; Ren, L.; Zhou, Q. Direct calculation of source impedance to adaptive maximum power point tracking for broadband vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2016, 28, 1105–1114. [Google Scholar] [CrossRef]
- Haroun, A.; Yamada, I.; Warisawa, S. Study of electromagnetic vibration energy harvesting with free/impact motion for low frequency operation. J. Sound Vib. 2015, 349, 389–402. [Google Scholar] [CrossRef]
- Han, Y.; Feng, Y.; Yu, Z.; Lou, W.; Liu, H. A Study on Piezoelectric Energy-Harvesting Wireless Sensor Networks Deployed in a Weak Vibration Environment. IEEE Sens. J. 2017, 17, 6770–6777. [Google Scholar] [CrossRef]
- Zhu, D.; Beeby, S.P.; Tudor, M.J.; Harris, N.R. A credit card sized self-powered smart sensor node. Sens. Actuators A Phys. 2011, 169, 317–325. [Google Scholar] [CrossRef]
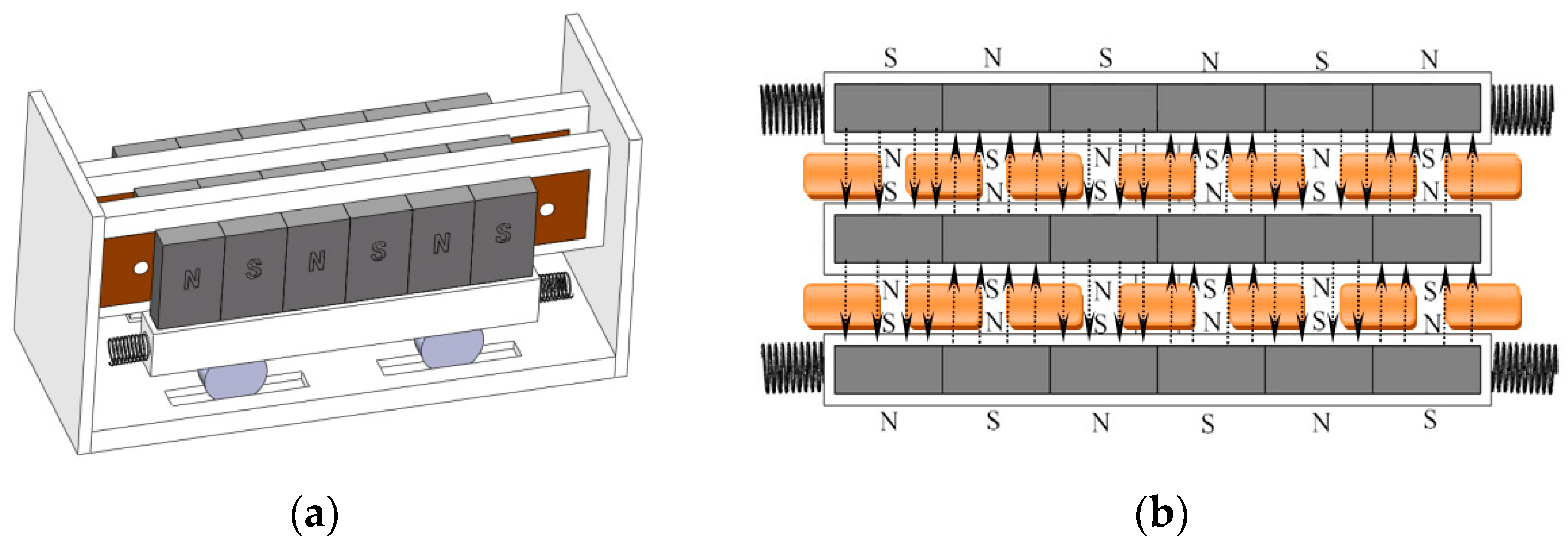
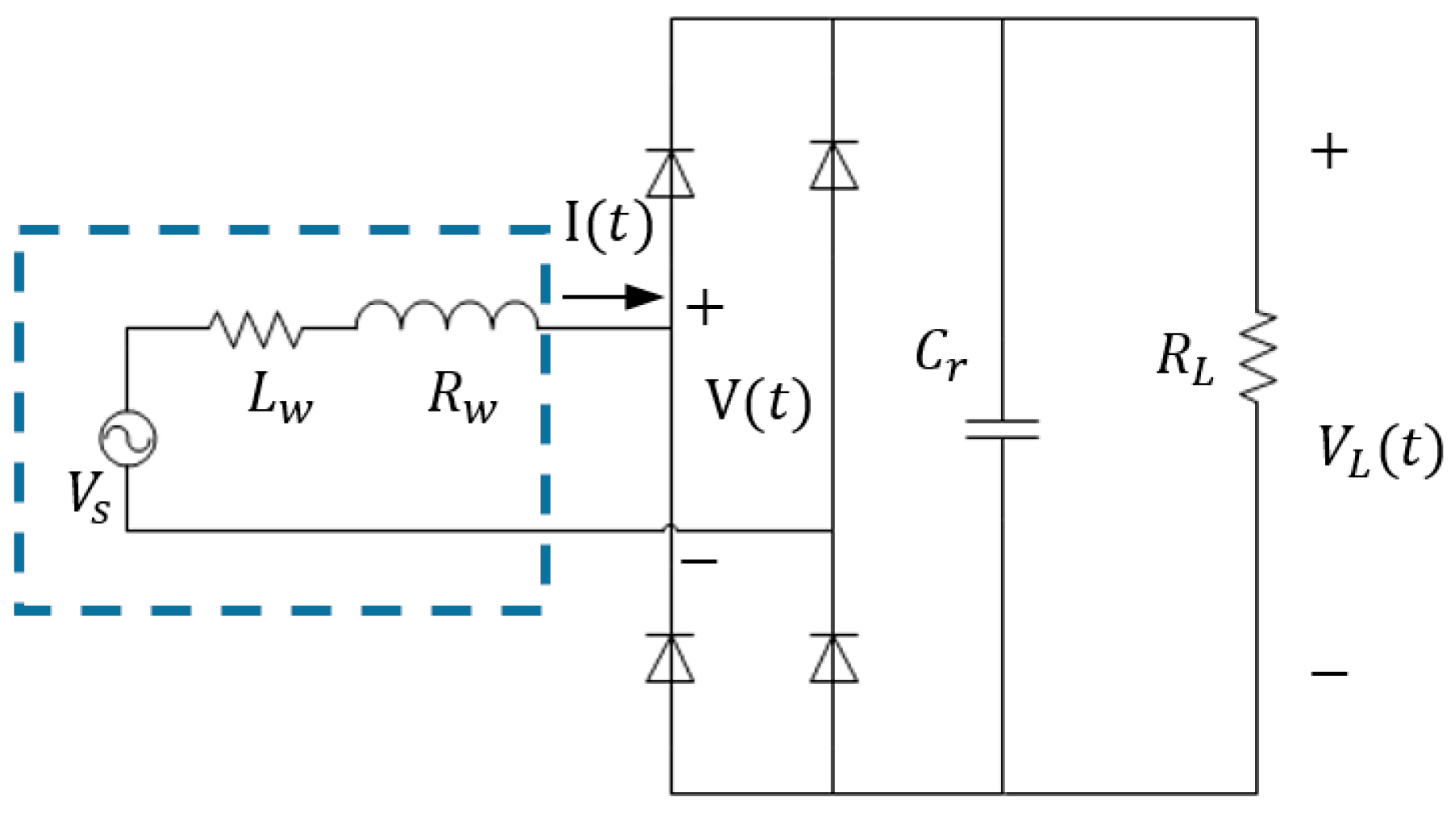
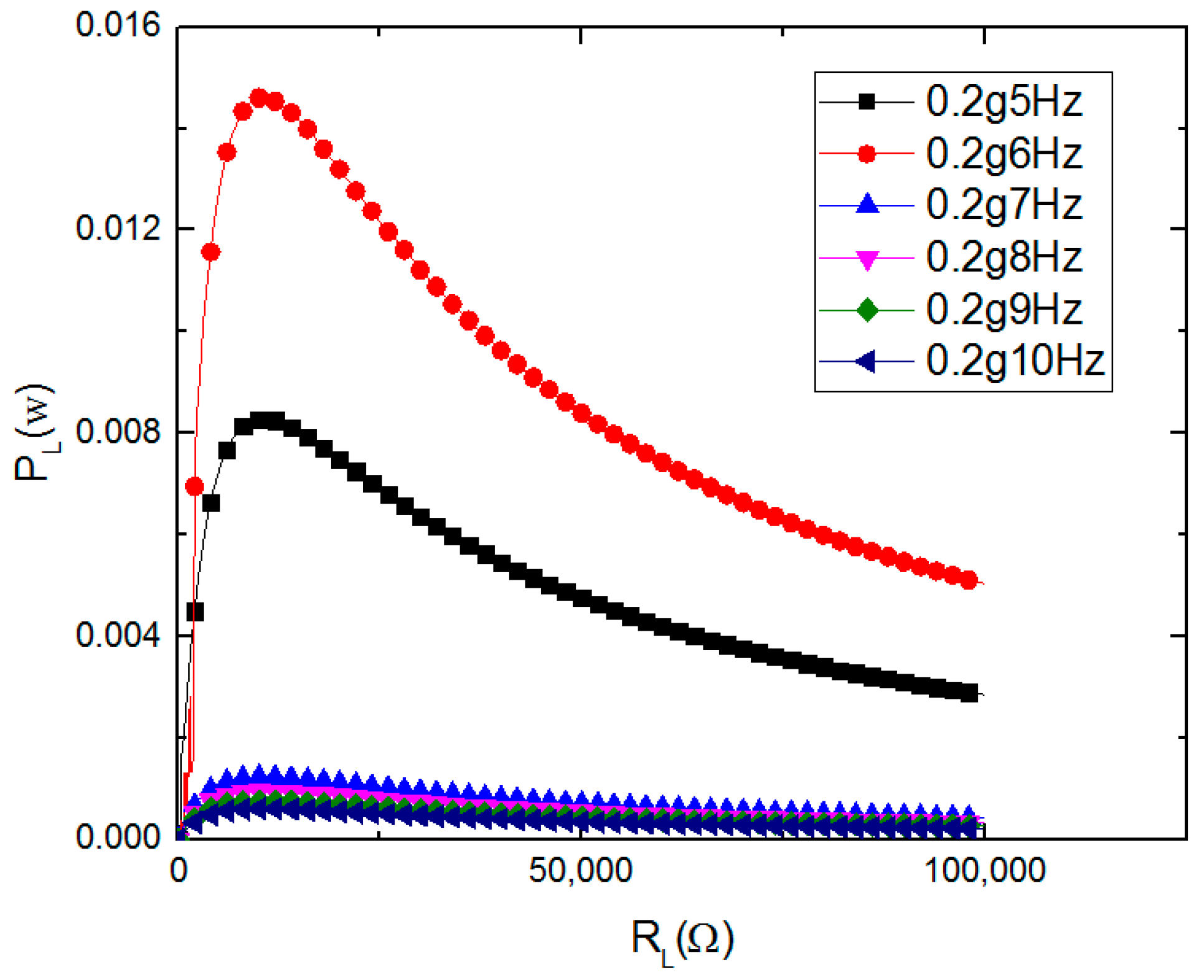

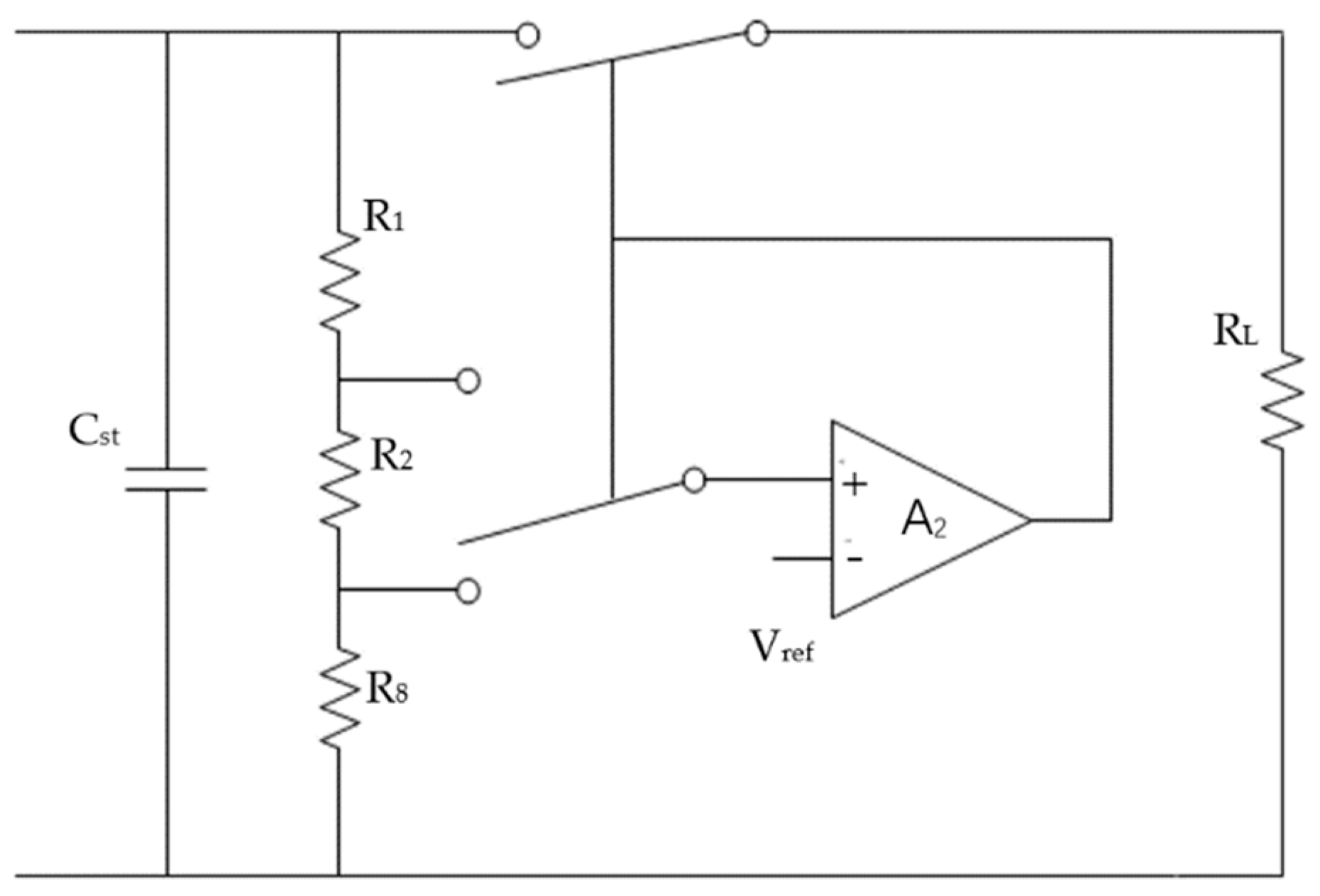




| Parameter | Value |
|---|---|
| Separation between two magnet rows | 5 mm |
| Magnet dimension | 20 mm × 10 mm × 4 mm |
| Coil dimension | 18 mm × 9 mm × 3 mm |
| Dimension of coil through a hole | 12 mm × 3 mm × 3 mm |
| Wire diameter | 50 µm |
| Number of magnets in each row | 6 |
| Number of magnet rows | 3 |
| Number of coils in each row | 7 |
| Number of coil rows | 2 |
| Component | Part Number | Comments |
|---|---|---|
| N-MOSFET | 2N7002 | 3.5 Ω; ; ; 22 pF; |
| Schottky diode | SS14 | |
| Comparator A1 | LTC1540 | |
| Inductor | - | L = 10 mH; DCR = 0.63 Ω |
| Comparator A2 | LTC1540 | |
| Voltage regulator | TPS70933 |
| Reference | Amplitude | Frequency | Storage Capacitor | Power | Efficiency | Charging Time Interval |
|---|---|---|---|---|---|---|
| Zhu 2011 [37] | 0.4 g | 67 Hz | 0.55 F | 240 μW | - | 800 s |
| Szarka 2012 [24] | 0.15 g | 43.6 Hz | 12.8 mF | 0.9 mW | 65% | 1440 s |
| Shen 2016 [29] | 0.99 g | 4 Hz | - | 31.6 mW | 16.9% | 600 s |
| Han 2017 [36] | 0.15 g | 40 Hz | 2 mF | 0.9–1.1 mW | 42% | 48–67 s |
| Xu 2017 [5] | 5 g | 52 Hz | 0.47 mF | 46.06 μW | - | 125 s |
| This work | 0.3 g | 8 Hz | 14.7 mF | 11.5 mW | 41.7% | 30 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; He, X.; Wang, X.; Jiang, S. A Nonlinear Electromagnetic Energy Harvesting System for Self-Powered Wireless Sensor Nodes. J. Sens. Actuator Netw. 2019, 8, 18. https://doi.org/10.3390/jsan8010018
Li K, He X, Wang X, Jiang S. A Nonlinear Electromagnetic Energy Harvesting System for Self-Powered Wireless Sensor Nodes. Journal of Sensor and Actuator Networks. 2019; 8(1):18. https://doi.org/10.3390/jsan8010018
Chicago/Turabian StyleLi, Kankan, Xuefeng He, Xingchang Wang, and Senlin Jiang. 2019. "A Nonlinear Electromagnetic Energy Harvesting System for Self-Powered Wireless Sensor Nodes" Journal of Sensor and Actuator Networks 8, no. 1: 18. https://doi.org/10.3390/jsan8010018
APA StyleLi, K., He, X., Wang, X., & Jiang, S. (2019). A Nonlinear Electromagnetic Energy Harvesting System for Self-Powered Wireless Sensor Nodes. Journal of Sensor and Actuator Networks, 8(1), 18. https://doi.org/10.3390/jsan8010018





