Abstract
Most existing dissemination schemes in Mobile Social Networks (MSNs) only consider the data dissemination. However, there are two types of messages: data and the control message (i.e., acknowledgment) in MSNs, and receiving acknowledgment is very important in many applications (e.g., the mobile trade and the incentive mechanism). In order to maximize the desired message delivery ratio, we have to identify the priority of each message in the network during the limited contact opportunity. Therefore, we propose a generic priority-based compare-split routing scheme, which proves to be the optimal buffer exchange strategy. During each contact opportunity, relays compare their forwarding abilities to different destinations based on two types of criteria: the contact probability and the social status. Ideally, each relay keeps the messages whose destinations meet the current relay frequently. Then, an adaptive priority-based exchange scheme, which considers the priority within each type of messages and the relative priority between two types of messages, is proposed to exchange the most benefit messages. The effectiveness of our scheme is verified through extensive simulations in synthetic and real traces.
1. Introduction
The wide usage of mobile devices (e.g., smartphones and tablets) and the evolution of high-speed short-distance wireless communication (e.g., Bluetooth 4.0 and WIFI Direct) in the recent years has stimulated lots of research in mobile social networks. Currently, we simply use centralized cellular networks (e.g., GSM and 3G) to transmit two types of data: immediate data (e.g., voice and video chat), and delay-tolerant data, (e.g., email and software update). With the increased amount of the data traffic, the cellular networks will not satisfy the increasing traffic demand, especially during peak times in the densely populated part area [1]. Therefore, Mobile Social Networks (MSNs) as complementary network communication technologies to cellular networks are suitable for delay-tolerant data for a local community in which the participants have frequent interactions, (e.g., people working in the same building, students studying in the same school). In MSNs, data are buffered for extended intervals of time until an appropriate forwarding opportunity is recognized in hopes that it will eventually reach its destination (i.e., store-carry-forward) [2]. As a result, MSNs extend communications between mobile devices from the restrictions of cellular infrastructure, mitigate the congestion for traditional centralized communication methods, and reduce the communication cost simultaneously.
Since the MSN is an autonomous network, a proper incentive scheme is imperative to stimulate nodal cooperation and to attract more participants. Without the centralized communication scheme, to apply incentive mechanism in MSNs, a common method is to collect the acknowledgment from the destination [3,4,5,6]. That is, the relays can inject information into the message. After the data reaches the destination node, the destination node will send the forwarding list, as an acknowledgment, back to the source. That is, there exist two types of messages in the network. In real scenarios, the buffer of the node is usually limited [7]. Therefore, how to utilize the limited buffer space to maximize the message delivery is the motivation of this paper. Ideally, we have two objectives: the data should be disseminated to the destination quickly, and acknowledgment should be sent back quickly. It might not be possible to achieve these two objectives at the same time. Then two challenges arise naturally: (1) How can a node compare the benefits of keeping the message and the benefits of exchanging it with others? (2) How can the benefit gain for each buffer exchange be quantified? The benefit can be regarded as the smaller delivery delay, or higher delivery ratio, and so on. An illustration of the two abovementioned challenges is shown in Figure 1, where nodes a, b have larger contact probabilities with node s and d, respectively. Thus, the acknowledgment for node s should be forwarded to node a, and the data and acknowledgment for node d should be forwarded to node b. However, sometimes, it is not easy to evaluate the nodes’ contact frequency with a special destination. In Figure 1, it is hard to compare the delay from nodes a to c and the delay from nodes b to c. Therefore, whether node b should keep the data for c is non-trivial. Furthermore, if we assume each node can only carry two messages at most, if the node b keeps the acknowledgment for c, the two messages for node d in node a cannot be forwarded to node b, due to the limited buffer space.
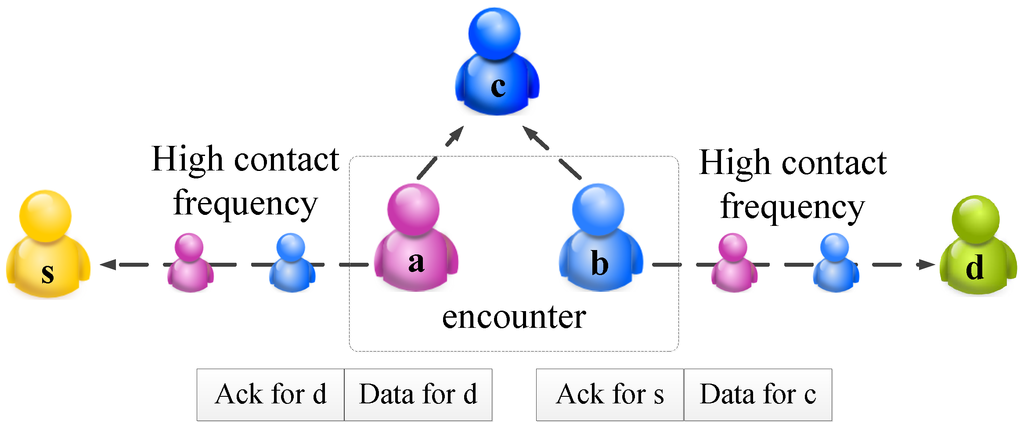
Figure 1.
An illustration of the network model.
For the first question, most existing methods try many different methods to estimate the contact probability between the encounter node and the destination of the message, and forward the message to the node with a higher contact probability. It is called the strongly connected relationship with destination in this paper. However, if we only consider this type of strongly connected relationship with the destination, we will miss lots of useful information. The node’s relationship with other nodes (excluding the destination) is called weakly connected relationship with destination in this paper, and it does matter for relay selection. In this paper, two types of criteria, social status, the centrality of a node in the network, and contact probability, the probability of a node to meet destination, are used as the weakly connected relationship with destination and the strongly connected relationship with destination, respectively. They are used together to estimate the ability that a node can act as a relay to send a message to the destination. By introducing the concept of social status, we combine the direct probability, two-hop indirect probability, and the influence of the other weakly-connected relationship with the destination, and estimate the probability more accurately.
As for the second question, we should set the priority of the message according to the possible beneficial gain. Two criteria are used in this paper: (1) Usefulness: If we forward it, it is highly likely to reach the destination before the deadline so that the work can pay off; (2) Urgency: The data which is close to the deadline should have a higher priority. A proposed priority setting leverages the two above criteria. The relative priority between data and acknowledgment is further proposed in different scenarios. In this paper, we focus on two scenarios (i.e., the data-first and acknowledgment-first). The idea for the data-first scenario is that nodes would like to send data to destinations as soon as possible, such as weather forecast updates and news feeds; otherwise, the data will expire. However, in the acknowledgment-first scenario, the acknowledgment is more important. The possible application scenarios are the mobile trade or source-incentive mechanisms. It is because the relays would like to get the reward as soon as possible, so that they try to send the acknowledgments back quickly. Otherwise, once the acknowledgment is expired, they cannot get any reward. Our proposed method is a generic routing scheme, which can be used in the abovementioned message dissemination.
The contribution of this paper is organized as follows: (1) We propose a generic routing scheme to accelerate the data and acknowledgment dissemination simultaneously, with time and buffer constraints; (2) We combine two types of criteria, the strongly connected relationship and the weakly connected relationship with the destination, together to estimate a node’s ability to act as a relay. Thus, the estimated contact probability is more accurate; (3) We propose an adaptive priority scheme for each type of message, so that message which contributes to performance most will be sent first.
The remainder of the paper is organized as follows. We review the related work in Section 2. The network model is introduced in Section 3. The proposed priority-based compare-split algorithm is presented in Section 4. After that, an analysis is provided in Section 5. The evaluation setting and the simulation results are shown in Section 6. We conclude the paper in Section 7.
2. Related Works
Routing in MSNs has attracted the attention of many people in the last few years [3,8,9,10,11,12,13,14,15,16]; how to achieve good performance with little system consumption is a major concern. The current research is mainly focused on the utility estimation of the relay node and the performance feedback by using the acknowledgment.
Relay utility estimation: For the relay node’s utility estimation, it initially begins from the direct contact probability and generally extends to criteria in multi-dimension. In [14], the author proposes the two-hop transitivity property. In [8,15], the weighted degree of nodes is also considered as a criterion for buffer exchange, so the routing decision is based on several criteria. In [10], the author first points out the intrinsic characteristics of MSNs, that is, the carrier of the smartphones (nodes) are people, so that MSNs share the social characters. They use two utilities called centrality and community locally and globally to make routing decisions more precisely. After that, a lot of the research about the social metric of MSNs were conducted [17,18]. Reference [19] proposed the centrality like PageRank, which is widely used in Internet searching. The idea is that your importance is decided by the importance of your neighbor. In [11], the author proposed a routing algorithm which considers the selfish characters of MSNs. It adjusts the utility by a factor called willingness. In this way, even though two nodes contact each other frequently, it might not be a good relay if its willingness is low. In [20], the author argues that most existing algorithms try to assign a majority of the workload on a few popular nodes, which is not fair and the resource of these nodes will soon be drawn up. A utility called assortativity is proposed to limit the system resource usage. However, all the aforementioned schemes only consider the direction contact probability between the node to the destination as the only forwarding criterion.
Acknowledgment in trust mechanism: A challenging problem is whether we should trust the information from the node in such an unsupervised environment. There might exist some selfish and malicious nodes in the network. In [21], the authors study the robustness of MSNs routing in the absence of authentication. The authors identify conditions for an attack to be effective and present an attack based on a combination of targeted flooding and acknowledgment counterfeiting that is highly effective, even with only a small number of attackers. Thus, a mechanism used to detect the attack is meaningful in MSNs. The results in [22] show that each node should forward the message which is most similar to its common interest, given an encounter between friends, or it should forward the message which is furthest to its common interest, given an encounter between the strangers. In [23], they propose a 2ACK scheme. The basic idea is that, when a node forwards a data packet successfully over the next hop, the destination node of the next-hop link will send back a special two-hop acknowledgment called 2ACK to indicate that the data packet has been received successfully.
Acknowledgment in incentive mechanism: Most existing methods introduce a credit-based scheme. That is, nodes get paid for providing services to other nodes. When they request other nodes to help them for packet forwarding, they use the same payment system to pay for such services. In [24], nodes keep acknowledgment of the received/forwarded messages. When they have a fast connection to a credit clearance service, they report all of these acknowledgments. The credit clearance service then decides the charge and credit for the reporting nodes. In [3], the authors introduce the trading mechanism to the receipt, that is, nodes would like to exchange their messages and receipts on the condition that both of them can increase their expected probability to successfully cash the receipt after exchanging the receipt.
In the above research, in the data dissemination problem, the acknowledgment is usually ignored. On the other hand, in the trust/incentive mechanism, the data dissemination is not considered. However, according to the research of [25], in a real data dissemination problem, there exist lots of data and acknowledgments. Due to the node’s buffer being limited, how to disseminate data with mixed data and acknowledgments is a fundamental problem. To the best of our knowledge, we are the first to jointly consider the data and acknowledgment exchange in MSNs with buffer constraint.
3. Network Model Overview
In this section, we first introduce the network model used in this paper. Then, we propose the problem based on the model and the corresponding applications.
3.1. System Model
There might not exist a contemporaneous end-to-end path for content dissemination in MSNs, and thus the messages suffer a relatively large delay. In many application scenarios, a certain delay is acceptable. However, it does not mean that delay can be any longer in MSNs. Let us take an example of news; we do not need to receive all the latest news in real time; a 2 h latency is acceptable, but we might not be interested in yesterday’s news anymore. Thus, a deadline or time-to-life (TTL) is needed, or the messages might be out-of-date and meaningless.
An illustration of the network model is shown in Figure 2. In our model, there exist two types of messages: data and acknowledgment. It is a single-copy scenario, which means that each message is unique in the network. If the source wants to send a message to a node, it can choose to send the message itself or ask other nodes for help. For the latter case, after the source forwards the message to relay, the relay will inject its ID into the message and later exchange the buffered messages with other encounter nodes to accelerate the message dissemination. If the message does not reach the corresponding destination before the deadline, the message is discarded. Otherwise, the message is forwarded to the destination in time, and the destination node will generate an acknowledgment to notify the corresponding source of the relays involving the data forwarding. This type of acknowledgment mechanism is used in many applications. For example, in the incentive model, if the source receives the acknowledgment, it will provide the promised reward to the listed relays through a centralized virtual bank. We further assume all the nodes are honest. They would not forge information to other nodes, or hide the messages that they carried. The security-related problems are out of the scope of this paper, and there exist some strong authentication schemes [26,27] that provide the verification of information.
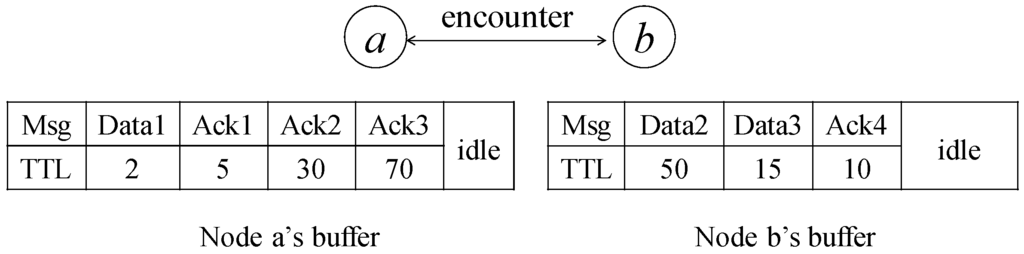
Figure 2.
An illustration of the network model where the value under the data and acknowledgment represents the TTL, and the blank region in the figure means the idle buffer.
The buffer size of the node is limited in our model, which matches the real application scenarios. In real application, the available buffer to carry messages for other nodes are limited [7]. Therefore, in each contact opportunity, we have to assign a priority to each message and let the most beneficial messages exchange first. In addition, we assume that nodes encounter each other in a pairwise manner, or we can use nodes’ IDs to decide the communication order. Some notations used in this paper are shown in Table 1. The message replacement policy is not discussed in this paper, since there are many existing works [28,29] that cover this problem. In our model, when the buffer is full, the oldest message is dropped first.

Table 1.
Summary of symbols.
3.2. Problem and Applications
The problem in this paper is how to find an optimal message exchange, due to the limited contact opportunity; as a result, the desired message delivery ratio is maximized.
Basically, we have the following two application scenarios:
- Data-first scenario: For mobile advertising, we want to disseminate as much as data as possible, in the hopes that data can reach more interested nodes. As for mobile trade, when the destination pays for the credit to relays, relays care more about whether the generated data can be delivered to the corresponding destinations as soon as possible so that they can earn credit.
- Acknowledgment-first scenario: For the incentive mechanism and mobile trade, the source might be more interested in checking whether the disseminated data have reached the corresponding destinations. Relays care more about whether they can cash the credit acknowledgment through the central credit center as soon as possible.
In the two above scenarios, both the sender and relays hope that data and acknowledgments can be transmitted soon. This is a win-win exchange strategy.
4. Priority-Based Compare-Split Scheme
In this section, we propose a priority-based compare-split scheme to maximize the achievable benefit during each exchange. Before that, we first introduce the relay selection criteria used in this paper. Then, we will present the two steps of the proposed scheme, and illustrate them by an example. The first step is compare-split, which collects the necessary information for routing. The second step is priority-based exchange, which decides how to exchange messages in order to maximize the achievable beneficial gain.
4.1. Relay Selection Criteria
In this paper, we not only estimate the node’s direct contact frequency with the destination node, called the strongly connected relationship with destination in this paper, as most existing schemes did, but also define the social status to distinguish a node’s weakly connected relationship with the destination. Then, we make a routing decision based on these two criteria. By combining the relationship of nodes with the destination and the other nodes together, we can estimate the ability of a node to act as relay more accurately.
Social status: a priori estimation of the node’s centrality in the network in a given period. It can be written in the following function:
where represents the nodes which encounter node a in a time interval. Along with time, nodes frequently contacting other nodes will have high value, and other nodes will keep a small value for social status.
Contact probability: a priori estimation of the contact with a destination in the network in a given period, which can be derived from the contact frequency to estimate the relationship between the relay and destination. The contact probability decays with time. The Exponentially Weighted Moving Average (EWMA) method is usually used to update the contact probability. The contact probability of node a with node d can be written in the following format:
where β is an empirical value that we can get a proper value from extensive experiments. In this paper, the β is set as during the experiments.
Let us take Figure 3 as an illustration. Consider nodes a and b, whose probabilities of reaching destination d is and respectively. Though the contact probability between node b and destination node d is larger than that of node a, node a should not forward the message to node b for the following two reasons: (1) Node a has a high indirect contact probability with node d. The probability that node a sends a message to d from node c is . (2) Node a has a high probability of meeting other nodes, and has a high probability of reaching the destination. The probability of node a meeting at least one of node e and f is . The probability of sending a message from node e or f is also . From this example, the observation is that the weakly connected relationship with the destination has an influence on the routing decision. That is, if a node is popular, even this node does not have a high contact probability with the destination, this node can still meet other nodes, which have quite a good relationship with the destination. If the current node always forwards the message to the encounter node based on the contact probability, without considering the weakly connected relationship with the destination, it might not be a good strategy. In the following, we use the contact probability and the social status to represent the strong and weak relationship with the destination.
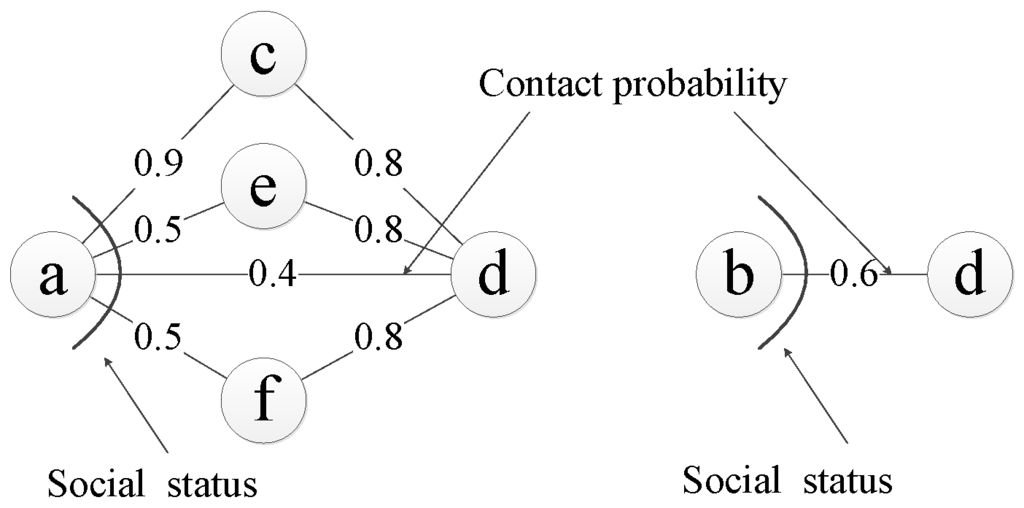
Figure 3.
An illustration about the contact probability and the social status for different nodes.
4.2. Step 1: Compare-Split
Upon the contact between nodes a and b, they exchange their probability vectors to corresponding destinations of messages they carry. Then, each node knows the combined destination set for messages buffered in them and the corresponding probability vector. Let’s denote the combined destination set D, , where m is the number of destinations. The probability vectors of node a and node b to destination set D as , and respectively. The social statuses of nodes are also changed during this step. Note that there exist two rounds of exchanges. One round is to exchange the destination of the messages in their buffer, and another round is to exchange their probability vectors.
Definition 1.
The forwarding difference vector of node a and node b for node a is the forwarding difference to the destination set of the messages they carried. Suppose the destination set is , and the forwarding difference vector is , , ..., , where .
The destination set splitting is based on the ratio of two encounter nodes’ forwarding difference vector.s That is, each node keeps the destination set that has better forwarding ability.
The following is the ratio-based split process, and it is shown in Figure 4.
- Both a and b generate the forwarding difference vector .
- Node a keeps messages for destinations that have higher values than, or equal to the 0, the size as k. When two forwarding probability differences are equal, the node’s ID/ available buffer space is used to break the tie, i.e., node with higher ID number/ larger available buffer space will keep messages for that destination.
- Node b keeps messages for the remaining destinations that have lower values than, or values equal to, the largest element.
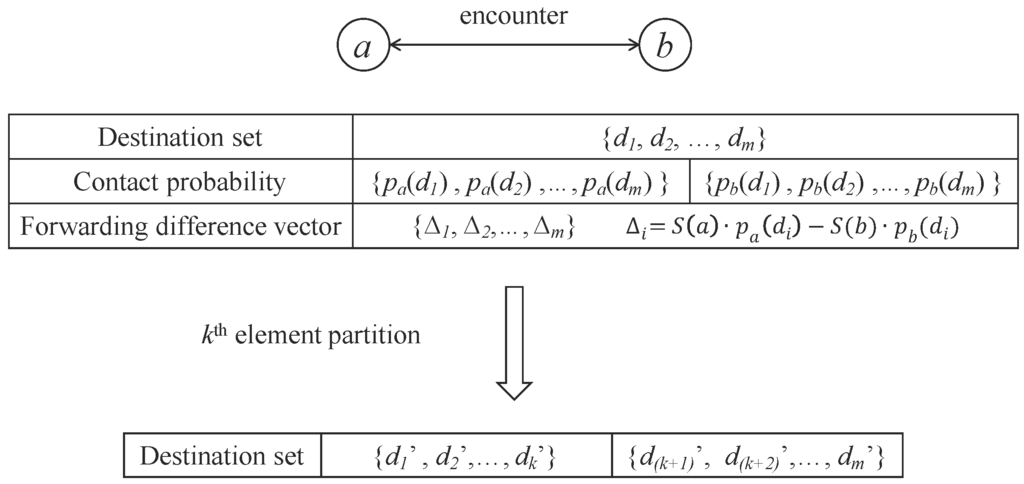
Figure 4.
An illustration of ratio-based-split where each node will carry the messages that they are more likely to encounter through a buffer exchange.
Note that in the compare-split scheme, even the current node has a larger contact probability for a special destination, this destination might be split to the other node, due to the current node’s low social status. The reason has been explained in Section 4.1.
Let us take Figure 5 as an example to illustrate the compare-split scheme. From the top of the figure, you can get the contact probability and social status of nodes a and b. During the contact, node a and node b first exchange the corresponding probability vectors. Node a sends probability vectors , , , , to node b, and node b sends probability vectors, , , ), , to node a. Then, both nodes form a destination set D, . In this example, we choose node a’s view to calculate the forwarding difference vector, is , and the remaining number of destinations are . Then, we will split messages of node a and node b. That is, node a should keep the messages for destination and node b should keep the messages for destination to maximize the combined probability.
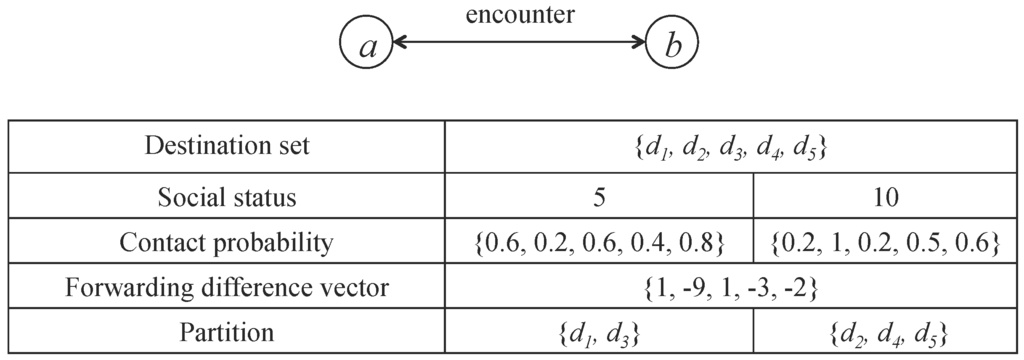
Figure 5.
An example of priority-based compare-split scheme.
There are two major advantages for the proposed compare-split scheme.
- It balances the influence of the contact probability and the social status. Therefore, it overcomes the situation in which the weakly connected relationship with the destination is ignored.
- The compare-split scheme is symmetric for the encountered two nodes. As a result, from each node’s viewpoint, they can get the same result. No further synchronization is needed.
4.3. Step 2: Priority-Based Exchange
Due to the limited buffer constraint and contact opportunity, different messages have different priorities. Intuitively, we hope that the message can be delivered to the destination in time, and the message which is close to its TTL should be transmitted first. In addition, the expected delivery delay should be considered during the priority setting. Here, the social status and the contact probability for the destination are jointly considered to estimate the expected delay.
Note that, in this setting, the social status of a node re-scales the expected delay.
As for the priority setting, we should not only consider the remaining time before the message expires but also consider the time that is expected to arrive at the destination. Thus, we define the priority as follows:
where the is the TTL of message a. The idea is that is the remaining time for message a, and thus we should set a lower priority for messages which have a long remaining time. However, the expected delay has an influence on the priority. For example, though the remaining time of message a is smaller than message b, the expected delay of message a is much smaller than that of message b. In this case, message a should have a lower priority since it can reach the destination before the deadline in a high probability. Thus, leverages the expected delay and the remaining time to represent the priority of the message. If the remaining time is smaller than the expected delay, we should set the priority of the message as 0, since it is highly possible that this message cannot reach its destination before the deadline, so that we do not waste the precious contact opportunity.
According to the different application scenarios in message dissemination, such as mobile advertising or public information dissemination, we should assign different priorities to data and acknowledgments. We define as the priority of a data, and as the priority of an acknowledgment. Furthermore, a relatively important factor α is defined in the priority setting, and the size of different types of messages are also embedded into this factor. In the data-first scenario, especially, , and in the acknowledgment-first scenario, .
We can illustrate the priority-based compare-split scheme in Figure 6. It continues the aforementioned example in Figure 5. The left-bottom table in Figure 6 shows the buffer information of nodes a and b before the split, where the value represents how much data or how many acknowledgments are destined to the corresponding destination. We consider the buffer constraint to get the number of messages that can be exchanged in each message. Then, we calculate the priority of the data and acknowledgment by Equation (4), and get a total dissemination order of the data and acknowledgment for nodes a and b. We further assume the size of the data is the same with the size of acknowledgment in this example for explanation simplicity, and each node can carry 4 messages at most. According to the compare-split step, node a has three messages to exchange, and node b has 2 messages to exchange. Due to the buffer constraint, only the two messages with the highest priority of each node have an opportunity to exchange in this encounter. For node a, that means the data to destination 2 and acknowledgment to destination 4. As for node b, that means the data to destination 3 and the acknowledgment to destination 3.
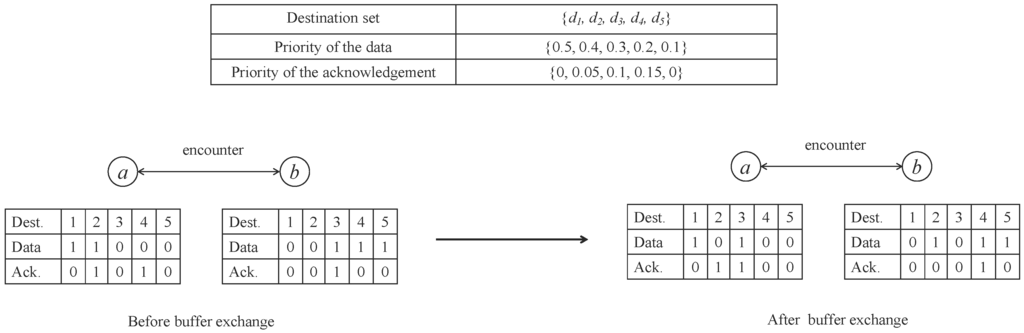
Figure 6.
An example of priority-based buffer exchange scheme.
Two types of TTL exist: one is for data, and one is for acknowledgments. We should distinguish these two types of TTL, since they might have different values in different scenarios. For example, in the data-first scenario, we might set the TTL of data longer to increase the opportunity for successful delivery, and vice versa in the acknowledgment-first scenario.
4.4. Discussion and Future Work
Our proposed scheme is used in the single-copy uni-cast scenario. However, it can be extended into the multiple-copy scenario. In this case, one node can encounter different nodes which buffer the same data more than one time. For example, source node s generates data i for node d. Then, node s encounters node a and node b, and relays data i to them (in order). Another node c later encounters node a and b buffered with data i in sequence and did buffer exchange. Node c should not assign the same priority of data i during these two buffer exchanges. A naive idea is that the priority of the data should decrease as the encountering times increase. That is, the priority of data i is determined by a tuple . As for the acknowledgment generation, the destination will only send back an acknowledgment when it receives data for the first time. In an incentive scenario, this situation is hard to handle. Should the source pay some credit for the relays which send the data to the destination late? If so, how can the source know their work, and how much credit should the source assign for them? Clearly, from the perspective of the source, this late delivery is meaningless. However, if it does not pay for the later relays, this type of incentive mechanism might not work. This is because the relays will very possibly get nothing to help the source. In addition, in multicast scenarios, there exist multiple acknowledgments for one piece of data from different destinations. Thus, there exists four types of relative priorities: different data, the same data, acknowledgments for different data, and acknowledgments for the same data. We should assign the four above relative priorities carefully, or the network can jam with a limited buffer.
| Algorithm 1: Priority-based compare-split routing |
| Input: Destination set D = , , …, , , …, , , …, . social status of and and relative priority α Output: The data exchange result of two nodes.
|
5. Performance Analysis
In this section, we analyze the theoretical result for the proposed compare-split scheme. We prove that the compare-split scheme is the optimal split algorithm. Furthermore, we address the expected delivery delay in the exponential contact frequency distribution between nodes.
5.1. Optimal Split Algorithm
The motivation for our proposed scheme is to ensure that each message can be buffered in the node, which has a relatively high probability of reaching the corresponding destination, and thus minimizes the expected delivery delay.
Suppose and is the destination set of messages in nodes a and b’s buffers, respectively. We would like to maximize the combined delivery probability of the messages in a and b as follows:
Lemma 1.
Suppose and are two subsets, as results of the destination partition. is called the forwarding difference between nodes a and b for destination i. Maximum combined probability occurs when for each and ,
Proof.
It is clear that any other partition can be generated through a sequence of swaps of messages between two nodes, a and b. We show that each such swap will deteriorate the combined probability. Suppose a message buffered from is assigned into . Based on the split process, we will always have the condition , that is, , or
Note that is the combined probability involving destinations i and j, whereas is the combined probability after the swap of i and j, which decreases the overall combined contact probability.
Theorem 1.
If we consider the priority of messages and buffer constraint, the proposed priority-based compare-split scheme achieves a maximum feasible combined probability.
Proof.
When the buffer sizes are enough, nodes a and b will exchange all the messages as the proposed partition, and thus achieve the maximum combined probability, according to Lemma 1. When the buffer sizes are not enough for nodes a and b to exchange all the messages, the changeable subset of messages are exchanged as the proposed partition, and thus achieve the partial maximal combined probability. This is because the remaining messages do not have an opportunity to exchange. Thus, our priority-based compare-split scheme achieves a maximum feasible combined probability according to Lemma 1.
This optimal split algorithm can partition the destinations to nodes with a higher probability; hence, the delivery latency of the message is reduced.
5.2. Case Study in the Exponential Contact Frequency Distribution
There is a case study, where the nodes’ contact probabilities follow the exponential distribution with a contact rate of λ. Literature [8,11] shows that people’s contact frequencies follow such distribution. It means that nodes have a probability of meeting each other within time T. In a realistic application scenario, we only care about whether the messages can be sent to the destination before the deadline or not. Based on the assumption above, the probability of the message being delivered to the destination at time t after it enters the buffer can be given by
As we are only interested in delivered messages, the probability function given above becomes a conditional probability for the messages that are delivered:
where denotes the probability that the destination is reached before τ, which is given by the cumulative probability distribution of . Therefore, the expected waiting time of a delivered message can be written as
From Equation (6), we can get the conclusion that the expected delay of delivered messages will be less than . Combined with Equation (5), we can calculate the priority of messages by using the proposed method.
6. Experiments
In this section, we will demonstrate that the proposed scheme is an efficient mechanism to accelerate message dissemination in MSNs. Two performance metrics are used: (1) Delivery ratio: the number of messages which arrive at corresponding destinations before TTL out of all the generated messages in a certain interval; (2) Latency: the average duration between a message’s generation and the arrival time at the destination. Efficient means that the message with a high priority can be transmitted to the destination in a low delay, and high delivery ratio.
6.1. Experiment Methods and Setting
During the experiment, we use not only synthetic mobility models, but also real traces, to verify the efficiency of the proposed scheme. We will compare the delivery ratio and latency in each trace.
(1) Uniform mobility: In synthetic mobility models, we set up a network with 20 nodes. Among them, five nodes are set as source nodes and five nodes are set as the destination nodes. The social status of nodes follows the uniform distribution model. The contact probability is generated based on the social status to satisfy Equation (1). We set a 10,000 s contact history in our simulation, and, every one second, new data generates in the network randomly within the source nodes. The contact event is randomly generated, and the contact number is proportional to the contact probability of nodes.
(2) The real trace: We use the real trace Infocom 2006 [30] in our simulation, which has been widely used in MSN routing simulations. This dataset consists of contact traces between short-range Bluetooth wearable devices (iMotes) carried by individuals. Groups of participants are asked to carry small devices (iMotes) for four days during the INFOCOM 2006 conference. The contact information of the 78 participants are recorded in the iMotes. Furthermore, 20 stationary (long range) iMotes are placed in the experiment. There are 223,657 contacts between these nodes during the 342,915 s. Every 50 s, new data is randomly generated in our simulation. In addition, among them, 10 nodes are set as the source nodes and 10 nodes are set as the destination nodes.
By using these synthetic mobility models and the real trace, we further set the buffer constraint. We do not consider the bandwidth constraint in this paper, which is reasonable since the current wireless communication speed is fast [31], e.g., more than 100 Mbps, compared with the size of the messages, typically less than 50 MB. To simplify the simulation, we assume that the size of data and acknowledgment is the same.
6.2. Compared Algorithms
For the contact probability estimation, we compare our algorithm with the direct probability estimations, which forwards messages based on the contact probability between nodes [14]. As for the priority, we can set the remaining time of messages as a criterion [32] and our proposed priority setting. The combination of the above probability estimation and priority setting is four algorithms. Furthermore, we use the epidemic algorithm [33] as the baseline, which copies the message once a relay encounters another relay. In the remainder of this paper, we will use compare-priority, compare-deadline, direct-priority, direct-deadline, and epidemic to represent these five algorithms, respectively. They are denoted as CP, CD, DP, DD, and EP algorithms in the following, respectively.
6.3. Simulation Results
The results can be seen from the Figure 7, Figure 8, Figure 9 and Figure 10. Since we set the same data generation ratio, the message delivery number can be used to represent the delivery ratio in our simulation.
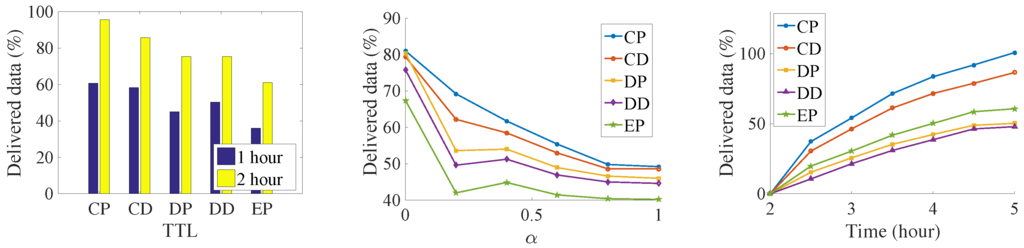
Figure 7.
Number of delivered data in the Infocom2006 trace.
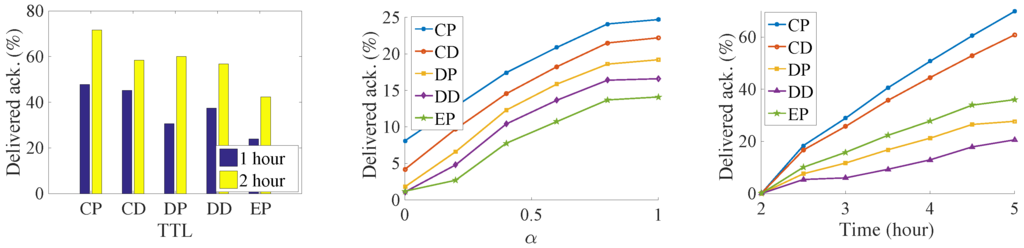
Figure 8.
Number of delivered acknowledgments in the Infocom2006 trace.
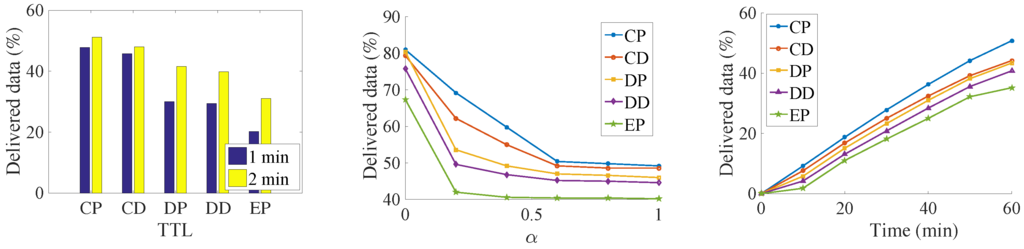
Figure 9.
Number of delivered data in the synthetic trace.
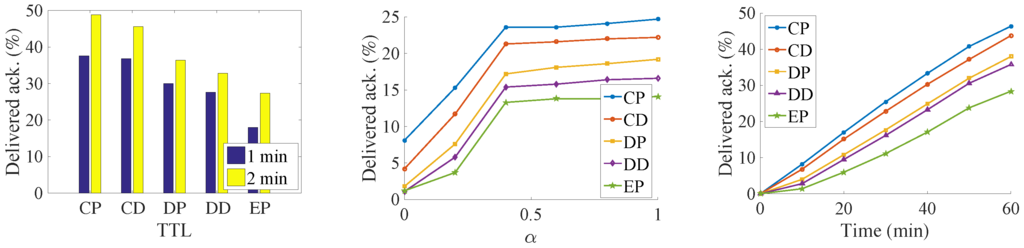
Figure 10.
Number of delivered acknowledgments in the synthetic trace.
We try to find the influence of the TTL for the delivery ratio, so we increase the TTL of the messages. Both the delivery number of data and the acknowledgment increase with an increase in data’s TTL. It is because that, along with the increasing of data’s TTL, data has a larger opportunity to be delivered before their deadline. At the same time, more acknowledgments are also generated. As a result, more acknowledgments are sent back to their sources. It is a near-linear increase in the Infocom2006 trace with the increase of the TTL. For the synthetic trace, the delivery number increases very quickly before convergence. Then, all the messages are sent to the destination when TTL is large. Any further increase of TTL is meaningless but consumes more buffer resources. Among the five algorithms, the CP algorithm always has the best performance. It is followed by the CD, DP, DD, and EP algorithms. The proposed method delivers 33% data and 22% more acknowledgments than the DD algorithms do. The EP algorithm achieves the worst performance; since lots of message are generated, the old message is soon dropped.
We try to find the impact of the relative priority in the message delivery ratio. The results show that, along with the increasing of α, the amount of delivered data decreases, and the number of delivered acknowledgments increase at the same time. This margin decreasing phenomenon appears clearly in the synthetic trace. For the Infocom2006 trace, this phenomenon just shows in the proposed CP and CD algorithms. The reason is that, with the increasing priority of acknowledgments, the messages cannot be exchanged for the better relays in the limit contact opportunity. Thus, more and more messages are buffered into the intermediate nodes until time is out, and thus the generation ratio of the data decreases.
In addition, we slice the time into small slots and want to find out how much data has been successfully delivered in each slot. The simulation shows that the dissemination delay also follows the same order as above—that is, CP, CD, DP, DD, and EP. This means that our proposed algorithm not only delivers more data, but also does so at a low delay. In the Infocom2006 trace, we notice that different contact estimations have a big influence on the number of messages that can be transmitted via the priority setting. However, the priority setting does not have such a big influence on the message delivery amount. There also exists a big performance gap between the CP, and the CD with the remaining three algorithms, which also show the importance of the weakly connected relationship with the destination. The CP algorithm delivers more than two times the data and three times the acknowledgment of the DD algorithms. In the synthetic trace, the difference between the five algorithms is not so significant; the reason might be the uniform setting of the encounter. Therefore, the influence of relay selection is not so important.
From the above experiments, we can clearly find that our proposed algorithm does the data dissemination in a low delay. At the same time, since data is transmitted faster, more data is transmitted into their destinations respectively, which, on the other hand, increases the delivery ratio of acknowledgment in the network. The results demonstrate the importance of the indirect relationship with the destination.
7. Conclusions
In this paper, we propose a generic scheme for the mixed data and acknowledgment dissemination problem with buffer constraint in mobile social networks. A generic routing algorithm, priority-based compare-split, is proposed. This algorithm evaluates relays’ forwarding abilities based on two criteria, social status and contact probability. Therefore, it evaluates relay’s ability more accurately. In addition, an adaptive priority-based exchange scheme is proposed within each type of message and the relative priority between different types of messages. Based on the new evaluation schemes to the relays and messages. Relays conduct buffer exchange, which thus maximizes achievable benefit. Two major application scenarios are further studied and explained in this paper. Extensive simulations show that our algorithm achieves a high delivery ratio in a low latency simultaneously. Our future work will focus on studying the situation where the size of messages is heterogeneous. In addition, contact durations will be considered in the network mode. Multiple copies of data and acknowledgments are another objective for future work.
Acknowledgments
This work is supported in part by NSF grants CNS 1461932, CNS 1460971, CNS 1449860, IIP 1439672, CNS 1156574 and CNS1461932.
Author Contributions
Ning Wang and Jie Wu worked on the high-level overview and solution. Ning Wang conceived and designed the experiments; Ning Wang analyzed the data and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The Global Mobile Data Traffic Forecast Update 2014-2019 White Paper. Available online: http://www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/whitepaperc11-520862.html (accessed on 2 February 2016).
- Fall, K. A delay-tolerant network architecture for challenged internets. In Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Karlsruhe, Germany, 25–29 August 2003; pp. 27–34.
- Ning, T.; Yang, Z.; Wu, H.; Han, Z. Self-interest-driven incentives for ad dissemination in autonomous mobile social networks. In Proceedings of the IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 2310–2318.
- Chen, B.; Chan, M.C. Mobicent: A credit-based incentive system for disruption tolerant network. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9.
- Hui, P.; Xu, K.; Li, V.O.; Crowcroft, J.; Latora, V.; Lio, P. Selfishness, altruism and message spreading in mobile social networks. In Proccedings of the 2009 IEEE INFOCOM Workshops, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1–6.
- Zhu, H.; Lin, X.; Lu, R.; Fan, Y.; Shen, X. Smart: A secure multilayer credit-based incentive scheme for delay-tolerant networks. Veh. Technol. 2009, 58, 4628–4639. [Google Scholar]
- Zhu, Z.; Liu, S.; Du, S.; Lin, X.; Zhu, H. Relative interpersonal-influence-aware routing in buffer constrained Delay-Tolerant Networks. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 4446–4451.
- Wu, J.; Wang, Y. A non-replication multicasting scheme in delay tolerant networks. In Proceedings of the 2010 IEEE 7th International Conference on Mobile Adhoc and Sensor Systems (MASS), San Francisco, CA, USA, 8–12 Novemebr 2010; pp. 89–98.
- Wang, N.; Wu, J. A general data and acknowledgement dissemination scheme in mobile social networks. In Proceedings of the 2014 IEEE 11th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Philadelphia, PA, USA, 28–30 October 2014; pp. 380–388.
- Hui, P.; Crowcroft, J.; Yoneki, E. Bubble rap: Social-based forwarding in delay-tolerant networks. IEEE Trans. Mob. Comput. 2011, 10, 1576–1589. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, S.; Cao, G. Routing in socially selfish delay tolerant networks. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9.
- Ramanathan, R.; Hansen, R.; Basu, P.; Rosales-Hain, R.; Krishnan, R. Prioritized epidemic routing for opportunistic networks. In Proceedings of the 1st international MobiSys workshop on Mobile Opportunistic Networking, San Juan, PR, USA, 11 June 2007; pp. 62–66.
- Burgess, J.; Gallagher, B.; Jensen, D.; Levine, B.N. MaxProp: Routing for Vehicle-Based Disruption-Tolerant Networks. In Proceedings of the IEEE INFOCOM 2006, Barcelona, Spain, 23–29 April 2006; pp. 1–11.
- Lindgren, A.; Doria, A.; Schelen, O. Probabilistic routing in intermittently connected networks. In Proceedings of the ACM SIGMOBILE Mobile Computing and Communications Review, San Diego, CA, USA, 19–20 September 2003; pp. 19–20.
- Guo, X.F.; Chan, M.C. Plankton: An efficient dtn routing algorithm. In Proceedings of the 2013 10th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), New Orleans, LA, USA, 24–27 June 2013; pp. 550–558.
- Mundur, P.; Seligman, M. Delay tolerant network routing: Beyond epidemic routing. In Proceedings of the 3rd International Symposium on Wireless Pervasive Computing, ISWPC 2008, Santorini, Greece, 7–9 May 2008; pp. 550–553.
- Wang, N.; Wu, J. InterestSpread: An efficient method for content transmission in mobile social networks. In Proceedings of the First International Workshop on Mobile Sensing, Computing and Communication, Philadelphia, PA, USA, 11 August 2014; pp. 13–18.
- Li, F.; Wu, J. LocalCom: A community-based epidemic forwarding scheme in disruption-tolerant networks. In Proceedings of the 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, SECON ’09, Rome, Italy, 22–26 June 2009; pp. 1–9.
- Mtibaa, A.; May, M.; Diot, C.; Ammar, M. Peoplerank: Social opportunistic forwarding. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–5.
- Pujol, J.M.; Toledo, A.L.; Rodriguez, P. Fair routing in delay tolerant networks. In Proceedings of the IEEE INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 837–845.
- Choo, F.C.; Chan, M.C.; Chang, E.C. Robustness of DTN against routing attacks. In Proceedings of the 2010 Second International Conference on Communication Systems and Networks (COMSNETS), Bangalore, India, 5–9 January 2010; pp. 78–85.
- Zhang, Y.; Zhao, J. Social network analysis on data diffusion in delay tolerant networks. In Proceedings of the Tenth ACM International Symposium on Mobile ad Hoc Networking and Computing, New Orleans, LA, USA, 18–21 May 2009; pp. 345–346.
- Liu, K.; Deng, J.; Varshney, P.K.; Balakrishnan, K. An acknowledgment-based approach for the detection of routing misbehavior in MANETs. IEEE Trans. Mob. Comput. 2007, 6, 536–550. [Google Scholar]
- Zhong, S.; Chen, J.; Yang, Y.R. Sprite: A simple, cheat-proof, credit-based system for mobile ad-hoc networks. Proc. IEEE INFOCOM 2003, 3, 1987–1997. [Google Scholar]
- Cha, M.; Kwak, H.; Rodriguez, P.; Ahn, Y.Y.; Moon, S. I tube, you tube, everybody tubes: Analyzing the world’s largest user generated content video system. In Proceedings of the 7th ACM SIGCOMM conference on Internet Measurement, San Diego, CA, USA, 23–26 October 2007; pp. 1–14.
- Kate, A.; Zaverucha, G.M.; Hengartner, U. Anonymity and security in delay tolerant networks. In Proceedings of the Third International Conference on Security and Privacy in Communications Networks and the Workshops, Nice, France, 17–21 September 2007; pp. 504–513.
- Chen, R.; Bao, F.; Chang, M.; Cho, J.H. Trust management for encounter-based routing in delay tolerant networks. In Proceedings of the 2010 IEEE Global Telecommunications Conference (GLOBECOM 2010), Miami, FL, USA, 6–10 December 2010; pp. 1–6.
- Liu, Y.; Wang, J.; Zhang, S.; Zhou, H. A buffer management scheme based on message transmission status in delay tolerant networks. In Proceedings of the 2011 IEEE Global Telecommunications Conference (GLOBECOM 2011), Houston, TX, USA, 5–9 December 2011; pp. 1–5.
- Pan, D.; Ruan, Z.; Zhou, N.; Liu, X.; Song, Z. A comprehensive-integrated buffer management strategy for opportunistic networks. J. Wirel. Commun. Netw. 2013, 2013, 1–10. [Google Scholar]
- James, S.; Richard, G.; Jon, C.; Pan, H.; Christophe, D.; Chaintreau, A. CRAWDAD Data Set Cambridge/haggle (v. 2006-01-31). 2006. Available online: http://crawdad.org/cambridge/haggle/ (accessed on 29 May 2009).
- Pyattaev, A.; Galinina, O.; Johnsson, K.; Surak, A.; Florea, R.; Andreev, S.; Koucheryavy, Y. Network-Assisted D2D Over WiFi Direct. In Smart Device to Smart Device Communication; Springer International Publishing: Cham, Switzerland, 2014; pp. 165–218. [Google Scholar]
- Balasubramanian, A.; Levine, B.; Venkataramani, A. DTN routing as a resource allocation problem. In Proceedings of the 2007 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Kyoto, Japan, 27–31 August 2007; pp. 373–384.
- Vahdat, A.; Becker, D. Epidemic Routing for Partially Connected ad Hoc Networks; Technical Report CS-200006; Duke University: Durham, NC, USA, 2000. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).