1. Introduction
Environmental monitoring has been an application domain with a large potential benefit from the utilization of wireless sensor networks since the development of this technology started. As wireless sensor networks do not require a fixed infrastructure, their flexibility of placement enables them to be used at practically any location. Environmental monitoring can thus utilize this technology in order to increase the amount of data being measured in an autonomous manner. As a result, a considerable number of case studies have been presented in the literature, which demonstrate the usage of wireless sensor networks in environmental monitoring applications, e.g., [
1,
2,
3,
4,
5,
6].
Despite the clear advantages of wireless sensor networks for increased temporal and spatial environmental measurements, a number of system challenges are yet to be overcome in order for wireless sensor networks to become a standard measurement instrument for the environmental sciences. One major challenge (though not limited to environmental monitoring) is the availability of a reliable long-term energy supply. In a similar manner to portable electronic devices, the individual sensor nodes within a wireless sensor network are typically powered by primary or secondary batteries. These energy sources, however, have a limited lifetime and energy storage capacity. Particularly, in application scenarios, which contain a large number of sensor nodes or are deployed in locations that are difficult to be revisited, the additional maintenance demands of manually exchanging or recharging depleted batteries are undesirable. Because the sensor nodes are required to operate autonomously over an extended period of time, however, the limited lifetime and the energy storage capacity of batteries are undesirable.
Energy harvesting—the extraction and conversion of ambient energy—in general and solar energy harvesting, in particular, have gained attraction in the research community in order to reduce the maintenance cost, which is introduced by the limitations of battery technology [
7,
8]. Utilizing an ambient energy source allows for the state-of-charge of an energy storage element to be continuously replenished. As a result, an optimally-dimensioned energy harvesting system can lead to the perpetual lifetime of the sensor node, which is only limited by the electronic degradation of the system itself, rather than its energy storage capacity.
In comparison to the energy supply from a battery, the dimensioning of a solar energy harvesting system requires a greater number of parameters to be taken into account. These parameters include the harvester architecture with its components to be dimensioned (e.g., the solar panel rating and storage element capacity), the application constraints and its effect on the load (e.g., the sensor node’s power consumption in a temporal manner), as well as the deployment location, which determines diurnal and annual cycles that have an effect on the available energy to be harvested. Consequently, the system dimensioning becomes a complex task and can typically not be performed in an easy manner. Nevertheless, the ability to efficiently dimension a solar energy harvesting architecture allows for a size and cost optimization to be performed without increasing the risk for system downtime, which has strong relevance to any wireless sensor system deployed outdoors.
Simulations have been proposed as a solution for the dimensioning problem. Using incoming and outgoing energy levels as the parameters, the behavior of the harvesting system, particularly, with respect to available energy, is simulated in order to evaluate its performance under the specific application constraints. As a result, a number of architectures and/or component choices can be evaluated prior to the deployment of the system. In order for these simulations to provide accurate results, however, the underlying harvesting system has to be modeled in an accurate manner. A number of modeling approaches have been proposed in the literature, but none of them seem to find wider attraction outside the research community.
The goal of this paper is to provide a review of the existing modeling approaches for solar-powered wireless sensor networks. We present, classify and analyze the common approaches in order to identify what hinders their adoption. The main focus lies on the utilization of simulations for dimensioning purposes, and each presented modeling approach will be evaluated in this regards. While the modeling of application and location parameters will be briefly addressed, the main focus lies on the modeling of the underlying hardware architectures for solar energy harvesting.
The structure of this paper is organized as follows.
Section 2 provides the background on solar energy harvesting architectures and a review of existing implementations, which demonstrates the variety of potential solutions and, thus, the challenge of choosing the most appropriate architecture and its components for a specific application at hand.
Section 3 introduces the underlying structure of solar energy harvesting models and reviews methods for the modeling of their individual modules. Based on the challenges of the existing methods that have been identified,
Section 4 proposes a data-driven modeling approach as a support method for the architecture selection and dimensioning. Finally,
Section 5 concludes the work and presents an outline for further investigations.
2. Solar Energy Harvesting Architectures
An energy harvesting system converts the energy from an ambient energy source to electrical energy in order to supply the connected load. In order for the system to accomplish this task, it typically contains a number of building blocks, which are depicted in
Figure 1 in a generalized manner. First and foremost, the system requires a conversion step, which allows for the incoming ambient energy to be converted to electrical energy. Moreover, as most ambient energy sources are intermittent or dynamic in the available energy levels, the energy harvesting systems commonly incorporate one, or several, energy buffers to enable a continuous supply. Finally, in order to perform safe and efficient charging of the energy buffers, as well as to provide acceptable voltage levels to the load, multiple regulation steps are commonly found in any energy harvesting system.
Figure 1.
Generalized architecture of an energy harvesting system.
Figure 1.
Generalized architecture of an energy harvesting system.
For solar energy harvesting, in particular, the energy conversion takes places through a solar panel, which provides an output current as a function of the solar irradiance and the terminal voltage. As the resulting I-Vcharacteristic is non-linear, the output power level is dependent on the working point of the panel. Maximum power point tracking (MPPT) is thus commonly integrated into the input regulation for large-scale solar energy harvesting systems, while it is argued upon whether it is also suitable for small-scale systems [
9,
10]. Because solar energy harvesting systems are required to equalize the diurnal and seasonal variations of the incoming solar energy, they typically include energy buffers in the form of batteries and/or capacitors. Furthermore, based on the energy storage technology that has been selected, additional charge management and protection circuits might be required.
The overall aim of the majority of solar energy harvesting systems is to supply a load with power in a continuous manner. Energy-neutral operation is a requirement for the system in order to fulfill this aim. Kansal
et al. [
11] defined energy-neutral operation through the condition:
where
is the supplied power by the energy converter and
is the consumed power by the load at time
t, respectively. Furthermore,
η denotes the charging efficiency,
the leakage power and
the initial state of charge of the energy storage at time
. In essence, energy-neutral operation is achieved if the energy demand of the load can be provided by the energy converter (
i.e., the solar panel) or the energy reservoir at any moment in time. The capability of the energy buffer to equalize insufficient ambient energy levels depends on the respective state of charge, which is affected by previous charge and discharge conditions, as well as the continuous losses.
Consequently, a solar energy harvesting system should be dimensioned in such a way that it enables an energy-neutral operation under predefined location and application constraints.
2.1. Solar Energy Harvesting Implementations
Solar energy harvesting has been identified early on as a potential solution to the power supply challenge in wireless sensor networks [
12,
13]. As a result, a plethora of different architectures and systems have been proposed in the literature [
14,
15,
16,
17,
18,
19,
20,
21]. This section provides an overview of the existing architectural solutions and implementations, and it illustrates the underlying challenge for the dimensioning task to be performed by the simulation tools. Due to the vast amount of existing systems, a selection has been made that covers the major variations in system architecture, component choice and implementation. For further details, we refer the reader to the respective literature of the individual systems, as well as survey papers, e.g., [
22].
A number of wireless sensor network case studies for environmental monitoring utilize off-the-shelf solar energy harvesting systems, which are typically composed of solar panels with ratings of the order of several watts, lead-acid batteries and commercial charge regulators [
2,
23]. While these solutions work well for applications with a large physical node size and considerable energy demands, they do not scale down in an efficient manner. Consequently, these solutions typically dominate the physical size of the sensor node and require additional resources in order to convert the 12 V battery voltage to adequate levels for the node’s power supply.
This has led to a number of solar energy harvesting systems that directly address the needs of wireless sensor nodes. An overview of these systems, along with their individual implementation choices, is given in
Table 1. The greatest variation in these systems can be observed in the implementation of the input regulation and the energy storage, which are, in addition, tightly linked to each other. The typical energy storage technologies include secondary batteries and double-layer capacitors (DLCs). While secondary batteries, commonly lithium- or nickel-based, provide a larger capacity and, thus, can support sensor nodes that have a greater energy consumption, DLCs allow for a greater number of charge cycles to be performed, which ultimately increases the system lifetime in a solar energy harvesting scenario. Moreover, in [
15,
18], both storage technologies have been combined in a hybrid solution in order to utilize the advantages of each individual technology. In addition to the technology selection itself, the systems vary in the energy storage implementation, which includes the device capacity and the number of cells.
Table 1.
Overview of solar energy harvesting system implementations. DLC, double-layer capacitor; MPPT, maximum power point tracking.
Table 1.
Overview of solar energy harvesting system implementations. DLC, double-layer capacitor; MPPT, maximum power point tracking.
| System | Solar Panel | Input Reg. | Storage | Output Reg. |
|---|
| Heliomote [14] | 400 mW | – | NiMH | DC-DC Boost |
| Prometheus [15] | 200 mW | Pulse Charging | 2x DLC (22 F) | – |
| (Mote Software) | Li ion (200 mA h) |
| Everlast [16] | 450 mW | MPPT | DLC (100 F) | DC-DC Boost |
| (Mote Software) |
| Alippi et al. [17] | 400 mW | MPPT | NiMH (300 mA h) | – |
| (Dedicated Software) |
| Ambimax [18] | 400 mW | MPPT | DLC (22 F) | DC-DC Boost |
| (Hardware) | Li-Ion |
| Enviromote [19] | 2.4 W | DC-DC Buck/Boost | NiMH (2x 2,000 mA h) | DC-DC Boost |
| Dondi et al. [20] | 500 mW | MPPT | DLC (50 F) | DC-DC Boost |
| (Pilot Cell) |
| Sunflower [21] | PIN Photodiodes | DC-DC Boost | DLC (0.2 F) | – |
With respect to input regulation, a distinction can be made between those architectures that purely regulate voltage level compliance and those that perform maximum power point tracking (MPPT). However, there are even considerable differences in the implementation for each respective group. Taking MPPT implementations as an example, the solutions range from pure hardware implementations to software-based control on dedicated MCUs or the sensor nodes themselves. In individual cases, the input regulation is omitted entirely [
14], which requires the careful matching between solar panel and energy storage ratings.
Furthermore, some variations in the implementation of the output regulation and the solar energy converter can be observed. In the majority of cases, the output regulation, if required at all, is implemented in the form of a DC-DC boost regulator. The necessity of an output regulation, however, has been avoided in several cases by selecting a storage technology with a sufficiently high voltage rating or by combining multiple storage cells. In regards to the solar energy converter, the majority of systems utilized solar panels of similar ratings. While a panel with an output power of the order of hundreds of appears to be a popular selection, in a few cases, larger and smaller converters have been used, respectively.
In conclusion, there exists a large number of solar energy harvesting systems with different underlying architectures and different component implementations. This number will only grow as development in the research community continues. In the majority of the existing systems proposed in the literature, clear reasoning for the choice of panel rating and energy buffer capacity are not to be found. In order to select the most appropriate architecture and dimension its components for a specific application scenario, clear methods for the comparison and the performance evaluation are required.
2.2. Solar Energy Harvesting Evaluation
Although the number of proposed solar energy harvesting systems is high, a comparative system evaluation has only been performed in a limited manner. In most cases that have been presented in the literature, the proposed solar energy harvesting architecture has been implemented and was evaluated in an application-specific context. This is commonly performed by a laboratory or real-world deployment, which generates the measurement results on the performance of the system.
While this type of result documents the suitability of the architecture for the respective application and its energy demands, it does not allow for a conclusion on the general system performance to be made. As the individual application scenarios, however, have their respective application and location constraints, it is essential to be able to judge a system’s suitability also for other scenarios than the one for which the system was initially intended.
Comparative experimental studies are a potential solution, as the performance of multiple systems can be analyzed under the same conditions. There are, however, a number of reasons for an experimental evaluation method to be regarded as infeasible. These reasons include the high cost and time requirements for system reimplementation, the great number of conditions to be tested for, the difficulty of generating these conditions and the continuous development of system architectures.
Consequently, solar energy harvesting simulations have been identified as a more efficient method for system comparison and dimensioning. In order for this method to be effective, however, accurate system models are required. In the remainder of this paper, existing methods for solar energy harvesting system modeling will be presented and analyzed. Moreover, we will argue for new approaches for the modeling of energy harvesting circuit architectures.
3. Modeling of Solar Energy Harvesting Systems
Simulations of asolar energy harvesting systems are used for various purposes, including the integration of energy awareness in communication and networking protocols, the optimization of the energy harvester design and the prediction of long-term operability, which, in turn, can be used for component dimensioning. Regardless of the individual purpose of the simulation, accurate system models of the energy harvesting system are required for the simulation output to become meaningful.
Figure 2 provides an abstracted depiction of the model components that are required for a full energy harvesting simulation. In individual cases, a subset of these model components can be sufficient.
A solar energy harvesting system model principally consists of three components, namely an environmental model, a model of the harvesting unit and an application model. The environmental model describes the amount of available energy in the ambient environment of the harvesting system. In a solar energy harvesting context, this is typically the solar irradiation that will be the input for the conversion technology, for example, a solar panel. While the available energy level in solar energy harvesting scenarios has basic temporal and spatial variations, it is additionally influenced by less predictable factors, such as weather conditions, system setup and physical objects in the surroundings. The application model, on the other hand, describes the energy requirements of the application, which is typically performed by describing the load on the power supply in a statical or dynamical manner. Finally, the harvester model describes how the available energy in the environment is extracted and processed in order to supply the application. This includes the energy conversion and, potentially, the energy buffer that is utilized in the harvesting architecture, as described in
Section 2.
Figure 2.
Overview of the model components for an energy harvesting system simulation.
Figure 2.
Overview of the model components for an energy harvesting system simulation.
3.1. Application Modeling Methods
The modeling of the energy requirements of wireless sensor nodes is not limited to its utilization in the simulation of solar energy harvesting systems. It is generally used to describe the energy requirements of an application and its implementation, which allows, for example, for the comparison of different implementation options to be performed. Any wireless sensor network application requires its nodes to execute a number of tasks (e.g., sensor reading, processing and communication). Each individual task poses a certain energy requirement that is defined by the components involved and the time period that is required for the task execution. The energy requirement of an application can thus be described by the number of times each individual task is performed.
Many environmental wireless sensor network applications follow a sample-and-send structure [
24], in which a certain group of tasks is executed in a periodical manner. These time-driven applications are commonly utilized for data gathering purposes. As the same order of tasks is performed in distinct time intervals, the energy requirement of these applications can easily be predicted. The most common approach for describing the energy requirement of an application in these cases is to utilize the duty cycling principle, which provides the continuous average power consumption of the application based on the power levels and time requirements of the involved tasks. In a simplified form, this can be described as:
where
and
are the power consumptions during active and inactive periods and
δ is the duty cycle of the application, being defined as the ratio of the active period
to the overall period
T:
While Equation (2) only distinguishes between an active and an inactive state, it can easily be extended in order to include each individual task in the model. In this approach, it is upon the user to accurately describe the power levels and time periods for the tasks of the application to be classified.
While time-driven applications are dominant in the design space of environmental wireless sensor networks, event-driven and query-driven applications application do occur. A prediction of the exact number of tasks in these scenarios is difficult to be performed, as it depends on the actual number of events and queries. This means that probability parameters have to be included in the modeling of the node’s energy consumption, which will introduce a number of uncertainties in the load estimation. A bounding approach would be the common choice in these scenarios, which uses the minimum and maximum number of events, or queries, to be expected in order to estimate the duty cycle.
3.2. Environmental Modeling Methods
In solar energy harvesting, the most important function of the environmental model is the estimation of solar irradiation. Nevertheless, other environmental parameters, such as temperature and humidity, can have an influence on the system performance. Due to the limited investigation in existing methods, we will limit the focus at this stage on the modeling of solar irradiation.
In order to predict solar irradiation, two families of modeling methods are commonly used, namely statistical models and astronomical models. In essence, a statistical model utilizes historic measurements of solar irradiation in order to predict future solar irradiation values. This approach is commonly found in large databases, such as Meteonorm (
http://www.meteonorm.com), which collect measurement values of a large number of stations over a long period of time. The collected data is used to predict the solar irradiation to be expected at a location close, or similar to, the measurement points. While this method includes detailed information, such as weather conditions, its accuracy depends on the amount of available measurement locations and the extent of available historic data. Furthermore, variations due to the system setup (e.g., panel orientation and inclination), as well as local obstructions are typically not considered in the database, as this would require an extensive amount of measurement stations. A number of use cases of this approach have been presented in the literature, and improvement methods, for example, in order to include local obstructions, have been proposed [
25,
26,
27,
28,
29].
An alternative approach is the utilization of an astronomical model. As opposed to the prediction of solar irradiation based on measurement data, the astronomical model calculates the ideal solar irradiation as a function of the angle between the Sun and the solar panel [
30]. This angle depends on the solar panel inclination, the panel orientation, the latitude, the time of the day and the day of the year. Although this method can be used to predict ideal irradiation levels at any location in an accurate manner, it does not include any weather conditions or local obstructions. Its main advantage over the statistical model is the flexibility provided by the lacking requirement of historical measurements. Moreover, several improvement methods have been proposed in the literature that extend the basic astronomical model in order to consider non-ideal conditions in the prediction procedure [
28,
31].
3.3. Harvesting Architecture Modeling Methods
Assuming the knowledge or accurate estimation of the ambient energy levels and the application energy requirements, the solar energy harvesting architecture models are required to describe the transfer of energy from the environment to the load. In order to utilize the simulation results for the selection of an appropriate architecture and its component sizing, the architectural model must be sufficiently accurate to model individual architectural properties.
The modeling methods proposed in the literature can roughly be distinguished between high-level and low-level models. In this, a high-level approach describes the system behavior as a whole, for example, by introducing an energy transfer efficiency between the actual irradiation and the sensor node. These models are typically independent of the actual hardware implementation, but attempt to abstract the parameters of interest with respect to the simulation purpose. As a result, the model can be formulated in an analytical fashion [
31,
32], which allows for an implementation in computational simulators to be performed in an easy manner. This is of particular interest if the model is used in combination with other analytical models in order to evaluate, for example, energy-aware network protocols or adaptive sampling algorithms. Because this modeling method does not have a direct representation of the underlying architecture, it is important that the abstraction includes all parameters that are required to describe the variations between any architecture to be selected. At the current state of the research, it is difficult to evaluate the existing models on this capability, as the proposed models are only evaluated on single architectures. It appears, however, that there will be difficulties in reflecting the consequences of specific architecture implementation choices, which is required in order to support the selection and dimensioning process in the system design.
Low-level modeling methods, on the other hand, are highly architecture specific. A common method is the modeling of the individual components or modules of which the harvesting architecture is composed. Similarly to the implementation of an electronic system, these component models are then combined into a system model in order to describe the system behavior. The majority of solutions that are presented in the literature are based on equivalent circuit models, which allow for an accurate electrical behavior of the respective components or component modules to be captured. Moreover, this approach allows for existing component models to be reused in order to model new architectures. While the underlying modeling methods remain similar, a number of different implementation methods have been proposed, which range from the derivation of analytical descriptions to the implementation in specific software environments, such as SPICE and Simulink [
33,
34,
35]. A limitation of the equivalent circuit modeling is the difficulty in accurately describing the behavior of integrated circuits. While the basic components of solar energy harvesting architectures,
i.e., the solar panel, supercapacitors and batteries, have well-developed models [
36,
37], the modeling of integrated circuits is more challenging, as their specific design is usually unknown to the end user. As a result, most systems that have been modeled in this manner are rather simple and avoid the electrical modeling of their integrated circuits. Instead, the behavior of the integrated circuits is simplified, for example, by efficiency factors. This, however, appears to become a challenge for the utilization of this approach, as the number of integrated circuits, and their complexity, increases in solar energy harvesting architectures. In addition, the component-based modeling method requires a great number of measurements to be performed in order to extract the parameters for matching the component models with the actually implemented components [
36,
37].
4. Data-Driven Architecture Modeling
Both of the previously presented architecture modeling approaches possess their individual advantages and disadvantage for usage as support to the architecture selection and component dimensioning problem. While the high-level modeling approach is applied on the system level and, thus, allows for a more flexible adaptation and a faster application, it does not reflect architecture-specific variations and detailed implementation choices. In contrast, the low-level approach is applied on the component level and, thus, provides a high level of detail. As a consequence, the architecture-specific variations and implementation choices can be accurately described by the model, but result in the requirement of a great number of measurements to be performed in order to classify the system to be modeled. For usage in the architecture comparison and the component dimensioning, a generic modeling method is required that can accurately reflect the differences of individual architectures and their components, but, at the same time, is easy to apply to a great number of architectures and implementations. Both modeling techniques, presented previously, require a detailed understanding of the underlying architecture in order to be applied, which hinders their adoption outside of the solar energy harvesting research community. In contrast, we believe that a data-driven approach has the capabilities to accomplish architecture-accurate, but easily-applied, modeling, and we propose that more research be focused on the evaluation of these methodologies.
4.1. State-of-Charge Modeling with Artificial Neural Networks
Data-driven modeling approaches are common in a number of different application areas. Even with respect to solar energy harvesting systems, data-driven approaches are used, for example, in order to predict solar irradiation based on historic measurement values [
25,
26]. Moreover, data-driven approaches have been utilized in order to capture the behavior of individual components, such as solar panels [
38]. A major benefit of artificial neural networks (ANNs) is their capability to learn from existing measurement data and to predict the system’s behavior without a detailed understanding of how the system or its underlying function actually look. In a solar energy harvesting context, this can be used in order to capture the behavior of a solar energy harvesting architecture implementation by mapping the significant output parameter to a number of relevant input parameters. Furthermore, this can be accomplished without the requirement of understanding the influence of each individual system component on the output parameter.
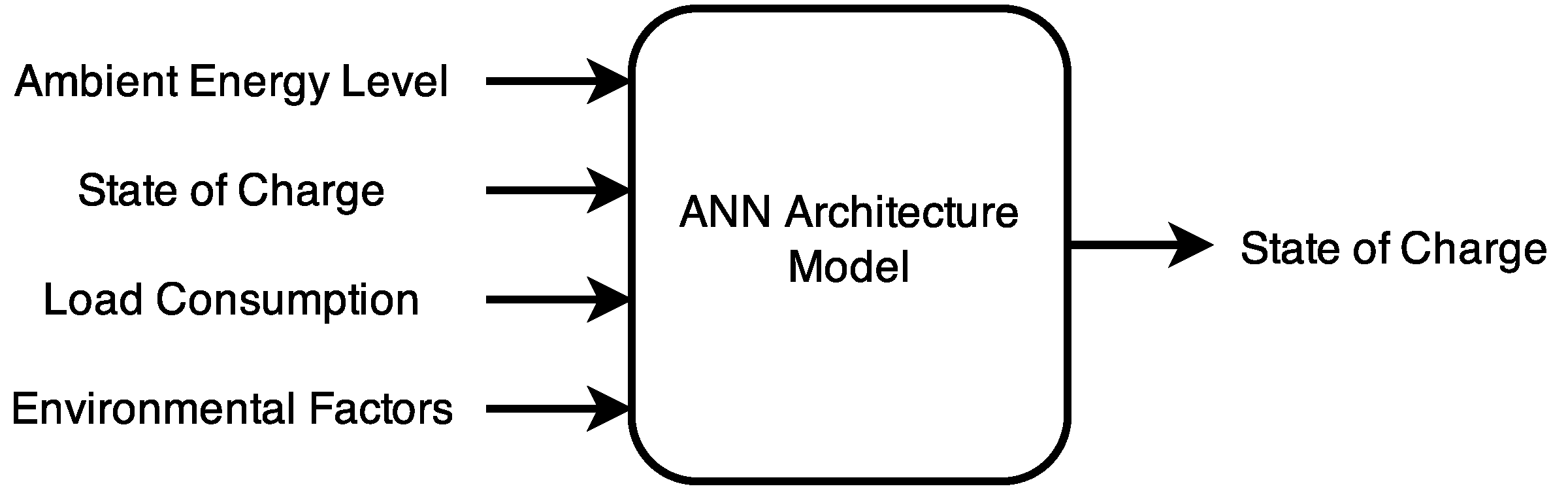
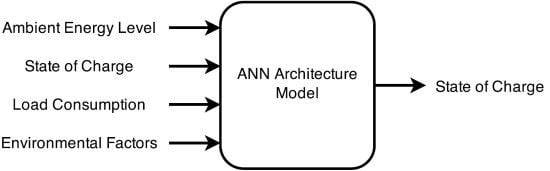
For the architecture comparison and component dimensioning, the state-of-charge (SOC) is the fundamental parameter to be modeled. Knowing the state-of-charge of the energy storage element at any moment in time enables the system designer to validate the suitability and performance of an architecture, or its component implementations, for a given application scenario (
i.e., the load conditions and the location).
Figure 3 depicts a high-level overview of this approach, in which a number of input parameters is utilized by an ANN model to predict the development of the state-of-charge. The most relevant input parameters, in this case, are the current solar irradiation, the current state-of-charge and the current load consumption. However, the method can easily be extended in order to include other input parameters, such as the ambient temperature. In order to generate the model in the first place, a supervised learning approach is utilized, which requires a dataset of the architecture for training purposes.
Figure 3.
Overview of the state-of-charge modeling with artificial neural networks.
Figure 3.
Overview of the state-of-charge modeling with artificial neural networks.
4.2. Training Dataset Generation
The generation of a training dataset for the supervised learning approach can principally occur in two manners. On the one hand, the dataset can be extracted from already gathered measurements (i.e., typically, the measurement results of a deployed architecture); on the other hand, it can be synthetically generated for training purposes.
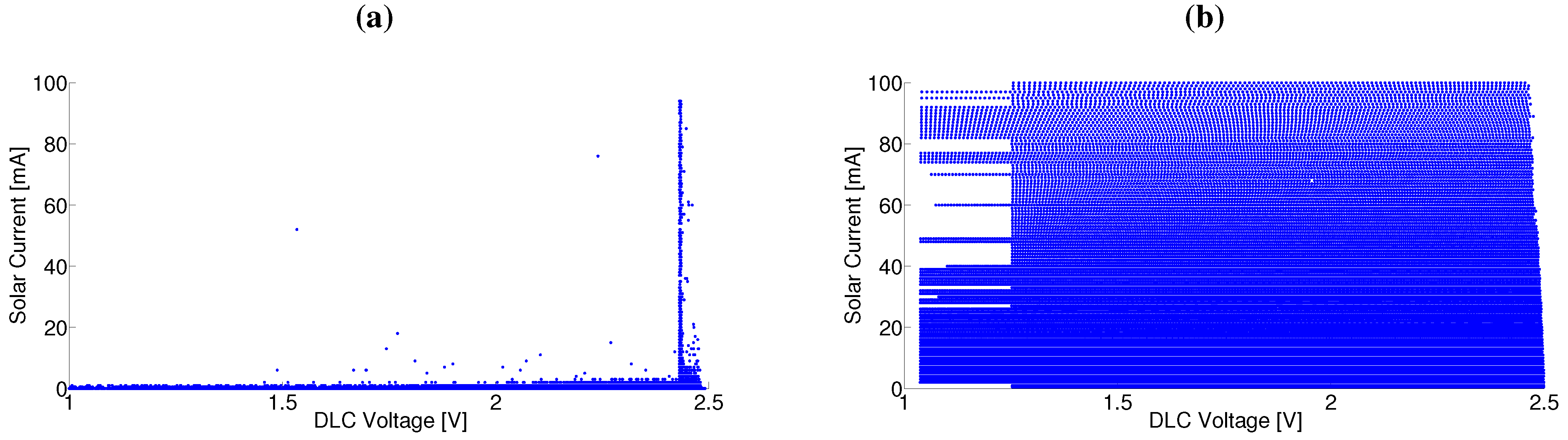
In the case that an architecture has been deployed previously and has generated a set of measurement values, the utilization of this dataset has the major advantage that no additional measurements have to be carried out. However, the likelihood that this empirical dataset will generate an accurate model is limited, which becomes obvious when investigating the example that is provided in
Figure 4a. The figure depicts the distribution of input parameters (
i.e., in this case, the input current and DLC voltage) in a two-dimensional space. For simplification, the load consumption and environmental factors are assumed to be constant. Moreover, the input current is used as a representation of the solar irradiation, while the DLC voltage is used to measure the state-of-charge. This example, which contains measurements of over 200 days with a five-minute resolution, indicates that an empirically generated dataset provides only limited coverage of possible input values. While the datasets includes a large number of both the state-of-charge values and the incoming energy, it is more likely that a large amount of incoming energy is observed when the state-of-charge is high. Due to the underlying architecture, which contains a double layer capacitor as its energy buffer element, this is not surprising, because the energy storage is rapidly charged during high irradiation conditions. The resulting distribution of the input parameter combinations, however, will provide training examples for only a subset of the possible input parameters. Therefore, the created model might be inaccurate in describing the behavior of the architecture for untrained conditions.
In order to overcome this challenge, a synthetically generated dataset can be used for training purposes. The main goal of this approach is the generation of a uniform dataset with high coverage of all potential input parameters in an efficient manner. This can be accomplished by using a controlled power source at the input of the architecture (
i.e., a controlled light source to bias the solar panel or a controlled current source in order to replace it) and a measurement unit in order to log the resulting effect on the state-of-charge.
Figure 4b illustrates the parameter distribution of this approach for one example case. In this case, a controlled current source has been used to generate the input energy parameter, whereas a multimeter measured the state-of-charge development of the DLC. Comparing the two parameter distribution plots in
Figure 4, it becomes clear that the synthetically generated dataset provides a much better fundament for the training of the architecture model. Moreover, the dataset can be generated in a highly effective manner, as the bias and measurements can be automated in a laboratory environment. Particularly in the case that deployment results are not gathered previously, the synthetically generated dataset can be obtained in a significantly shorter time period than collecting the required data empirically.
Figure 4.
Comparison of (a) an empirical training dataset that is extracted from deployment data and (b) a synthetically generated training dataset.
Figure 4.
Comparison of (a) an empirical training dataset that is extracted from deployment data and (b) a synthetically generated training dataset.
4.3. Preliminary Method Evaluation
Initial evaluation results of the proposed ANN modeling method have been obtained using a simple solar energy harvesting architecture. This architecture contains a double-layer capacitor as its energy buffer and has a direct coupling of the solar panel to this capacitor. A current rectification and over-voltage protection is used at the input stage to protect the solar panel and DLC, respectively. The output stage is composed of a DC-DC boost regulator in order to apply a constant supply voltage to the node, even in the case that the state-of-charge is low. For a more detailed description of the architecture, we refer the reader to the work presented in [
39].
In order to generate the ANN model, the MATLAB Neural Network Fitting Toolbox is utilized. The underlying model to be trained uses a two-layer feed-forward network with sigmoid hidden neurons and linear output neurons. A Levenberg–Marquardt back-propagation algorithm is used for training. Both, an empirical dataset and a synthetically generated dataset have been used to develop the models, respectively.
For the evaluation purpose, the models have been tested with a dataset of real-world measurements, containing more than 60,000 samples. The evaluation contains a model validation step and a full simulation step. During validation, the capability of the model to predict individual outputs based on input parameters is observed. The predicted state-of-charge is compared to the true state-of-charge based on true input parameters. In contrast, during simulation, the predicted state-of-charge is used as the new input parameter (i.e., estimation errors propagate to the input parameter), which results in a time series of the state-of-charge prediction.
Table 2 gives an overview of the performance of the modeling technique, both for a model created from empirical data and a synthetically generated dataset. Both evaluation steps (
i.e., validation and simulation) demonstrate the accurate prediction capability of the models with average percentage errors below 0.1% for validation and below 5% for simulation. Although the amount of small simulation errors increases for the model that has been trained with a synthetic dataset, the overall percentage error is reduced to
. A considerable difference between the validation error and the simulation error can be observed and was found to originate from error propagation. Single significant prediction errors in the model will result in an erroneous input parameter for the next prediction until the model corrects itself. In the architecture under evaluation, this is typically the case when the DLC is fully charged.
Table 2.
Overview of the model error distribution for models created from an empirical training dataset (TDS) and a synthetic TDS.
Table 2.
Overview of the model error distribution for models created from an empirical training dataset (TDS) and a synthetic TDS.
| Absolute Deviation | Empirical TDS | | Synthetic TDS |
|---|
| Validation | Simulation | | Validation | Simulation |
|---|
| 0.016% | 2.99% | | 0.013% | 15.88% |
| 0.006% | 2.17% | | 0.003% | 2.96% |
| 0.002% | 1.62% | | 0.002% | 1.41% |
| 0.008% | 1.16% | | 0.002% | 1.12% |
| 0.003% | 1.01% | | – | 0.35% |
| – | 0.3% | | – | – |
5. Conclusions
Solar energy harvesting is a suitable option to prolong the lifetime of environmental wireless sensor networks and can, potentially, lead to perpetual system operation. In order to optimize the solar energy harvesting module for a specific application, however, accurate and time-efficient methods are required. In particular, the selection of a hardware architecture and its component implementation lacks clear approaches to be performed.
In this paper, we have presented a summary of the existing work on solar energy harvesting architectures and their evaluation, which demonstrates the large variety of systems from which to select. Due to the large number of potential architectures, experimental comparison and evaluation methods become inefficient, which leaves system simulation as the remaining approach for the system comparison and dimensioning task. In order for the simulation to meet the accuracy requirements, however, accurate system models must be utilized. We have presented the existing modeling methods for available ambient energy, the energy consumption of the load and the solar energy harvesting architecture itself. Because the harvesting architecture and its implementation is the decisive module for the comparison and dimensioning task, the focus of this work lies in this unit.
A study of the existing methods has shown that the architecture modeling is typically performed in one of two manners. As the first option, the architecture can be modeled on a high abstraction level, which attempts to generate an analytical description of the architecture’s behavior on the system level. While this approach allows for a flexible implementation to be carried out and requires only a small number of parameters to be classified, its capability to reflect architectural differences and implementation choices in an accurate manner is uncertain. Alternatively, the architecture can be modeled on a low abstraction level, which includes the modeling of individual components within the architecture. As opposed to the high-level model, the low-level model reflects architectural differences in a more detailed manner, but requires a large number of measurements to be performed in order to classify all parameters.
As a consequence of these challenges, a data-driven approach based on artificial neural networks is proposed for the architecture modeling task. The goal of this model is to provide an accurate, but efficient, method for the description of an architecture’s behavior. Using experimentally obtained training data, the model can learn to predict the significant output parameter (e.g., state-of-charge) from a number of input biases and, thus, captures the behavior of the underlying system. The approach has been evaluated in a preliminary study, and the results show that the state-of-charge prediction occurs in an accurate manner with an average percentage error of <0.1% during validation and <2% during simulation. Moreover, the modeling development is highly efficient, as the training dataset generation occurs on the system level (i.e., no classification of individual components is required). Because a detailed understanding of the underlying architecture is not required in order to apply this modeling technique, the approach can easily be automated, which simplifies adoption outside the research community.
Nevertheless, the evaluation of the proposed method has been conducted in a limited scope only. In order to provide a clearer picture on the general applicability of this approach, it must be tested on a variety of system architectures and implementations. Moreover, additional investigations on the influences of the underlying ANN model are required. This includes, for example, the number of layers and neurons used in the network.