MIMO Underwater Acoustic Communications in Ports and Shallow Waters at Very High Frequency
Abstract
:1. Introduction
2. System Model
2.1. Source Signals
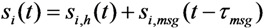
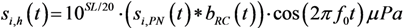
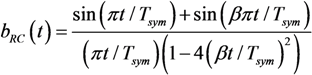
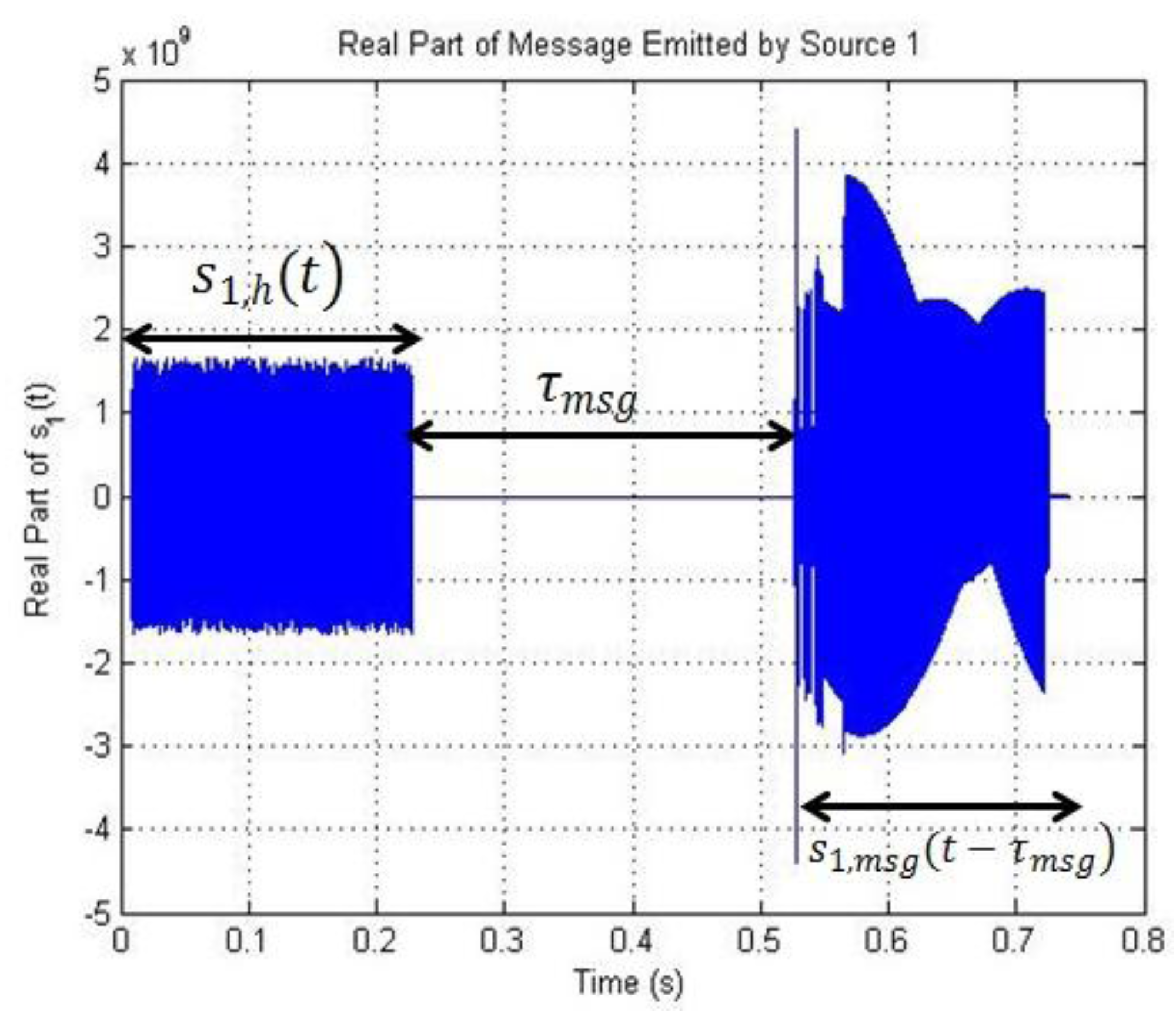
2.2. Received Signals
2.2.1. Channel Estimation
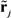 at receiver j can be written in matrix form [4,17]:
at receiver j can be written in matrix form [4,17]:
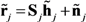
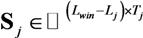 represents the augmented source signal array at the j th receiver.
represents the augmented source signal array at the j th receiver. 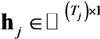 represents the augmented channel impulse response array.
represents the augmented channel impulse response array. 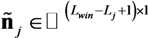 represents the noise array.
represents the noise array.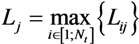 . Finally, Tj is the sum of the channel lengths over the total number of transmitters Nt, so that
. Finally, Tj is the sum of the channel lengths over the total number of transmitters Nt, so that 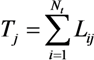 .
.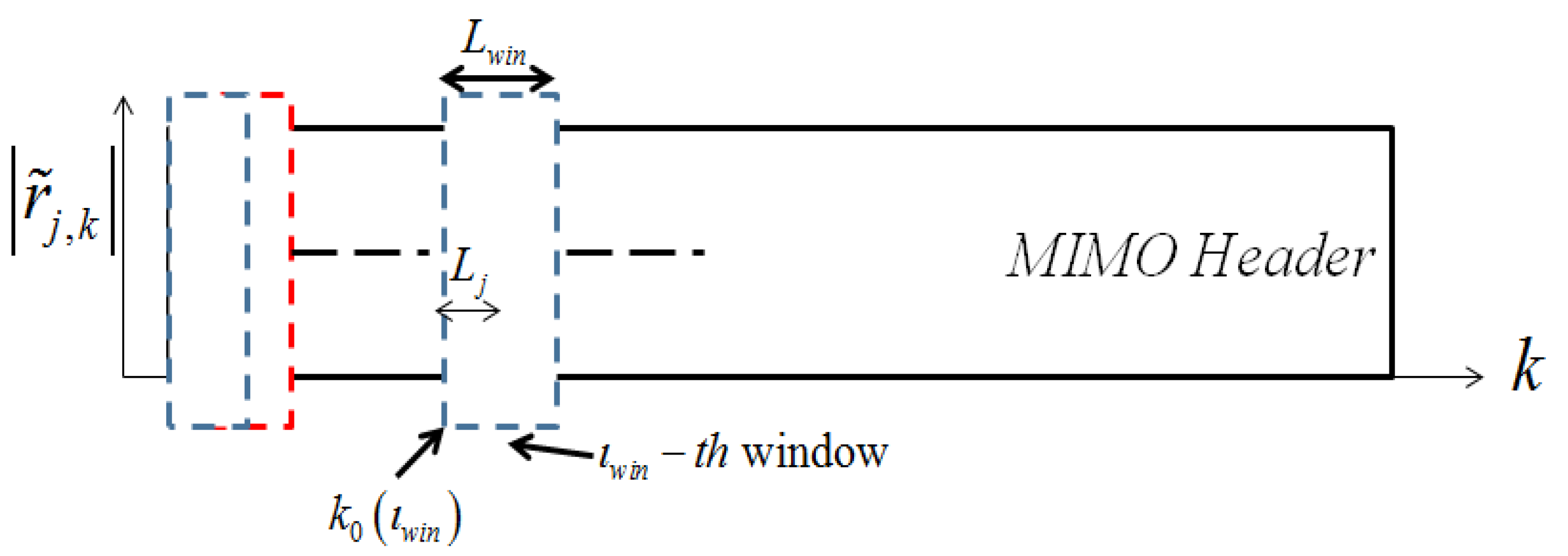
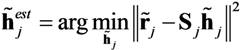
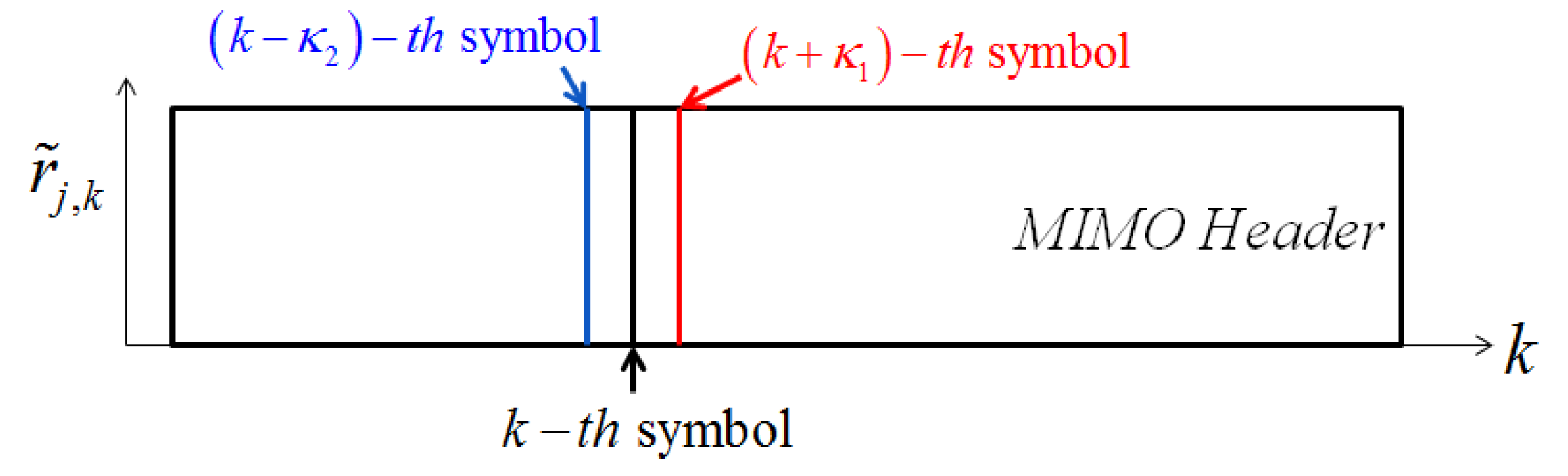
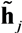 for every time window index twin,
for every time window index twin,
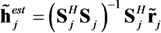
2.2.2. MIMO Deconvolution
2.2.2.1. Minimum Mean Squared Error Linear Equalization
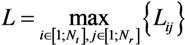
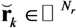 and
and 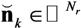 as the received signal and noise over the total number of hydrophones:
as the received signal and noise over the total number of hydrophones:
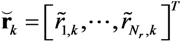
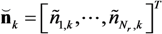
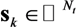 and channel impulse responses
and channel impulse responses 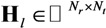 as:
as:
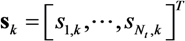
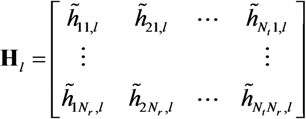
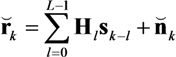
 ,
, 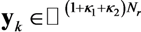 and
and  are defined as
are defined as
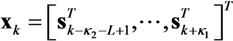
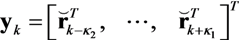
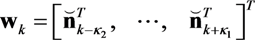
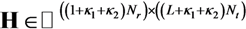 ,
,
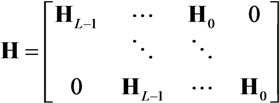
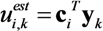
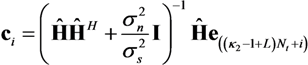
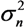 is the variance of the noise and
is the variance of the noise and 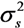 is the variance of the original sequence SI,K.
is the variance of the original sequence SI,K.  denotes a column vector of size (L + κ1 + κ2) Nt with 1 at index i and 0 at other positions.
denotes a column vector of size (L + κ1 + κ2) Nt with 1 at index i and 0 at other positions. 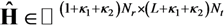 is the estimates of augmented channel matrix H or time window index twin Here, the estimated signal
is the estimates of augmented channel matrix H or time window index twin Here, the estimated signal  depends on length of the time window, which in turns depends on the measured channel response. If Nwin = 1, the channel is stationary over a message duration and
depends on length of the time window, which in turns depends on the measured channel response. If Nwin = 1, the channel is stationary over a message duration and
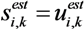
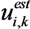 becomes a function of twin. In this case, the equalized signal for each sliding window is cropped and forms a section of the equalized output
becomes a function of twin. In this case, the equalized signal for each sliding window is cropped and forms a section of the equalized output  ,
,
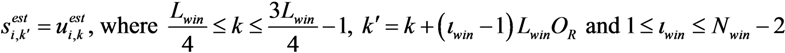
2.2.2.2. MMSE Interference Cancellation Linear Equalizer
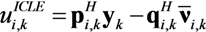
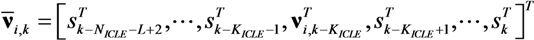
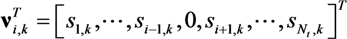
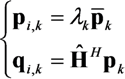
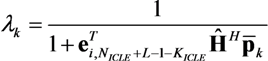
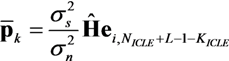
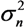 represents the noise variance. The ICLE estimate
represents the noise variance. The ICLE estimate 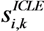 depend on the number of time windows used to perform the channel estimation, thus Equations (23)–(25) also apply to
depend on the number of time windows used to perform the channel estimation, thus Equations (23)–(25) also apply to 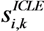 .
.3. Simulated and Experimental Results
3.1. Experimental Setup
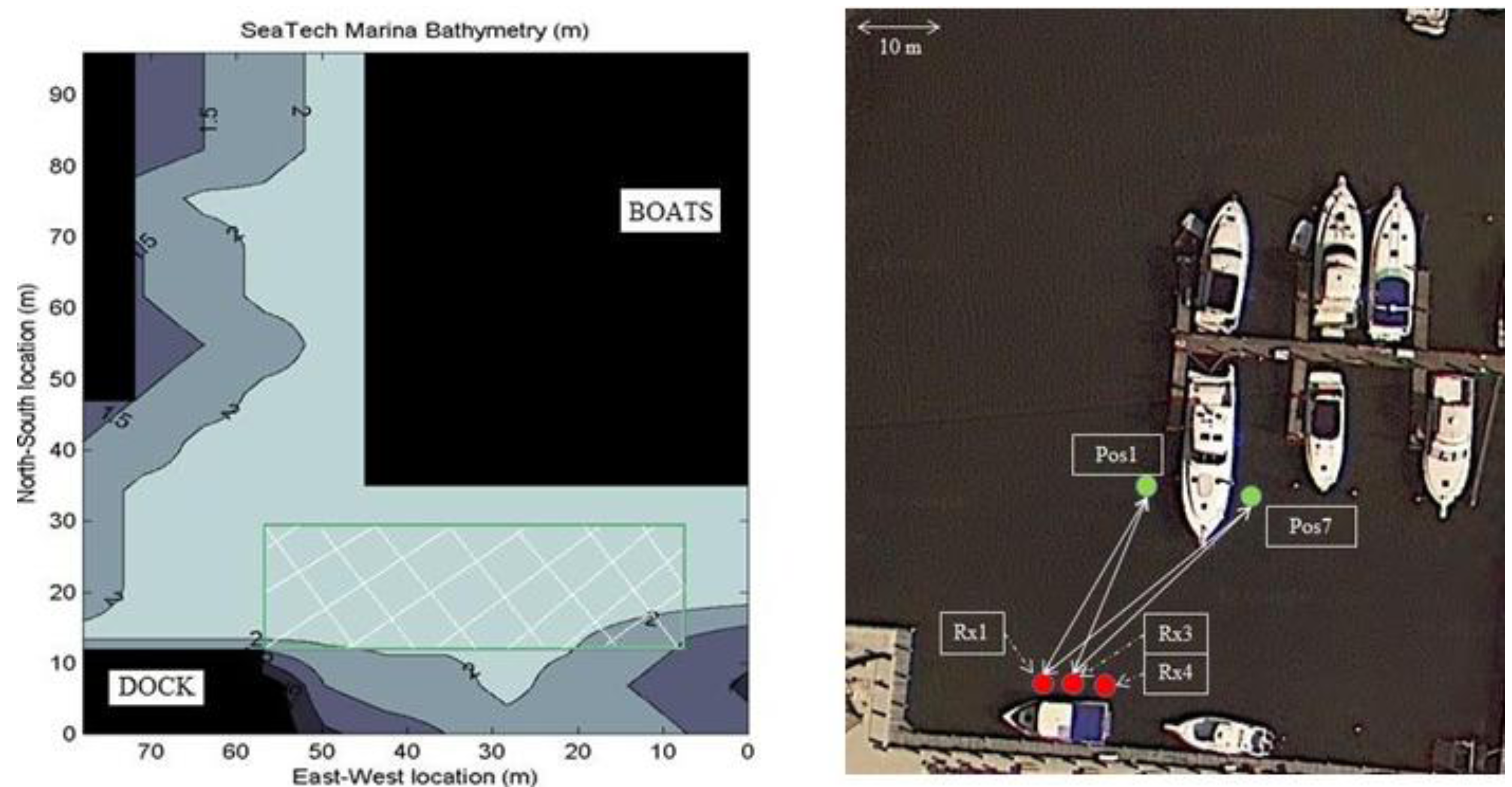
| Mission Number and Date | Source 1 Position | Source 2 Position | Receiver 1 Position | Receiver 2 Position | Number of Messages Retained |
|---|---|---|---|---|---|
| 1-07/27/2011 | Pos1 | Pos7 | Rx1 | Rx3 | 50 |
| 2-07/27/2011 | Pos7 | Pos1 | Rx1 | Rx3 | 50 |
| 3-08/29/2011 | Pos7 | Pos1 | Rx1 | Rx3 | 100 |
| 4-08/29/2011 | Pos1 | Pos7 | Rx1 | Rx3 | 100 |
| Distance on Figure 4 | Distance (m) |
|---|---|
| Rx1-Pos1 | 24 |
| Rx1-Pos7 | 27 |
| Rx3-Pos1 | 23.3 |
| Rx3-Pos7 | 25.8 |
| Pos1-Pos7 | 6.15 |
| Rx1-Rx3 | 2.68 |
| Mission Number and Date | SNR1(dB) | SNR2(dB) |
|---|---|---|
| 1-07/27/2011 | 27.1 | 27.3 |
| 2-07/27/2011 | 28.8 | 27.8 |
| 3-08/29/2011 | 30.9 | 34.3 |
| 4-08/29/2011 | 29.2 | 33.2 |
3.2. Simulation Parameters
| Name | Symbol | Value (units) | Name | Symbol | Value (units) |
|---|---|---|---|---|---|
| Sources Depth [4,17] | DSi | 1 m | Source Level | SL | 179 dB re 1 µPa @ 1 m |
| Receivers Depth [4,17] | DRj | 1.5 m | Noise Level | NL | 83.7 dB re 1 µPa |
| Water Depth [4,17] | DW | 3 m | Sampling Frequency | FS | 150 kHz in base band 750 kHz in pass band |
| Water Sound Speed [4,17] | C | 1,500 m/s | Symbol Rate | Dsym | 75 kHz |
| Water Density [4,17] | ρ | 1,023 kg/m3 | Carrier Frequency | f0 | 0 kHz in base band 300 kHz in pass band |
| Sandy Sediment Sound Speed [4,17] | Cb | 1,800 m/s | MIMO Sequence Duration | τh | 218.5 ms |
| Sandy Sediment Density [4,17] | ρb | 1,800 kg/m3 | Dead-Time Duration | τmsg | 300 ms |
| Sea Bottom Loss [4,17] | LSB | 5 dB | Correlation Threshold Parameter | Kthr | 20 |
| Beginning of Time Window [4,17] | k0 | 0 | Time Window Length | τwin | 518.5 ms |
| Number of Transmitters [4,17] | Nt | 2 | Number of Receivers | Nr | 2 |
| Distance Source 1 Receiver 1 [4,17] | R11 | 23.3 m | Distance Source 1 Receiver 2 [4,17] | R12 | 24 m |
| Distance Source 2 Receiver 1 [4,17] | R21 | 25.8 m | Distance Source 2 Receiver 2 [4,17] | R22 | 27 m |
3.3. Performance Metrics
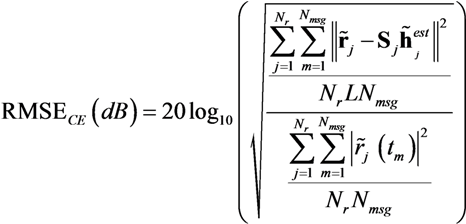
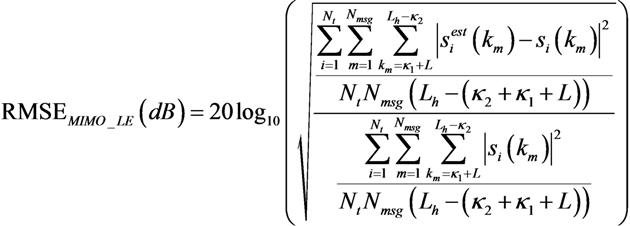
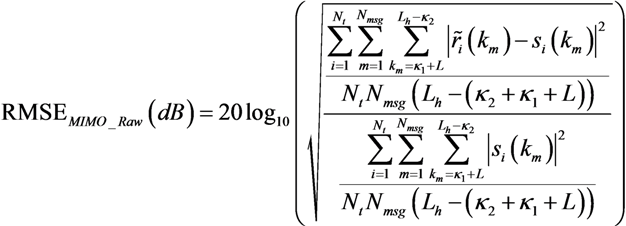
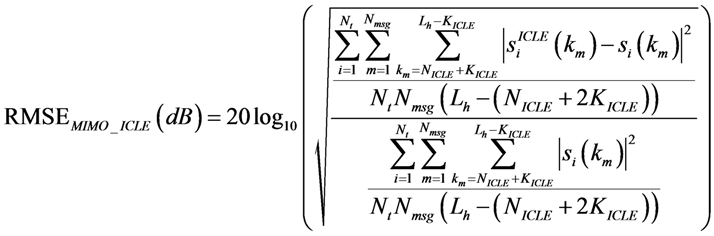
3.4. MIMO Channel Estimation Results
| TL(ms) | Simulated RMSECE (dB) | Experimental RMSECE (dB) |
|---|---|---|
| 0.667 | −9.5 | −0.4 |
| 1.333 | −12.5 | −0.9 |
| 2.0 | −18.8 | −4.1 |
| 2.667 | −34.7 | −4.9 |
| 3.333 | −34.7 | −6.2 |
| 4.0 | −34.7 | −9.1 |
| 4.667 | −34.8 | −11.4 |
| 5.33 | −34.8 | −25.7 |
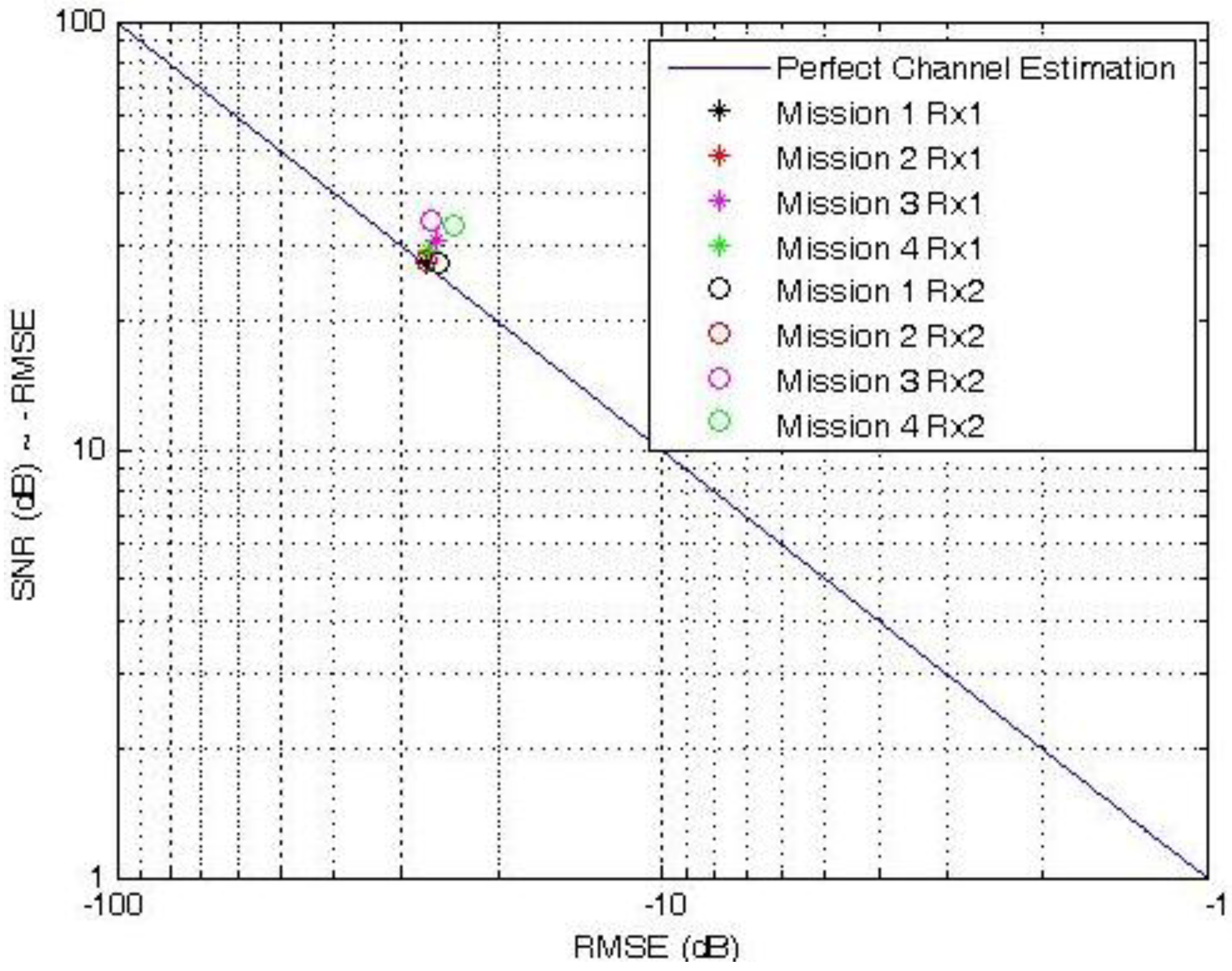
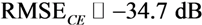 ), the experimental results on RMSECE differ. Indeed, the minimum RMSECE is obtained for TL = 5.33 ms (RMSECE = −25.7 dB) as shown in Table 5 and Figure 5. If, as explained earlier on, values higher than TL = 5.33 ms cannot be considered, the minimum value of RMSECE using experimental data is of the same order of magnitude as RMSECE in the simulation framework. The channel estimation can therefore be considered as very accurate.
), the experimental results on RMSECE differ. Indeed, the minimum RMSECE is obtained for TL = 5.33 ms (RMSECE = −25.7 dB) as shown in Table 5 and Figure 5. If, as explained earlier on, values higher than TL = 5.33 ms cannot be considered, the minimum value of RMSECE using experimental data is of the same order of magnitude as RMSECE in the simulation framework. The channel estimation can therefore be considered as very accurate. 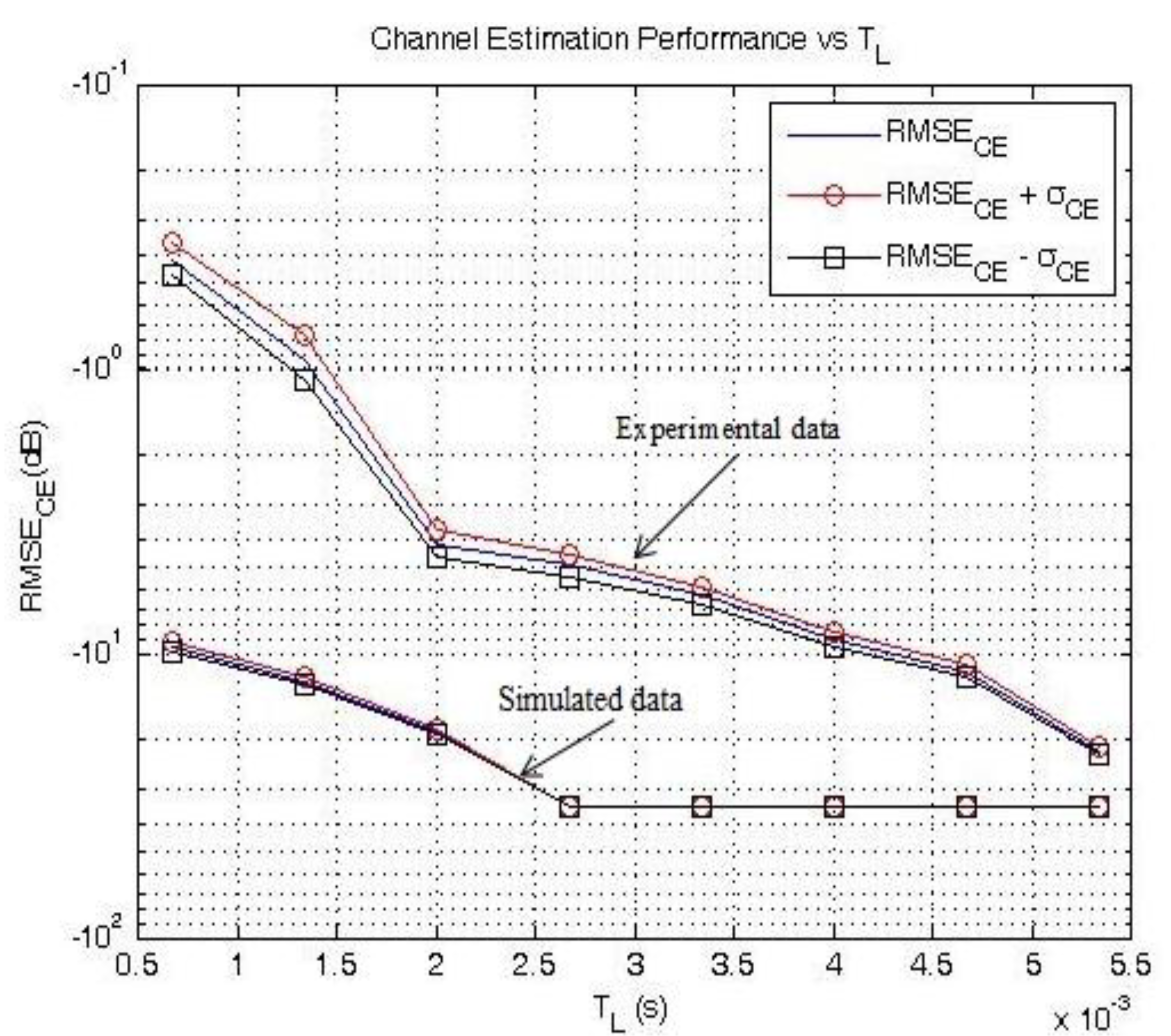
 , such that:
, such that:
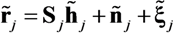
3.5. MIMO Deconvolution Results
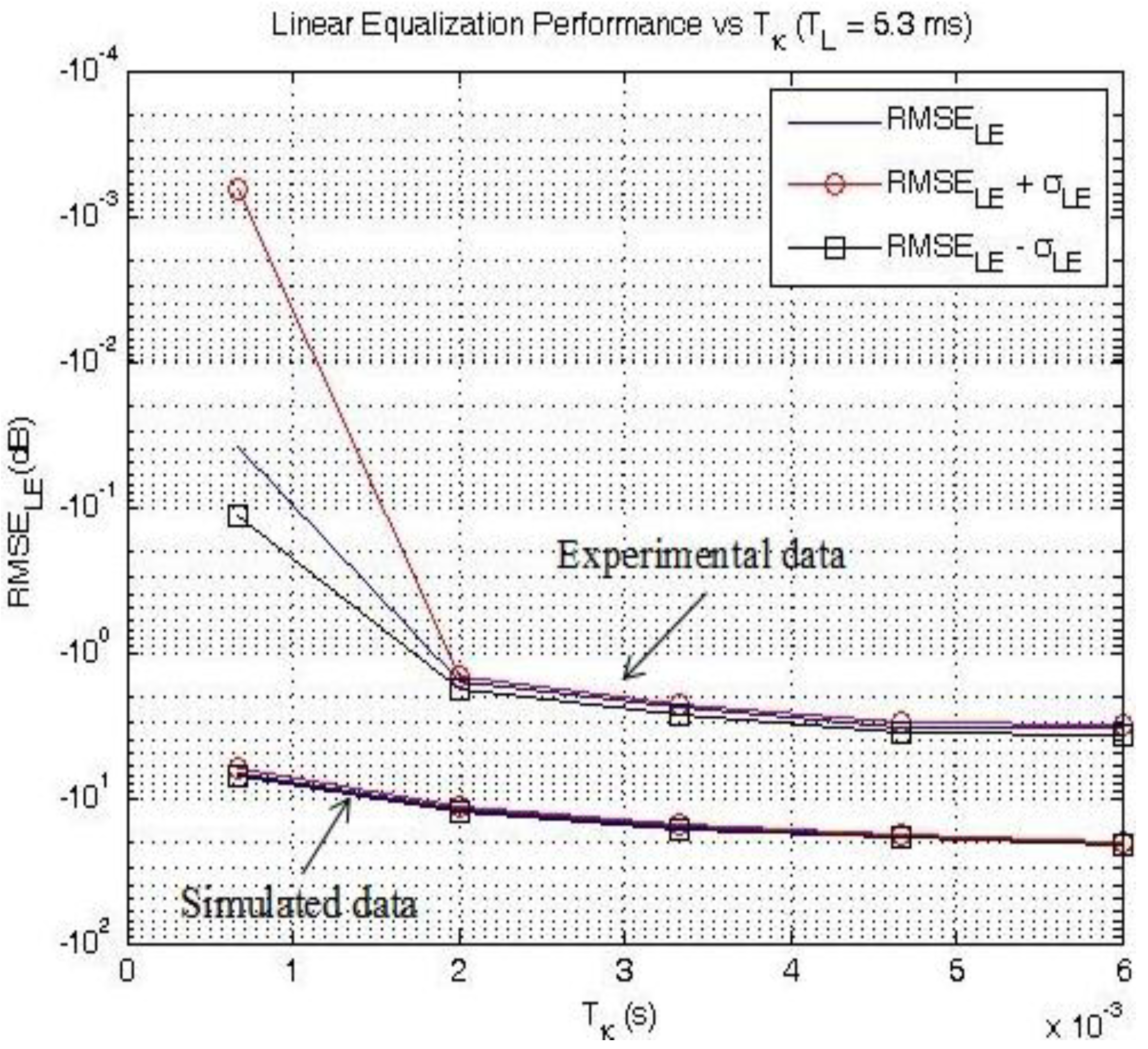
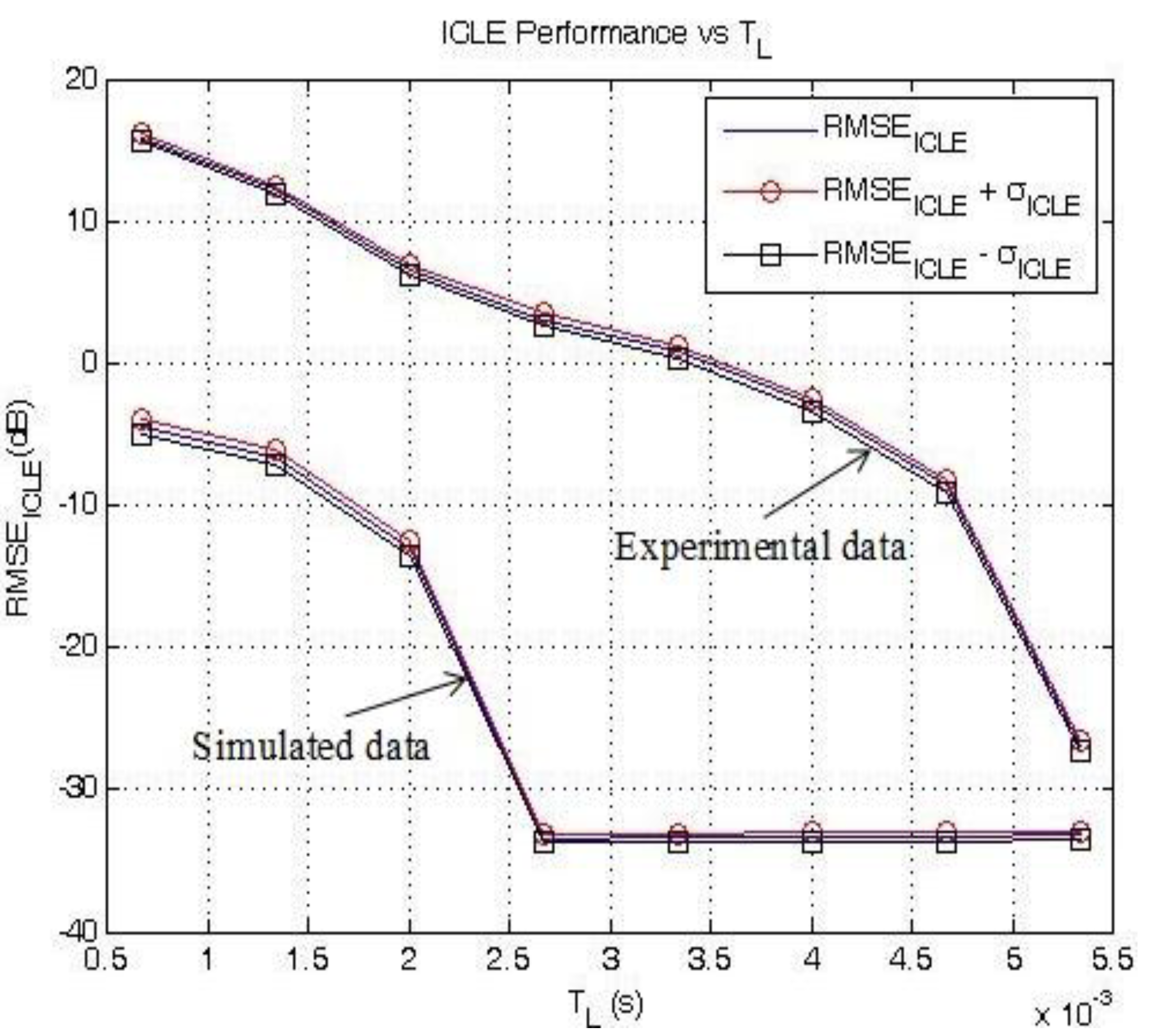
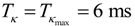 , which lead to the lowest RMSE values [17]. Both simulations and experimental results (averaged over the total number of missions carried out) are presented in Table 6. Clearly, RMSEMIMO_LE and RMSEMIMO_ICLE decrease as TL increases using either simulated or field data. Note that the equalizer length is limited to TL = 5.33 ms, as higher values of TL led to singularities.
, which lead to the lowest RMSE values [17]. Both simulations and experimental results (averaged over the total number of missions carried out) are presented in Table 6. Clearly, RMSEMIMO_LE and RMSEMIMO_ICLE decrease as TL increases using either simulated or field data. Note that the equalizer length is limited to TL = 5.33 ms, as higher values of TL led to singularities.| TL (ms) | RMSE MIMO_Raw (dB) | |
|---|---|---|
| Simulations | Experiments | |
| 0.667 ms, 1.333 ms, 2 ms, 2.667 ms, 3.333 ms, 4 ms, 4.667 ms, 5.33 ms | 0.04 | 3 |
| RMSE MIMO_Raw (dB) | RMSE MIMO_ICLE (dB) | ||||
|---|---|---|---|---|---|
| Simulations | Experiments | Simulations | Experiments | ||
| TL (ms) | 0.667 | 0.4 | 19.7 | −4.5 | 15.8 |
| 1.333 | −3.4 | 14.4 | −6.7 | 12.1 | |
| 2.0 | −10.3 | 8.3 | −13 | 6.4 | |
| 2.667 | −20.5 | 5.5 | −33.4 | 3.1 | |
| 3.333 | −20.5 | 2.2 | −33.4 | 0.7 | |
| 4.0 | −20.5 | −1.9 | −33.3 | −3 | |
| 4.667 | −20.5 | −3.9 | −33.3 | −8.8 | |
| 5.33 | −20.5 | −3.3 | −33.2 | −26.9 | |
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Beaujean, P.P.J.; Carlson, E.A. HERMES a high bit-rate underwater acoustic modem operating at high frequencies for ports and shallow water applications. Mar. Technol. Soc. J. 2009, 43, 21–32. [Google Scholar] [CrossRef]
- Beaujean, P.P.; Carlson, E. Combined Vehicle Control, Status Check and High-Resolution Acoustic Images Retrieval Using a High-Frequency Acoustic Modem on a Hovering AUV. In Proceedings of OCEANS 2010, Seattle, WA, USA, 20–23 September 2010; pp. 1–10.
- Beaujean, P.P. A Performance Study of the High-Speed, High-Frequency Acoustic Uplink of the Hermes Underwater Acoustic Modem. In Proceedings of OCEANS 2009-EUROPE, Bremen, Germany, 11–14 May 2009; pp. 1–6.
- Real, G.; Beaujean, P.P.; Bouvet, P.J. A Channel Model and Estimation Technique for MIMO Underwater Acoustic Communications in Ports and Very Shallow Waters at very High Frequencies. In Proceeding of OCEANS 2011, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–9.
- Tao, J.; Zheng, Y.R.; Xiao, C.; Yang, T.C.; Yang, W.B. Time-Domain Receiver Design for MIMO Underwater Acoustic Communications. In Proceedings of OCEANS 2008, Quebec City, QC, USA, 15–18 September 2008; pp. 1–6.
- Tuchler, M.; Singer, A.C.; Koetter, R. Minimum mean squared error equalization using a priori information. IEEE Trans. Signal Process. 2002, 50, 673–683. [Google Scholar] [CrossRef]
- Bouvet, P.J.; Hélard, M.; le Nir, V. Simple iterative receivers for MIMO LP-OFDM systems. In Annales des telecommunications; Springer-Verlag: Berlin, Germany, 2006; Volume 61, pp. 578–601. [Google Scholar]
- Bouvet, P.J.; Loussert, A. Capacity Analysis of Underwater Acoustic MIMO Communications. In Proceedings of OCEANS 2010 IEEE-Sydney, Sydney, Australia, 24–27 May 2010; pp. 1–8.
- Kilfoyle, D.B.; Preisig, J.C.; Baggeroer, A.B. Spatial modulation experiments in the underwater acoustic channel. IEEE J. Ocean. Eng. 2005, 30, 406–415. [Google Scholar] [CrossRef]
- Roy, S.; Duman, T.M.; McDonald, V.; Proakis, J.G. High-rate communication for underwater acoustic channels using multiple transmitters. IEEE J. Ocean. Eng. 2007, 32, 663–688. [Google Scholar] [CrossRef]
- Li, B.; Huang, J.; Zhou, S.; Ball, K.; Stojanovic, M.; Freitag, L.; Willett, P. MIMO-OFDM for high-rate underwater acoustic communications. IEEE J. Ocean. Eng. 2009, 34, 634–644. [Google Scholar] [CrossRef]
- Ceballos Carrascosa, P.; Stojanovic, M. Adaptive channel estimation and data detection for underwater acoustic MIMO-OFDM systems. IEEE J. Ocean. Eng. 2010, 35, 635–646. [Google Scholar] [CrossRef]
- Song, A.; Badiey, M. Time reversal multiple-input/multiple-output acoustic communication enhanced by parallel interference cancellation. J. Acoust. Soc. Am. 2012, 131, 281–291. [Google Scholar] [CrossRef]
- Stojanovic, M.; Catipovic, J.A.; Proakis, J.G. Phase-coherent digital communications for underwater acoustic channels. IEEE J. Ocean. Eng. 1994, 19, 100–111. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zheng, X. Signal synthesis and receiver design for MIMO radar imaging. IEEE Trans. Signal Process. 2008, 56, 3959–3968. [Google Scholar] [CrossRef]
- Song, A.; Badiey, M.; McDonald, V.K. Multi-Channel Combining and Equalization for UWA MIMO Channels. In Proceedings of IEEE Oceans Conference, Quebec City, QC, USA, 15–18 September 2008; pp. 1–6.
- Real, G. Very High Frequency, MIMO Underwater Acoustic Communications in Ports and Shallow Waters. Master’s Thesis, Florida Atlantic University, FL, USA, 2011. [Google Scholar]
- Proakis, J.G. Digital Communications, 4th ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Laot, C.; le Bidan, R.; Leroux, D. Low-complexity MMSE turbo equalization: a possible solution for EDGE. IEEE Trans. Wirel. Commun. 2005, 4, 965–974. [Google Scholar] [CrossRef]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography; Academic Press: Waltham, MA, USA, 1997. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Real, G.; Beaujean, P.-P.; Bouvet, P.-J. MIMO Underwater Acoustic Communications in Ports and Shallow Waters at Very High Frequency. J. Sens. Actuator Netw. 2013, 2, 700-716. https://doi.org/10.3390/jsan2040700
Real G, Beaujean P-P, Bouvet P-J. MIMO Underwater Acoustic Communications in Ports and Shallow Waters at Very High Frequency. Journal of Sensor and Actuator Networks. 2013; 2(4):700-716. https://doi.org/10.3390/jsan2040700
Chicago/Turabian StyleReal, Gaultier, Pierre-Philippe Beaujean, and Pierre-Jean Bouvet. 2013. "MIMO Underwater Acoustic Communications in Ports and Shallow Waters at Very High Frequency" Journal of Sensor and Actuator Networks 2, no. 4: 700-716. https://doi.org/10.3390/jsan2040700
APA StyleReal, G., Beaujean, P.-P., & Bouvet, P.-J. (2013). MIMO Underwater Acoustic Communications in Ports and Shallow Waters at Very High Frequency. Journal of Sensor and Actuator Networks, 2(4), 700-716. https://doi.org/10.3390/jsan2040700





