EMG-Based Simulation for Optimization of Human-in-the-Loop Control in Simple Robotic Walking Assistance
Abstract
1. Introduction
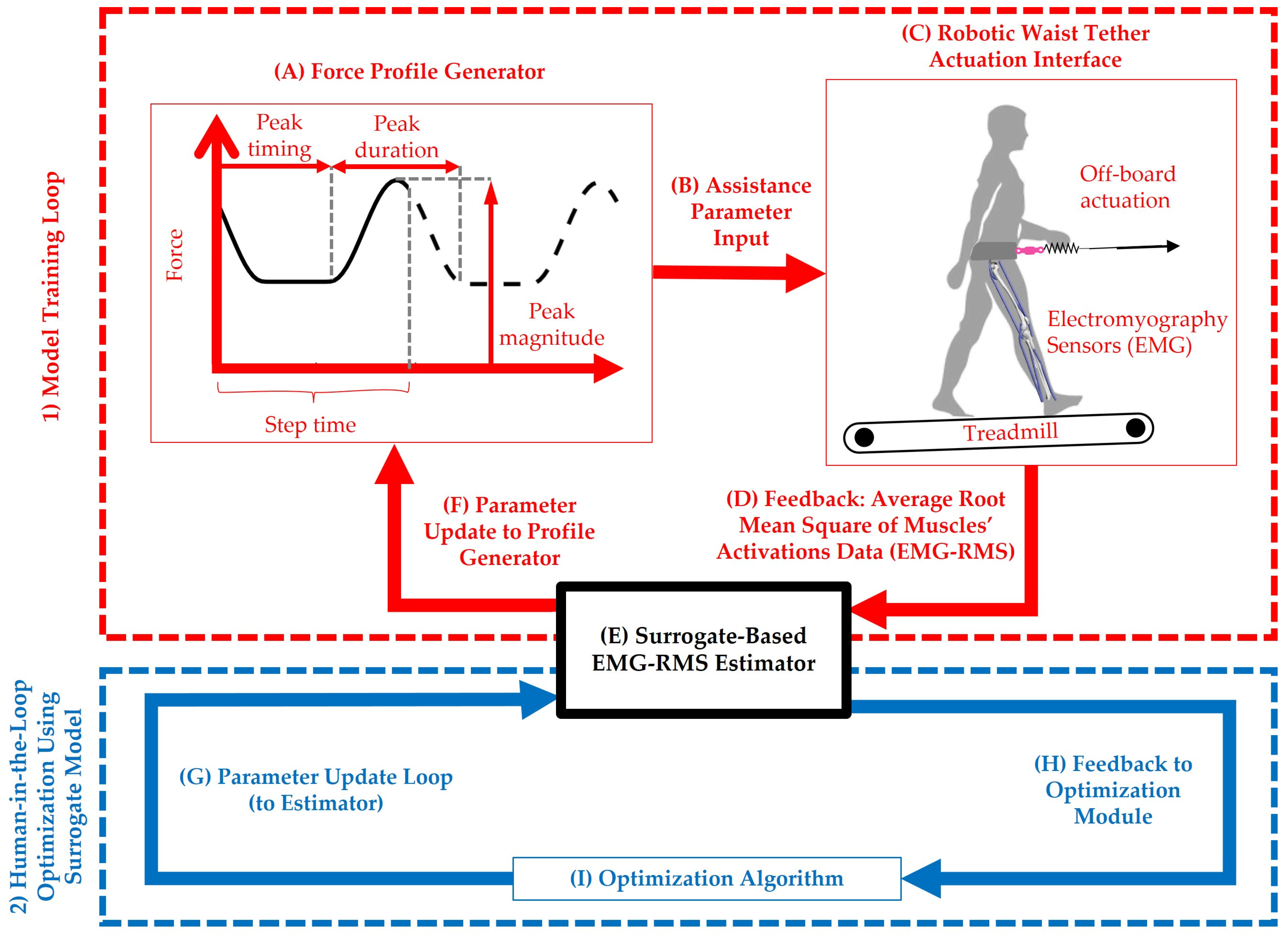
2. Materials and Methods
2.1. System Overview and Data Collection
2.2. Model Development and Optimization Setup
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARI | Average Rate of Improvement |
| AUC | Area Under the Curve |
| BO | Bayesian Optimization |
| CE | Cross-Entropy |
| CMAES | Covariance Matrix Adaptation Evolution Strategy |
| CMC | Computed Muscle Control |
| EBO | Exploitative Bayesian Optimization |
| EEG | Electroencephalogram |
| EMG | Electromyography |
| EMG-RMS | Average of The Root Mean Square of The Muscles’ Activations |
| ESN | Echo State Network |
| GA | Genetic Algorithm |
| GB | Gradient Boosting |
| GP | Gaussian Process |
| GPAE | Gaussian Process—Absolute Exponential |
| GPM | Gaussian Process—Matern 3/2 |
| GPRQ | Gaussian Process—Rational Quadratic |
| GPSE | Gaussian Process—Squared Exponential |
| GRF | Ground Reaction Force |
| GSA | Gravitational Search Algorithm |
| HIL | Human-in-the-Loop |
| IMU | Inertial Measurement Unit |
| LR | Linear Ridge |
| ML | Machine Learning |
| PR | Polynomial Ridge |
| PSO | Particle Swarm Optimization |
| RF | Random Forest |
| RMS | Root Mean Square |
| SVR | Support Vector Regression |
References
- Kutulakos, Z.; Slade, P. Simulating Human-in-the-Loop Optimization of Exoskeleton Assistance to Compare Optimization Algorithm Performance. Biorxiv 2024. [Google Scholar] [CrossRef]
- Mohammadzadeh Gonabadi, A.; Pipinos, I.I.; Myers, S.A.; Fallahtafti, F. Optimizing Hip Exoskeleton Assistance Pattern Based on Machine Learning and Simulation Algorithms: A Personalized Approach to Metabolic Cost Reduction. Front. Robot. AI 2025, 12, 1669600. [Google Scholar] [CrossRef]
- Kim, J.; Quinlivan, B.T.; Deprey, L.A.; Arumukhom Revi, D.; Eckert-Erdheim, A.; Murphy, P.; Orzel, D.; Walsh, C.J. Reducing the Energy Cost of Walking with Low Assistance Levels through Optimized Hip Flexion Assistance from a Soft Exosuit. Sci. Rep. 2022, 12, 11004. [Google Scholar] [CrossRef]
- Echeveste, S.; Bhounsule, P.A. Electromyography-Based Human-in-the-Loop Bayesian Optimization to Assist Free Leg Swinging. Biomechanics 2025, 5, 21. [Google Scholar] [CrossRef]
- Mohammadzadeh Gonabadi, A.; Fallahtafti, F.; Pipinos, I.I.; Myers, S.A. Predicting Lower Body Joint Moments and Electromyography Signals Using Ground Reaction Forces during Walking and Running: An Artificial Neural Network Approach. Gait Posture 2025, 117, 323–331. [Google Scholar] [CrossRef]
- Zabre-Gonzalez, E.V.; Amieva-Alvarado, D.; Beardsley, S.A. Prediction of EMG Activation Profiles from Gait Kinematics and Kinetics during Multiple Terrains. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Guadalajara, Mexico, 1–5 November 2021; IEEE: New York City, NY, USA, 2021; pp. 6326–6329. [Google Scholar]
- Lim, H.; Kim, B.; Park, S. Prediction of Lower Limb Kinetics and Kinematics during Walking by a Single IMU on the Lower Back Using Machine Learning. Sensors 2019, 20, 130. [Google Scholar] [CrossRef]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of Lower Limb Joint Angles and Moments during Gait Using Artificial Neural Networks. Med. Biol. Eng. Comput. 2020, 58, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P.; Gordon, K.E.; Sawicki, G.S.; Peethambaran, A. An Improved Powered Ankle-Foot Orthosis Using Proportional Myoelectric Control. Gait Posture 2006, 23, 425–428. [Google Scholar] [CrossRef] [PubMed]
- Ferris, D.P.; Czerniecki, J.M.; Hannaford, B. An Ankle-Foot Orthosis Powered by Artificial Pneumatic Muscles. J. Appl. Biomech. 2005, 21, 189–197. [Google Scholar] [CrossRef]
- Mohammadzadeh Gonabadi, A.; Antonellis, P.; Malcolm, P. Differences between Joint-Space and Musculoskeletal Estimations of Metabolic Rate Time Profiles. PLoS Comput. Biol. 2020, 16, e1008280. [Google Scholar] [CrossRef] [PubMed]
- Byfield, R.; Guess, M.; Sattari, K.; Xie, Y.; Guess, T.; Lin, J. Machine Learning Full 3-D Lower-Body Kinematics and Kinetics on Patients with Osteoarthritis from Electromyography. Biomed. Eng. Adv. 2023, 5, 100088. [Google Scholar] [CrossRef]
- Amrani El Yaakoubi, N.; McDonald, C.; Lennon, O. Prediction of Gait Kinematics and Kinetics: A Systematic Review of EMG and EEG Signal Use and Their Contribution to Prediction Accuracy. Bioengineering 2023, 10, 1162. [Google Scholar] [CrossRef]
- Hernández, Ó.G.; Lopez-Castellanos, J.M.; Jara, C.A.; Garcia, G.J.; Ubeda, A.; Morell-Gimenez, V.; Gomez-Donoso, F. A Kinematic, Imaging and Electromyography Dataset for Human Muscular Manipulability Index Prediction. Sci. Data 2023, 10, 132. [Google Scholar] [CrossRef]
- Myunghee, K.; Ding, Y.; Malcolm, P.; Speeckaert, J.; Siviy, C.J.C.; Walsh, C.J.; Kuindersma, S.; Kim, M.; Ding, Y.; Malcolm, P.; et al. Human-in-the-Loop Bayesian Optimization of Wearable Device Parameters. PLoS ONE 2017, 12, e0184054. [Google Scholar] [CrossRef]
- Ding, Y.; Kim, M.; Kuindersma, S.; Walsh, C.J. Human-in-the-Loop Optimization of Hip Assistance with a Soft Exosuit during Walking. Sci. Robot. 2018, 3, eaar5438. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, D.; Yan, Z.; Yu, L.; Gui, L.; Yang, C.; Yang, W. Optimizing Exoskeleton Assistance: Muscle Synergy-Based Actuation for Personalized Hip Exoskeleton Control. Actuators 2024, 13, 54. [Google Scholar] [CrossRef]
- Li, L.-L.; Zhang, Y.-P.; Cao, G.-Z.; Li, W.-Z. Human-in-the-Loop Trajectory Optimization Based on SEMG Biofeedback for Lower-Limb Exoskeleton. Sensors 2024, 24, 5684. [Google Scholar] [CrossRef] [PubMed]
- Desplenter, T.; Trejos, A. Evaluating Muscle Activation Models for Elbow Motion Estimation. Sensors 2018, 18, 1004. [Google Scholar] [CrossRef] [PubMed]
- Slade, P.; Kochenderfer, M.J.; Delp, S.L.; Collins, S.H. Personalizing Exoskeleton Assistance While Walking in the Real World. Nature 2022, 610, 277–282. [Google Scholar] [CrossRef]
- Antonellis, P.; Mohammadzadeh Gonabadi, A.; Myers, S.A.; Pipinos, I.I.; Malcolm, P. Metabolically Efficient Walking Assistance Using Optimized Timed Forces at the Waist. Sci. Robot. 2022, 7, eabh1925. [Google Scholar] [CrossRef]
- Dzewaltowski, A.C.; Antonellis, P.; Mohammadzadeh Gonabadi, A.; Song, S.; Malcolm, P. Perturbation-Based Estimation of within-Stride Cycle Metabolic Cost. J. Neuroeng. Rehabil. 2024, 21, 131. [Google Scholar] [CrossRef]
- Eke-Okor, S. An Electromyographic Examination of the Effects of Load on Human Gait. Clin. Biomech. 1988, 3, 111–120. [Google Scholar] [CrossRef]
- Zhu, M.; Guan, X.; Li, Z.; He, L.; Wang, Z.; Cai, K. SEMG-Based Lower Limb Motion Prediction Using CNN-LSTM with Improved PCA Optimization Algorithm. J. Bionic Eng. 2023, 20, 612–627. [Google Scholar] [CrossRef]
- Buchanan, T.S.; Shreeve, D.A. An Evaluation of Optimization Techniques for the Prediction of Muscle Activation Patterns During Isometric Tasks. J. Biomech. Eng. 1996, 118, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Tibold, R.; Fuglevand, A.J. Prediction of Muscle Activity during Loaded Movements of the Upper Limb. J. Neuroeng. Rehabil. 2015, 12, 6. [Google Scholar] [CrossRef]
- Samarakoon, S.M.U.S.; Herath, H.M.K.K.M.B.; Yasakethu, S.L.P.; Fernando, D.; Madusanka, N.; Yi, M.; Lee, B.-I. Long Short-Term Memory-Enabled Electromyography-Controlled Adaptive Wearable Robotic Exoskeleton for Upper Arm Rehabilitation. Biomimetics 2025, 10, 106. [Google Scholar] [CrossRef]
- Nasiri, R.; Shushtari, M.; Arami, A. An Adaptive Assistance Controller to Optimize the Exoskeleton Contribution in Rehabilitation. Robotics 2021, 10, 95. [Google Scholar] [CrossRef]
- Rahman, M.H.; Ochoa-Luna, C.; Saad, M. EMG Based Control of a Robotic Exoskeleton for Shoulder and Elbow Motion Assist. J. Autom. Control Eng. 2015, 3, 270–276. [Google Scholar] [CrossRef]
- Peternel, L.; Noda, T.; Petrič, T.; Ude, A.; Morimoto, J.; Babič, J. Adaptive Control of Exoskeleton Robots for Periodic Assistive Behaviours Based on EMG Feedback Minimisation. PLoS ONE 2016, 11, e0148942. [Google Scholar] [CrossRef]
- Ranathunga Arachchilage Ruwan Chandra GOPURA; KIGUCHI, K. An Exoskeleton Robot for Human Forearm and Wrist Motion Assist -Hardware Design and EMG-Based Controller. J. Adv. Mech. Des. Syst. Manuf. 2008, 2, 1067–1083. [Google Scholar] [CrossRef]
- Carvalho, C.R.; Fernández, J.M.; Del-Ama, A.J.; Oliveira Barroso, F.; Moreno, J.C. Review of Electromyography Onset Detection Methods for Real-Time Control of Robotic Exoskeletons. J. Neuroeng. Rehabil. 2023, 20, 141. [Google Scholar] [CrossRef]
- Koller, J.R.; Gates, D.H.; Ferris, D.P.; David Remy, C. “Body-in-the-Loop” Optimization of Assistive Robotic Devices: A Validation Study. In Proceedings of the Robotics: Science and Systems XII, Ann Arbor, MI, USA, 18–22 June 2016; Science and Systems Foundation: College Station, TX, USA, 2016; pp. 1–7. [Google Scholar]
- Li, X.; Lu, L.; Fu, X.; Li, H.; Yang, W.; Guo, H.; Guo, K.; Huang, Z. Systematic Review and Meta-Analysis of the Efficacy and Safety of Electroacupuncture for Poststroke Dysphagia. Front. Neurol. 2023, 14, 1270624. [Google Scholar] [CrossRef]
- Ward, R.E.; Boudreau, R.M.; Caserotti, P.; Harris, T.B.; Zivkovic, S.; Goodpaster, B.H.; Satterfield, S.; Kritchevsky, S.; Schwartz, A.V.; Vinik, A.I.; et al. Sensory and Motor Peripheral Nerve Function and Longitudinal Changes in Quadriceps Strength. J. Gerontol. Ser. A 2015, 70, 464–470. [Google Scholar] [CrossRef]
- Chen, S.J.; Pipinos, I.; Johanning, J.; Radovic, M.; Huisinga, J.M.; Myers, S.A.; Stergiou, N. Bilateral Claudication Results in Alterations in the Gait Biomechanics at the Hip and Ankle Joints. J. Biomech. 2008, 41, 2506–2514. [Google Scholar] [CrossRef]
- Dingwell, J.B.; Ulbrecht, J.S.; Boch, J.; Becker, M.B.; O’Gorman, J.T.; Cavanagh, P.R. Neuropathic Gait Shows Only Trends towards Increased Variability of Sagittal Plane Kinematics during Treadmill Locomotion. Gait Posture 1999, 10, 21–29. [Google Scholar] [CrossRef]
- Wurdeman, S.R.; Koutakis, P.; Myers, S.A.; Johanning, J.M.; Pipinos, I.I.; Stergiou, N. Patients with Peripheral Arterial Disease Exhibit Reduced Joint Powers Compared to Velocity-Matched Controls. Gait Posture 2012, 36, 506–509. [Google Scholar] [CrossRef] [PubMed]
- Mohammadzadeh Gonabadi, A.; Fallahtafti, F. Gait Stability Under Hip Exoskeleton Assistance: A Phase-Dependent Analysis Using Gait Tube Methodology. Appl. Sci. 2025, 15, 7530. [Google Scholar] [CrossRef]
- Russell, D.M.; Haworth, J.L.; Martinez, C. Coordination Dynamics of (a) Symmetrically Loaded Gait. Exp. Brain Res. 2016, 234, 867–881. [Google Scholar] [CrossRef] [PubMed]
- Heitkamp, L.N.; Stimpson, K.H.; Dean, J.C. Application of a Novel Force-Field to Manipulate the Relationship between Pelvis Motion and Step Width in Human Walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2051–2058. [Google Scholar] [CrossRef]
- Woollacott, M.; Shumway-Cook, A. Attention and the Control of Posture and Gait: A Review of an Emerging Area of Research. Gait Posture 2002, 16, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-Loop Optimization of Exoskeleton Assistance during Walking. Science 2017, 356, 1280–1284. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, S.; Figueiredo, J.; Fonseca, P.; Vilas-Boas, J.P.; Santos, C.P. Human-in-the-Loop Optimization of Knee Exoskeleton Assistance for Minimizing User’s Metabolic and Muscular Effort. Sensors 2024, 24, 3305. [Google Scholar] [CrossRef] [PubMed]








| Study/Reference | Target Joint | Optimization Method | Objective Function | Personalization Type | Simulation or Real-Time | Key Contribution | Gap Addressed by Present Work |
|---|---|---|---|---|---|---|---|
| Desplenter & Trejos [19] | Elbow | None (model evaluation) | RMS torque error (1.67–2.19 Nm) | EMG-driven model | Simulation | Compared 7 EMG activation models for motion estimation | No optimization; not hip-focused. Our work adds HIL optimization and hip-specific EMG modeling. |
| Slade et al. [20] | Ankle | Data-driven (logistic regression) | Metabolic energy (17–23% reduction) | Wearable sensors | Real-time | Real-time HIL optimization for ankle assistance | Real-time only, ankle-specific. Our work provides a multi-optimizer simulation for hip optimization. |
| Ma et al. [17] | Hip | HIL (Thompson sampling) | Muscle synergy (6.3% improvement) | sEMG feedback | Real-time | EMG-based synergy optimization for hip torque | Single optimizer; real-time only. Our work generalizes to multiple optimizers in simulation. |
| Li et al. [18] | Lower limbs | HIL (Thompson + collocation) | sEMG biofeedback | Hybrid (offline + online) | Hybrid | Combined trajectory and feedback optimization | Focused on multiple joints; not EMG-RMS optimization. Our work isolates hip neuromuscular control. |
| Kutulakos & Slade [1] | Ankle | Multiple (CMA-ES, PSO, GA) | Metabolic cost | Simulated HIL | Simulation | Compared optimizers for metabolic-based HIL | Ankle-focused and metabolic. Our work extends to hip with EMG-RMS surrogates. |
| Echeveste & Bhounsule [4] | Leg (swing) | Bayesian HIL | EMG for leg swing | Adaptive | Real-time | Demonstrated EMG-based fast convergence | Limited to Bayesian optimization and leg swing; not full gait. Our work extends to hip walking optimization. |
| Gonabadi et al. [2] | Hip | Seven global optimizers (GSA, PSO, CMA-ES, BO, CE, GA, EBO) | EMG-RMS (neuromuscular effort) | Simulated HIL with nine ML surrogates | Simulation | First multi-optimizer, EMG-based surrogate framework for hip personalization | Bridges metabolic and neuromuscular optimization; reduces real-time burden; establishes algorithm sensitivity and reproducibility. |
| # | Machine Learning Models | Optimization Algorithms |
|---|---|---|
| 1 | Linear Ridge (LR) | Covariance Matrix Adaptation Evolution Strategy (CMAES) |
| 2 | Polynomial Ridge (PR) | Bayesian Optimization (BO) |
| 3 | Support Vector Regression (SVR) | Exploitative Bayesian Optimization (EBO) |
| 4 | Random Forest (RF) | Cross-Entropy Method (CE) |
| 5 | Gradient Boosting (GB) | Genetic Algorithm (GA) |
| 6 | Gaussian Process—Absolute Exponential (GPAE) | Gravitational Search Algorithm (GSA) |
| 7 | Gaussian Process—Matern 3/2 (GPM) | Particle Swarm Optimization (PSO) |
| 8 | Gaussian Process—Rational Quadratic (GPRQ) | - |
| 9 | Gaussian Process—Squared Exponential (GPSE) | - |
| Algorithm | Population Size/Agents | Initialization Mean/Method | Key Parameters | Random Seed Used |
|---|---|---|---|---|
| CMA-ES | 150 | Mean: (0.5, 0.5, 0.5); σ = 0.3 | λ = 15; Elite size = 3 | rng(42) |
| Bayesian Optimization (BO) | N/A (sequential) | Uniform sampling in [0, 1]3 | Acquisition: EI+; Exploration constant = 2.6 | rng(42) |
| Exploitative BO (EBO) | N/A (sequential) | Uniform sampling in [0, 1]3 | Acquisition: EI+; Exploration constant = 0.93 | rng(42) |
| Cross-Entropy (CE) | 150 | Mean: (0.5, 0.5, 0.5); σ = 0.3 | Elite fraction = 0.5; λ = 30 (2 × CMAES) | rng(42) |
| Genetic Algorithm (GA) | 200 | Uniform sampling in [0, 1]3 | Crossover fraction = 0.8; Generations = ceil(200/20) | rng(42) |
| Gravitational Search Algorithm (GSA) | 200 | Uniform sampling in [0, 1]3 | G0 = 100; α = 20; Max iterations = ceil (200/20) | rng(42) |
| Particle Swarm Optimization (PSO) | 200 | Uniform sampling in [0, 1]3 | Inertia-based updates; Swarm size = 20; Iterations = ceil (200/20) | rng(42) |
| # | Machine Learning Models | Relative Absolute Error of EMG-RMS (RAEP) (%) |
|---|---|---|
| 1 | Linear Ridge (LR) | 2.14 |
| 2 | Polynomial Ridge (PR) | 1.82 |
| 3 | Support Vector Regression (SVR) | 1.65 |
| 4 | Random Forest (RF) | 1.65 |
| 5 | Gradient Boosting (GB) | 1.57 |
| 6 | Gaussian Process—Absolute Exponential (GPAE) | 1.66 |
| 7 | Gaussian Process—Matern 3/2 (GPM) | 1.66 |
| 8 | Gaussian Process—Rational Quadratic (GPRQ) | 1.65 |
| 9 | Gaussian Process—Squared Exponential (GPSE) | 1.73 |
| # | Algorithm | Total Number of Evaluations | Mean Convergence Time (s) | Peak Magnitude | Peak Timing | Peak Duration | Normalized EMG-RMS | Mean AUC | Mean ARI |
|---|---|---|---|---|---|---|---|---|---|
| 1 | CMAES | 100.00 | 0.33 | 0.01 | 0.73 | 0.52 | 0.23 | 0.13 | 1.55 × 10−5 |
| 2 | BO | 100.00 | 9.90 | 0.02 | 0.73 | 1.00 | 0.16 | 0.12 | 2.51 × 10−5 |
| 3 | EBO | 100.00 | 8.74 | 0.09 | 0.71 | 1.00 | 0.20 | 0.13 | 2.47 × 10−5 |
| 4 | CE | 100.00 | 0.33 | 0.09 | 0.93 | 0.17 | 0.22 | 0.13 | 2.17 × 10−5 |
| 5 | GA | 100.00 | 1.69 | 0.49 | 0.35 | 0.77 | 0.21 | 0.13 | 2.53 × 10−5 |
| 6 | GSA | 100.00 | 0.32 | 0.15 | 0.72 | 0.97 | 0.17 | 0.12 | 2.84 × 10−5 |
| 7 | PSO | 100.00 | 1.61 | 0.29 | 0.15 | 0.31 | 0.36 | 0.10 | 0.62 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadzadeh Gonabadi, A.; Hunt, N.H.; Fallahtafti, F. EMG-Based Simulation for Optimization of Human-in-the-Loop Control in Simple Robotic Walking Assistance. J. Sens. Actuator Netw. 2025, 14, 113. https://doi.org/10.3390/jsan14060113
Mohammadzadeh Gonabadi A, Hunt NH, Fallahtafti F. EMG-Based Simulation for Optimization of Human-in-the-Loop Control in Simple Robotic Walking Assistance. Journal of Sensor and Actuator Networks. 2025; 14(6):113. https://doi.org/10.3390/jsan14060113
Chicago/Turabian StyleMohammadzadeh Gonabadi, Arash, Nathaniel H. Hunt, and Farahnaz Fallahtafti. 2025. "EMG-Based Simulation for Optimization of Human-in-the-Loop Control in Simple Robotic Walking Assistance" Journal of Sensor and Actuator Networks 14, no. 6: 113. https://doi.org/10.3390/jsan14060113
APA StyleMohammadzadeh Gonabadi, A., Hunt, N. H., & Fallahtafti, F. (2025). EMG-Based Simulation for Optimization of Human-in-the-Loop Control in Simple Robotic Walking Assistance. Journal of Sensor and Actuator Networks, 14(6), 113. https://doi.org/10.3390/jsan14060113








