DAR-MDE: Depth-Attention Refinement for Multi-Scale Monocular Depth Estimation
Abstract
1. Introduction
- We develop a depth estimation framework that integrates a Multi-Scale Feature Aggregation (MSFA) module to enable robust learning across objects of varying sizes and scene perspectives.
- We incorporate a Refining Attention Network (RAN) module that selectively emphasizes structurally important regions by learning the relationship between coarse depth probabilities and local feature maps.
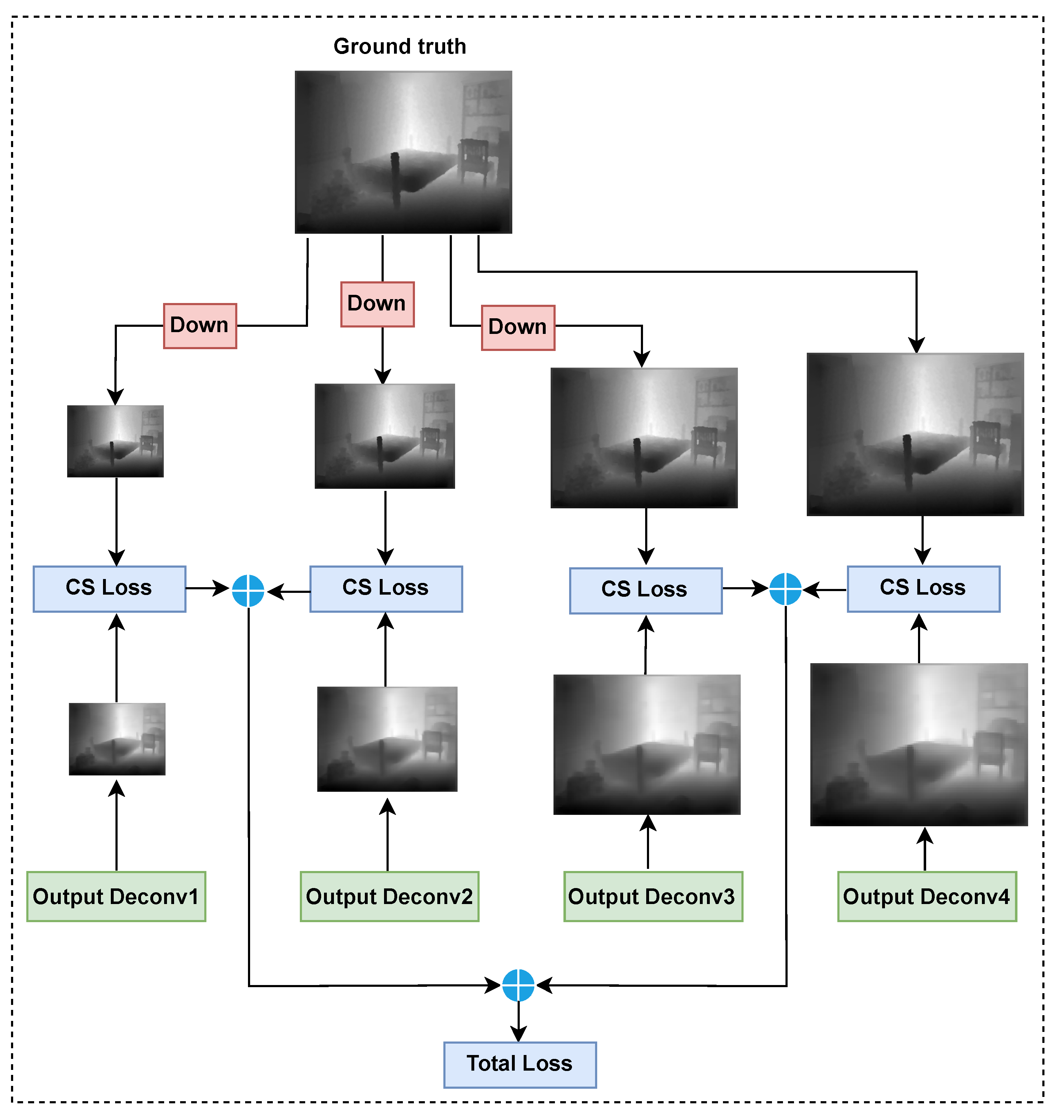
- We introduce a multi-scale loss strategy based on curvilinear saliency that enforces depth consistency at multiple resolutions, leading to sharper boundaries and better small object representation.
- We validate our approach extensively on both indoor (NYU Depth v2, SUN RGB-D) and outdoor (Make3D) datasets, demonstrating superior generalization without reliance on additional sensors such as LiDAR or infrared. The results highlight its light weight and applicability for monocular scenarios.
2. Related Work
2.1. Depth Estimation
2.2. Multi-Scale Networks
2.3. Refining Attention Depth Network
3. Proposed Methodology
3.1. Problem Formulation
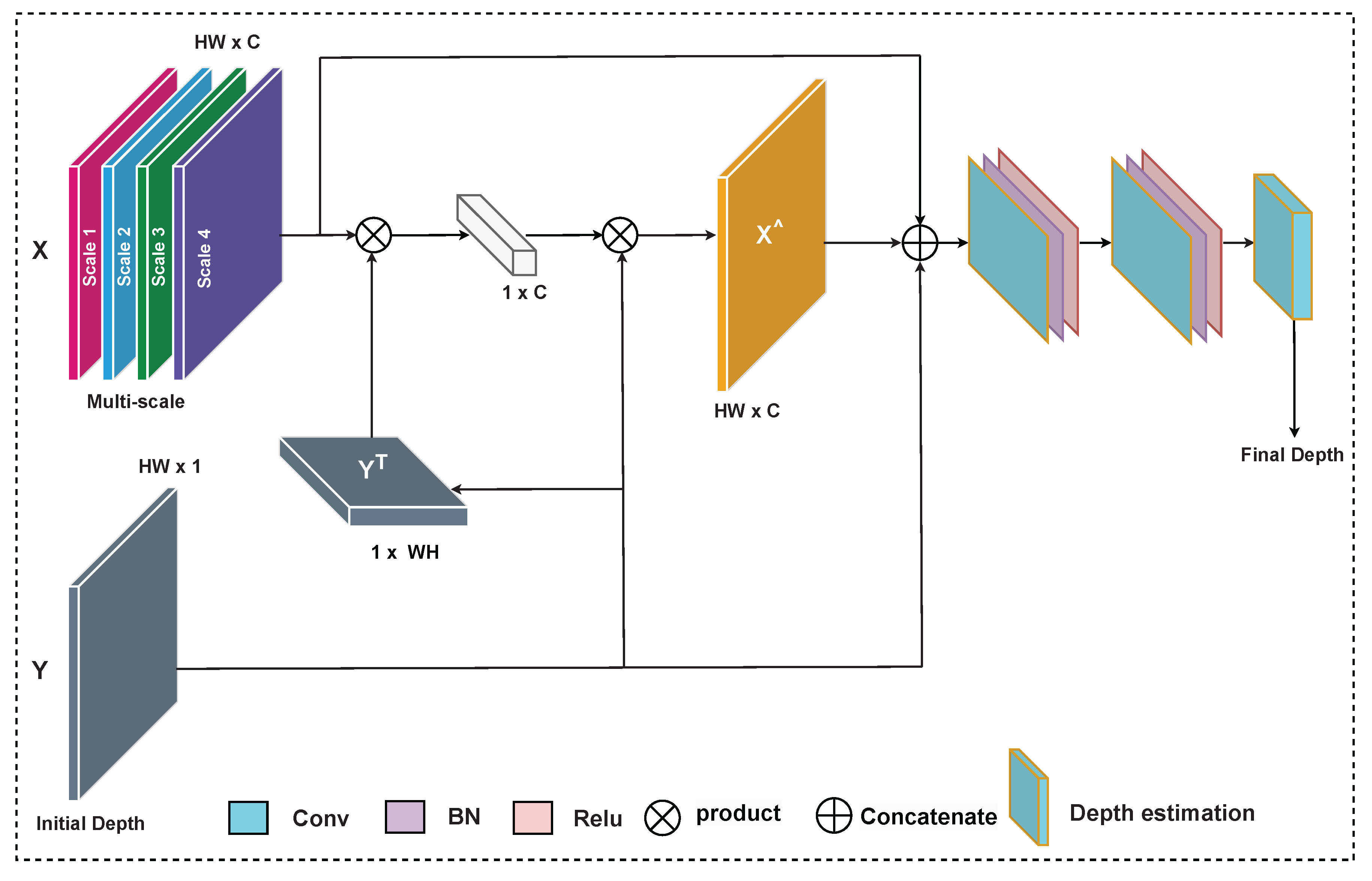
3.2. Model Architecture
3.2.1. Autoencoder Network
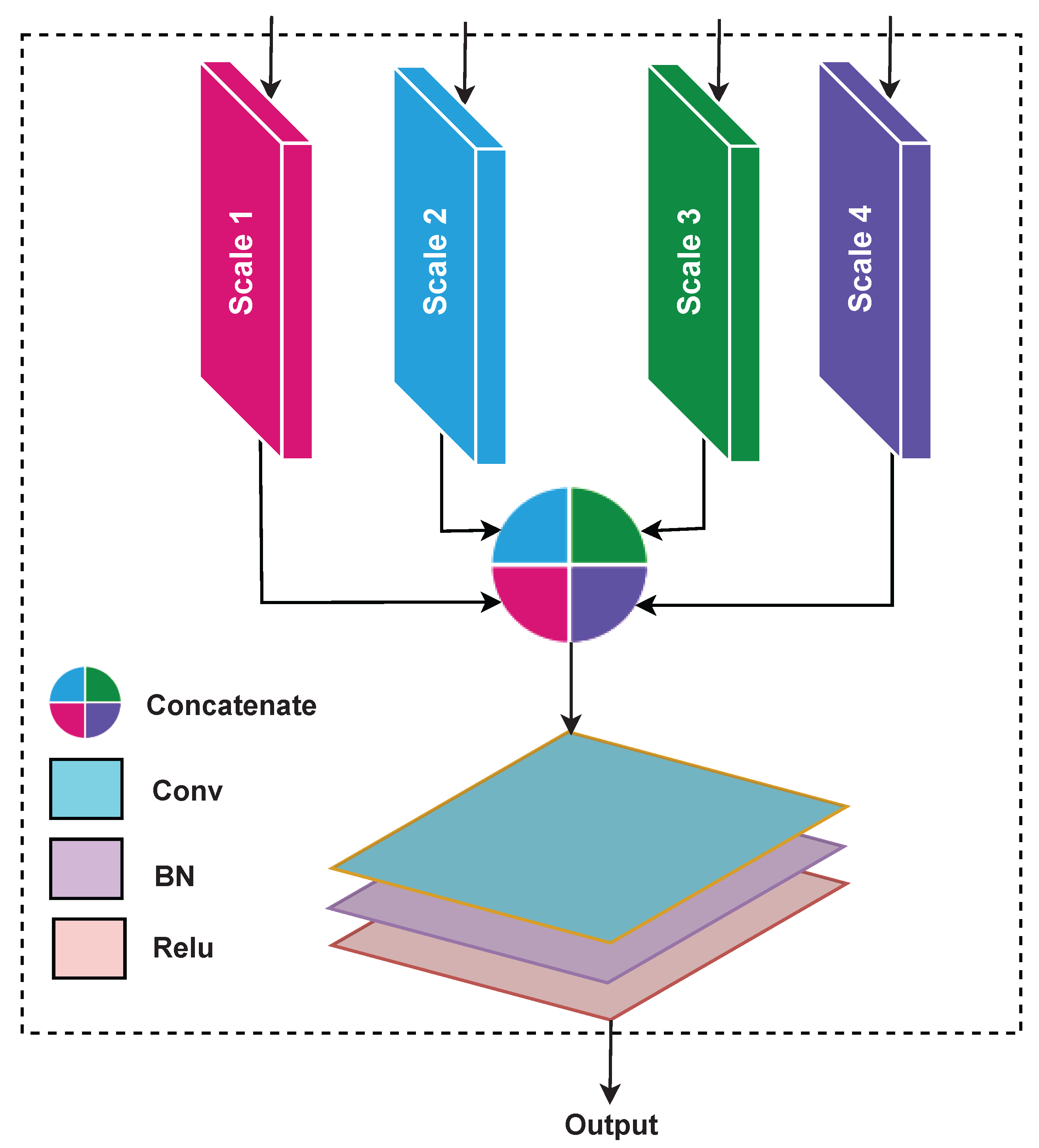
3.2.2. Multi-Scale Feature Aggregation Network
3.2.3. Refining Attention Network
3.3. Loss Functions
3.3.1. Multi-Scale Loss Function
3.3.2. Content Loss Function
3.3.3. Total Loss Function
4. Experiments and Results
4.1. Dataset
4.1.1. Indoor Scenes
- NYU Depth-v2 dataset
- II.
- SUN RGB-D dataset
4.1.2. Outdoor Scenes
- Make3D dataset
4.2. Data Augmentation
- Scaling: Random scaling in which each input image and its corresponding depth map underwent a random scale transformation with a factor S ∈ [0.5, 1.7].
- Rotation: Random rotation involving adjustments of the input image and its corresponding depth map by angles R ∈ [−60, −45, −30, 30, 45, 60] degrees.
- Gamma Correction: Variation in gamma correction for each input RGB image, with random adjustments G ∈ [1, 2.8].
- Flipping: Random flipping, in which each input image and its corresponding depth map experienced horizontal flipping with a factor F ∈ [−1, 0, 1].
- Translation: Random translation, entailing shifts of each input image and its corresponding depth map by T ∈ [−6, −4, −2, 2, 4, 6] pixels.
4.3. Parameter Settings
4.4. Evaluation Measures
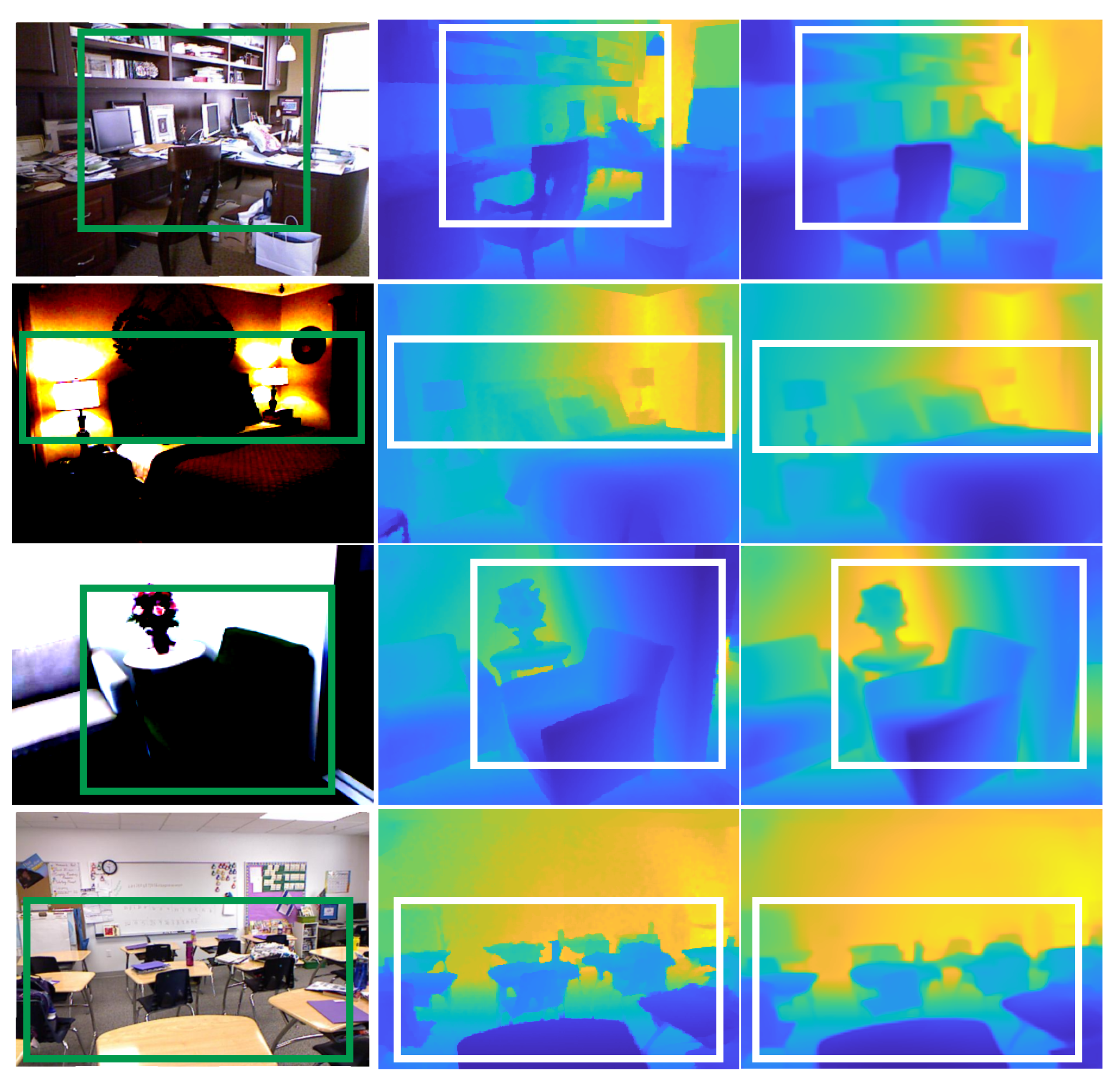
4.5. Results and Discussion
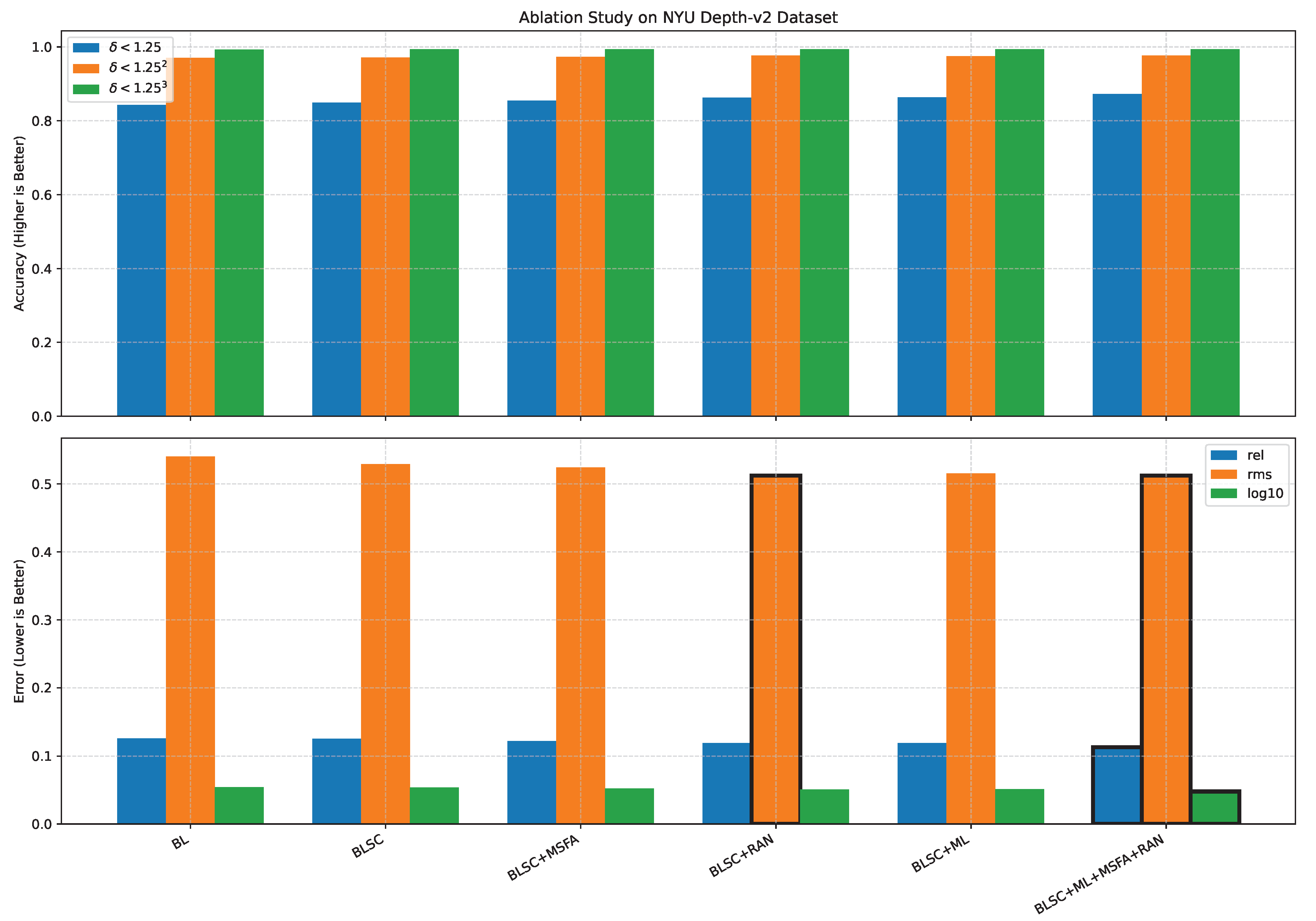
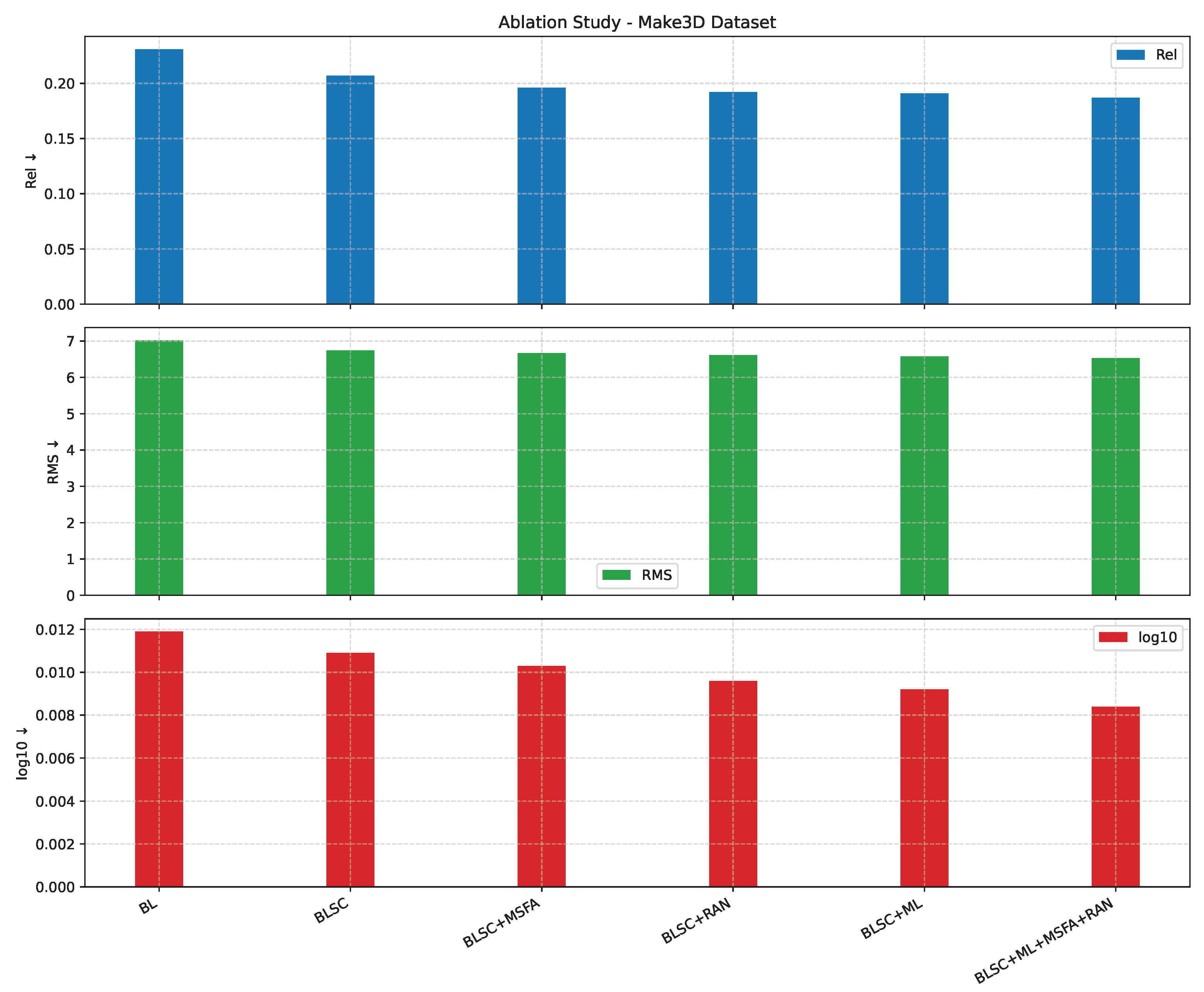
4.5.1. Ablation Study
- Baseline (BL): Basic autoencoder with four content loss functions: point-wise () loss, mean squared error () loss, the logarithm of depth errors () loss, and structural similarity index measure () loss.
- BLSC: BL model with skip connections from the encoder layers to the corresponding decoder layers.
- BLSC + MSFA: BLSC model with Multi-Scale Feature Aggregation Network (MSFA).
- BLSC + RAN: BLSC model with Refining Attention Network (RAN).
- BLSC + ML: BLSC model with multi-loss function.
- BLSC + ML + MSFA + RAN: BLSC model with multi-loss function, MSFA, and RAN.
4.5.2. Performance Analysis
| Method | Accuracy: Higher Is Better | Error: Lower Is Better | ||||
|---|---|---|---|---|---|---|
| rel ↓ | rms ↓ | log10 ↓ | ||||
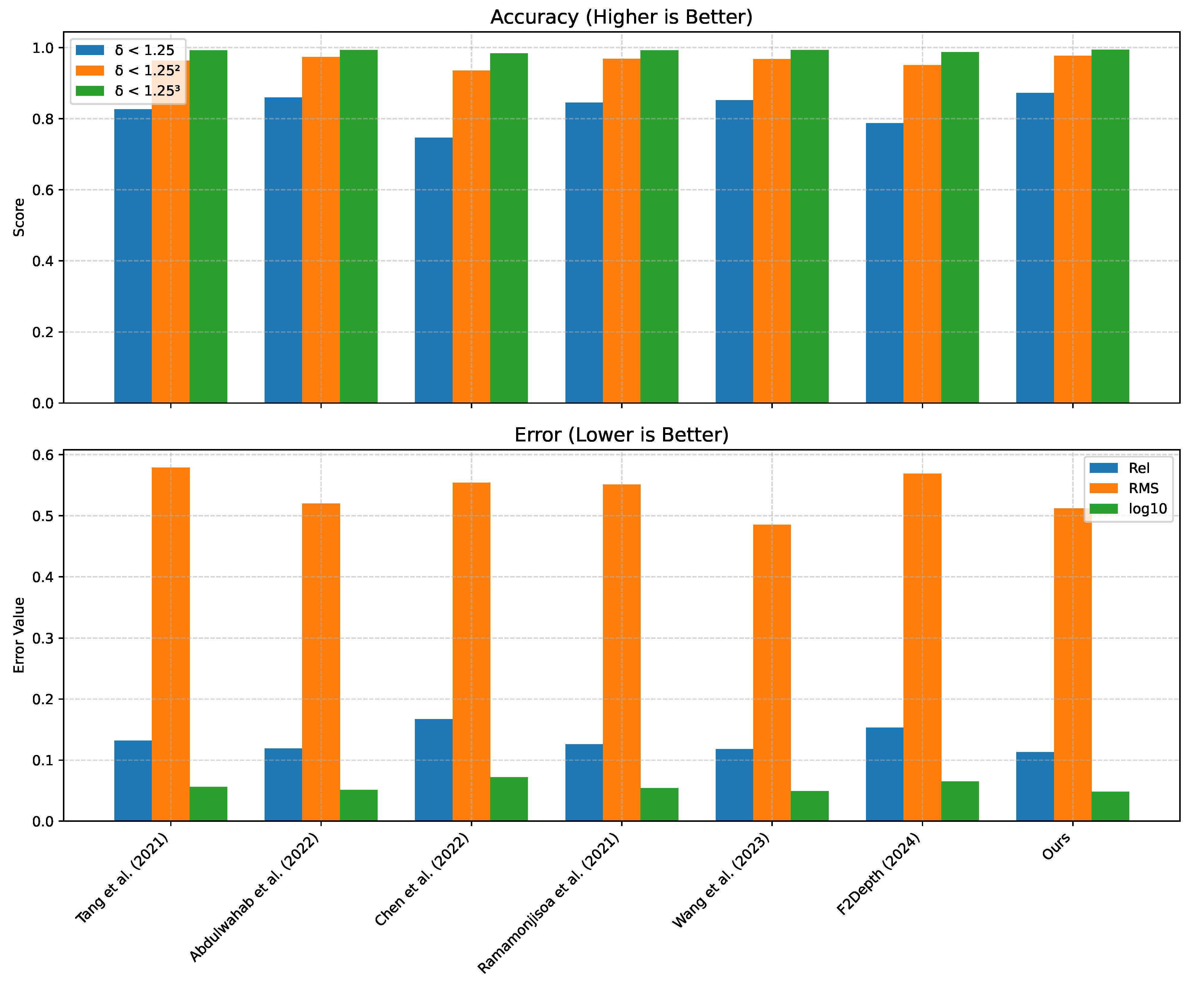
| Tang et al. [53] | 0.826 | 0.963 | 0.992 | 0.132 | 0.579 | 0.056 |
| Abdulwahab et al. [29] | 0.8591 | 0.9733 | 0.9932 | 0.119 | 0.520 | 0.051 |
| Chen et al. [51] | 0.746 | 0.935 | 0.984 | 0.167 | 0.554 | 0.072 |
| Ramamonjisoa et al. [52] | 0.8451 | 0.9681 | 0.9917 | 0.1258 | 0.551 | 0.054 |
| WangandPiao et al. [25] | 0.852 | 0.967 | 0.993 | 0.118 | 0.485 | 0.049 |
| Guo et al. [54] | 0.787 | 0.950 | 0.987 | 0.153 | 0.569 | 0.065 |
| Our model (DAR-MDE) | 0.8725 | 0.9766 | 0.994 | 0.113 | 0.512 | 0.048 |
| Method | rel ↓ | rms ↓ | log10 ↓ |
|---|---|---|---|
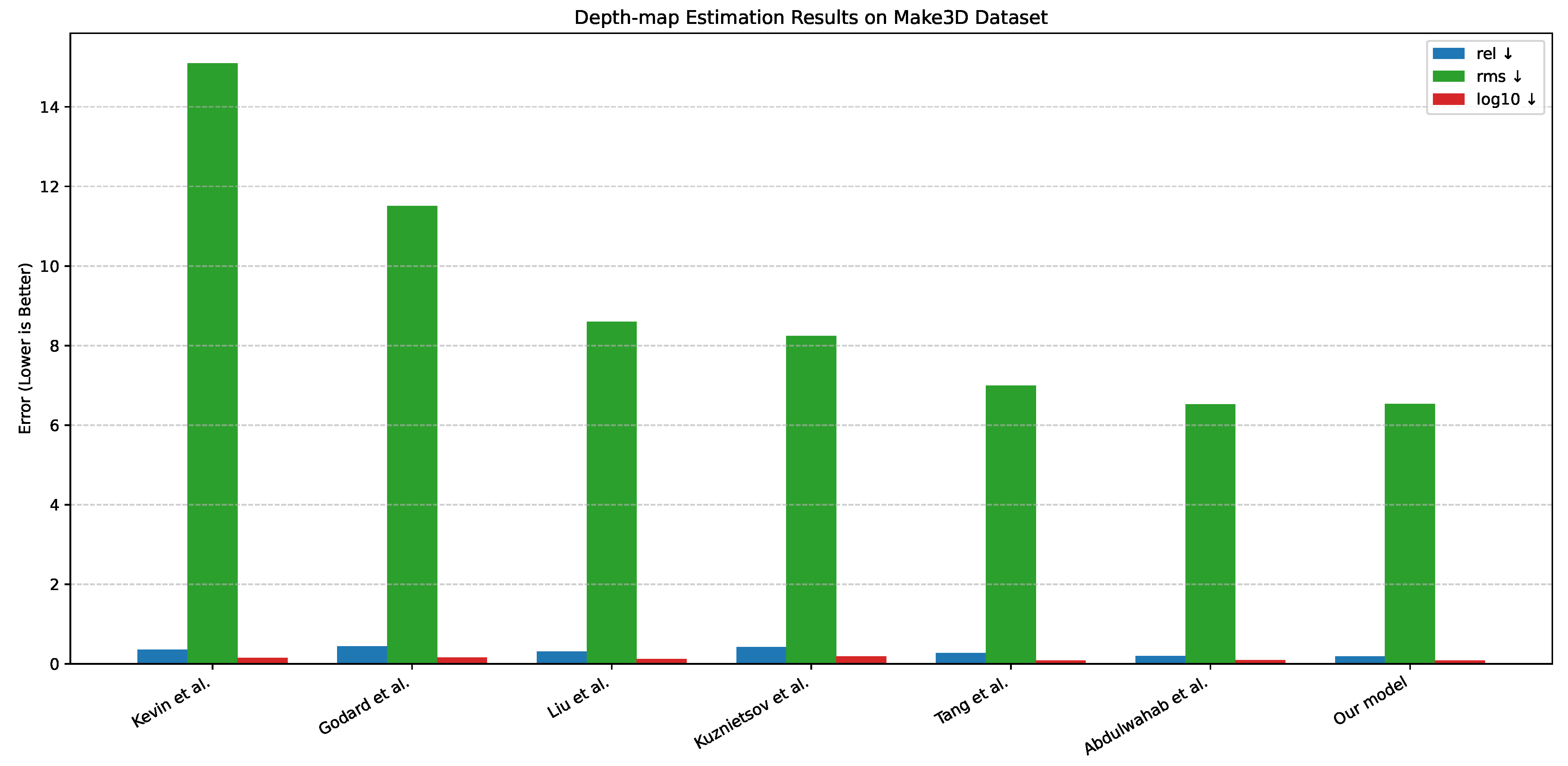
| Kevin et al. [55] | 0.361 | 15.1 | 0.148 |
| Godard et al. [56] | 0.443 | 11.513 | 0.156 |
| Liu et al. [50] | 0.314 | 8.60 | 0.119 |
| Kuznietsov et al. [57] | 0.421 | 8.24 | 0.190 |
| Tang et al. [53] | 0.276 | 6.99 | 0.086 |
| Abdulwahab et al. [29] | 0.195 | 6.522 | 0.091 |
| Our model (DAR-MDE) | 0.187 | 6.531 | 0.084 |
| Method | Encoder | Accuracy: Higher Is Better | Error: Lower Is Better | ||||
|---|---|---|---|---|---|---|---|
| ↑ | ↑ | ↑ | rel ↓ | rms ↓ | log10 ↓ | ||
| Chen et al. [59] | SENet-154 | 0.757 | 0.943 | 0.984 | 0.166 | 0.494 | 0.071 |
| Yin et al. [60] | ResNeXt-101 | 0.696 | 0.912 | 0.973 | 0.183 | 0.541 | 0.082 |
| Lee et al. [20] | DenseNet-161 | 0.740 | 0.933 | 0.980 | 0.172 | 0.515 | 0.075 |
| Bhat et al. [61] | E-B5 + Mini-ViT | 0.771 | 0.944 | 0.983 | 0.159 | 0.476 | 0.068 |
| Li et al. [62] | ResNet-18 | 0.738 | 0.935 | 0.982 | 0.175 | 0.504 | 0.074 |
| Li et al. [62] | Swin-Tiny | 0.760 | 0.945 | 0.985 | 0.162 | 0.478 | 0.069 |
| Li et al. [62] | Swin-Large | 0.805 | 0.963 | 0.990 | 0.143 | 0.421 | 0.061 |
| Zhao et al. [58] | SwinV2-Large | 0.861 | – | – | 0.121 | 0.355 | – |
| Li et al. [62] | Swin-Large | 0.805 | 0.963 | 0.99 | 0.143 | 0.421 | 0.061 |
| Hu et al. [63] | SwinV2-Large | 0.807 | 0.967 | 0.992 | 0.139 | 0.421 | 0.061 |
| Our Model (DAR-MDE) | ResNet-50 | 0.860 | 0.957 | 0.977 | 0.124 | 0.410 | 0.057 |
| Our Model (DAR-MDE) | SENet-154 | 0.865 | 0.960 | 0.980 | 0.120 | 0.405 | 0.054 |
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDE | Monocular Depth Estimation |
| CNN | Convolutional Neural Network |
| MSFA | Multi-Scale Feature Aggregation |
| RAN | Refining Attention Network |
| DAR-MDE | Dual-Attention Refining Monocular Depth Estimation |
| NYU Depth v2 | New York University Depth Dataset v2 |
| SUN RGB-D | SUN RGB-D Dataset |
| MSE | Mean Squared Error |
| RMSE | Root Mean Square Error |
| SSIM | Structural Similarity Index Measure |
| rel | Average Relative Error |
| MS | Multi-Scale |
| GT | Ground Truth |
| GPU | Graphics Processing Unit |
| LiDAR | Light Detection and Ranging |
| ADAM | Adaptive Moment Estimation |
| GAN | Generative Adversarial Network |
| SOTA | State-of-the-Art |
References
- Chiu, C.H.; Astuti, L.; Lin, Y.C.; Hung, M.K. Dual-Attention Mechanism for Monocular Depth Estimation. In Proceedings of the 2024 16th International Conference on Computer and Automation Engineering (ICCAE), Melbourne, Australia, 14–16 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 456–460. [Google Scholar]
- Yang, Y.; Wang, X.; Li, D.; Tian, L.; Sirasao, A.; Yang, X. Towards Scale-Aware Full Surround Monodepth with Transformers. arXiv 2024, arXiv:2407.10406. [Google Scholar] [CrossRef]
- Tang, S.; Lu, T.; Liu, X.; Zhou, H.; Zhang, Y. CATNet: Convolutional attention and transformer for monocular depth estimation. Pattern Recognit. 2024, 145, 109982. [Google Scholar] [CrossRef]
- Liu, J.; Cao, Z.; Liu, X.; Wang, S.; Yu, J. Self-supervised monocular depth estimation with geometric prior and pixel-level sensitivity. IEEE Trans. Intell. Veh. 2022, 8, 2244–2256. [Google Scholar] [CrossRef]
- Hu, D.; Peng, L.; Chu, T.; Zhang, X.; Mao, Y.; Bondell, H.; Gong, M. Uncertainty Quantification in Depth Estimation via Constrained Ordinal Regression. In Proceedings of the European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; Available online: https://www.ecva.net/papers/eccv_2022/papers_ECCV/papers/136620229.pdf (accessed on 14 August 2025).
- Wang, Y.; Piao, X. Scale-Aware Deep Networks for Monocular Depth Estimation. In Proceedings of the CVPR, Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Wang, W.; Yin, B.; Li, L.; Li, L.; Liu, H. A Low Light Image Enhancement Method Based on Dehazing Physical Model. Comput. Model. Eng. Sci. (CMES) 2025, 143, 1595–1616. [Google Scholar] [CrossRef]
- Zhang, Z. Lightweight Deep Networks for Real-Time Monocular Depth Estimation. In Proceedings of the ICRA, London, UK, 29 May–2 June 2023. [Google Scholar]
- Yoon, S.; Lee, J. Context-Aware Depth Estimation via Multi-Modal Fusion. In Proceedings of the CVPR, Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Shakibania, H.; Raoufi, S.; Khotanlou, H. CDAN: Convolutional dense attention-guided network for low-light image enhancement. Digit. Signal Process. 2025, 156, 104802. [Google Scholar] [CrossRef]
- Ding, L. Attention-Guided Depth Completion from Sparse Data. In Proceedings of the European Conference on Computer Vision (ECCV), Milan, Italy, 29 September–4 October 2024. [Google Scholar]
- Chen, Y.; Zhao, H.; Hu, Z.; Peng, J. Attention-based context aggregation network for monocular depth estimation. Int. J. Mach. Learn. Cybern. 2021, 12, 1583–1596. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process. Syst. 2014, 2, 2366–2374. [Google Scholar]
- Xu, D.; Ricci, E.; Ouyang, W.; Wang, X.; Sebe, N. Multi-scale continuous CRFs as sequential deep networks for monocular depth estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5354–5362. [Google Scholar]
- Liu, C.; Gu, J.; Kim, K.; Narasimhan, S.G.; Kautz, J. Neural RGB(r)D sensing: Depth and uncertainty from a video camera. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10986–10995. [Google Scholar]
- Masoumian, A.; Rashwan, H.A.; Cristiano, J.; Asif, M.S.; Puig, D. Monocular depth estimation using deep learning: A review. Sensors 2022, 22, 5353. [Google Scholar] [CrossRef]
- Simsar, E.; Örnek, E.P.; Manhardt, F.; Dhamo, H.; Navab, N.; Tombari, F. Object-Aware Monocular Depth Prediction with Instance Convolutions. IEEE Robot. Autom. Lett. 2022, 7, 5389–5396. [Google Scholar] [CrossRef]
- Ji, W.; Yan, G.; Li, J.; Piao, Y.; Yao, S.; Zhang, M.; Cheng, L.; Lu, H. DMRA: Depth-induced multi-scale recurrent attention network for RGB-D saliency detection. IEEE Trans. Image Process. 2022, 31, 2321–2336. [Google Scholar] [CrossRef]
- Aich, S.; Vianney, J.M.U.; Islam, M.A.; Liu, M.K.B. Bidirectional attention network for monocular depth estimation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 11746–11752. [Google Scholar]
- Lee, J.H.; Han, M.K.; Ko, D.W.; Suh, I.H. From big to small: Multi-scale local planar guidance for monocular depth estimation. arXiv 2019, arXiv:1907.10326. [Google Scholar]
- Jung, H.; Kim, Y.; Min, D.; Oh, C.; Sohn, K. Depth prediction from a single image with conditional adversarial networks. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1717–1721. [Google Scholar]
- Wofk, D.; Ma, F.; Yang, T.J.; Karaman, S.; Sze, V. Fastdepth: Fast monocular depth estimation on embedded systems. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6101–6108. [Google Scholar]
- Moukari, M.; Picard, S.; Simon, L.; Jurie, F. Deep multi-scale architectures for monocular depth estimation. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2940–2944. [Google Scholar]
- Abdulwahab, S.; Rashwan, H.A.; Garcia, M.A.; Jabreel, M.; Chambon, S.; Puig, D. Adversarial learning for depth and viewpoint estimation from a single image. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2947–2958. [Google Scholar] [CrossRef]
- Wang, Q.; Piao, Y. Depth estimation of supervised monocular images based on semantic segmentation. J. Vis. Commun. Image Represent. 2023, 90, 103753. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Y.; Zhang, L. DeMT: Deformable Mixer Transformer for Multi-Task Learning of Dense Prediction. arXiv 2023, arXiv:2301.03461. [Google Scholar]
- Chen, L. Multi-Scale Adaptive Feature Fusion for Monocular Depth Estimation. In Proceedings of the NeurIPS, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Tan, M. Hierarchical Multi-Scale Learning for Monocular Depth Estimation. In Proceedings of the NeurIPS, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Abdulwahab, S.; Rashwan, H.A.; Garcia, M.A.; Masoumian, A.; Puig, D. Monocular depth map estimation based on a multi-scale deep architecture and curvilinear saliency feature boosting. Neural Comput. Appl. 2022, 34, 16423–16440. [Google Scholar] [CrossRef]
- Lin, G.; Liu, F.; Milan, A.; Shen, C.; Reid, I. Refinenet: Multi-path refinement networks for dense prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 1228–1242. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, P.; Huang, Q.; Zhang, H.; Gan, Z.; Huang, X.; He, X. Attngan: Fine-grained text to image generation with attentional generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1316–1324. [Google Scholar]
- Hao, S.; Zhou, Y.; Zhang, Y.; Guo, Y. Contextual attention refinement network for real-time semantic segmentation. IEEE Access 2020, 8, 55230–55240. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, L.; Yang, D.; Yang, L. KRAN: Knowledge Refining Attention Network for Recommendation. ACM Trans. Knowl. Discov. Data (TKDD) 2021, 16, 39. [Google Scholar] [CrossRef]
- Koenderink, J.J. The structure of images. Biol. Cybern. 1984, 50, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2noise: Learning image restoration without clean data. arXiv 2018, arXiv:1803.04189. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, T.; Zhang, H.; Long, L.R.; Huang, X. SegAN: Adversarial network with multi-scale L1 loss for medical image segmentation. Neuroinformatics 2018, 16, 383–392. [Google Scholar] [CrossRef]
- Xue, Y.; Xu, T.; Huang, X. Adversarial learning with multi-scale loss for skin lesion segmentation. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 859–863. [Google Scholar]
- Liu, J.; Zhang, Y.; Cui, J.; Feng, Y.; Pang, L. Fully convolutional multi-scale dense networks for monocular depth estimation. IET Comput. Vis. 2019, 13, 515–522. [Google Scholar] [CrossRef]
- Lin, L.; Huang, G.; Chen, Y.; Zhang, L.; He, B. Efficient and high-quality monocular depth estimation via gated multi-scale network. IEEE Access 2020, 8, 7709–7718. [Google Scholar] [CrossRef]
- Rashwan, H.A.; Chambon, S.; Gurdjos, P.; Morin, G.; Charvillat, V. Using curvilinear features in focus for registering a single image to a 3D object. IEEE Trans. Image Process. 2019, 28, 4429–4443. [Google Scholar] [CrossRef]
- Alhashim, I.; Wonka, P. High quality monocular depth estimation via transfer learning. arXiv 2018, arXiv:1812.11941. [Google Scholar]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor segmentation and support inference from rgbd images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 746–760. [Google Scholar]
- Song, S.; Lichtenberg, S.P.; Xiao, J. Sun RGB-D: A RGB-D scene understanding benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 567–576. [Google Scholar]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3D: Depth Perception from a Single Still Image. In Proceedings of the AAAI, Chicago, IL, USA, 13–17 July 2008; Volume 3, pp. 1571–1576. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. PyTorch: An Open Source Machine Learning Framework; Facebook AI Research: Menlo Park, CA, USA, 2017; Available online: https://pytorch.org (accessed on 14 August 2025).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G. Deep convolutional neural fields for depth estimation from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5162–5170. [Google Scholar]
- Chen, S.; Fan, X.; Pu, Z.; Ouyang, J.; Zou, B. Single image depth estimation based on sculpture strategy. Knowl.-Based Syst. 2022, 250, 109067. [Google Scholar] [CrossRef]
- Ramamonjisoa, M.; Firman, M.; Watson, J.; Lepetit, V.; Turmukhambetov, D. Single Image Depth Estimation Using Wavelet Decomposition. arXiv 2021, arXiv:2106.02022. [Google Scholar]
- Tang, M.; Chen, S.; Dong, R.; Kan, J. Encoder-Decoder Structure with the Feature Pyramid for Depth Estimation from a Single Image. IEEE Access 2021, 9, 22640–22650. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, H.; Shao, S.; Li, X.; Zhang, B. F2-Depth: Self-supervised Indoor Monocular Depth Estimation via Optical Flow Consistency and Feature Map Synthesis. arXiv 2024, arXiv:2403.18443. [Google Scholar] [CrossRef]
- Karsch, K.; Liu, C.; Kang, S.B. Depth transfer: Depth extraction from video using non-parametric sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2144–2158. [Google Scholar] [CrossRef]
- Godard, C.; Mac Aodha, O.; Brostow, G.J. Unsupervised monocular depth estimation with left-right consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 270–279. [Google Scholar]
- Kuznietsov, Y.; Stuckler, J.; Leibe, B. Semi-supervised deep learning for monocular depth map prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6647–6655. [Google Scholar]
- Zhao, W.; Rao, Y.; Liu, Z.; Liu, B.; Zhou, J.; Lu, J. Unleashing text-to-image diffusion models for visual perception. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 5729–5739. [Google Scholar]
- Chen, X.; Chen, X.; Zha, Z.J. Structure-aware residual pyramid network for monocular depth estimation. arXiv 2019, arXiv:1907.06023. [Google Scholar] [CrossRef]
- Yin, W.; Liu, Y.; Shen, C.; Yan, Y. Enforcing geometric constraints of virtual normal for depth prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5684–5693. [Google Scholar]
- Bhat, S.F.; Alhashim, I.; Wonka, P. Adabins: Depth estimation using adaptive bins. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 4009–4018. [Google Scholar]
- Li, Z.; Wang, X.; Liu, X.; Jiang, J. Binsformer: Revisiting adaptive bins for monocular depth estimation. IEEE Trans. Image Process. 2024, 33, 3964–3976. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Rao, Y.; Yu, H.; Wang, G.; Fan, H.; Pang, W.; Dong, J. Out-of-distribution monocular depth estimation with local invariant regression. Knowl.-Based Syst. 2025, 319, 113518. [Google Scholar] [CrossRef]






| Method | Accuracy: Higher Is Better | Error: Lower Is Better | ||||
|---|---|---|---|---|---|---|
| rel ↓ | rms ↓ | log10 ↓ | ||||
| BL | 0.8425 | 0.9701 | 0.9932 | 0.1260 | 0.540 | 0.0542 |
| BLSC | 0.8491 | 0.9712 | 0.9939 | 0.1252 | 0.529 | 0.0536 |
| BLSC + MSFA | 0.8549 | 0.973 | 0.9937 | 0.1219 | 0.524 | 0.052 |
| BLSC + RAN | 0.8629 | 0.9763 | 0.9940 | 0.1193 | 0.512 | 0.0509 |
| BLSC + ML | 0.8636 | 0.9753 | 0.9940 | 0.1189 | 0.515 | 0.0512 |
| BLSC + ML + MSFA + RAN | 0.8725 | 0.9766 | 0.994 | 0.113 | 0.512 | 0.048 |
| Method | rel ↓ | rms ↓ | log10 ↓ |
|---|---|---|---|
| BL | 0.231 | 7.02 | 0.0119 |
| BLSC | 0.207 | 6.74 | 0.0109 |
| BLSC + MSFA | 0.196 | 6.67 | 0.0103 |
| BLSC + RAN | 0.192 | 6.61 | 0.0096 |
| BLSC + ML | 0.191 | 6.58 | 0.0092 |
| BLSC + ML + MSFA + RAN | 0.187 | 6.531 | 0.0084 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulwahab, S.; Rashwan, H.A.; El-Melegy, M.T.; Puig, D. DAR-MDE: Depth-Attention Refinement for Multi-Scale Monocular Depth Estimation. J. Sens. Actuator Netw. 2025, 14, 90. https://doi.org/10.3390/jsan14050090
Abdulwahab S, Rashwan HA, El-Melegy MT, Puig D. DAR-MDE: Depth-Attention Refinement for Multi-Scale Monocular Depth Estimation. Journal of Sensor and Actuator Networks. 2025; 14(5):90. https://doi.org/10.3390/jsan14050090
Chicago/Turabian StyleAbdulwahab, Saddam, Hatem A. Rashwan, Moumen T. El-Melegy, and Domenec Puig. 2025. "DAR-MDE: Depth-Attention Refinement for Multi-Scale Monocular Depth Estimation" Journal of Sensor and Actuator Networks 14, no. 5: 90. https://doi.org/10.3390/jsan14050090
APA StyleAbdulwahab, S., Rashwan, H. A., El-Melegy, M. T., & Puig, D. (2025). DAR-MDE: Depth-Attention Refinement for Multi-Scale Monocular Depth Estimation. Journal of Sensor and Actuator Networks, 14(5), 90. https://doi.org/10.3390/jsan14050090






