Can Differential Privacy Hinder Poisoning Attack Detection in Federated Learning?
Abstract
1. Introduction
1.1. Summary of Contributions
- We formally pose the following novel research question: Does differential privacy hinder or help in detecting poisoning attacks in federated learning? This is a question that has gone largely unexplored in the literature.
- We analyze the effect of DP-SGD noise on detection and identification accuracy under different model sizes, numbers of clients, and poisoning intensities, supported by mathematical reasoning.
- We design and implement two lightweight poisoning detection algorithms based on model performance deviation and a third algorithm to identify malicious clients. We also adapt an existing AE-based detection method [17] for benchmarking.
- We evaluate the detection and identification performance across three different FL tasks: (i) image classification on MNIST using a CNN and (ii) anomaly detection on CSE-CIC-IDS2018 and CIC-IoT2023 using autoencoder-based neural networks.
- We evaluate the detection and identification performance of data- and model-level poisoning attacks under varying levels of DP noise, including strong ( = 0.1), moderate ( = 1.0), weak ( = 10.0), and no privacy ( → ∞).
- Our results show that both the detection and identification of poisoned clients remain effective even under strong DP constraints, thereby validating the robustness of the proposed approach.

| Algorithm 1 Global Model-Assisted Poisonous Data Attack Detector (GAPDAD) |
|
| Algorithm 2 Client-Assisted Poisonous Data Attack Detector (CAPDAD) |
|
| Algorithm 3 Identification of Malicious Clients (IMC) |
|
1.2. Related Work
| Method | Detection Strategy | DP | Server Requirement | Remarks |
|---|---|---|---|---|
| REC-Fed [28] | Cluster-based anomaly filtering | ✗ | Client clustering and similarity checks | Strong for edge networks but not DP-compatible |
| FLDetector [29] | Behavioral consistency tracking | ✗ | History of client updates required | May fail with unstable training dynamics |
| SafeFL [30] | Synthetic validation dataset testing | ✗ | Needs generative model at server | Effective detection; impractical where synthetic data are not feasible |
| FedDMC [31] | PCA and tree-based clustering | ✗ | Low-dimensional projections from clients | Efficient but untested under DP settings |
| SecureFed [32] | Dim. reduction + contribution scoring | ✗ | Requires client-side projections | Lightweight, trade-off between privacy and accuracy |
| VFEFL [33] | Functional encryption-based validation | ✗ | Verifiable crypto setup between clients and server | Strong privacy guarantees but computationally heavy |
| Ours | Accuracy trend deviation under DP noise | ✔ | Test accuracy evaluation only | Lightweight, privacy-preserving, and works even under strong DP noise |
2. Problem Statement
2.1. Preliminaries on Differential Privacy
2.2. Distributed Setup
2.3. Adversary Model and Attack Assumptions
- In each FL round, at least clients are honest. A round here refers to one complete cycle where the central server distributes the global model to clients, who then perform local training on their data and send the updated model back to the server, and the server aggregates these updates to refine the global model.
- Each client updates its model for T iterations locally before sharing it with the server.
- Each client performs -DP locally by using a Gaussian mechanism on globally agreed-upon values for and , as described in Section 2.
- No zero-day attack is expected; we have some genuine prior models.
- The data distribution of a client does not change during a training round.
3. Detection of Poisonous Data in the Presence of DP
3.1. Attack Detection at the Server
3.1.1. Global Model-Assisted Poisonous Data Attack Detection
3.1.2. Client-Assisted Poisonous Data Attack Detection
3.2. Identification of the Adversarial Clients
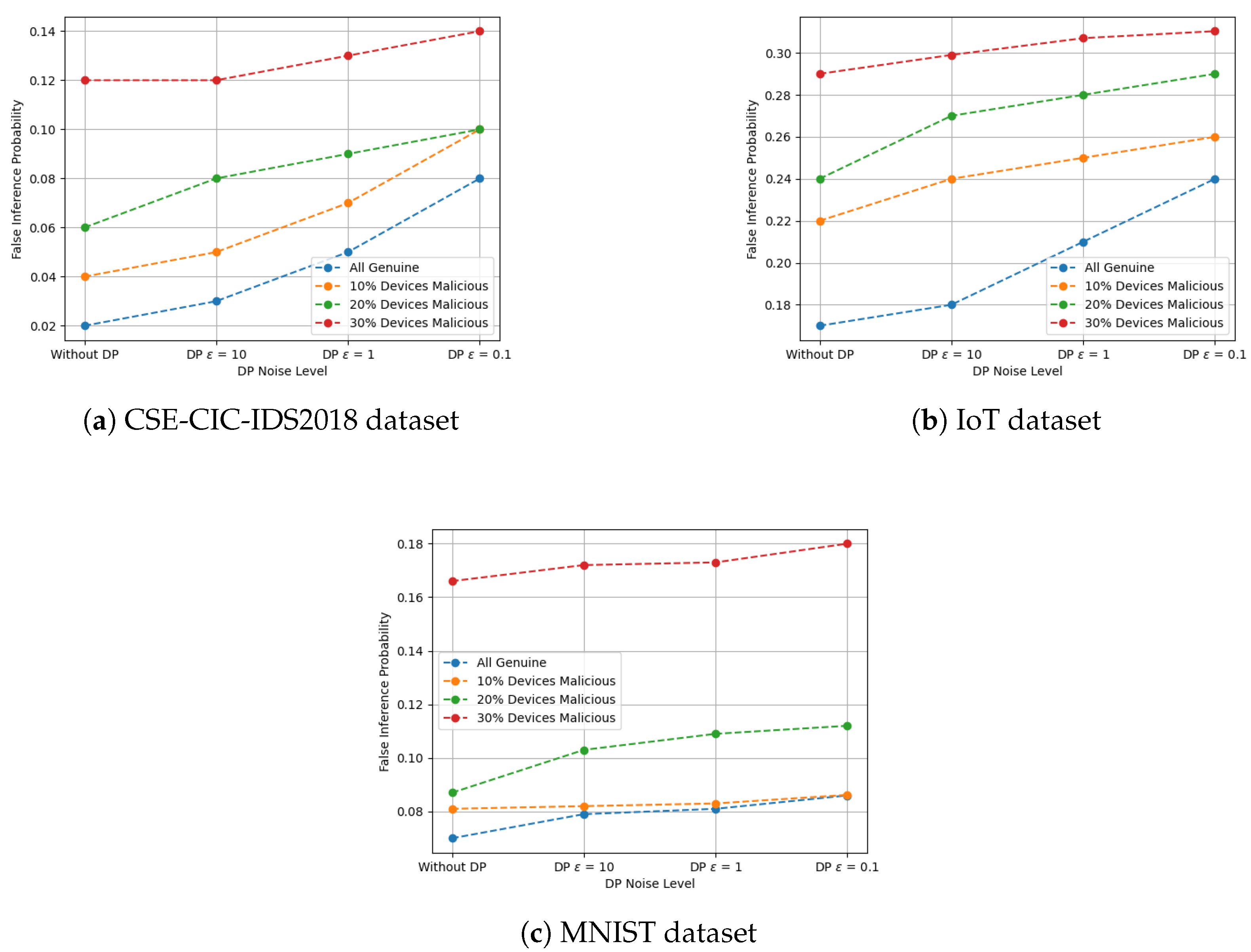
3.3. The Effect of DP Noise on the Detection Performance
4. Experiments and Results
4.1. Simulation Setup and Datasets
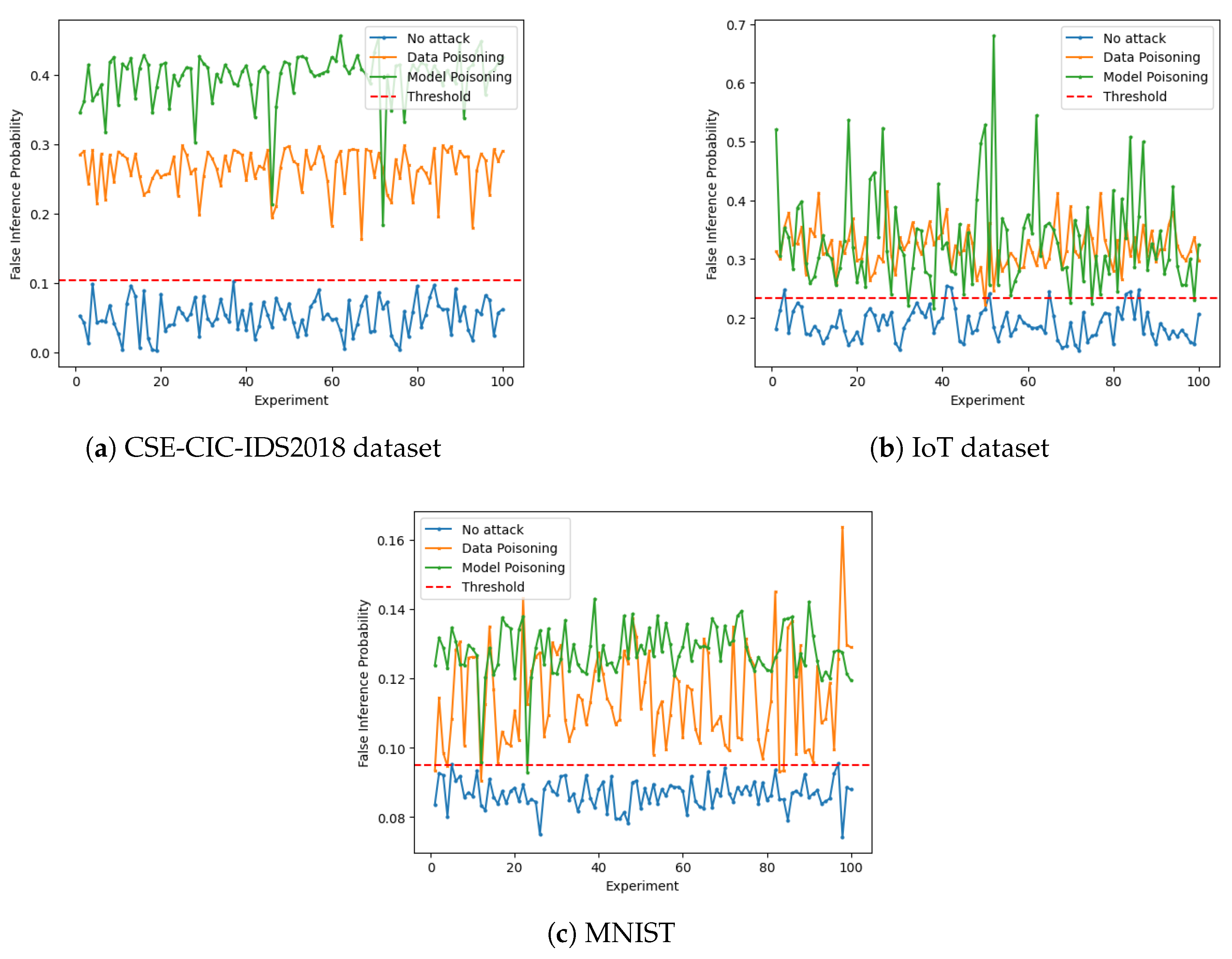
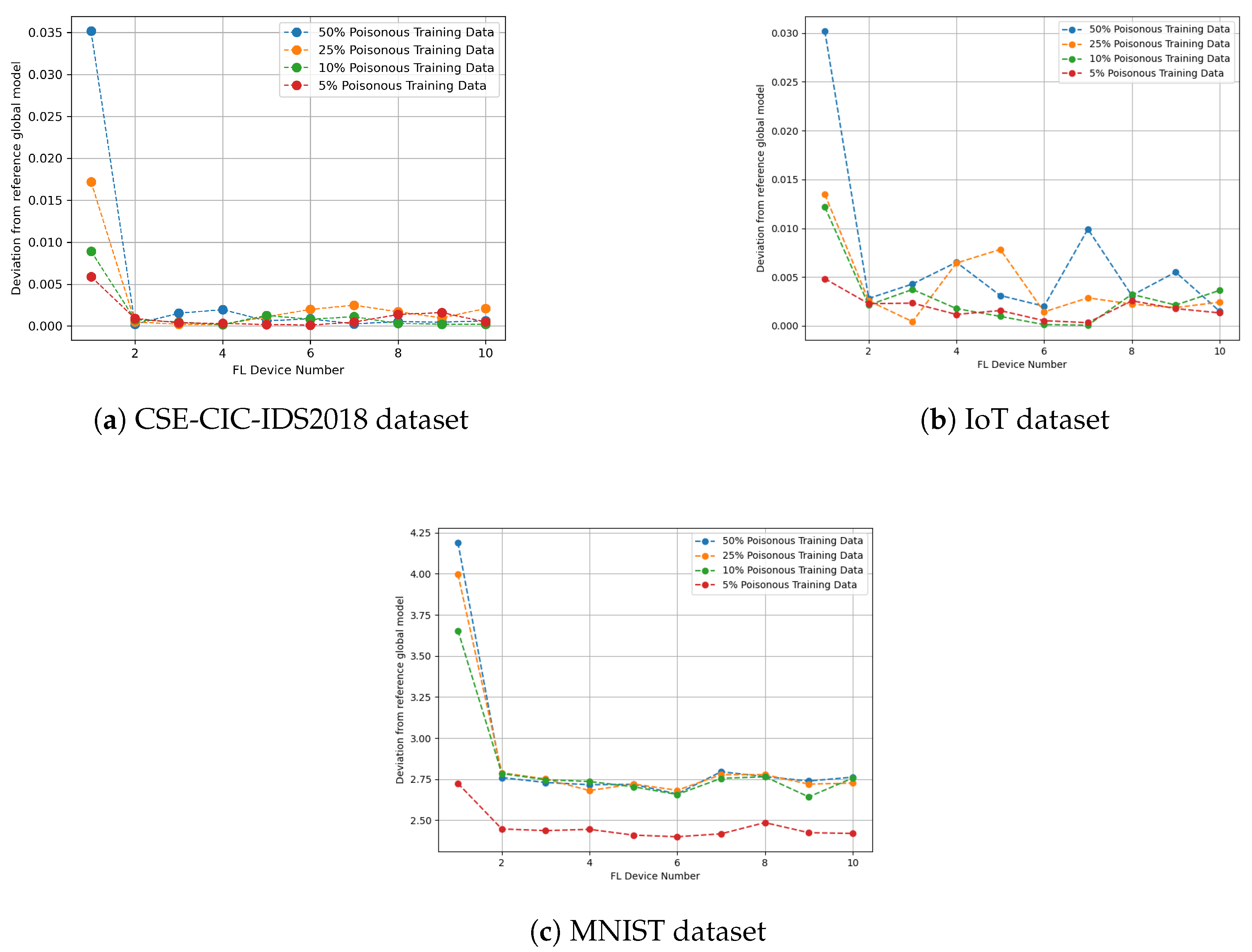
4.2. Experiment I: Impact of Poisoning Attacks with FL and DP
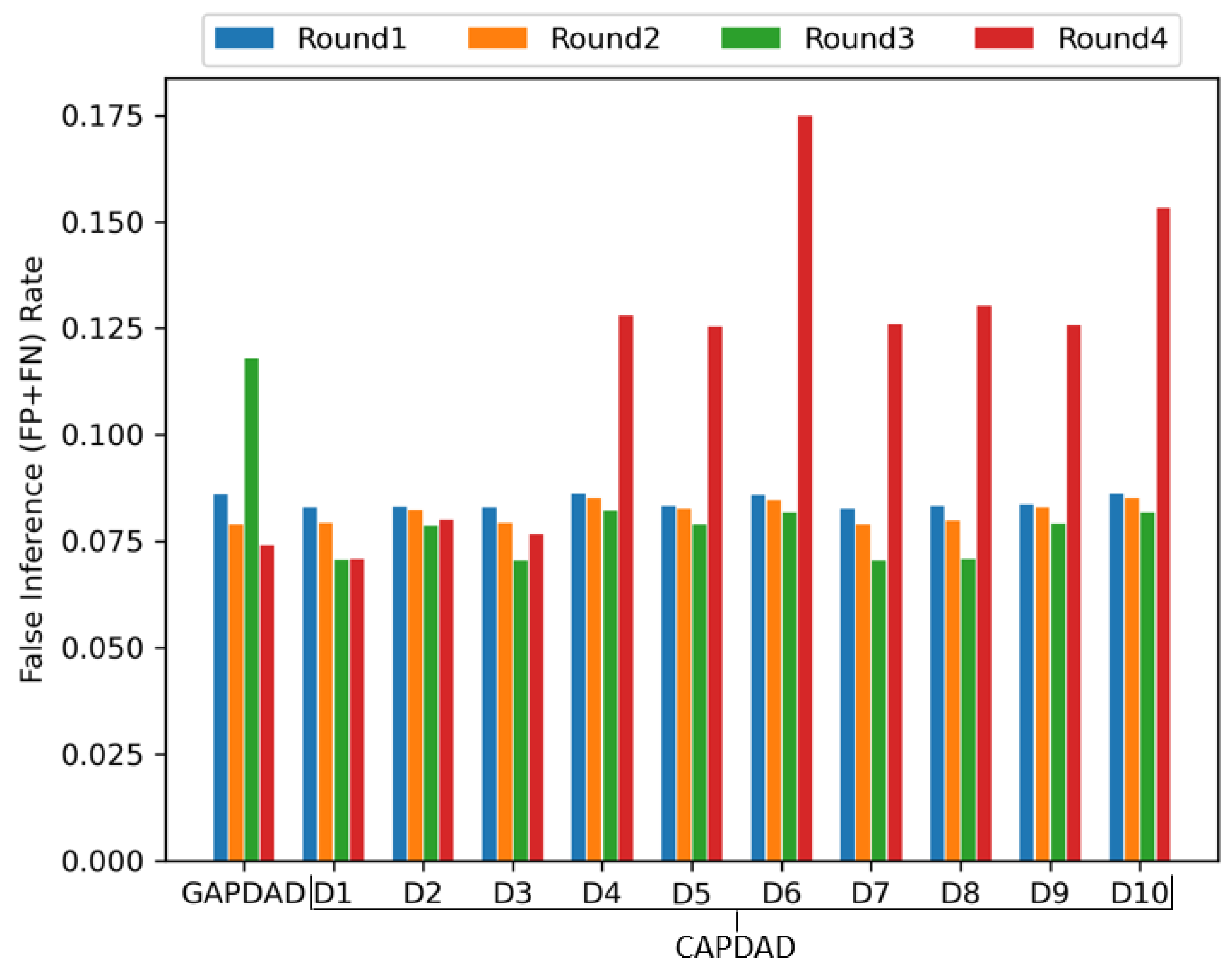
4.3. Experiment II: Detection of Poisoning Attacks Using the GAPDAD and CAPDAD Algorithms 1 and 2
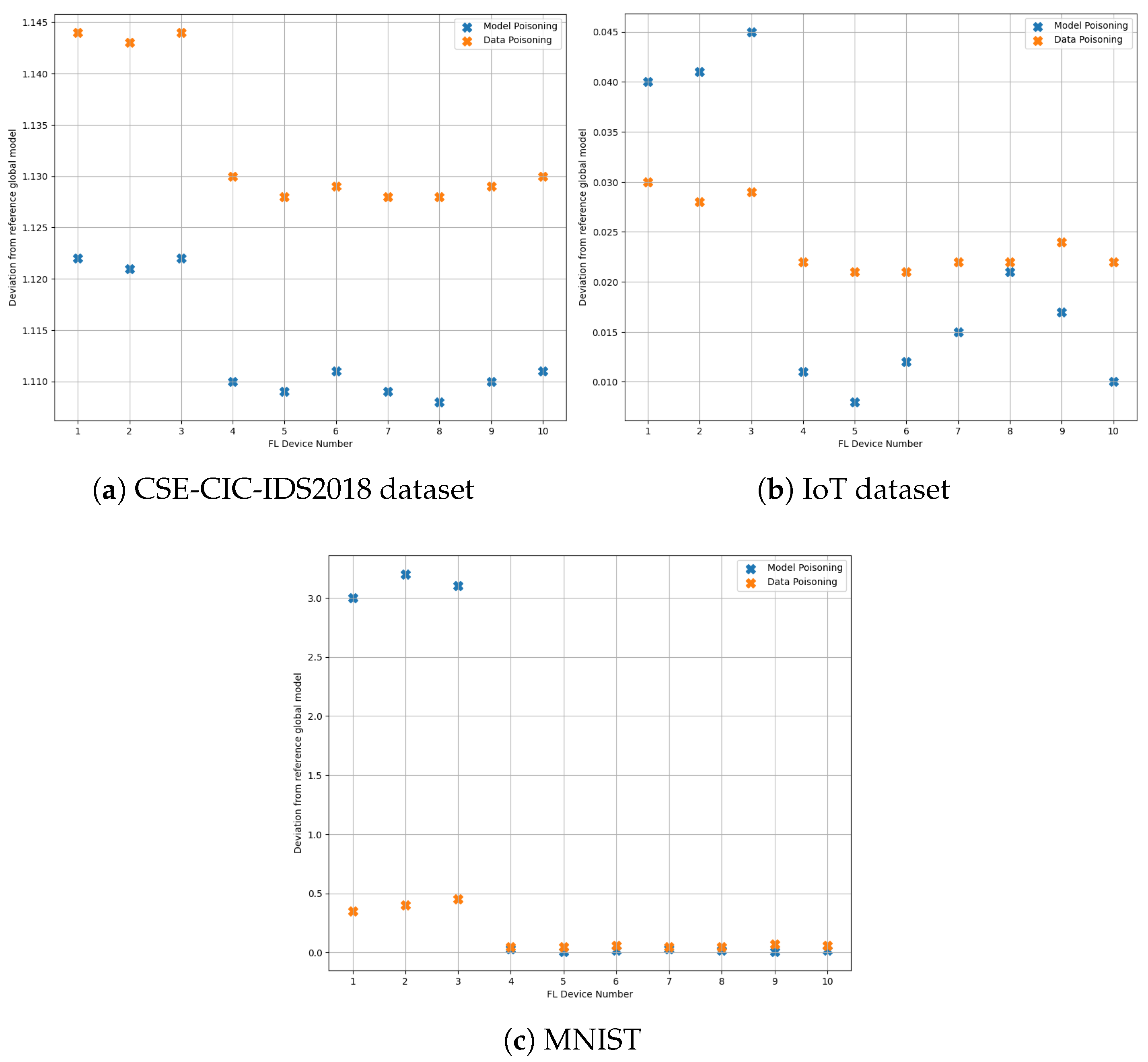
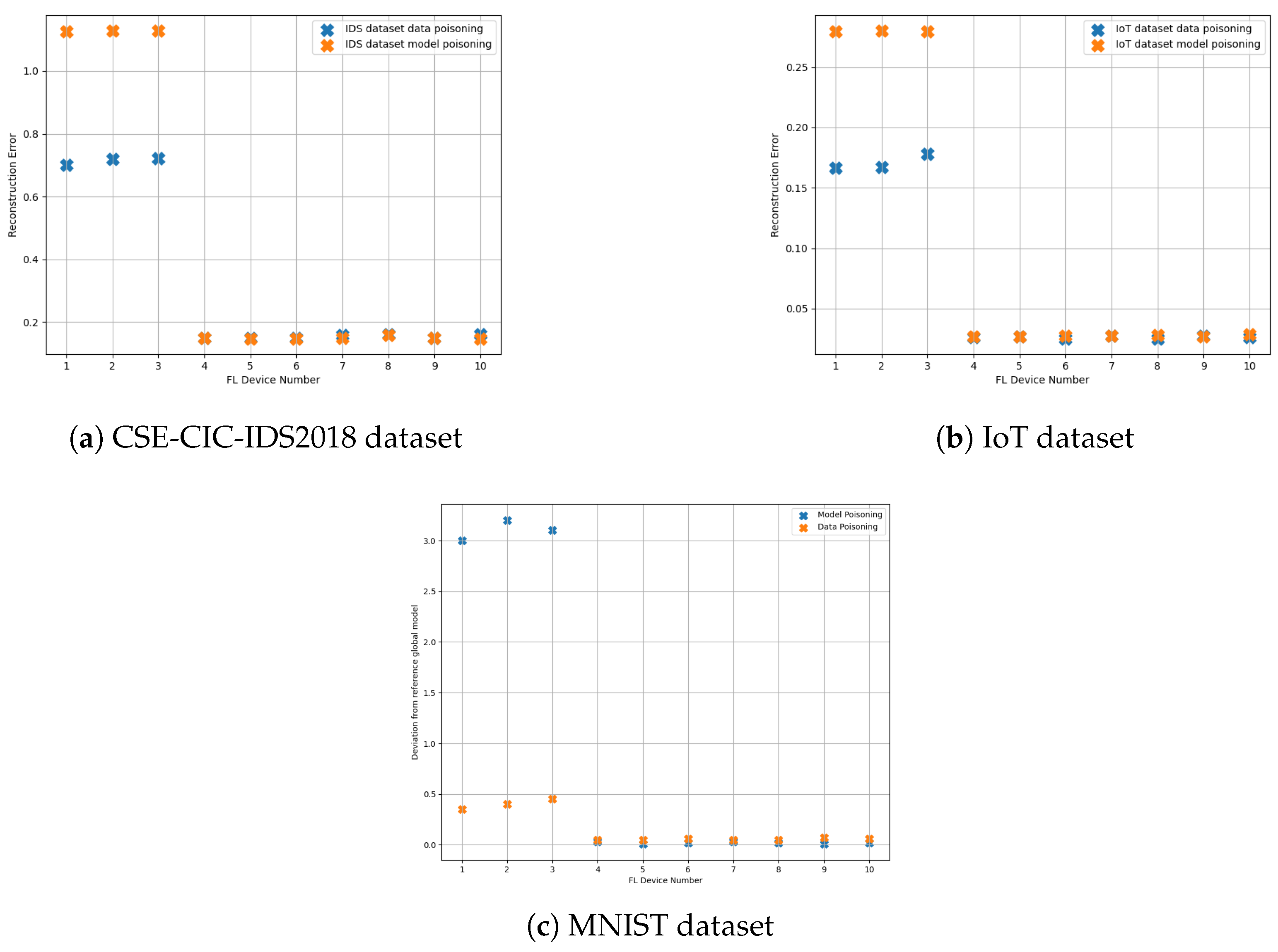
4.4. Experiment III: Identification of Malicious Clients
4.5. Experiment IV: AeNN-Based Identification of Malicious Clients
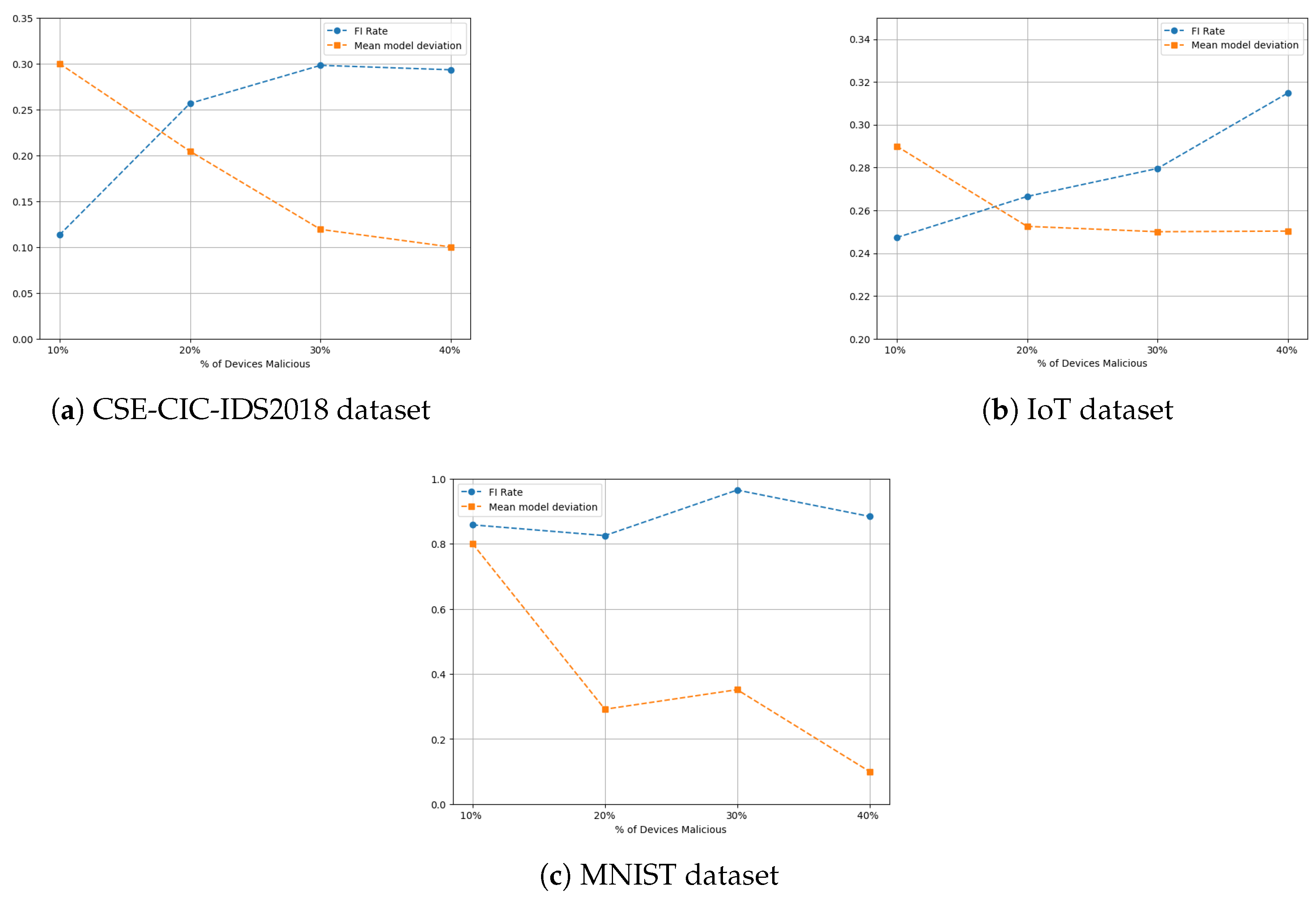
4.6. Experiment V: Analysis of Detection and Identification Trends Across Datasets
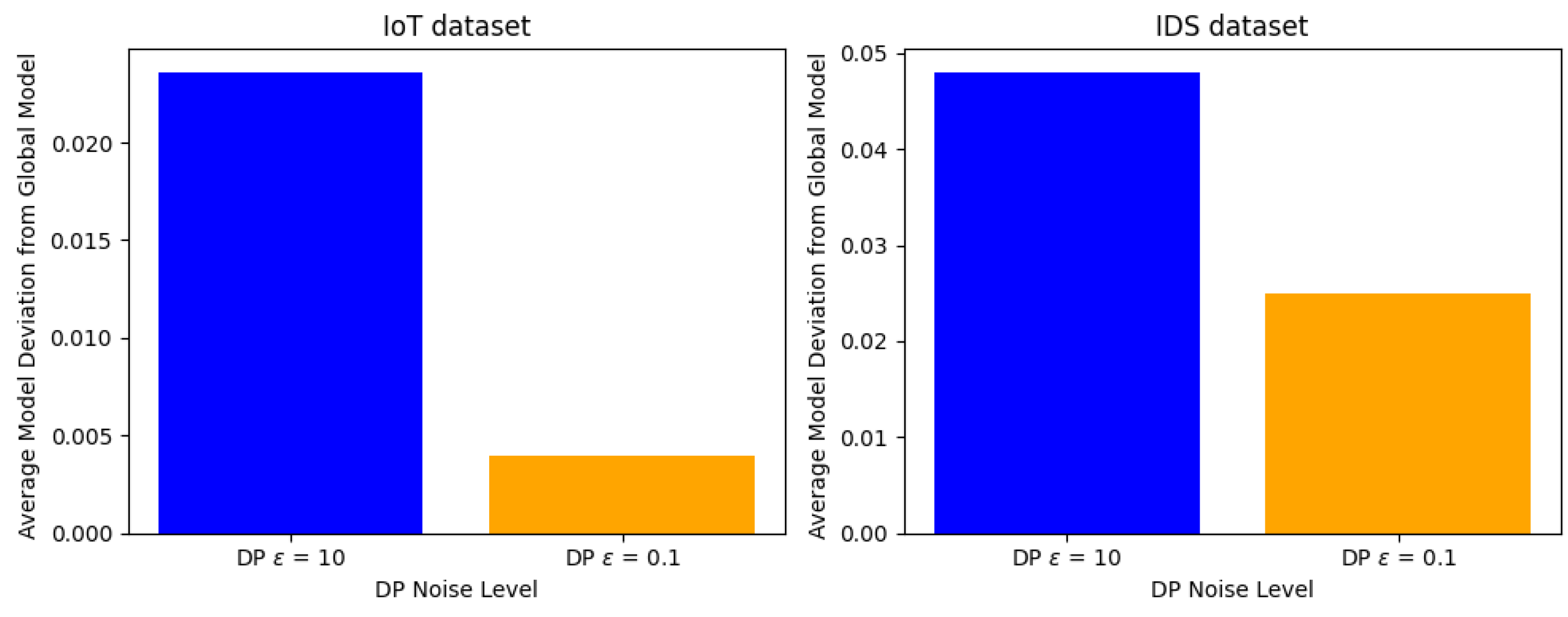
4.7. Experiment VI: Impacts of Differential Privacy Across Varying Model Architectures
5. Conclusions and Future Scope
Author Contributions
Funding
Conflicts of Interest
References
- Kairouz, P.; McMahan, H.B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A.N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. Advances and open problems in federated learning. Found. Trends® Mach. Learn. 2021, 14, 1–210. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating Noise to Sensitivity in Private Data Analysis. In Proceedings of the Third Conference on Theory of Cryptography, New York, NY, USA, 4–7 March 2006; pp. 265–284. [Google Scholar] [CrossRef]
- Dwork, C.; Talwar, K.; Thakurta, A.; Zhang, L. Analyze Gauss: Optimal Bounds for Privacy-preserving Principal Component Analysis. In Proceedings of the 46th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 31 May–3 June 2014; pp. 11–20. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; ACM: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.; Poor, H.V. Federated learning with differential privacy: Algorithms and performance analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef]
- Sun, Z.; Kairouz, P.; Suresh, A.T.; McMahan, H.B. Can You Really Backdoor Federated Learning? 2019. Available online: http://arxiv.org/abs/1911.07963 (accessed on 30 July 2025).
- Bouacida, N.; Mohapatra, P. Vulnerabilities in Federated Learning. IEEE Access 2021, 9, 63229–63249. [Google Scholar] [CrossRef]
- Koh, P.; Steinhardt, J.; Liang, P. Stronger Data Poisoning Attacks Break Data Sanitization Defenses. arXiv 2018, arXiv:1811.00741. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, S.; Aafer, Y.; Lee, W.C.; Zhai, J.; Wang, W.; Zhang, X. Trojaning Attack on Neural Networks. In Proceedings of the Network and Distributed System Security Symposium, San Diego, CA, USA, 18–21 February 2018. [Google Scholar]
- Steinhardt, J.; Koh, P.W.; Liang, P. Certified Defenses for Data Poisoning Attacks. 2017. Available online: http://arxiv.org/abs/1706.03691 (accessed on 30 July 2025).
- Raghunathan, A.; Steinhardt, J.; Liang, P. Certified Defenses Against Adversarial Examples. 2020. Available online: http://arxiv.org/abs/1801.09344 (accessed on 30 July 2025).
- Ma, Y.; Zhu, X.; Hsu, J. Data Poisoning Against Differentially-Private Learners: Attacks and Defenses. 2019. Available online: http://arxiv.org/abs/1903.09860 (accessed on 30 July 2025).
- IDS 2018 | Datasets | Research | Canadian Institute for Cybersecurity | UNB—unb.ca. Available online: https://www.unb.ca/cic/datasets/ids-2018.html. (accessed on 31 July 2023).
- Neto, E.C.P.; Dadkhah, S.; Ferreira, R.; Zohourian, A.; Lu, R.; Ghorbani, A.A. CICIoT2023: A real-time dataset and benchmark for large-scale attacks in IoT environment. Sensors 2023, 23, 5941. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Raza, A.; Li, S.; Tran, K.P.; Koehl, L. Using Anomaly Detection to Detect Poisoning Attacks in Federated Learning Applications. 2023. Available online: http://arxiv.org/abs/2207.08486 (accessed on 30 July 2025).
- Yang, Z.; Chen, M.; Wong, K.K.; Poor, H.V.; Cui, S. Federated learning for 6G: Applications, challenges, and opportunities. Engineering 2022, 8, 33–41. [Google Scholar] [CrossRef]
- Nair, D.G.; Nair, J.J.; Reddy, K.J.; Narayana, C.A. A privacy preserving diagnostic collaboration framework for facial paralysis using federated learning. Eng. Appl. Artif. Intell. 2022, 116, 105476. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, N.; Wang, Y.; Gu, S.; Cao, Z.; Dong, X.; Choo, K.K.R. A differentially private federated learning model against poisoning attacks in edge computing. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1941–1958. [Google Scholar] [CrossRef]
- Chhetri, B.; Gopali, S.; Olapojoye, R.; Dehbash, S.; Namin, A.S. A Survey on Blockchain-Based Federated Learning and Data Privacy. arXiv 2023, arXiv:2306.17338. [Google Scholar] [CrossRef]
- Venkatasubramanian, M.; Lashkari, A.H.; Hakak, S. IoT Malware Analysis using Federated Learning: A Comprehensive Survey. IEEE Access 2023, 11, 5004–5018. [Google Scholar] [CrossRef]
- Balakumar, N.; Thanamani, A.S.; Karthiga, P.; Kanagaraj, A.; Sathiyapriya, S.; Shubha, A. Federated Learning based framework for improving Intrusion Detection System in IIOT. Network 2023, 3, 158–179. [Google Scholar]
- Li, S.; Cheng, Y.; Liu, Y.; Wang, W.; Chen, T. Abnormal client behavior detection in federated learning. arXiv 2019, arXiv:1910.09933. [Google Scholar] [CrossRef]
- Xing, L.; Wang, K.; Wu, H.; Ma, H.; Zhang, X. FL-MAAE: An Intrusion Detection Method for the Internet of Vehicles Based on Federated Learning and Memory-Augmented Autoencoder. Electronics 2023, 12, 2284. [Google Scholar] [CrossRef]
- Sáez-de Cámara, X.; Flores, J.L.; Arellano, C.; Urbieta, A.; Zurutuza, U. Clustered federated learning architecture for network anomaly detection in large scale heterogeneous IoT networks. Comput. Secur. 2023, 131, 103299. [Google Scholar] [CrossRef]
- Yazdinejad, A.; Dehghantanha, A.; Karimipour, H.; Srivastava, G.; Parizi, R.M. A robust privacy-preserving federated learning model against model poisoning attacks. IEEE Trans. Inf. Forensics Secur. 2024, 19, 6693–6708. [Google Scholar] [CrossRef]
- Li, X.; Guo, Y.; Zhang, T.; Yang, Y. REC-Fed: A robust and efficient clustered federated system for dynamic edge networks. IEEE Trans. Mob. Comput. 2024, 23, 15256–15273. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q.; Liu, J. FLDetector: Detecting adversarial clients in federated learning via update consistency. arXiv 2022, arXiv:2207.09209. [Google Scholar]
- Dou, Z.; Wang, J.; Sun, W.; Liu, Z.; Fang, M. Toward Malicious Clients Detection in Federated Learning (SafeFL). arXiv 2025, arXiv:2505.09110. [Google Scholar]
- Mu, X.; Cheng, K.; Shen, Y.; Li, X.; Chang, Z.; Zhang, T.; Ma, X. FedDMC: Efficient and Robust Federated Learning via Detecting Malicious Clients. IEEE Trans. Dependable Secur. Comput. 2024, 21, 5259–5274. [Google Scholar] [CrossRef]
- Kavuri, L.A.; Mhatre, A.; Nair, A.K.; Gupta, D. SecureFed: A two-phase framework for detecting malicious clients in federated learning. arXiv 2025, arXiv:2506.16458. [Google Scholar]
- Cai, N.; Han, J. Privacy-Preserving Federated Learning against Malicious Clients Based on Verifiable Functional Encryption. arXiv 2025, arXiv:2506.12846. [Google Scholar] [CrossRef]
- Tasnim, N.; Mohammadi, J.; Sarwate, A.D.; Imtiaz, H. Approximating Functions with Approximate Privacy for Applications in Signal Estimation and Learning. Entropy 2023, 25, 825. [Google Scholar] [CrossRef] [PubMed]
- Imtiaz, H.; Mohammadi, J.; Silva, R.; Baker, B.; Plis, S.M.; Sarwate, A.D.; Calhoun, V.D. A Correlated Noise-Assisted Decentralized Differentially Private Estimation Protocol, and its Application to fMRI Source Separation. IEEE Trans. Signal Process. 2021, 69, 6355–6370. [Google Scholar] [CrossRef] [PubMed]
- Imtiaz, H.; Mohammadi, J.; Sarwate, A.D. Distributed Differentially Private Computation of Functions with Correlated Noise. 2021. Available online: http://arxiv.org/abs/1904.10059 (accessed on 30 July 2025).
- Dwork, C. Differential Privacy. In Proceedings of the Automata, Languages and Programming, Venice, Italy, 10–14 July 2006; pp. 1–12. [Google Scholar]
- Dwork, C.; Roth, A. The Algorithmic Foundations of Differential Privacy. Found. Trends Theor. Comput. Sci. 2013, 9, 211–407. [Google Scholar] [CrossRef]
- McSherry, F.; Talwar, K. Mechanism Design via Differential Privacy. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS ’07), Providence, RI, USA, 21–23 October 2007; pp. 94–103. [Google Scholar] [CrossRef]
- Chen, Z.; Yeo, C.K.; Lee, B.S.; Lau, C.T. Autoencoder-based network anomaly detection. In Proceedings of the 2018 Wireless telecommunications symposium (WTS), Phoenix, AZ, USA, 18–20 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Liu, P.; Xu, X.; Wang, W. Threats, attacks and defenses to federated learning: Issues, taxonomy and perspectives. Cybersecurity 2022, 5, 4. [Google Scholar] [CrossRef]
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics. Part Two, 2nd ed.; D. Van Nostrand Company, Inc.: Princeton, NJ, USA, 1951. [Google Scholar]
- Hasanpour, S.H.; Rouhani, M.; Fayyaz, M.; Sabokrou, M. Lets keep it simple, using simple architectures to outperform deeper and more complex architectures. arXiv 2016, arXiv:1608.06037. [Google Scholar]
- Authors, T.F. Flower: A Friendly Federated Learning Framework—flower.dev. Available online: https://flower.dev/ (accessed on 31 July 2023).
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef]



| Dataset | Experiment | Accuracy | False Inference | Precision | Recall |
|---|---|---|---|---|---|
| CICIDS | FL | 98.60 | 0.01 | 0.95 | 1.0 |
| FL with DP | 91.41 | 0.08 | 0.99 | 0.74 | |
| Data Poisoning | 88.30 | 0.12 | 0.93 | 0.69 | |
| Model Poisoning | 63.20 | 0.36 | 0.47 | 0.94 | |
| IoT | FL | 85.88 | 0.14 | 0.67 | 0.98 |
| FL with DP | 72.64 | 0.27 | 0.52 | 0.54 | |
| Data Poisoning | 68.94 | 0.31 | 0.45 | 0.49 | |
| Model Poisoning | 38.73 | 0.61 | 0.26 | 0.66 | |
| MNIST | FL | 92.05 | 0.07 | 0.92 | 0.92 |
| FL with DP | 91.76 | 0.08 | 0.91 | 0.92 | |
| Data Poisoning | 85.53 | 0.14 | 0.88 | 0.85 | |
| Model Poisoning | 69.81 | 0.31 | 0.70 | 0.70 |
| Poisoning Type | Dataset | Precision | Recall | Accuracy | Robustness |
|---|---|---|---|---|---|
| Data Poisoning | CSE-CIC-IDS2018 | 0.970 | 1 | 0.985 | 0.97 |
| CIC-IoT-2023 | 0.832 | 0.940 | 0.875 | 0.76 | |
| MNIST | 0.971 | 0.95 | 0.965 | 0.93 | |
| Model Poisoning | CSE-CIC-IDS2018 | 0.970 | 1 | 0.985 | 0.97 |
| CIC-IoT-2023 | 0.840 | 1.000 | 0.905 | 0.83 | |
| MNIST | 0.98 | 0.99 | 0.985 | 0.97 |
| Architecture | Layer Composition | Parameter Count |
|---|---|---|
| SmallCNN | Conv(1,8,3) + ReLU + MaxPool + FC(1352,10) | 13.6 K |
| MediumCNN | 2 Conv + ReLU + MaxPool + FC(3872,10) | 43.5 K |
| ExtendedMediumCNN | 3 Conv + ReLU + MaxPool + FC(5184,256) + FC(256,10) | 1.35 M |
| DeepCNN | 3 Conv + ReLU + MaxPool + FC(5184,256) + FC(256,128) + FC(128,10) | 1.38 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aggarwal, C.; Nair, D.G.; Mohammadi, J.A.; Nair, J.J.; Ott, J. Can Differential Privacy Hinder Poisoning Attack Detection in Federated Learning? J. Sens. Actuator Netw. 2025, 14, 83. https://doi.org/10.3390/jsan14040083
Aggarwal C, Nair DG, Mohammadi JA, Nair JJ, Ott J. Can Differential Privacy Hinder Poisoning Attack Detection in Federated Learning? Journal of Sensor and Actuator Networks. 2025; 14(4):83. https://doi.org/10.3390/jsan14040083
Chicago/Turabian StyleAggarwal, Chaitanya, Divya G. Nair, Jafar Aco Mohammadi, Jyothisha J. Nair, and Jörg Ott. 2025. "Can Differential Privacy Hinder Poisoning Attack Detection in Federated Learning?" Journal of Sensor and Actuator Networks 14, no. 4: 83. https://doi.org/10.3390/jsan14040083
APA StyleAggarwal, C., Nair, D. G., Mohammadi, J. A., Nair, J. J., & Ott, J. (2025). Can Differential Privacy Hinder Poisoning Attack Detection in Federated Learning? Journal of Sensor and Actuator Networks, 14(4), 83. https://doi.org/10.3390/jsan14040083






