Parallel Eclipse-Aware Routing on FPGA for SpaceWire-Based OBC in LEO Satellite Networks
Abstract
1. Introduction
- We verified the feasibility of implementing a K-Shortest Paths (KSP) algorithm, tailored for LEO satellites, on an FPGA and secured real-time performance by reducing computation time through acceleration and parallelization; additionally, we incorporated the Eclipse-Aware Routing (EAR) algorithm, which considers eclipse conditions and energy consumption rates.
- We demonstrated the practical applicability of our approach by integrating the FPGA with SpaceWire-based systems and implementing dynamic routing-table updates on actual SpaceWire network hardware, SpaceWire Brick MK4.
2. Problem Description
2.1. Characteristics of LEO Network Topologies
2.2. Energy Efficiency Problem in LEO Networks
2.3. Problem of Real-Time Routing on OBCs with Limited Resources
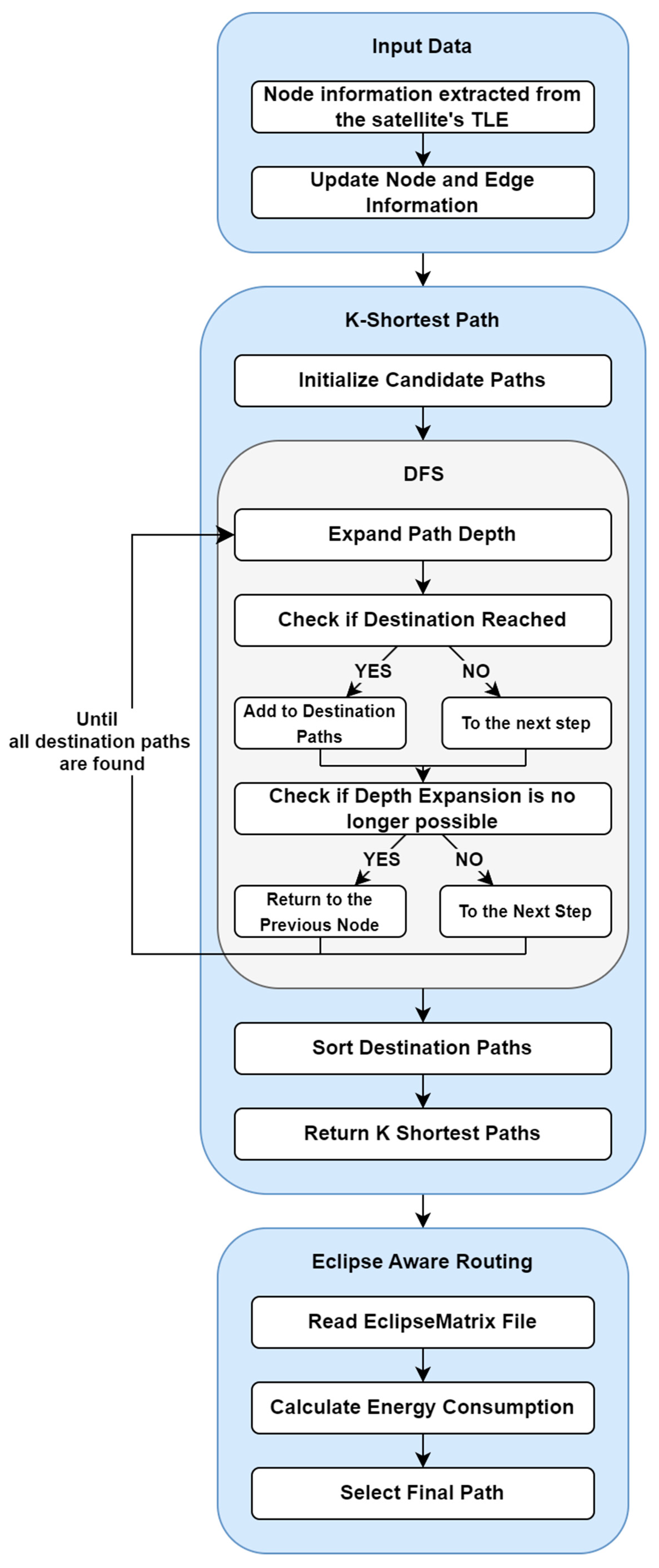
3. Proposed Method
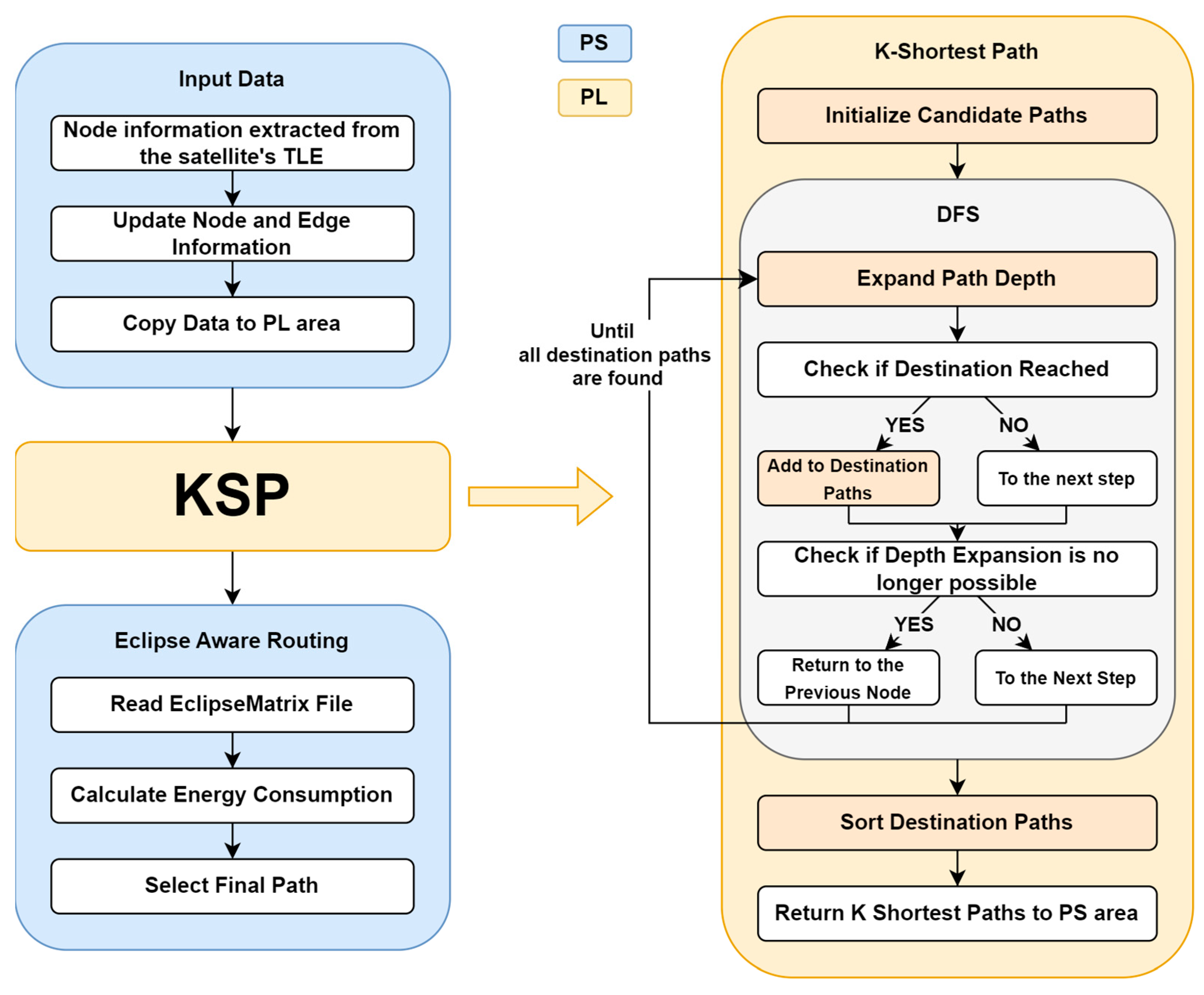
3.1. Overall Structure
3.2. Description for Eclipse-Aware Routing (EAR)
| Algorithm 1 Eclipse-Aware Routing | |
| Input | eclipseMatrix[time][nodes] paths[]: result of KSP sampleTime NoE, TxE, RxE nTimeStep |
| Output | minPath |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. | Initialize Constants: NoE, TxE, RxE Initialize energyTable[pathCount][maxLength] = 0 For each pathIdx from 0 to topPath − 1; currentPath <= Paths[pathIdx]; For satIdx from 0 to length(currentPath) − 1; currentSat <= currentPath[satIdx] If eclipseMatrix[timeIndex][currentSat] == 1; (startIdx, endIdx) <= locateEclipseInterval(eclipseMatrix, timeIndex,currentSat) eclipseDuration = (endIdx − startIdx) × sampleTime; txEstimate <= round(eclipseDuration × random(0.01, 0.1)); Compute Energy Consumption: baseEnergy <= eclipseDuration × NoE; commEnergy <= (txEstimate + 1) × (TxE + RxE) energyTable[pathIdx][satIdx] <= baseEnergy + commEnergy End if End for End for Compute Maximum Energy Consumtion per Path: For each pathIndex from 0 to topPath −1; maxEnergyPerPath[pathIdx] <= maximum value in energyTable[pathIdx]); End for Select Optimal Path: minPath <= index of Minimum value in maxEnergyPerPath Return minPath; |
3.3. DFS-Based K-Shortest Path Search Algorithm
| Algorithm 2 DFS-based K-Shortest Path Algorithm | |
| Input | numEdges[], startVertex, endVertex, K edges[MAX EDGES] ⟵ list of (src, dest, weight) |
| Output | paths[] |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. | Initialize allPaths[300][MAX VERTICES] <= 0 Initialize allCosts[300] <= 0, pathCount <= 0, maxDepth <= 0 stack <= (startVertex, depth = 0, cost = 0) visited[MAX VERTICES] <= false while stack not empty do (current, depth, cost) <= stack.pop() if visited[current] then continue visited[current] <= true path[depth] <= current maxDepth <= max(maxDepth, depth) if current == endVertex then allPaths[pathCount] <= path[0.depth] allCosts[pathCount] <= cost pathCount <= pathCount + 1 visited[current] <= false continue end if hasChild <= false for each (src, dest, weight) in edges do if src == current and not visited[dest] then stack.push(dest, depth + 1, cost + weight) hasChild <= true end if end for if not hasChild then visited[current] <= false end if end while sort allpaths in allcosts ascending order Save the top K paths from allPaths and their costs from allCosts into paths return paths |
3.4. IP Design for Eclipse-Aware Routing on FPGA with Parallelization Achieved Through Pipelining
4. Experimental Results
4.1. Experimental Setups
4.2. LEO Network Topologies for Experiments
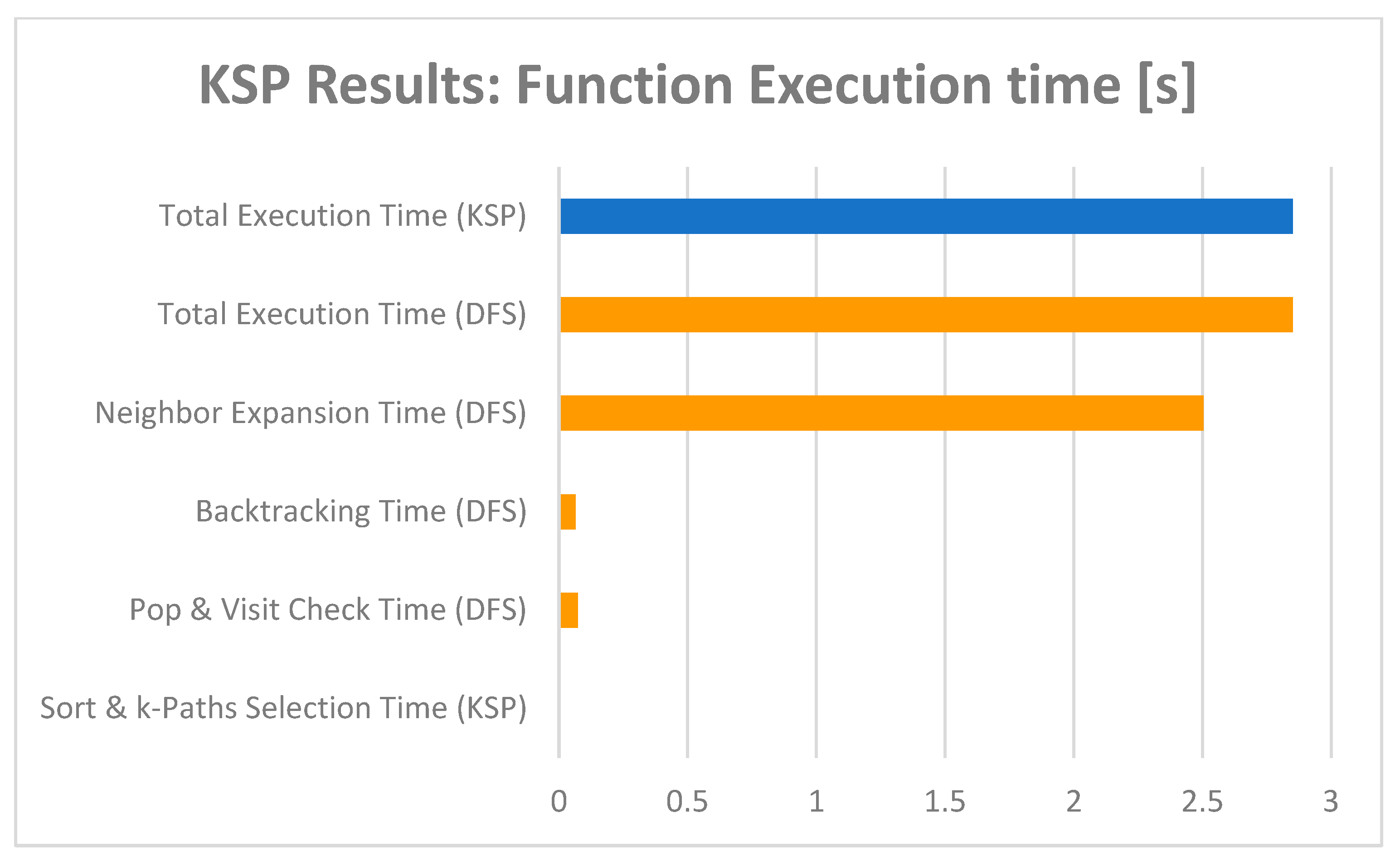
4.3. K-Shortest Paths and Eclipse-Aware Routing Results
4.4. Comparison Results Between Only PS and PS + PL
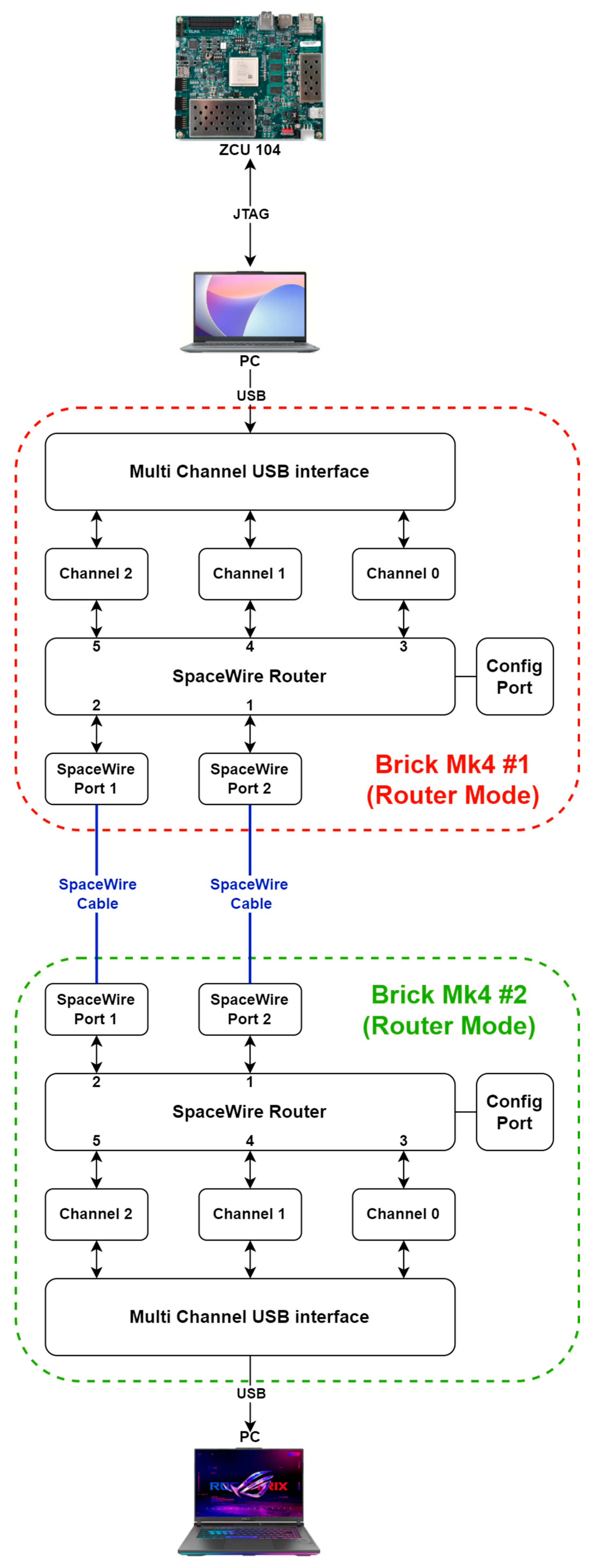
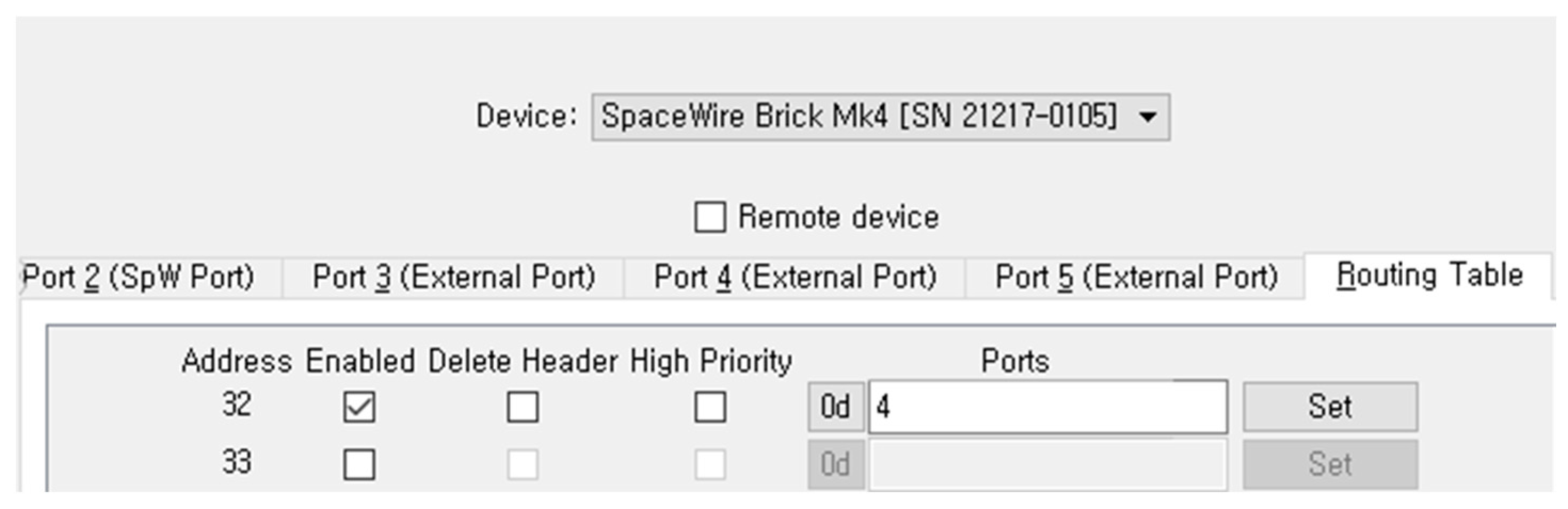
4.5. Results with SpaceWire-Based Devices
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leyva-Mayorga, I.; Soret, B.; Röper, M.; Wübben, D.; Matthiesen, B.; Dekorsy, A.; Popovski, P. LEO Small-Satellite Constellations for 5G and Beyond-5G Communications. IEEE Access 2020, 8, 184955–184964. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Yuan, H.; Yang, K.; Kang, J.; Wang, P.; Niyato, D. Joint UAV trajectory and power allocation with hybrid FSO/RF for secure space–air–ground communications. IEEE Internet Things J. 2024, 11, 31407–31421. [Google Scholar] [CrossRef]
- Parkes, S.M.; Armbruster, P. SpaceWire: A spacecraft onboard network for real-time communications. IEEE Trans. Nucl. Sci. 2005, 52, 2277–2283. [Google Scholar]
- Rani, S.; Malhotra, S. Comparative Study Of LEO, MEO & GEO Satellites. Int. J. Res. (IJR) 2014, 1, 1181–1186. [Google Scholar]
- Wang, J.; Li, L.; Zhou, M. Topological dynamics characterization for LEO satellite networks. Comput. Netw. 2007, 51, 43–53. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L. Resource allocation algorithm for space-based LEO satellite network based on satellite association. KSII Trans. Internet Inf. Syst. 2024, 18, 1638–1658. [Google Scholar]
- Zheng, X.; Liu, J.; Li, J.; Lv, D.; Liao, J.; Chen, X.; Hsu, T. A routing strategy for GEO/LEO satellite network based on dynamic delay prediction and link control. In Proceedings of the Communications and Networking—17th EAI International Conference, ChinaCom 2022, Xi’an, China, 19–20 November 2022; Gao, F., Wu, J., Li, Y., Gao, H., Eds.; Lecture Notes of the Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering; Springer: Berlin, Germany, 2023; Volume 500, pp. 3–17. [Google Scholar]
- Guo, Z.; Zhao, Y.; Li, J.; Sun, L. Load-balancing routing for LEO satellite network with distributed hops-based back-pressure. Sensors 2023, 23, 9789. [Google Scholar]
- Macambira, R.D.N.M.; Carvalho, C.B.; de Rezende, J.F. Energy-efficient routing in LEO satellite networks for extending satellites’ lifetime. Comput. Commun. 2022, 195, 463–475. [Google Scholar] [CrossRef]
- Suchida, H.; Kawamoto, Y.; Kato, N.; Kaneko, K.; Tani, S.; Uchida, S.; Aruga, H. Efficient Power Control for Satellite-Borne Batteries Using Q-Learning in Low-Earth-Orbit Satellite Constellations. IEEE Wirel. Commun. Lett. 2020, 9, 809–812. [Google Scholar] [CrossRef]
- Hussein, M.; Jakllari, G.; Paillassa, B. On Routing for Extending Satellite Service Life in LEO Satellite Networks. In Proceedings of the Globecom 2014—Symposium on Selected Areas in Communications: GC14 SAC Satellite & Space Communication, Austin, TX, USA, 8–12 December 2014; pp. 2832–2837. [Google Scholar]
- Kim, D.; Lee, H.; Won, D.; Han, M. FPGA-based Inference Parallelization for Onboard RL-based Routing in Dynamic LEO Satellite Networks. Int. J. Aeronaut. Space Sci. 2024, 25, 1135–1145. [Google Scholar] [CrossRef]
- Kim, H.; Lee, H.; Han, M. GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks. Aerospace 2025, 12, 422. [Google Scholar] [CrossRef]
- Qasaimeh, M.; Denolf, K.; Lo, J.; Vissers, K.; Zambreno, J.; Jones, P.H. Comparing energy efficiency of CPU, GPU and FPGA implementations for vision kernels. arXiv 2019, arXiv:1906.11879. [Google Scholar]
- Vaithianathan, M.; Patil, M.; Ng, S.F.; Udkar, S. Comparative study of FPGA and GPU for high-performance computing and AI. ESP Int. J. Adv. Comput. Technol. 2023, 1, 37–46. [Google Scholar]
- STAR-Dundee Ltd. SpaceWire Brick Mk4 Datasheet; STAR-Dundee Ltd.: Dundee, UK, 2023. [Google Scholar]
- Vissicchio, S.; Handley, M. Reliable Low-Delay Routing In Space with Routing-Oblivious LEO Satellites. arXiv 2024, arXiv:2401.11490. [Google Scholar]
- Bhosale, V.; Saeed, A.; Bhardwaj, K.; Gavrilovska, A. A Characterization of Route Variability in LEO Satellite Networks. In Proceedings of the Passive and Active Measurement Conference (PAM 2023), Virtual Event, 21–23 March 2023; pp. 313–342. [Google Scholar]
- Sumanth, R.M. Computation of Eclipse Time for Low-Earth Orbiting Small Satellites. Int. J. Aviat. Aeronaut. Aerosp. 2019, 6, 15. [Google Scholar]
- Tsuchida, H.; Kawamoto, Y.; Kato, N.; Kaneko, K.; Tani, S.; Hangai, M.; Aruga, H. Improvement of Battery Lifetime Based on Communication Resource Control in Low-Earth-Orbit Satellite Constellations. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1388–1398. [Google Scholar] [CrossRef]



| Category | Specification |
|---|---|
| SOC | Zunq UltraScale+™ MPSoc ZU7EV |
| Programmable-logic resources | 504 K system logic cells, 461 K CLB flip-flops, 6.2 Mb distributed RAM, 11 Mb block RAM, 27 Mb UltraRAM, 1728 DSP slices |
| On-board memory | 2 GB DDR4 component memory |
| Power consumption | 15 W |
| K paths | Paths | Cost |
|---|---|---|
| 1 | 38 ⟶ 39 ⟶ 40 ⟶ 63 ⟶ 64 ⟶ 87 (7980) ⟶ 98 (7300) | 6 |
| 2 | 38 ⟶ 39 ⟶ 40 ⟶ 63 ⟶ 74 ⟶ 75 ⟶ 86 ⟶ 87 (7980) ⟶ 98 (7300) | 8 |
| 3 | 38 ⟶ 37 ⟶ 114 ⟶ 103 ⟶ 102 ⟶ 101 ⟶ 100 (7300) ⟶ 99 (7300) ⟶ 98 (7300) | 8 |
| PS (ms) | PS + PL (ms) | |
|---|---|---|
| 160 edge data/Departure 38/Destination 98 | 8.893 | 2.621 |
| 160 edge data/Departure 2/Destination 98 | 71.098 | 19.090 |
| 300 edge data/Departure 38/Destination 98 | 226.378 | 59.304 |
| 300 edge data/Departure 2/Destination 98 | 2450.603 | 638.854 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.H.; Lee, H.; Han, M. Parallel Eclipse-Aware Routing on FPGA for SpaceWire-Based OBC in LEO Satellite Networks. J. Sens. Actuator Netw. 2025, 14, 73. https://doi.org/10.3390/jsan14040073
Park JH, Lee H, Han M. Parallel Eclipse-Aware Routing on FPGA for SpaceWire-Based OBC in LEO Satellite Networks. Journal of Sensor and Actuator Networks. 2025; 14(4):73. https://doi.org/10.3390/jsan14040073
Chicago/Turabian StylePark, Jin Hyung, Heoncheol Lee, and Myonghun Han. 2025. "Parallel Eclipse-Aware Routing on FPGA for SpaceWire-Based OBC in LEO Satellite Networks" Journal of Sensor and Actuator Networks 14, no. 4: 73. https://doi.org/10.3390/jsan14040073
APA StylePark, J. H., Lee, H., & Han, M. (2025). Parallel Eclipse-Aware Routing on FPGA for SpaceWire-Based OBC in LEO Satellite Networks. Journal of Sensor and Actuator Networks, 14(4), 73. https://doi.org/10.3390/jsan14040073







