Abstract
Channel estimation is a critical component in orthogonal frequency division multiplexing (OFDM) systems for ensuring reliable wireless communication. In this study, we propose a fast super-resolution convolutional neural network (FSRCNN) model for channel estimation, designed to reduce computational complexity while maintaining high estimation accuracy. The proposed FSRCNN model incorporates modifications such as replacing linear interpolation with zero padding and leveraging a new fast CNN architecture to estimate channel coefficients. Our numerical experiments and simulations demonstrate that the FSRCNN model significantly outperforms traditional methods, such as least square (LS) and linear minimum mean square error (LMMSE), in terms of mean square error (MSE) across various signal-to-noise ratios (SNRs). Specifically, the FSRCNN model achieves MSE values comparable to MMSE estimation, particularly at higher SNRs, while maintaining lower computational complexity. At an SNR of 20 dB, the FSRCNN model shows a notable improvement in MSE performance compared to the ChannelNet and LS methods. The proposed model also demonstrates robust performance across different SNR levels, with optimal results observed when the training SNR is close to the operating SNR. These findings validate the effectiveness of the FSRCNN model in providing a low-complexity, high-accuracy alternative for channel estimation, making it suitable for real-time applications and devices with limited computational resources. This advancement holds significant promise for enhancing the reliability and efficiency of current and future wireless communication networks.
1. Introduction
The exponential growth in wireless data traffic, driven by the proliferation of smart devices and the increasing demand for high-speed, low-latency communication, has spurred the development of fifth-generation (5G) networks. These networks aim to deliver significantly enhanced performance compared to their predecessors, offering higher data rates, improved reliability, and lower latency. However, as the limitations of 5G begin to surface, particularly in handling extreme connectivity and mobility scenarios, there is a growing focus on beyond 5G (B5G) technologies, which promise to push the boundaries of wireless communication even further. The introduction of 5G and the subsequent exploration of B5G technologies bring about new challenges in the design and implementation of wireless communication systems. Among these challenges, channel estimation emerges as a critical area of focus. Effective channel estimation is essential for achieving reliable communication, especially in the context of massive multiple-input multiple-output (MIMO) systems and millimeter-wave (mmWave) frequencies, both of which are central to 5G and B5G networks. Traditional channel estimation methods, such as LS and MMSE, while effective in previous generations, struggle to meet the demands of the high-mobility and high-frequency environments characteristic of 5G and beyond networks.
In the field of wireless communication, channel estimation stands as a pivotal component, essential for the reliable transmission and reception of signals [1]. As wireless networks grow increasingly complex and demand higher data rates, traditional channel estimation methods face challenges in terms of accuracy and efficiency [2,3]. This is where deep learning, an advanced branch of machine learning, presents a groundbreaking approach. Deep learning techniques, renowned for their ability to discern intricate patterns and dependencies in large datasets, offer a novel paradigm in channel estimation [4,5]. Unlike conventional algorithms, which often rely on simplified statistical models and can struggle with the dynamic and complex nature of wireless channels, deep learning models are capable of adapting to these complexities [6]. They can efficiently process vast amounts of channel data, learning from the environment to accurately predict channel characteristics. The application of deep learning in channel estimation represents a significant shift from traditional methods. These techniques enable more accurate predictions of channel states, even in scenarios with high mobility or rapidly fluctuating conditions. This advancement is crucial not only for enhancing the performance of current wireless networks but also for paving the way for future technologies where adaptive and intelligent network management becomes indispensable. Incorporating deep learning into channel estimation offers a promising avenue for addressing the limitations of existing methods [7]. This approach has the potential to significantly improve the efficiency, reliability, and overall performance of wireless communication systems.
Achievement of the desired performance in wireless communication requires accurate channel state information (CSI). Channel estimation is a bit of a challenging task due to the limited observation of the high-dimensional channel. There are two types of approaches used to estimate the channel: Time Division Duplexing (TDD) and Frequency Division Duplexing (FDD). In TDD, the system relies on the assumption of channel reciprocity between both the uplink and the downlink channel due to the same frequency band, whereas in FDD, both uplink and downlink channels have different frequencies. Due to different bands, the downlink channel is neither the same nor can it be inferred from the uplink channel without any downlink training [8,9,10]. The CSI is obtained by exploiting the channel sparsity of mmWave frequencies, which is addressed by authors in [11,12]. By representing the channel in a parametric model, only the angles of departure/arrival (AoD/AoA) of the strong path and corresponding channel gains can be used to obtain CSI discussed in [13,14] instead of estimating the whole channel. An adaptive compressed sensing algorithm is proposed based on the angular sparsity of the mmWave channel. Due to the high scattering path in the mmWave channel, the system requires more resources to obtain the desired resolution which complicates the system [11,15].
In [16], the author introduced a joint hybrid-field channel estimation scheme that does not differentiate between far-field and near-field channels. The author employed the Simultaneous Weighted Orthogonal Matching Pursuit (SWOMP) algorithm to effectively estimate the hybrid-field channels even when the sparsity is unknown. To address the high computational complexity typically associated with matrix inversion operations, they proposed using the “Woodbury” transformation method and further refined the approach using a low-complexity SWOMP (LC-SWOMP) algorithm based on the Gauss–Seidel iterative method.
2. Related Work
In recent years, significant research has focused on improving channel estimation techniques to meet the stringent requirements of 5G and beyond networks. These advancements are driven by the need for higher data rates, lower latency, and more reliable connections in increasingly complex wireless environments. One of the key challenges in communication networks is the need to handle massive MIMO systems, where traditional channel estimation methods often fall short due to the high dimensionality and rapidly varying channel conditions. To tackle this situation, deep learning has emerged as a powerful tool, offering innovative solutions that outperform conventional techniques in several aspects.
In 2024 [17], an approach was introduced to tackle the challenge of beamspace channel estimation, which arises due to the limited number of RF chains compared to the large number of transmit/receive antennas. The SL-AMP network was designed to pre-learn the prior parameters of the beamspace channel using a Bernoulli Gaussian mixture distribution. The network was further enhanced by leveraging Wasserstein Generative Adversarial Networks (GANs) to generate channel samples for training, which helps in overcoming the issue of insufficient training data. The proposed network achieved better performance with reduced training complexity compared to existing methods, making it a valuable contribution to mmWave communications. In 2021 [18], a deep learning-assisted channel estimation framework was proposed specifically designed for MIMO-OFDM systems in 5G and beyond networks. The authors introduced a novel architecture that leverages machine learning techniques, particularly deep learning models like CNN, FDNN, and bi-LSTM, to enhance channel estimation accuracy. The study compares traditional methods like LS and LMMSE estimation with the proposed deep learning models. It is found that the bi-LSTM model significantly improves estimation accuracy by effectively capturing time-varying and frequency-selective characteristics of the 5G channels. The research demonstrates that deep learning-based approaches can outperform conventional methods, especially in environments with high mobility and Doppler effects. In 2023 [19], the integration of deep learning with advanced channel estimation techniques in 5G and beyond networks was explored, particularly focusing on the challenges posed by high mobility and frequency selectivity. The study introduced innovative neural network architectures tailored for massive MIMO systems operating in complex environments. The authors conducted extensive simulations and show that the proposed deep learning models, including hybrid approaches combining different network architectures, provided superior performance in terms of MSE and bit error rate (BER) compared to traditional estimation methods. The research highlighted the potential of deep learning to adapt to dynamic channel conditions, making it a robust solution for next-generation wireless networks. On the other hand, Deep Learning (DL) has also gained much attention in communication systems. In 2018 [20], CsiNet, a deep learning-based CSI sensing and recovery mechanism for massive MIMO systems, was presented. This innovative approach used a deep neural network to transform CSI into a compressed representation, significantly improving reconstruction quality and reducing time complexity compared to traditional compressive sensing methods. CsiNet demonstrated its effectiveness even in low compression ratios, highlighting its potential for efficient and accurate CSI feedback in massive MIMO systems. In 2019 [21], a deep learning-based channel estimation technique for OFDM systems was demonstrated. The authors modeled the time-frequency response of fast fading channels as 2D images. They used deep image processing techniques, specifically image super-resolution (SR) and image restoration (IR), to enhance channel estimation. The proposed method showed performance comparable to MMSE estimation, outperforming an approximation to linear MMSE. This work contributes to the field by efficiently applying image processing algorithms in deep learning for improved channel estimation in communication systems. In 2020 [22], TS-ChannelNet, a deep learning-aided temporal spectral channel network for channel estimation in vehicular communications using IEEE 802.11p, was presented. This approach, inspired by image super-resolution techniques, used a two-phase process involving an Average Decision-Directed Estimation with Time Truncation (ADD-TT) and a Super Resolution Convolutional Long Short-Term Memory (SR-ConvLSTM) network. The method demonstrated significant performance gains over existing methods, particularly in high signal–noise-ratio regions, offering a robust solution for accurate channel estimation in high-speed vehicular scenarios. Furthermore, in 2022 [23], a deep learning-based weighted interpolation (WI) estimator was introduced for channel estimation in vehicular communications, specifically for the IEEE 802.11p standard. The study proposed a novel approach that modified pilot allocation to achieve higher transmission data rates. It demonstrated that the developed estimator significantly outperforms existing deep learning-based frame-by-frame estimators in various vehicular scenarios while also reducing computational complexity. This work represents a substantial advancement in robust and efficient channel estimation for high-mobility vehicular environments. Recently, in 2023 [24], a novel Bi-RNN-based channel estimation scheme was introduced for doubly selective environments, particularly for high-mobility communications using Bi-RNN networks. This scheme significantly outperformed the state-of-the-art CNN-based channel estimators in various mobility scenarios while also considerably reducing computational complexity. The paper demonstrates the effectiveness of the Bi-RNN approach, emphasizing its superiority in terms of performance and lower computational demand, making it a promising alternative for accurate and efficient channel estimation in high mobility scenarios.
Table 1 highlights the key aspects of related work such as methodology, techniques, performance metrics, and computational complexity.

Table 1.
Novelty analysis.
In this work, we propose low-complexity super resolution-based CNN used for estimating fast-fading channels in OFDM systems. The proposed modifications also include replacing linear interpolation with zero padding. We also propose to apply the new fast CNN model to estimate the channel coefficients. These changes significantly reduce the computational complexity of the estimation process and improved MSE as well. Numerical results confirm that the proposed modifications achieve an MSE performance comparable to that of linear minimum MSE estimation. This paper makes several significant contributions to the field of channel estimation for 5G and beyond networks, particularly through the application of deep learning techniques:
- Development of a Novel Deep Learning-Based Channel Estimation Framework: We propose a FSRCNN tailored for channel estimation in 5G and beyond networks. This framework effectively addresses the challenges posed by high-mobility and high-frequency environments, offering a robust solution for modern wireless communication systems.
- Enhanced Accuracy and Robustness in High-Mobility Scenarios: Our FSRCNN-based method significantly improves the accuracy of channel estimation, particularly in scenarios with high Doppler shifts and frequency selectivity, where traditional methods such as LS and MMSE estimation often struggle.
- Comprehensive Comparative Analysis: We conduct extensive simulations comparing the performance of our proposed method against conventional channel estimation techniques. The results demonstrate superior performance in terms of MSE, highlighting the practical benefits of our approach.
- Scalability to Future Wireless Networks: The proposed FSRCNN framework is designed with scalability in mind, making it adaptable to future wireless communication systems, including beyond 5G (B5G) and 6G networks. This adaptability ensures that the framework remains relevant as wireless technologies continue to evolve.
Table 2 and Table 3 present a comprehensive summary of the abbreviations and parameters that are integral to this article, serving as a valuable reference for understanding the technical terminology and key metrics.

Table 2.
List of Abbreviations.

Table 3.
List of Parameters.
3. Conventional Methods
We consider single-input single-output (SISO) OFDM in which the subframe size is where is the total number of time slots and is the total number of subcarriers. For the th time slot and the th subcarrier, the received signal is given by
where is the transmitted symbol, channel coefficient is the element of channel matrix , which contains channel coefficients of all subcarriers and time slots for the subframe, and is a white Gaussian noise symbol with zero mean and variance . To estimate channel coefficients, conventional methods are least squares (LS) and linear minimum mean square error (LMMSE) estimates. Both are used as a reference in our work.
For given pilot symbols, the LS estimate of the channel coefficients at pilot positions in the subframe is obtained by solving
where is an vector of pilot symbols, is an vector of received symbols, and is a diagonal matrix whose diagonal entries are obtained from channel vector , which contains the channel coefficients of pilots. The complexity of LS, which comes mainly from the solving of (2), is low, and channel statistics are not required for LS. To obtain an estimate of the remaining channel coefficients in the current OFDM subframe, interpolation can be applied.
After the LS estimates are obtained, they can be used to calculate the LMMSE estimates of the channel coefficients for all symbols in the subframe as follows:
where the filter matrix is
The autocorrelation matrix for is denoted by , the cross-correlation matrix between all channel coefficients in the subframe and the channel coefficients at only pilot positions in the subframe , and is an identity matrix. The accuracy of the estimate can be measured by the mean square error given by
LMMSE estimation is computationally complex due to inversion of a large matrix and requires channel and noise statistics unlike the LS estimation.
4. Motivation for Using CNNs in Applications for Channel Estimation
A deep learning-based channel estimator is proposed in [21] to acquire the time-frequency channel response from available pilots. It is a data-driven approach. Traditional channel estimation methods often rely on assumptions about the channel model. CNNs, by learning directly from the data, can provide more accurate estimates by capturing complex relationships and patterns.
- Feature Extraction Capabilities: CNN are highly effective at automatically extracting features from data, particularly images. In the context of channel estimation, the channel state information can be treated as an image where spatial correlations and patterns are present. CNNs can effectively capture these patterns.
- Spatial Invariance: CNNs are designed to recognize patterns regardless of their position in the input image. This property is known as spatial invariance. For channel estimation, this means that CNNs can detect important features such as signal strength variations and interference patterns consistently across different regions of the input data.
- Robustness to Noise by Learning Local Patterns: The use of convolutional layers enables CNNs to learn local patterns efficiently. In wireless communications, local variations in the channel characteristics can significantly affect performance. CNNs can learn these local variations through filters that capture local dependencies, leading to more accurate channel estimation. The ability of CNNs to filter out noise while preserving important features improves the reliability of channel estimation.
5. Proposed Fast Super-Resolution Convolutional Neural Network (FSRCNN)
To enhance the performance by overcoming the limitations of SRCNN, we adapted a modified version of SRCNN. By utilizing a deeper but narrower network architecture, FSRCNN enhances feature extraction capabilities. FSRCNN employs a more efficient upsampling strategy, reducing the need for extensive pre-processing and enabling faster inference times. This makes FSRCNN more suitable for real-time applications and devices with limited computational resources [26].
Architecture of FSRCNN
FSRCNN is designed to enhance the efficiency and speed of image super-resolution tasks while maintaining high-quality output. Figure 1 represents the detailed structure of FSRCNN as discussed earlier. Below is a detailed breakdown of its architecture.
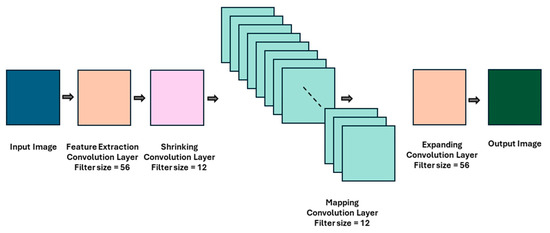
Figure 1.
FSRCNN layers for the proposed estimator.
- Input Layer: A low-resolution image fed directly into the network without any pre-processing upscaling step. This input is represented by a tensor of shape (H, W, C), where H and W are the height and width of the image and C is the number of color channels.
- Feature Extraction Layer: The first layer of FSRCNN performs convolution to extract initial features from the input image. A Parametric Rectified Linear Unit (PReLU) activation function is applied to introduce non-linearity and help the network learn more complex features.
- III.
- Shrinking Layer: A second convolution layer reduces the dimensionality of the feature maps to decrease computational complexity while retaining essential information.
- IV.
- Mapping Layers: These layers perform the mapping from low-resolution to high-resolution feature space. Multiple convolution layers are used here to transform the shrunken feature maps. Each layer is followed by a PReLU activation.
- V.
- Expanding Layer: A convolution layer increases the dimensionality of the feature maps back to a higher resolution, preparing the data for the final deconvolution step.
- VI.
- Deconvolution Layer: This final layer performs the upscaling to convert the low-resolution feature maps into high-resolution images.
6. System Model
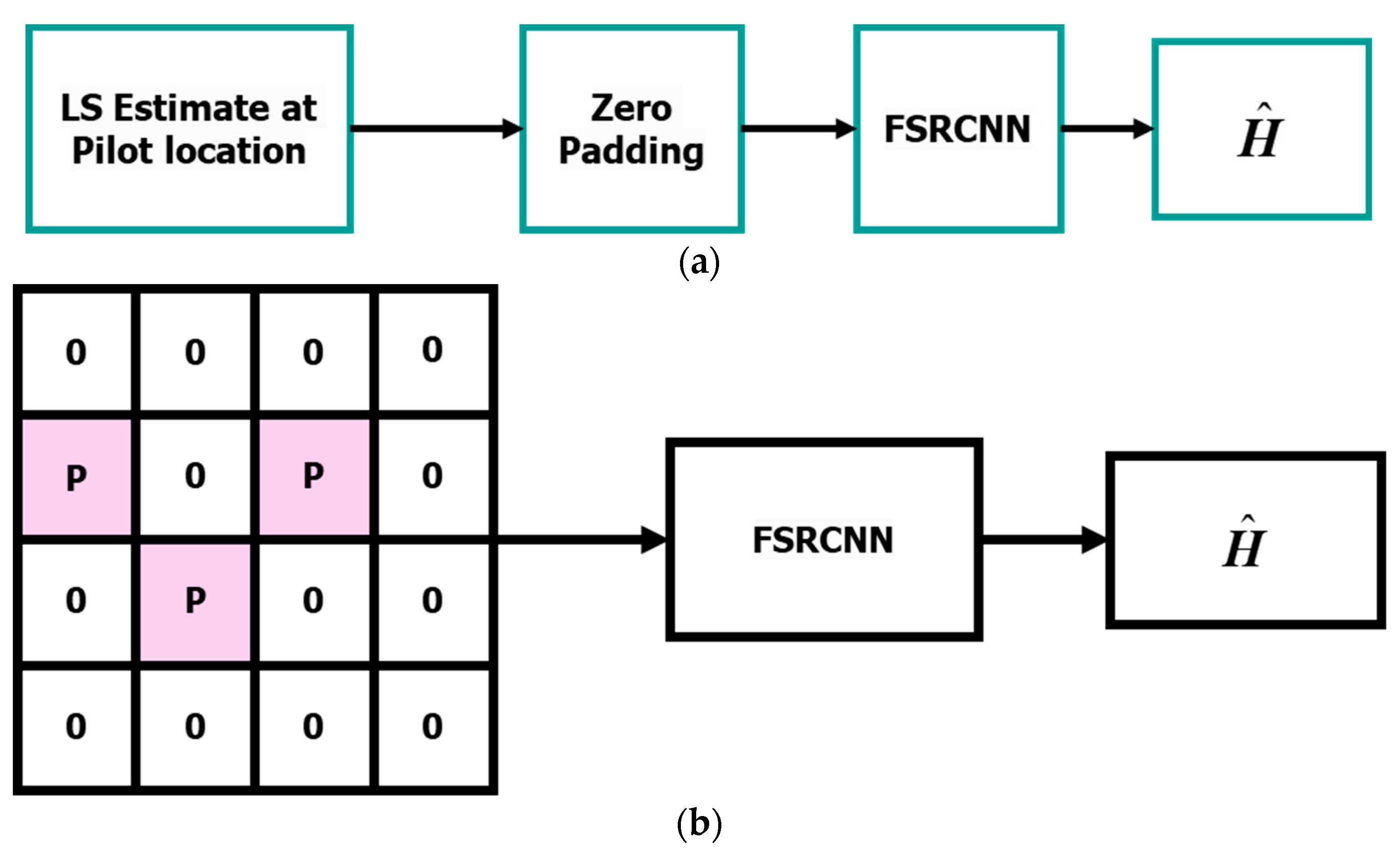
In this work, we proposed a DL-based channel estimation by deploying fast super-resolution. We propose to reduce the simplified channel estimation as shown in Figure 2a,b. FSRCNN is trained using the LS estimates of the pilot marked by P in Figure 2b. The remaining inputs are padded by zero. A properly trained FSRCNN should be able to learn the channel coefficients directly from the received pilots without interpolated symbols.
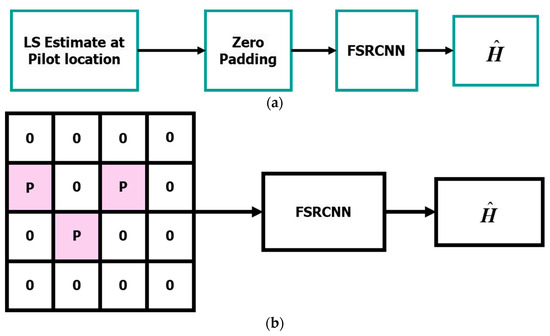
Figure 2.
Our proposed channel estimation (a) Detailed process of channel estimation (b) A simplified example for channel estimation.
Complexity Discussion
The complexity analysis for SRCNN and DnCNN including LMMSE is calculated in this section. The parameter for each layer is summarized in Table 4.

Table 4.
Structures of different CNNs.
The complexity of convolution layer which is computed by height , width , length of filter and the number of input and output features maps denoted as and , respectively, can be given by Equation (11) [27]:
So, the complexity of SRCNN is given by Equation (12):
and the complexity of DnCNN and the output layer becomes approximately as in Equation (13),
The complexity of linear interpolation is given by Equation (14),
The total time complexity of the ChannelNet is given by Equation (15),
The complexity of the LMMSE method can be analyzed by estimating the number of multiplication and addition requirements which can be given by Equation (17),
Thus, the computational complexity of the LMMSE method is dominated by the matrix inversion step, which requires operations, and the matrix multiplications, making the method computationally intensive for large matrices.
In the proposed method, FSRCNN is adapted. So, the complexity of the proposed model is equal to .
When using a combination of DnCNN and SRCNN, the overall computational complexity is determined by the cumulative FLOPs of both models which are computed during simulation. This combined approach, while potentially more accurate and effective in certain applications, significantly increases the computational demand compared to using FSRCNN with interpolation and FSRCNN alone.
SRCNN involves fewer layers but larger filters, resulting in substantial computational requirements for each operation. DnCNN incorporates many layers with smaller filters and batch normalization, which increases the model complexity and computational load due to the depth of the network. The proposed method simplifies the system architecture, resulting in lower computational complexity and faster processing times as shown in Figure 3 in terms of MSE execution time. The combined use of SRCNN and DnCNN significantly increases both the number of parameters and computational complexity compared to using SRCNN and FSRCNN alone.
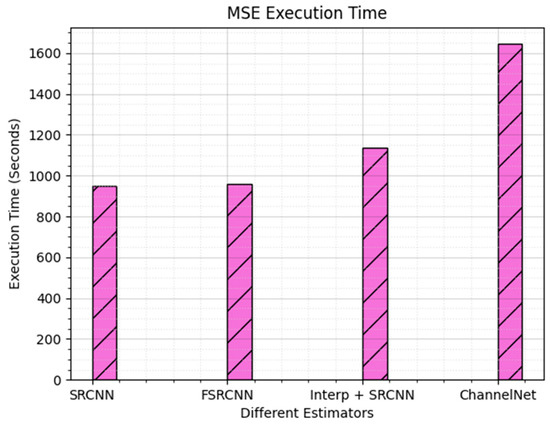
Figure 3.
Execution time comparison for different CNN structures.
7. Results and Discussions
In this section, we train the network and evaluate the MSE across a range of SNRs, comparing the results with widely used baseline algorithms. The simulation parameter is discussed in Table 5. The setup involves a single antenna at both the transmitter and receiver.

Table 5.
Key Simulation Parameters for the Experiment.
For channel modeling and pilot transmission, we utilize the well-known Vienna LTE-A simulator developed by the University of Vienna [28]. The dataset is divided into 32,000 channels for training, 4000 channels for testing, and 4000 channels for validation. Consistent with LTE standards, each simulation frame comprises 14 time slots with 72 subcarriers. We consider the VehicularA (VehA) channel model, which represents a long delay spread environment, at a carrier frequency of 2.1 GHz. The user equipment (UE) speed is set at 50 km/h.
To implement the proposed scheme, we use Keras and Tensorflow with a batch size of 128 and a training rate of 0.001 for 50 epochs. For numerical results, the VehA channel data set from GitHub [29] is used. One-ninth of the data set is used for testing, while the rest is used for training. Each OFDM frame consists of 14 time slots and 72 subcarriers with 48 pilot symbols. The performance of the ideal MMSE and LS estimations is used as a reference. MSE of various channel estimation schemes is shown in Figure 4. The ideal MMSE estimate provides the lower bound, whereas the LS estimates with interpolation offer the upper bound. Our CNN model is trained and tested for SNR 12 dB to 22 dB. The input to the model is the LS channel estimates. The result in Figure 4a,b shows that MSE decreases with SNR during the testing phase as expected. In Figure 4a, the MSE for SRCNN with zero padding and the proposed CNN with zero padding are compared. The proposed model performs similarly to the MMSE for an SNR below 15 dB when trained at a low SNR of 12 dB. For testing the sSNR greater than or equal to 20 dB, the performance of the model trained for a high SNR of 22 dB is the best. The model performs well when the SNR at which it was trained is close to the operating SNR. MSE performance degrades when the difference between the operating and training SNRs is large. Satisfactory performance close to MMSE performance is achieved when the SNR is low. Figure 4a shows the MSE vs. SNR curves for different CNNs including FSRCNN as proposed (12 dB and 22 dB) and SRCNN zero padding (12 dB and 22 dB). Figure 4b shows the MSE vs. SNR curves for various methods including LS MMSE, LS Interp, ChannelNet (12 dB and 22 dB), and the proposed network (12 dB and 22 dB). The curves demonstrate that the proposed network achieves lower MSE compared to traditional LS methods and ChannelNet at different SNR levels. Specifically, the proposed FSRCNN and the generalized approach show improved performance over ChannelNet, particularly at higher SNRs. The results indicate that the proposed schemes effectively reduce MSE, validating their superiority over existing methods.
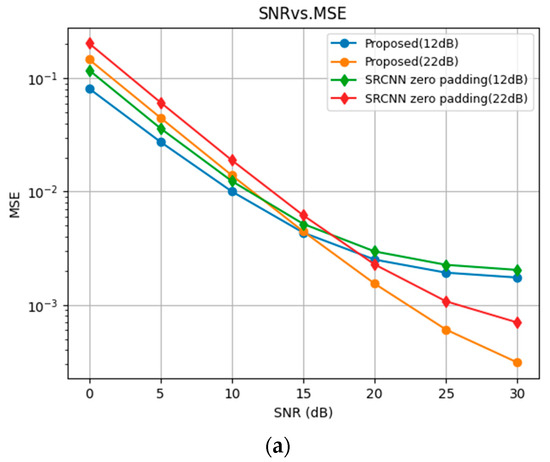
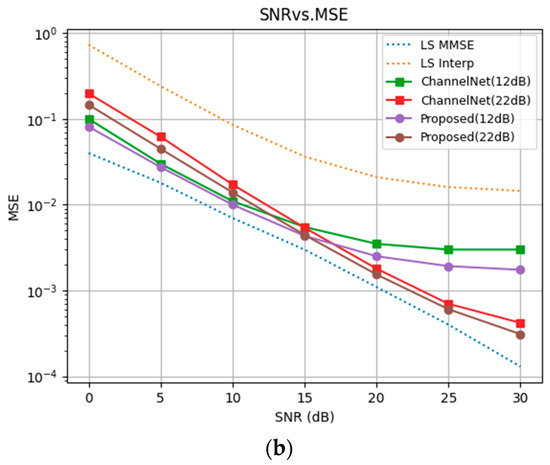
Figure 4.
MSE of various channel estimation methods for VehA channel model (a) MSE comparison of FSRCNN (zero padding) and SRCNN (zero padding) only (b) MSE comparison of Proposed model with state of the art and other tradition techniques.
The proposed FSRCNN model is designed to balance computational efficiency with estimation accuracy, making it suitable for real-time applications in 5G and beyond networks. When compared to the optimal non-linear estimators such as the MMSE, our method achieves performance close to the MMSE, particularly at higher SNR levels, as indicated by the MSE results presented in Figure 4 and Figure 5. The MMSE estimator represents a theoretical bound In terms of estimation accuracy, as it minimizes the MSE under the assumption of perfect knowledge of channel and noise statistics. However, the computational complexity of MMSE, which involves large matrix inversions, makes it less practical for real-time implementations, especially in high-dimensional scenarios typical of massive MIMO.
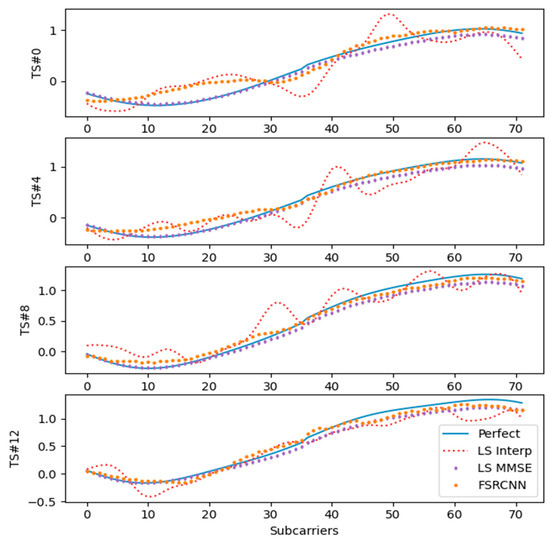
Figure 5.
The real parts of the estimates of the channel response from various estimation methods are compared with the actual response shown in solid blue lines. The channel response and the estimates are plotted for all subcarriers and 4 time slots as indicated.
In contrast, the FSRCNN model reduces this complexity significantly by avoiding matrix inversions and leveraging the power of deep learning to approximate the channel characteristics. While it may not always achieve the absolute minimum MSE that the MMSE offers, it provides a practical trade-off between accuracy and computational load, making it a viable alternative in scenarios where real-time processing and resource constraints are critical.
Figure 5 shows the real part of the channel estimates for the 72 subcarriers in four different time slots, which are the zeroth, fourth, eighth, and twelfth. Estimates are obtained from different methods and compared with the real part of the actual channel response. Note that within each timeslot, the channel is assumed unchanged. The MMSE estimator shown in purple dots yields a close estimate to the actual response shown by solid blue lines. The orange dot which represents our proposed method estimates very close to the perfect channel.
Figure 5 illustrates the performance of our proposed FSRCNN-based channel estimation method in a high-mobility scenario. The results clearly demonstrate the superiority of our approach, particularly in terms of MSE reduction as the SNR increases. Compared to traditional methods including LS with interpolation and LS MMSE, our approach significantly improves channel estimation accuracy, which is crucial for maintaining reliable communication in dynamic environments. The enhanced performance is attributed to the deep learning architecture’s ability to learn and adapt to complex channel conditions, including high Doppler shifts and frequency selectivity.
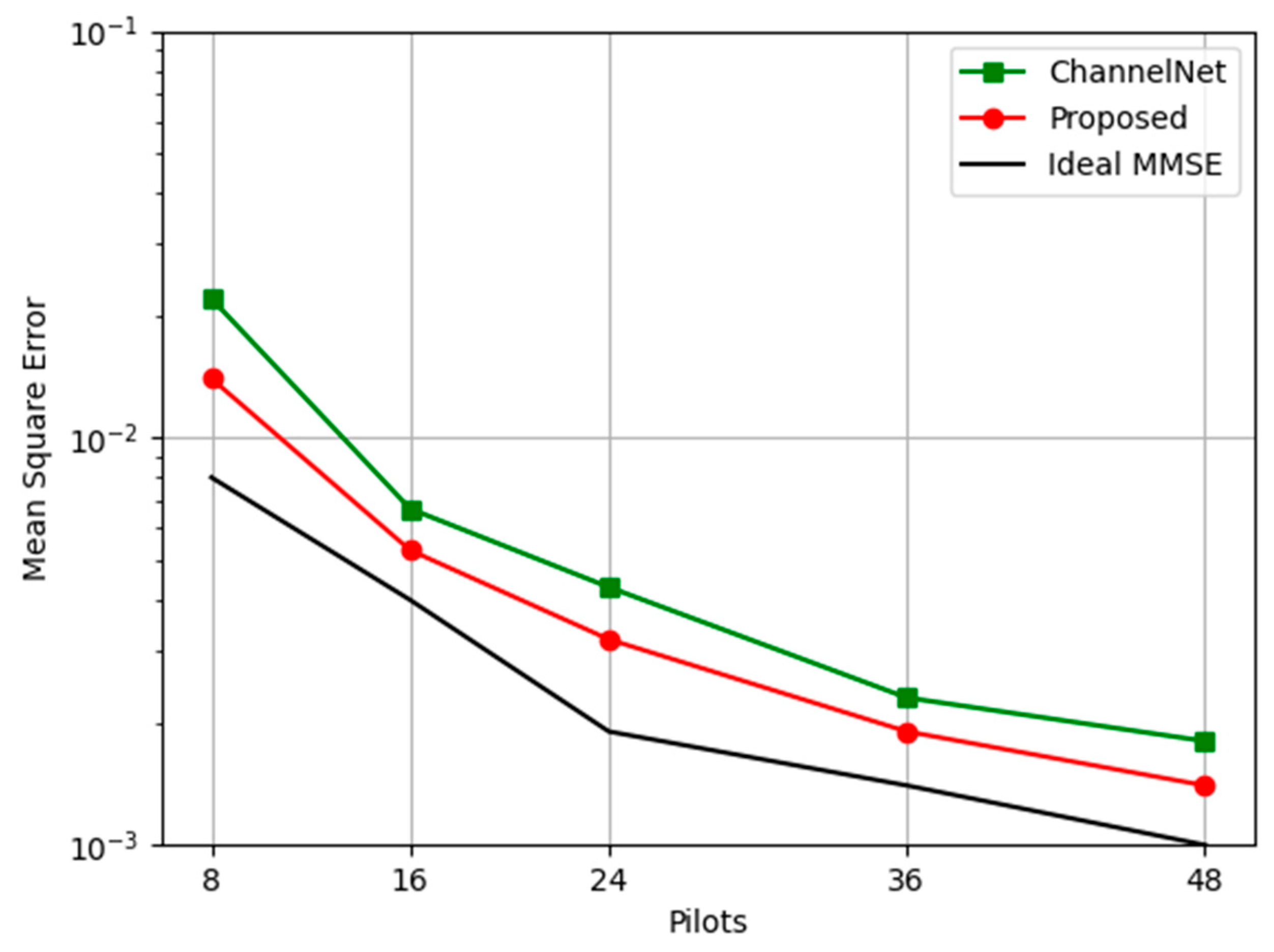
Figure 6 illustrates the MSE performance of three different methods, ChannelNet, the proposed one, and Ideal MMSE, by varying numbers of pilots. To demonstrate the performance of the proposed algorithm, simulations are conducted with various numbers of pilots at an SNR level of 20 dB. As the number of pilots increases from 8 to 48, all three methods demonstrate a decrease in Mean Square Error, indicating improved performance. The Ideal MMSE method consistently achieves the lowest MSE across all pilot numbers, showing its superior accuracy. The proposed method follows, exhibiting better performance than ChannelNet. This comparative analysis highlights the efficiency of the proposed method in reducing MSE as the number of pilots increases with lower complexity. Figure 6 further highlights the robustness of our approach by comparing its performance across different SNR levels with other conventional methods and the deep learning approach ChannelNet (state of the art). The results confirm that our FSRCNN-based method consistently outperforms traditional linear and non-linear estimators, even under varying channel conditions. This is particularly evident when comparing our results with those shown in Figure 4, where the conventional approach struggles to maintain accuracy in high-mobility scenarios. Comparative analysis clearly indicates that our method not only achieves better performance but also offers a more reliable solution for channel estimation.
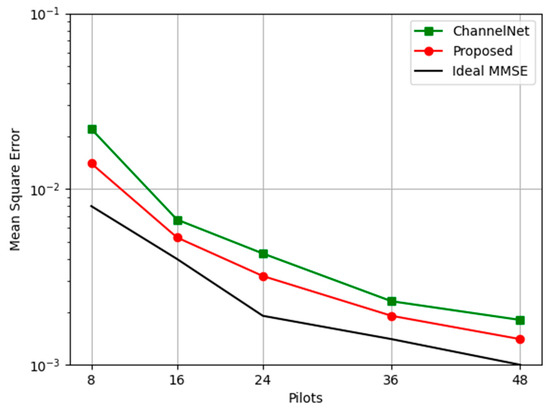
Figure 6.
Effect of different pilot lengths on MSE of channel estimation.
8. Conclusions
In this study, we proposed a novel FSRCNN model for channel estimation in OFDM systems, aimed at reducing computational complexity while maintaining high estimation accuracy. The modifications include replacing linear interpolation with zero padding and applying a new fast CNN model to estimate channel coefficients. Our extensive numerical experiments and simulations demonstrated that the proposed FSRCNN model significantly outperforms traditional methods, such as LS and LMMSE, in terms of MSE SNRs. Specifically, the proposed FSRCNN model shows performance comparable to MMSE estimation, particularly at higher SNRs, while maintaining lower computational complexity. The key findings from our results are as follows: the proposed FSRCNN model achieves lower MSE compared to traditional LS methods and the ChannelNet at different SNR levels, indicating the model’s superior accuracy in estimating channel states. Additionally, the FSRCNN model demonstrates reduced computational complexity compared to traditional LMMSE and the combined SRCNN and DnCNN approaches, making it suitable for real-time applications and devices with limited computational resources. Furthermore, the FSRCNN model performs well across different SNR levels, with the best performance observed when the training SNR is close to the operating SNR, ensuring reliable channel estimation under varying conditions. The proposed model consistently outperforms ChannelNet, particularly in high SNR regions, validating the effectiveness of the modifications in improving channel estimation accuracy. In conclusion, the proposed FSRCNN model offers a promising solution for efficient and accurate channel estimation in wireless communication systems, addressing the limitations of existing methods by providing a low-complexity alternative that does not compromise on performance. This advancement has significant implications for enhancing the reliability and efficiency of current and future wireless networks.
9. Future Scope
While this research made significant strides in advancing channel estimation techniques for 5G and beyond networks, several avenues for future exploration remain. One promising direction is the application of the FSRCNN-based framework to more diverse and complex scenarios, such as ultra-dense networks and environments with extreme mobility, which are anticipated to be characteristic of 6G networks. Additionally, enhancing the robustness of the proposed method against varying channel conditions and imperfections in real-world deployments is an important area for further investigation. Incorporating advanced deep learning architectures, such as transformers or attention mechanisms, could improve the adaptability and accuracy of the model in dynamic environments.
Expanding the application of this framework to other aspects of wireless communication, such as resource allocation and interference management, presents an exciting opportunity. Integrating the channel estimation process with other network optimization tasks could lead to more efficient and intelligent communication systems. Moreover, as B5G and 6G technologies continue to evolve, the scalability and generalizability of the FSRCNN framework is crucial. Future research should explore its adaptability to emerging technologies, including terahertz communication, reconfigurable intelligent surfaces (RIS), and AI-driven network management systems. These advancements could further solidify the role of deep learning in shaping the future of wireless communication.
10. Contribution to Sensor and Actuator Networks
The research presented in this paper makes a significant contribution to the field of wireless sensor and actuator networks (WSANs), particularly in the context of next-generation networks such as B5G. WSANs are crucial in various applications, including smart cities, industrial automation, healthcare, and environmental monitoring, where reliable and efficient communication is essential. The development of a FSRCNN for channel estimation directly addresses the challenges faced by WSANs in these demanding environments. The proposed FSRCNN framework enhances the underlying system architecture of WSANs by improving the accuracy and robustness of channel estimation, which is vital for maintaining reliable communication between sensors and actuators, especially in high-mobility and high-frequency environments typical of 5G networks. This improvement contributes to smarter and more intelligent sensing and actuation, as the framework’s ability to adapt to dynamic channel conditions enables better decision-making processes within the network, thereby enhancing overall efficiency and responsiveness.
Moreover, the scalability and robustness of the FSRCNN framework make it particularly well suited for large-scale deployments in Industry 4.0 environments, where embedded wireless sensor and actuator systems are integral to automation and manufacturing processes. As WSANs continue to evolve with the integration of 5G and future 6G networks, the FSRCNN framework ensures that these systems can meet the rigorous demands of next-generation applications, maintaining high-quality communication in complex and rapidly changing environments. Additionally, by improving the accuracy of channel predictions, this framework enhances the reliability and security of WSAN operations, which is crucial for critical applications such as healthcare and industrial control systems. The implementation of the FSRCNN framework also provides valuable support for experimental facilities and test beds designed to optimize WSAN performance, offering a robust method for simulating and testing these networks under various conditions. Overall, this research aligns closely with the goals of advancing WSANs, particularly in their integration with next-generation networks and their applications across diverse and critical domains.
Author Contributions
Conceptualization, S.K.; methodology, S.K.; software, S.K.; validation, S.K., L.W.; formal analysis, S.C. and A.P.; writing—original draft preparation, S.K.; writing—review and editing, S.K., L.W. and W.S.; visualization, S.K.; supervision, L.W. and W.S.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data are created. All the data are mentioned in the manuscript.
Acknowledgments
This research project is supported by the Second Century Fund (C2F), Chulalongkorn University, Thailand and also by Thailand Science research and Innovation Fund Chulalongkorn University (CU_FRB65_ind (12)_160_21_26).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, Y.; Tan, Z.; Hu, H.; Cimini, L.J.; Li, G.Y. Channel estimation for OFDM. IEEE Commun. Surv. Tutor. 2014, 16, 1891–1908. [Google Scholar] [CrossRef]
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-wave cellular wireless networks: Potentials and challenges. Proc. IEEE 2014, 102, 366–385. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A survey of deep learning and its applications: A new paradigm to machine learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Saikia, P.; Paul, S.; Tsalavoutis, V.; Atiah, F.; Ravi, V.; Peters, A. A review of deep learning with special emphasis on architectures, applications and recent trends. Knowl.-Based Syst. 2020, 194, 105596. [Google Scholar] [CrossRef]
- Mao, Q.; Hu, F.; Hao, Q. Deep learning for intelligent wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2018, 20, 2595–2621. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, C.-K.; Liang, L.; Jin, S. Universal Model-Driven Deep Learning for MIMO Transceiver Design. IEEE Commun. Mag. 2023, 62, 74–80. [Google Scholar] [CrossRef]
- Sheikhi, A.; Razavizadeh, S.M.; Lee, I. A comparison of TDD and FDD massive MIMO systems against smart jamming. IEEE Access 2020, 8, 72068–72077. [Google Scholar] [CrossRef]
- Xie, H.; Gao, F.; Jin, S.; Fang, J.; Liang, Y.-C. Channel estimation for TDD/FDD massive MIMO systems with channel covariance computing. IEEE Trans. Wirel. Commun. 2018, 17, 4206–4218. [Google Scholar] [CrossRef]
- Amadid, J.; Belhabib, A.; Boulouird, M.; Hassan, M.M.R.; Zeroual, A. On Channel Estimation and Power Control for Multi-cell Multi-path Massive MIMO TDD System. 2022. [CrossRef]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Méndez-Rial, R.; Rusu, C.; González-Prelcic, N.; Alkhateeb, A.; Heath, R.W. Hybrid MIMO architectures for millimeter wave communications: Phase shifters or switches? IEEE Access 2016, 4, 247–267. [Google Scholar] [CrossRef]
- Iwen, M.A.; Tewfik, A.H. Adaptive strategies for target detection and localization in noisy environments. IEEE Trans. Signal Process. 2012, 60, 2344–2353. [Google Scholar] [CrossRef]
- Heath, R.W.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Mi, D.; Wang, Z.; Imran, M.A.; Shakir, M.Z. MmWave massive-MIMO-based wireless backhaul for the 5G ultra-dense network. IEEE Wirel. Commun. 2015, 22, 13–21. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, J.; Jiang, J. Low complexity hybrid-field channel estimation based on simultaneous weighted OMP algorithm in Extreme Large-scale MIMO systems. IEEE Access 2024, 12, 46551–46561. [Google Scholar] [CrossRef]
- Ruan, C.; Zhang, Z.; Jiang, H.; Zhang, H.; Dang, J.; Wu, L. Simplified learned approximate message passing network for beamspace channel estimation in mmWave massive MIMO systems. IEEE Trans. Wirel. Commun. 2023, 23, 5142–5156. [Google Scholar] [CrossRef]
- Le, H.A.; Van Chien, T.; Nguyen, T.H.; Choo, H.; Nguyen, V.D. Machine learning-based 5G-and-beyond channel estimation for MIMO-OFDM communication systems. Sensors 2021, 21, 4861. [Google Scholar] [CrossRef]
- Sufyan, A.; Khan, K.B.; Khashan, O.A.; Mir, T.; Mir, U. From 5G to beyond 5G: A comprehensive survey of wireless network evolution, challenges, and promising technologies. Electronics 2023, 12, 2200. [Google Scholar] [CrossRef]
- Wen, C.-K.; Shih, W.-T.; Jin, S. Deep learning for massive MIMO CSI feedback. IEEE Wirel. Commun. Lett. 2018, 7, 748–751. [Google Scholar] [CrossRef]
- Soltani, M.; Pourahmadi, V.; Mirzaei, A.; Sheikhzadeh, H. Deep learning-based channel estimation. IEEE Commun. Lett. 2019, 23, 652–655. [Google Scholar] [CrossRef]
- Zhu, X.; Sheng, Z.; Fang, Y.; Guo, D. A deep learning-aided temporal spectral ChannelNet for IEEE 802.11 p-based channel estimation in vehicular communications. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 94. [Google Scholar] [CrossRef]
- Gizzini, A.K.; Chafii, M.; Nimr, A.; Shubair, R.M.; Fettweis, G. CNN aided weighted interpolation for channel estimation in vehicular communications. IEEE Trans. Veh. Technol. 2021, 70, 12796–12811. [Google Scholar] [CrossRef]
- Gizzini, A.K.; Chafii, M. Deep Learning Based Channel Estimation in High Mobility Communications Using Bi-RNN Networks. arXiv 2023, arXiv:2305.00208. [Google Scholar]
- Li, Y.; Jiang, M. ADMM-Based Hybrid-Field Uplink Channel Estimation for Extremely Large-Scale MIMO Systems. In Proceedings of the 2023 IEEE/CIC International Conference on Communications in China (ICCC), Dalian, China, 10–12 August 2023; pp. 1–5. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14, 2016. pp. 391–407. [Google Scholar]
- Wei, T.; Tian, Y.; Chen, C.W. Rethinking Convolution: Towards an Optimal Efficiency. 2020. Available online: https://openreview.net/forum?id=-oeKiM9lD9h (accessed on 29 August 2024).
- Mehlführer, C.; Colom Ikuno, J.; Šimko, M.; Schwarz, S.; Wrulich, M.; Rupp, M. The Vienna LTE simulators-Enabling reproducibility in wireless communications research. EURASIP J. Adv. Signal Process. 2011, 2011, 1–14. [Google Scholar] [CrossRef]
- ChannelNet. Available online: https://github.com/MehranSoltani94/DeepPilotDesign (accessed on 15 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).