Abstract
For a multiuser multiple-input–multiple-output (MIMO) overlay cognitive radio (CR) network, an opportunistic interference alignment (IA) technique has been proposed that allows spectrum sharing between primary users (PUs) and secondary users (SUs) while ensuring zero interference to the PU. The CR system consists of one PU and K SUs where the PU uses space-time water-filling (ST-WF) algorithm to optimize its transmission and in the process, frees up unused eigenmodes that can be exploited by the SU. The SUs make use of an optimal power allocation algorithm to align their transmitted signals in such a way their interference impairs only the PUs unused eigenmodes. Since the SUs optimal power allocation algorithm turns out to be an optimal beamformer with multiple eigen-beams, this work initially proposes combining the diversity gain property of space-time block codes, the zero-forcing function of IA and beamforming to optimize the SUs transmission rates. This proposed solution requires availability of channel state information (CSI), and to eliminate the need for CSI, this work then combines Differential Space-Time Block Coding (DSTBC) scheme with optimal IA precoders (consisting of beamforming and zero-forcing) to maximize the SUs data rates. Simulation results confirm the accuracy of the proposed solution.
1. Introduction
The scarcity of the licensed frequency spectrum has not hindered the development of wireless communications services [1]. Studies have shown under-utilization of the licensed spectrum due to the fixed spectrum access (FSA) policy [2], which grants exclusive rights to licensed users. This inefficiency has led to the demand for dynamic spectrum access (DSA), an alternative policy allowing both licensed users and unlicensed secondary users (SUs) to access the spectrum. To support DSA, cognitive radio (CR) are required to sense the radio frequency spectrum [3,4,5]. CR can sense and utilize idle portions/spectrum holes of the licensed spectrum in an opportunistic manner when licensed/primary users (PUs) are idle or concurrently with the PUs [4,5]. Since the SU’s transmission is considered of a lower priority than that of the PU, a crucial task in the design of CR is about how best the SU can avoid interfering with the PU in their vicinity [4,5,6]. This is particularly challenging due to the increased deployment of wireless communications services such that the PU is seldom idle [7].
In trying to find solutions to this problem, the focus of research has shifted towards an interference management strategy [8,9,10] that linearly encodes signals over multiple signaling dimensions, such that the resulting interference signal observed at each receiver lies in a lower dimensional subspace and is orthogonal to the one spanned by the signal of interest at each receiver. There have been several research endeavors conducted towards implementing interference alignment (IA) in CR networks, most notably the work in [11] and later in [12], where an opportunistic IA (OIA) technique was proposed. In this work, the PU link makes use of a water-filling power allocation (PA) scheme to maximize its transmission over its spatial directions (SDs), leaving some of these SDs unused due to power limitations. The SU link then opportunistically takes advantage of these unused SDs (called transmit opportunities (TOs)) with a linear pre-coder that aligns the SU’s transmission with the unused SDs of the PU link, thereby avoiding any interference to the PU.
Some of these are depicted in [11,12,13,14,15], where all of their models make use of a single-user MIMO SU link thus ignoring the effect of multiple SUs on the performance of a CR network. In fact, a single SU is unlikely to reliably detect the presence of a PU due to factors such as multipath fading impairments, low Signal-to-Noise Ratios (SNRs) and sensing time constraints [16]. Further work conducted in [17,18,19,20,21,22,23] take these impairments into consideration by employing multi-user MIMO SUs to take advantage of multi-user diversity [20], with [22,23] employing cooperative spectrum sensing (CSS). The work conducted in [21,22,23] also represented a paradigm shift because they employed the space–time water-filling algorithm for power allocation (PA) of the PU link, unlike the spatial water-filling algorithm used in [11,12,13,14,15,16,17,18,19,20] given that space–time water-filling (ST-WF) achieves higher capacity per antenna than spatial water-filling (SWF) in conditions more suited to CR networks [24,25,26]. The above observations, combined with the prospect of improved spectrum utilization through CSS provided the motivation to propose an OIA technique that utilizes ST-WF for the PU link optimization in which three different IA constraints are satisfied. The first two constraints deal with SUs aligning their transmission to orthogonal subspaces at both the PU-Rx and SU-Rx. The third constraint deals with ensuring that all SUs avoid interference with the PU transmission. However, simultaneously aligning all SU transmissions at the PU-Rx is always limited by availability of spatial dimensions as well as typical user loads [27]. Therefore, this work proposes a user selection algorithm by the FC, in which only a set of SUs, i.e., the SUs that are closest to the FC, are aligned at each PU-Rx.
Naturally, the success of the SUs communication depends on the accurate availability of unused Degrees of Freedoms (DoFs), as shown in the work in [15] which provides a more accurate outcome on the absence/presence of individual TOs. Thus, to further enhance accuracy of detection of TOs without the huge computational complexity of [15], this paper makes use of a double-threshold energy detection (ED) scheme [28,29] for the purpose of enhancing detection accuracy and availability of DoFs. Typically, the sensing condition states that if the SD exceeds the water-level value, then the SU reports unavailability of used SD. Alternatively, if it is less than , then the SU reports availability of unused SD. However, if the detected value is between and (i.e., values that are slightly above or below ), the SUs still reports this energy value, implying that the FC receives two kinds of information from which to base its decision on. This increased range of values available to the FC leads to higher detection accuracy and thus increased DoFs.
This research is also focused on maximizing the achievable transmission rate as well as diversity gain for the opportunistic SU links. The more legacy work of [11,12] use two PA schemes to find a covariance matrix that maximizes the achievable transmission rate for the opportunistic SU link. It was shown in [12] that the PA technique turns out to be a beamformer with multiple beams formed using the orthogonal eigenvectors of the correlation matrix of the estimated channel at the SU-Tx according to the “spatial water-filling” principle. The water-level saturates the power constraints, which makes the -user cognitive SU MIMO network equivalent to a standard interference channel with multiple antennas at each node. To increase the data rate performance, parallel transmissions equipped with space–time block coding (STBC) across eigen-beams were developed in [30,31,32], which yielded a two-directional eigen-beamformer that performs better than the conventional one-directional beamformer with negligible increase in computational complexity [32,33]. Conversely, to achieve full transmit diversity without losing sum rates, new IA schemes were proposed in [34,35] that use STBC to achieve full transmit diversity, where the STBC structure of the equivalent channels were preserved after zero-forcing the interfering users [36]. These IA schemes were shown to achieve higher diversity gain than other conventional methods [37] with only local CSI. Since the work in [37,38,39,40] reveals that the SU transmission is not changed by the transmit eigen-beamforming matrices, we can therefore propose wedding optimal precoding with orthogonal STBC and IA that will achieve higher transmit diversity at the same symbol rates as the work conducted in [12].
The ST-WF scheme is not without its drawbacks as shown in [24,25] to be associated with a higher channel outage probability, thereby setting a lower-bound in terms of the SUs’ transmission rates. In order to solve this problem of maximizing the SUs’ rates in the presence of channel outage, this paper proposes that the multiple SUs employ a differential STBC (DSTBC) scheme that is then combined with optimal IA precoders [38,39] that align interference at unintended receivers thereby eliminating the need for local CSI. DSTBC encodes the transmitted information into phase differences between two consecutive symbols, where information is essentially transmitted by first providing reference symbols which determine whether the SUs transmit or remain silent. The linearly encoded combinations of the original phase-shifted symbols and their conjugates are then processed. After zero forcing, the multiple SU-Rxs decode the current symbol by comparing its phase to the previous symbol’s phase. This scheme achieves a significantly higher sum rate and reliability. The contribution of this paper can be summarized as follows:
- Firstly, the PU’s PA technique is based on an SVD scheme that employs the ST-WF algorithm for the PU link to free up some unused eigenmodes and achieve better channel capacity and;
- Secondly, this paper takes advantage of multiple SUs, similar to [22,23], to enhance performance by employing CSS, and proposing a double-threshold ED scheme; the FC receives two kinds of information from which to base its decision which improves the probability of detection;
- Finally, to optimize the transmission rates of SUs; this work proposes an IA technique that combines the merits of DSTBC and linear precoding, yielding a two-dimensional (2-D) beamforming solution that shows better performance in terms of the SUs’ transmission rates.
The remainder of this paper is organized as follows. In Section 2, the system model is described, and the main assumptions required for analysis are introduced. In Section 3, a comparative analysis is conducted between the MEB, SWF, and ST-WF schemes for the PU link as well as an analysis on the outage probability of the ST-WF algorithm. Section 4 presents the opportunistic IA scheme (OIA) by presenting the sensing phase (along with the double-threshold method) and the IA phase with the SU selection process. Section 5 presents OIA with STBC by briefly reviewing the literature before presenting the algorithms required for the STBC–beamforming–IA technique. Section 6 then presents the OIA with DSTBC approach that describes the steps taken towards achieving diversity and higher data rates through DSTBC. Section 7 provides an overview of simulation results as well as a performance comparison between this work and that of [12,22]. Finally, Section 8 presents the concluding remarks.
2. System Model and Assumptions
The system model for this paper is a MIMO CR network that consists of a single PU link (PU-Tx and PU-Rx) and SU-Tx/Rx pairs (, …, ) as shown in Figure 1 below. Every user is assumed to have transmit and receiver antennas. The PU link is a point-to-point MIMO link, while the SU network is a multi-user MIMO network. The following assumptions are made for the purpose of the system model: (I) The PU and SUs operate in the same frequency band and all channels are Rayleigh fading. (II) The PU link is a single user MIMO channel which is represented as a matrix, with channel coefficients between transmitter and receiver , where elements of are drawn i.i.d. from a continuous distribution. The channels are assumed to be block fading, and the CSI is known to all the nodes. The signal received at the PU-Rx can be defined as
where is the precoding matrix of the th user and represents the number of transmitted streams, is the transmitted vector, is the additive Gaussian noise vector at the th receiver. The transmitted power is subject to an average power constraint . (III) It is assumed that the PU-Tx is oblivious to the presence of the SUs. We also assume that the PU channel matrix is known at the PU-Tx and PU-Rx [4]. The PU-Tx chooses its precoding matrix and the PU-Rx chooses its post-processing matrix such that the PU link channel transfer matrix is diagonalized. Then, once SVD has taken place on of the PU, each SU will receive independent parallel non-interfering channels [11,23].
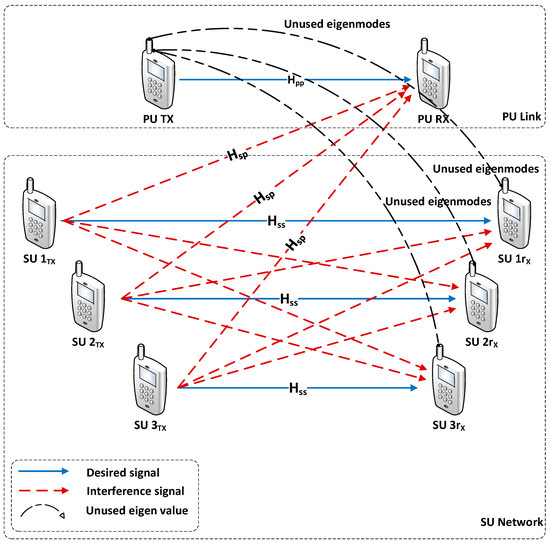
Figure 1.
Multiuser CR network model consisting of one PU link and multiple SUs.
The received signal at each SU-Rx is thus defined as
The transmit covariance of the input signal is which is subject to an average power constraint. In the standard IA conditions, each transmitter therefore transmits a sequence of Gaussian encoded symbols to its corresponding receiver by processing its symbols using a precoding matrix to form the transmitted signal vector . The received signal at the th receiver is linearly processed by the post-processing matrix to extract the symbols sent by the th transmitter. The IA condition states that the primary and secondary received signals are represented by
where denotes the received signal vector at the th receiver; denotes the zero mean unit variance circularly symmetric AWGN noise vector at the receiver; denotes the signal vector transmitted from the transmitter; is the matrix of the channel coefficients between the transmitter and the th receiver; and , where is the transmit power of the transmitter [20]. It should be noted that and are used as a generalization denoting each transmitter and receiver pair.
3. PU Link Optimization
3.1. The Numerical Comparison
With the comparative study carried out in [24,25], it is clear that the ST-WF offers improved SU performance for the same PU parameters. Most significant though is the fact that the ST-WF achieves significantly higher capacity than SWF at low-to-moderate SNR regimes, which fits well with CR networks [25,26]. In order to implement the ST-WF algorithm, we take a look at the original approach for water-filling [12], i.e., the SWF approach. For a single MIMO PU channel, recall that
where is the input covariance matrix, is the MIMO channel, is the autocorrelation matrix of the input vector , defined as , P is the instantaneous power limit, denotes the determinant of , and denotes the trace of matrix and is the noise variance. SWF can be used to optimally allocate power to the parallel channels as defined by the following equation [26]:
where is the power of . The water-fill level is chosen such that as defined in Equation (5). Once the PA matrix using SWF is set up according to [12], the diagonal matrix contains non-zero/used entries and zero/unused entries which crucially translate into a set of used receive dimensions and a set of unused receive dimensions with no PU signal. In terms of implementing the ST-WF algorithm, the PU-Tx also chooses precoding matrices as the columns of that corresponds to a non-zero power allocation that is used to maximize the rate of the PU link under power constraints as shown below
It should be noted that for ST-WF, the function is present in all MIMO channel realizations, implying that the symbol rate changes faster than the channel variation where can be computed from all symbols but within one channel realization. For computation of the diagonal PA matrix by applying the so-called ST-WF algorithm, can be found as follows:
where is the mean water level that can be solved by the equation provided below:
and is the marginal probability density function (pdf) of the random variable . To gain more insight into this issue, Figure 2 above shows the average sum rate versus the SNR for a single user PU MIMO link with the SWF, ST-WF, and MEB PA schemes. For the Rayleigh channels in this work, Rayleigh fading is assumed to be pure due to the PU-Tx and PU-Rx assumed to be in close proximity and hence the shadowing effect is negligible.
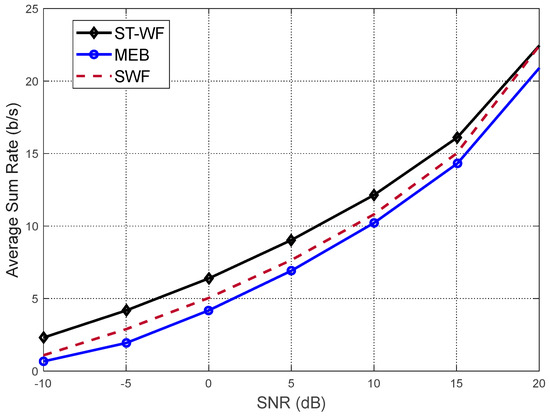
Figure 2.
Average sum rate vs. the SNR at the PUs link for water-filling (SWF and ST-WF) and MEB.
The ST-WF algorithm with no shadowing variance achieves higher spectral efficiency over SWF at low SNRs and has the highest gain of 5 dB in the SNR over equal power distribution at a spectral efficiency of 2.5 bps/Hz/antenna. Furthermore, Figure 2 shows that the numerical results obtained from the simulations corroborate with theoretical results [24,25]. The simulation results shows that the ST-WF scheme outperforms the other schemes and shows the possibility of increased sum rates in two-tier CR networks when the PU participates in IA.
3.2. Outage Probability of ST-WF
A condition exists for the ST-WF algorithm, when SDs from the PU channel matrix are not high enough to properly utilize transmission power. This can result in blockage of transmission, or more specifically channel outage. The channel outage probability defined in [41] is equivalent to the probability that the largest eigenvalue of is smaller than . Since the eigenvalues of are in descending order, the channel outage probability can be expressed as
The exact channel outage probability is expressed in terms of the maximal eigenvalue distribution, denoted as . If , where is the shadowing random variable and is the maximal eigenvalue of , the distribution of is denoted as and can be obtained by integrating out , that is,
Differentiating Equation above yields the pdf of given as
Given the closed-form nature of the outage probability calculations, solving for is seen to be computationally complex, and as such, only an approximated value of will be utilized to simplify the calculation of . The achievable spectral efficiencies per antenna of the two cases of SWF and ST-WF are compared using Monte Carlo simulations performed over channel realizations.
Since we are considering practical multi-antenna systems where the channel coefficients fluctuate relatively fast, their antennas may exhibit strong correlation among fading channels, which implies that the channel’s spatial correlations will typically change slowly, even when the channel coefficients fluctuate relatively fast [42,43,44]. The channel’s spatial correlation is considered as a slowly varying effect similar to log-normal shadowing. Therefore, the Rayleigh MIMO channel has variance of for both real and imaginary parts with a standard deviation of for a pure Rayleigh scenario, and for log-normal distribution [45].
With the average power set to be 1, Figure 3 shows the channel outage probabilities for both water-filling techniques for Rayleigh channels with and without shadowing. For , it can be seen that the SWF technique incurs a higher channel outage probability than the ST-WF technique. The case of pure Rayleigh fading for the ST-WF technique results in lower channel outage because the increase in in log-normal shadowing conditions changes much slower than fast fading. Therefore, the distribution of the shadowing variable dominates the outage probability. ST-WF typically achieves a higher average capacity per antenna compared to SWF due to its ability to adapt power allocation over both space and time, leading to a more balanced and efficient use of the available resources.
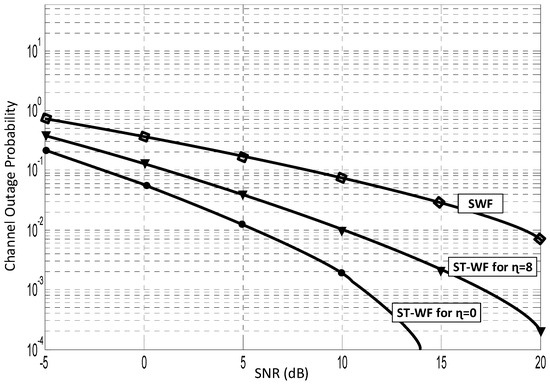
Figure 3.
Outage probability curves for SWF and ST-WF.
4. Opportunistic Interference Alignment
The proposed approach will be divided into two phases, the first being the sensing phase and the second being the interference alignment phase.
4.1. The Sensing Phase
It should be noted that because both PU and SU have been assumed to be operating in the same frequency band, the SUs will opportunistically always make use of the licensed spectrum as long as the TOs are available. Recall from the system model that the PU–SU link is assumed to be operating as a MIMO channel with the PU seemingly broadcasting to many SUs [26,31] such that at a low SNR, the ST-WF algorithm allocates all power to the strongest parallel channels while at a high SNR, it allocates equal power to each of the channels. The strongest channels are the used dimensions, while the others can be classified as the unused dimensions or TOs.
Energy detection is especially useful in scenarios where prior information about the signal is unavailable, thanks to its simplicity and efficiency. When compared to other traditional spectrum sensing methods—such as matched filtering, cyclostationary feature detection, and eigenvalue-based detection—energy detection offers distinct advantages, including ease of implementation and applicability in diverse environments. The advantages of energy detection compared to other traditional spectrum sensing techniques [46] can be found in Table 1.

Table 1.
Spectrum sensing techniques comparison [46].
Each SU can sense the absence or presence of the unused TO such as is the case in conventional energy detection theory [4,47], where each SU makes its local decisions by comparing its observational value with a pre-fixed threshold , as shown in Figure 4a, and a decision is made when is greater or less than the threshold value under the following binary hypothesis test [22]:
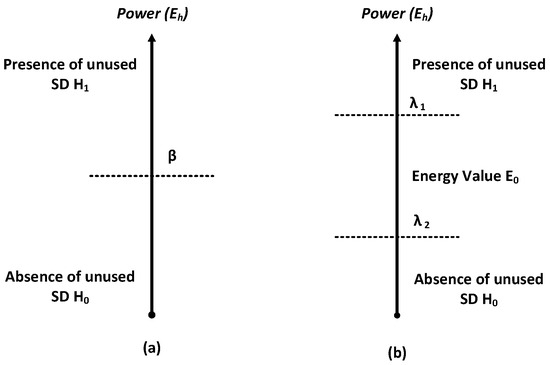
Figure 4.
(a) Single detection (b) Double detection.
In this paper, a double-threshold method as shown in Figure 4b is introduced, where two thresholds are used to help the decision of the SU [28,29]. The condition for the conventional detection method states that “if the energy value exceeds , then the SU reports . If is less than , SU reports . However, there are some sub-carriers that are just slightly below the water level, i.e., , that the normal single-threshold detection classifies as used. However, the channels of these sub-carriers are actually too poor for it to be worthwhile for transmission by the PU [48], with the same applying for the reverse situation of the sub-carriers being slightly above water-level (), which are classified as unused. Therefore, the double-detection technique states that if is between and , then the SU also reports this observational energy value “”; hence, the FC receives two kinds of information, the local decision and the observational value of the SU.
It is assumed that each SU has identical threshold values. If satisfies , then the SU sends the measured energy value to the FC. Otherwise, it reverts back to reporting its local decision according to , i.e., the conventional detection technique. Each SU sends a summary of its own observations to the FC in the form of where and denote the probabilities of missed detection and false alarm for the SUs.
Let denote the information that the FC receives from the SU expressed as
and
Hence, the FC collects their observational values and makes an upper decision on the availability of used and unused SDs. The FC then uses the hard combination fusion rule [1,4,47] for making the final decision based on the received information. This work utilizes the probability of missed detection as one of the parameters for measuring performance. It can be observed that the simulation results in Figure 5 are quite optimal, yielding near-perfect results when sensing ONLY for TOs. Figure 5 illustrates that the detection probability of the proposed double-threshold CSS scheme increases compared with the conventional detection scheme. Figure 6 illustrates the performance variation of the in relationship to the SNR (dB) with multiple cognitive relays (2, 4, and 6). It can be observed that by increasing the number of SUs, is increased. Additionally, the increases as the SNR increases, which is consistent with performance criteria in CR networks.
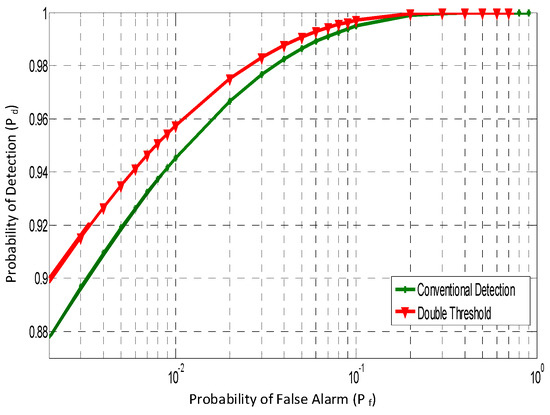
Figure 5.
Performance comparison of a conventional ED and a double-threshold ED scheme.
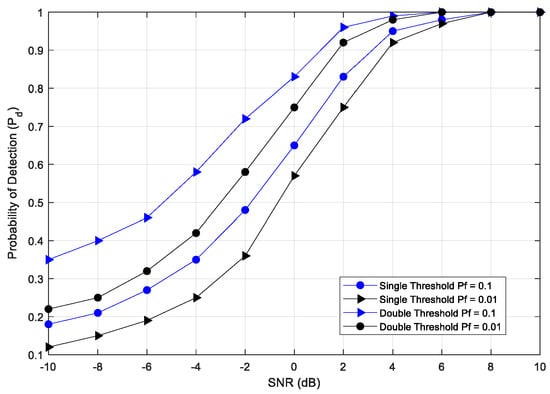
Figure 6.
Pd vs. SNR with Pf = and using a conventional ED and a double-threshold ED with an scheme.
4.2. The Interference Alignment Phase
The main goal of this subsection is to derive appropriate pre- and postcoding matrices which align the SU transmissions to the unused dimensions. In order to achieve that, an OIA strategy is proposed in which three separate conditions must be satisfied. Firstly, given the SVD channel matrix of the PU link as where and are the and singular-vector matrices and is a diagonal matrix containing singular values, the cognitive IA problem is formulated by defining the required conditions for IA.
Given that the received signal at the th receiver due to the th transmitter lies in the subspace spanned by the columns of , the SU-Tx’s are guaranteed not to generate any interference on the PU-Rx as long as the following precoding and post-processing condition are met
Equation is the post-processing matrix that satisfies the orthogonality between the SU-Rxs and the PU-Tx, thus guaranteeing that the PU link achieves similar data rates as an equivalent single-tier system despite the opportunistic transmission of the SUs. is defined as the DoFs [8], thus satisfying the first condition.
The second condition requires that the SU and PU signals be aligned to orthogonal subspaces at not only the PU receiver, but the SU receiver as well. Therefore, a different strategy is used to design the SUs postcoding matrix in order to satisfy the second interference constraint. The first part of this constraint, defined in ensures that interference from each SU-Tx is aligned at the output of its corresponding unintended receivers.
Similar to , the constraint in guarantees that the th SU can achieve DoFs. However, because this work consists of multiple SUs, the third condition that must be satisfied requires that ALL the SUs do not impose any interference on the PU receiver. Similar to the approach proposed in [27,49], this work proposes to perform IA with user selection in order to optimize the performance of this third condition. While the work conducted in [14,15,16,17,18,19,20] relies strictly on the feasibility conditions of IA [50,51] to ensure multiple SUs are aligned along the PU null spaces, the number of SUs that can actually be aligned at the PU’s null spaces is generally limited by the spatial dimensions available for IA based on the number of antennas at the PU-Rx. Therefore, simultaneously aligning all SUs at the PU-Rx is not feasible for typical user loads. Instead of attempting to align the entire set of SUs at every PU, this work proposes an efficient clustering strategy for the SUs network.
The objective of this strategy is to ensure that SUs that are closest to the FC are aligned at each PU-Rx into the same cluster. In order to select appropriate SUs, the FC collects information from each SU node, which includes the distance from the FC and the SUs’ received signal power from the PU. Based on the information gathered, the FC elects the SUs that will form a cluster according to a given election algorithm and broadcasts the election to all nodes. The message broadcasted contains the node ID of the elected SUs and also information about time synchronization, resource allocation, and the maximum number of permitted access nodes in one cluster. The number of nodes in a cluster is limited to avoid too many nodes crowding in one cluster. Let denote the average distance from nodes to the FC, and the selected SUs are expected to be located at minimal away from FC. The SU election algorithm is described in Table 2.

Table 2.
SU election algorithm.
The number of SUs aligned at each PU-Rx cannot exceed , which is introduced to control the maximum number of elements of each set. It should be noted that limiting the selection of SUs to a bare minimum can negate the benefits of multi-user diversity. However, our selection scheme will be justified in the next section of this paper.
4.3. Feasibility Conditions of IA
This section discusses the feasibility of the proposed method as well as the conditions for perfect IA. The conditions for which the system is proper are first determined by establishing that the number of variables to be determined is greater than or equal to the number of equations in the IA system defined in [51] as follows:
Our model looks to design a cluster of SUs based on geographical proximity as discussed in Section 4.2 above, and for the sake of simplicity, we limit our initial design to two SUs per cluster with each SU having two Tx/Rx antennas. It is well known from Bezout’s theorem that generic polynomial systems are solvable if and only if the number of equations does not exceed the number of variables [52]. As such, signal space IA problems can either be proper or improper [51,53]. Thus, from the Theorem of Proper Characterization [50], a symmetric system is proper if and only if
Likewise, an asymmetric system defined as is improper if
Thus, based on the Equations and , this system can be designed according to the algorithms to satisfy the IA condition. The advantage of this is that it will follow directly on the cognitive IA system [18]. For example, it was shown that for single-beam IA systems, i.e., systems where each user requests only one DoF [50], IA is almost surely feasible if the system is proper.
5. Opportunistic Interference Alignment with Space–Time Coding
5.1. Background
In [12], a source covariance matrix was chosen in which the SU-Tx can allocate power to maximize its achievable rate. This was achieved by using uniform power allocation (UPA) and optimal power allocation (OPA) schemes. In the UPA case, the opportunistic SU-Tx does not perform any optimization on its transmit power, but rather uniformly spreads its total power among the previously identified TOs, which saturates the transmit power constraint. The OPA scheme, on the other hand, takes on a water-filling solution with an SVD matrix such that the OP can be rewritten as
Given that the SVD of the matrix is given as , where the columns of and contain the singular vectors, and is the diagonal matrix containing the corresponding singular values . The optimal solution is thus given as . The diagonal matrix is used to represent the OPA solution and the optimal values of its diagonal elements translate into the water-filling solution
where is the Lagrangian multiplier chosen to satisfy Equation (23). This optimal SU precoder described above turns out to be a generalized beamformer formed using the eigenvectors of the matrix of the optimized channel at the SU-Tx. A perfect illustration of this is the work conducted in [22], where, even after the SUs use a covariance matrix to maximize their throughput, a power-allocation strategy called threshold beam forming (TBF) is proposed to improve both the spectral and power efficiency of the SUs. The TBF scheme is an effective tool for saving SU-Tx power and improving the spectrum efficiency in poor channel conditions. If the receiver can acquire the CSI reliably as shown in [22] or when partial CSI is available at the transmitter, coherent detection along with orthogonal space–time block coding (STBC) [31,37,54] can be employed to increase the data rate. As such, parallel transmissions equipped with STBC [31,32,33,34] across optimally loaded eigen-beams have been developed that lead to the so-called two-directional (2D) eigen-beamforming. With minimal variation in computational complexity compared with traditional one-directional (1D) beamforming, 2D beamforming was shown to achieve better performance.
In addition to network throughput, reliability in terms of diversity gain is another dimension of performance measurement for the SUs. When channels experience fading, the SNR level at the receiver becomes low and dominated by outage events. As a result, techniques such as Alamouti codes and STBC in point-to-point MIMO channels [34] have been proposed to explore the spatial diversity gain. Recently, the work in [34] presented the scenario where a trade-off between symbol rate, diversity, and IA was possible in a multi-user network, thus motivating the work in [35,36,55] that use Alamouti codes to achieve full transmit diversity without losing rate. The transmitters in this proposed scheme only require CSI from itself to both receivers instead of global CSI as assumed in [10].
It is clear that the scope of the literature on wedding optimal precoding/eigen-beamforming with orthogonal STBC to improve throughput does not delve into the full process of IA through zero forcing at the multiple receivers. The scope of the literature on achieving higher diversity gain, on the other hand, does incorporate STBC with beamforming where zero forcing is used to decouple symbols at the interfering users, but obviously without optimal precoding. As such, this work finds an opportunity to propose an IA scheme where each transmitter needs only channel information from itself to both receivers that achieves the same maximum symbol rate as the scheme in [10] but with a higher diversity gain. Given the fact that Alamouti codes achieve full transmit spatial diversity in point-to-point MIMO systems [37], this work incorporates Alamouti codes in the design of optimal precoding matrices, the product of which is a two-dimensional (2-D) eigen-beamformer without rate reduction. Since the equivalent channels are linearly independent, zero-forcing (ZF) is conducted at each receiver, to cancel interference and separate useful symbols to obtain symbol-by-symbol decoding.
Given that channel estimation becomes difficult or requires too many training symbols, especially when the channel is rapidly changing in a mobile environment, unitary space–time modulation and differential space–time modulation [46,54,56,57,58,59,60,61,62,63] are well motivated because they bypass CSI acquisition at the SU-Rx. As such, this work considers differential space–time modulation based on orthogonal STBC, without partial CSI at the SU-Tx for independent, identically distributed (i.i.d.) fading channels. One of the advantages of MIMO systems is their ability to exhibit strong correlation in the presence of fading due to multiple transmit antennas. This implies that the channel’s spatial correlations in fast-fading channels will still fluctuate slowly [56,57]. Thus, while there is no knowledge of CSI in differential space–time transmission, the channel’s spatial correlations can easily be estimated at the SU-Rx due to slower fluctuation and be fed back to the SU-Tx. Similar to [37], the differential modulation based on orthogonal STBC is also much easier to construct and leads to low-complexity symbol-by-symbol decoding. Given its inherent advantages, this paper will consider incorporating differential STBC (DSTBC) into the STBC beamforming solution described earlier. The next sections will look at how the STBC–beamforming–IA process with local CSI will be used to achieve both higher sum rates and diversity gain. This will then be followed by the DSTBC–beamforming–IA (DSTBC–BF–IA) solution to save the SU-Tx power in rapidly changing channel conditions.
5.2. STBC Beamforming IA Process
The initial approach considers a two-user IC channel as shown in Figure 7 where are used to denote the channel matrices. and are perfectly known at SU-Rx 1, and and are known at SU-Rx 2, and each of the entries are i.i.d. Gaussian distributed. It is assumed that the channels are block fading (or constant), i.e., all channels keep unchanged during transmission in which all the desired signals at SU-Rx 1 are from SU-Tx 1 while the interference at SU-Rx 1 only comes from SU-Tx 2 [34]. At a given symbol period, two signals with fixed Binary Phase-shift keying (BPSK) constellation for each of the two receivers are simultaneously transmitted from the SU-Tx antennas, denoted as .
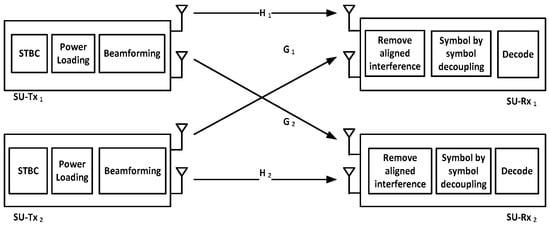
Figure 7.
STBC process.
At the next symbol period, two complex conjugate signals are then transmitted from the two antennas of the SU, denoted as . The superscript in denotes the index of the symbol, the first subscript denotes the index of the transmitter, and denotes the index of the receiver. SU-Tx linearly combines four symbols and generates a block code . The equivalent transmitted vectors can be expressed as
where denotes the beamforming matrix from Tx to Rx . The symbols intended for SU-Rx 1 become interference for SU-Rx 2 and are aligned with SU-Rx 2. The decompositions in and for the precoding and post-processing matrices of the SUs can be modified due to the presence of the PU link to get the following equations:
The modified equations in and represent a standard IA problem with the variables and . Given that and are the beamforming matrices at the th SU-Tx and SU-Rx, ensures that all the interfering signals at th SU-Rx lie in the subspace orthogonal to , while assures that the signal subspace has dimension and is linearly independent of the interference subspace. The constant is a diagonal matrix which contains power loading coefficients. By exploiting the knowledge of the covariance matrix, the power loading coefficients will be derived based on the symbol error rate (SER) values. From [12], the SNR of the covariance matrix for a fixed channel realization can be found as follows:
where denotes the independent eigenvalue channels, is the Rayleigh distribution of the th sub-channels, denotes the th eigenvalue of that is non-negative, and denoting the th sub-channel’s SNR [31]. This implies that we can approximately compute the SER.
where , and is the moment generating function of the probability density function of the Rayleigh distribution. The power loading coefficients contained in the diagonal matrix based on the approximate SER values are shown to also come very close to the actual SER values at a low SNR.
where is the eigenvalue of the channel covariance matrix . To select power loading coefficients, we now formulate the following optimization problem:
Using the Lagrange multiplier method, we can find power loading coefficients as follows:
where is the number of beamformers that transmit signals, given the transmitted power budget . Each transmitter sends two symbols to one receiver. The transmitted block codes are designed as follows:
The coefficients and are the average SNR and the normalization factor at each SU-Rx, respectively, that are introduced to ensure that the average energy of the coded symbols are unitary across all the antennas. Each symbol is sent using Alamouti codes, and each transmitter sends linear combinations of both the original symbol and their conjugate. To this end, is transmitted along the eigenvectors of the channel correlation matrix with power loaded on each eigenvector. Recalling that the received signal matrix at Rx can be represented as
where denotes the additive white Gaussian noise (AWGN) matrix at Rx , therefore
Both the second terms in and represent interference, which then makes it clear to see how the post-processing filters of and align symbols and at SU-Rx 1, while and are aligned at SU-Rx 2. After completing IA at both SU-Rxs, the individual symbols can be decoded using symbol-by-symbol decoding. As mentioned earlier, the Alamouti structure ensures that the corresponding definite channel matrices at the SU-Rx retain the same structure due to the completeness of its multiplication and addition properties [37]. Therefore, can be decoded with the following equation:
Equation therefore applies to the remaining symbols at SU-Rx 1 and SU-Rx 2 to have four separate procedures for symbol-by-symbol decoding to recover the desired symbols.
6. Opportunistic Interference Alignment with Differential-STBC
The spectral efficiency gain of ST-WF is typically associated with a higher channel outage probability, which sets a lower-bound on optimizing the SUs transmission rates. It is therefore necessary to find a solution that not only helps with optimizing transmission rates, but also encourages the SUs to use their power more efficiently. Thus, similar to the work conducted in [22], where the SU-Rx depends on pilot signals transmitted at the start of each transmission to estimate its own channel matrix (local CSI) and determine whether the SU-Tx remains silent or transmits, this paper considers using DSTBC, but without local CSI at SU-Txs for independent, identically distributed (i.i.d.) fading channels. This solution states that if the channel is approximately constant for a time of at least two symbol periods without any outage, i.e., within 3 dB of the coherent demodulation in Gaussian channels, then the SUs transmit. Otherwise, the SUs remain silent.
6.1. Differential Encoding
To implement DSTBC, information is encoded in the phase differences between consecutive transmitted symbols, rather than in the absolute phases of the symbols themselves. This approach offers several advantages, particularly when it comes to simplifying receiver design and improving robustness in wireless communication systems. In order to implement DSTBC for the SUs, signal transmissions begin by sending a reference codeword matrix which consists of an arbitrary pair of symbols and at time from the two SU-Txs followed by the related pair of symbols and at time that provide the receiver with a known frame of reference for facilitating the DSTBC process. Where the channel has a phase response that is approximately constant from one symbol period to the next, defined by a threshold , the SU-Rx is able to decode the information in the current symbol. Specifically, the information matrix is transmitted according to its matrix structure defined in , first collected in an STBC matrix comprising the linear combinations of both original symbols and their conjugate as follows:
It follows that the DSTBC matrix can be written as follows:
where the codeword matrix also has the following structure:
Similar to the STBC solution, will be transmitted along the eigenvectors of the correlation matrix with power loaded on each channel eigenvector. As such, the transmitted signal at the th block can be expressed as follows:
where contains power loading coefficients. Due to the unitary property of the codeword matrix and the works in [37,53], the SU-Tx power remains unchanged, implying that the fundamental differential transmission equation is not changed by the power-loaded eigen-beamforming matrices. Similar to the STBC-beamforming solution, the SER is also used to derive power loading coefficients using . Using the Lagrange multiplier method, we can find power loading coefficients as follows [37]:
Equation above is similar to for coherent STBC except for a factor 2 in the second term, which is used to compensate for the dB discrepancy between the for DSTBC and its counterpart in coherent STBC [48,53].
6.2. Differential Decoding
The first step towards differential decoding entails removing the aligned interference. Given that the equivalent channels spanned by the useful signals have an Alamouti structure, and since the equivalent channels for interference are constant, the aligned interference can simply be cancelled. From and , and . For clarity, we first consider a single Rx antenna. The received data are processed by computing the differential phases between any two consecutive symbols. The receiver detects this phase difference to decode the transmitted data without needing to know the exact channel coefficients. The scheme uses the relative phase between consecutive transmissions; it is inherently robust to slow fading and phase noise. The decoding process is less affected by these variations, leading to more reliable communication. By not requiring the transmission of pilot symbols which are typically used for channel estimation in other schemes, DSTBC can use the available bandwidth more efficiently. This allows for a higher sum rate because more symbols can be transmitted within a given timeframe. DSTBC offers advantages in certain scenarios, these come at the cost of increased computational demands, especially when compared to traditional, centralized STBC schemes [64].
7. Simulation Results and Analysis
In this section, numerical results have been provided to evaluate the performance of the OIA-STBC algorithm against the SU-IA-OPA and SU-IA-TBF algorithms. It is quite clear from the results obtained that this scheme provides improved throughput when compared with other schemes. The performance curves of conventional STBC with coherent detection are shown to be parallel to those of the DSTBC schemes, indicating that the DSTBC schemes also achieve full transmission diversity due to the orthogonal designs. Traditionally, the one drawback of the differential scheme is that it is almost always 3 dB worse than the respective STBC with coherent detection since it does not require any CSI. The inherent requirement of perfect CSI in the coherent STBC scheme introduces channel estimation errors as well as additional power consumed by training symbols, particularly in this work that employs optimal power loading, making it inapplicable to fast-fading channels. DSTBC, on the other hand, does not require CSI at the SU-Rx, making it well suited to perform well in fast-fading channels. A summary of the simulation parameters is shown in Table 3.

Table 3.
Summary of the simulation parameters.
In our simulations, both coherent STBC and DSTBC use BPSK, where the channel is both fixed and independent over a pair of successive blocks in each run (i.e., channel variation is negligible in two consecutive blocks) making our simulations valid for fast-fading channels. As stated earlier, practical multi-antenna systems may exhibit strong correlation among fading channels, which implies that the channel’s spatial correlations will typically change slowly, even when the channel coefficients fluctuate relatively fast, which is a requirement common to all differential schemes. The SER performance curves of coherent STBC and DSTBC with beamforming with two Tx antennas and both one and two RX antennas are evaluated via simulations as shown in Figure 8 below. If we take into account the channel estimation error and the transmitted power consumed by training, coherent STBC with two Rx antennas shows better performance than with one Rx antenna. On the other hand, we see that for one Rx antenna, the proposed DSTBC–beamforming scheme initially outperforms the coherent STBC at a very low SNR since DSTBC does not require CSI at the Rx.
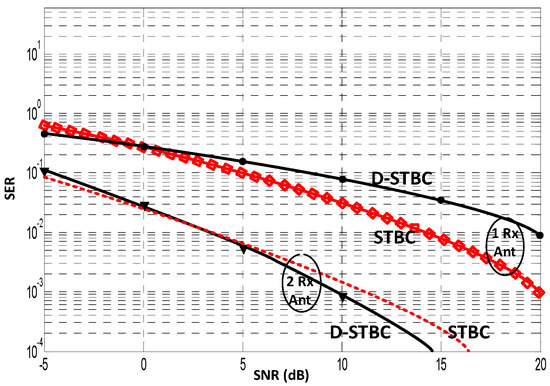
Figure 8.
SER Curves for coherent STBC and DSTBC–beamforming schemes.
With two Rx antennas, the DSTBC–beamforming scheme eventually shows better performance than coherent STBC with an increasing margin as the SNR was increased. Therefore, our results demonstrate that in highly correlated channels, the proposed DSTBC modulation scheme has better or comparable error probability performance to coherent STBC, proving the point that the training symbols used in coherent STBC incur a significant loss in data rate. This is a clear demonstration that combining DSTBC with optimally loaded beamforming offers higher data rates. The analysis of the performance curves presented in Figure 9 and Figure 10 provide further insight into the improved data rates of the DSTBC–beamforming scheme. Monte-Carlo simulations using MATLAB were carried out for two SU pairs (Tx and Rx) and a single PU link with each node equipped with two antennas. As shown in Figure 9, three separate techniques are compared, namely the legacy SU–IA–PA [12], the SU–IA–TBF [22], and of course the proposed STBC–BF–IA scheme.
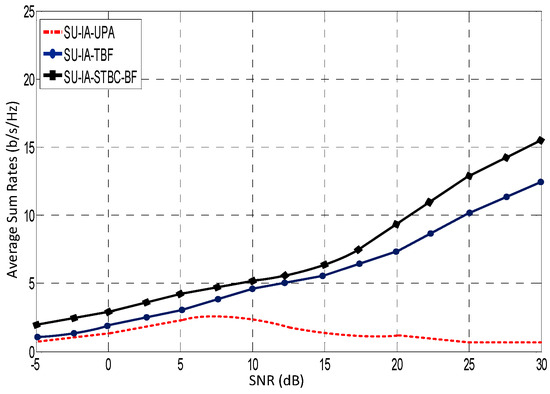
Figure 9.
Average sum rate (b/s) against SNR (dB) for two SUs.
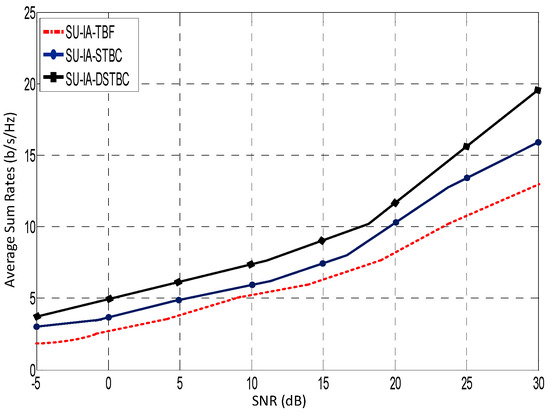
Figure 10.
Average sum rate (b/s) against SNR (dB) for two SUs with DSTBC.
For the SU–IA–PA scheme, it is observed that at low and high SNRs for the PU link, the performances of both the uniform PA and optimal PA are unsatisfactory and almost identical, even when the SU-Tx spreads its power amongst all the available TOs or performs optimal PA which translates into a water-filling solution. This poor outcome is most probably due to the transmission power of the PU-Tx being at lower and higher ends of the transmit power spectrum, thus not leaving any unused SDs. Indeed, in that case, we are faced with the conventional CR system in which SUs can only utilize the PUs frequency band in an opportunistic manner to avoid imposing interference on the PU, i.e., when the PU is idle. At intermediate SNR values, however, significant data rates for the IA–OPA and IA–UPA approaches are achieved by the SUs. For the TBF scheme shown in Figure 9, the discrepancy in performance of the PU link optimization using the MEB technique is small in comparison to the ST-WF algorithms but the throughput performance of the SUs, on the other hand, increases exponentially at high SNR values when compared to the SU–IA–OPA scheme at almost no cost to the PU. The improved performance of the SUs’ sum rates can be attributed to two things: Firstly, the MEB algorithm ensures that at least one of the PUs’ eigenmode will always be available to convey the SUs’ data. Secondly, the SUs with a poor channel condition stay silent as per TBF to cooperate with the other SU links to enhance the performance of the network through controlling the interference. It could also be suggested that as the number of candidate SUs increases, the average sum rate also increases. It should be noted that the observations are all predicated on the fact that the achievable rates of the SUs have to be computed using the following equation: for all .
From Figure 9, the proposed STBC–BF solution clearly performs better than the TBF solution even with the TBF solution seemingly enjoying the advantage of an increased number of candidate SUs and its efficient SU rate optimization scheme that is applied after threshold beamforming to help keep the sum rates above a prespecified threshold level. This improved performance is initially founded on the fact that the SU selection scheme limits the number of SUs in a cluster, which was otherwise not the case in other works such as in [22]. While an increased number of SUs can improve detection accuracy, it could also be an additional source of interference to the PU transmission. Helped by the double-detection scheme, the SUs are therefore almost assured free TOs that they could align their transmission with. Secondly, the increased sum rates of this scheme are a direct manifestation of employing coherent STBC with beamforming and optimal power loading to improve reliability in terms of diversity gain without much discrepancy in terms of computational complexity.
The graph shown in Figure 10 demonstrates the performance comparison between SU–IA–STBC and SU–IA–DSTBC where the channel’s spatial correlations are considered to have a slowly varying effect similar to shadowing. Both the DSTBC and the STBC technique are seen to significantly outperform the SU–IA–UPA technique because implementing 2D eigen-beamforming minimizes the error probability and outperforms 1D beamforming especially at a moderate-to-high SNR. This is indicative of the fact that for the SU–IA–UPA scheme, the TOs become almost non-existent at the highest SNR. However, this work shows that for practical values of the SNR, there are a non-zero number of TOs that the SUs can always exploit. At an intermediate-to-high SNR, the SU–IA–DSTBC scheme performs better than the SU–IA–STBC scheme. The graph shown in Figure 10 demonstrates the difference in performance between the SU–IA–TBF scheme against the SU–IA–DSTBC schemes. It has been shown that even though the ST-WF PA scheme provides efficient performance for the SUs only in the intermediate SNRs, this work combines the benefits of double ED as well as the SU–IA–STBC algorithm to release even more eigenmodes, thus achieving higher data rate performance than the SU–IA–TBF algorithm. The essential drawback of the MEB algorithm is that it is less dynamic than ST-WF and more susceptible to lower data rates. It can also be seen in Figure 8 that the data rate performance of the SU–IA–DSTBC is higher than that of the SU–IA–DSTBC schemes, owing to the fact that the threshold function of the DSTBC scheme is an effective tool for saving the PU’s transmit power due to the WPA’s channel outage conditions (see Figure 3). The consequence of saving the SUs’ transmit power can be seen in Figure 8, where the sum rate performance of the SU–IA–DSTBC curve increases even further especially at a moderate-to-high SNR, when compared with the SU–IA–STBC curve. Also, with two SU-Rx antennas, the DSTBC–beamforming scheme shows better SER performance than coherent STBC with an increasing margin as the SNR was increased, demonstrating that in highly correlated channels, training symbols used in coherent STBC incur a significant loss in data rate.
Implementing the proposed scheme in real-world CR networks involves significant challenges such as hardware limitations, synchronization, channel variability, energy consumption, and interference management. Although the approach offers benefits, these practical issues must be addressed to realize its potential.
8. Conclusions
An opportunistic interference alignment (OIA) scheme has been proposed that is based on the literature described in [11,12,13,14,15,16,17,18,19,20,21,22,23]. However, this work differentiates itself in a number of key areas to achieve significantly higher data rate performance. Firstly, the SVD that is performed on the PU channel matrix applies a ST-WF algorithm to free up some unused eigenmodes. Both the PU and SU can utilize the licensed spectrum by aligning the interference from the SUs to these unused eigenmodes. The ST-WF achieves higher capacity per antenna than SWF, and even though ST-WF has a higher channel outage probability than that of SWF, its transmission is similar to block transmission, which makes this scheme operate in conditions more suited to CR networks. Secondly, to further enhance the accuracy of detection of TOs, this work makes use of a double-threshold energy detection (ED) scheme where the FC receives two kinds of information from which to base its decision on. This increased range of values available to the FC leads to higher detection accuracy and thus an increased number of TOs. Thirdly, to increase the SUs’ sum rate performance, a new IA scheme equipped with STBC across eigen-beams were combined to yield a two-directional eigen-beamformer that performs better than the conventional one-directional beamformer with negligible increase in computational complexity. The incremental gains in performance achieved from the ST-WF and double-ED schemes coupled with a careful SU selection scheme that always ensures a for the SUs combine with the SU–IA–STBC scheme to yield higher data rates. Lastly, the new IA scheme was used to achieve full transmit diversity without losing sum rates by wedding optimal precoding with orthogonal DSTBC, where the DSTBC structure of the equivalent channels were preserved after zero-forcing the interfering users. Since the fundamental SU transmission is not changed by the transmit eigen-beamforming matrices, these IA schemes were shown to achieve higher diversity gain than other conventional methods.
Author Contributions
Conceptualization, Y.A., O.S. and Y.S.; Data curation, Y.A. and Y.S.; Formal analysis, Y.A., O.S. and Y.S.; Investigation, Y.A., O.S. and Y.S.; Methodology, Y.A., O.S. and Y.S.; Project administration, O.S.; Resources, O.S. and Y.S.; Software, Y.A. and O.S.; Supervision, Y.S.; Validation, Y.A. and O.S.; Writing—original draft, Y.A.; Writing—review and editing, O.S., Y.A. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, X.L.; Li, Y.X.; Gao, Y.; Tang, X.W. Q-Learning-Based Spectrum Access for Multimedia Transmission Over Cognitive Radio Networks. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 110–119. [Google Scholar] [CrossRef]
- Dong, L.; Wang, H.M.; Xiao, H. Secure Cognitive Radio Communication via Intelligent Reflecting Surface. IEEE Trans. Commun. 2021, 69, 4678–4690. [Google Scholar] [CrossRef]
- Mitola, J.; Maguire, G.Q. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef]
- Nobar, S.K.; Ahmed, M.H.; Morgan, Y.; Mahmoud, S.A. Resource Allocation in Cognitive Radio-Enabled UAV Communication. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 296–310. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, X. Deep Reinforcement Learning Optimal Transmission Algorithm for Cognitive Internet of Things With RF Energy Harvesting. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1216–1227. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered Wireless Communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Ghosh, S.; Acharya, T.; Maity, S.P. Outage Analysis in SWIPT Enabled Cooperative AF/DF Relay Assisted Two-Way Spectrum Sharing Communication. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1434–1443. [Google Scholar] [CrossRef]
- Jafar, S.A. Interference Alignment—A New Look at Signal Dimensions in a Communication Network; Now Publishers: Norwell, MA, USA, 2011. [Google Scholar]
- El-Ayach, O.; Peters, S.W.; Heath, R.W. The Practical Challenges of Interference Alignment. IEEE Wirel. Commun. 2013, 20, 35–42. [Google Scholar] [CrossRef]
- Jafar, S.A.; Shamai, S. Degrees of Freedom Region of the MIMO X Channel. IEEE Trans. Inf. Theory 2008, 54, 151–170. [Google Scholar] [CrossRef]
- Perlaza, S.M.; Debbah, M.; Lasaulce, S.; Chaufray, J.M. Opportunistic Interference Alignment in MIMO Interference Channels. In Proceedings of the IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications, Cannes, France, 15–18 September 2008; pp. 1–5. [Google Scholar]
- Perlaza, S.M.; Fawaz, N.; Lasaulce, S.; Debbah, M. From Spectrum Pooling to Space Pooling: Opportunistic Interference Alignment in MIMO Cognitive Networks. IEEE Trans. Signal Process. 2010, 58, 3728–3741. [Google Scholar] [CrossRef]
- Krikidis, I. A SVD-Based Location Coding for Cognitive Radio in MIMO Uplink Channels. IEEE Commun. Lett. 2010, 14, 912–914. [Google Scholar] [CrossRef]
- Tang, J.; Lambotharan, S.; Pomeroy, S. Interference Cancellation and Alignment Techniques for multiple-input and multiple-output Cognitive Relay Networks. IET Signal Process. 2013, 7, 188–200. [Google Scholar] [CrossRef]
- Alizadeh, A.; Bahrami, H.R.; Maleki, M.; Sastry, S. Spatial Sensing and Cognitive Radio Communication in the Presence of a K-User Interference Primary Network. IEEE J. Sel. Areas Commun. 2015, 33, 741–754. [Google Scholar] [CrossRef]
- Sboui, L.; Ghazzai, H.; Rezki, Z.; Alouini, M.S. Achievable Rate of a Cognitive MIMO Multiple Access Channel With Multi-Secondary Users. IEEE Commun. Lett. 2015, 19, 403–406. [Google Scholar] [CrossRef]
- Shen, C.; Fitz, M.P. Opportunistic Spatial Orthogonalization and Its Application in Fading Cognitive Radio Networks. IEEE J. Sel. Top. Signal Process. 2011, 5, 182–189. [Google Scholar] [CrossRef]
- Amir, M.; El-Keyi, A.; Nafie, M. Constrained Interference Alignment and the Spatial Degrees of Freedom of MIMO Cognitive Networks. IEEE Trans. Inf. Theory 2011, 57, 2994–3004. [Google Scholar] [CrossRef]
- Yang, H.J.; Shin, W.Y.; Jung, B.C.; Paulraj, A. Opportunistic Interference Alignment for MIMO Interfering Multiple-Access Channels. IEEE Trans. Wirel. Commun. 2013, 12, 2180–2192. [Google Scholar] [CrossRef]
- Baferani, M.H.; Abouei, J.; Yazdi, Z.Z. Interference Alignment in Overlay Cognitive Radio Femtocell Networks. IET Commun. 2016, 10, 1401–1410. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Berberidis, K. Blind Opportunistic Interference Alignment in MIMO Cognitive Radio Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 626–639. [Google Scholar] [CrossRef]
- Mosleh, S.; Abouei, J.; Aghabozorgi, M.S. Distributed Opportunistic Interference Alignment Using Threshold-Based Beamforming in MIMO Overlay Cognitive Radio. IEEE Trans. Veh. Technol. 2014, 63, 3783–3793. [Google Scholar] [CrossRef]
- Abdulkadir, Y.; Simpson, O.; Nwanekezie, N.; Sun, Y. Space-Time Opportunistic Interference Alignment in Cognitive Radio Networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Doha, Qatar, 3–6 April 2016. [Google Scholar]
- Shen, Z.; Heath, J.; Andrews, J.; Evans, B.L. Comparison of Space-time Water-filling and Spatial Water-filling for MIMO Fading Channels. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), Dallas, TX, USA, 29 November–3 December 2004. [Google Scholar]
- Shen, Z.; Heath, J.; Andrews, J.; Evans, B.L. Space-Time Water-Filling for Composite MIMO Fading Channels. EURASIP J. Wirel. Commun. Netw. 2006, 2006, 016281. [Google Scholar] [CrossRef][Green Version]
- Goldsmith, A.; Jafar, S.A.; Jindal, N.; Vishwanath, S. Capacity limits of MIMO channels. IEEE J. Sel. Areas Commun. 2003, 21, 684–702. [Google Scholar] [CrossRef]
- Guler, B.; Yener, A. Selective Interference Alignment for MIMO Cognitive Femtocell Networks. IEEE J. Sel. Areas Commun. 2015, 32, 439–450. [Google Scholar] [CrossRef]
- Simpson, O.; Abdulkadir, Y.; Sun, Y.; Chi, B. Relay-Based Cooperative Spectrum Sensing with Improved Energy Detection in Cognitive Radio. In Proceedings of the International Conference on Broadband and Wireless Computing, Communications and Applications, Krakow, Poland, 4–6 November 2015. [Google Scholar]
- Kalamkar, S.S.; Banerjee, A. Improved Double Threshold Energy Detection for Cooperative Spectrum Sensing in Cognitive Radio. Def. Sci. J. 2013, 63, 34–40. [Google Scholar] [CrossRef]
- Jöngren, G.; Skoglund, M.; Ottersten, B. Combining Beamforming and Orthogonal Space–Time Block Coding. IEEE Trans. Inf. Theory 2003, 48, 611–627. [Google Scholar] [CrossRef]
- Zhou, S.; Giannakis, G.B. Optimal Transmitter Eigen-Beamforming and Space—Time Block Coding Based on Channel Correlations. IEEE Trans. Inf. Theory 2003, 49, 1673–1689. [Google Scholar] [CrossRef]
- Bhatnagar, M.R.; Hjørungnes, A. Linear Precoding of STBC over Correlated Ricean MIMO Channels. IEEE Trans. Wirel. Commun. 2010, 9, 1832–1836. [Google Scholar] [CrossRef]
- Abdel-Samad, A.; Davidson, T.N.; Gershman, A.B. Robust Transmit Eigen Beamforming Based on Imperfect Channel State Information. IEEE Trans. Signal Process. 2010, 54, 1596–1608. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, W.; Xia, X.G. On Designs of Full Diversity Space-Time Block Codes for Two-User MIMO Interference Channels. IEEE Trans. Wirel. Commun. 2012, 11, 4184–4191. [Google Scholar]
- Li, L.; Jafarkhani, H. Maximum-Rate Transmission With Improved Diversity Gain for Interference Networks. IEEE Trans. Inf. Theory 2013, 59, 5313–5330. [Google Scholar]
- Naguib, A.; Seshadri, N.; Calderbank, A. Applications of Space-time Block Codes and Interference Suppression for High Capacity and High Data Rate Wireless Systems. In Proceedings of the Asilomar Conference, Pacific Grove, CA, USA, 1–4 November 1998. [Google Scholar]
- Alamouti, A. Simple Transmitter Diversity scheme for Wireless Communications. IEEE J. Sel. Areas Commun. 1998, 16, 1451–1458. [Google Scholar] [CrossRef]
- Cai, X.; Giannakis, G.B. Differential Space—Time Modulation With Eigen-Beamforming for Correlated MIMO Fading Channels. IEEE Trans. Signal Process. 2006, 54, 1279–1288. [Google Scholar]
- Bhatnagar, M.R.; Hjørungnes, A.; Song, L. Precoded Differential Orthogonal Space-Time Modulation Over Correlated Ricean MIMO Channels. IEEE J. Sel. Top. Signal Process. 2011, 2, 124–134. [Google Scholar] [CrossRef]
- Li, F.; Jafarkhani, H. Space-time Processing for X Channel using Precoders. IEEE Trans. Signal Process. 2011, 60, 1849–1861. [Google Scholar] [CrossRef]
- Alotaibi, F.T.; Chambers, J.A. Outage Probability of Cooperative Cognitive Networks Based on Distributed Orthogonal Space–Time Block Codes. IEEE Trans. Veh. Technol. 2011, 61, 3759–3765. [Google Scholar] [CrossRef]
- Telatar, I.E. Capacity of Multi-antenna Gaussian Channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Guo, X.; Xia, X.G. On Full Diversity Space—Time Block Codes With Partial Interference Cancellation Group Decoding. IEEE Trans. Inf. Theory 2009, 55, 4366–4385. [Google Scholar] [CrossRef]
- StÄuber, G.L. Principles of Mobile Communication, 2nd ed.; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Simpson, O. Optimal Cooperative Spectrum Sensing for Cognitive Radio. Ph.D. Thesis, University of Hertfordshire, Hatfield, UK, 2016. [Google Scholar]
- Atapattu, S.; Tellambura, C.; Jiang, H. Energy Detection Based Cooperative Spectrum Sensing in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2011, 10, 1232–1241. [Google Scholar] [CrossRef]
- Palomar, D.P.; Fonollosa, J.R. Practical Algorithms for a Family of Water-filling Solutions. IEEE Trans. Signal Process. 2005, 53, 686–695. [Google Scholar] [CrossRef]
- Abdulkadir, Y.; Simpson, O.; Nwanekezie, N.; Sun, Y. A Differential Space-Time Coding Scheme for Cooperative Spectrum Sensing in Cognitive Radio Networks. In Proceedings of the IEEE 26th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Hong Kong, China, 30 August–2 September 2015; pp. 1386–1391. [Google Scholar]
- Yetis, C.M.; Gou, T.; Jafar, S.A.; Kayran, A.H. On Feasibility of Interference Alignment in MIMO Interference Networks. IEEE Trans. Signal Process. 2010, 58, 4771–4782. [Google Scholar] [CrossRef]
- Gomadan, K.; Cadambe, V.R.; Jafar, S.A. A Distributed Numerical Approach to Interference Alignment and Applications to Wireless Interference Networks. IEEE Trans. Inf. Theory 2011, 57, 3309–3322. [Google Scholar] [CrossRef]
- Guo, C.; Peng, T.; Xu, S.; Wang, H.; Wang, W. Cooperative Spectrum Sensing with Cluster-Based Architecture in Cognitive Radio Networks. In Proceedings of the IEEE 69th Vehicular Technology Conference (VTC), Barcelona, Spain, 26–29 April 2009; pp. 1–5. [Google Scholar]
- Gomadam, K.S.; Cadambe, V.R.; Jafar, S.A. Approaching the Capacity of Wireless Networks through Distributed Interference Alignment. In Proceedings of the IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6. [Google Scholar]
- Tarokh, V.; Jafarkhani, H. A Differential Detection Scheme for Transmit Diversity. IEEE J. Sel. Areas Commun. 2000, 18, 1161–1174. [Google Scholar] [CrossRef]
- Ganesan, A.; Rajan, B.S. Interference Alignment With Diversity for the 2 × 2 X-Network With Four Antennas. IEEE Trans. Inf. Theory 2014, 60, 3576–3592. [Google Scholar] [CrossRef]
- Jafarkhani, H.; Tarokh, V. Multiple Transmit Antenna Differential detection from Generalized Orthogonal Designs. IEEE Trans. Inf. Theory 2001, 47, 2626–2631. [Google Scholar] [CrossRef]
- Ganesan, G.; Stoica, P. Differential Modulation using Space–time Block Codes. IEEE Signal Process. Lett. 2002, 9, 57–60. [Google Scholar] [CrossRef]
- Abdulkadir, Y.; Simpson, O.; Sun, Y. Interference Alignment for Cognitive Radio Communications and Networks: A Survey. J. Sens. Actuator Netw. 2019, 8, 50. [Google Scholar] [CrossRef]
- Slaney, A.; Sun, Y. Space-time coding for wireless communications. IEE Proc. Commun. 2006, 153, 509–518. [Google Scholar] [CrossRef][Green Version]
- Yang, J.; Sun, Y.; Senior, J.M.; Pem, N. Channel estimation for wireless communications using space-time block coding techniques. In Proceedings of the IEEE International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003. [Google Scholar]
- Delestre, F.; Masoud, E.; Sun, Y.; Slaney, A. Detection scheme for space-time block coded wireless communications without channel state information. In Proceedings of the IEEE International Conference on Communication Systems, Guangzhou, China, 19–21 November 2008. [Google Scholar]
- Bani, K.; Kulkarni, V. Hybrid Spectrum Sensing Using MD and ED for Cognitive Radio Networks. J. Sens. Actuator Netw. 2022, 11, 36. [Google Scholar] [CrossRef]
- Abdulkadir, Y. Optimizing Cooperative Spectrum Sensing in Cognitive Radio Networks Using Interference Alignment and Space-Time Coding. Ph.D. Thesis, University of Hertfordshire, Hatfield, UK, 2017. [Google Scholar]
- Nnamdi, N.; Simpson, O.; Wojaiye, G.O.; Sun, Y. Co-Efficient Vector Based Differential Distributed Quasi-Orthogonal Space Time Frequency Coding. Sensors 2023, 23, 7540. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).