Beta Maximum Power Extraction Operation-Based Model Predictive Current Control for Linear Induction Motors
Abstract
1. Introduction
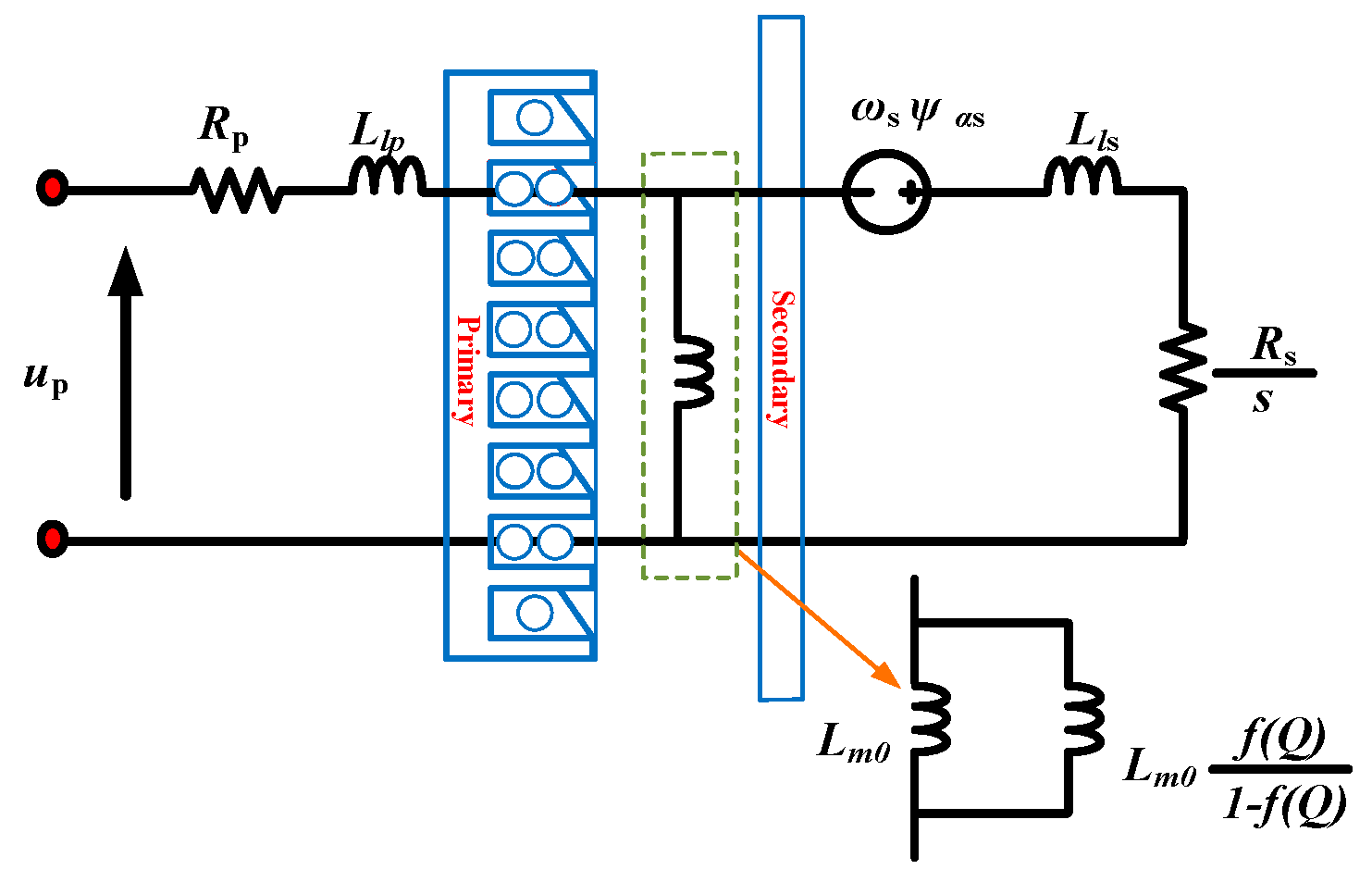
2. Modeling of the LIM
3. Description of the Overall System
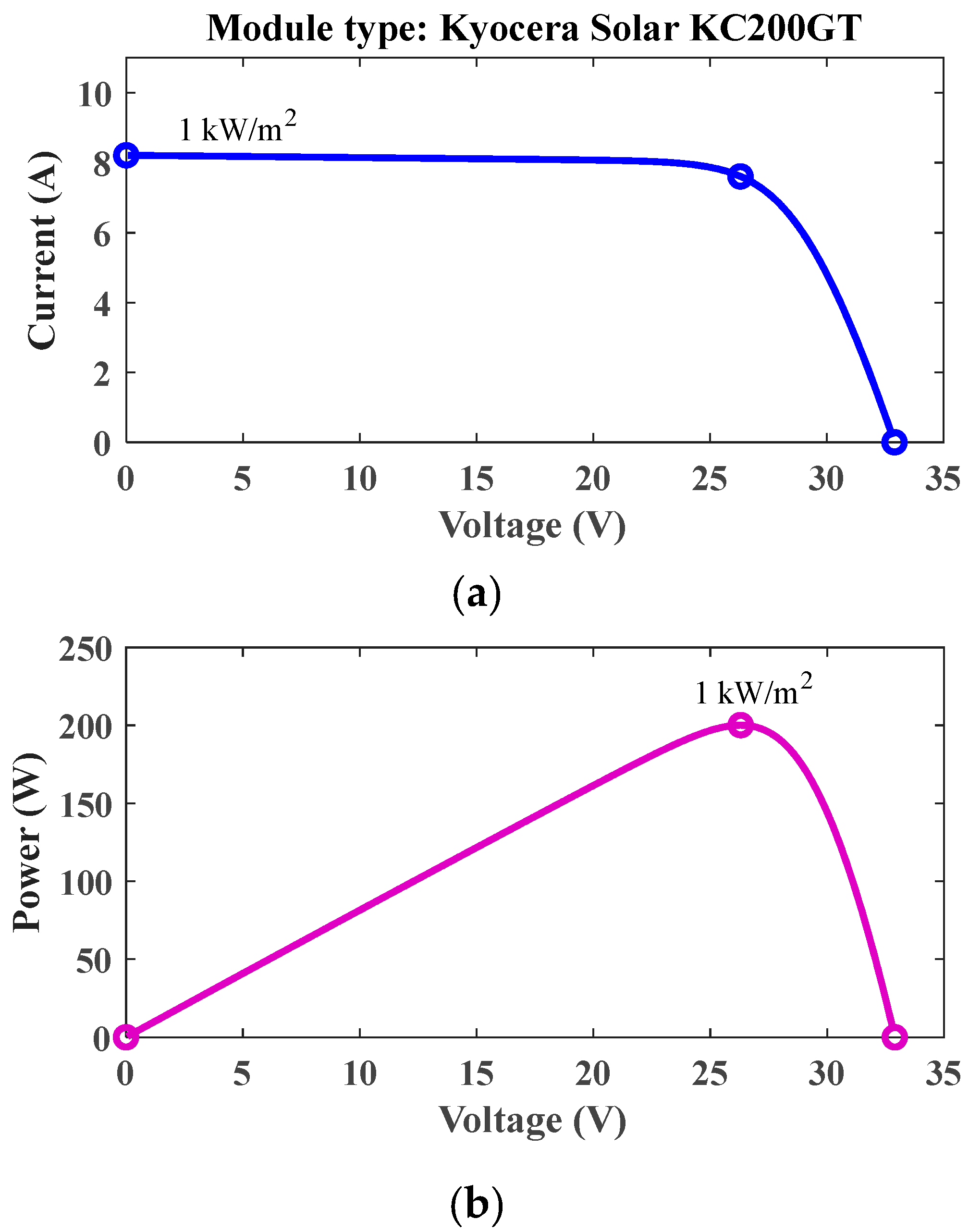
3.1. PV Panel
3.2. Boost Converter
3.3. Beta-Based MPE Technique
3.4. Finite Set-Model Predictive-Based Current Control Technique
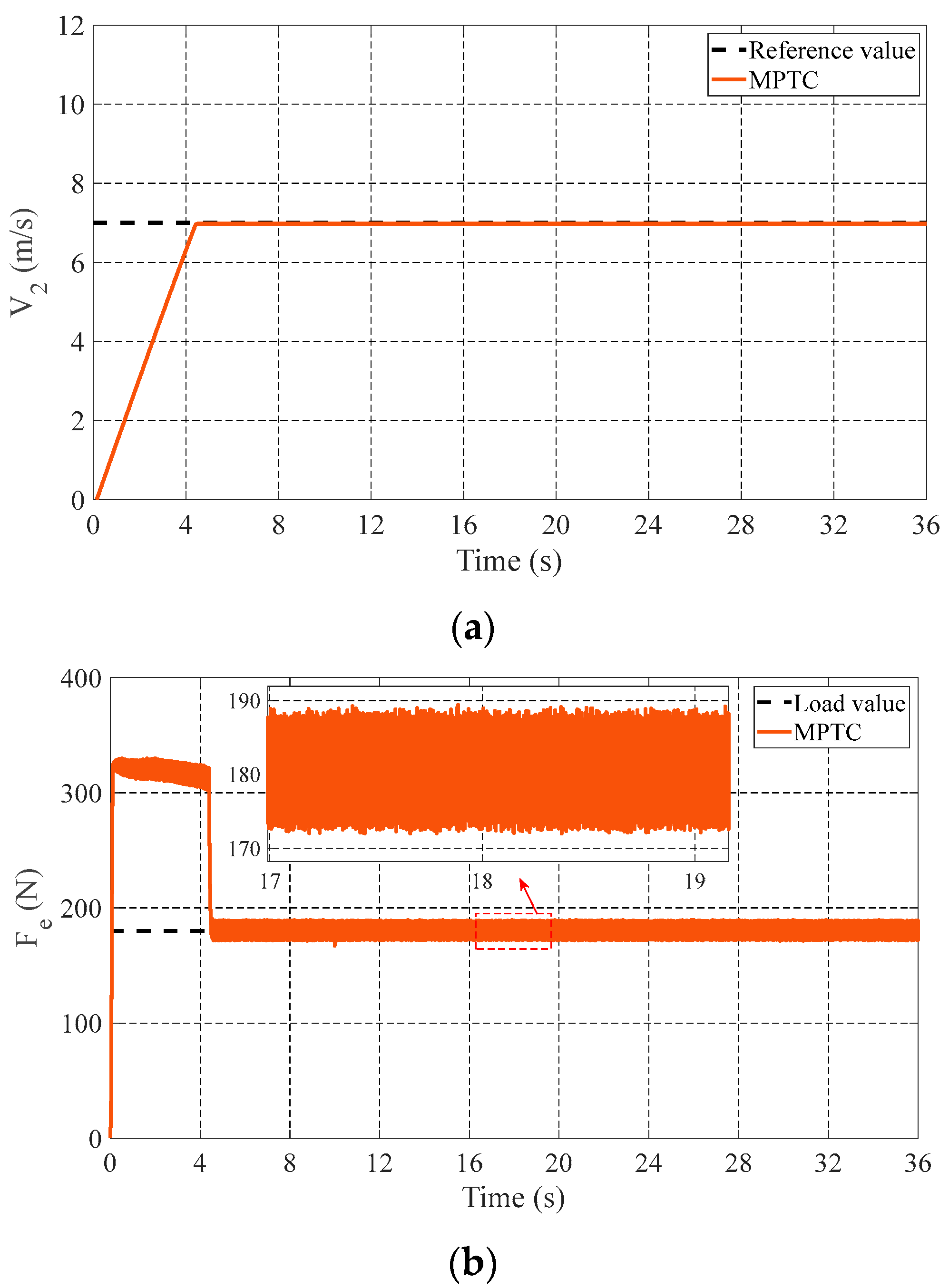
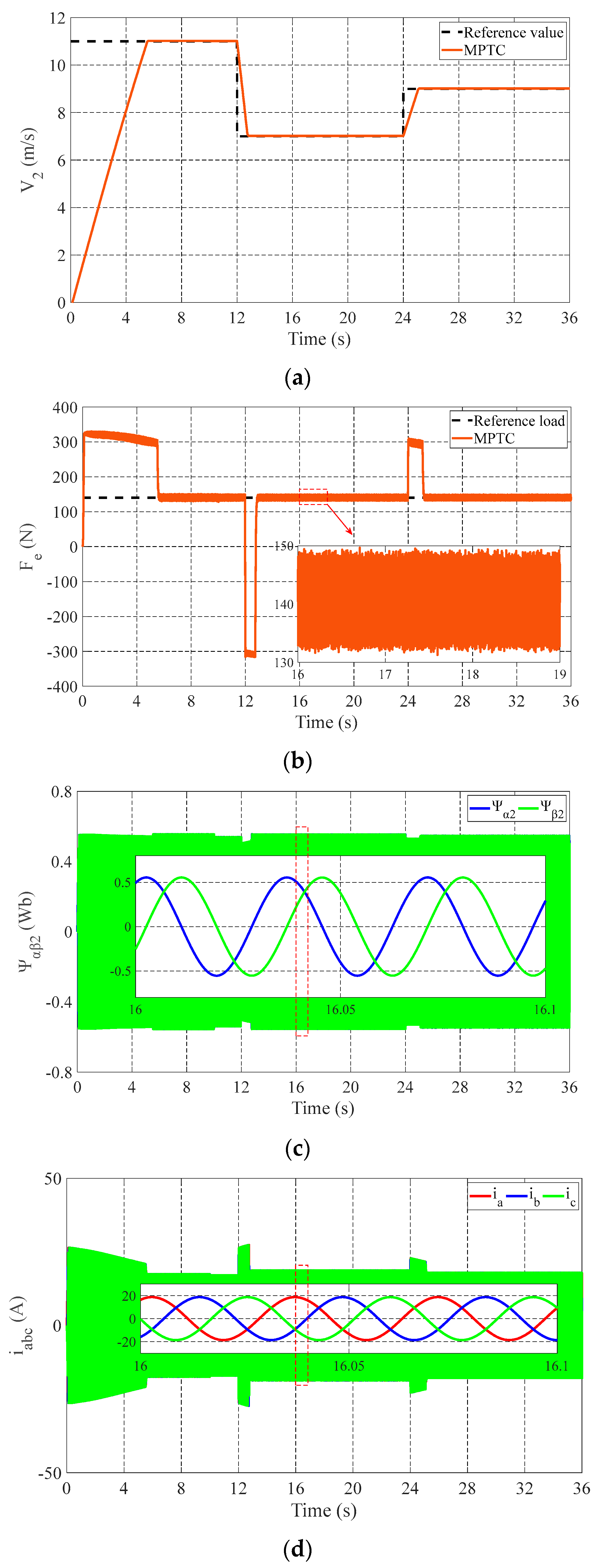
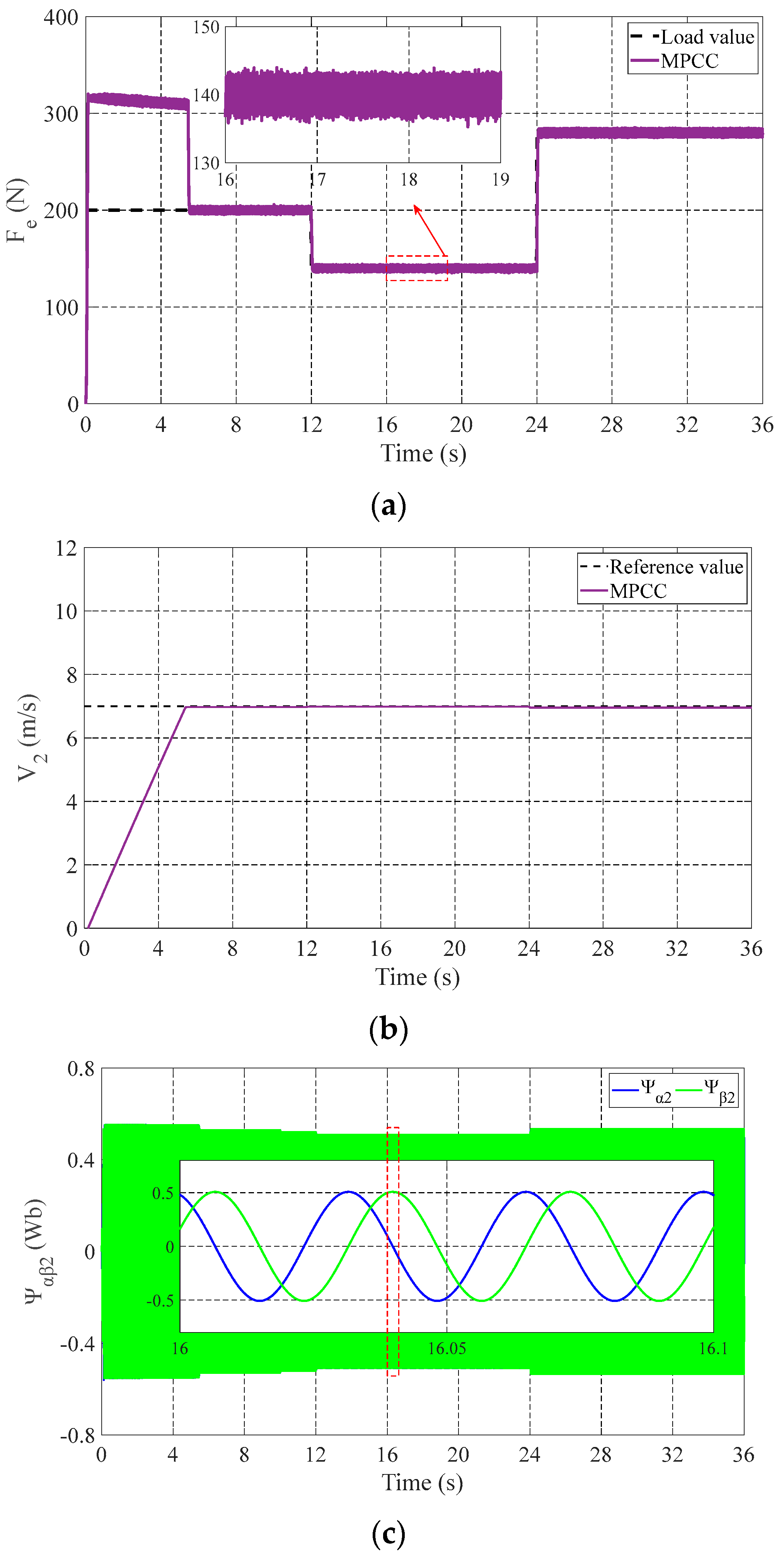
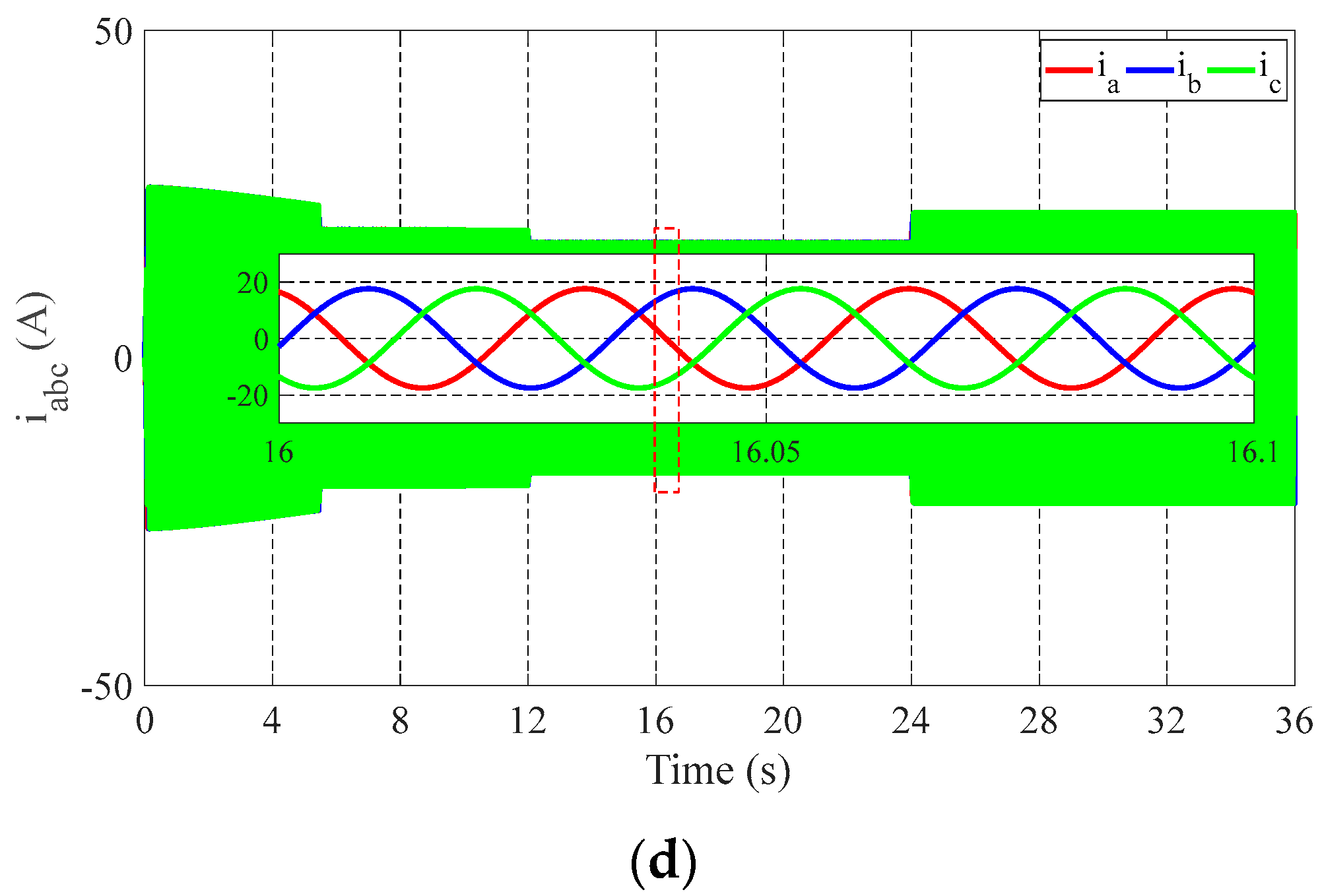
4. Simulation Results and Discussion
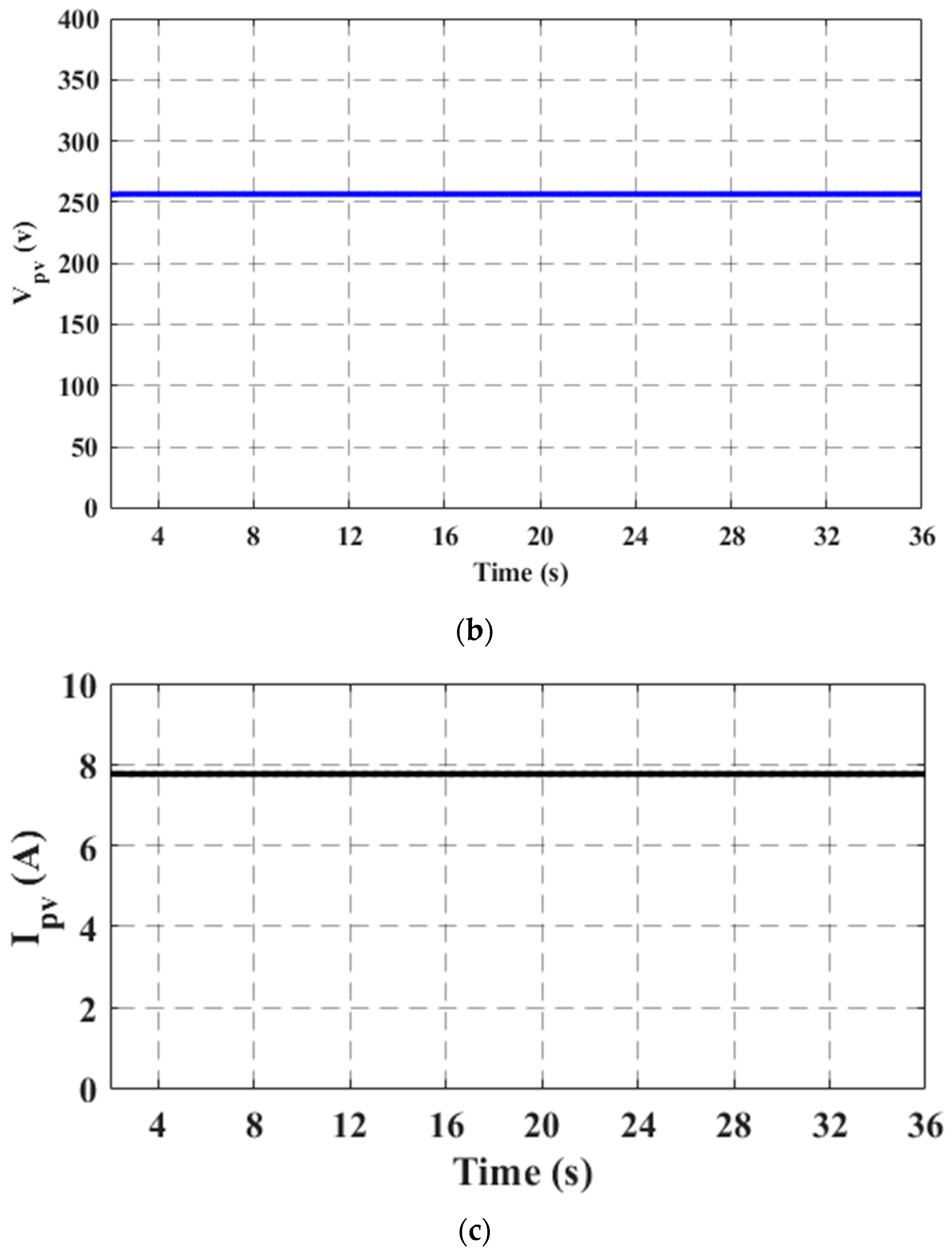
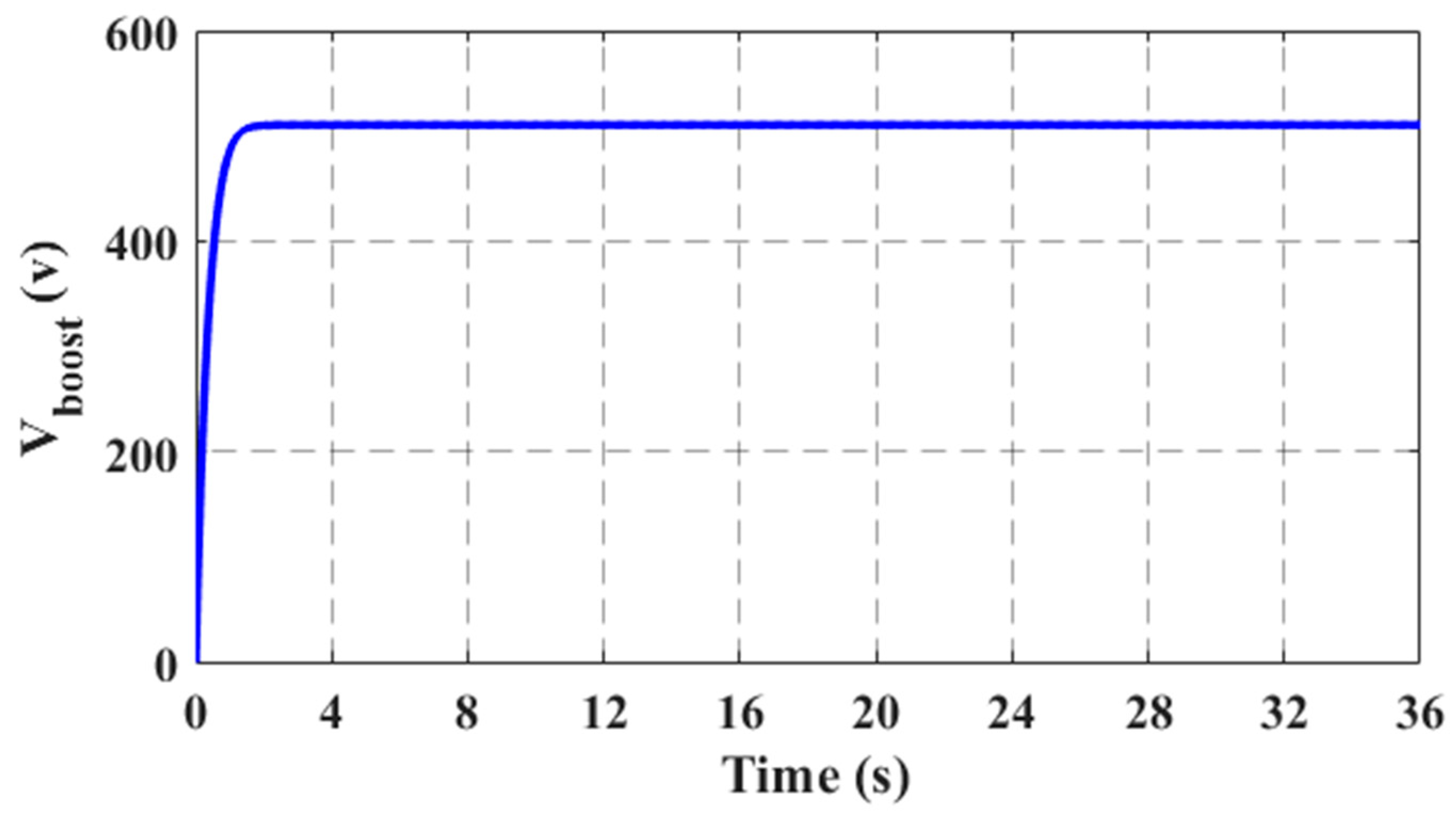
4.1. Case 1: Starting Process
4.2. Case 2: Speed Change Process
4.3. Case 3: Load Change Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, C.E.; Phan, B.C. Optimal Hybrid Energy Solution for Island Micro-Grid. In Proceedings of the 2016 IEEE International Conferences on Big Data and Cloud Computing (BDCloud), Social Computing and Networking (SocialCom), Sustainable Computing and Communications (SustainCom) (BDCloud-SocialCom-SustainCom), Atlanta, GA, USA, 8–10 October 2016; pp. 461–468. [Google Scholar] [CrossRef]
- Sharma, S.; Varshney, L.; Elavarasan, R.M.; Vardhan, A.S.S.; Vardhan, A.S.S.; Saket, R.K.; Subramaniam, U.; Hossain, E. Performance Enhancement of PV System Configurations Under Partial Shading Conditions Using MS Method. IEEE Access 2021, 9, 56630–56644. [Google Scholar] [CrossRef]
- De, S.; Swathika, O.V.G.; Tewari, N.; Venkatesan, A.K.; Subramaniam, U.; Bhaskar, M.S.; Padmanaban, S.; Leonowicz, Z.; Mitolo, M. Implementation of Designed PV Integrated Controlled Converter System. IEEE Access 2020, 8, 100905–100915. [Google Scholar] [CrossRef]
- Ramli, M.A.; Twaha, S.; Ishaque, K.; Al-Turki, Y.A. A review on maximum power point tracking for photovoltaic systems with and without shading conditions. Renew. Sustain. Energy Rev. 2017, 67, 144–159. [Google Scholar] [CrossRef]
- Priyadarshi, N.M.; Bhaskar, S.; Modak, P.; Kumar, N. Hybrid Firefly-PSO MPPT Based Single Stage Induction Motor for PV Water Pumping With Deep Fuzzy-Neural Network Learning. In Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Sarkar, P.R.; Minai, A.F.; Bhaskar, M.S.; Pachauri, R.K.; Sashikant. Examination of MPPT Algorithm on Three Step DC-DC Converter. In Proceedings of the 2022 IEEE 9th Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON), Prayagraj, India, 2–4 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Mohapatra, A.; Nayak, B.; Das, P.; Mohanty, K.B. A review on MPPT techniques of PV system under partial shading condition. Renew. Sustain. Energy Rev. 2017, 80, 854–867. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. An improved perturb and observe (P&O) maximum power point tracking (MPPT) algorithm for higher efficiency. Appl. Energy 2015, 150, 97–108. [Google Scholar] [CrossRef]
- Xu, W.; Hamad, S.A.; Bukhari, S.A.; Elmorshedy, M.F.; Ali, M.M.; Diab, A. Thrust Ripple Suppression for Linear Induction Machines Based on Improved Finite Control Set-Model Predictive Voltage Control. IEEE Trans. Ind. Appl. 2022, 58, 7263–7274. [Google Scholar] [CrossRef]
- Bukhari, S.A.; Xu, W.; Elmorshedy, M.F.; Junejo, A.K.; Hamad, S.A. Upgraded Limited-Step Predictive Current Control Strategy for Linear Induction Machine based on Linear Metro. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zou, J.; Xu, W.; Zhu, J.; Liu, Y. Low-Complexity Finite Control Set Model Predictive Control With Current Limit for Linear Induction Machines. IEEE Trans. Ind. Electron. 2018, 65, 9243–9254. [Google Scholar] [CrossRef]
- Sun, X.; Shi, L.; Zhang, Z.; Zhu, H. Thrust Control of a Double-Sided Linear Induction Motor With Segmented Power Supply. IEEE Trans. Ind. Electron. 2018, 66, 4891–4900. [Google Scholar] [CrossRef]
- Xu, W.; Sun, G.; Wen, G.; Wu, Z.; Chu, P.K. Equivalent Circuit Derivation and Performance Analysis of a Single-Sided Linear Induction Motor Based on the Winding Function Theory. IEEE Trans. Veh. Technol. 2012, 61, 1515–1525. [Google Scholar] [CrossRef]
- Ali, M.M.; Xu, W.; Elmorshedy, M.F.; Hamad, S.A.; Junejo, A.K.; Ismail, M. Improved Drive Performance of Linear Induction Machine Based on Direct Thrust Control and Sliding Mode Control with Extended State Observer Applied for Linear Metro. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Q.G.; Yaohua, L.; Liming, S. A novel switching scheme for direct thrust control of LIM with reduction of thrust ripple. In Proceedings of the 2010 International Conference Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 1491–1494. [Google Scholar]
- Zhang, Y.; Wang, Q.; Liu, W. Direct Torque Control Strategy of Induction Motors Based on Predictive Control and Synthetic Vector Duty Ratio Control. In Proceedings of the 2010 International Conference on Artificial Intelligence and Computational Intelligence, Sanya, China, 23–24 October 2010; pp. 96–101. [Google Scholar] [CrossRef]
- Hamad, S.A.; Ghalib, M.A. Fuzzy MPPT operation-based model predictive flux control for linear induction motors. Int. J. Hydrogen Energy 2024, 50, 1035–1044. [Google Scholar] [CrossRef]
- Hamad, S.A.; Xu, W.; Diab, A.; Ali, M.M.; Bukhari, S.A. Model Predictive Voltage Control for Linear Induction Machine Without Weighting Factor. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Ismail, M.M.; Xu, W.; Tang, Y.; Liu, Y.; Hussien, M.G.; Rodriguez, J.; Hamad, S.A. Performance Enhancement of Salient Permanent-Magnet Motors over Wide Speed Range Based on Finite-Set Model Predictive Control. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021; pp. 75–80. [Google Scholar] [CrossRef]
- Xie, W.; Wang, X.; Wang, F.; Xu, W.; Kennel, R.M.; Gerling, D.; Lorenz, R.D. Finite-Control-Set Model Predictive Torque Control With a Deadbeat Solution for PMSM Drives. IEEE Trans. Ind. Electron. 2015, 62, 5402–5410. [Google Scholar] [CrossRef]
- Xu, W.; Zou, J.; Liu, Y.; Zhu, J. Weighting Factorless Model Predictive Thrust Control for Linear Induction Machine. IEEE Trans. Power Electron. 2019, 34, 9916–9928. [Google Scholar] [CrossRef]
- Hamad, S.A.; Xu, W.; Elmorshedy, M.F.; Ali, M.M. Improved Model Predictive Flux Control of Linear Induction Machine Applied for Linear Metro. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020. [Google Scholar] [CrossRef]
- Hamad, S.A.; Xu, W.; Liu, Y.; Ali, M.M.; Ismail, M.M.; Rodriguez, J. Improved MPCC with Duty Cycle Modulation Strategy for Linear Induction Machines based on Linear Metro. In Proceedings of the 2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 20–22 November 2021. [Google Scholar]
- Park, Y.-S. Investigation on Connected System of Axial-Flux Permanent Magnet Synchronous Generator and Linear Induction Motor. IEEE Can. J. Electr. Comput. Eng. 2021, 45, 18–23. [Google Scholar] [CrossRef]
- Hai, T.; Zhou, J.; Muranaka, K. An efficient fuzzy-logic based MPPT controller for grid-connected PV systems by farmland fertility optimization algorithm. Optik 2022, 267, 1–9. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics: Circuits, Devices & Applications, 4th ed.; Pearson: London, UK, 2004. [Google Scholar]
- Li, X.; Wen, H.; Jiang, L.; Lim, E.G.; Du, Y.; Zhao, C. Photovoltaic Modified β-Parameter-based MPPT Method with Fast Tracking. J. Power Electron. 2016, 16, 9–17. [Google Scholar] [CrossRef]
- Jansen, P.; Lorenz, R. A physically insightful approach to the design and accuracy assessment of flux observers for field oriented induction machine drives. IEEE Trans. Ind. Appl. 1994, 30, 101–110. [Google Scholar] [CrossRef]










| Parameter | Unit | Value |
|---|---|---|
| Motor speed | m/s | 11 |
| Thrust force | N | 280 |
| Input filter inductor | 440 | |
| Input filter capacitor | 21 | |
| Motor power | Kw | 3 |
| Motor current | A | 22 |
| Input voltage | V | 500 |
| Primary resistance | Ω | 1 |
| Primary length | m | 1.3087 |
| Primary pole pitch | 0.1485 | |
| Mutual inductance | 31.725 |
| Quantity | FS-MPTC | FS-MPCC |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghalib, M.A.; Hamad, S.A.; Elmorshedy, M.F.; Almakhles, D.; Ali, H.H. Beta Maximum Power Extraction Operation-Based Model Predictive Current Control for Linear Induction Motors. J. Sens. Actuator Netw. 2024, 13, 37. https://doi.org/10.3390/jsan13040037
Ghalib MA, Hamad SA, Elmorshedy MF, Almakhles D, Ali HH. Beta Maximum Power Extraction Operation-Based Model Predictive Current Control for Linear Induction Motors. Journal of Sensor and Actuator Networks. 2024; 13(4):37. https://doi.org/10.3390/jsan13040037
Chicago/Turabian StyleGhalib, Mohamed. A., Samir A. Hamad, Mahmoud F. Elmorshedy, Dhafer Almakhles, and Hazem Hassan Ali. 2024. "Beta Maximum Power Extraction Operation-Based Model Predictive Current Control for Linear Induction Motors" Journal of Sensor and Actuator Networks 13, no. 4: 37. https://doi.org/10.3390/jsan13040037
APA StyleGhalib, M. A., Hamad, S. A., Elmorshedy, M. F., Almakhles, D., & Ali, H. H. (2024). Beta Maximum Power Extraction Operation-Based Model Predictive Current Control for Linear Induction Motors. Journal of Sensor and Actuator Networks, 13(4), 37. https://doi.org/10.3390/jsan13040037







