Data-Driven Position and Stiffness Control of Antagonistic Variable Stiffness Actuator Using Nonlinear Hammerstein Models
Abstract
1. Introduction
- Modeled subsystems can be used for a local controller design (cascaded design [29]).
- Unmeasurable variables (e.g., stiffness) can be theoretically modeled; hence, the model-based control design is possible for them.
- The control performance depends on the parameter estimation accuracy; that is, the parameters should be measured or estimated accurately enough to have less model uncertainty.
- Many undesired effects are not considered in the theoretical model, such as the dead zone, backlash, and friction.
- Some of the plant subsystems may have unknown behaviors or are hard to model theoretically.
1.1. Related Works
1.2. Contributions
- The stiffness of the output link is created by applying a voltage difference between the input voltages of the motors.
- Nonlinear Hammerstein models are employed to model the position dynamics, effectively capturing nonlinearities inherent in the AVSA setup, including gearbox friction.
- PID gains are optimized using a genetic algorithm for predetermined stiffness and position values.
- Utilizing a single PID controller with interpolated optimal gains enables seamless control over both position and stiffness, facilitating smooth transitions in stiffness and position.
2. Hardware Overview
2.1. Setup Specifications
2.2. Nonlinear Spring Mechanism
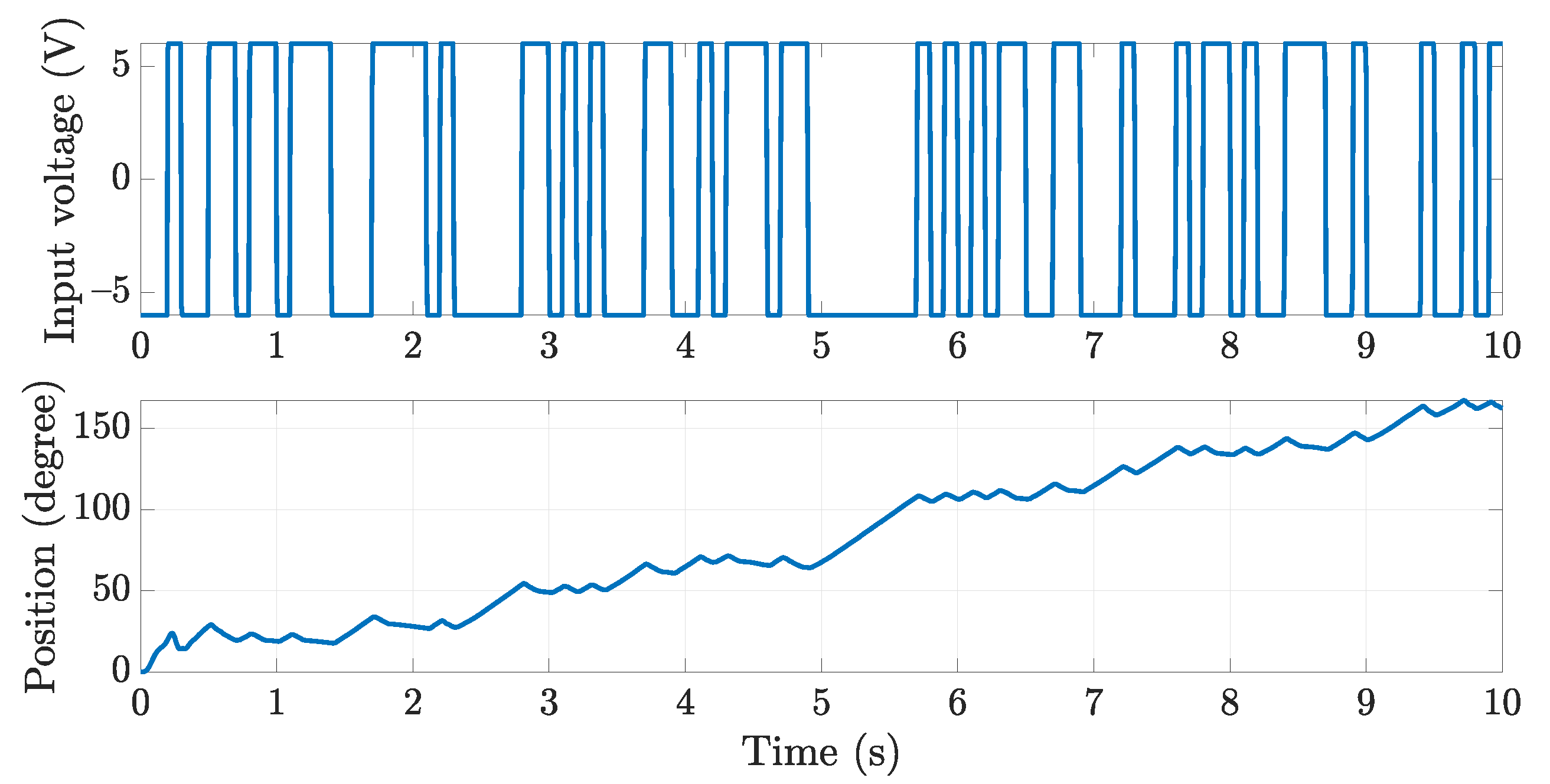
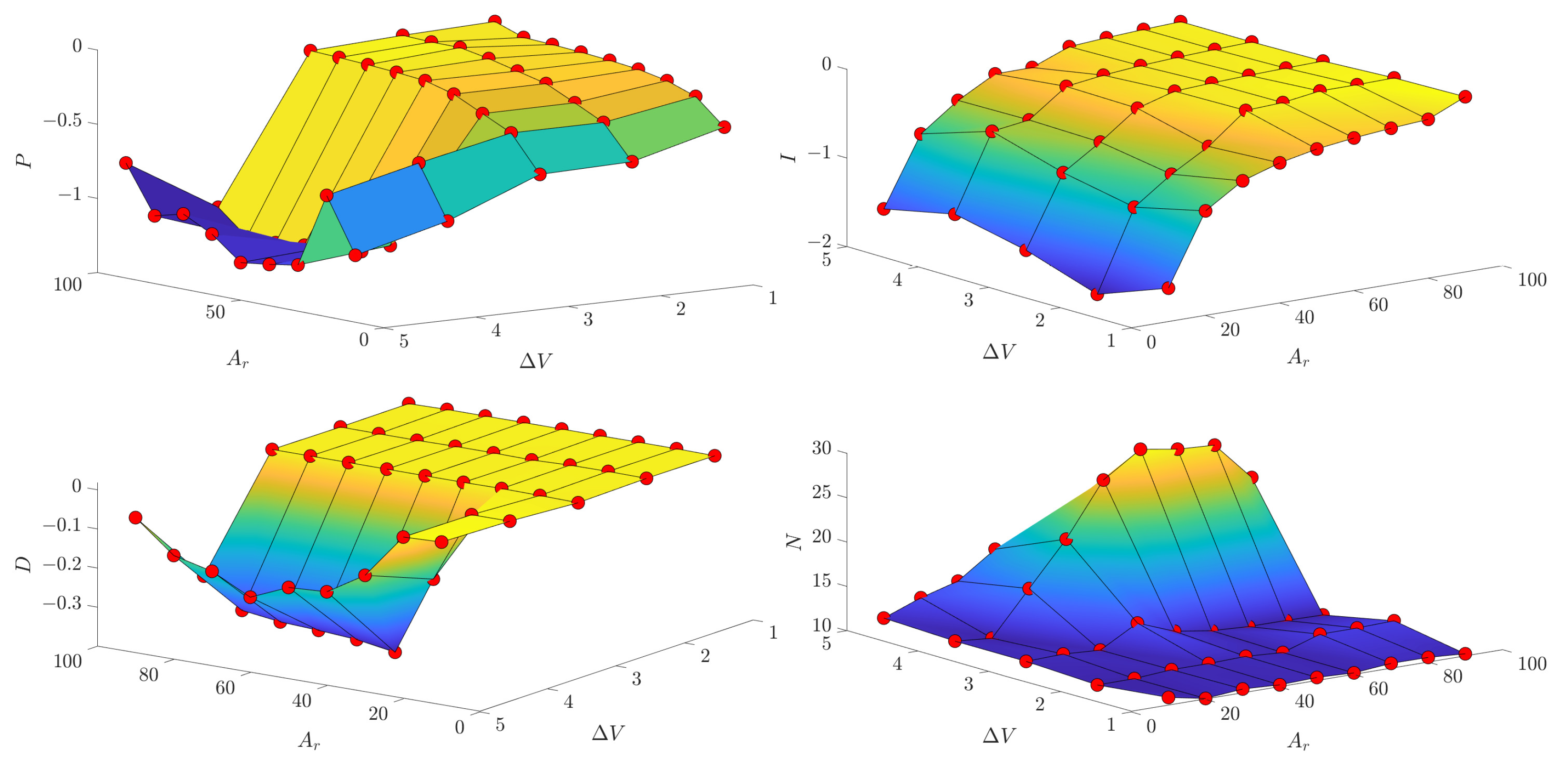
3. Identification of AVSA
3.1. Stiffness Estimation
3.2. Linear Models
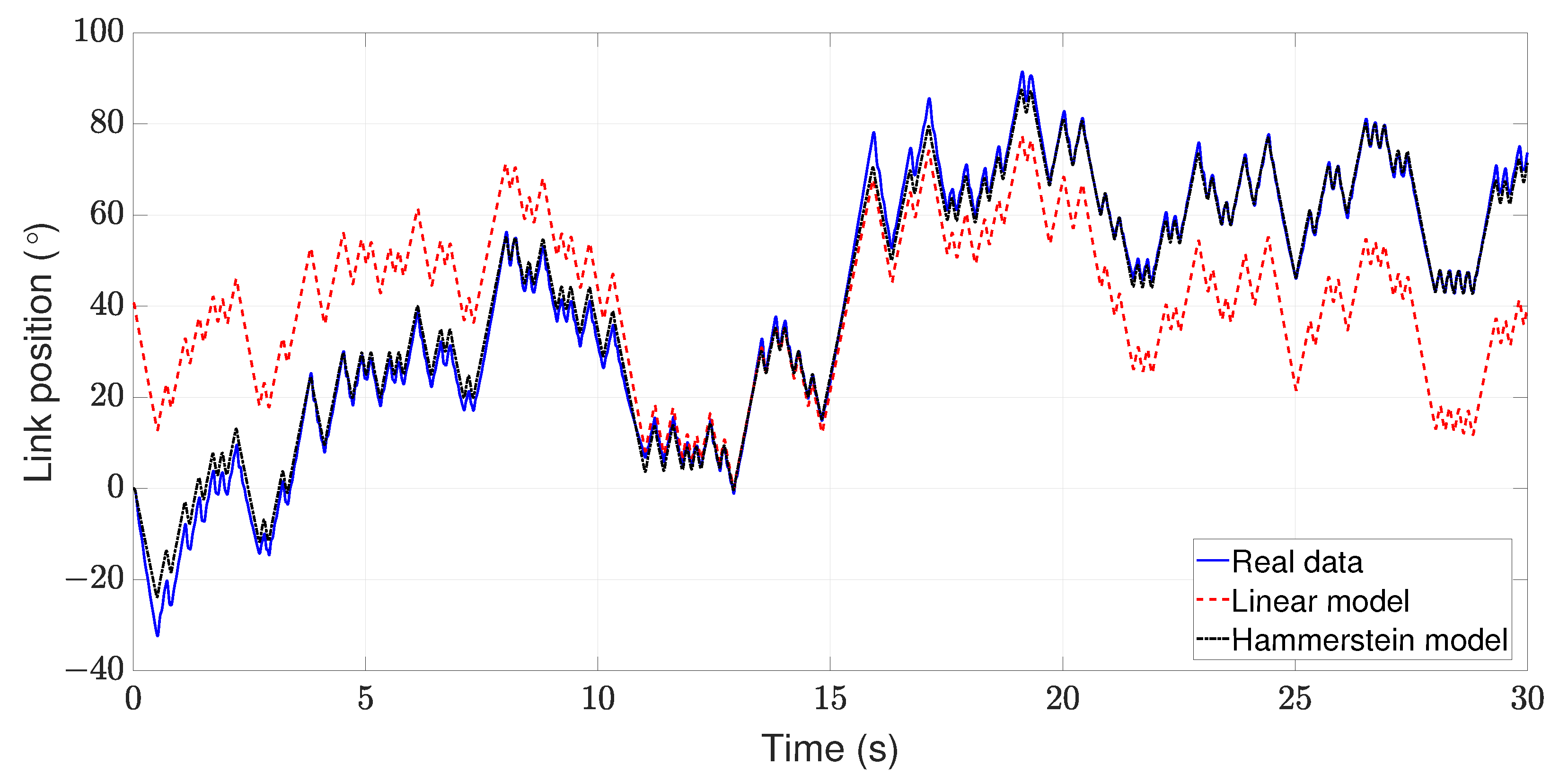
3.3. Nonlinear Hammerstein Models
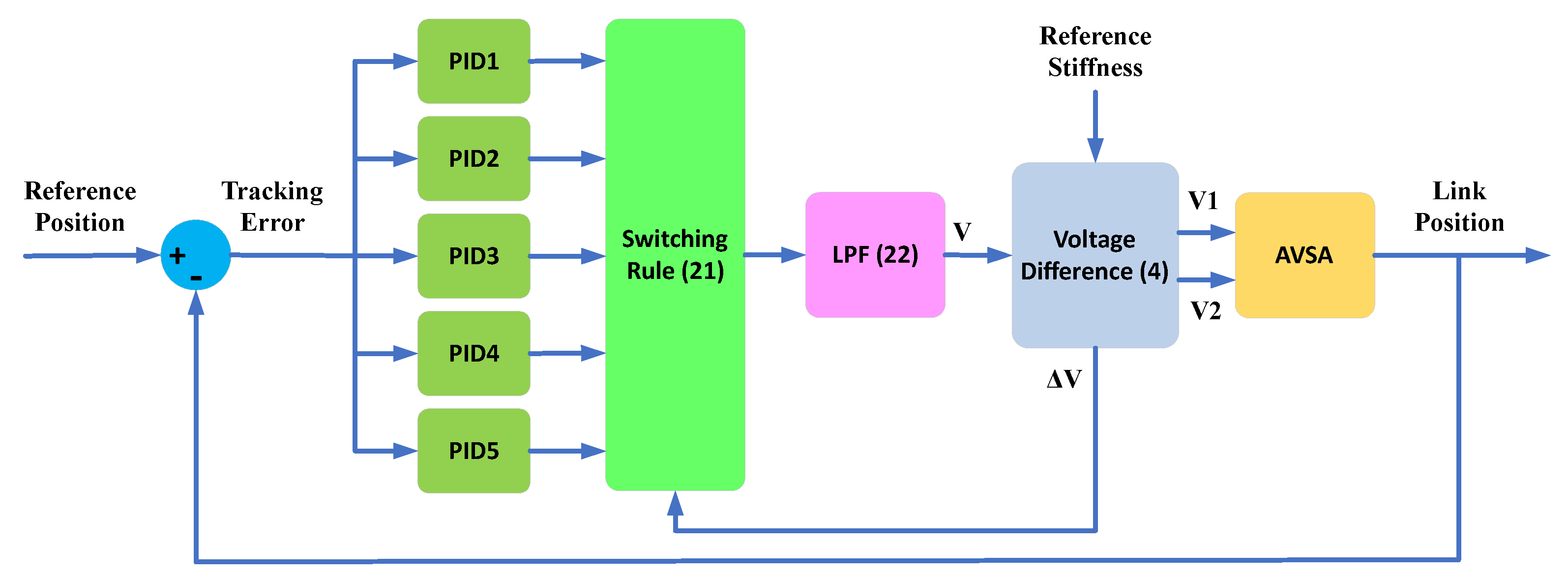
4. Control Design
4.1. Switching PID Control for Linear Models
Soft Switching among Controllers
4.2. PID Control for Hammerstein Models
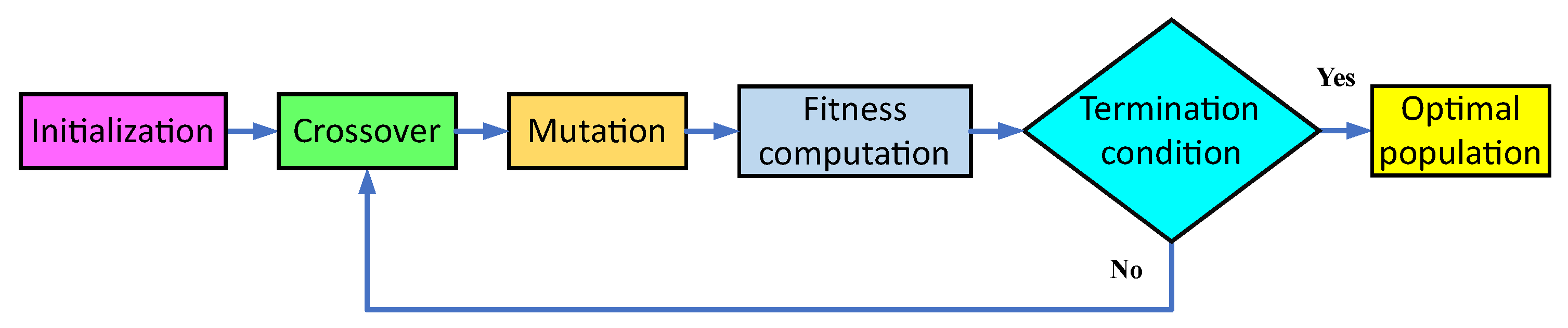
Optimization with GA
5. Experimental Results
5.1. Square Position and Stiffness Tracking
5.2. Sinusoidal Position and Stiffness Tracking
5.3. Sawtooth Position and Sinusoidal Stiffness Tracking
5.4. Square Position and Sawtooth Stiffness Tracking
5.5. Disturbance Rejection Property
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APRBS | Amplitude-modulated Pseudo Random Binary Sequence |
| AVSA | antagonistic variable stiffness actuator |
| CW | clockwise |
| CCW | counterclockwise |
| EMAVSA | electromechanical antagonistic variable stiffness actuators |
| FAVSA | fluidic antagonistic variable stiffness actuators |
| GA | genetic algorithm |
| HIL | hardware in the loop |
| LPF | low-pass filter |
| MIMO | multi input multi output |
| MPC | model predictive control |
| PEA | parallel elastic actuator |
| PID | proportional integral derivative |
| PRBS | pseudo random binary sequence |
| PSO | particle swarm optimization |
| RMSE | root mean square error |
| SA | simulated annealing |
| SEA | serial elastic actuator |
| SISO | single input, single output |
| SMA | shape memory alloy |
| SMC | sliding mode control |
| SVSA | serial variable stiffness actuator |
| VD | voltage difference |
| VSA | variable stiffness actuator |
References
- Nishimura, S.; Chaichaowarat, R.; Krebs, H.I. Human-Robot Interaction: Controller Design and Stability. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 1096–1101. [Google Scholar]
- Javadi, A.; Chaichaowarat, R. Position and stiffness control of an antagonistic variable stiffness actuator with input delay using super-twisting sliding mode control. Nonlinear Dyn. 2023, 111, 5359–5381. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Chaichaowarat, R. Sensorless Estimation of Human Joint Torque for Robust Tracking Control of Lower-Limb Exoskeleton Assistive Gait Rehabilitation. J. Sens. Actuator Netw. 2023, 12, 53. [Google Scholar] [CrossRef]
- Tantagunninat, T.; Wongkaewcharoen, N.; Pornpipatsakul, K.; Chuengpichanwanich, R.; Chaichaowarat, R. Modulation of Joint Stiffness for Controlling the Cartesian Stiffness of a 2-DOF Planar Robotic Arm for Rehabilitation. In Proceedings of the 2023 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Seattle, WA, USA, 28–30 June 2023; pp. 598–603. [Google Scholar]
- Grioli, G.; Wolf, S.; Garabini, M.; Catalano, M.; Burdet, E.; Caldwell, D.; Carloni, R.; Friedl, W.; Grebenstein, M.; Laffranchi, M.; et al. Variable stiffness actuators: The user’s point of view. Int. J. Robot. Res. 2015, 34, 727–743. [Google Scholar] [CrossRef]
- Zhao, W.; Liao, J.; Qian, W.; Yu, H.; Guo, Z. A novel design of series elastic actuator using tensile springs array. Mech. Mach. Theory 2024, 192, 105541. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Mutlu, R.; Roberts, J.; Kuo, C.H.; Ugurlu, B. Design and Control of a Novel Variable Stiffness Series Elastic Actuator. IEEE/ASME Trans. Mechatron. 2023, 28, 1534–1545. [Google Scholar] [CrossRef]
- Penzlin, B.; Enes Fincan, M.; Li, Y.; Ji, L.; Leonhardt, S.; Ngo, C. Design and Analysis of a Clutched Parallel Elastic Actuator. Actuators 2019, 8, 67. [Google Scholar] [CrossRef]
- Mohseni, O.; Shahri, M.A.; Davoodi, A.; Ahmadabadi, M.N. Adaptation in a variable parallel elastic actuator for rotary mechanisms towards energy efficiency. Robot. Auton. Syst. 2021, 143, 103815. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, K.; Sun, J.; Li, J. Design, modeling and control of a reconfigurable variable stiffness actuator. Mech. Syst. Signal Process. 2021, 160, 107883. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Z.; Zhang, Y.; Xiao, X.; Tan, J. A Novel Design of Serial Variable Stiffness Actuator Based on an Archimedean Spiral Relocation Mechanism. IEEE/ASME Trans. Mechatron. 2018, 23, 2121–2131. [Google Scholar] [CrossRef]
- Chaichaowarat, R.; Nishimura, S.; Krebs, H.I. Design and Modeling of a Variable-Stiffness Spring Mechanism for Impedance Modulation in Physical Human–Robot Interaction. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7052–7057. [Google Scholar]
- Lu, H.; Zhang, X.; Huang, X. Robust Adaptive Control of Antagonistic Tendon-Driven Joint in the Presence of Parameter Uncertainties and External Disturbances. J. Dyn. Syst. Meas. Control 2017, 139, 101003. [Google Scholar] [CrossRef]
- Luong, T.; Kim, K.; Seo, S.; Jeon, J.; Koo, J.C.; Choi, H.R.; Moon, H. Simultaneous position-stiffness control of antagonistically driven twisted-coiled polymer actuators using model predictive control. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 8610–8616. [Google Scholar]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Grebenstein, M.; Höppner, H.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.G.; et al. Variable Stiffness Actuators: Review on Design and Components. IEEE/ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Best, C.M.; Rupert, L.; Killpack, M.D. Comparing model-based control methods for simultaneous stiffness and position control of inflatable soft robots. Int. J. Robot. Res. 2020, 40, 470–493. [Google Scholar] [CrossRef]
- Lugo, J.H.; Caligiuri, A.; Zoppi, M.; Cannata, G.; Molfino, R. Position and Stiffness Control of One DoF Revolute Joint Using a Biphasic Media Variable Stiffness Actuator. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; pp. 308–314. [Google Scholar]
- Liu, L.; Hong, Z.; Penzlin, B.; Misgeld, B.J.E.; Ngo, C.; Bergmann, L.; Leonhardt, S. Low Impedance-Guaranteed Gain-Scheduled GESO for Torque-Controlled VSA With Application of Exoskeleton-Assisted Sit-to-Stand. IEEE/ASME Trans. Mechatron. 2021, 26, 2080–2091. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, P.; Sun, F.; Sun, X.; Xu, F.; Jin, J.; Fang, L. Dynamic Modeling and Control of Antagonistic Variable Stiffness Joint Actuator. Actuators 2021, 10, 116. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, P.; Zhu, H.; Xia, K.; Ren, T.; Shen, Y.; Li, Y. A variable stiffness soft robotic manipulator based on antagonistic design of supercoiled polymer artificial muscles and shape memory alloys. Sens. Actuators Phys. 2024, 366, 114999. [Google Scholar] [CrossRef]
- Nalini, D.; Dhanalakshmi, K. Synergistically configured shape memory alloy for variable stiffness translational actuation. J. Intell. Mater. Syst. Struct. 2019, 30, 844–854. [Google Scholar] [CrossRef]
- Hamid, Q.Y.; Wan Hasan, W.Z.; Azmah Hanim, M.A.; Nuraini, A.A.; Hamidon, M.N.; Ramli, H.R. Shape memory alloys actuated upper limb devices: A review. Sens. Actuators Rep. 2023, 5, 100160. [Google Scholar] [CrossRef]
- She, Y.; Gu, Z.; Song, S.; Su, H.-J.; Wang, J. A Continuously Tunable Stiffness Arm With Cable-Driven Mechanisms for Safe Physical Human-Robot Interaction. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2020; p. V010T010A060. [Google Scholar]
- Yang, H.; Wei, G.; Ren, L. A Novel Soft Actuator: MISA and Its Application on the Biomimetic Robotic Arm. IEEE Robot. Autom. Lett. 2023, 8, 2373–2380. [Google Scholar] [CrossRef]
- Schiavi, R.; Grioli, G.; Sen, S.; Bicchi, A. VSA-II: A Novel Prototype of Variable Stiffness Actuator for Safe and Performing Robots Interacting with Humans. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 2171–2176. [Google Scholar]
- Abroug, N.; Laroche, E. Transforming series elastic actuators into Variable Stiffness Actuators thanks to structured H∞ control. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 734–740. [Google Scholar]
- Palli, G.; Pan, L.; Hosseini, M.; Moriello, L.; Melchiorri, C. Feedback linearization of variable stiffness joints based on twisted string actuators. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2742–2747. [Google Scholar]
- Buondonno, G.; Luca, A.D. Efficient Computation of Inverse Dynamics and Feedback Linearization for VSA-Based Robots. IEEE Robot. Autom. Lett. 2016, 1, 908–915. [Google Scholar] [CrossRef]
- Lukic, B.; Jovanovic, K.; Sekara, T.B. Cascade Control of Antagonistic VSA—An Engineering Control Approach to a Bioinspired Robot Actuator. Front. Neurorobot. 2019, 13, 69. [Google Scholar] [CrossRef]
- Guo, J.; Guo, J.; Xiao, Z. Robust tracking control for two classes of variable stiffness actuators based on linear extended state observer with estimation error compensation. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420911774. [Google Scholar] [CrossRef]
- Trumic, M.; Jovanovic, K.; Fagiolini, A. Decoupled nonlinear adaptive control of position and stiffness for pneumatic soft robots. Int. J. Robot. Res. 2020, 40, 277–295. [Google Scholar] [CrossRef]
- Zhakatayev, A.; Rubagotti, M.; Varol, H.A. Closed-Loop Control of Variable Stiffness Actuated Robots via Nonlinear Model Predictive Control. IEEE Access 2015, 3, 235–248. [Google Scholar] [CrossRef]
- Lukic, B.Z.; Jovanovic, K.M.; Kvasccev, G.S. Feedforward neural network for controlling qbmove maker pro variable stiffness actuator. In Proceedings of the 2016 13th Symposium on Neural Networks and Applications (NEUREL), Belgrade, Serbia, 22–24 November 2016; pp. 1–4. [Google Scholar]
- Flacco, F.; De Luca, A.; Sardellitti, I.; Tsagarakis, N.G. On-line estimation of variable stiffness in flexible robot joints. Int. J. Robot. Res. 2012, 31, 1556–1577. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Sardellitti, I.; Caldwell, D.G. A New Actuator With Adjustable Stiffness Based on a Variable Ratio Lever Mechanism. IEEE/ASME Trans. Mechatron. 2014, 19, 55–63. [Google Scholar] [CrossRef]
- Luong, T.; Seo, S.; Kim, K.; Jeon, J.; Yumbla, F.; Koo, J.C.; Choi, H.R.; Moon, H. Realization of a Simultaneous Position-Stiffness Controllable Antagonistic Joint Driven by Twisted-Coiled Polymer Actuators Using Model Predictive Control. IEEE Access 2021, 9, 26071–26082. [Google Scholar] [CrossRef]
- Isermann, R.; Münchhof, M. Identification of Dynamic Systems: An Introduction with Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 85. [Google Scholar]
- Guo, J.; Tian, G. Mechanical Design and Analysis of the Novel 6-DOF Variable Stiffness Robot Arm Based on Antagonistic Driven Joints. J. Intell. Robot. Syst. 2016, 82, 207–235. [Google Scholar] [CrossRef]
- Tanaka, S.; Nabae, H.; Suzumori, K. Back-Stretchable McKibben Muscles: Expanding the Range of Antagonistic Muscle Driven Joints. IEEE Robot. Autom. Lett. 2023, 8, 5331–5337. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Li, Y. Design and Dynamic Modeling of Variable Stiffness Joint Actuator Based on Archimedes Spiral. IEEE Access 2018, 6, 43798–43807. [Google Scholar] [CrossRef]
- Astrom, K.J.; Hagglund, T. Advanced PID Control; ISA-The Instrumentation, Systems and Automation Society: Raleigh, NC, USA, 2006. [Google Scholar]
- Ogata, K. Discrete-Time Control Systems; Prentice-Hall, Inc.: Bergen County, NJ, USA, 1995. [Google Scholar]
- Liu, H.; Abraham, A.; Hassanien, A.E. Scheduling jobs on computational grids using a fuzzy particle swarm optimization algorithm. Future Gener. Comput. Syst. 2010, 26, 1336–1343. [Google Scholar] [CrossRef]
- Ozsoy, V.S.; Unsal, M.G.; Orkcu, H.H. Use of the heuristic optimization in the parameter estimation of generalized gamma distribution: Comparison of GA, DE, PSO and SA methods. Comput. Stat. 2020, 35, 1895–1925. [Google Scholar] [CrossRef]
- Kramer, O. Genetic Algorithm Essentials; Springer: Cham, Switzerland, 2017; p. 92. [Google Scholar]
- Beck, O.N.; Shepherd, M.K.; Rastogi, R.; Martino, G.; Ting, L.H.; Sawicki, G.S. Exoskeletons need to react faster than physiological responses to improve standing balance. Sci. Robot. 2023, 8, eadf1080. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Casas, R.; Lum, P.S. An elbow exoskeleton for upper limb rehabilitation with series elastic actuator and cable-driven differential. IEEE Trans. Robot. 2019, 35, 1464–1474. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Mao, Z. Robust adaptive control of Hammerstein nonlinear systems and its application to typical CSTR problems. Int. J. Adapt. Control Signal Process. 2017, 31, 163–190. [Google Scholar] [CrossRef]

















| Parameters | V | V | V | V | V |
|---|---|---|---|---|---|
| Voltage Difference (V) | Linear Model | Hammerstein Model | Improvement Percentage |
|---|---|---|---|
| PID Coefficients | ||||
|---|---|---|---|---|
| i | ||||
| 1 | −0.476 | −0.544 | 0.0115 | 10.42 |
| 2 | −0.421 | −0.421 | 0.013 | 7.5 |
| 3 | −0.907 | −0.961 | −0.025 | 21.75 |
| 4 | −0.905 | −0.772 | 0 | 0 |
| 5 | −0.96 | −0.673 | −0.04 | 8.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javadi, A.; Haghighi, H.; Pornpipatsakul, K.; Chaichaowarat, R. Data-Driven Position and Stiffness Control of Antagonistic Variable Stiffness Actuator Using Nonlinear Hammerstein Models. J. Sens. Actuator Netw. 2024, 13, 29. https://doi.org/10.3390/jsan13020029
Javadi A, Haghighi H, Pornpipatsakul K, Chaichaowarat R. Data-Driven Position and Stiffness Control of Antagonistic Variable Stiffness Actuator Using Nonlinear Hammerstein Models. Journal of Sensor and Actuator Networks. 2024; 13(2):29. https://doi.org/10.3390/jsan13020029
Chicago/Turabian StyleJavadi, Ali, Hamed Haghighi, Khemwutta Pornpipatsakul, and Ronnapee Chaichaowarat. 2024. "Data-Driven Position and Stiffness Control of Antagonistic Variable Stiffness Actuator Using Nonlinear Hammerstein Models" Journal of Sensor and Actuator Networks 13, no. 2: 29. https://doi.org/10.3390/jsan13020029
APA StyleJavadi, A., Haghighi, H., Pornpipatsakul, K., & Chaichaowarat, R. (2024). Data-Driven Position and Stiffness Control of Antagonistic Variable Stiffness Actuator Using Nonlinear Hammerstein Models. Journal of Sensor and Actuator Networks, 13(2), 29. https://doi.org/10.3390/jsan13020029







