Abstract
In decentralized environments, such as mobile ad hoc networks (MANETs) and wireless sensor networks (WSNs), traditional reputation management systems are not viable due to their dependence on a central authority that is both accessible and trustworthy for all participants. This is particularly challenging in light of the dynamic nature of these networks. To overcome these limitations, our proposed solution utilizes blockchain technology to maintain global reputation information while remaining fully decentralized, and to secure multiparty computation to ensure privacy. Our system is not limited to specific settings, such as buyer/seller or provider/client scenarios, where only a subset of the network are raters while the others are ratees. Instead, it allows all nodes to participate in both rating and being rated. In terms of security, the system maintains feedback privacy in the semi-honest model, even in the presence of up to dishonest parties, while requiring only messages and having an computation overhead. Furthermore, the adopted techniques enable the system to achieve unique characteristics such as accessibility, consistency, and verifiability, as supported by the security analysis provided.
1. Introduction
The reputation of a party is a metric that reflects the level of trust and confidence that other parties have in it. This metric is derived from the actions and conduct of the party in question, as well as the judgments made by other parties regarding those actions. Depending on the context, a party may be expected to adhere to certain codes of conduct or perform specific actions, and the quality of those actions will be evaluated by other parties, leading to the formation of a rating [1,2]. A party’s reputation can be influenced by a multitude of factors, including its past actions, behavior, and the opinions of others. A strong reputation can be beneficial for a party as it can lead to increased trust and cooperation from other parties, whereas a poor reputation can have the opposite effect. To facilitate the monitoring and evaluation of a party’s reputation, reputation management systems are often utilized, providing a basis for other parties to make informed decisions about their interactions with the party in question.
E-commerce platforms often include built-in reputation systems that gather user feedback on items and sellers. They present this aggregated data to consumers, helping them make decisions about which products to buy and from whom. This type of reputation system is known as a centralized reputation system, which relies on a trusted central authority, such as a market operator (Airbnb, eBay, or Amazon), to provide oversight and ensure the authenticity of the feedback.
However, there are certain contexts where a central authority is not present. This includes decentralized social networks (DSNs), MANETs, peer-to-peer systems (P2P), WSNs, and other types of systems. In such scenarios, traditional centralized reputation systems are not effective. This is where decentralized reputation systems (DRSs) come into play [3,4,5]. These systems are designed to operate without a central authority and instead rely on the collective input of network participants to establish trust and evaluate reputations.
It is worth mentioning that centralized and decentralized reputation systems are two distinct approaches to managing and evaluating reputation within systems or networks.
Centralized reputation systems are characterized by the presence of a central authority, such as a company or organization, that is responsible for collecting, analyzing, and determining reputational scores [2]. This central authority also makes decisions about access or privileges based on those scores. However, this approach can be vulnerable to manipulation or bias due to the reliance on a single source of truth for reputation data.
On the other hand, decentralized reputation systems do not rely on a central authority for managing reputation data [6]. Instead, the reputation data is distributed across a network of individuals or entities, and decisions about access or privileges are made based on consensus among those individuals or entities, which increases the fairness and resilience of those systems, making them less prone to failure or censorship as they have no central point of control.
It is evident that the centralized paradigm does not apply in situations where there is a lack of a central authority. In such scenarios, distributed reputation systems (DRSs) provide an alternative solution. DRSs employ various techniques for the collection and distribution of reputation data [3,4,5]. In (MANETs), for instance, a node can gather reputation information about its peers through previous interactions and use this information to inform its future decisions. When a node has no prior experience with a peer or is new to the network, the conventional approach is to seek out the reputation information of other peers in the network and use it to make decisions regarding interactions with the targeted node.
One of the key considerations in implementing DRSs is feedback privacy [6]. If peers’ feedback is disclosed for any reason, particularly when their identities are publicly known, they may face retaliation attacks and receive low ratings, for example, [7]. Additionally, there is a potential for ratings to be provided for the purpose of reciprocation, with a user giving an unjustified high rating in anticipation of receiving a similar rating in future interactions.
To address the challenges associated with the protection of privacy in decentralized reputation systems, researchers have proposed various privacy-preserving decentralized reputation systems (PDRSs) [6,7,8,9,10]. These systems enable parties to avoid directly transmitting their reputation information to the requesting party and instead employ protocols that allow them to compute reputation as a function of their rating values while maintaining the privacy of these values. The outcome of this computation is then revealed to the requesting party.
However, it should be noted that the reputation information gathered by such systems is typically limited to the users’ direct experiences and recommendations from neighbors and acquaintances, resulting in incomplete and inconsistent reputation data across the network. This raises the question of how to aggregate ratings effectively in a decentralized network and maintain global reputation scores while preserving the ratings’ privacy.
1.1. Contributions
In this paper, we propose an efficient and dynamic decentralized reputation system that maintains global reputation information by integrating secure multiparty computation techniques [11] with blockchain technology [12]. The proposed system guarantees the privacy of individual ratings while making the aggregated reputation scores publicly accessible.
Additionally, we analyze several reputation system models in the literature and develop a general-purpose reputation system that is not restricted to scenarios where nodes are either raters or ratees, such as buyers/sellers or providers/clients. Instead, any participant in the network can function both as a rater and a ratee simultaneously.
Furthermore, we design a blockchain-based architecture that implements the proposed reputation system while reducing the on-chain storage and computation overhead with an off-chain phase. Security analysis demonstrates the reliability of the proposed system.
In contrast to previous works on the subject, the proposed system achieves unique properties such as accessibility, consistency, conservation, and verifiability.
In summary, the main contributions of this paper can be summarized as:
- Propose an efficient and dynamic decentralized reputation system that maintains global reputation scores;
- Develop a general-purpose reputation system that is not restricted to scenarios where nodes are either raters or ratees;
- Design a blockchain-based architecture that reduces the on-chain storage and computation overhead with an off-chain phase;
- Achieve unique properties such as privacy, accessibility, consistency, conservation, and verifiability.
Remarkably, some of the properties mentioned above can be trivial in the context of centralized reputation systems. But in dynamic PDRSs, they are challenging.
1.2. Organization
The rest of the paper is structured as follows: the second section comprises a review of the relevant literature in the field, followed by an introduction of the key components of our system, including any modifications or adaptations made. We also provide definitions for the concepts of trust and reputation, which are vital for the system’s operation, and discuss the security considerations that informed our design choices. The third section offers a comprehensive overview of the system and its various phases. The fourth section presents the results of our testing and evaluation efforts, including the methods used to assess the system’s performance. In addition, the security proof and analysis are included in Appendix A. The conclusion summarizes the main contributions of the paper and identifies potential areas for future research that could build upon the work presented here.
2. Preliminaries
In this section, we first provide an overview of the current state of the art in decentralized reputation systems. We then present an introduction to both blockchain and SMC (Secure Multi-Party Computation), including any modifications or adaptations that have been made, and highlight specific features that are suitable for our proposed use case. Finally, we provide definitions for relevant concepts related to the proposed system and discuss important security considerations.
2.1. Related Works
In PDRSs, there are two primary approaches to ensuring privacy [13]. The first approach prioritizes user anonymity, while the second approach emphasizes feedback confidentiality. The distinction between these two approaches can be summarized as follows [13]:
- The first approach, known as user anonymity-oriented systems, assigns one or more pseudonyms to users that cannot be linked to their true identities to preserve anonymity. These systems allow the users to conduct transactions and provide feedback without hiding it because they are not associated with their true identities.
- The second approach, known as feedback confidentiality-oriented systems, assigns unique pseudonyms to each user, and feedback is kept private. These systems do not aim to conceal the identities of the users providing feedback, but rather to hide the specific feedback values. In theory, these systems should not reveal any information about feedback other than the aggregated reputation.
The current study adopts the second approach as it is more pragmatic and realistic. This is because, in reality, complete anonymity is not always feasible in everyday situations. For instance, on e-commerce platforms, even if anonymity can be maintained online, the exchange of physical goods sold on them may reveal customers’ identities. From this perspective, feedback-confidentiality systems are a more viable option for enabling users to give honest feedback without fear of retaliation.
Most traditional works in the field of PDRSs (e.g., [6,8,9,10]) focus on a scenario where a querying party, denoted as , wishes to interact with a target party, denoted as , but is uncertain of ’s trustworthiness. This may be due to a lack of information about ’s past behavior, or limited or outdated experience with . Let represent the set of parties that possess reputation information about , referred to as witnesses or source parties. In such cases, can consult a selected subset of source parties, namely (), who will execute a protocol to compute ’s reputation score securely and then send the result to .
In line with this setting, one of the earliest works in the field is presented in [6]. The authors proposed a system that relies on random witness selection and additive secret sharing. The system offers three different levels of security and demonstrates the feasibility of witness selection schemes that produce at least two honest witnesses with high probability. Despite being fully decentralized and suitable for general use, the system is not able to compute and store global reputation scores. Instead, each party in the system must retain its gathered information locally, and reputation is determined solely by feedback from neighboring parties. Additionally, the system demands the exchange of messages for each reputation request.
The authors of [7,9] expanded upon the work presented in [6] with the k-shares reputation system, which is designed for the semi-honest and malicious adversarial model, respectively. Their system enhances efficiency by reducing communication costs to messages. Furthermore, it increases the probability of keeping reputation information private by enabling users to choose witnesses with good reputation scores while avoiding those they do not trust.
The previous systems presented in [6,7,9] are not well-suited for dynamic networks due to a number of limitations. Specifically, in dynamic networks, the number of available source parties, or parties currently participating in the network, may be smaller than in a static network. Furthermore, when a party leaves the network, all of its reputation information becomes inaccessible, as each party stores its information locally. As a result, reputation is likely to be computed with a different set of present parties each time a party requests it, leading to inconsistent and changing reputation information at each request.
To address these challenges, authors in [10] proposed a system that enables parties leaving the network to delegate their reputation information in order to prevent its loss. However, this approach comes with an increase in computation and communication costs and requires the leaving user to divide the entrusted information among a group of users (through secret-sharing) before leaving. Additionally, if a member of the delegation group leaves, the information must be re-delegated, making the recovery and reconstruction of the delegated information more challenging as the number of parties involved increases and the data become fragmented.
Despite the efforts made to prevent the loss of reputation information, it is evident that the previously mentioned solutions remain incapable of computing and storing global reputation scores. These methods rely on users’ direct experiences and recommendations from neighbors and acquaintances, resulting in incomplete and inconsistent reputation data that are primarily shared locally.
To structure the literature review effectively, we assess and classify related works according to the following criteria:
- 1.
- Full Decentralization: Reputation systems that do not depend on central entities for the collection, computation, or dissemination of reputation scores [14]. Instead, the information is distributed among parties, who share it to evaluate the trustworthiness of potential transactional partners.
- 2.
- General-Purpose Reputation Systems: These systems are designed to be utilized in various network environments and are not limited to specific settings such as service providers/consumers in online marketplaces or servers/clients in IoT [6,9,10]. They are flexible enough to adapt to various networks, including P2P, MANETs, or WSNs.
- 3.
- Global Reputation Systems: These systems collect ratings from all over the network and aggregate them into global reputation scores that are accessible to all users across the network [15].
- 4.
- Privacy: refers to the ability of a reputation system to compute and disseminate reputation scores while preserving feedback privacy [7,10].
It is worth noting that many proposed systems in the literature are not general-purpose systems. Rather, they are tailored to specific contexts such as online marketplaces [16,17,18] or the Internet of Things (IoT) [19,20,21,22], where the network is divided into two distinct groups: ratees and raters. In online marketplaces, users are either consumers (raters) or service providers (ratees), while in IoT, they are either server nodes or clients. However, in other contexts, such as P2P networks, MANETs, VANETs, DSNs, and WSNs, users often have to play both the role of a rater and a ratee.
We emphasize that such proposed systems are often too specific or incompatible with fully distributed settings such as P2P networks, MANETs, or WSNs. One example is PrivBox [23], a verifiable reputation system for online marketplaces. It enables consumers to rate retailers and submit their feedback in an encrypted form using homomorphic encryption to a public bulletin board (PBB). The system makes reputation information publicly accessible and verifiable without disclosing the individual ratings. However, the system leaves the reputation computation task to any customer who wishes to compute the reputation of a particular vendor. The system employs zero-knowledge proofs to demonstrate that the ratings are well-formed.
Another example of such a system is PrivRep [24], which builds upon the work presented in [23]. The system utilizes a public bulletin board (PBB) in combination with a reputation engine (RE) to calculate reputation from homomorphically encrypted feedback. The RE is controlled and operated by the marketplace, rather than regular users, and it has the authority to reject feedback deemed untrustworthy. It is evident that the use of two central entities, namely the RE for computation and the PBB for storage, undermines the decentralized nature of the proposed system.
Similarly, the system proposed in [15] for the Social Internet of Things also relies on a PBB. However, the authors mention the possibility of implementing it as a blockchain or a mirrored server, which may address the issue of centralization and enhance the decentralized aspect of the system.
In [17], the authors proposed a blockchain-based cross-platform reputation system for e-commerce, referred to as RepChain. The system interconnects various e-commerce platforms and enables them to share their users’ reputations through a consortium blockchain. While the system is not entirely decentralized, as each platform relies on its centralized entity, the top layer interconnecting platforms are decentralized owing to the use of blockchain technology.
The authors in [25] propose a solution to blockchain usage limitations in the Internet of Things (IoT) reputation systems, especially their lack of scalability. They introduce a distributed ledger combining Tangle and blockchain as a reputation framework. Combining Tangle with blockchain is destined to provide maintainability of the former and scalability of the latter. Consequently, the proposed ledger could handle a more significant number of IoT devices and transactions.
Blockchain has had a wide range of applications due to its outstanding features such as security and reliability, especially in distributed settings [26,27,28,29]. Among other applications is fog computing, where blockchain may achieve secure decentralized reputation systems and identity management [30].
Similarly, the authors in [21] proposed a decentralized reputation management system for the Internet of Things (IoT) that takes into account geospatial information. The proposed system recognizes that the trustworthiness of a device can be affected by various factors, including its geographical location. The system utilizes a cloud–fog–edge architecture, in which the fog layer employs blockchain technology to create a decentralized network among fog nodes, allowing for transparent and decentralized management. The location-based system component stores geographical information in smart contracts, enabling reputation values to vary based on the device’s location.
In the field of VANETs, decentralized reputation systems were proposed in works such as [31], where the authors utilized a Bayesian filter to enable nodes to detect malicious vehicles based on their trust scores. Additionally, the authors in [32] proposed a two-layered blockchain-based reputation system comprising a local, one-day message blockchain and a global vehicle reputation blockchain. The local blockchain efficiently manages local traffic information, reducing the memory overhead for vehicles, while the global one maintains reputation scores.
Based on the literature review and the classification of related works according to four criteria, namely: Full Decentralization, General-Purpose, Global Reputation, and Privacy (as summarized in Table 1), it is clear that a portion of the related works are fully decentralized reputation systems and general-purpose, but do not maintain global reputation scores and rely on locally stored information. As a result, their produced reputation information is partial and inconsistent across the network, as it is limited to users’ direct experience and recommendations from neighbors and acquaintances. On the other hand, another portion of related works is proposed for specific settings and achieves global reputation and some form of decentralization, but they are not general-purpose systems. The current work objective is to fill this gap by proposing a global reputation system that is both general-purpose and fully decentralized.

Table 1.
A Comparative study of privacy-preserving decentralized reputation systems.
2.2. Blockchain
Typically, a blockchain can be seen as a distributed public database from which every user can read, but not any user can write. Rather, users need to reach a consensus over the network before the writing is accepted [33]. All actions that modify this database are recorded and broadcast to all users in blocks. Once a block is received and accepted by network users, it becomes immutable after a few following blocks. Furthermore, blockchain is reputed for recording transactions efficiently in a verifiable and permanent way. Owing to this fact, it is considered an append-only database.
From another point of view, blockchain can be regarded as a data structure composed of an ordered list of blocks as depicted in Figure 1. The result of all actions in all blocks at a given moment constitutes the state of the blockchain.

Figure 1.
Blockchain structure.
Let be a blockchain, where the first block is the genesis block, while is the last validated block. Each block contains a cryptographic hash of its precedent block , which makes the blockchain resistant to modification by design. Once recorded, the data in any given block cannot be modified without altering all the previous blocks, which requires the consensus of the network majority. A blockchain is typically managed by a P2P network adhering to a communication protocol.
The block is composed of a block header and a series of transactions . The block header includes a collection of relevant data fields, whereas the transactions series is the list of transactions comprised in this block. Specifically, transactions are organized in each block as a Merkle tree data structure. In addition, the Merkle tree has its root hash called TransactionsRoot in the block header.
For simplicity, a block can be formulated as:
where includes several data fields, among them [33,34]:
- PreviousBlockHash: The hash of the previous block’s header.
- StateRoot: The hash of the root node of the state tree.
- TransactionsRoot: The hash of the root node of the transactions’ Merkle tree.
A transaction is a single instruction constructed by a party and signed cryptographically. It is traditionally used to transfer a sum of coins (virtual money). In our context, it is also used to submit parties’ feedback to the blockchain and to join source parties’ lists (c.f. Section 3). Mainly, it contains some common data fields, namely:
- Nonce: A scalar value equal to the number of transactions issued by the sender;
- Recipient: The address of the recipient.
- Type: The transaction type: for coins transfer; for rating peers; and for the joining recipient’s source parties list.
- Data: A value that depends on the transaction type.
- Signature: The transaction signature, also used to recover the sender’s address.
2.2.1. State
The state, as described in [34,35], is a mapping between parties’ addresses and their state accounts. It is implemented and maintained in the form of a modified Merkle tree. It is a simple database linked to blocks, but not stored on the blockchain. The state database can be considered a condensed version of the blockchain, as it only contains the essential information for regular users, specifically accounts and balances. It is the only data structure, in addition to the blocks’ headers, required for non-miner users to participate in the network. In the context of this work, reputation scores are also stored in the state. Ethereum is an example of a blockchain that implements a state database, unlike Bitcoin, which does not have an equivalent structure, as stated in [36].
We denote the state database as and use a party’s address a to reference its account denoted by . In the context of this research, the account state includes the following data fields:
- Nonce: The number of transactions sent from this address, denoted .
- Balance: The number of coins owned by this address, denoted .
- Reputation: The reputation score, denoted .
- Weight: The number of feedback received so far, denoted .
- Source Parties List: The list of source parties’ addresses, denoted .
Figure 2 shows all the blockchain components and how they are linked.
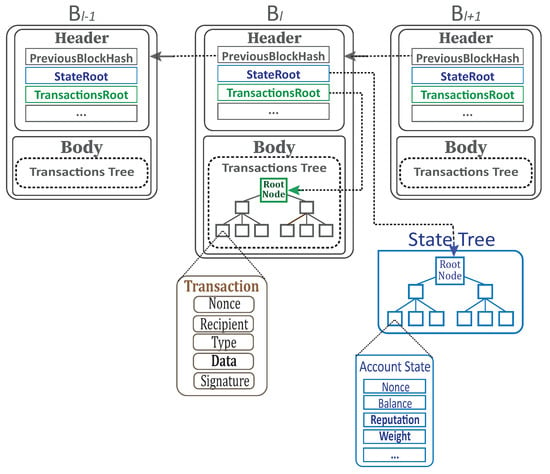
Figure 2.
Blockchain components with the state.
2.2.2. Consensus
The creation of blocks is controlled by a mechanism that varies between different blockchain algorithms. The first mechanism used to reach consensus [37] on newly created blocks was the Proof-of-Work (PoW). The concept started with the blockchain/currency Bitcoin [12] and was followed by several alternative coins launched using similar ideas.
The mechanism of PoW requires block creators, called miners, to prove that they performed a certain amount of work to write to the blockchain. Usually called mining, this task consists of finding a partial collision using hash functions, which is a power-consuming process often requiring dedicated hardware [38].
With the advent of PPCoin [39] developed further by BlackCoin [40], NXT [41], and NeuCoin [42], a new family of blockchain-based systems was born, replacing PoW with the concept of Proof-of-Stake (PoS).
With the PoS, every participant randomly gains the right to write to the blockchain with a probability proportional to their stake, i.e., the number of coins they staked. Therefore, the additional computing power used in PoW becomes useless. Accordingly, it is less costly to run the PoS and particularly much faster to create new blocks under it. After some of its inherent issues were tackled [39,40,42], it is perfectly reasonable today to maintain a distributed consensus using the PoS. In this regard, we consider the PoS more appropriate in our context than the PoW.
During the block creation process, miners, also known as validators, perform various tasks. Among them, they record new transactions and validate new blocks. Usually, a new block is validated on regular periods. When transactions become part of an accepted block, they are considered confirmed. Consequently, all the concerned users’ state accounts are updated to reflect the changes made by the transactions in that block.
Whether the consensus mechanism uses mining in the case of PoW or validation in the case of PoS, block creation has a cost for miners/validators. This task is attractive for them only because they are rewarded by earning transaction fees. In this regard, it is crucial to highlight that the role of a reputation system is to support the network’s operation by establishing trust between the users and encouraging participation and good behavior. Thus, it is counterproductive to impose fees on users that provide their feedback, as it is already challenging to persuade them to do so without fees. Additionally, assuming some activity and transactions in the network other than rating and reputation—otherwise, the very existence of the network would be pointless—it is those types of transactions that have to pay for the block creation process. Because reputation functionalities are essential functionalities just like security, we cannot compare them with financial transactions, for example.
2.3. Secure Multiparty Computation
Using SMC, a set of parties can collaboratively compute a function over their private inputs without disclosing them. With n parties , each one holding a secret input , and f an agreed-upon function that accepts n inputs: A protocol is a SMC one if it allows to compute while meeting the following criteria:
- Correctness: The protocol correctly computes the value of y;
- Privacy: The parties cannot learn any information about , but y from the protocol.
In order to calculate a function f, which is typically represented as a Boolean or arithmetic circuit, one must evaluate the equivalent circuit gate by gate. There are currently two paradigms for Secure Multi-Party Computation (SMC) implementation: secret sharing [43,44,45,46], and garbled circuits [47,48,49]. Each paradigm has its own advantages and development trajectory. In our system, we use secret sharing, as it is more adapted to arithmetic circuits.
In the following paragraphs, we will introduce the variant of SMC used in our system, which is adapted from [50] for arithmetic circuits. This protocol is considered in the semi-honest adversarial model. However, we do not use the entire protocol. Instead, we only include the elements of the protocol that are pertinent to our setting and particularly appropriate for the reputation-related functions we are focusing on (c.f. Section 2.4.1).
Reputation functions typically determine reputation scores from ratings provided by users. They usually take the form of a sum, an average, or a weighted average, which we can represent as linear functions of the kind where are private values and are public. Remarkably, these functions employ only addition and multiplication by public values.
Let us assume that the desired function f is given as an arithmetic circuit composed of only addition and multiplication by public values.
In accordance with this protocol, secret-sharing a value entails sampling uniform random shares and taking the share as . The outcome is an additive secret sharing of x, which is represented by , where for . Practically speaking, a party can generate as indicated and send a share to each party if it wishes to share its secret x with parties. The value of x will remain private as long as the party keeps the share secret, and adding the n shares is sufficient to recover x.
The SMC protocol for n parties computing from their respective private inputs, works as follows:
- 1.
- Input: Every party secret-shares its private input by generating and sending , respectively, to while keeping secret.
- 2.
- Computation: Each party calculates f over the shares they received by evaluating operations in the order and precedence. The operations are realized as follows:
- (a)
- Addition: For example, is realized by each party computing .
- (b)
- Multiplication by a public value: For example, for a public and x private is computed by each party evaluating .
- 3.
- Output: A party can learn the result of computation y by each party sending to and party reconstructing .
It is simple to check that the protocol computes f precisely. The protocol is secure against any passive adversary controlling up to parties. Indeed, the adversary cannot unveil the value of x unless he knows all shares in the representation .
From the previously mentioned operations, the SMC protocol can handle any linear function , which is amply sufficient for reputation functions.
The original protocol is broader than described above. It can handle the multiplication of two private values and, by extension, any arithmetic circuit since addition and multiplication form a complete basis for arithmetic circuits.
2.4. Problem Setting & Definitions
We model our environment as a multi-agent environment, where each agent represents a user or any devices executing the necessary computation and communication on behalf of them. We often use the word “party” instead of “agent” without changing the meaning. Let be the set of all parties existing in the environment and . We associate with each party an account that is controlled by a pair of private/public keys, denoted (, ). A party and its associated account are usually identified by a short address derived from its public key by taking the right-most 160-bits of its 256-bit SHA-3 hash [34]:
2.4.1. Trust and Reputation
Let us introduce the following notations:
- denote the set of all trust relationships between parties in , where (or ) implies that the party a has a trust relationship towards a target party t. Mainly, is a binary relation that is not necessarily symmetric, as trust is a directional relation.
- denotes the set of all actions, e.g., “upload authentic content”, or “report an event”.
- refers to the functionsuch that outputs if party t executes the action anticipated by party a, or outputs if t does not perform the anticipated action. Let the subjective probability denote party a’s belief that party t will accomplish the action.
Without a loss of generality and for practicality’s sake, we can assign to the subjective belief mentioned above an equivalent integer value in the interval where M is a fixed positive integer. The integer value is obtained by normalizing the probability to the scale , which is done by multiplying by M, adding and taking the floor. The result is an integer in the range .
Definition 1
(Trust). Let be the set of all parties, be the set of all actions and . The trust of party a in party t expressed as an integer and reported to the scale is given as:
where and with p a prime number.
A party a is said to be a source party of a target party t in the context of an action if a has trust in t in the context . The set of all source parties of a party t in context is denoted . When the context (action) is clear, the notation is used. We also refer to a’s trust in party t as a’s feedback on t or the rating.
Definition 2
(Reputation). A reputation function is any chosen function such that (). Let be the set of source parties of party t in the context ψ. If is the adopted reputation function, then the reputation of party t in the context ψ is defined as:
where is the trust of party in party t for . is also denoted when the context is clear.
Reputation, in general, is the outcome of evaluations from various sources. It is often represented as a function of these evaluations, such as the sum or average [2]. There are a variety of methods for aggregating reputation from ratings, including counting [51], probabilistic [52], discrete [53], flow [54], and fuzzy approaches [55]. However, a comprehensive examination of these methods is beyond the scope of this study. In this work, we adopt the counting approach for reputation, which is implemented as the average of feedback values due to its simplicity and ease of comprehension by human users. Other linear functions, such as the weighted average, could also be utilized without any alteration to the proposed system. The reputation is recorded on the blockchain as a pair (refer to Section 2.2.1), where represents the reputation score and represents the number of ratings, also known as weight. This way, the weight of this measure is preserved.
The weight of a reputation score is an essential factor in determining its overall value, as it reflects the number of ratings or evaluations that have been used to calculate the reputation score. The higher the weight, the more evaluations have been taken into account, making the reputation score more reliable and representative of the overall perception of an entity. To ensure that the weight of the reputation score is preserved, we record it alongside the reputation score on the blockchain. For further discussions on reputation aggregation, one can refer to the works of [1,2].
2.4.2. Security Definition and Adversary Model
In the following, we present the adversary model for our system, some important assumptions, and system requirements.
- Adversary Model: In this paper, we consider the model of multiparty computation in the presence of static semi-honest adversaries. Parties in such a model are supposed to follow the protocol, but may try to learn more information than allowed during the execution of the protocol using intermediate information and their internal states. We call any coalition of dishonest parties adversaries.
- Random Number Generator & Hash Function: All parties in the network are granted access to a random number generator, denoted RandGen(), to achieve privacy for our system and use the Keccak 256 algorithm [56] as the default hash function denoted . Keccak is a robust hashing algorithm at the core of SHA-3 and is also part of Solidity [57] and Ethereum.
- Authentication: Our system uses public-key cryptography. It authenticates each user through digital signatures enabling them to exchange messages and perform transactions. Every user obtains a public and a private key forming his digital identity. They use the private key to sign messages and transactions linking them to their identity, while other users can verify the signer’s identity using the public key visible to all network participants. A valid signature gives a recipient confidence that the message was created by a known sender (authenticity) and was not altered in transit (integrity). Regularly, a signature scheme is a tuple of algorithms (Gen(), Sign(), Verify()) where Gen() generates a private key and a corresponding public key ; Sign() returns a tag t on the inputs of the private key , and a message m; and Verify() outputs accepted or rejected on the inputs of a public key , a message m, and a tag t. In our context, the system uses the elliptic curve digital signature algorithm (ECDSA) [58] specifically, the recoverable version of it [34] consisting of three functions that are PUBKEY, SIGN and RECOVER, defined as follows:
- returns , a 512-bit public key on the input of a randomly generated 256-bit private key.
- returns a tag as a signature on the inputs of a public key and a message m.
- returns the public key of the signer if is a valid signature or nothing otherwise.
- Recoverable ECDSA is a variant of the ECDSA that allows for the recovery of the public key used to generate a signature from the signature itself. This is useful in certain situations, especially when multiple parties are signing a message, as it allows for a more efficient verification process without the need to store multiple copies of each party’s public key.
- Encryption: On the other hand, for privacy purposes, the Elliptic Curve Integrated Encryption Scheme (ECIES) [59] is used to encrypt messages between parties.
- Communication channels: We assume that point-to-point channels exist between every pair of parties and postulate that they are reliable and guarantee the authenticity of the data sent through them. In addition, we assume they are private, so the adversary cannot obtain messages sent between honest parties. Point-to-point private channels are emulated in our context through signature and encryption.
- Privacy in the Semi-Honest Model: Recall that in the semi-honest model, it is assumed that the parties involved in SMC will follow the protocol as prescribed, but they may attempt to gain additional information beyond what they are supposed to learn during the computation. Privacy in this model refers to the ability of the parties to keep their inputs confidential from one another during the computation, while still permitting the correct output to be computed.
- A SMC protocol is considered to privately compute a function f if the information obtained by any subset of semi-honest parties during the execution of the protocol is the same as what they could learn by just looking at their inputs and the outputs. In other words, the protocol ensures that the parties do not learn any additional information about the inputs of other parties beyond what can be inferred from their own inputs and the outputs.
- In formal terms [60]: Let be the parties participating in a SMC with the inputs , respectively, a subset of semi-honest parties representing the adversary, and denotes their view on the protocol , which is the set of all the information obtained by the adversary I from the protocol during its execution. There exists a polynomial-time algorithm known as a simulator that can produce the same view from just the inputs of I and the output . In computational security, this is expressed and equivalent to the indistinguishability of two distributions and .
- O. Goldreich [60] specifies the security definition of privacy for multiparty computation in the semi-honest model as follows:
Definition 3.
Let and where . Let a deterministic functionality. We say that a protocol Π privately computes f if there is a probabilistic polynomial time algorithm denoted (a simulator) such that for every , it holds that:
- 1.
- (Correctness)
- 2.
- (Privacy)
where “Correctness” means that the protocol computes and outputs the desired function , namely .
- Accessibility: Accessibility refers to the ability of a reputation system to facilitate the utilization and access of reputation information for all users. In decentralized reputation systems, this entails ensuring that all individuals, regardless of their location and the data they possess, can utilize and benefit from others’ reputation scores.
Definition 4.
We say that a reputation system Π achieves Accessibility if a can query for the reputation score of t at any time and always obtains a copy of according to its request time.
- Consistency: Consistency refers to the uniformity or unchanging nature of the reputation system across the network. In decentralized reputation systems, consistency is crucial as it ensures that the output reputation scores are comparable and reliable across the network when requested simultaneously.
Definition 5.
We say that a reputation system Π is Consistent if , if a and b query for the reputation score of t at the same time and obtain and , respectively, then .
- Conservation: Conservation in the context of decentralized reputation systems refers to the safeguarding and preservation of reputation and feedback information. In more straightforward terms, it entails ensuring that valuable information is not lost, even when the provider of feedback leaves the network.
Definition 6.
We say that a reputation system Π conserves the reputation information if such that a party a has rated t before, then remains a function of its rating even if a leaves the network.
- Verifiability: In decentralized reputation systems, verifiability refers to the capability for reputation scores and rating transactions to be independently examined and confirmed by any user, rather than being accepted solely based on trust or authority. This process involves verifying the qualifications of raters, signatures, nonces, and the calculation of reputation scores.
Definition 7.
We say that a reputation system Π achieves verifiability if such that the system has received for t so far n feedback from parties , respectively: then any party can check that the reputation score of t at this time is and that the number of ratings is .
2.4.3. Problem Definition
Let be the set of source parties of a target party t in the context of a given action . We assume that is known and unique for simplicity. We examine the situation where the set of t’s source parties execute a reputation system , which takes their private feedback , securely computes the functionality , and outputs the reputation score of target party t. The reputation system is required to be decentralized and secure under the semi-honest model.
3. The Reputation System
3.1. System Overview
The proposed system is structured into three distinct phases, as described below. Each one has its specific objective and task. A graphical overview of the system is presented in Figure 3 in addition to a summary of the system parameter choices in Table 2:

Figure 3.
System overview.

Table 2.
System parameters.
- In the first phase, each witness joins the list of source parties by submitting a JOIN transaction. After successful validation, the witness is assigned to a subgroup U consisting of k parties. The purpose of this phase is to ensure that witnesses are legitimate and have the necessary credentials to participate in the rating process.
- The second phase is where most of the actual reputation calculation takes place. Each subgroup runs the Secure Multi-Party Computation protocol, which allows parties to jointly compute a reputation rating without revealing their individual inputs. Once the joint rating is calculated, it is submitted to the blockchain via a RATE transaction. This phase aims to ensure that the reputation calculation is secure, accurate, and tamper-proof.
- In the final phase, the miners execute the RATE transaction and calculate the final reputation score based on the received ratings. The reputation value is then updated on the blockchain, making it publicly available for all participants. This phase aims to ensure that the reputation value is accurate, transparent, and accessible to all parties on the network.
3.2. System Specification
The system presumes that a particular action has been executed by the targeted party and that the participating parties have based their evaluations on the quality of that action. Furthermore, it is assumed that all participating parties possess a piece of data, referred to as , as evidence of the interaction that has transpired. Based on this evidence, they can be added to the list of source parties and compute reputation collectively. Subsequently, the resulting score is submitted to the blockchain for integration.
If a party is new to the network or possesses a poor reputation, it is unable to be added to the list of source parties and, as a result, is unable to evaluate other parties. However, it can enhance its reputation by exhibiting positive behavior and receiving positive feedback from its peers. Nevertheless, only parties with reputation scores higher than a predefined threshold and the number of received evaluations exceeding are permitted to evaluate others (see Section 3.3).
Let be the set of source parties of a party t. We recall that, if , then represents the source party address and its account state. If the source parties want to share their feedback and n is large, they are divided into subgroups that do not exceed k parties, and each party is assigned to a subgroup. k is a system-wide fixed parameter chosen to be as small as possible (see Section 3.4).
- 1.
- In the first phase specified in Algorithm 1, the source parties join the list of source parties and are assigned to a subgroup U of k parties from the list.
- 2.
- Each subgroup runs the second phase specified in Algorithm 2 independently and submits its result as a transaction to the blockchain. Any source party can initiate the second phase by requesting parties in its subgroup U for SMC computation. We refer to that party by for simplicity and to the set of selected parties by .
- 3.
- In the third phase specified in Algorithm 3, the miner that gained the right to form the new block executes the transactions and updates the state.
| Algorithm 1 Phase 1: Joining the list of source parties and forming subgroups. |
|
| Algorithm 2 Phase 2: Secure multiparty computation. |
|
| Algorithm 3 Phase 3: Reputation aggregation on-chain (performed by miners). |
|
3.3. Reputation Threshold
The system uses thresholds to ensure a minimum level of trustworthiness within the network. Newcomers or parties with low reputations are not allowed to participate in witness groups and cannot rate other parties. However, they can improve their reputation score by exhibiting good behavior and receiving positive feedback from their peers. Both the reputation score and the number of received ratings, called reputation weight, are taken into account, with a threshold set for each. Therefore, the thresholds and represent the minimum reputation score and weight required for parties to participate in the network.
The threshold on reputation weight is included in the system to ensure that feedback from parties is coming from a diverse group of participants. By requiring a minimum number of ratings before a party’s feedback is considered, the system aims to prevent a single or small group of parties from having an outsized influence on the reputation of others.
However, the threshold on reputation weight could also make it difficult for new parties to establish a reputation and participate in the network, limiting the diversity of the network, hence the need for a trade-off between security and decentralization. The threshold can be adjusted depending on the desired balance between security and decentralization for the network.
3.4. Which Value k for the System
Conducting a secure multiparty computation with all n source parties participating simultaneously, especially in dynamic networks where parties may enter and exit the network, is a challenging task. Furthermore, the task requires messages, which can be significantly reduced by dividing the set of source parties into subgroups of a fixed number k. As per Theorem A1, privacy is ensured if each subgroup contains at least two honest parties. The probability of having at least two honest parties in each subgroup, when parties are selected uniformly at random, is equal to , where k is the number of participating parties, n is the total number of source parties, and b is the total number of corrupt parties. We denote this probability as in relation to the value of k.
from that we have:
In the following, we take the number of corrupt parties b as a percentage of the total number of source parties n. Figure 4 shows how behaves according to k values with b set to different percentages of n. In Table 3, we vary b from 10% to 95% of the total number of source parties n. We set some target values for to achieve and determine the thresholds of k that ensure the probability is higher than the desired values:
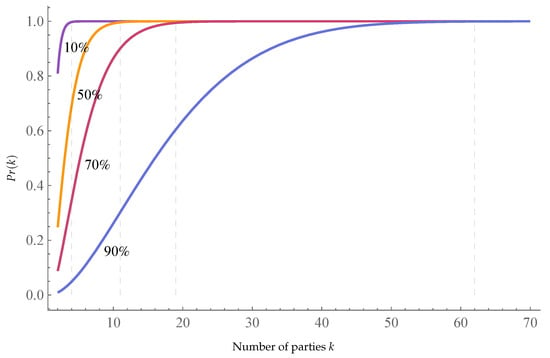
Figure 4.
The Probability for different percentages of corrupt parties.

Table 3.
Minimal values of k for desired according to b.
3.5. Security Proof and Analysis
To demonstrate the robustness and dependability of the proposed system, we present a security proof and analysis in Appendix A. This enables a thorough examination of its security characteristics and renders a comprehensive understanding of the system and its capabilities.
4. Performance Evaluation
In this section, we evaluate our proposed system’s effectiveness by measuring its performance and analyzing its strengths and weaknesses. This evaluation is conducted in two phases. Firstly, the communication and computation overhead complexity is estimated and compared exclusively with fully decentralized reputation systems, as presented in Table 4. Subsequently, a series of experiments are conducted on an Intel-Core i7-8750H laptop under the Windows operating system. The experiments were repeated over a total of ten sessions to ensure the reliability and robustness of the results. The results reported in this paper are the average of the ten sessions.

Table 4.
The complexity of reputation computation.
The proposed system efficiently computes reputation scores, as it necessitates only a linear number of messages related to the number of feedback providers (n). Specifically, with a fixed parameter k, the maximum number of messages that need to be exchanged is , thus the system’s complexity is . In terms of computation overhead, the system requires the generation of up to random numbers, the signature and recovery of messages, the computation of addresses, and the encryption and decryption of , which also results in a complexity of .
In order to simulate the blockchain functionality in our system, we utilized Ganache [61], an Ethereum simulator that enables the development of smart contracts on top of the Ethereum blockchain. Ganache provides all of the necessary remote procedure call (RPC) functions and features and can be programmatically accessed via Python or JavaScript. Our on-chain logic is implemented using two smart contracts written in the Solidity programming language [57], a widely-used object-oriented language on various blockchain platforms, specifically Ethereum. These smart contracts are then deployed to Ganache via Web3.js [62], the Ethereum JavaScript API, which facilitates interaction with Ethereum nodes through RPC.
The first smart contract manages the list of source parties (refer to the listing in Appendix B), while the second simulates the computation and updating of reputation data on the blockchain, as well as performing signature, nonce, and membership verification (refer to the listing in Appendix C). To estimate the computation cost of the RATE smart contract, it was taken off-chain before testing.
The off-chain phase of our simulation was written in JavaScript, utilizing the Web3 RandomHex function for randomness generation, ECDSA for authentication, and ECIES for encryption. It is worth noting that the JavaScript code does not use HTTP or Websocket. Instead, it was run on the Node.js runtime environment [63] as a standalone application. The parameters and settings used in our simulation are outlined in Table 5.

Table 5.
Simulation parameters.
Our simulation verifies the soundness of the proposed system by demonstrating that the generated reputation scores match the ratings’ averages. In addition, we conduct an analysis of the effects of varying parameters, such as the subgroups cardinality k and the shares bitlength, on system performance. Our simulation results provide insight into the practical implementation of the proposed system and its potential performance in real-world applications.
Experiment 1: We know from Section 3.4 that the minimal value of parameter k required to maintain targeted privacy is proportional to the ratio of corrupt parties in the system. Hence, to study the impact of increasing malicious parties’ ratio on performance, it is sufficient to raise k and monitor the execution time. Figure 5, Figure 6, and Figure 7 illustrate the experiment’s results and show a running time quasi-linear in k.

Figure 5.
Computation cost of shares generation plus signature and encryption.

Figure 6.
Cost of shares decryption and signatures verification.
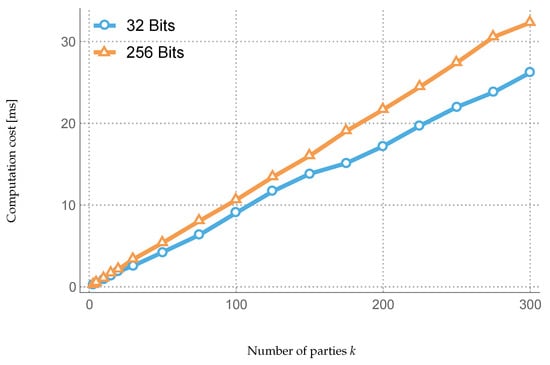
Figure 7.
Rate transaction computation cost.
Experiment 2: The second parameter studied was the shares bitlength, which depends solely on the finite field prime number p. Shares are primarily generated randomly in , and they have the same bitlength as the parameter p regardless of the rating domain. The experiment consists of changing shares’ bitlength by changing p accordingly and checking any effect on the system performance/execution time. Namely, we set p’s bitlength to 32- and 256-bit, as shown in Figure 5, Figure 6, Figure 7 and Figure 8. The results reveal a mild effect on performance.
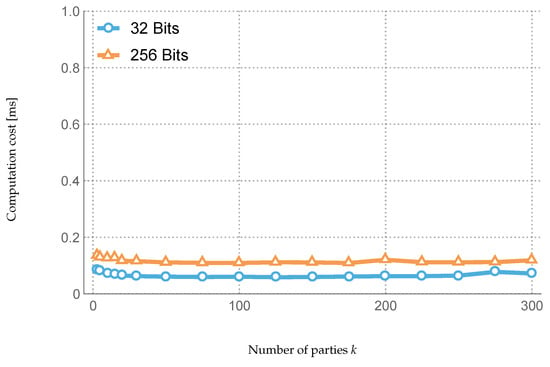
Figure 8.
Cost of the function computation over shares plus signature.
5. Conclusions and Future Directions
In this study, we propose a new dynamic, decentralized, and privacy-preserving reputation system. Our system utilizes blockchain technology to store and update reputation data and secure multiparty computation (SMC) to ensure the confidentiality of feedback. By leveraging these technologies, we have developed a fully decentralized system that maintains global reputation information without relying on a central authority. Our system is suitable for general-purpose use cases where nodes can both provide and receive feedback, and has been proven secure under the semi-honest adversarial model. However, future work could investigate the system’s robustness under more advanced threat models, such as covert and malicious attacks. Additionally, our system demonstrates an efficient design, requiring only messages and having an computation complexity.
Future research directions include addressing other challenges that reputation systems often face, such as oscillation, self-promotion, defamation, and whitewashing. To address these challenges, advanced cryptographic techniques such as data obfuscation, homomorphic encryption, and homomorphic secret-sharing could be explored. Additionally, we plan to investigate the application of reputation systems in location-sensitive networks, such as MANETs and VANETs. In these environments, feedback is often relayed by closely-located nodes, which poses a risk of identity violation. Our objective in these scenarios is to develop a system that enables parties to submit feedback while remaining anonymous.
Another important consideration for decentralized systems like ours is scalability. The number of transactions that a blockchain can handle in a given period is limited, and thus, future work could investigate methods such as sharding or nested blockchains to increase the capacity of our system.
Author Contributions
Conceptualization, K.M., F.E.B. and H.B.-A.; methodology, K.M., F.E.B. and H.B.-A.; software, K.M., F.E.B. and H.B.-A.; validation, K.M., F.E.B. and H.B.-A.; formal analysis, K.M., F.E.B. and H.B.-A.; resources, K.M.; writing—original draft preparation, K.M.; writing—review and editing, K.M., F.E.B. and H.B.-A.; visualization, F.E.B. and H.B.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| P2P | Peer-To-Peer |
| MANETs | Mobile Ad-hoc Networks |
| WSNs | Wireless Sensor Networks |
| VANETs | Vehicular Ad-hoc Networks |
| DSNs | Decentralized Social Networks |
| DRSs | Decentralized Reputation Systems |
| PDRSs | Privacy-Preserving Decentralized Reputation Systems |
| PoW | Proof of Work |
| PoS | Proof of Stake |
| PBB | Public Bulletin Board |
| SMC | Secure Multiparty Computation |
Appendix A. Security Proof and Analysis
Let and . Our system securely computes a deterministic functionality that is the average of its inputs: the feedback values . We can say that privately computes if there is a probabilistic polynomial time algorithm denoted (a simulator) such that for every , it holds that:
- 1.
- (Correctness)
- 2.
- (Privacy)
Appendix A.1. Correctness
Each party of address prepares the shares of its feedback value such that . The sum of the trust values of all parties in is given as . Thus, it can be stated as , which is the sum of all shares of all parties in U. After preparing its shares, every party sends one share to each party in U while keeping the share private. Each party then in U computes the sum of the received shares and its private share , signs it, and sends it to . issues a transaction with the sums and corresponding signatures. The miner then verifies the transaction and computes the average of , which equals the average of the trust values of all parties, in showed as follows:
Let us assume and are the values in the account state of the party t before executing the transaction. R represents the average of the N previous ratings received so far. Since is the average of the k new ratings, then, after executing the transaction, the new state becomes and the average of the total ratings □
We note that a new account state is initiated with the values and .
Appendix A.2. Privacy
During the execution of the protocol on the feedback values , the view of the party () denoted by is:
The adversary here is semi-honest; therefore, its view is exactly as in the case where the parties follow the protocol specification. Considering a participant party in the protocol, has to prepare k shares of its secret feedback value as follows:
- The shares are random numbers generated uniformly over the interval , where p is a prime chosen large enough as stated in the problem settings.
- The last share is computed as . Thus, it is also uniformly distributed over since it is a function of the previous shares.
We conclude that all the shares are uniformly random, which means that one of them does not reveal any information individually about . The only way to gain information about is to know all k shares.
We note also that the sums are sums of uniformly distributed random numbers , and hence are also uniformly distributed.
According to the protocol, every party then sends each share exclusively to the corresponding party and keeps private. So, from the party ’s perspective (), it receives from other parties the shares , which are independent and uniformly distributed over a large interval. Then it broadcasts the sum . From the previous discussion, we can say that:
- To learn the shares prepared by , all the parties would have to collude (to be dishonest).
- If the parties are colluding, then they can also learn the private share of from the known as: .
Thus, the protocol does not guarantee feedback privacy in the presence of dishonest parties.
Theorem A1.
The protocol Π guarantees feedback privacy in the presence of at least two honest parties.
Let us assume that at least two parties are honest. This means that the adversary can form a coalition of up to dishonest parties out of k. Let any coalition of s parties such that . For simplicity, we suppose that the first s parties represent the coalition, and are the honest parties. The view of the coalition during the execution of on the feedback values is:
which means the coalition has knowledge of all the feedback values except and has all the shares except those of parties , namely . Knowing that all shares and sums in the coalition view are uniformly distributed values, we show that there exists a probabilistic polynomial time algorithm that can derive any information the coalition can derive from its view by taking as input only the coalition’s feedback values , the output , and some randomness. Let be:
where and are random numbers uniformly generated over the same corresponding large interval as the shares and the sums .
The two distributions generated by and are computationally indistinguishable,
which means that any information the coalition can derive from its view can be derived just from its input and output. Looking at what is possible to derive from the coalition input and output, we can state that it is infeasible to uncover feedback values such as from them. Consequently, is secure with dishonest parties.
We highlight that even if the miner is part of the adversary, their view does not add any information to the coalition, as its view is poorer than a regular participating party:
The target party t can also attempt to uncover parties’ ratings by corrupting other participating parties. Fortunately, unless t controls parties it cannot reach its goal. □
Appendix A.3. Accessibility
, querying for the reputation score of t comes down to searching the state database for after updating its copy to the last one. Since each party has the right to download and maintain a full copy of the blockchain or a light copy including only headers and the state, then it has full access to all reputation scores. Therefore, we can say that the reputation system achieves Accessibility.
Appendix A.4. Consistency
, if a and b query for the reputation score of t at the same time, assuming that they have updated their copies of the state, therefore their copies are identical, and they include the changes introduced by the last confirmed block. Intuitively, a and b are querying the same database. So they will obtain the same reputation value. We can say then that the reputation system is Consistent through the network.
Appendix A.5. Conservation
such that the party a has already rated t at least one time. We can say that a’s rating is part of a transaction recorded in a specific block on the blockchain, which accordingly affects the resulting version of the state, and it especially affects the account state of t and its reputation score.
We recall that transactions are recorded on the blockchain in an immutable way and that all the following blocks and resulting state versions after are affected accordingly. Therefore, if the party a leaves the network, then all its ratings remain part of the blockchain, and the reputation score of t remains a function of its mentioned rating.
As a result, we can say that the reputation system conserves the reputation information.
Appendix A.6. Verifiability
Verifiability is an immediate result of blockchain properties that allow any user that joins the network to grab a copy of the entire blockchain and to go through the list of blocks and transactions that are all public, verifying their integrity and correctness. Indeed, the user can go through the blockchain block by block, from the Genesis block to the last one, executing every single transaction and reflecting on the state. By searching for RATE transactions sent to a target party t, for example, counting the number of feedbacks included in them and computing their average, the user can easily compare the results with the reputation score and weight in t’s state account.
Appendix B. Source Parties’ Manager Smart Contract
| Listing A1. Source Paries Management Smart Contract. |
 |
Appendix C. Reputation Manager Smart Contract
| Listing A2. Reputation Management Smart Contract. |
 |
 |
References
- Jøsang, A.; Ismail, R.; Boyd, C. A Survey of Trust and Reputation Systems for Online Service Provision. Decis. Support Syst. 2007, 43, 618–644. [Google Scholar] [CrossRef]
- Hendrikx, F.; Bubendorfer, K.; Chard, R. Reputation Systems: A Survey and Taxonomy. J. Parallel Distrib. Comput. 2015, 75, 184–197. [Google Scholar] [CrossRef]
- Aberer, K.; Despotovic, Z. Managing Trust in a Peer-2-peer Information System. In Proceedings of the Tenth International Conference on Information and Knowledge Management, Atlanta, GR, USA, 5–10 October 2001; CIKM ’01; ACM: New York, NY, USA, 2001; pp. 310–317. [Google Scholar] [CrossRef]
- Kamvar, S.D.; Schlosser, M.T.; Garcia-Molina, H. The Eigentrust Algorithm for Reputation Management in P2P Networks. In Proceedings of the 12th International Conference on World Wide Web, Budapest, Hungary, 20–24 May 2003; ACM: New York, NY, USA, 2003. WWW ’03. pp. 640–651. [Google Scholar] [CrossRef]
- Ganeriwal, S.; Srivastava, M.B. Reputation-Based Framework for High Integrity Sensor Networks. In Proceedings of the SASN ’04: The 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks, Washington, DC, USA, 25 October 2004; ACM Press: New York, NY, USA, 2004; pp. 66–77. [Google Scholar] [CrossRef]
- Pavlov, E.; Rosenschein, J.S.; Topol, Z. Supporting Privacy in Decentralized Additive Reputation Systems. In Proceedings of the Trust Management; Jensen, C., Poslad, S., Dimitrakos, T., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2004; pp. 108–119. [Google Scholar]
- Hasan, O.; Brunie, L.; Bertino, E. Preserving Privacy of Feedback Providers in Decentralized Reputation Systems. Comput. Secur. 2012, 31, 816–826. [Google Scholar] [CrossRef][Green Version]
- Dimitriou, T.; Michalas, A. Multi-Party Trust Computation in Decentralized Environments. In Proceedings of the 2012 5th International Conference on New Technologies, Mobility and Security (NTMS), Istanbul, Turkey, 7–10 May 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Hasan, O.; Brunie, L.; Bertino, E.; Shang, N. A Decentralized Privacy Preserving Reputation Protocol for the Malicious Adversarial Model. IEEE Trans. Inf. Forensics Secur. 2013, 8, 949–962. [Google Scholar] [CrossRef]
- Clark, M.R.; Stewart, K.; Hopkinson, K.M. Dynamic, Privacy-Preserving Decentralized Reputation Systems. IEEE Trans. Mob. Comput. 2017, 16, 2506–2517. [Google Scholar] [CrossRef]
- Goldreich, O. Foundations of Cryptology; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2003; Volume 1. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Bitcoin. 2008; Volume 4, no 2. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 3 November 2022).
- Hasan, O. A Survey of Privacy Preserving Reputation Systems. (Doctoral dissertation, LIRIS UMR 5205 CNRS/INSA de Lyon/Université Claude Bernard Lyon 1/Université Lumière Lyon 2/École Centrale de Lyon), 2017. Available online: https://hal.science/hal-01635314/document (accessed on 12 January 2023).
- Tian, C.; Yang, B. R2Trust, a Reputation and Risk Based Trust Management Framework for Large-Scale, Fully Decentralized Overlay Networks. Future Gener. Comput. Syst. 2011, 27, 1135–1141. [Google Scholar] [CrossRef]
- Azad, M.A.; Bag, S.; Hao, F.; Shalaginov, A. Decentralized Self-Enforcing Trust Management System for Social Internet of Things. IEEE Internet Things J. 2020, 7, 2690–2703. [Google Scholar] [CrossRef]
- Kugblenu, C.; Vuorimaa, P. Decentralized Reputation System on a Permissioned Blockchain for E-Commerce Reviews. In Proceedings of the 17th International Conference on Information Technology–New Generations (ITNG 2020), Las Vegas, NV, USA, 5–8 April 2020; Advances in Intelligent Systems and Computing. Latifi, S., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 177–182. [Google Scholar] [CrossRef]
- Li, M.; Zhu, L.; Zhang, Z.; Lal, C.; Conti, M.; Alazab, M. Anonymous and Verifiable Reputation System for E-Commerce Platforms Based on Blockchain. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4434–4449. [Google Scholar] [CrossRef]
- Qi, S.; Li, Y.; Wei, W.; Li, Q.; Qiao, K.; Qi, Y. Truth: A Blockchain-Aided Secure Reputation System With Genuine Feedbacks. IEEE Trans. Eng. Manag. 2022, 1–15. [Google Scholar] [CrossRef]
- Debe, M.; Salah, K.; Rehman, M.H.U.; Svetinovic, D. IoT Public Fog Nodes Reputation System: A Decentralized Solution Using Ethereum Blockchain. IEEE Access 2019, 7, 178082–178093. [Google Scholar] [CrossRef]
- Liu, D.; Alahmadi, A.; Ni, J.; Lin, X.; Shen, X. Anonymous Reputation System for IIoT-Enabled Retail Marketing Atop PoS Blockchain. IEEE Trans. Ind. Inform. 2019, 15, 3527–3537. [Google Scholar] [CrossRef]
- Weerapanpisit, P.; Trilles, S.; Huerta, J.; Painho, M. A Decentralised Location-Based Reputation Management System in the IoT Using Blockchain. IEEE Internet Things J. 2022, 9, 15100–15115. [Google Scholar] [CrossRef]
- Singh, S.K.; Park, J.H. TaLWaR: Blockchain-Based Trust Management Scheme for Smart Enterprises With Augmented Intelligence. IEEE Trans. Ind. Inform. 2023, 19, 626–634. [Google Scholar] [CrossRef]
- Azad, M.A.; Bag, S.; Hao, F. PrivBox: Verifiable Decentralized Reputation System for Online Marketplaces. Future Gener. Comput. Syst. 2018, 89, 44–57. [Google Scholar] [CrossRef]
- Bag, S.; Azad, M.A.; Hao, F. A Privacy-Aware Decentralized and Personalized Reputation System. Comput. Secur. 2018, 77, 514–530. [Google Scholar] [CrossRef]
- Mirhosseini, S.A.M.; Fanian, A.; Gulliver, T.A. A Trust and Reputation System for IoT Exploiting Distributed Ledger Technology. arXiv 2021, arXiv:2111.13500. [Google Scholar]
- Wang, J.; Chen, W.; Wang, L.; Sherratt, R.; Alfarraj, O.; Tolba, A. Data Secure Storage Mechanism of Sensor Networks Based on Blockchain. Comput. Mater. Contin. 2020, 65, 2365–2384. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, S.; Wang, J.; Yu, X.; Alfarraj, O. A Storage Optimization Scheme for Blockchain Transaction Databases. Comput. Syst. Sci. Eng. 2021, 36, 521–535. [Google Scholar] [CrossRef]
- Guruprakash, J.; Koppu, S. EC-ElGamal and Genetic Algorithm-Based Enhancement for Lightweight Scalable Blockchain in IoT Domain. IEEE Access 2020, 8, 141269–141281. [Google Scholar] [CrossRef]
- Jayabalasamy, G.; Koppu, S. High-Performance Edwards Curve Aggregate Signature (HECAS) for Nonrepudiation in IoT-based Applications Built on the Blockchain Ecosystem. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 9677–9687. [Google Scholar] [CrossRef]
- Alzoubi, Y.I.; Al-Ahmad, A.; Kahtan, H. Blockchain Technology as a Fog Computing Security and Privacy Solution: An Overview. Comput. Commun. 2022, 182, 129–152. [Google Scholar] [CrossRef]
- Najafi, M.; Khoukhi, L.; Lemercier, M. Decentralized Reputation Model Based on Bayes’ Theorem in Vehicular Networks. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Xiamen, China, 28–30 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, S.; Seo, S.H. Design of a Two Layered Blockchain-Based Reputation System in Vehicular Networks. IEEE Trans. Veh. Technol. 2022, 71, 1209–1223. [Google Scholar] [CrossRef]
- Antonopoulos, A.M. Mastering Bitcoin: Programming the Open Blockchain; O’Reilly Media, Inc. 1005 Gravenstein Highway North: Sebastopol, CA, USA, 2017. [Google Scholar]
- Wood, D.G.; Ethereum: A Secure Decentralised Generalised Transaction Ledger. Ethereum Project Yellow Paper; 2014. Available online: https://ethereum.github.io/yellowpaper/paper.pdf (accessed on 26 February 2022).
- Tschorsch, F.; Scheuermann, B. Bitcoin and Beyond: A Technical Survey on Decentralized Digital Currencies. IEEE Commun. Surv. Tutorials 2016, 18, 2084–2123. [Google Scholar] [CrossRef]
- Garay, J.; Kiayias, A.; Leonardos, N. The Bitcoin Backbone Protocol: Analysis and Applications. In Proceedings of the Advances in Cryptology—EUROCRYPT 2015; Oswald, E., Fischlin, M., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2015; pp. 281–310. [Google Scholar] [CrossRef]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine Generals Problem. ACM Trans. Program. Lang. Syst. 2016, 4, 382–401. [Google Scholar] [CrossRef]
- Peck, M. The Bitcoin Arms Race Is On!—IEEE Spectrum. 2013. Available online: https://spectrum.ieee.org/computing/networks/the-bitcoin-arms-race-is-on (accessed on 14 February 2022).
- King, S.; Nadal, S. PPCoin: Peer-to-Peer Crypto-Currency with Proof-of-Stake. Self-Published Paper, August, 2012, Volume 19, no 1. Available online: https://bitcoin.peryaudo.org/vendor/peercoin-paper.pdf (accessed on 3 May 2022).
- Vasin, P. BlackCoin’s Proof-of-Stake Protocol V2 2014. 2014, Volume 71, p. 2. Available online: https://blackcoin.co/blackcoin-pos-protocol-v2-whitepaper.pdf (accessed on 3 May 2022).
- Nxt Community. Nxt Whitepaper—Introduction: Nxt Whitepaper. Available online: https://nxtdocs.jelurida.com/Nxt_Whitepaper (accessed on 29 January 2023).
- Davarpanah, K.; Kaufman, D.; Pubellier, O. NeuCoin: The First Secure, Cost-Efficient and Decentralized Cryptocurrency. arXiv 2015, arXiv:1503.07768. Available online: https://arxiv.org/pdf/1503.07768 (accessed on 3 May 2022). [CrossRef]
- Damgård, I.; Pastro, V.; Smart, N.; Zakarias, S. Multiparty Computation from Somewhat Homomorphic Encryption. In Proceedings of the Advances in Cryptology–CRYPTO 2012, Barbara, CA, USA, 19–23 August 2012; Lecture Notes in Computer Science. Safavi-Naini, R., Canetti, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 643–662. [Google Scholar] [CrossRef]
- Damgård, I.; Keller, M.; Larraia, E.; Pastro, V.; Scholl, P.; Smart, N.P. Practical Covertly Secure MPC for Dishonest Majority – Or: Breaking the SPDZ Limits. In Proceedings of the Computer Security–ESORICS 2013, Egham, UK, 9–13 September 2013; Crampton, J., Jajodia, S., Mayes, K., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–18. [Google Scholar] [CrossRef]
- Keller, M.; Pastro, V.; Rotaru, D. Overdrive: Making SPDZ Great Again. In Proceedings of the Advances in Cryptology–EUROCRYPT 2018; 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, 29 April–3 May 2018; pp. 158–189. [Google Scholar] [CrossRef]
- Keller, M. MP-SPDZ: A Versatile Framework for Multi-Party Computation. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, USA, 9–13 November 2020; pp. 1575–1590. [Google Scholar] [CrossRef]
- Rindal, P.; Rosulek, M. Faster Malicious 2-Party Secure Computation with Online/Offline Dual Execution. In Proceedings of the 25th USENIX Conference on Security Symposium, Austin, TX, USA, 10–12 August 2016; SEC’16; USENIX Association: Berkeley, CA, USA, 2016; pp. 297–314. [Google Scholar]
- Wang, X.; Ranellucci, S.; Katz, J. Authenticated Garbling and Efficient Maliciously Secure Two-Party Computation. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; CCS ’17; Association for Computing Machinery: New York, NY, USA, 2017; pp. 21–37. [Google Scholar] [CrossRef]
- Gueron, S.; Lindell, Y.; Nof, A.; Pinkas, B. Fast Garbling of Circuits Under Standard Assumptions. J. Cryptol. 2018, 31, 798–844. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play ANY Mental Game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; STOC ’87; Association for Computing Machinery: New York, NY, USA, 1987; pp. 218–229. [Google Scholar] [CrossRef]
- Dimitriou, T.; Karame, G.; Christou, I. SuperTrust – A Secure and Efficient Framework for Handling Trust in Super Peer Networks. In Proceedings of the Twenty-Sixth Annual ACM Symposium on Principles of Distributed Computing, Portland, OR, USA, 12–15 August 2007; pp. 374–375. [Google Scholar] [CrossRef]
- Jøsang, A.; Luo, X.; Chen, X. Continuous Ratings in Discrete Bayesian Reputation Systems. In Proceedings of the Trust Management II, IFIP – The International Federation for Information Processing, Trondheim, Norway, 18–20 June 2008; Karabulut, Y., Mitchell, J., Herrmann, P., Jensen, C.D., Eds.; Springer US: Boston, MA, USA, 2008; pp. 151–166. [Google Scholar] [CrossRef]
- Abdul-Rahman, A.; Hailes, S. Supporting Trust in Virtual Communities. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 4–7 January 2000; pp. 1–9. [Google Scholar] [CrossRef]
- Zhou, R.; Hwang, K. PowerTrust: A Robust and Scalable Reputation System for Trusted Peer-to-Peer Computing. IEEE Trans. Parallel Distrib. Syst. 2007, 18, 460–473. [Google Scholar] [CrossRef]
- Nithyanand, R.; Raman, K. Fuzzy Privacy Preserving Peer-to-Peer Reputation Management. Cryptology ePrint Archive.. 2009. Available online: https://eprint.iacr.org/2009/442.pdf (accessed on 12 February 2022).
- Bertoni, G.; Peeters, M.; Assche, G.V.; Daemen, J. The KECCAK Reference; 2011. Available online: https://keccak.team/files/Keccak-reference-3.0.pdf (accessed on 10 February 2022).
- Solidity. Solidity 0.8.17 Documentation. Available online: https://docs.soliditylang.org/en/v0.8.17/ (accessed on 11 November 2022).
- Johnson, D.; Menezes, A.; Vanstone, S. The Elliptic Curve Digital Signature Algorithm (ECDSA). Int. J. Inf. Secur. 2001, 1, 36–63. [Google Scholar] [CrossRef]
- Martínez, V.G.; Encinas, L.H.; Ávila, C.S. A Survey of the Elliptic Curve Integrated Encryption Scheme. J. Comput. Sci. Eng. 2010, 2, 7–13. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ganache. Ganache|Overview–Truffle Suite. Available online: https://trufflesuite.com/docs/ganache/ (accessed on 10 November 2022).
- Web3.js. Ethereum JavaScript API—Web3.Js 1.8.0 Documentation. Available online: https://web3js.readthedocs.io/en/v1.8.0/ (accessed on 11 November 2022).
- Node.js. Available online: https://nodejs.org/en/ (accessed on 8 November 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).