MANET Performance Optimization Using Network-Based Criteria and Unmanned Aerial Vehicles

Abstract

In this contribution we consider the problem of optimal drone positioning for improving the operation of a mobile ad hoc network. We build upon our previous results devoted to the application of game-theoretic methods for computing optimal strategies. One specific problem that arises in this context is that the optimal solution cannot be uniquely determined. In this case, one has to use some other criteria to choose the best (in some sense) of all optimal solutions. It is argued that centrality measures as well as node ranking can provide a good criterion for the selection of a unique solution. We showed that for two specific networks most criteria yielded the same solution, thus demonstrating good coherence in their predictions.

1. Introduction

In this paper we consider the problem of optimizing information transmission in self-organizing networks of various configurations using a game-theoretic approach. Self-organization means that the considered networks are formed by agents (transceivers) without any pre-existing network infrastructure (cell towers, routers, etc.) Such mobile networks are commonly referred to as Mobile Ad Hoc Networks (MANET) or Wireless Ad Hoc Networks (WANET) [1]. Since recently, there has been an increased interest in studying such systems, see, e.g., an overview in [1]. One specific direction of study that proved to be very useful in solving different problems related to the optimization of mobile networks consists in the application of game-theoretic methods [2,3]. Another important aspect is related to the resilience analysis of such networks, [4,5,6], see also the papers [7,8], where the issue of network resilience is addressed using the game-theoretic methods.

Often, mobile ad-hoc networks are used in situations when it is necessary to organize communication between groups of people in an area where cellular communication is not available. The application of this technology could potentially save lives. For instance, during search and rescue operations communication between search parties is a key requirement. When natural disasters occur, there is disruption to the communications infrastructure, the faster that communication can be established the faster search efforts can be coordinated. A mobile ad-hoc network does not rely on a predefined communications infrastructure and can be deployed quickly; a further advantage of this network is the mobility of the communicating nodes.

To consider more specific examples, MANETs are widely used to support the actions of rescue groups in mountains, swamps and other difficult-to-pass areas, [9,10]. Some groups use portable equipment to communicate with others. Moreover, due to restrictions on the transmission range of the radio signal, as well as landscape restrictions of the terrain, information often does not go directly, but through other network nodes, which act as intermediaries, broadcasting the message over the network.

When deploying a mobile network it is important to ensure that all agents can enjoy an efficient and stable communication. It is thus of particular importance to develop some approaches aimed at increasing network connectivity. Most results are focused on optimizing the routing protocols as in [11,12], possibly combined with topology management [13]. Among several paper developing alternative approaches we wish to mention [14], where the authors analyzed a MANET formed by unmanned air vehicles (UAV) and considered several approaches for computing the location and movement of UAVs based upon different connectivity models. While the mobile network formed by UAVs enjoys great flexibility, it is often not possible to use a large number of UAVs. There has been a number of papers analyzing the effect of introducing a limited number of UAVs to increase the overall performance of a MANET, see e.g., [15,16,17]. However, these papers consider the problem of placing an UAV in a broader context, without specifically taking into account the topology of a given MANET.

In this contribution we consider a particular problem statement in which the agents belong to several groups [18]. Each group is controlled by the respective control center (which we will refer to as the player later on) and contains a certain fixed set of agents (nodes). Only agents of the same player can transfer information to each other. In the considered variant of the problem, network agents are motionless. Optimization of the network operation is performed by changing its structure by adding new agents to it. Each player has a drone with a transceiver that can be placed in a certain position and connected to the network, and in addition, unlike stationary agents, a drone can interact with agents of any player.

It is to be stressed that the main feature of drones that we exploit in this paper is their mobility. In contrast to nearly static terrestrial nodes, a drone can be placed at any location at players’ will. Most papers on the use of drones do not address the problem of optimal drone location, but rather analyze their transmission, energy or protocol characteristics. The only paper that considers a similar setup is by Han et al. [14]. However, in this paper the authors assume that all agents can be arbitrarily placed, which is quite a strong assumption.

Within the stated research program, there have been several papers dealing with the problem of optimal placing of drones under different assumptions about the players’ strategies, see [18,19,20]. However, as was previously shown, the computed optimal solutions are in general non-unique. Hence, in this paper we address the problem of determining the best in some sense optimal solution based upon certain characteristics developed within the context of network theory [21] (see the recent paper [22] for an example of using different centrality measures). It should be noted that there have been a number of results devoted to the application of methods from network theory to the analysis and optimization of MANETs, see e.g., [23,24,25,26]. However, none of the mentioned works considered the problem of optimizing the interconnection structure of the mobile network.

This paper is organized as follows: Section 2 introduces the mathematical ingredients that are needed to formalize the obtained results. In Section 3, we consider different centrality measures and the node ranking algorithm used in the paper. Section 4 describes the application of considered measures to specific mobile networks, while Section 5 illustrates the obtained results with numerical simulation. The discussion section concludes the paper.

2. Mathematical Model

In the following, the mobile network is considered in the form of a graph. The task is to find positions for the drones of each player in order to maximize the total payoff of the players, where the individual payoff of each player is the amount of decrease in the diameter of its subgraph after the drone is “launched”. Each of the found positions will be the desired strategy of the corresponding player. The problem is solved in a cooperative version, since it is the total gain that is optimized. As a result, there are many optimal solutions that give the same maximum total payoff. Therefore, it is necessary to determine the criterion for selecting a solution. Below, we present the necessary mathematical notation and definitions that will be used in the sequel.

2.1. Game-Theoretic Description of the Problem

We consider the set $\mathcal{N}=\{1,\dots ,N\}$ of N players and assume that each player $i\in \mathcal{N}$ has a non-empty set ${\mathcal{A}}_i=\left\{a_i^j\right\}$, $j=1,\dots ,k_i$, of agents. We associate an agent with its coordinates $(x_i^j,y_i^j)$ and write $a_i^j=(x_i^j,y_i^j)$. Any agent can communicate with the adjacent agents of the same player.

We further assume that the agents can be located at the vertices of a uniform grid spanning a connected subset of the Euclidean plane $X\subset {\mathbb{R}}^2$. In practice, one considers three kinds of grids: the triangular, the Cartesian (integer), and the hexagonal grids, which are formed by arranging the nodes in a mesh of equilateral triangles, squares, and hexagons. This implies, in particular, that in the respective grids an agent can have at most 6, 4, resp. 3 neighbors, i.e., adjacent agents. Henceforth we will denote the set of all admissible coordinates by $W\subset X$.

While a MANET typically has a dynamic topology, we look at a snapshot of the network at a given point in time. Thus, we assume that the communication network formed by the respective agents does not change with time.

The key aspect of the considered setup consists in the use of drones. Each player has a mobile agent (drone), denoted ${\delta }_i$, at their disposal. This drone can be placed at any point of the grid at player’s will. It is further assumed that a drone can communicate with all agents within its reach and can be used to transmit information by the agents of all players. The considered problem fits well the game-theoretic framework as different players may have stride to achieve distinct, not necessarily aligned goals. Considering the problem from this viewpoint, the player’s strategy corresponds to choosing the location of the drone. The respective optimization problem consists in determining an optimal strategy such that the payoff function of the respective player is maximized. The formal definition of the respective payoff functions will be defined in Section 2.4.

2.2. Network Structure

The considered networks can well be described by undirected graphs as detailed in the following.

An undirected graph G is defined as a tuple $G=(V,E)$, where V is the set of vertices, and $E\subseteq V\times V$ is the set of edges. We let $N_V$ denote the number of the vertices and $N_E$ the number of edges in the graph, i.e., $N_V=\left|V\right|$ and $N_E=\left|E\right|$. We consider graphs without self-loops, i.e., $(v_i,v_i)\notin E$ for all $v_i\in V$. The graph is said to be fully connected if any two distinct vertices are connected by an edge. In this case, $N_E=N_V(N_V-1)$, which is the maximal possible number of edges, denoted ${\overline{N}}_E$.

In a MANET, all vertices correspond to agents and hence are characterized by their physical coordinates. We define a location function $\sigma :\mathcal{V}\to {\mathbb{R}}^2$ that associates to any vertex its physical coordinates. As was said above, these coordinates do not need to be the physical coordinates, but can belong to the grid space and hence be restricted to a particular subset of ${\mathbb{R}}^2$. There is an edge between two vertices if the respective agents are located in the adjacent nodes of the respective grid. Thus, the set of edges is determined on the basis of the agents’ coordinates. We will reflect this by writing a graph as a triple $\mathcal{G}=(\mathcal{V},\sigma ,{\mathcal{E}}_{\sigma })$, where the coordinate function is introduced above and the set of edges ${\mathcal{E}}_{\sigma }$ is defined on the base of vertices adjacency. The definition of $\sigma$ and ${\mathcal{E}}_{\sigma }$ depends on the specific aspects of the network realization and will not be addressed here.

In this paper, we will consider the situations when the existing network is extended by an additional vertex (e.g., a drone). We formalize this as follows. Let $\mathcal{G}=(\mathcal{V},\sigma ,{\mathcal{E}}_{\sigma })$ be a graph and w be a vertex that does not belong to the set $\mathcal{V}$. We define the union $\tilde{\mathcal{G}}=\mathcal{G}\cup \left\{w\right\}$ to be a new graph with an extended set of vertices $\tilde{\mathcal{V}}=\mathcal{V}\cup \left\{w\right\}$ and the accordingly adjusted set of edges ${\tilde{\mathcal{E}}}_{\sigma }$. The union operation can obviously be extended to the case $\mathcal{G}\cup S$, where S is a set of agents $S={\left\{s_i\right\}}_{i=1}^k$. The exclusion operation $\mathcal{G}=\tilde{\mathcal{G}}\backslash \left\{w\right\}$ is defined in a similar way. Note that $\tilde{\mathcal{G}}$ can be disconnected if the location of the added vertex is such that no edge can form between this vertex and the remaining vertices of the graph.

The diameter of the graph $\mathcal{G}$, denoted by $D\left(\mathcal{G}\right)$, is defined as

$$D\left(\mathcal{G}\right)=\underset{(v_i,v_j)\in \mathcal{V}\times \mathcal{V}}{max}d(v_i,v_j),$$

where $d(v_i,v_j)$ is the shortest path between two vertices $v_i$ and $v_j$. If no such path exists, $d(v_i,v_j)=\infty$. This implies, in particular, that a disconnected graph has an infinite diameter.

2.3. Mobile Agent: Drone

Each player has a drone ${\delta }_i$ at their disposal. The drone can be placed at any admissible point in W. While all the (stationary) agents have fixed coordinates, the position of the moving agent ${\delta }_i$, $i\in \mathcal{N}$ can be changed during the game. The edge between the moving agent and another agent is defined on the base of adjacency, similarly to the way the edges between the stationary agents are formed. In general, the moving agent ${\delta }_i$ can have a larger transmissibility radius and hence can establish a link with other moving agents ${\delta }_j$ and other stationary agents $v_i^p\in {\mathcal{A}}_i$, $i\in \mathcal{N}$, that are located at a larger distance. However, this formulation does not lead to a substantial improvement in terms of theoretical analysis, except for increased notation. We thus stick to the original formulation in which a drone can communicate only with the adjacent vertices.

The set of all drones is denoted by by $\Delta ={\left\{{\delta }_i\right\}}_{i=1}^N$ and the set of all drones except the ith one by ${\Delta }_{-i}=\Delta \backslash \left\{{\delta }_i\right\}$.

2.4. Optimization Problem

For any type of communication structure the ith player solves the following optimization problem:

$${\overline{q}}_i=\underset{q_i\in W_i^{\ast }}{\arg \min }D({\mathcal{G}}_i^{\ast },{\mathcal{V}}_i),$$

(1)

where ${\mathcal{G}}^{\ast }$ is the extended graph and $W_i^{\ast }=W\backslash Q_{-i}$ is the set of admissible locations for the ith drone. The latter notation means that a drone cannot be placed at the position currently occupied by another drone. We have ${\mathcal{G}}_i^{\ast }={\mathcal{G}}_i\cup Q$, that is each player aims at placing its moving agent $q_i$ such that it minimizes the diameter of the player’s graph. Note that the drones themselves are not considered when computing the diameter of the graph as they are not assumed to be the sources of any useful information, but merely transmit information between the agents. Within this framework, we assume that each drone can be used by the agents of any player, i.e., the players cooperate through the collective use of transmission capabilities provided by drones.

Accordingly, the pay-off (utility) function of the ith player is defined as the difference between the diameter of the respective graph before placing the drone and afterwards:

$$H_i(\mathcal{G},Q)=D({\mathcal{G}}_i,{\mathcal{V}}_i)-D({\mathcal{G}}_i^{\ast },{\mathcal{V}}_i)\ge 0,$$

(2)

where $\overline{{\mathcal{G}}_i^{\ast }}={\mathcal{G}}_i^S\cup Q$. Note that the pay-off function is always non-negative as the drone is not considered when computing the diameter and hence cannot increase its value.

Within a game-theoretical framework one typically considers one of two possible optimal solutions: cooperative solution and a Nash equilibrium solution. The former one corresponds to the case when all players act together and aim at maximizing their total pay-off, while the latter one appears when each player maximizes their own pay-off function. In [18,19,20], the problem of determining the Nash equilibrium and best-reply solutions was was studied in detail within the framework of multi-stage and one-stage (static) games.

One specific issue that arose in the context of game-theoretic analysis of the problem consists in the non-uniqueness of the obtained solution. While this fact does not restrict the application of suggested techniques, it is desirable to exploit the additional degree of freedom that appears because of this non-uniqueness.

Specifically, we consider the cooperative scenario in which the players aim at maximizing their joint profit. In most considered problems the solution turns out to be non-unique, that is there are several possible positions for the drones that result in the same decrease in the network diameter. We thus consider several possibilities to further improve the performance of the overall mobile network using the methods from network theory as specified in the subsequent sections.

3. Centrality Measures and Node Ranking

After finding the set of optimal solutions to the problem, the question arises-how to choose the only solution? To answer it, it is necessary, first, to pay attention to the contribution of the installed drones to the speed of information transfer in the network as a whole. Secondly, one has to go beyond the stated goal and pay attention to other aspects of the system’s functioning. One of the most important of these aspects is the resilience of the network to the failure of some nodes. For example, if the most “extreme” node that interacts with only one of the nodes fails, then the interaction within the rest of the network will not be disrupted in any way. But if the failed node turns out to be the only one connecting between two separate parts of the network, then the structure will split in two parts that will not be able to interact with each other. Accordingly, the drone should be placed in a position that, to some extent, preserves the overall structure of the network when the central nodes fail. Both of these tasks-improving the operation of the network as a whole and increasing its resilience to breakdowns can be solved simultaneously using the measures of centrality [21] of network nodes.

Measures of centrality of network nodes allow to determine the value of the “contribution” that each of the nodes makes to the overall structure. The larger this value is, the more important the node is from the point of view of the network structure. That is to say, if it fails (i.e., when the corresponding vertex is removed from the network graph), the interaction of the remaining nodes will be significantly disrupted.

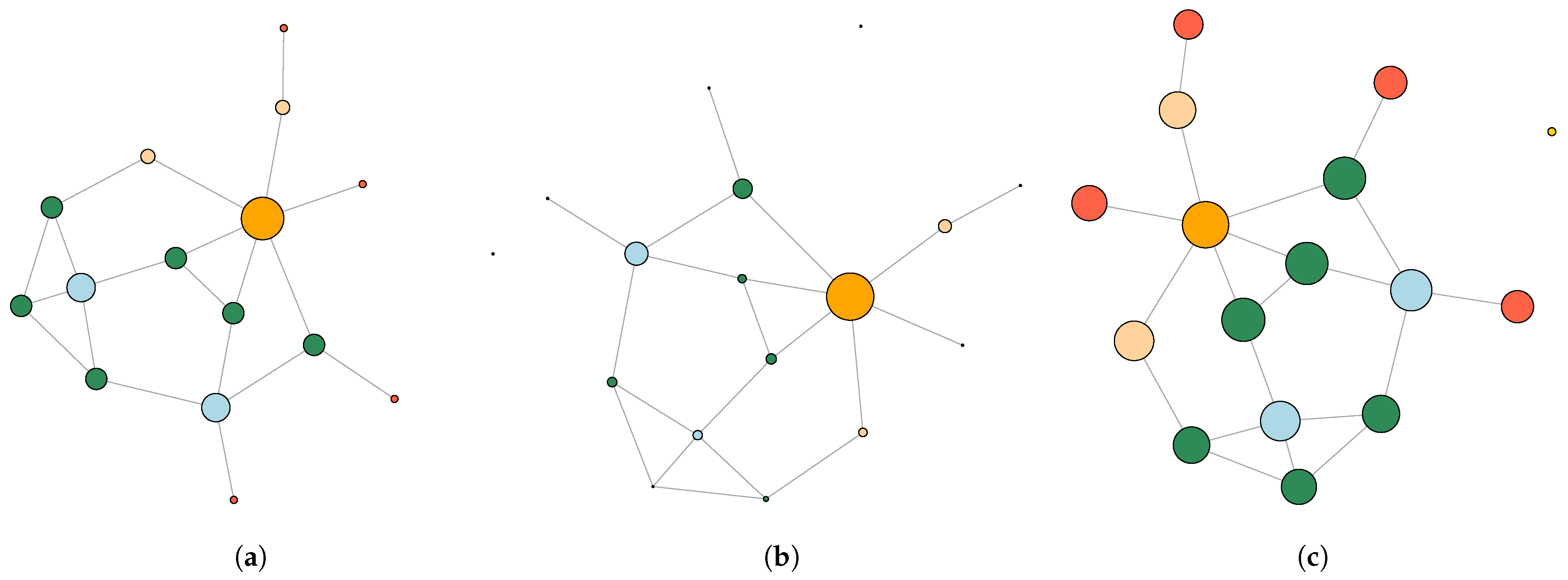
To evaluate the contribution of the respective node we will use different centrality measures. Below we consider several most widely used centrality measures. The simplest one the number of neighbors of a node, called the degree centrality:

$$C_D\left(v\right)=deg\left(v\right),$$

where $deg\left(v\right)$ is the number of neighbors of the vertex $v\in V$. In Figure 1, three different centrality measures are shown for a sample graph. Apart from degree centrality, also the betweenness centrality and closeness centrality, described below, are shown.

The next measure called the betweenness centrality appears to be better suited for this problem as it addresses the problem of optimizing the transmission of information in the network as a whole, as well as the requirement described above to preserve the structure of the network in the event of failure of the key nodes that gate the largest amount of information. When calculating this measure, the shortest paths between different pairs of nodes in the network are considered, while taking into account which nodes these paths pass through. The more shortest paths pass through a certain node, the greater its measure of centrality from the point of view of information transmission, since routing algorithms calculate exactly the shortest possible paths in the network. Thus, the formula for calculating this measure is as follows:

$$C_B\left(v\right)=\sum _{s\ne v\ne t}\frac{{\pi }_{st}\left(v\right)}{{\pi }_{st}},$$

where ${\pi }_{st}\left(v\right)$ is the number of the shortest paths between nodes s and t passing through the node v, and ${\pi }_{st}$ is the total number of shortest paths between nodes s and t.

Finally, the last measure, called the closeness centrality, measures the centrality of nodes by determining how close a node is to the others. The degree of closeness of a node in the network is thus computed as the inverse value of the sum of its distances to all other nodes:

$$C_C\left(v\right)=\frac{1}{{\sum }_{u\ne v}\mathrm{dist}(u,v)},$$

where the distance function $\mathrm{dist}(u,v)$ is defined in an appropriate way. For instance, for the mobile network defined on a Manhattan grid, the distance between two nodes can be taken as the Euclidean distance.

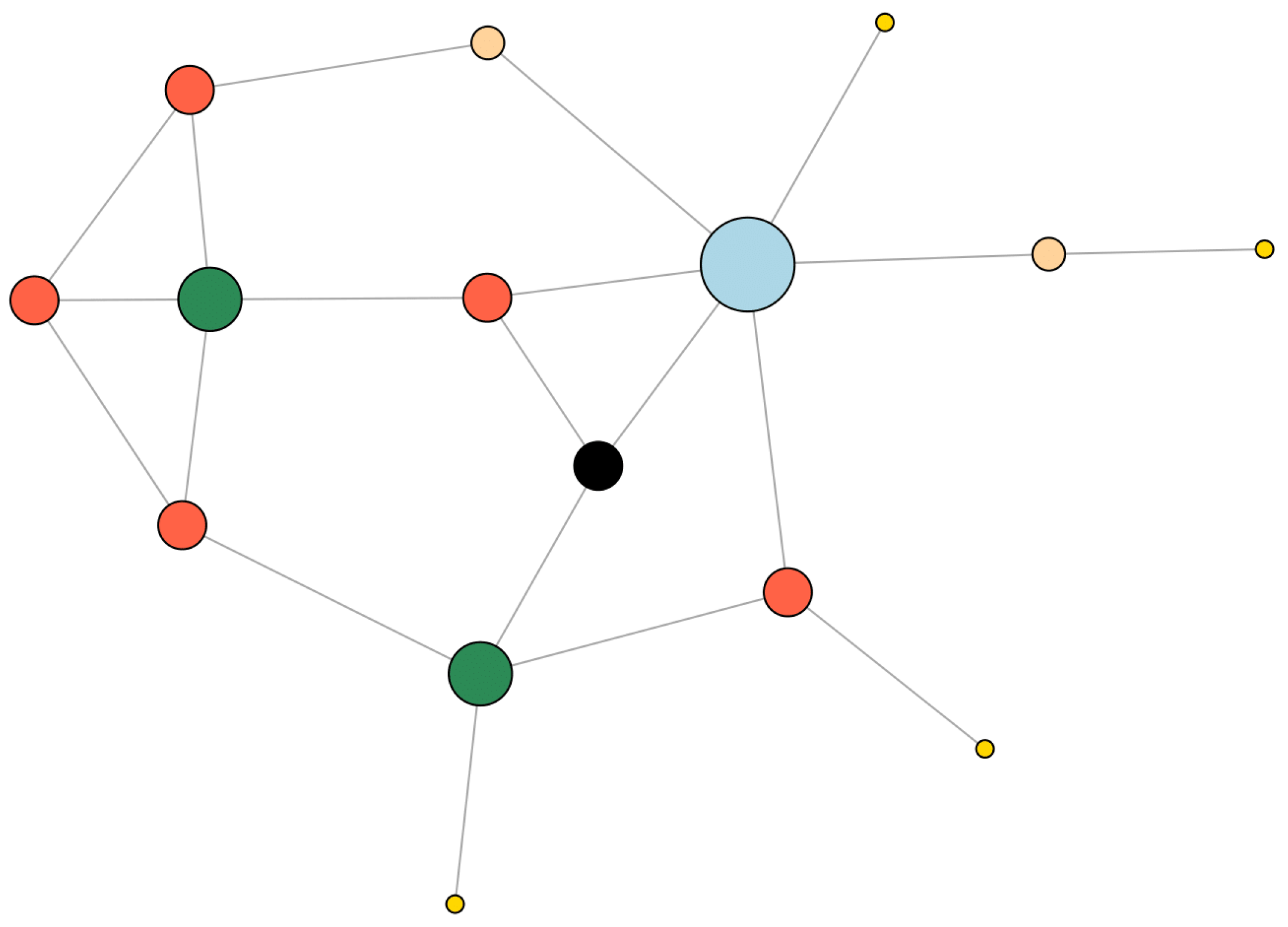
  PageRank  

The PageRank algorithm [27] can be seen as an extension of the centrality measures described above. The idea of this algorithm is that any node has its value that it shares with all neighboring nodes and itself in equal proportion (sometimes the share of the value that the node shares with itself is assumed to be slightly larger: this is controlled by the parameter $\alpha$). To describe this formally, we introduce the normalized adjacency matrix $\tilde{A}\left(G\right)$ of the graph G, whose elements are defined as follows:

$$a_{ij}=\left\{\begin{array}{cc}\alpha ,\hfill & i=j\hfill \\ \frac{1}{deg\left(j\right)},\hfill & \left(ij\right)\in E\left(G\right)\hfill \\ 0,\hfill & \left(ij\right)\notin E\left(G\right).\hfill \end{array}\right.$$

The values of the nodes are thus obtained as the solution of the fixed point problem $\tilde{A}\left(G\right)w=w$ or, put differently, $w=\mathcal{N}(I-\tilde{A}\left(G\right))$, where $\mathcal{N}$ denotes the null space. Note that there are some modifications of the described scheme aimed at improving its numerical stability. However, these differences will not be addressed in this contribution.

Figure 2 illustrates the application of the PageRank algorithm to the same sample graph as in Figure 1c.

4. Results

4.1. First Mobile Network

To illustrate the described approach we consider a specific configuration of the mobile network shown in Figure 3.

There, two sets of agents, indicated by dark red and yellow circles, form two networks. This scheme illustrates a rather common situation when a group of agents is deployed to a difficult region where there are some obstacles preventing the group from forming a dense mobile network. The goal of the players is to place the drones in the way that the sum of the respective payoff is maximal. We recall that the payoffs of the players are defined as the decrease in the diameter of the network after placing the drones, (2). The original diameters of the respective networks are $D\left(R_1\right)=15$ and $D\left(R_2\right)=16$.

The described optimization problem has 4 solutions which are presented in

Table 1. Optimal strategies: Network 1.

Strategy	Drone of the 1st Player	Drone of the 2nd Player	Payoff Function
1	(3; 4)	(3; 3)	(6; 6)
2	(4; 4)	(4; 3)	(6; 6)
3	(3; 3)	(3; 4)	(6; 6)
4	(4; 3)	(4; 4)	(6; 6)

. Two of the listed solutions are shown in Figure 4.

Thus, one faces the problem that was mentioned above: there are several optimal solutions that yield the same value of the total payoff function. To chose a unique solution we use different centrality measures introduced above.

Table 2. Centrality measures computed for two optimal positions of the drones. The respective values for the first and the second drone are separated by a slash: $C_x\left({\delta }_1\right)/C_x\left({\delta }_2\right)$.

1st Drone	2nd Drone	Degree Centrality	Betweenness Centrality	Closeness Centrality	PageRank
(3; 4)	(3; 3)	2/2	42/42	0.016/0.016	0.054/0.054
(4; 4)	(4; 3)	2/2	45.5/45.5	0.018/0.018	0.053/0.053

contains the values of several centrality measures computed for specific positions of the drones. In there, we considered only two cases as the remaining two are equivalent to the original ones up to relabeling the drones.

One can see that while Degree centrality is not informative as it yields the same result for all positions, other centrality measures allow to distinguish between two positions. It can also be observed that while both the betweenness centrality and closeness centrality indicate that the second solution is better in terms of the respective measures, the rank of the second solution is slightly smaller than the rank of the first solution. This apparent contradiction disappears if we consider the normalized ranks of the nodes, i.e., the ranks divided by the maximal rank over all nodes. In this case, the normalized rank of the first solution is equal to $\frac{0.054}{0.079}=0.676$, while the normalized rank of the second solution is $\frac{0.053}{0.077}=0.680$, which is larger than the preceding number. It should be noted that both betweenness and closeness centrality measures the normalized values demonstrate the same order pattern: the normalized centrality measures for the second solution are larger than those of the first solution. Thus we conclude that the second solution outperforms the first one in terms of both centrality measures and PageRank weights.

4.2. Second Mobile Network

To provide a further illustration we consider a different configuration of the mobile network shown in Figure 5. There, two sets of agents, indicated by dark blue and light blue circles, form two networks. The original diameters of the respective networks are $D\left(R_1\right)=10$ and $D\left(R_2\right)=14$.

Similar to the previous case, there are 4 optimal solutions. Two of them are shown in

Table 3. Optimal strategies: Network 2.

Strategy	Drone of the 1st Player	Drone of the 2nd Player	Payoff Functions
1	(5; 4)	(5; 3)	(0; 6)
2	(5; 4)	(4; 4)	(3; 3)

, the remaining two are obtained by interchanging the roles of the drones. The respective positions of the drones are shown in Figure 6.

However, the considered situation differs quite a lot from the previous case in that the position of drones influences the respective subgraphs to a different extent. While the first strategy results in a dramatic reduction of the diameter of the second subgraph, the diameter of the first subgraph remains unchanged. The second strategy is more balanced in contrast to the first one: it reduces the diameters of both graphs, but to a lesser extent.

Similarly to the previous case, the respective centrality measures for both drones are presented in

Table 4. Centrality measures computed for two optimal positions of the drones. The respective values for the first and the second drone are separated by a slash: $C_x\left({\delta }_1\right)/C_x\left({\delta }_2\right)$. Normalized values of PageRank measures are shown in round brackets.

1st Drone	2nd Drone	Degree Centrality	Betweenness Centrality	Closeness Centrality	PageRank	Subgraph
(5; 4)	(5; 3)	2/1	12/0	0.016/0.013	0.08/0.045 (0.722/0.403)	1
		2/2	37/36	0.015/0.015	0.055/0.055 (0.669/0.670)	2
(5; 4)	(4; 4)	2/2	17.7/21.7	0.025/0.028	0.067/0.065 (0.659/0.636)	1
		2/3	28/60.5	0.018/0.021	0.051/0.071 (0.65/0.916)	2

. We present the computed characteristics for each subgraph separately. It can be readily seen that the centrality measures differ quite a lot for both subgraphs: for the first solution the centrality measures of the respective are quite small for the first subgraph (with the only exception for the rank of the first drone) and somewhat larger for the second subgraph (there is a substantial increase in Betweenness centrality). However, the second solution yields a substantial increase in all centrality measures compared to the first solution.

It is worth noting that while the first solution was locally better than the second one, the total value of all centrality measures corresponding to the second solution substantially exceeded the respective characteristics computed for the first solution. The numerical analysis supports the conclusion that the second solution results in a better overall performance than the first one.

We thus conclude that the total value of the respective centrality measure can serve as an appropriate measure for determining the better among several alternative choices.

5. Numerical Simulation

5.1. Simulation Environment

In this work, the NS-3 network simulator [28,29] was chosen as the simulation environment. NS-3 is a discrete event simulator that was designed to provide an open, flexible network modeling platform for research and education. NS-3 can be used to model various packet data networks and simulate their work. This tool is widely used to study the operation of large networks, as well as a validation tool for analytical models and algorithms under study. The network simulator allows one to conduct experiments without the need to deploy a real network, which can significantly reduce costs, reduce the labor intensity of the process and ensure sufficient speed and efficiency in organizing the simulation.

While the existing models set in NS-3 focus on simulating the operation of internet protocols and networks, the simulator is not limited to internet systems: it is possible to use NS-3 to simulate non-internet systems such as human behavior in society, analysis of the epidemiological dynamics, transport system functioning, etc. This flexibility is determined by the modular structure the simulator, which is designed as a set of libraries that can be combined with each other as well as with other external software libraries. The NS-3 can also use external animators and data analysis and visualization tools.

5.2. Problem Formulation and Analysis

The simulation model was written in C ++ using third party libraries provided by the NS-3 simulator. The program takes as input the file that has the following format: the first line is the number of nodes in the network. Next come the coordinates of all the nodes of the network to be simulated. The rest of the file contains the binary adjacency matrix A of all network nodes. The adjacency matrix is formed on the basis of the physical location of the nodes in the considered network.

We use the reactive topology-based table-driven protocol DSDV as it may be considered as a good choice when network contains not too many nodes [30]. It should be noted that routing protocol selection is a hot area in MANET/FANET performance optimisation, see for example [31]. The problem of choosing the most appropriate protocol remains open and will be addressed in our future work.

We consider two scenarios illustrating the above concept, i.e., the nodes chosen accordingly for Network 1 (see Section 4.1) and Network 2 (see Section 4.2). The physical distance between the agents is measured in units that are equal to 100 meters. We used Internet protocols setting for data transmission as well as the Friis propagation loss model [32]. The latter model is good for the line-of-sight free space propagation.

In order to analyze the quality of the constructed network, it is necessary to choose a specific characteristic that can be used to evaluate the performance of the system. The transmission parameters were set such that the nodes at distance 100 m from each other get clear connection, and the transmission decays fast for the distances above that. This was necessary to realistically test conditions of theoretical Networks 1 and 2, and we used the parameters indicated in

Table 5. Simulation parameters.

Parameter	Value
Transmission Radius	105
Number of Nodes (player 1)	16 (Network 1) and 12 (Network 2)
Number of Nodes (player 2)	17
Physical Mode	DSSS at 11 Mbps
Transfer Rate	CBR at 11 Mbps
Routing Protocol	DSDV
Transport Protocol	UDP
Propagation model	FriisPropagationLossModel
Simulation time	100 sec.

. A part of the presented results was previously demonstrated in [33].

We have chosen information delivery ratio, i.e., the ration of successfully received bytes to transmitted bytes as the network performance measure. The required information can be obtained using the built-in technology for monitoring flows in the NS-3 network. Namely, we use the Flow Monitor module which is developed to provide a flexible system for measuring the performance of network protocols. The module uses sensors installed in network nodes to track packets exchanged between nodes, thus providing required information on the amount of data successfully sent and received.

During the execution of the program, information about all flows that traverse the network is stored in the .flowmon file. From there, one can observe at what point in the simulation time the stream began, at what time it ended, how many packets were transmitted during the data transfer, and of what size.

For either theoretical network, both sources and sinks were randomly allocated to the regular nodes using uniform distribution, and 100 simulation have been run to obtain the mean packet delivery ratio. Furthermore, to simulate a realistic process of data transmission the number of packages sent was chosen to be high enough such that the networks gets congested. In such a situation, there are numerous packets that get lost, resp., are dropped due to many reasons such as buffer overflow, insufficient room in pending queue, packet damage etc. In this way we emulated a realistic scenario in which agents send and receive large amounts of data such a video streams.

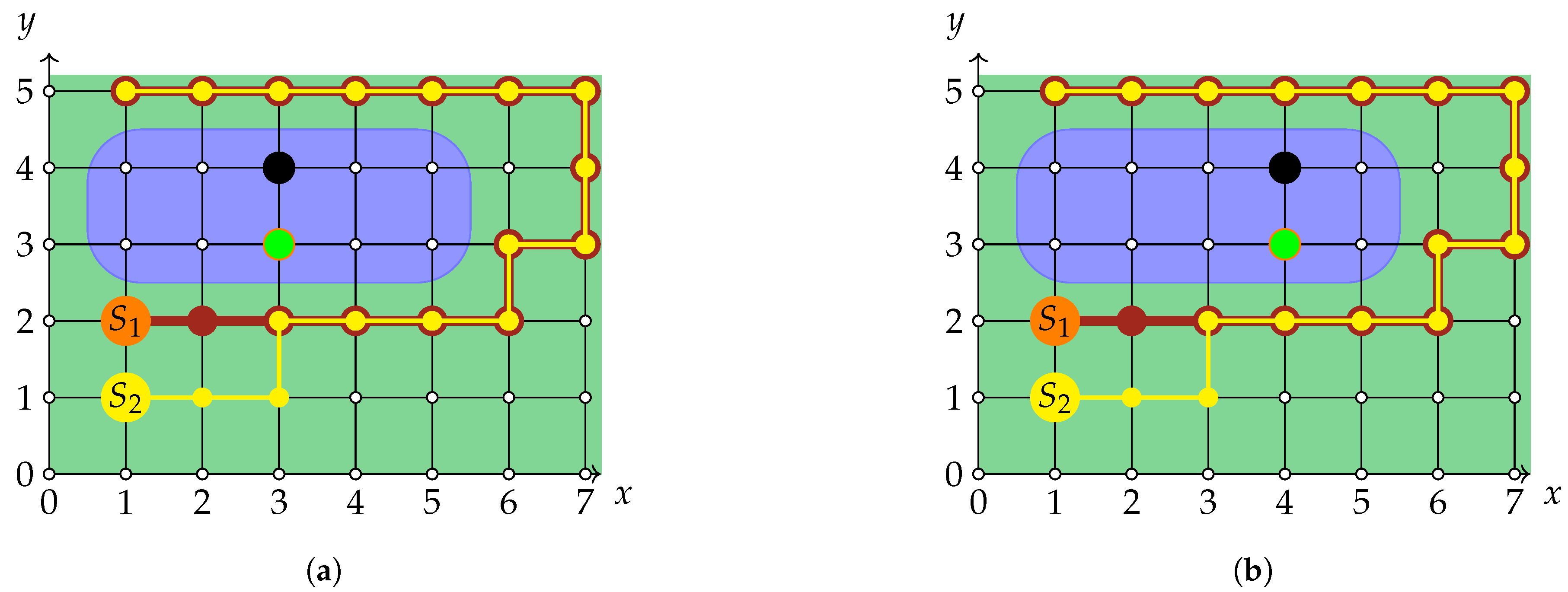
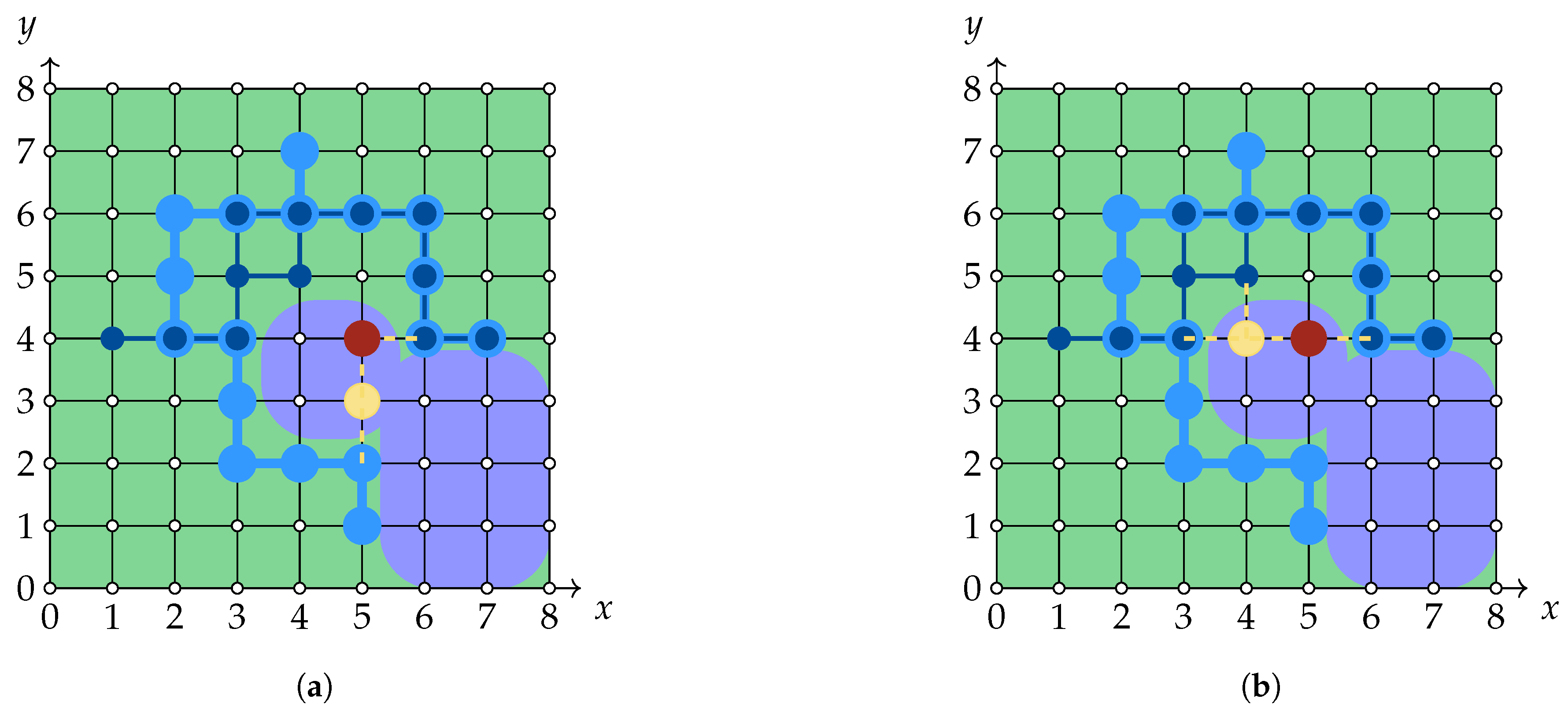
For both Networks 1 and 2 we have compared two solutions, both Pareto-optimal solution, but different according to centrality measures.

5.2.1. Simulation Results for Network 1

For the network described in Section 4.1, the results for both agents shown an improvement of slightly less than 2%: for the solution $(3;4)/(3;3)$ the sent-to-receive ratio was $0.3262$, while the solution $(4;4)/(4;3)$ corresponded to the sent-to-receive ratio equal to $0.3302$ (both numbers rounded to the fourth digit). This minute improvement can be attributed to the fact that both solutions are rather similar and hence do not allow to clearly see the difference. In contrast to Network 1, the case described in the next subsection correspond to the solutions that are structurally very different. In this case, the improvement is better pronounced as demonstrated below.

5.2.2. Simulation Results for Network 2

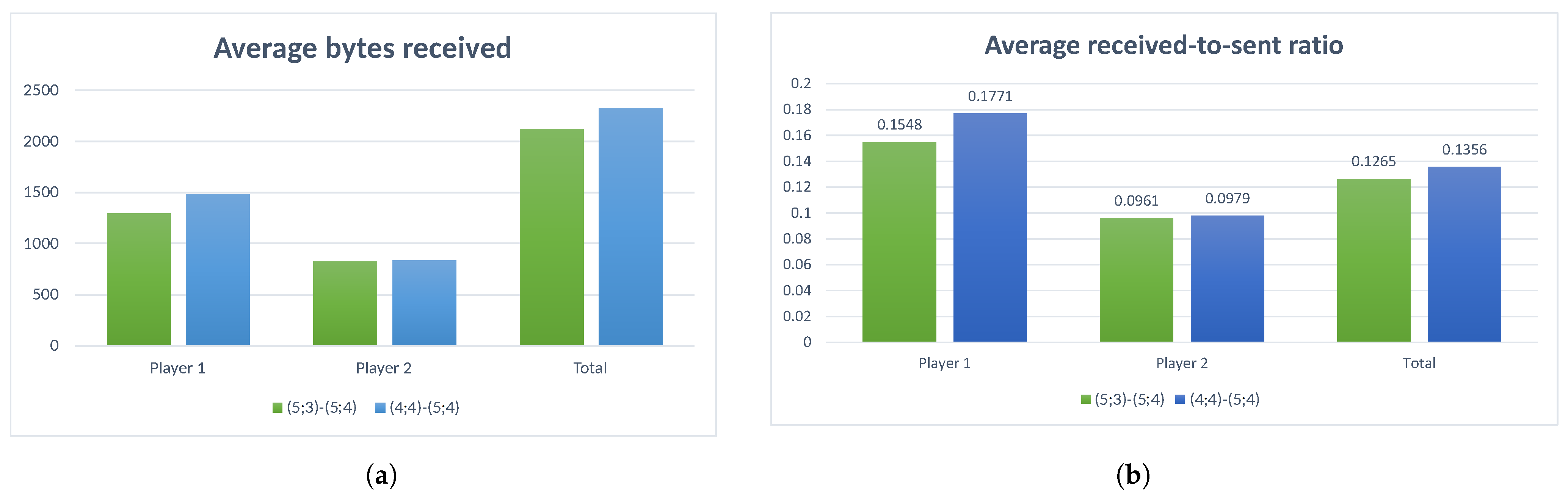
The resulted simulation data are visualized in Figure 7 (see Supplementary Materials for more details). This Figure contains aggregated information for both Players separately and also provides the average performance characteristic of the whole system. We recall that we simulated two solutions, $(5;3)/(5;4)$ and $(4;4)/(5;4)$. Both solutions yielded the same improvement in the diameter of the overall network, but the second solution was better according to the centrality measures. One can see that the second solution brought an approximate 14% increase in information delivery ratio for Player 1, approximate 2% increase for Player 2, and 7% increase for the whole of the network. All the data were average over 100 simulations with uniformly distributed sources and destinations.

Thus the numerical results indicate that the solution $(4;4)/(5;4)$ does indeed yields a substantial performance improvement for the total network. It is interesting to note that while the first solution resulted in a larger decrease of diameter than the second one, it did not lead to any substantial improvement in received-to-sent ratio. This might indicate that the performance of the network can depend on the network diameter in a more complex way that was initially assumed. This aspect requires a thorough investigation with a larger set of test networks.

6. Discussion

In this contribution we considered the problem of determining the best solution to the problem of mobile agent (drone) placement in a mobile ad-hoc network. Typically, the optimal position of a drone is chosen to minimize the diameter of the network. However, as was often demonstrated in other papers, such solution can be non-unique. In this case, the additional degree of freedom can be exploited to increase the quality of the network even further performing a higher-order optimization with respect to additional criteria. We studied different centrality measures and also PageRank weights of the nodes. It was shown that while the degree centrality did not provide any useful information, both betweenness and closeness centrality agreed with PageRank and yielded the solution that was both more resilient and also outperformed the alternative one. Further, it has been shown that when the subgraphs of the respective players are different, the total value of the centrality measures can be used to choose the better solution. This is a promising illustration of how the optimization procedure introduced previously could be better improved by considering centrality measures.

While the obtained results were demonstrated for relatively small mobile networks, it remains open if the observed regularities can be extended to larger networks, in particular networks with a less regular structure. The analysis of large networks of a general structure will be carried out in our future work. It is hoped that such analysis can not only help improving the performance of mobile networks, but can also shed a new light to the role and function of different centrality measures.

Another direction of future investigations will consist in establishing the connection between the computed network characteristics and the actual performance of the network evaluated in terms of amount of information transferred and received, minimal time required for transmitting a fixed amount of information between two nodes and so on. It is expected that these performance criteria strongly depend on the protocols used in the network. This interplay adds to the complexity of the considered problem and will be the subject our future analysis.