Abstract
Cryptography is considered indispensable among security measures applied to data concerning insecure means of transmission. Among various existent algorithms on asymmetric cryptography, we may cite Elliptic Curve Cryptography (ECC), which has been widely used due to its security level and reduced key sizes. When compared to Rivest, Shamir and Adleman (RSA), for example, ECC can maintain security levels with a shorter key. Elliptic Curve Point Multiplication (ECPM) is the main function in ECC, and is the component with the highest hardware cost. Lots of ECPM implementations have been applied on hardware targeting the acceleration of its calculus. This article presents a systematic review of literature on ECPM implementations on both Field-Programmable Gate Array (FPGA) and Application-Specific Integrated Circuit (ASIC). The obtained results show which methods and technologies have been used to implement ECPM on hardware and present some findings of the choices available to the hardware designers.
1. Introduction
The rapid development and widespread application of information technology have deeply affected the entire economy and society. Many electronic devices need to exchange confidential information securely, and one of the best defenses to preserve the data secrecy and confidentiality from unpermitted users is cryptography. One approach to provide public-key cryptography relies on the use of Elliptic Curve Cryptography (ECC), which is based on the algebraic structure of elliptic curves over finite fields. ECC was proposed by Neal Koblitz [1] and Victor Miller [2], and requires smaller keys to obtain the same security level when compared to other algorithms. For instance, considering a 3072-bit Rivest, Shamir and Adleman (RSA) key, ECC will need a 256-bit key to ensure the same security level [3]. As the keys for ECC are smaller than those for other algorithms, ECC’s requirements are also smaller and conform to the requirements of size- and resource-constrained devices.
ECC is widely implemented on software and hardware approaches to increase security when sharing information through unsafe networks. Software applications involve Bitcoin digital signature scheme [4], OpenSSL protocols [5], image encryption [6,7], and others. Hardware implementations of ECC for size constraint devices, such as the Internet of Things (IoT), include Radio Frequency Identification (RFID) [8], wireless medical devices [9], Android chat applications [10], and others. Its applications can be made in devices with or without limited resources; the manner they are implemented will vary depending on the environment. Thus, IoT applications are suitable for devices with limited hardware resources, unlike other cryptographic schemes.
Applications of ECC under hardware approaches usually aim to speed up critical operations. Elliptic Curve Point Multiplication (ECPM), also referred to in the literature as scalar multiplication, is the main operation and most computing-intensive part of the algorithm [11]. So, it has been subjected to countless attempts to improve its performance when applied to hardware. Depending on the purpose of implementation, different sets of techniques can be utilized on ECC over prime and binary fields. These techniques include area reduction [12], performance and efficiency increase [13,14], adjustments to fit size constraint devices [12,15], and development of custom crypto-processors [11,14,16]. For instance, Hossain, Saeedi, and Kong [13] proposed an architecture to speed up ECPM utilizing Jacobian projective coordinates and a combination of Point Addition (PA) and Point Doubling (PD) in parallel. Liu, Liu, and Zou [16] proposed a flexible processor with multi-algorithm support, which enables different fields and curves with random point generation. Salarifard, Bayat-Sarmadi, and Mosanaei-Boorani [17] implemented a fixed-base-comb method in two architectures and reached significant results in energy and latency reduction on ECPM, and the implementation is Simple Power Analysis (SPA) and timing attack resistant.
While similarities can be found among sets of algorithms for ECC in literature, a roadmap of desired characteristics must be previously traced based on the purpose of the implementation. An algorithm applied to aim area reduction is usually slower than another that is not recommended for resource-constrained devices. Several parameters must be defined once the roadmap is constructed, including finite field, algorithms for field arithmetic, a curve selection, point representation, and algorithms to perform Elliptic Curve (EC) arithmetic, among others [18]. The perfect selection can be a little tricky; thus, it should always be done considering the environment first of all. If the environment requires a small code due to area limitations, the chosen algorithms must fit this requirement or lose efficiency and performance. In view of this, it is difficult to reach a custom best set of algorithms to apply on hardware implementations with no size constraints, in which the focus lies over efficiency and performance values. Papers often trace a customized set of algorithms for their own purposes, whereas different possibilities can be found on books or surveys without recommendations of the best choice.
In this paper, we present a comparison involving recently selected ECPM implementations over hardware approaches. Focusing on implementations of ECPM over binary fields on Integrated Circuit (IC) technologies such as Field-programmable Gate Array (FPGA) and Application-specific Integrated Circuit (ASIC), our comparison aims to find the techniques that favor reaching the best efficiency. While environments and purposes differ in each work, thus, affecting the selection of algorithms and techniques, it is possible to trace similarities among some sets of algorithms and trace a basic roadmap. The sets of algorithms these works implemented were cataloged to provide a recommendation of a path to follow. Thus, as the main contribution, this paper indicates which combinations of methods and technologies reach the best efficiency, thus pointing out directions for hardware implementations of ECPM over binary fields.
The remainder of this paper is organized as follows. Section 2 presents an approach to the context of the research, involving finite fields, curves, point multiplication, coordinates, and existing attacks on ECC. Section 3 describes the methodology applied in this study, including research questions, document search, paper selection, and data extraction. Next, Section 4 discusses the gathered information on the selected papers, describing the techniques applied to those and making a comparative analysis of silicon cost and performance. Finally, Section 5 presents the final remarks.
2. Background
The development process of embedded systems mainly includes the design of hardware and software. The system must ensure reliability, maintainability, availability, safety, and security [19]. A system designer must take precautions regarding energy consumption, code size, usage of resources, weight, and cost to enhance efficiency [20]. Since the code must be compact, designers must select the functions properly to provide efficiency without compromising the primary function.
It is well-known that selecting the best cryptographic scheme and algorithms has a preponderant role in the design task. According to Loi and Ko [21], ECC needs smaller keys than RSA to provide the same level of security. Therefore, this aspect is why we defined ECC as our object of study. While smaller keys do not guarantee smaller code, the advantages of ECC rely on the security aspect.
ECC uses the Discrete Logarithm Problem (DLP), which is classified as a one-way function because it is easy to calculate but challenging to reverse. According to Ciet and Joye [22], there is no sub-exponential algorithm capable of solving Elliptic Curve Discrete Logarithm Problem (ECDLP), although one of the algorithms that can be applied is Pollard’s Rho method [23]. Other methods, such as brute-force, have an impractical performance.
2.1. The Elliptic Curve over Finite Fields
ECC is an approach for public-key cryptography on the algebraic structure of elliptic curves over finite fields or Galois fields, .
The elliptic curve over , here denoted by or , is defined by the general Weierstrass equation [24]:
in which . Prime fields are usually called , with , where p is a prime number and . We denote Binary fields by , with . There also exist elliptic curves defined over other fields for cryptography, which are not discussed in this paper.
The set of all points on the elliptic curve and the point at infinity, , forms an Abelian group in which is the identity element. An Abelian group is a nonempty set with a binary operation + defined on such that the following conditions hold:
- i.
- Identity: ,
- ii.
- Negatives: If , then and is called the negative of P and . Also, .
- iii.
- Point addition: Let , where , then, .
- iv.
- Point doubling: Let where . Then .
A hierarchy must be followed to define the sets of algorithms needed to create an ECC cryptographic scheme. Figure 1 demonstrates this hierarchy. First, it is necessary to select the type of protocol to be used, Elliptic Curve Diffie-Hellman (ECDH) or Elliptic Curve Digital Signature Algorithm (ECDSA). In sequence, the algorithms to perform ECPM must be defined, followed by the algorithms to perform field arithmetic.
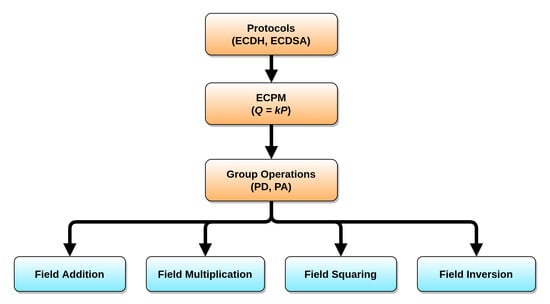
Figure 1.
Elliptic Curve Cryptography (ECC) implementation hierarchy.
Finite field requires that a basis is selected to perform field arithmetic. Figure 2 represents what needs to be defined accordingly to the chosen basis. For binary field, if the polynomial basis is chosen, each element is a polynomial, and therefore, field operations make use of polynomial arithmetic [25]. A reduction polynomial must be defined to reduce the results of its arithmetic into elements of Galois field [26]. Reduction polynomial will ensure that the given result belongs to the field.
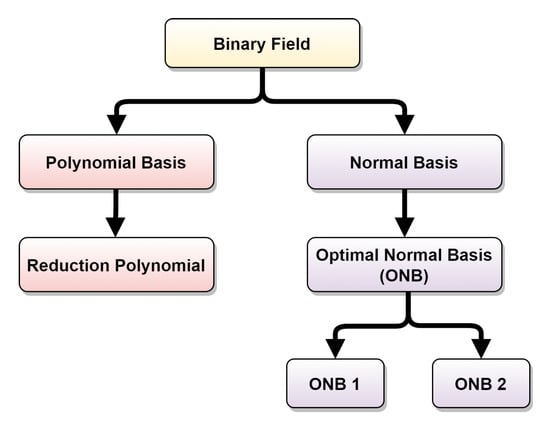
Figure 2.
Binary Field.
Normal basis is defined for any finite field . An example of a normal basis is Gaussian normal basis, commonly utilized on ECC. Optimal Normal Basis (ONB) aims at reducing hardware complexity when multiplying field elements [18]. In a normal basis representation, elements of are expressed in terms of a basis of the form . One advantage of a normal basis representation is that squaring a field element is a simple rotation of its vector representation [25]. Mullin et al. [27] introduced the concept of an ONB to reduce the hardware complexity of multiplying field elements in . Table 1 presents two types of ONB, concerning the value of m [25]. If m does not satisfy any of three statements mentioned in the table, then does not contain an ONB [25]. According to Hankerson, Menezes, and Vanstone [18], ONB does not have any significant advantages over a polynomial basis for hardware implementation. Furthermore, field multiplication in software for normal basis representations is very slow compared to multiplication with a polynomial basis. In this way, the polynomial basis is the best choice for hardware implementation.

Table 1.
Summary of the Optimal Normal Basis (ONB).
2.2. Curves over Binary Fields
An elliptic curve over binary fields is defined by:
There are two types of a curve over a binary field : (i) random elliptic curves over a binary field ; and () Koblitz elliptic curves over a binary field . Some parameters must be defined previously to generate a curve over binary fields. According to the authors of [18], the domain parameters for both are the following:
- m, which is the extension degree of the binary field .
- , which is the reduction polynomial of degree m.
- The coefficients of the elliptic curve .
- The prime order of the base point P, which is given by n.
- The cofactor is given by , in which is the order of over .
- The , which are the coordinates of the base point P.
In addition to these parameters, if random curves are being used, a seed will be applied to randomly generate the elliptic curve’s coefficients.
- A.
- Random Elliptic Curve (REC) (REC is part of National Institute of Standards and Technology (NIST)’s recommended curves [25].): Its advantages lie in the security aspect, in which the coefficients of the curve are randomly generated. Once the randomness requires more computational processing power, this curve may not be the better implementation choice [25].
- B.
- Koblitz Curve (KEC) (KEC is part of NIST’s recommended curves and easy to create [25].): Also known as anomalous binary curves, this curve is defined over binary fields and is a non-supersingular elliptic curve. ECPM in KEC is fastest than in REC [18]. Because KEC is presented on NIST’s recommendations, it is a popular chosen curve [13,28].
Regardless of the curve selection, domain parameters must be carefully chosen. Brown [29] presents an efficient generation for the Elliptic curve domain parameters over , in which the output of the presented steps is the septuple . In such a way, the logarithm derivation on the associated elliptic curve requires approximately operations, where t is the security level in bits required from the elliptic curve domain parameters.
2.3. Elliptic Curve Point Multiplication
To generate the public key, cryptosystems based on elliptic curves must perform point multiplication, also called scalar multiplication. Elliptic Curve Point Multiplication (ECPM) is the most computationally expensive part of ECC and consists of repeated steps of point adding and point doubling to reach:
in which P is a point of the curve , k is a randomly selected integer from the range of defining the private key, and Q is the public key resultant of the multiplication [18]. From Equation (3), the private key is defined, and posteriorly the public key is created. Thus, both keys are related to each other. There are numerous ECPM algorithms, although the simplest algorithm is composed of point adding and point doubling operations. We can define the point adding and point doubling operations as follows:
- A.
- Point Addition: Consists in adding a point with another point. Assume two points and , in which and . Then, [25]. Point should be reflected the in x-axis to compute point R. Figure 3 shows the point addition on ECC.
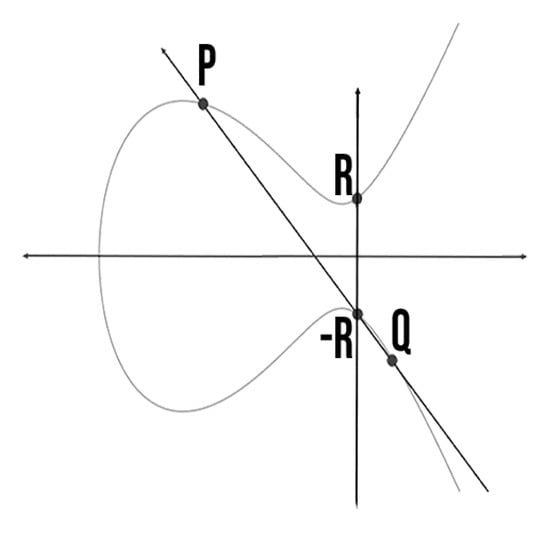 Figure 3. Point addition on ECC.
Figure 3. Point addition on ECC. - B.
- Point Doubling: Is the addition to a point with itself, when . Let , where , then [18]. Point doubling is evaluated in the same way as point addition, as also generates first , which is reflected in x-axis to compute point . Figure 4 shows the point doubling on ECC.
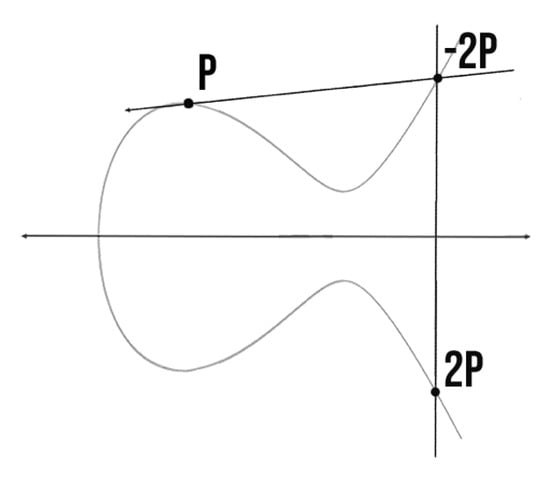 Figure 4. Point doubling on ECC.
Figure 4. Point doubling on ECC.
Double-and-Add method is a known algorithm for scalar multiplication. According to [25], the scalar should be written as in binary notation and consider . Finally, the result follows of the sum . The Double-and-Add method requires doubling operations and likely additions. This method is one of the most basic algorithms to perform scalar multiplication and can be modified or combined with other techniques to accelerate it. As other algorithms, we can mention the addition-subtraction method using Nonadjacent form (NAF), Right-to-left binary method, Left-to-right binary method, Montgomery, Fixed-base comb, and Window methods [18]. The best algorithm is selected based on the project environment, whereas the indicated algorithm for one project will not necessarily be indicated for another.
2.4. Projective Coordinates
The projective coordinates systems offer an alternative method for the efficient performance of the arithmetic of the elliptic curve [30]. These methods avoid the expensive cost of the field multiplication inversion involved in both points doubling and point addition operation with the arithmetic of the affine coordinates . In these methods, the elliptic curve points are usually substituted with the projective coordinates system as follows.
In standard projective coordinates, the projective point , in which , corresponds to the affine point [31]. Therefore, in (2) can be rewritten as
In the Jacobian coordinates system, a point in affine coordinates system is recovered as , in which [31], in (2) yields
These operations directly impact efficiency and performance metrics. Therefore, before selecting the projective coordinates, we need to know the context of ECPM.
2.5. Attacks on ECC
For any cryptosystem, there will always be an attempt to break it and steal information. For instance, although ECC is a very secure cryptographic scheme, attacks aim to break it. Some examples are divided into [25]:
- i.
- Algorithms on DLP: Shank’s Baby-step-Giant-step, Pohlig-Hellman’s method, Pollard’s -method, -method, Index-calculus algorithm, Number field sieve algorithm, and function field sieve algorithm.
- ii.
- Algorithms on ECDLP: Shank’s Baby-step-Giant-step, Pollard’s -method, Pohlig-Hellman’s method, method of solving multiple ECDLP, and Index-calculus method.
- iii.
- Weil pairing and MOV reduction attack.
- iv.
- Semaev-Smart-Satoh-Araki (SSA) attack.
- v.
- Differential and power attacks: SPA and Differential Power Analysis (DPA).
- vi.
- Electromagnetic Analysis Attack (EAA).
- vii.
- Error message analysis.
Some approaches for mitigating attacks have been studied [32]. These countermeasures heavily depend on the hardware platform’s characteristics, operating environment, and invaders’ skills. These aspects must be evaluated on a case-by-case basis.
In implementations of ECC, point multiplication algorithms are particularly vulnerable because the usual formulas for adding and doubling points are quite different and, therefore, may have its power traces readily be distinguished by SPA [25]. However, some precautions can be taken to prevent these attacks. In this case, a modified algorithm uses the power alignment for the adding and doubling points operation [18]. Thus, the equals power traces are certainly no longer distinguishable by SPA.
3. Materials and Methods
In this paper, we applied the Systematic Literature Review (SLR) method. According to Kitchenham et al. [33], this method is a secondary study on a subject to identify, analyze, and interpret all possible evidence related to the main studies on that subject. The motivation behind these studies is to gather knowledge about a particular field of study.
A systematic review of the literature has some requirements to succeed. The first step should be to define a subject and its motivation. In second, the search strategy must be well-defined. Similarly, the selection method must lead to the primary studies in the literature and its contribution to the current research [33].
In this paper, we present an analytical discussion about the previous research based on ECPM to identify the possible opportunities and challenges where new studies may be applied. The strategies applied in this systematic review of the literature relied on: (i) the database and research query used; and () the inclusion and exclusion criteria. Both are presented in the following subsections.
3.1. Research Strategy
Our work brings a new contribution to the discussion about ECPM implementation by providing a study of the most efficient algorithms on hardware. Table 2 presents the research question for this study.

Table 2.
Research Question.
3.2. Research Query
As the primary database, we selected Elsevier’s Scopus, the largest abstract and citation database of peer-reviewed literature. We focused on the most recent publications, ranging from 2015 to 2020. The Scopus query was performed using the following expression:
| TITLE-ABS-KEY ((elliptic AND curve AND point AND multiplication) AND (fpga)) AND (LIMIT-TO (PUBYEAR, 2020) OR LIMIT-TO (PUBYEAR, 2019) OR LIMIT-TO (PUBYEAR, 2018) OR LIMIT-TO (PUBYEAR, 2017) OR LIMIT-TO (PUBYEAR, 2016) OR LIMIT-TO(PUBYEAR, 2015)) AND (LIMIT-TO(DOCTYPE, “ar”)). |
3.3. Inclusion and Exclusion Criteria
To assess the relevance of the journal in which each paper was published, we used SCImago Journal Rank (SJR) indicator [34]. SJR measures the scientific influence of scholarly journals by accounting for both: (i) the number of citations received by a journal; and () the prestige of the journals from where the citations come. Then, the set of journals is ranked according to their SJR and divided into four equal groups, four quartiles. Our study considered only articles published in journals classified in the two upper quartiles, i.e., Q1 and Q2.
After selecting the papers retrieved from the query, we analyzed their abstracts, results, and conclusions. We then selected only the works presenting implementations over 163-bit binary curves and single point multiplication. This constraint enabled us to make a fair comparison among the works analyzed in this review. We also applied a set of exclusion criteria to reduce the number of papers to the most representative set of works for a full analysis. The inclusion and exclusion criteria are summarized in Table 3.

Table 3.
Inclusion and Exclusion Criteria.
4. Results
The review protocol returned 55 papers. After applying the inclusion and exclusion criteria (Table 3), we selected 13 works for analysis, including: [11,13,14,16,17,28,35,36,37,38,39,40,41]. For each paper, we gathered information (when available) about its curve, field, coordinates, inversion, multiplier, and other techniques applied to ECPM itself. We observed that most papers implemented a customized algorithm with enhanced functions to speed up point multiplication. It is worth to mention that we collected data about the entire environment, covering all the information provided, as every technique influences the final result. This section presents a review of the techniques applied to each primary study concerning the whole used environment. It should be underlined that information about all the techniques used is not always available for all papers. Thus, we elaborated on the following description based on the available information.
4.1. Curves
Table 4 presents the curves utilized by each of the selected papers. We can see that most papers made use of generic curves, while others did not specify. For the works concerned about the choice of the curve, most of them used the Koblitz curve. For a better understanding, we present below a brief description of each other curves.

Table 4.
Summary of implemented curves.
- Koblitz curves: According to Hankerson, Menezes, and Vanstone [18], the primary advantage of the Koblitz curves consists of the opportunity of implementing ECC without point doublings when performing ECPM.
- Generic curves: They are non-supersingular elliptic curves defined over the general Weierstrass Equation (1). Generic elliptic curves are the most general form of curves found in literature and can be defined over prime or binary fields.
- Random curves: This type of curve is generated randomly due to the parameters’ choice. The curve’s coefficients are generated from the output of a seeded cryptographic hash [42], thus providing more security to the cryptosystem [43]. According to Hankerson, Menezes, and Vanstone [18], when the curve is generated randomly, it is provided some assurance to the user as proof that the curve was not generated with intentional weaknesses that could be exploited lately. Even though the curve’s randomness increases security, other questions must be considered, such as the area of the device where the encryption will be applied.
- Hessian curves: Hessian curves are defined over a symmetric cubic equation. Its addition formulas can also be used for doubling and subtraction when generating points on the curve, making this an interesting choice against side-channel attacks. Generalized Hessian curves have some differences from Hessian curves, covering more isomorphic classes of elliptic curves. The equation for Generalized Hessian curves can be written aswhere , , and [43].
- Binary Edwards Curves (BEC): These curves are defined over the equationwhere and and . This curve is symmetric in x-axis and y-axis, i.e., if , then [44].
- Binary Huff Curves (BHC): These curves are defined over the equationwhere and . This equation is related to the curve when using projective coordinates, although there exists an equation directed to the use of affine coordinates [45].
The curves chosen by the authors vary due to the purpose of each implementation. While some of them opted for NIST recommended curves (Koblitz, Random, and others, which belong to the “did not specify” row, were referred only as “NIST recommended”), others preferred to construct a curve based on other equations, such as binary Edwards or Hessian curves. Li and Li [28] state that Koblitz curves could execute ECPM faster than generic curves when utilizing Frobenius mapping. According to Azarderakhsh and Reyhani-Masoleh [14], binary Edwards curves belong to a special type of generic elliptic curves defined over binary fields. Imran et al. [11] showed that BHC requires less computation than BEC, even though both require more computation than generic EC.
4.2. IC Technologies
All selected papers had prototyped their ECC implementations on Xilinx FPGA devices, and some included ASIC deployments, both using different lithographies. Table 5 shows the circuit technologies used in each work. While it is preferred to implement the circuit in newer devices, such as the Virtex-7 family, for fair comparisons among related works, we also consider older FPGAs.

Table 5.
Type of Integrated Circuit (IC) technology used for implementations.
4.3. Basis
As Table 6 shows, 71% of the works analyzed in this review employ a polynomial basis. This evidence suggests that the polynomial basis is more suitable for hardware implementation. At this point, we note that the Gaussian normal basis provides an efficient implementation of field multiplication that requires simple hardware for the shift, rotation, and XOR operations [38]. The squaring operation is simple as it needs only the right cyclic shift [14].

Table 6.
Basis for the field.
A polynomial basis requires smaller hardware than a Gaussian basis. On the other hand, a Gaussian basis enables substantial gain in area and performance for inversion operations. Furthermore, both bases can be implemented with a small footprint and provide high performance for square operations. While there may exist small differences in these results, the differences in performance are caused mainly by inversion operations. This effect results from the fact that affine coordinates need many inversions, and projective coordinates need only one inversion [46].
Thus, if we use affine coordinates in a Gaussian basis, the performance will be superior compared to a polynomial basis. For projective coordinates, both bases have similar performance. However, a polynomial basis hardware implementation is more area efficient than a normal basis.
4.4. Coordinates
Table 7 shows the coordinates utilized by the works we address in this paper. We can see that most of them (71%) made use of projective coordinates (Lopez–Dahab or Jacobian), which we briefly described in Section 2.4.

Table 7.
Coordinates used in each ECC environment.
4.5. Inversion
Table 8 relates to the use of algorithms to speed up inversion operation. Even though most works use projective coordinates, which requires a single inversion at the end of scalar multiplication, an algorithm to speed up this operation can be utilized. In this case, most works use the Itoh-Tsujii algorithm [47]. While this algorithm requires intermediate results storage, it is the most efficient to compute inversion [25].

Table 8.
Inversion algorithm.
4.6. Multiplication
In Section 2.1, we discussed multiplication as an arithmetic operation in a field. In this case, efficiency and speed are fundamental for the performance in applications that use the field multiplication operation [48]. Field multiplications involving integers and polynomials are used in finite field arithmetic, and there are different algorithms to solve field multiplication, which depend on the size of the numbers.
Table 9 presents the multiplication methods applied to each selected paper. We note that there are several methods to perform field multiplication. In the works analyzed in this review, the field multiplications are specific implementations. Karatsuba-Ofman Algorithm (KOA) was the only algorithm to speed up field multiplication that was applied. In our analysis, we encounter KOA in single [17] and combined versions [28].

Table 9.
Multiplication methods.
4.7. Point Multiplication
Point multiplication, ECPM, or scalar multiplication is the repeated PA and PD operations. Specifically, these are methods to compute , being k the private key and P a point in the curve. This operation will generate, as output, the public key [49]. Table 10 identifies the ECPM methods used in the works analyzed in this review. We can see that the Montgomery algorithm is prevalent for point multiplication, probably because it is well-known for providing faster modular multiplication on hardware and software implementations.

Table 10.
Elliptic Curve Point Multiplication (ECPM) methods.
4.8. Efficiency Analysis
Based on the results presented above, we shall use some metric to compare the primary studies fairly. Considering the implementations over 163-bits, we calculate the efficiency of each analyzed work by applying the equation presented in [17], which is given by
where m is the order of the finite field (number of bits), a is the area, and t is the processing time. This metric indicates the processing throughput achieved by each slice (or gate) used. Its unit of measurement is Kbps/slice (or Kbps/gate). Efficiency enables us to compare implementations that use different orders of finite field. In principle, the higher the order, the greater the efficiency. However, increasing it also leads to an increase in area and processing time. So, a trade-off must be found. Moreover, the equation also enables comparison of implementations that use the same finite field order (as done in this paper) but explore different architectures to increase performance (i.e., use of barrier registers, pipelining, and spatial parallelism). Some solutions reduce processing time but increase the area of the circuit (and, consequently, the dissipated power), which does not necessarily result in increased efficiency. For a given order of the finite field, the most efficient circuits reach the lowest processing time using fewer resources.
Table 11 and Table 12 summarizes the works which obtained the higher efficiency for each IC technology. The tables show the area of the circuits—a (in Kslices or Kgates), the maximum operating frequency— (in MHz), the processing latency—ℓ (in cycles), the processing time—t (in s), and the efficiency (in kbps/slice ou kbps/gate). Except for efficiency, which is computed by (10), we obtained the other indicators from the primary studies. Considering the FPGA-based implementations, we note that Low Complexity (LC) in Virtex-7 is the best choice—it would be expected that the implementation using Virtex-7 would produce a better result due to the smaller lithography used in this device family (i.e., 28 nm). The next two methods that obtained high efficiency were Lopez–Dahab Montgomery (LDM), which combines the Lopez–Dahab projective coordinate system and the Montgomery scalar multiplication method, and Low Latency (LL). The use of -adic nonadjacent form (-NAF) in Virtex-5 [28] also provided good efficiency. Regarding the ASIC-based implementations, the best results were obtained using the 65 nm lithography. Combined Point Doubling and Point Addition (PDPA) for Koblitz and Random curves [13] achieved higher efficiency. On the other hand, Salarifard, Bayat-Sarmadi, and Mosanaei-Borani [17] obtained a higher efficiency for generic curves.

Table 11.
Field-Programmable Gate Array (FPGA)-based implementations for .

Table 12.
Application-Specific Integrated Circuit (ASIC) (65 nm)-based implementation for .
By analyzing the hardware implementations, we note that the combinations that provided the higher efficiency are the ones used in works [17] for FPGA- and [13] for ASIC-based implementations. The former combined generic curves, polynomial basis, and Lopez–Dahab projective coordinates and employed the Itoh-Tsujii algorithm to implement the inversion, the KOA method to perform field multiplication, and the fixed-base comb for ECPM. The latter also used polynomial basis but employed different curves (Koblitz and Random), projective coordinates (Jacobian), and field and point multiplication methods (Custom Multiplication Module (CMM) and Combined PDPA, respectively). It is worth noting that standardization in the choice of metrics for comparison and the difficulty of reproducing results due to the used devices makes a fair comparison unfeasible. A sensitivity analysis would help to understand the real effects of choosing together methods of inversion, multiplication, and ECPM.
5. Conclusions
In this article, we presented a review of techniques for implementing elliptic curve point multiplication on FPGA and ASIC devices. We note that the analyzed works use different types of curves according to the implementation goals. However, most studies use the polynomial basis and the projective coordinates, which points out that this combination is the most suitable for hardware implementation. Concerning the operations, we have not identified any preferred method for implementing field or point multiplications. On the other hand, most of the works used the Itoh-Tsujii algorithm to accelerate the inversion. However, there is no sufficient evidence to indicate its use to produce a gain in efficiency or performance. From the study, we also note that the best combination of algorithms, techniques, and IC technologies depends on the project’s goal, and a system designer must take into account the requirements of the target application to select the choices that best fit those requirements. For instance, if we use affine coordinates, we should know that the algorithm uses more inversion operations than projective coordinates, requiring enhancements in implementation to compensate for this cost. Moreover, resource-constrained devices may need algorithms that enable cost reduction; however, such algorithms may exhibit lower efficiency and performance. Finally, although this article has presented an analysis of ECPM implementations on hardware, further studies are needed to define a set of guidelines to aid designers in choosing the best combination of methods and algorithms for different application classes.
Author Contributions
Conceptualization, A.V.L., G.A.M.S., C.A.Z. and W.D.P.; methodology, A.V.L., G.A.M.S., C.A.Z. and W.D.P.; analysis, A.V.L., C.A.Z. and W.D.P.; writing—original draft preparation, A.V.L., V.R.Q.L., M.B., C.A.Z. and W.D.P.; writing—review and editing, A.V.L., V.R.Q.L., M.B., C.A.Z. and W.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brasil (CAPES)—Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq)—Grants 315287/2018-7 and 436982/2018-8, Fundação de Amparo à Pesquisa do Estado de Santa Catarina (FAPESC)—Grant 2019TR169, Fundação para a Ciência e a Tecnologia under Projects UIDB/04111/2020 and foRESTER PCIF/SSI/0102/2017.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASIC | Application-specific Integrated Circuit |
| BHC | Binary Huff Curves |
| CMM | Custom Multiplication Module |
| DPA | Differential Power Analysis |
| ECC | Elliptic Curve Cryptography |
| ECDH | Elliptic Curve Diffie-Hellman |
| ECDLP | Elliptic Curve Discrete Logarithm Problem |
| ECDSA | Elliptic Curve Digital Signature Algorithm |
| ECPM | Elliptic Curve Point Multiplication |
| EAA | Electromagnetic Analysis Attack |
| FPGA | Field-programmable Gate Array |
| HBPKOA | Hybrid Bit-Parallel KOA |
| HDC | Hybrid-Double Multiplication |
| IC | Integrated Circuit |
| IoT | Internet of Things |
| KEC | Koblitz Curve |
| KOA | Karatsuba-Ofman Algorithm |
| LC | Low Complexity |
| LDM | Lopez–Dahab Montgomery |
| LL | Low Latency |
| MDSM | Most Significant Digit Serial Multiplier |
| MSBSM | Most-Signicant Bit-Serial Multiplier |
| NAF | Nonadjacent form |
| NIST | National Institute of Standards and Technology |
| ONB | Optimal Normal Basis |
| PA | Point Addition |
| PD | Point Doubling |
| R4IM | Radix-4 Interleaved Multiplication |
| REC | Random Elliptic Curve |
| RFID | Radio Frequency Identification |
| RSA | Rivest, Shamir and Adleman |
| SLR | Systematic Literature Review |
| SJR | SCImago Journal Rank |
| SPA | Simple Power Analysis |
| SSA | Semaev-Smart-Satoh-Araki |
| TPFPM | Two Parallel Balanced Full-Precision Multipliers |
| ZPA | Zero Power Analysis |
Symbols
The following symbols are used in this manuscript:
| Elliptic curve | |
| Finite fields or Galois field | |
| Nonempty set | |
| p | Prime number |
| m | Extension degree of binary or primary field |
| Coefficients of elliptic curve | |
| Reduction polynomial for the binary field | |
| h | Cofactor of an elliptic curve |
| Number at infinity | |
| P | Base point on elliptic curve |
| k | Scalar |
| Q | Point on elliptic curve |
| R | Point on elliptic curve |
| S | Point on elliptic curve |
| Primitive element | |
| Binary digit of k | |
| Ordered pair | |
| Ordered triple | |
| a | Area |
| Maximum operating frequency | |
| ℓ | Latency |
| t | Time |
References
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Linz, Austria, 9–11 April 1985; pp. 417–426. [Google Scholar] [CrossRef]
- Cheung, D.; Maslov, D.; Mathew, J.; Pradhan, D.K. On the design and optimization of a quantum polynomial-time attack on elliptic curve cryptography. In Proceedings of the Workshop on Quantum Computation, Communication, and Cryptography, Tokyo, Japan, 30 January–1 February 2008; pp. 96–104. [Google Scholar] [CrossRef]
- Kikwai, B.K. Elliptic curve digital signatures and their application in the bitcoin crypto-currency transactions. Int. J. Sci. Res. Publ. 2017, 7, 135–138. [Google Scholar]
- Käsper, E. Fast Elliptic Curve Cryptography in OpenSSL. In Proceedings of the 2011 International Conference on Financial Cryptography and Data Security, Gros Islet, St. Lucia, 28 February–4 March 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 27–39. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Xie, E.Y. When an attacker meets a cipher-image in 2018: A year in review. J. Inf. Secur. Appl. 2019, 48, 102361. [Google Scholar] [CrossRef]
- Khoirom, M.S.; Laiphrakpam, D.S.; Themrichon, T. Cryptanalysis of multimedia encryption using elliptic curve cryptography. Optik 2018, 168, 370–375. [Google Scholar] [CrossRef]
- Dahshan, H. An elliptic curve key management scheme for Internet of Things. Int. J. Appl. Eng. Res. 2016, 11, 10241–10246. [Google Scholar]
- Shankar, S.K.; Tomar, A.; Tak, G. Secure Medical Data Transmission by Using ECC with Mutual Authentication in WSNs. Procedia Comput. Sci. 2015, 70, 455–461. [Google Scholar] [CrossRef][Green Version]
- Natanael, D.; Faisal; Suryani, D. Text Encryption in Android Chat Applications using Elliptical Curve Cryptography (ECC). Procedia Comput. Sci. 2018, 135, 283–291. [Google Scholar] [CrossRef]
- Imran, M.; Rashid, M.; Jafri, A.R.; Najam-ul Islam, M. ACryp-Proc: Flexible asymmetric crypto processor for point multiplication. IEEE Access 2018, 6, 22778–22793. [Google Scholar] [CrossRef]
- Pateriya, R.; Vasudevan, S. Elliptic Curve Cryptography in Constrained Environments: A Review. In Proceedings of the 2011 International Conference on Communication Systems and Network Technologies, Jammu, India, 3–5 June 2011; pp. 120–124. [Google Scholar] [CrossRef]
- Hossain, M.S.; Saeedi, E.; Kong, Y. Parallel point-multiplication architecture using combined group operations for high-speed cryptographic applications. PLoS ONE 2017, 12, e0176214. [Google Scholar] [CrossRef]
- Azarderakhsh, R.; Reyhani-Masoleh, A. Parallel and high-speed computations of elliptic curve cryptography using hybrid-double multipliers. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1668–1677. [Google Scholar] [CrossRef]
- Dhillon, P.K.; Kalra, S. Elliptic curve cryptography for real time embedded systems in IoT networks. In Proceedings of the 2016 5th International Conference on Wireless Networks and Embedded Systems (WECON), Rajpura, India, 14–16 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, D.; Zou, X. An efficient and flexible hardware implementation of the dual-field elliptic curve cryptographic processor. IEEE Trans. Ind. Electron. 2017, 64, 2353–2362. [Google Scholar] [CrossRef]
- Salarifard, R.; Bayat-Sarmadi, S.; Mosanaei-Boorani, H. A low-latency and low-complexity point-multiplication in ECC. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2869–2877. [Google Scholar] [CrossRef]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to elliptic curve cryptography. Comput. Rev. 2005, 46, 13. [Google Scholar] [CrossRef]
- Marwedel, P. Embedded System Design; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1. [Google Scholar]
- Vahid, F.; Givargis, T. Embedded System Design: A Unified Hardware/Software Approach; Department of Computer Science and Engineering University of California: La Jolla, CA, USA, 1999. [Google Scholar]
- Loi, K.C.; Ko, S.B. Flexible elliptic curve cryptography coprocessor using scalable finite field arithmetic blocks on FPGAs. Microprocess. Microsyst. 2018, 63, 182–189. [Google Scholar] [CrossRef]
- Ciet, M.; Joye, M. Elliptic Curve Cryptosystems in the Presence of Permanent and Transient Faults. Des. Codes Cryptogr. 2005, 36, 33–43. [Google Scholar] [CrossRef]
- Pollard, J.M. A monte carlo method for factorization. BIT Numer. Math. 1975, 15, 331–334. [Google Scholar] [CrossRef]
- Silverman, J.H. Advanced Topics in the Arithmetic of Elliptic Curves; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994; Volume 151. [Google Scholar] [CrossRef]
- San, C.V. A Survey of Elliptic Curve Cryptosystems, Part I: Introductory; Technical Report, NAS Technical Report-NAS-03-012. 2003. Available online: https://nas.nasa.gov/assets/pdf/techreports/2003/nas-03-012.pdf (accessed on 20 June 2020).
- Ning, P.; Yin, Y.L. Efficient Software Implementation for Finite Field Multiplication in Normal Basis. In Information and Communications Security; Qing, S., Okamoto, T., Zhou, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 177–188. [Google Scholar] [CrossRef]
- Mullin, R.C.; Onyszchuk, I.M.; Vanstone, S.A.; Wilson, R.M. Optimal normal bases in GF (pn). Discret. Appl. Math. 1988, 22, 149–161. [Google Scholar] [CrossRef]
- Li, L.; Li, S. High-performance pipelined architecture of point multiplication on Koblitz curves. IEEE Trans. Circuits Syst. II Express Briefs 2017. [Google Scholar] [CrossRef]
- Brown, D. Standards for efficient cryptography, SEC 1: Elliptic curve cryptography. Released Stand. Version 2009, 1. Available online: https://www.secg.org/SEC1-Ver-1.0.pdf (accessed on 20 June 2020).
- Jebrila, I.H.; Sallehb, R.; Mc, A.S. Efficient Algorithm in Projective Coordinates for EEC Over. Int. J. Comput. Internet Manag. 2007, 15, 43–50. [Google Scholar]
- Saffar, N.A.; Said, M. Improved Arithmetic on Elliptic Curves over Prime Field. Int. J. Comput. Netw. Commun. Secur. 2014, 2, 462–471. [Google Scholar]
- Fan, J.; Guo, X.; De Mulder, E.; Schaumont, P.; Preneel, B.; Verbauwhede, I. State-of-the-art of secure ECC implementations: A survey on known side-channel attacks and countermeasures. In Proceedings of the 2010 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST), Anaheim, CA, USA, 13–14 June 2010; pp. 76–87. [Google Scholar] [CrossRef]
- Kitchenham, B.; Charters, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; Technical Report EBSE 2007-001, Keele University and Durham University Joint Report. 2007. Available online: https://www.elsevier.com/__data/promis_misc/525444systematicreviewsguide.pdf (accessed on 20 June 2020).
- Scimago. Scimago Journal and Country Rank. 2019. Available online: www.scimagojr.com (accessed on 10 November 2020).
- Rashidi, B.; Sayedi, S.M.; Farashahi, R.R. High-speed hardware architecture of scalar multiplication for binary elliptic curve cryptosystems. Microelectron. J. 2016, 52, 49–65. [Google Scholar] [CrossRef]
- Khan, Z.U.; Benaissa, M. High-Speed and Low-Latency ECC Processor Implementation Over GF (2m) on FPGA. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 165–176. [Google Scholar] [CrossRef]
- Benaissa, M.; Khan, Z. Throughput/area-efficient ECC processor using Montgomery point multiplication on FPGA. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 1078–1082. [Google Scholar] [CrossRef]
- Al-Somani, T.F. High-performance generic-point parallel scalar multiplication. Arab. J. Sci. Eng. 2017, 42, 507–512. [Google Scholar] [CrossRef]
- Li, J.; Zhong, S.; Li, Z.; Cao, S.; Zhang, J.; Wang, W. Speed-Oriented Architecture for Binary Field Point Multiplication on Elliptic Curves. IEEE Access 2019, 7, 32048–32060. [Google Scholar] [CrossRef]
- Harb, S.; Jarrah, M. FPGA implementation of the ECC over GF(2m) for small embedded applications. ACM Trans. Embed. Comput. Syst. 2019, 18. [Google Scholar] [CrossRef]
- Kumar, N.; Shirisha, C. An area-efficient ECC architecture over GF(2m) for resource-constrained applications. AEU Int. J. Electron. Commun. 2020, 125. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. FIPS PUB 186-2: Digital Signature Standard (DSS); NIST: Gaithersburg, MD, USA, 2000.
- Farashahi, R.R.; Joye, M. Efficient arithmetic on Hessian curves. In Proceedings of the International Workshop on Public Key Cryptography, Paris, France, 26–28 May 2010; pp. 243–260. [Google Scholar] [CrossRef]
- Kocabaş, Ü.; Fan, J.; Verbauwhede, I. Implementation of binary Edwards curves for very-constrained devices. In Proceedings of the ASAP 2010-21st IEEE International Conference on Application-specific Systems, Architectures and Processors, Rennes, France, 7–9 July 2010; pp. 185–191. [Google Scholar] [CrossRef]
- Devigne, J.; Joye, M. Binary Huff curves. In Proceedings of the Cryptographers Track at the RSA Conference, San Francisco, CA, USA, 14–18 February 2011; pp. 340–355. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kim, M.S.; Lee, H.R.; Kim, H.W. Implementation and Analysis of Elliptic Curve Cryptosystems over Polynomial Basis and Onb; World Academy of Science, Engineering and Technology: Istanbul, Turkey, 2005; Volume 10. [Google Scholar] [CrossRef]
- Itoh, T.; Tsujii, S. A Fast Algorithm for Computing Multiplicative Inverses in GF(2M) Using Normal Bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef]
- Patil, S.; Manjunatha, D.V.; Kiran, D. Design of speed and power efficient multipliers using vedic mathematics with VLSI implementation. In Proceedings of the 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 10–11 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Menezes, A.J.; Vanstone, S.A. Elliptic curve cryptosystems and their implementation. J. Cryptol. 1993, 6, 209–224. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).