The Pitfalls of Heterosis Coefficients
Abstract
1. Introduction
2. The Dominance and Heterosis Coefficients
- (i)
- Wright [1] defined:where , and are, respectively, the phenotypic values of genotypes , and , with . varies from 0, when is fully dominant over , to 1, when is fully recessive with respect to . corresponds to semi-dominance or additivity () (Table 1). Note that is strictly equivalent to the dominance coefficient h used in evolutionary genetics [4].
- (ii)
- Falconer [5] proposed the following coefficient:where . varies in the opposite direction to : its value is 1 if (complete dominance of over ), if ( is fully recessive with respect to ) and 0 if there is additivity. In the case of overdominance, and , and in the case of underdominance, and (Table 1).
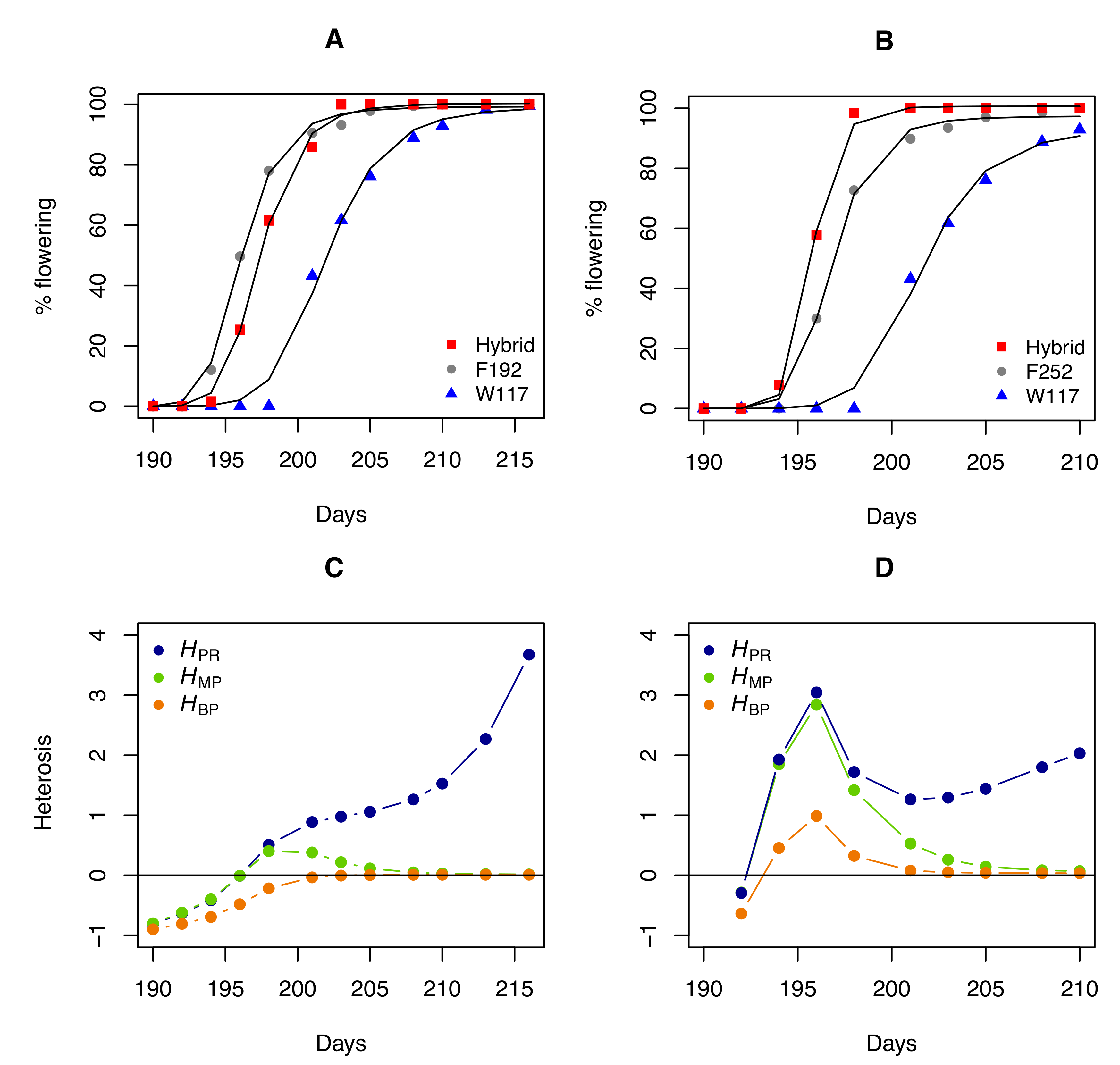
3. Relationship between the Potence Ratio and the other Heterosis Coefficients
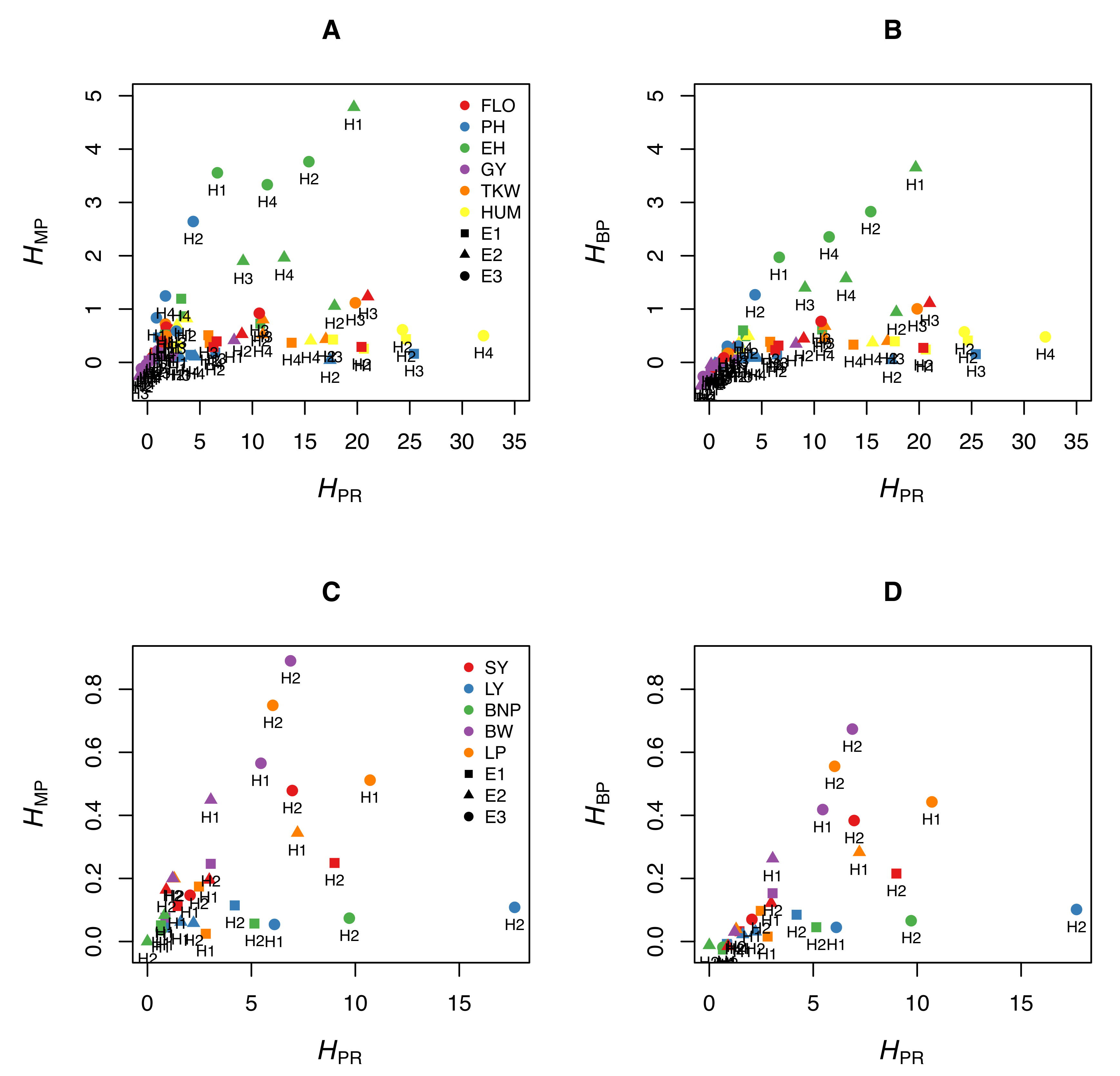
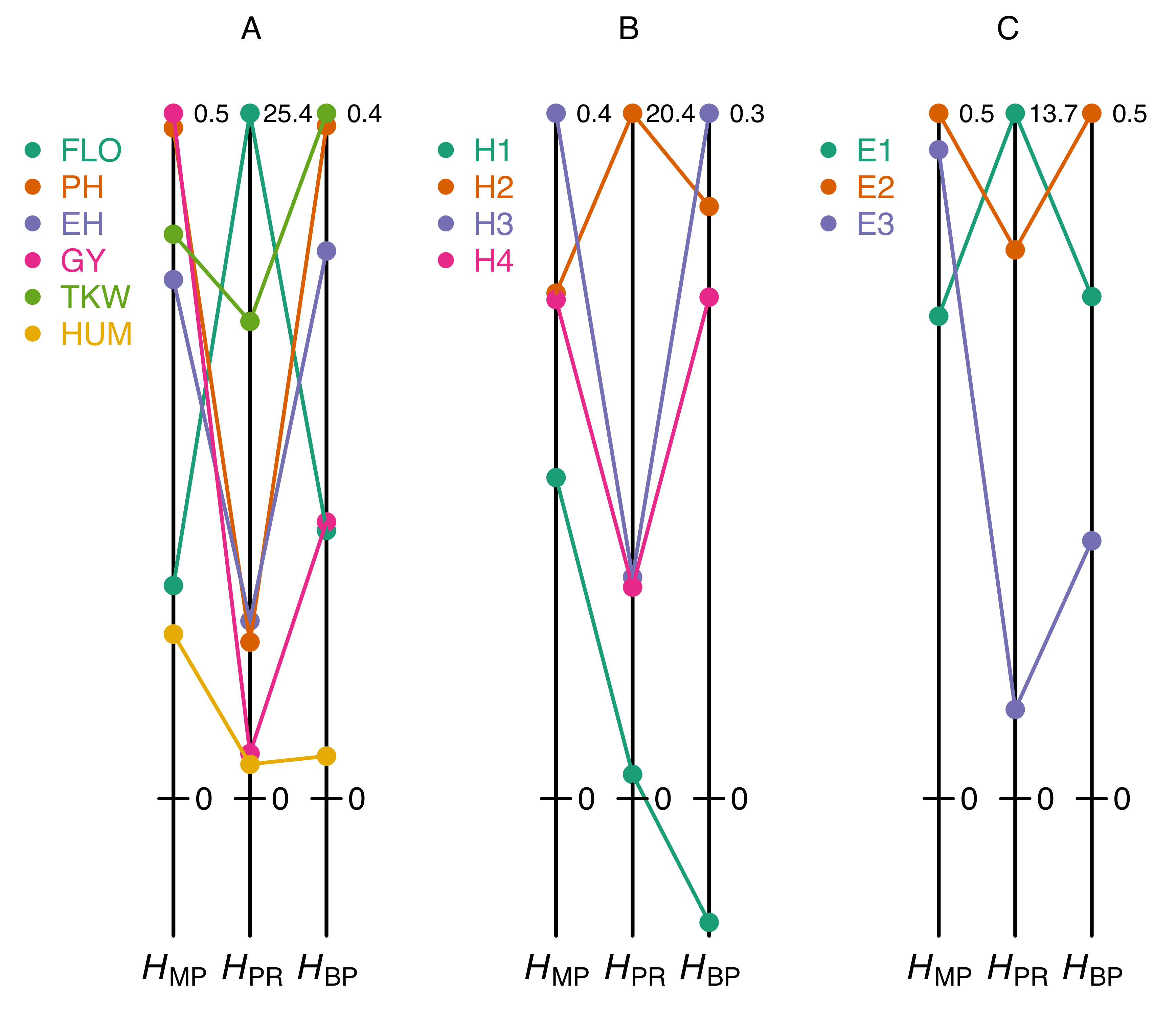
4. The Pitfalls of the Most Commonly Used Heterosis Coefficients
5. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wright, S. Physiological and evolutionary theories of dominance. Am. Nat. 1934, 68, 24–53. [Google Scholar] [CrossRef]
- Fiévet, J.B.; Nidelet, T.; Dillmann, C.; de Vienne, D. Heterosis is a systemic property emerging from non-linear genotype-phenotype relationships: Evidence from in vitro genetics and computer simulations. Front. Genet. 2018, 9, 159. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, F.; Fouqueau, L.; de Vienne, D.; Nidelet, T.; Violle, C.; Weigel, D. Nonlinear phenotypic variation uncovers the emergence of heterosis in Arabidopsis thaliana. PLoS Biol. 2019, 17, e3000214. [Google Scholar] [CrossRef] [PubMed]
- Crow, J.F.; Kimura, M. An Introduction to Population Genetics Theory; The Blackburn Press: Caldwell, NJ, USA, 1970. [Google Scholar]
- Falconer, D.S. Introduction to Quantitative Genetics; Oliver and Boyd: Edinburgh, UK; London, UK, 1960. [Google Scholar]
- Gowen, J.W. Heterosis; Iowa State College Press: Ames, IA, USA, 1952. [Google Scholar]
- Frankel, R. Heterosis: Reappraisal of Theory and Practice; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1983. [Google Scholar]
- Fonseca, S.; Patterson, F.L. Hybrid Vigor in a Seven-Parent Diallel Cross in Common Winter Wheat (Triticum aestivum L.). Crop. Sci. 1968, 8, 85–88. [Google Scholar] [CrossRef]
- Mather, K. Biometrical Genetics; Methuen: London, UK, 1949. [Google Scholar]
- Shang, L.; Wang, Y.; Cai, S.; Wang, X.; Li, Y.; Abduweli, A.; Hua, J. Partial Dominance, Overdominance, Epistasis and QTL by Environment Interactions Contribute to Heterosis in Two Upland Cotton Hybrids. G3 Genes Genomes Genet. 2016, 6, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Shull, G.H. The composition of a field of maize. Am. Breeder’s Assoc. Rep. 1908, 4, 296–301. [Google Scholar] [CrossRef]
- East, E.M. Heterosis. Genetics 1936, 21, 375–397. [Google Scholar] [PubMed]
| Reference | Coefficient | Coefficient Scales with Their Characteristic Values |
|---|---|---|
| High homozygote |  | |
| Mean homozygote | 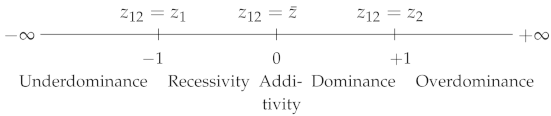 | |
| Mid-parent | 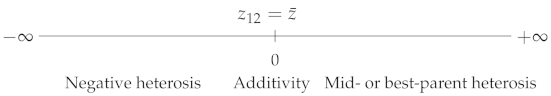 | |
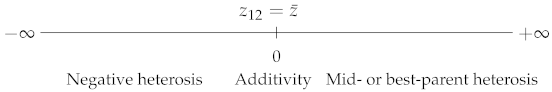 | ||
 | ||
| Best-parent | 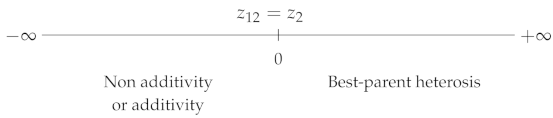 | |
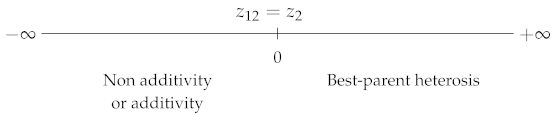 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Vienne, D.; Fiévet, J.B. The Pitfalls of Heterosis Coefficients. Plants 2020, 9, 875. https://doi.org/10.3390/plants9070875
de Vienne D, Fiévet JB. The Pitfalls of Heterosis Coefficients. Plants. 2020; 9(7):875. https://doi.org/10.3390/plants9070875
Chicago/Turabian Stylede Vienne, Dominique, and Julie B. Fiévet. 2020. "The Pitfalls of Heterosis Coefficients" Plants 9, no. 7: 875. https://doi.org/10.3390/plants9070875
APA Stylede Vienne, D., & Fiévet, J. B. (2020). The Pitfalls of Heterosis Coefficients. Plants, 9(7), 875. https://doi.org/10.3390/plants9070875





