Rice Growth Estimation and Yield Prediction by Combining the DSSAT Model and Remote Sensing Data Using the Monte Carlo Markov Chain Technique
Abstract
1. Introduction
2. Result
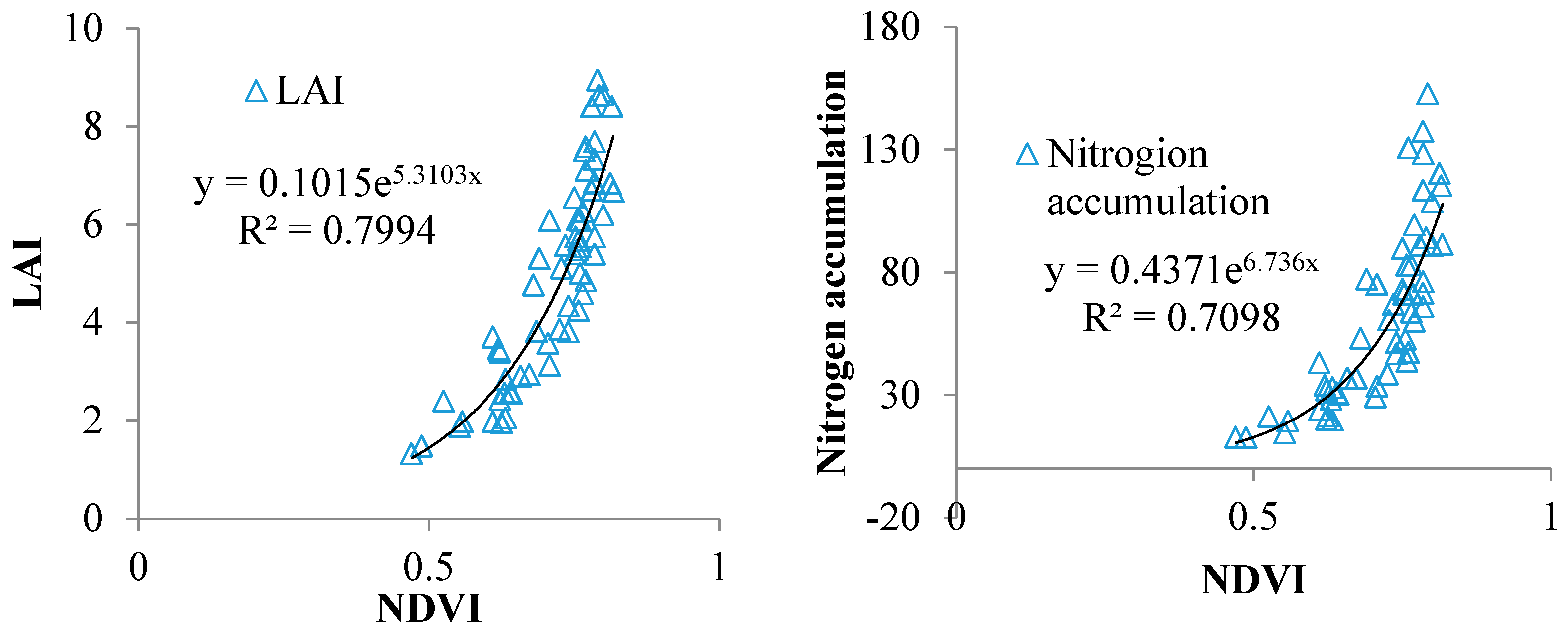
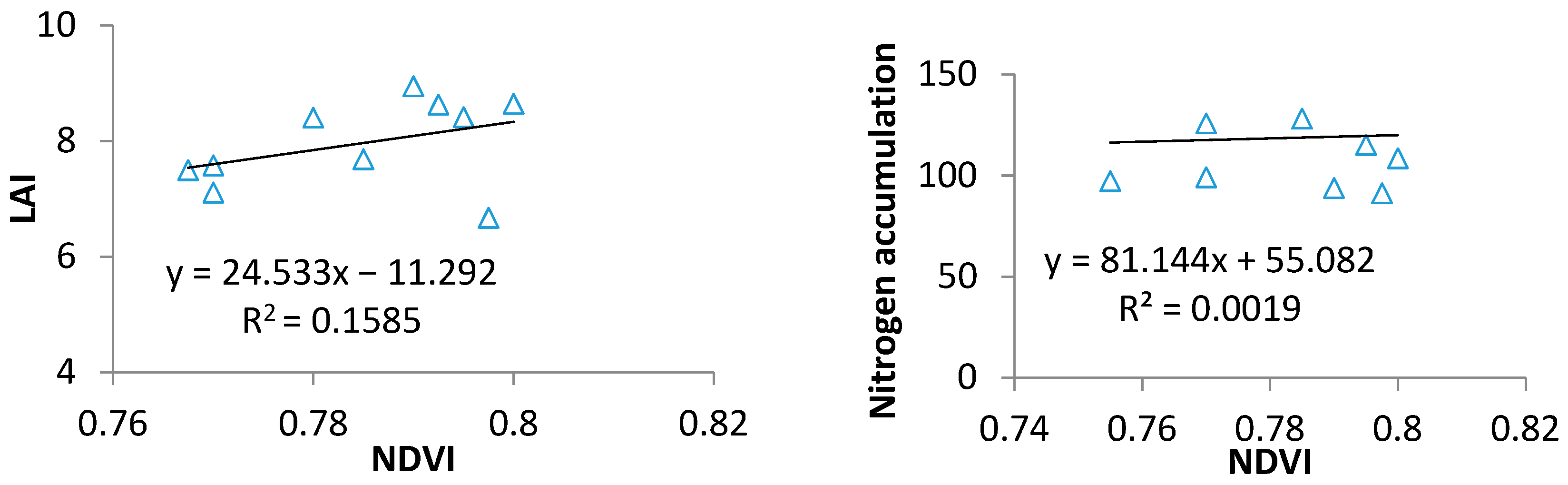
2.1. Spectral Index for LAI and VNA Estimation
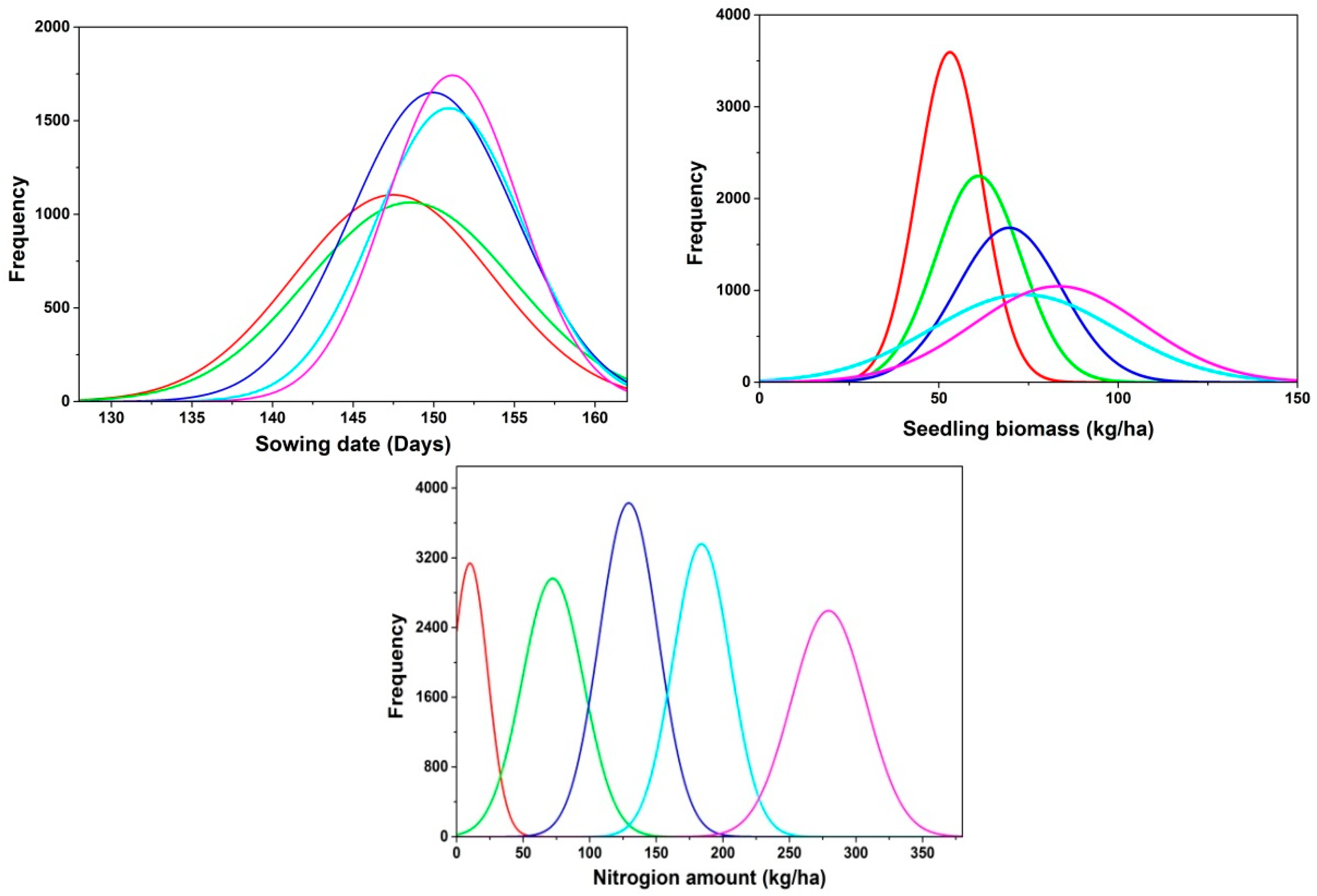
2.2. The Probability Distribution of Inverted Initial Parameters
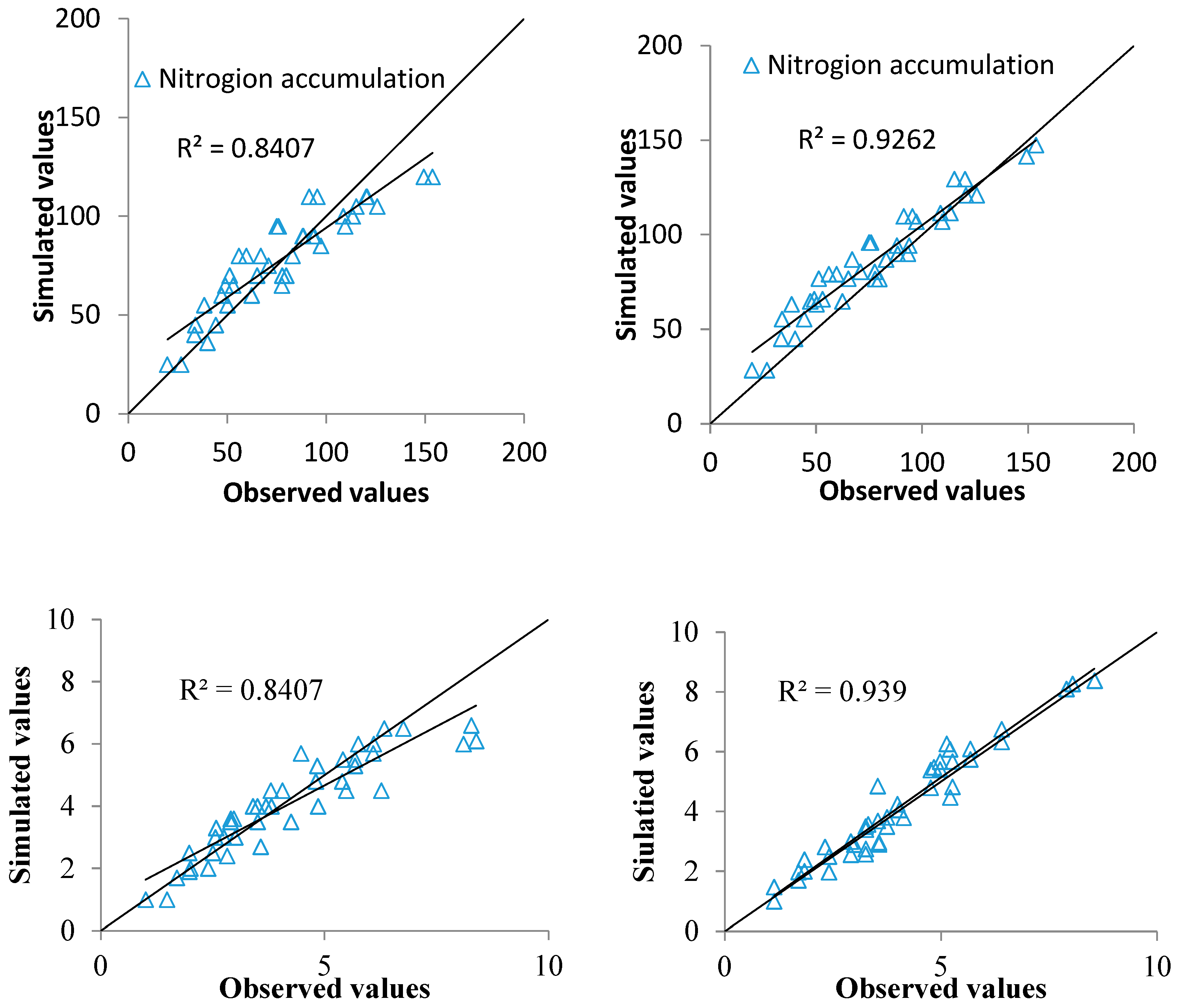
2.3. Data Assimilation for LAI and PNA Estimation
2.4. Data Assimilation for LAI and PNA Prediction and Uncertainty Analysis
2.5. Data Assimilation for Yield Prediction and Uncertainty Analysis
3. Materials and Methods
3.1. Experimental Design
3.2. Data Acquisition
3.2.1. Measurement of Canopy Spectral Reflectance
3.2.2. Plant Sampling and Analysis
3.3. CERES-Rice Model
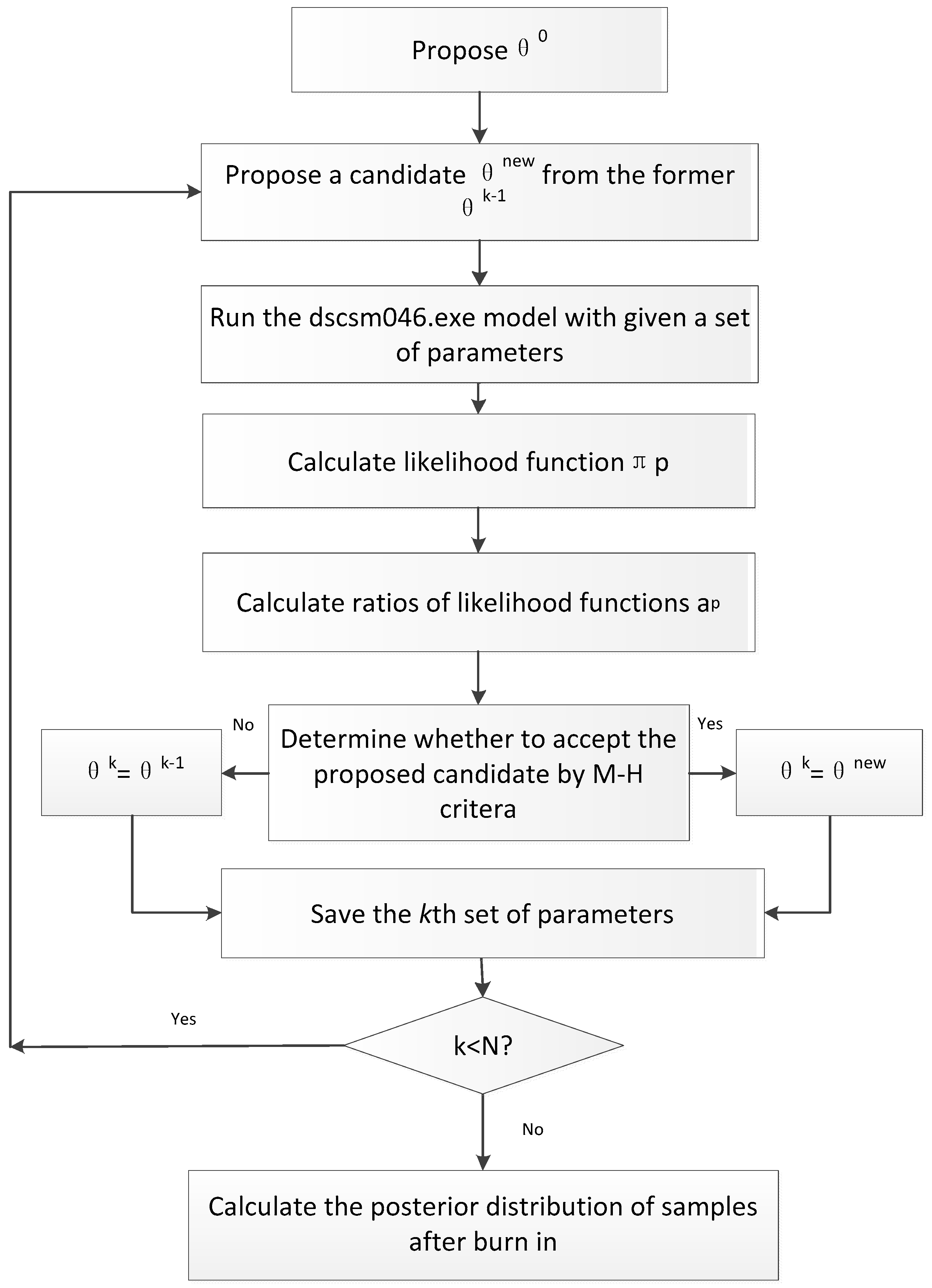
3.4. Integrating the MCMC Technique for Data Assimilation
3.5. Statistical Analysis
4. Discussion
4.1. Integration of Crop Model and Remote Sensing
4.2. MCMC Method
4.3. Uncertainty Analysis
4.4. Yield Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, L.; Fang, S.; Fan, J.; Wang, Y.; Zhan, L.; He, Y. Rice Yield Estimation Using Machine Learning and Feature Selection in Hilly and Mountainous Chongqing, China. Agriculture 2024, 14, 1615. [Google Scholar] [CrossRef]
- Xia, T.; Miao, Y.; Wu, D.; Shao, H.; Khosla, R.; Mi, G. Active optical sensing of spring maize for in-season diagnosis of nitrogen status based on nitrogen nutrition index. Remote Sens. 2016, 8, 605. [Google Scholar] [CrossRef]
- Anthony, N.R.; Anatoly, G.; Yi, P.; Viña, A.; Timothy, A.; Donald, R. Green leaf area index estimation in maize and soybean: Combining vegetation indices to achieve maximal sensitivity. Agron. J. 2012, 104, 1336. [Google Scholar]
- González-Sanpedro, M.C.; Le Toan, T.; Moreno, J.; Kergoat, L.; Rubio, E. Seasonal variations of leaf area index of agricultural fields retrieved from Landsat data. Remote Sens. Environ. 2008, 112, 810–824. [Google Scholar] [CrossRef]
- Gitelson, A.A. Remote sensing estimation of crop biophysical characteristics at various scales. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 1–36. [Google Scholar]
- Wang, H.; Zhu, Y.; Li, W.; Cao, W.; Tian, Y. Integrating remotely sensed leaf area index and leaf nitrogen accumulation with ricegrow model based on particle swarm optimization algorithm for rice grain yield assessment. J. Appl. Remote Sens. 2014, 8, 083674. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Xu, X.; Zhao, C.; Jin, X.; Yang, G.; Feng, H. Assimilation of two variables derived from hyperspectral data into the DSSAT-CERES model for grain yield and quality estimation. Remote Sens. 2015, 7, 12400–12418. [Google Scholar] [CrossRef]
- Akumaga, U.; Gao, F.; Anderson, M.; Dulaney, W.P.; Houborg, R.; Russ, A.; Hively, W.D. Integration of remote sensing and field observations in evaluating DSSAT model for estimating maize and soybean growth and yield in Maryland, USA. Agron. J. 2023, 13, 1540. [Google Scholar] [CrossRef]
- Thirumeninathan, S.; Pazhanivelan, S.; Mohan, R.; Pouchepparadjou, A.; Sudarmanian, N.S.; Ragunath, K.; Aruna, L.; Satheesh, S. Integrating S1A microwave remote sensing and DSSAT CROPGRO simulation model for groundnut area and yield estimation. Eur. J. Agron. 2024, 161, 127348. [Google Scholar] [CrossRef]
- Ma, G.; Huang, J.; Wu, W.; Fan, J.; Zou, J.; Wu, S. Assimilation of MODIS-LAI into the WOFOST model for forecasting regional winter wheat yield. Math. Comput. Model. 2013, 58, 634–643. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Dong, Y.; Zhao, C.; Yang, G.; Chen, L.; Wang, J.; Feng, H. Integrating a very fast simulated annealing optimization algorithm for crop leaf area index variational assimilation. Math. Comput. Model. 2013, 58, 877–885. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, S.; Shen, S. Assimilating remote sensing information with crop model using Ensemble Kalman Filter for improving LAI monitoring and yield estimation. Ecol. Model. 2013, 270, 30–42. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Yang, G.; Yang, H.; Feng, H.; Xu, X.; Wang, J.; Li, X.; Luo, J. Winter wheat yield estimation based on multi-source medium resolution optical and radar imaging data and the AquaCrop model using the particle swarm optimization algorithm. ISPRS J. Photogramm. Remote Sens. 2017, 126, 24–37. [Google Scholar] [CrossRef]
- De Wit, A.D.; Van Diepen, C. Crop model data assimilation with the Ensemble Kalman filter for improving regional crop yield forecasts. Agric. For. Meteorol. 2007, 146, 38–56. [Google Scholar] [CrossRef]
- Nearing, G.S.; Crow, W.T.; Thorp, K.R.; Moran, M.S.; Reichle, R.H.; Gupta, H.V. Assimilating remote sensing observations of leaf area index and soil moisture for wheat yield estimates: An observing system simulation experiment. Water Resour. Res. 2012, 48, W05525. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, X.; Tang, L.; Liu, L.; Cao, W.; Zhu, Y. Estimation of ecotype-specific cultivar parameters in a wheat phenology model and uncertainty analysis. Agric. For. Meteorol. 2016, 221, 219–229. [Google Scholar] [CrossRef]
- Siriwardene, J.A.D.S.; Thomas, A.J.; Evans, R.A.; Axford, R.F. Automated analysis of total nitrogen in solid biological material. J. Sci. Food Agric. 1966, 17, 456–460. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Hastings, W. Monte Carlo sampling methods using Markov chains and their application. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Erdle, K.; Mistele, B.; Schmidhalter, U. Comparison of active and passive spectral sensors in discriminating biomass parameters and nitrogen status in wheat cultivars. Field Crops Res. 2011, 124, 74–84. [Google Scholar] [CrossRef]
- Serrano, L.; Gamon, J.A.; Peñuelas, J. Estimation of canopy photosynthetic and nonphotosynthetic components from spectral transmittance. Ecology 2000, 81, 3149–3162. [Google Scholar] [CrossRef]
- Wang, W.; Yao, X.; Yao, X.; Tian, Y.; Liu, X.; Ni, J.; Cao, W.; Zhu, Y. Estimating leaf nitrogen concentration with three-band vegetation indices in rice and wheat. Field Crops Res. 2012, 129, 90–98. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.X.; Chen, X.P.; Zhang, H.; Jia, L.; Bareth, G. Estimating winter wheat biomass and nitrogen status using an active crop sensor. Intell. Autom. Soft Comput. 2010, 16, 1221–1230. [Google Scholar]
- Takahashi, W.; Vu, N.C.; Kawaguchi, S.; Minamiyama, M.; Ninomiya, S. Statistical models for prediction of dry weight and nitrogen accumulation based on visible and near-infrared hyperspectral reflectance of rice canopies. Plant Prod. Sci. 2000, 3, 377–386. [Google Scholar] [CrossRef]
- Ntakos, G.; Prikaziuk, E.; ten Den, T.; Reidsma, P.; Vilfan, N.; van der Wal, T.; van der Tol, C. Coupled WOFOST and SCOPE model for remote sensing-based crop growth simulations. Comput. Electron. Agric. 2024, 225, 109238. [Google Scholar] [CrossRef]
- Naud, C.; Mitchell, K.L.; Muller, J.P.; Clothiaux, E.E.; Albert, P.; Preusker, R.; Fischer, J.; Hogan, R.J. Comparison between ATSR-2 stereo, MOS O2-A band and ground-based cloud top heights. Int. J. Remote Sens. 2007, 28, 1969–1987. [Google Scholar] [CrossRef]
- Chen, Y.; Cournède, P.H. Data assimilation to reduce uncertainty of crop model prediction with convolution particle filtering. Ecol. Model. 2014, 290, 165–177. [Google Scholar] [CrossRef]
- Huang, J.; Song, J.; Huang, H.; Zhuo, W.; Niu, Q.; Wu, S.; Ma, H.; Liang, S. Progress and perspectives in data assimilation algorithms for remote sensing and crop growth model. Sci. Remote Sens. 2024, 10, 100146. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, Z.; Chen, J.; Ren, J.; Li, Z.; Sun, L. The estimation of regional crop yield using ensemble-based four-dimensional variational data assimilation. Remote Sens. 2014, 6, 2664–2681. [Google Scholar] [CrossRef]
- Li, Q.; Gao, M.; Duan, S.; Yang, G.; Li, Z.L. Integrating remote sensing assimilation and SCE-UA to construct a grid-by-grid spatialized crop model can dramatically improve winter wheat yield estimate accuracy. Comput. Electron. Agric. 2024, 227, 1–10. [Google Scholar] [CrossRef]
- Ren, S.; Chen, H.; Hou, J.; Zhao, P.; Dong, Q.; Feng, H. Based on historical weather data to predict summer field-scale maize yield: Assimilation of remote sensing data to WOFOST model by ensemble Kalman filter algorithm. Comp. Electron. Agric. 2024, 219, 108822. [Google Scholar] [CrossRef]
- Wang, D.; Struik, P.C.; Liang, L.; Yin, X. Developing remote sensing- and crop model-based methods to optimize nitrogen management in rice fields. Comput. Electron. Agric. 2024, 220, 108899. [Google Scholar] [CrossRef]
- Shi, C.; Jin, Z.; Gao, L.; Ge, D.; Wei, X. Application and Analysis of Ceres-Rice in Rice Nitrogen Fertilizer Management. Jiangsu Agric. Sci. 2003, 19, 1–4. [Google Scholar]
- Hansen, J.W.; Jones, J.W. Short Survey: Scaling-up crop models for climate variability. Agric. Syst. 2000, 65, 43–72. [Google Scholar] [CrossRef]

| Treatments | Sowing Date (%) | Seeding Rate (%) | Nitrogen Amount (%) |
|---|---|---|---|
| E1N0 | −2 | −16.2 | / |
| E1N1 | −1.33 | 3.2 | 7.2 |
| E1N2 | 0 | 17.9 | −7.3 |
| E1N3 | 0.67 | 27.2 | −11.9 |
| E1N4 | 1.33 | 32.1 | 1.8 |
| E2N0 | −1.6 | −12.4 | / |
| E2N1 | −1.4 | 4.3 | −5.2 |
| E2N2 | −0.7 | 13.6 | 8.4 |
| E2N3 | 1 | 23.2 | −9.3 |
| E2N4 | 1.4 | 29.4 | 7.5 |
| E3N0 | −2.2 | −15.2 | / |
| E3N1 | −1.3 | −1 | 8.53 |
| E3N2 | −0.4 | 12.7 | −3.7 |
| E3N3 | 1.3 | 24.1 | 5.8 |
| E3N4 | 1.2 | 32.5 | 11.7 |
| Experiment No | Site | Cultivar | N Rate (Kg ha−1) | Planting Date | Soil Parameters |
|---|---|---|---|---|---|
| Experiment 1 2015 | Deqing | Yongyou538 | N0(0) N1(70) N2(140) N3(210) N4(280) | 28-May | Soil organic matter: 22 g kg−1 Total N: 1.37 g kg−1 P2O5: 32.59 mg kg−1 K2O: 98.96 mg kg−1 |
| Experiment 2 2016 | Deqing | Xiushui134 | N0(0) N1(70) N2(140) N3(210) N4(280) | 28-May | Soil organic matter: 21.1 g kg−1 Total N: 1.27 g kg−1 P2O5: 38.12 mg kg−1 K2O: 90.23 mg kg−1 |
| Experiment 3 2017 | Deqing | Yongyou1540 | N0(0) N1(70) N2(140) N3(210) N4(280) | 30-May | Soil organic matter: 22.4 g kg−1 Total N: 1.24 g kg−1 P2O5: 40.14 mg kg−1 K2O: 94.56 mg kg−1 |
| LAI | PNA | |||||||
|---|---|---|---|---|---|---|---|---|
| Tilling | Jointing | Booting | Flowering | Tilling | Jointing | Booting | Flowering | |
| N0 | 0.17 | 0.10 | 0.16 | 0.15 | 5.30 | 3.28 | 2.92 | 3.07 |
| N1 | 0.26 | 0.11 | 0.17 | 0.17 | 6.02 | 4.25 | 3.66 | 3.93 |
| N2 | 0.23 | 0.12 | 0.16 | 0.16 | 5.06 | 3.98 | 3.59 | 3.92 |
| N3 | 0.22 | 0.13 | 0.16 | 0.13 | 4.85 | 4.12 | 3.64 | 4.03 |
| N4 | 0.15 | 0.13 | 0.13 | 0.14 | 3.84 | 3.85 | 3.61 | 3.78 |
| Yield | |||
|---|---|---|---|
| R2 | RMSE (kg/ha) | RMSD (kg/ha) | |
| E1 | 0.86 | 960 | 678 |
| E2 | 0.83 | 338 | 764 |
| E3 | 0.7 | 685 | 792 |
| Total | 0.79 | 661 | 745 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, S.; Xue, Z.; Hu, J.; Chen, S.; Lv, Z. Rice Growth Estimation and Yield Prediction by Combining the DSSAT Model and Remote Sensing Data Using the Monte Carlo Markov Chain Technique. Plants 2025, 14, 1206. https://doi.org/10.3390/plants14081206
Chen Y, Wang S, Xue Z, Hu J, Chen S, Lv Z. Rice Growth Estimation and Yield Prediction by Combining the DSSAT Model and Remote Sensing Data Using the Monte Carlo Markov Chain Technique. Plants. 2025; 14(8):1206. https://doi.org/10.3390/plants14081206
Chicago/Turabian StyleChen, Yingbo, Siyu Wang, Zhankui Xue, Jijie Hu, Shaojie Chen, and Zunfu Lv. 2025. "Rice Growth Estimation and Yield Prediction by Combining the DSSAT Model and Remote Sensing Data Using the Monte Carlo Markov Chain Technique" Plants 14, no. 8: 1206. https://doi.org/10.3390/plants14081206
APA StyleChen, Y., Wang, S., Xue, Z., Hu, J., Chen, S., & Lv, Z. (2025). Rice Growth Estimation and Yield Prediction by Combining the DSSAT Model and Remote Sensing Data Using the Monte Carlo Markov Chain Technique. Plants, 14(8), 1206. https://doi.org/10.3390/plants14081206





