Modeling the Effect of the Biological Control of Pseudococcus viburni Signoret (Hemiptera: Pseudococcidae) on Grapevine Leafroll Virus Spread
Abstract
1. Introduction
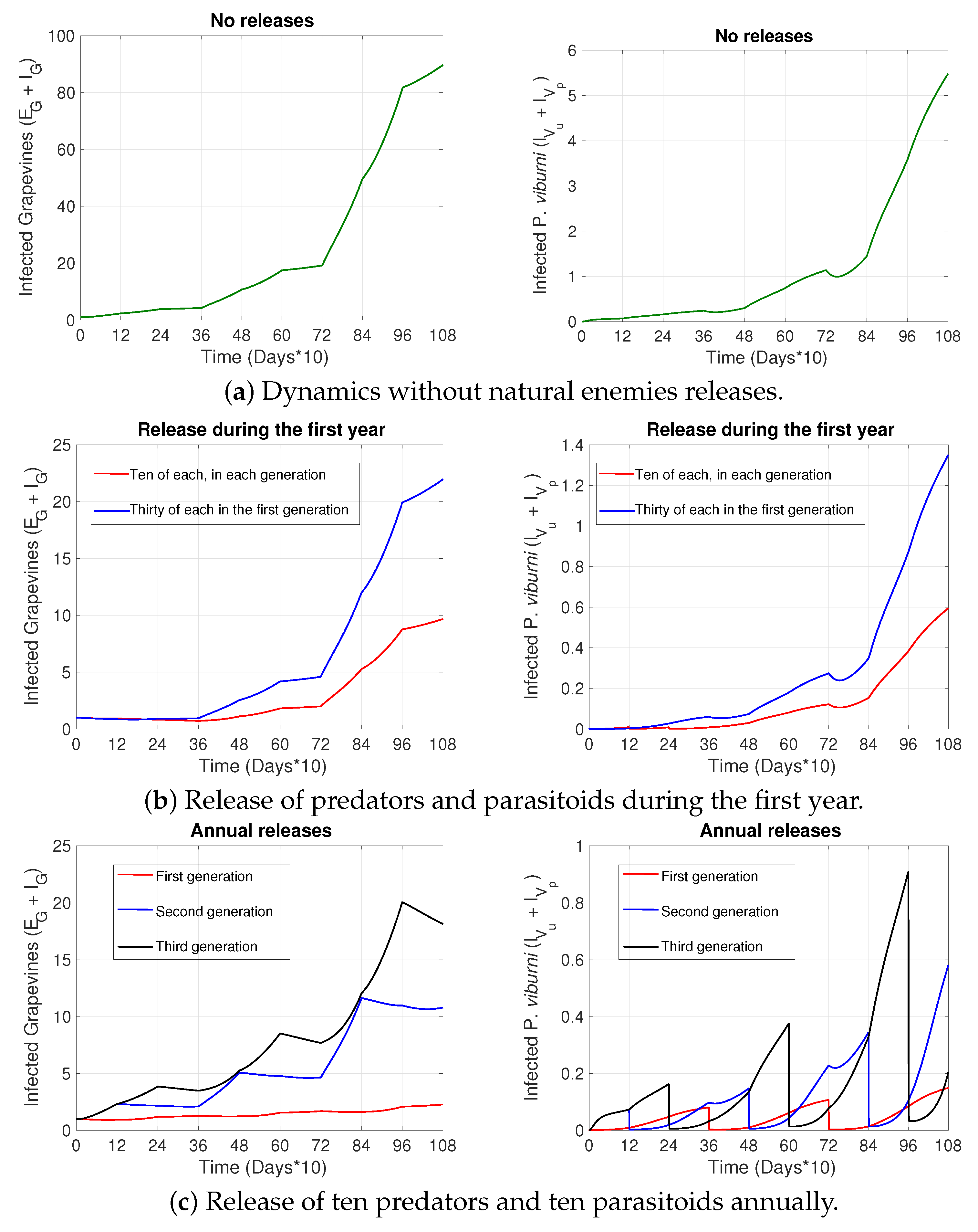
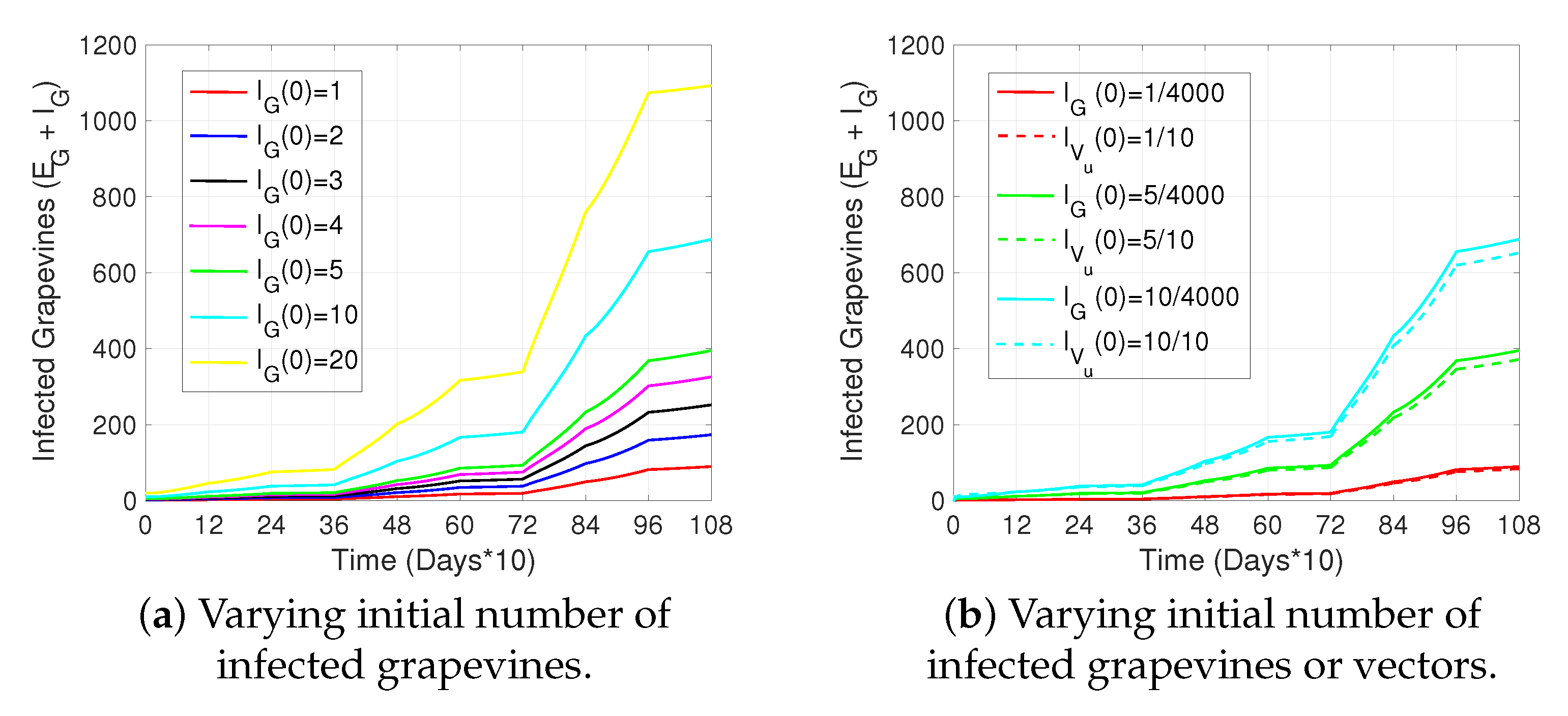
2. Results
3. Discussion
4. Materials and Methods
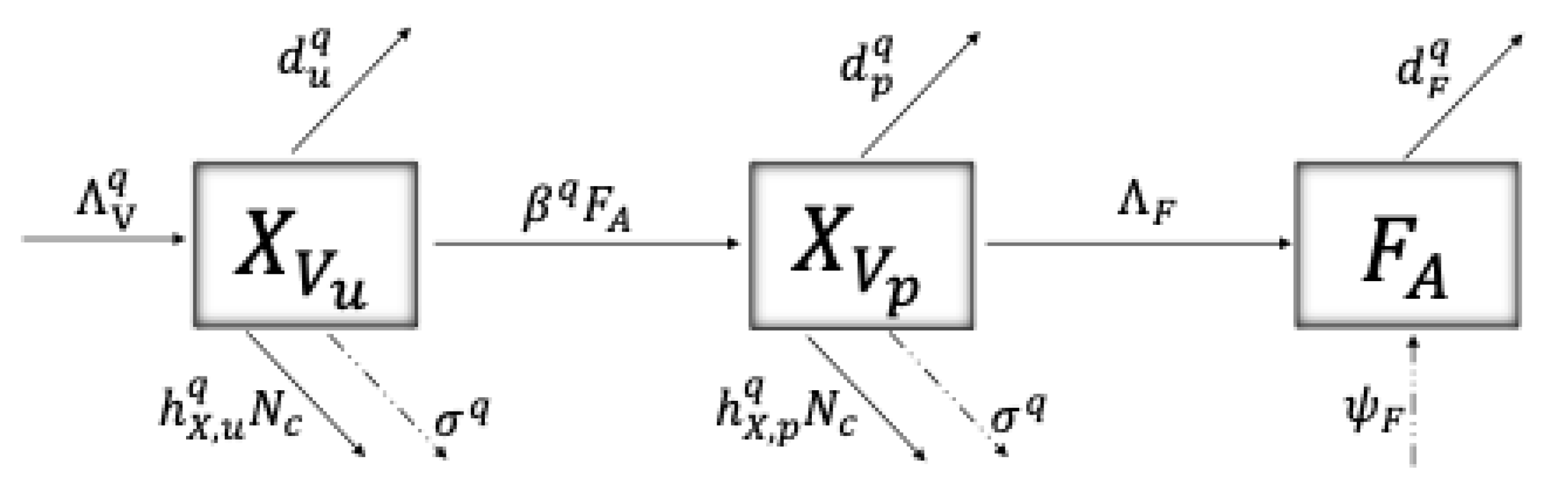
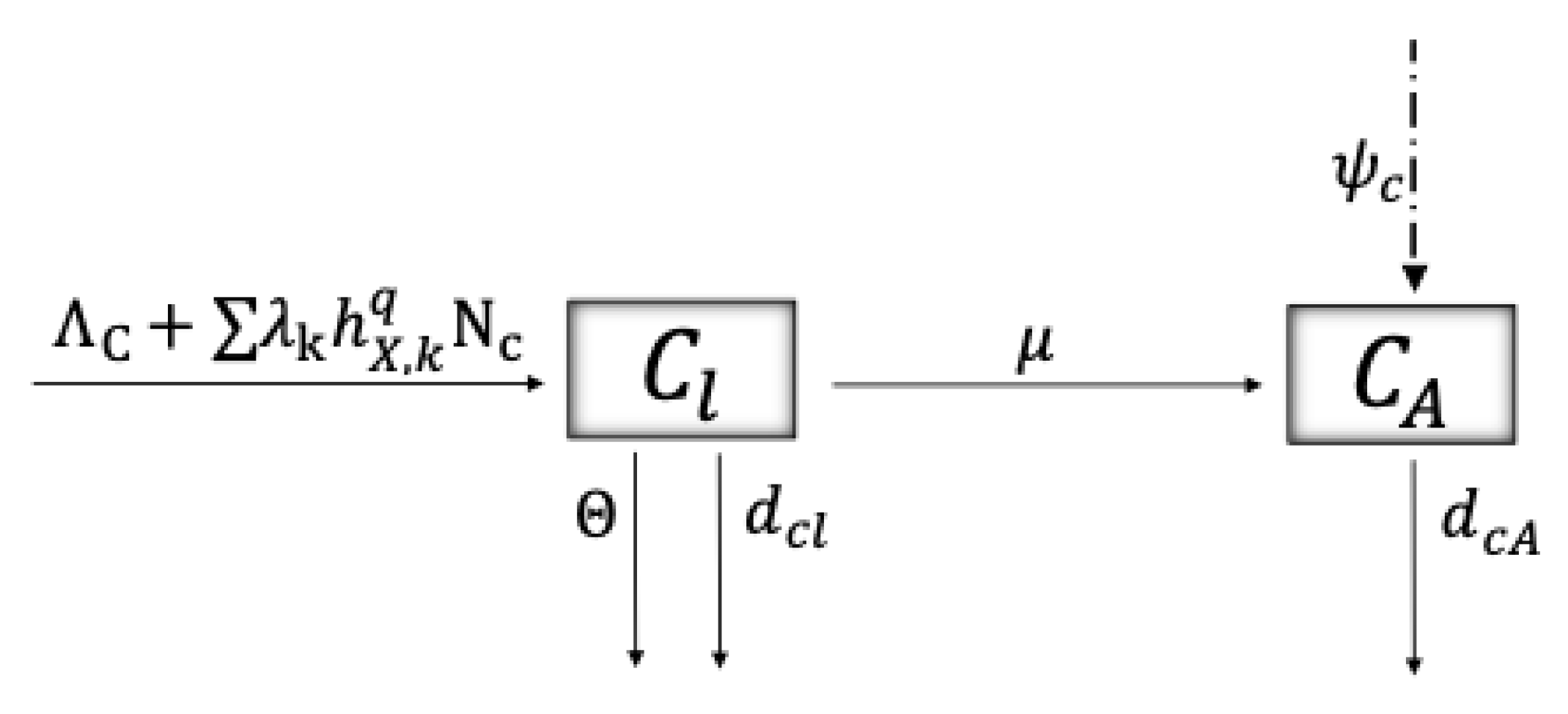
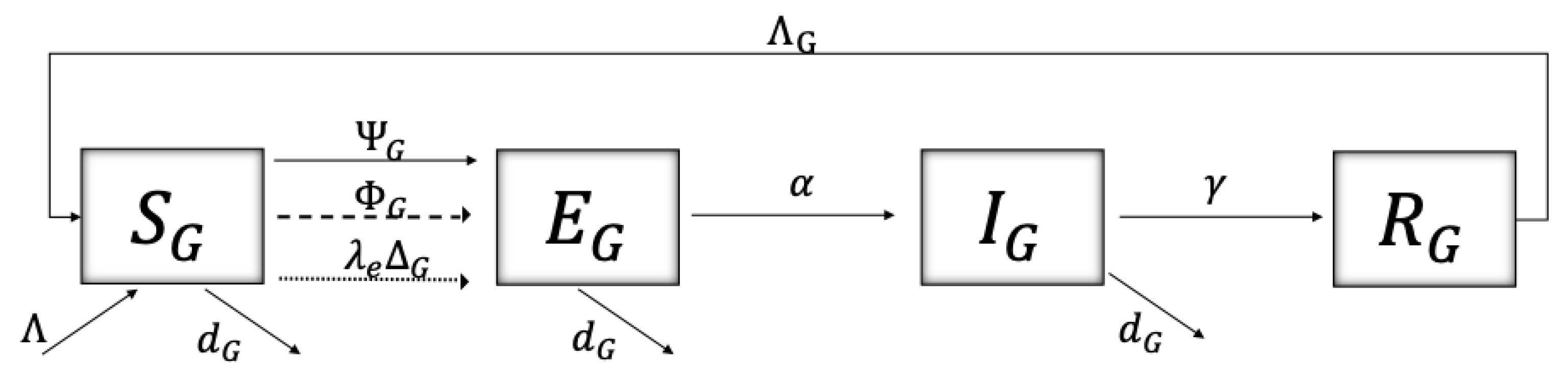
4.1. The Model
4.2. Model Description
| Variable | Description | Units |
|---|---|---|
| P. viburni | ||
| Susceptible () or infectious () state at development | v | |
| stage , | ||
| Unparasitized population of P. viburni at time t | v | |
| Parasitized population of P. viburni at time t | v | |
| A. flavidulus | ||
| Population at time t | f | |
| C. montrouzieri | ||
| Population at larval stage, at time t | m | |
| Population at adult stage, at time t | m | |
| Grapevines | ||
| Susceptible grapevines at time t | g | |
| Exposed grapevines at time t | g | |
| Infectious grapevines at time t | g | |
| Removed (uprooted) grapevines at time t | g | |
| Param. | Description | Units | Baseline | Value | Ref. |
|---|---|---|---|---|---|
| Recruitment rate. | [57] | ||||
| Parasitation rate of P. viburni by A. flavidulus. | 0.5 | [58] | |||
| , | Natural mortality rate. | 1/30, 1/30 | [58] | ||
| Predator preference proportion for unparasitized, parasitized P. viburni, | Ul | [0,1] | 0.6, 0.4 | [38] | |
| Mortality incremental factor due to vector prevention and control measures differentiated by season . | Ul | [1,∞[ | 3/10, 3/100, 0 | [58] | |
| Constant in the functional response of the predation rate. | [1,∞[ | 1000 | [58] | ||
| Transmission rate from infectious vine to susceptible vector. | 65/100 | ||||
| Vector–host transmission rate reduction due to vector movement. | Ul | ]0,1] | 1/4 | [40,59,60] | |
| Average time a vector remains infectious. | d | ]0,16] | 10 | [17,61] |
| Param. | Description | Units | Baseline | Value | Ref. |
|---|---|---|---|---|---|
| A. flavidulus | |||||
| Recruitment rate. | – | 1/10 | [48] | ||
| Natural mortality rate. | 0.1 | [48] | |||
| Release incremental factor at instants . | Ul | - | CA | ||
| C. montrouzieri | |||||
| Recruitment rate. | 0.1 | [48] | |||
| Predation conversion rate from P. viburni to C. montrouzieri. | [0,1] | 0.001 | [48] | ||
| Cannibalism rate. | [0,1] | 1 | [38] | ||
| Mean larval stage duration before becoming adult. | d | 25 | [48] | ||
| Natural mortality rate of adults. | 0.02 | [48] | |||
| Natural mortality rate of larvae. | [48] | ||||
| Release incremental factor at instants . | Ul | - | CA | ||
| . d = day, m = C. montrouzieri, Ul = Unitless, CA = Chosen by author | |||||
| Param. | Description | Units | Baseline | Value | Ref. |
|---|---|---|---|---|---|
| Transmission rate to grapevine through P. viburni at both of its kth stages (), differentiated by seasonal generations of P. viburni | 1, 1/2, 1/8 | [18] | |||
| Transmission rate to grapevine through pruning, differentiated by seasonal generations of P. viburni | 0.01 × 0, 0.01 × 1/3, 0.01 × 1 | [37] | |||
| Average virus incubation time | d | 180 | [37] | ||
| Average time an infectious vine is uprooted | d | 720 | [37] | ||
| Replacement rate of removed grapevines. | 1/360 | [62] | |||
| Recruitment rate | 1/9000 | ||||
| Grafting rate | 0 | [63,64] | |||
| Proportion of infected grafts | Ul | 0 | [37] | ||
| Natural mortality rate | 1/9000 | [13] | |||
| Time instants where grafting occurs | d | 0 | [63,64] | ||
| Time instants where pruning occurs | d | , , | [63,64] |
 |
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sastry, K.S.; Zitter, T.A.; Sastry, K.S.; Zitter, T.A. Management of virus and viroid diseases of crops in the tropics. In Plant Virus and Viroid Diseases in the Tropics: Volume 2: Epidemiology and Management; Springer: Berlin/Heidelberg, Germany, 2014; pp. 149–480. [Google Scholar]
- Jones, R.A.; Naidu, R.A. Global dimensions of plant virus diseases: Current status and future perspectives. Annu. Rev. Virol. 2019, 6, 387–409. [Google Scholar] [CrossRef]
- Krishnareddy, M. Impact of Climate Change on Insect Vectors and Vector-Borne Plant Viruses and Phytoplasma. In Climate-Resilient Horticulture: Adaptation and Mitigation Strategies; Singh, H.C.P., Rao, N.K.S., Shivashankar, K.S., Eds.; Springer: Chennai, India, 2013; pp. 255–277. [Google Scholar] [CrossRef]
- Canto, T.; Aranda, M.A.; Fereres, A. Climate change effects on physiology and population processes of hosts and vectors that influence the spread of hemipteran-borne plant viruses. Glob. Change Biol. 2009, 15, 1884–1894. [Google Scholar] [CrossRef]
- Montes, N.; Pagán, I. Challenges and opportunities for plant viruses under a climate change scenario. Adv. Virus Res. 2022, 114, 1–66. [Google Scholar] [PubMed]
- Shah, F.M.; Razaq, M.; Ahmad, F.; ur Rehman, A.; ud Din Umar, U. Crop Protection Under Climate Change: The Effect on Tri-trophic Relations Concerning Pest Control. In Climate Change Impacts on Agriculture: Concepts, Issues and Policies for Developing Countries; Springer: Berlin/Heidelberg, Germany, 2023; pp. 329–354. [Google Scholar]
- Daane, K.M.; Cooper, M.L.; Triapitsyn, S.V.; Andrews, J.W.; Ripa, R. Parasitoids of obscure mealybug, Pseudococcus viburni (Hem.: Pseudococcidae) in California: Establishment of Pseudaphycus flavidulus (Hym.: Encyrtidae) and discussion of related parasitoid species. Biocontrol Sci. Technol. 2008, 18, 43–57. [Google Scholar] [CrossRef]
- Harutyunyan, M.; Malfeito-Ferreira, M. The Rise of Wine among Ancient Civilizations across the Mediterranean Basin. Heritage 2022, 5, 788–812. [Google Scholar] [CrossRef]
- Almeida, R.; Daane, K.; Bell, V.; Blaisdell, G.K.; Cooper, M.; Herrbach, E.; Pietersen, G. Ecology and management of grapevine leafroll disease. Front. Microbiol. 2013, 4, 94. [Google Scholar] [CrossRef]
- Golino, D.A.; Weber, E.; Sim, S.T.; Rowhani, A. Leafroll disease is spreading rapidly in a Napa Valley vineyard. Calif. Agric. 2008, 62, 156–160. [Google Scholar] [CrossRef][Green Version]
- Credi, R.; Babini, A.R. Effects of Virus and Virus-Like Infections on Growth, Yield, and Fruit Quality of Albana and Trebbiano Romagnolo Grapevines. Am. J. Enol. Vitice 1997, 48, 7–12. [Google Scholar] [CrossRef]
- Martelli, G.P.; Agranovsky, A.; Bar-joseph, M.; Boscia, D.; Candresse, T.; Coutts, R.H.A.; Dolja, V.V.; Falk, B.W.; Gonsalves, D.; Jelkmann, W.; et al. The family Closteroviridae revised. Arch. Virol. 2002, 147, 2039–2044. [Google Scholar] [CrossRef]
- Atallah, S.S.; Gómez, M.I.; Fuchs, M.F.; Martinson, T.E. Economic Impact of Grapevine Leafroll Disease on Vitis vinifera cv. Cabernet franc in Finger Lakes Vineyards of New York. Am. J. Enol. Vitic. 2012, 63, 73–79. [Google Scholar] [CrossRef]
- Maree, H.J.; Almeida, R.P.; Bester, R.; Chooi, K.M.; Cohen, D.; Dolja, V.V.; Fuchs, M.F.; Golino, D.A.; Jooste, A.E.; Martelli, G.P.; et al. Grapevine leafroll-associated virus 3. Front. Microbiol. 2013, 4, 82. [Google Scholar] [CrossRef]
- Cooper, M.L.; Daugherty, M.P.; Jeske, D.R.; Almeida, R.P.; Daane, K.M. Incidence of grapevine leafroll disease: Effects of grape mealybug (Pseudococcus maritimus) abundance and pathogen supply. J. Econ. Entomol. 2018, 111, 1542–1550. [Google Scholar] [CrossRef]
- Tsai, C.W.; Chau, J.; Fernandez, L.; Bosco, D.; Daane, K.; Almeida, R. Transmission of Grapevine leafroll-associated virus 3 by the vine mealybug (Planococcus ficus). Phytopathology 2008, 98, 1093–1098. [Google Scholar] [CrossRef]
- Herrbach, E.; Alliaume, A.; Prator, C.A.; Daane, K.; Cooper, M.; Almeida, R.P. Vector transmission of grapevine leafroll-associated viruses. In Grapevine Viruses: Molecular Biology, Diagnostics and Management; Springer: Dordrecht, The Netherlands, 2017; pp. 483–503. [Google Scholar]
- Swallow, W.H. Group testing for estimating infection rates and probabilities of disease transmission. Phytopathology 1985, 75, 882–889. [Google Scholar] [CrossRef]
- Tsai, C.W.; Rowhani, A.; Golino, D.A.; Daane, K.M.; Almeida, R.P.P. Mealybug Transmission of Grapevine Leafroll Viruses: An Analysis of Virus–Vector Specificity. Phytopathology 2010, 100, 830–834. [Google Scholar] [CrossRef]
- Daane, K.M.; Almeida, R.P.; Bell, V.A.; Walker, J.T.; Botton, M.; Fallahzadeh, M.; Mani, M.; Miano, J.L.; Sforza, R.; Walton, V.M.; et al. Biology and management of mealybugs in vineyards. In Arthropod Management in Vineyards: Pests, Approaches, and Future Directions; Springer: Dordrecht, The Netherlands, 2012; pp. 271–307. [Google Scholar]
- Correa, M.C.; Palero, F.; Malausa, T.; Crochard, D.; Zaviezo, T.; Lombaert, E. European bridgehead effect in the worldwide invasion of the obscure mealybug. Biol. Invasions 2019, 21, 123–136. [Google Scholar] [CrossRef]
- Blaisdell, G.; Zhang, S.; Bratburd, J.; Daane, K.; Cooper, M.; Almeida, R. Interactions within susceptible hosts drive establishment of genetically distinct variants of an insect-borne pathogen. J. Econ. Entomol. 2015, 108, 1531–1539. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Venkatesan, T.; Jalali, S.; Ramya, S.; Prathibha, M. Insecticide resistance and its management in mealybugs. In Mealybugs and Their Management in Agricultural and Horticultural Crops; Springer: Berlin/Heidelberg, Germany, 2016; pp. 223–229. [Google Scholar][Green Version]
- Bostanian, N.J.; Vincent, C.; Isaacs, R. Arthropod Management in Vineyards: Pests, Approaches, and Future Directions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar][Green Version]
- Charles, J.; Bell, V.; Lo, P.; Cole, L.; Chhagan, A. Mealybugs (Hemiptera: Pseudococcidae) and their natural enemies in New Zealand vineyards from 1993–2009. N. Z. Entomol. 2010, 33, 84–91. [Google Scholar] [CrossRef]
- Pacheco da Silva, V.C.; Aquino, D.A.; Crochard, D.; Malausa, T.; Botton, M.; Palero, F. Parasitoids (Hymenoptera) of Mealybug Pests (Hemiptera: Pseudococcidae) from Southern Brazil: Molecular and Morphological Characterization. Neotrop. Entomol. 2021, 50, 759–766. [Google Scholar] [CrossRef] [PubMed]
- Hamid, H.; Michelakis, S. The importance of Cryptolaemus montrouzieri Mulsant (Col., Coccinellidae) in the control of the citrus mealybug Planococcus citri (Risso) (Hom., Coccoidea) under specific conditions. J. Appl. Entomol. 1994, 118, 17–22. [Google Scholar] [CrossRef]
- Kairo, M.T.; Pollard, G.V.; Peterkin, D.D.; Lopez, V.F. Biological control of the hibiscus mealybug, Maconellicoccus hirsutus Green (Hemiptera: Pseudococcidae) in the Caribbean. Integr. Pest Manag. Rev. 2000, 5, 241–254. [Google Scholar] [CrossRef]
- Kreiter, P.; Graille, G.; Thaon, M.; Lanza, R.; Tamonte, M.; Germain, C.; Germain, J.F.; Hantzberg, H. Biological control against two mealybugs, newly present on strawberries in Southern France. Phytoma 2004, 568, 38–40. [Google Scholar]
- Li, H.S.; Huang, Y.H.; Chen, M.L.; Ren, Z.; Qiu, B.Y.; De Clercq, P.; Heckel, G.; Pang, H. Genomic insight into diet adaptation in the biological control agent Cryptolaemus montrouzieri. BMC Genom. 2021, 22, 135. [Google Scholar] [CrossRef]
- Bell, V.A.; Hedderley, D.I.; Pietersen, G.; Lester, P.J. Vineyard-wide control of grapevine leafroll-associated virus 3 requires an integrated response. J. Plant Pathol. 2018, 100, 399–408. [Google Scholar] [CrossRef]
- Müller, C.B.; Brodeur, J. Intraguild predation in biological control and conservation biology. Biol. Control 2002, 25, 216–223. [Google Scholar] [CrossRef]
- Rosenheim, J.A.; Kaya, H.K.; Ehler, L.E.; Marois, J.J.; Jaffee, B.A. Intraguild predation among biological-control agents: Theory and evidence. Biol. Control 1995, 5, 303–335. [Google Scholar] [CrossRef]
- Benchohra, M.; Henderson, J.; Ntouyas, S. Impulsive differential equations and inclusions. In Contemporary Mathematics and Its Applications; Hindawi Publishing Corporation: London, UK, 2006. [Google Scholar]
- Córdova-Lepe, F.; Pinto, M.; González-Olivares, E. A new class of differential equations with impulses at instants dependent on preceding pulses. Applications to management of renewable resources. Nonlinear Anal. Real World Appl. 2012, 13, 2313–2322. [Google Scholar] [CrossRef]
- Gutiérrez-Jara, J.P.; Córdova-Lepe, F.; Muñoz-Quezada, M.T.; Chowell, G. Pesticide application, educational treatment and infectious respiratory diseases: A mechanistic model with two impulsive controls. PLoS ONE 2020, 15, 0243048. [Google Scholar] [CrossRef]
- Gutiérrez-Jara, J.P.; Vogt-Geisse, K.; Correa, M.C.; Vilches-Ponce, K.; Pérez, L.M.; Chowell, G. Modeling the Impact of Agricultural Mitigation Measures on the Spread of Sharka Disease in Sweet Cherry Orchards. Plants 2023, 12, 3442. [Google Scholar] [CrossRef]
- Correa, M.C.; Gutiérrez-Jara, J.P.; Vogt-Geisse, K.; Benitez, H.; Pérez, L.M.; Fleisch, A.; Malausa, T.; Queguiner, L.; Rodríguez, S.; Ris, N.; et al. Better alone than in bad company? Modeling the intra-guild predation and release timing in the biological control of Pseudococcus viburni. J. Pest Sci. 2024, 97, 1913–1926. [Google Scholar] [CrossRef]
- Jose, S.A.; Raja, R.; Zhu, Q.; Alzabut, J.; Niezabitowski, M.; Balas, V.E. An Integrated Eco-Epidemiological Plant Pest Natural Enemy Differential Equation Model with Various Impulsive Strategies. Math. Probl. Eng. 2022, 2022, 4780680. [Google Scholar] [CrossRef]
- Arias, J.H.; Gómez-Gardenes, J.; Meloni, S.; Estrada, E. Epidemics on plants: Modeling long-range dispersal on spatially embedded networks. J. Theor. Biol. 2018, 453, 1–13. [Google Scholar] [CrossRef]
- Goleniewski, G. Modelling cultivar mixtures using SEIR compartmental models. Biom. J. 1996, 38, 281–297. [Google Scholar] [CrossRef]
- Jeger, M.; Van den Bosch, F.; Madden, L. Modelling virus-and host-limitation in vectored plant disease epidemics. Virus Res. 2011, 159, 215–222. [Google Scholar] [CrossRef]
- Jeger, M.; Madden, L.; Van Den Bosch, F. Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018, 102, 837–854. [Google Scholar] [CrossRef]
- Savary, S.; Nelson, A.; Willocquet, L.; Pangga, I.; Aunario, J. Modeling and mapping potential epidemics of rice diseases globally. Crop Prot. 2012, 34, 6–17. [Google Scholar] [CrossRef]
- Tankam-Chedjou, I.; Touzeau, S.; Mailleret, L.; Tewa, J.J.; Grognard, F. Modelling and control of a banana soilborne pest in a multi-seasonal framework. Math. Biosci. 2020, 322, 108324. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Chen, L. Modelling and analysis of integrated pest management strategy. Discret. Contin. Dyn. Syst. Ser. B 2004, 4, 759–768. [Google Scholar] [CrossRef]
- Shi, R.; Jiang, X.; Chen, L. A predator–prey model with disease in the prey and two impulses for integrated pest management. Appl. Math. Model. 2009, 33, 2248–2256. [Google Scholar] [CrossRef]
- Mathulwe, L.; Malan, A.; Stokwe, N. A Review of the Biology and Control of the Obscure Mealybug, Pseudococcus viburni (Hemiptera: Pseudococcidae), with Special Reference to Biological Control Using Entomopathogenic Fungi and Nematodes. Afr. Entomol. 2021, 29, 1–16. [Google Scholar] [CrossRef]
- Wei, J.; Lu, Y.; Niu, M.; Cai, B.; Shi, H.; Ji, W. Novel insights into hotspots of insect vectors of GLRaV-3: Dynamics and global distribution. Sci. Total Environ. 2024, 925, 171664. [Google Scholar] [CrossRef]
- Vu, M.; McFadden-Smith, W.; Poojari, S. Monitoring the Spread of Grapevine Viruses in Vineyards of Contrasting Agronomic Practices: A Metagenomic Investigation. Biology 2023, 12, 1279. [Google Scholar] [CrossRef]
- Pietersen, G.; Kellerman, U.; Oosthuizen, W.; Spreeth, N. Effect of rouging on natural spread of grapevine leafroll disease in two vineyards in South Africa. In Proceedings of the 8th International Congress of Plant Pathology, Christchurch, New Zealand, 2–7 February 2003; pp. 2–7. [Google Scholar]
- Pietersen, G.; Spreeth, N.; Oosthuizen, T.; van Rensburg, A.; van Rensburg, M.; Lottering, D.; Rossouw, N.; Tooth, D. Control of grapevine leafroll disease spread at a commercial wine estate in South Africa: A case study. Am. J. Enol. Vitic. 2013, 64, 296–305. [Google Scholar] [CrossRef]
- Bell, V.; Bonfiglioli, R.; Walker, J.; Lo, P.; Mackay, J.; McGregor, S. Grapevine leafroll-associated virus 3 persistence in Vitis vinifera remnant roots. J. Plant Pathol. 2009, 91, 527–533. [Google Scholar]
- Fuchs, M. Grapevine viruses: A multitude of diverse species with simple but overall poorly adopted management solutions in the vineyard. J. Plant Pathol. 2020, 102, 643–653. [Google Scholar] [CrossRef]
- Grasswitz, T.R.; James, D.G. Movement of grape mealybug, Pseudococcus maritimus, on and between host plants. Entomol. Exp. Appl. 2008, 129, 268–275. [Google Scholar] [CrossRef]
- Diaz-Lara, A.; Aguilar-Molina, V.H.; Monjarás-Barrera, J.I.; Vončina, D.; Erickson, T.M.; Al Rwahnih, M. Potential Implications and Management of Grapevine Viruses in Mexico: A Review. Int. J. Plant Biol. 2023, 14, 177–189. [Google Scholar] [CrossRef]
- Waterworth, R.A.; Wright, I.M.; Millar, J.G. Reproductive biology of three cosmopolitan mealybug (Hemiptera: Pseudococcidae) species, Pseudococcus longispinus, Pseudococcus viburni, and Planococcus ficus. Ann. Entomol. Soc. Am. 2011, 104, 249–260. [Google Scholar] [CrossRef]
- Karamaouna, F.; Copland, M.J. Fitness and life history parameters of Leptomastix epona and Pseudaphycus flavidulus, two parasitoids of the obscure mealybug Pseudococcus viburni. BioControl 2009, 54, 65–76. [Google Scholar] [CrossRef]
- Bosch, M.J.; Ives, A.R. Identifying environmental factors affecting the production of pea aphid dispersal morphs in field populations. Ecol. Entomol. 2023, 48, 597–609. [Google Scholar] [CrossRef]
- Kansman, J.T.; Nersten, C.E.; Hermann, S.L. Smelling danger: Lady beetle odors affect aphid population abundance and feeding, but not movement between plants. Basic Appl. Ecol. 2023, 71, 1–8. [Google Scholar] [CrossRef]
- McGreal, B.; Sandanayaka, M.; Gough, R.; Rohra, R.; Davis, V.; Marshall, C.W.; Richards, K.; Bell, V.A.; Chooi, K.M.; MacDiarmid, R.M. Retention and Transmission of Grapevine Leafroll-Associated Virus 3 by Pseudococcus calceolariae. Front. Microbiol. 2021, 12, 663948. [Google Scholar] [CrossRef]
- Nicaise, V. Crop immunity against viruses: Outcomes and future challenges. Front. Plant Sci. 2014, 5, 660. [Google Scholar] [CrossRef]
- Nasr, M.M.; Darwesh, D.R.; Swelam, S.S. Grafting. Egypt. J. Agric. Res. 2022, 100, 653–660. [Google Scholar]
- Tedesco, S.; Fevereiro, P.; Kragler, F.; Pina, A. Plant grafting and graft incompatibility: A review from the grapevine perspective. Sci. Hortic. 2022, 299, 111019. [Google Scholar] [CrossRef]
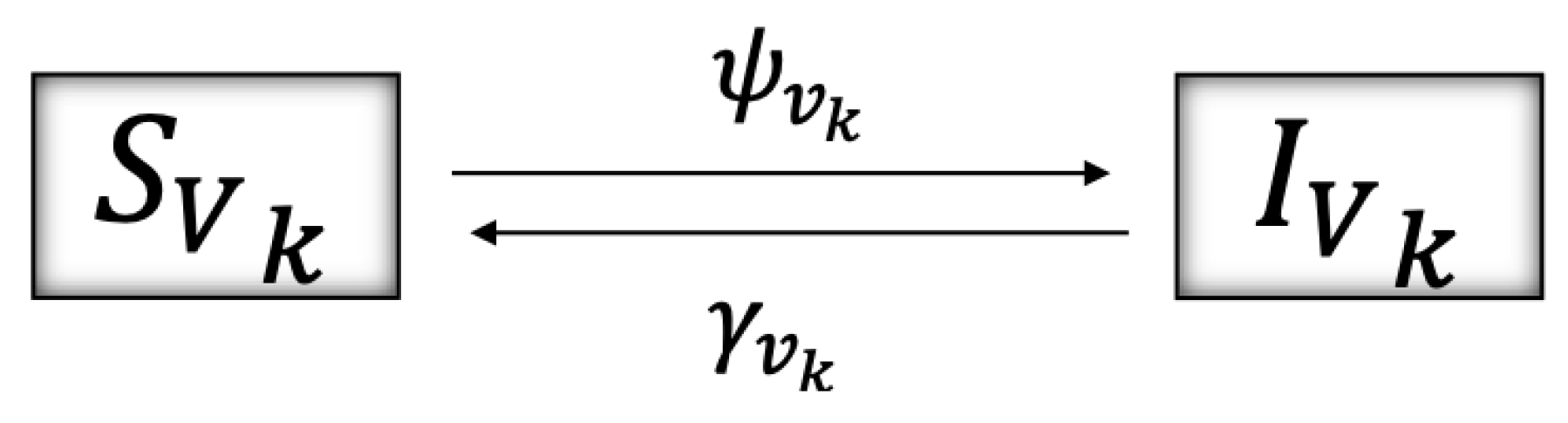
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogt-Geisse, K.; Correa, M.C.G.; Gutiérrez-Jara, J.P.; Daane, K.M. Modeling the Effect of the Biological Control of Pseudococcus viburni Signoret (Hemiptera: Pseudococcidae) on Grapevine Leafroll Virus Spread. Plants 2025, 14, 3043. https://doi.org/10.3390/plants14193043
Vogt-Geisse K, Correa MCG, Gutiérrez-Jara JP, Daane KM. Modeling the Effect of the Biological Control of Pseudococcus viburni Signoret (Hemiptera: Pseudococcidae) on Grapevine Leafroll Virus Spread. Plants. 2025; 14(19):3043. https://doi.org/10.3390/plants14193043
Chicago/Turabian StyleVogt-Geisse, Katia, Margarita C. G. Correa, Juan Pablo Gutiérrez-Jara, and Kent M. Daane. 2025. "Modeling the Effect of the Biological Control of Pseudococcus viburni Signoret (Hemiptera: Pseudococcidae) on Grapevine Leafroll Virus Spread" Plants 14, no. 19: 3043. https://doi.org/10.3390/plants14193043
APA StyleVogt-Geisse, K., Correa, M. C. G., Gutiérrez-Jara, J. P., & Daane, K. M. (2025). Modeling the Effect of the Biological Control of Pseudococcus viburni Signoret (Hemiptera: Pseudococcidae) on Grapevine Leafroll Virus Spread. Plants, 14(19), 3043. https://doi.org/10.3390/plants14193043





