Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians
Abstract
1. Introduction
- (i).
- Develop models for estimating the aboveground biomass of young, planted beech trees using basic tree characteristics;
- (ii).
- Model aboveground biomass accumulation in relation to stand age;
- (iii).
- Quantify ANPP and leaf litter productivity regarding stand age;
- (iv).
- Compare results from artificially regenerated beech plantations with those obtained from naturally regenerated stands shown in Konôpka et al. [16].
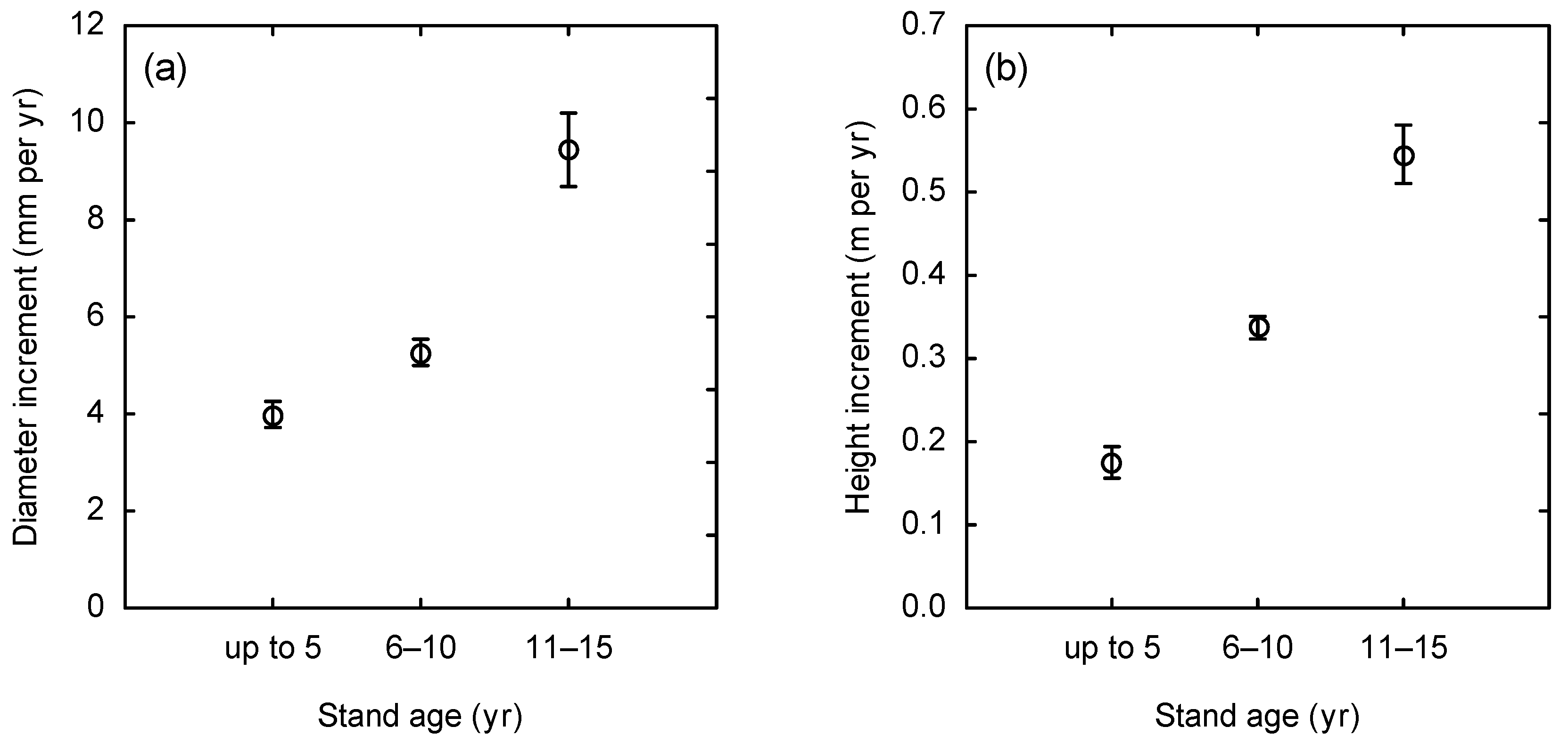
2. Results
3. Discussion
3.1. Biomass Stock and Productivity in Planted Stands
3.2. Differences Between Planted and Naturally Regenerated Stands
4. Materials and Methods
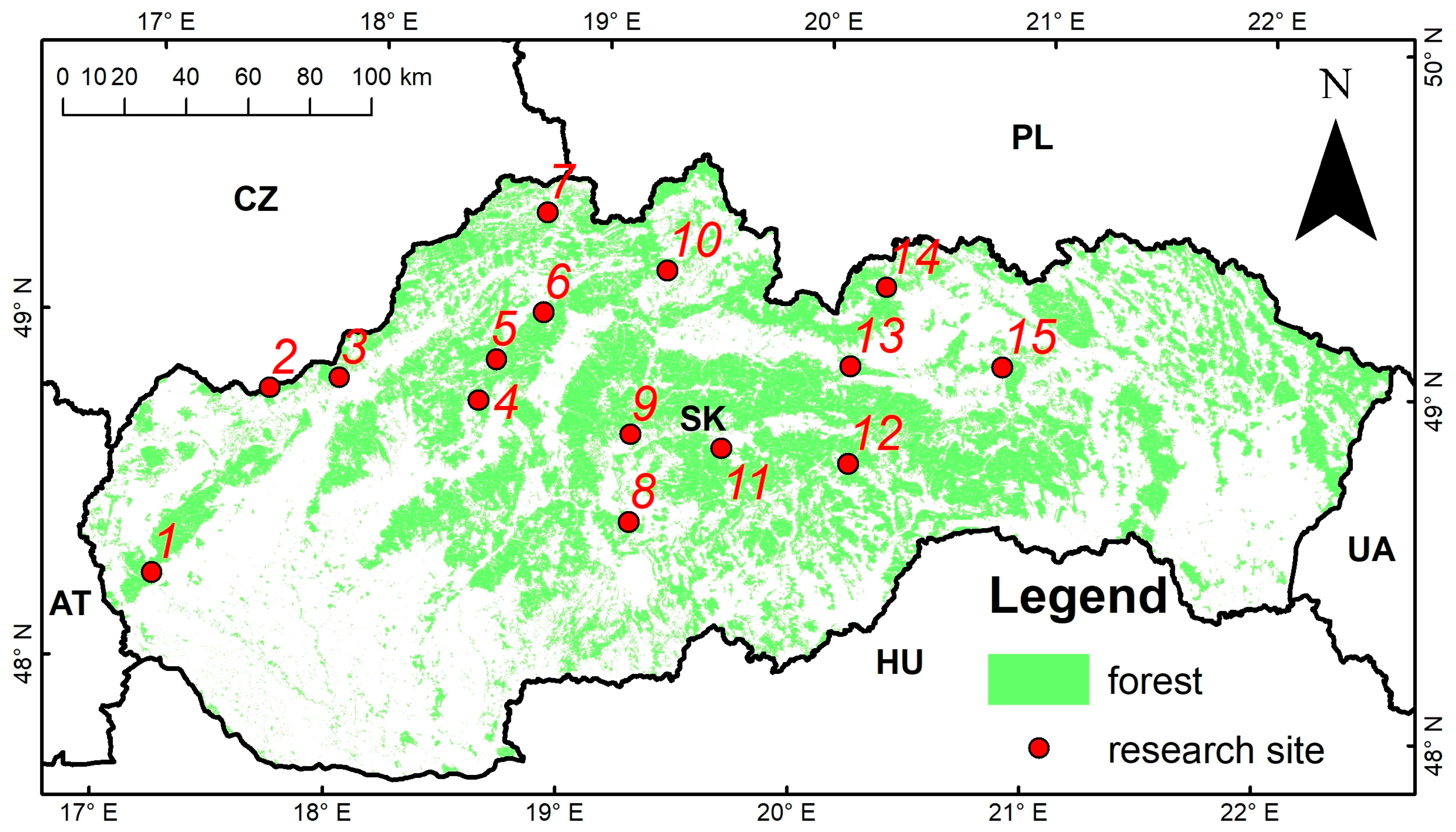
4.1. Selection of Stands and Tree Measurements
- (i).
- To cover a range of locations across Slovakia, with a focus on moderately fertile sites,
- (ii).
- The contribution of beech had to be nearly 100%, with minimal admixture of other tree species,
- (iii).
- All trees had to be planted, with no individuals originating from natural regeneration,
- (iv).
- The stands had to be established with regular spacing between trees and be up to 12 years old (excluding the 2–3 years the seedlings spent in the forest nursery prior to planting),
- (v).
- Seedlings had to be either undamaged or only minimally affected by harmful agents (e.g., browsing by game).
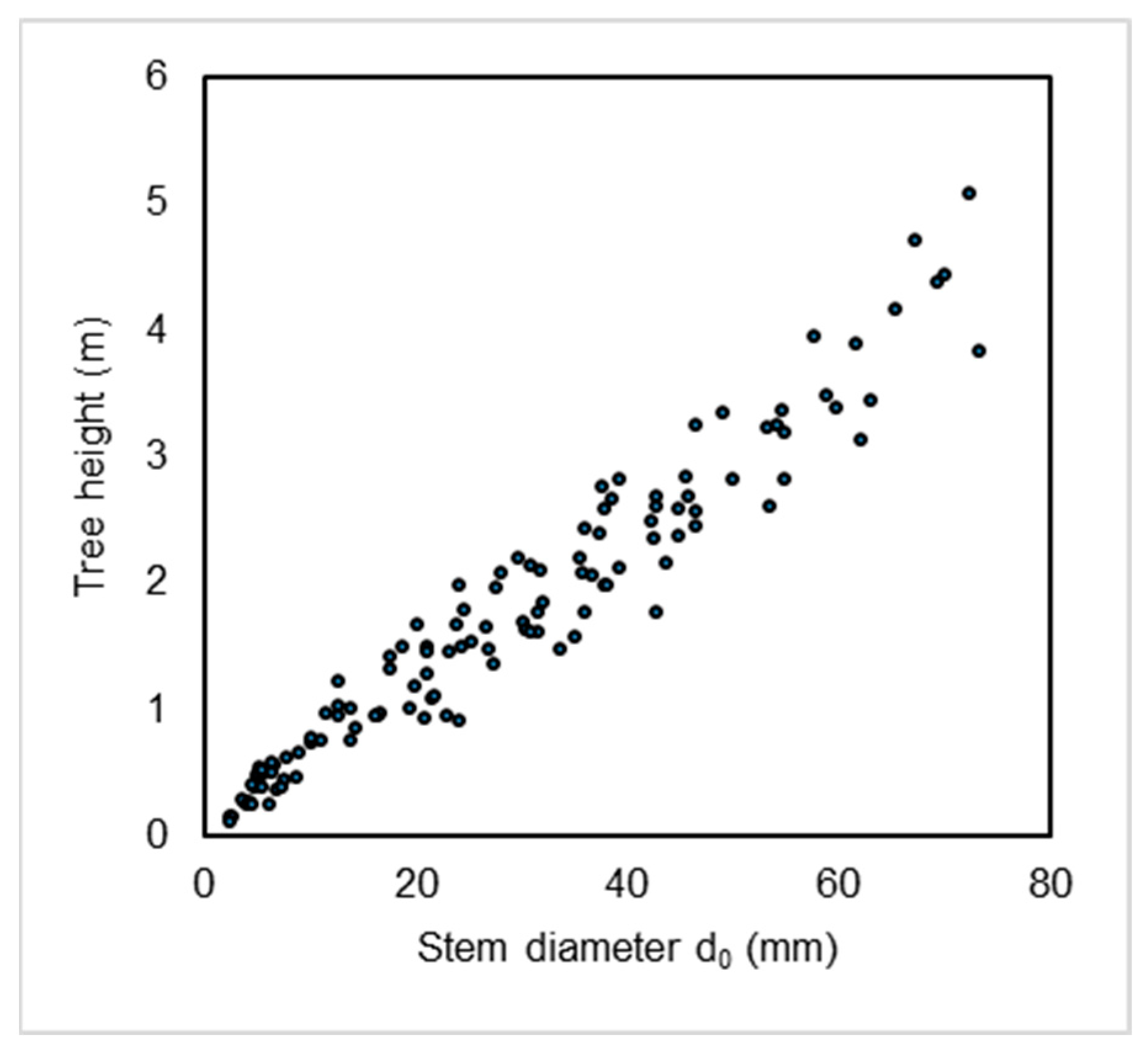
4.2. Tree Sampling and Quantification of Aboveground Biomass
- Procedure 1
- Procedure 2
4.3. Estimates on Aboveground Biomass Stock and Net Primary Productivity
- is biomass stock per area (Mg per ha);
- S is area size (m2);
- a, b is tree spacing, i.e., 1.6 m × 1.6 m;
- wavg is average stock of a single tree in the subplot (Mg);
- w is total biomass stock of all trees in the subplot (Mg);
- N is number of trees in the subplot.
- y is dependent variable, i.e., biomass stock (Mg per ha) or NPP (Mg per ha and year);
- t is stand age (years);
- b0, b1 are equation parameters.
4.4. Comparisons Among Planted and Naturally Regenerated Beech Stands
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- San-Miguel-Ayanz, J.; de Rigo, D.; Caudullo, G.; Durrant, T.H.; Mauri, A. European Atlas of Forest Tree Species; Publication Office of European Commission: Luxembourg, 2016; p. 200. [Google Scholar]
- Martinez Del Castillo, E.; Zang, C.S.; Buras, A.; Hacket-Pain, A.; Esper, J.; Serrano-Notivoli, R.; Hartl, C.; Weigel, R.; Klesse, S.; Resco de Dios, V.; et al. Climate-change-driven growth decline of European beech forests. Commun. Biol. 2022, 5, 163. [Google Scholar] [CrossRef]
- Pramreiter, M.; Grabner, M. The Utilization of European Beech Wood (Fagus sylvatica L.) in Europe. Forests 2023, 14, 1419. [Google Scholar] [CrossRef]
- Brunet, J.; Fritz, O.; Richnau, G. Biodiversity in European beech forests—A review with recommendations for sustainable forest management. Ecol. Bull. 2010, 53, 77–94. [Google Scholar]
- Huang, W.; Lundqvist, S.-O.; Thygesen, L.G. Effects of climate variability on secondary xylem formation and anatomy in Fagus sylvatica trees grown in Denmark. Bot. Lett. 2025, 172, 87–100. [Google Scholar] [CrossRef]
- Hlásny, T.; Mátyás, C.; Seidl, R.; Kulla, L.; Merganičová, K.; Trombík, J.; Dobor, L.; Barcza, Z.; Konôpka, B. Climate change increases the drought risk in Central European forests: What are the options for adaptation? Cen. Eur. For. J. 2014, 60, 5–18. [Google Scholar] [CrossRef]
- Cerioni, M.; Brabec, M.; Bače, R.; Baders, E.; Boncina, A.; Brůna, J.; Chećko, E.; Cordonnier, T.; de Koning, J.; Diaci, J.; et al. Recovery and resilience of European temperate forests after large and severe disturbances. Glob. Change Biol. 2024, 30, e17159. [Google Scholar] [CrossRef]
- Šebeň, V. Národná Inventarizácia a Monitoring Lesov Slovenskej Republiky 2015–2016; Lesnícke štúdie 65; Národné Lesnícke Centrum: Zvolen, Slovakia, 2017; p. 256. (In Slovak) [Google Scholar]
- Ministry of Agriculture and Rural Development Report on the Forest Sector of the Slovak Republic—Green Report, Abridged version; Ministry of Agriculture and Rural Development: Bratislava, Slovakia, 2024; p. 68.
- Kunca, A.; Zúbrik, M.; Galko, J.; Vakula, J.; Leontovyč, R.; Konôpka, B.; Nikolov, C.; Gubka, A.; Longauerová, V.; Maľová, M.; et al. Salvage felling in the Slovak forests in the period 2004–2013. Lesn. Čas.-For. J. 2015, 61, 188–195. [Google Scholar] [CrossRef]
- Kunca, A.; Zúbrik, M.; Galko, J.; Vakula, J.; Leontovyč, R.; Konôpka, B.; Nikolov, C.; Gubka, A.; Longauerová, V.; Maľová, M. Salvage felling in the Slovak Republic’s forests during the last twenty years (1998–2017). Cen. Eur. J. 2019, 65, 3–11. [Google Scholar] [CrossRef]
- Larsen, J.B.; Angelstam, P.; Bauhus, J.; Carvalho, J.F.; Diaci, J.; Dobrowolska, D.; Gazda, A.; Gustafsson, L.; Krumm, F.; Knoke, T.; et al. Closer-to-Nature Forest Management. From Science to Policy 12; EFI: Joensuu, Finland, 2022; p. 53. [Google Scholar]
- Barna, M.; Kulfan, J.; Bublinec, E. Beech and Beech Ecosystems of Slovakia; Veda: Bratislava, Slovakia, 2011; p. 636. [Google Scholar]
- Repáč, I.; Parobeková, Z.; Sendecký, M. Reforestation in Slovakia: History, current practice and perspectives. Reforesta 2017, 3, 53–88. [Google Scholar] [CrossRef]
- Axer, M.; Schlicht, R.; Kronenberg, R.; Wagner, S. The Potential for Future Shifts in Tree Species Distribution Provided by Dispersal and Ecological Niches: A Comparison between Beech and Oak in Europe. Sustainability 2021, 13, 3067. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Šebeň, V.; Lukac, M. 2024: Decadal forest mensuration cycle significantly underestimates net primary production in dense young beech stands. For. Ecol. Manag. 2024, 555, 121711. [Google Scholar] [CrossRef]
- Holgén, P.; Hånell, B. Performance of planted and naturally regenerated seedlings in Picea abies-dominated shelter wood stands and clearcuts in Sweden. For. Ecol. Manag. 2000, 127, 129–138. [Google Scholar] [CrossRef]
- Stark, H.; Nothdurft, A.; Bauhus, J. Allometries for Widely Spaced Populus ssp. and Betula ssp. in Nurse Crop Systems. Forests 2013, 4, 1003–1031. [Google Scholar] [CrossRef]
- Wang, T.; Domng, L.; Liu, Z. Factors driving carbon accumulation in forest biomass and soil organic carbon across natural forests and planted forests in China. Front. For. Glob. Change 2024, 6, 3389. [Google Scholar] [CrossRef]
- Paton, D.; Nunez, J.; Bao, D.; Munoz, A. Forage biomass of 22 shrub species from Monfragüe Natural Park (SW Spain) assessed by log–log regression models. J. Arid Environ. 2002, 52, 223–231. [Google Scholar] [CrossRef]
- Clifford, D.; Cressie, N.; England, J.R.; Roxburgh, S.H.; Paul, K.I. Correction factors for unbiased, efficient estimation and prediction of biomass from log–log allometric models. For. Ecol. Manag. 2013, 310, 375–381. [Google Scholar] [CrossRef]
- Jenkins, D.G. Estimating ecological production from biomass. Ecosphere 2015, 6, 49. [Google Scholar] [CrossRef]
- Parresol, B.R. Assessing Tree and Stand Biomass: A Review with Examples and Critical Comparisons. For. Sci. 1999, 45, 573–593. [Google Scholar] [CrossRef]
- Dutcă, I.; McRoberts, R.E.; Næsset, E.; Blujdea, V.N. Accommodating heteroscedasticity in allometric biomass models. For. Ecol. Manag. 2022, 505, 119865. [Google Scholar] [CrossRef]
- Tian, L.; Tao, Y.; Joanna, S.; Mäkelä, A.; Li, M. How forest age impacts on net primary productivity: Insights from future multi-scenarios. For. Ecosyst. 2024, 11, 100228. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Pan, Y.; Birdsey, R.; Katgge, J. Relationships between net primary productivity and forest stand age in U.S. forests. GBC 2012, 26, 2010GB003942. [Google Scholar] [CrossRef]
- Persson, H. Fine-root production, mortality and decomposition in forest ecosystems. Plant Ecol. 1980, 41, 101–109. [Google Scholar] [CrossRef]
- Brunner, I.; Bakker, M.R.; Björk, R.G.; Hirano, Y.; Lukac, M.; Aranda, X.; Børja, I.; Eldhuset, T.D.; Helmisaari, H.S.; Jourdan, C.; et al. Fine-root turnover rates of European forests revisited: An analysis of data from sequential coring and ingrowth cores. Plant Soil 2013, 362, 357–372. [Google Scholar] [CrossRef]
- Zianis, D.; Mencuccini, M. Aboveground net primary productivity of a beech (Fagus moesiaca) forest: A case study of Naousa forest, northern Greece. Tree Physiol. 2005, 25, 713–722. [Google Scholar] [CrossRef]
- Husmann, K.; Rumf, S.; Nagel, J. Biomass functions and nutrient contents of European beech, oak, sycamore maple and ash and their meaning for the biomass supply chain. J. Clean. Prod. 2018, 172, 4044–4056. [Google Scholar] [CrossRef]
- Becknell, J.M.; Vegas, G.; Pérez-Aviles, D.; Medvigy, D.; Powers, J.S. Above-ground net primary productivity in regenerating seasonally dry tropical forest: Contributions of rainfall, forest age and soil. J. Ecol. 2021, 109, 3903–3915. [Google Scholar] [CrossRef]
- Cienciala, E.; Černý, M.; Apltauer, J.; Exnerová, Z. Biomass functions applicable to European beech. J. For. Sci. 2005, 51, 147–154. [Google Scholar] [CrossRef]
- Qi, L.; Liu, X.; Jiang, Z.; Yue, X.; Li, Z.; Fu, J.; Liu, G.; Guo, B. Combining diameter-distribution function with allometric equation in biomass estimates: A case study of Phyllostachys edulis forests in South Anhui, China. Agrofor. Syst. 2016, 90, 1113–1121. [Google Scholar] [CrossRef]
- Le Goff, N.; Ottorini, J.-M. Biomass distribution allocation and growth efficiency in European beech trees of different ages in pure even aged stands in northeast France. Cent. Eur. For. J. 2022, 3, 117–138. [Google Scholar] [CrossRef]
- Beets, P.N.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; Graham, J.D.; Brandon, A. Allometric Equations for Estimating Carbon Stocks in Natural Forest in New Zealand. Forests 2012, 3, 818–839. [Google Scholar] [CrossRef]
- Pajtík, J.; Konôpka, B.; Šebeň, V. Allometric models for estimating aboveground biomass of young Norway spruce trees in Western Carpathians, Slovakia. Cent. Eur. For. J. 2022, 3, 154–162. [Google Scholar] [CrossRef]
- Asigbaase, M.; Dawoe, E.; Abugre, S.; Kyereh, B.; Nsor, C.A. Allometric relationships between stem diameter, height and crown area of associated trees of cocoa agroforests of Ghana. Sci. Rep. 2023, 13, 14897. [Google Scholar] [CrossRef]
- Vejpustková, M.; Zahradník, D.; Čihák, T.; Šrámeke, V. Models for predicting aboveground biomass of European beech (Fagus sylvatica L.) in the Czech Republic. J. For. Sci. 2015, 61, 45–54. [Google Scholar] [CrossRef]
- Chakraborty, T.; Saha, S.; Reif, A. Biomass equations for European beech growing on dry sites. IForest 2016, 9, 754–757. [Google Scholar] [CrossRef]
- Bartelink, H. Allometric relationships for biomass and leaf area of beech (Fagus sylvatica L.). Ann. Sci. For. 1997, 54, 39–50. [Google Scholar] [CrossRef]
- Barna, M.; Kodrík, M. Beech biomass distribution after shelterwood cutting according to tree social status. Ekológia 2002, 21, 61–73. [Google Scholar]
- Xin, S.; Shahzad, M.K.; Mahardika, S.B.; Wang, W.; Jiang, L. An Alternative Method for Estimation of Stand-Level Biomass for Three Conifer Species in Northeast China. Forests 2023, 14, 1247. [Google Scholar] [CrossRef]
- Pajtík, J.; Konôpka, B.; Marušák, R. Above-ground net primary productivity in young stands of beech and spruce. Lesn. Čas.-For. J. 2013, 59, 154–162. [Google Scholar] [CrossRef][Green Version]
- Repáč, I. Estimation of development pf European beech and Norway spruce plantations five years after application of mycorrhizal and water-holding additive at planting. Rep. For. Res. 2019, 64, 57–64. [Google Scholar][Green Version]
- Houšková, K.; Mauer, O. Effect of the density of transplants in reforestation on themorphological quality of the above-ground part of European beech (Fagus sylvatica L.) six years after planting. Acta Univ. Agric. Silvic. Mendel. Brun. 2013, 61, 1703–1713. [Google Scholar] [CrossRef]
- Close, D.C.; Beadle, C.L.; Brown, P.H. The physiological basis of containerised tree seedling tranplant shock: A review. Austrian For. 2005, 68, 112–120. [Google Scholar]
- Preece, N.D.; van Oosterzee, P.; Lawes, M.J. Reforestation success can be enhanced by improving tree planting methods. J. Environ. Manag. 2023, 336, 117645. [Google Scholar] [CrossRef] [PubMed]
- Blaško, R.; Forsmark, B.; Gundale, M.J.; Lim, H.; Lundmark, T.; Nordin, A. The carbon sequestration response of aboveground biomass and soils to nutrient enrichment in boreal forests depends on baseline site productivity. Sci. Total Environ. 2022, 838, 156327. [Google Scholar] [CrossRef]
- Campioli, M.; Gielen, B.; Granier, A.; Verstraeten, A.; Neirynck, J.; Janssens, I.A. Carbon allocation to biomass production of leaves, fruits and woody organs at seasonal and annual scale in a deciduous- and evergreen temperate forest. Biogeosci. Discuss. 2010, 7, 7575–7606. [Google Scholar]
- Marčiš, P.; Pajtík, J.; Konôpka, B.; Lukac, M. Height-based biomass models differ for naturally regenerated and planted young trees. For. Ecosyst. 2025; in press. [Google Scholar]
- Breusch, T.S.; Pagan, A.R. A Simple Test for Heteroskedasticity and Random Coefficient Variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Spiess, A. Propagation of Uncertainty. R Package Version 1.0-7. Available online: https://CRAN.R-project.org/package=propagate (accessed on 1 September 2025).
- Wang, C.M.; Iyer, H.K. On higher-order corrections for propagating uncertainties. Metrologia 2005, 42, 406. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 1 September 2025).




| Site Name | Number of Measured Trees | Mean Tree Height (m) | Mean Stem Diameter d0 (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Age (Years) | Subplot A | Subplot B | Subplot C | Subplot A | Subplot B | Subplot C | Subplot A | Subplot B | Subplot C | |
| Zdychava | 2 | 35 | 34 | 36 | 0.26 | 0.25 | 0.22 | 4.52 | 4.70 | 4.24 |
| Myjava | 2 | 31 | 28 | 33 | 0.53 | 0.53 | 0.49 | 6.01 | 5.96 | 5.17 |
| Svaty Jur | 4 | 34 | 31 | 32 | 0.75 | 0.63 | 0.73 | 12.20 | 9.47 | 11.06 |
| Chocholna | 4 | 30 | 30 | 30 | 0.93 | 0.85 | 0.91 | 13.93 | 12.82 | 13.90 |
| Poruba | 4 | 30 | 30 | 30 | 0.63 | 0.63 | 0.72 | 16.02 | 16.12 | 16.64 |
| Racibor | 5 | 33 | 33 | 34 | 0.89 | 0.85 | 1.08 | 15.47 | 15.45 | 18.85 |
| Bijacovce | 5 | 31 | 31 | 34 | 1.23 | 0.93 | 1.25 | 21.49 | 19.54 | 19.98 |
| Fackov | 6 | 32 | 34 | 32 | 1.67 | 1.74 | 1.90 | 32.40 | 31.51 | 34.07 |
| Zdiar | 7 | 33 | 31 | 33 | 1.77 | 1.87 | 1.89 | 38.97 | 40.30 | 40.96 |
| Turie | 8 | 34 | 32 | 31 | 2.12 | 2.40 | 2.36 | 39.75 | 42.37 | 41.43 |
| Husarik | 8 | 30 | 28 | 30 | 2.28 | 2.16 | 2.34 | 35.99 | 36.61 | 33.56 |
| Lopusna dolina | 8 | 31 | 31 | 33 | 2.27 | 2.46 | 2.43 | 42.84 | 41.81 | 38.64 |
| Geberanica | 9 | 29 | 27 | 27 | 1.34 | 1.18 | 1.42 | 18.23 | 16.78 | 18.11 |
| Priechod | 9 | 31 | 24 | 28 | 2.68 | 2.83 | 2.44 | 36.34 | 38.07 | 34.39 |
|
Cierny Balog | 10,11,12 | 30 | 30 | 25 | 2.64 | 3.84 | 3.33 | 35.57 | 64.66 | 43.68 |
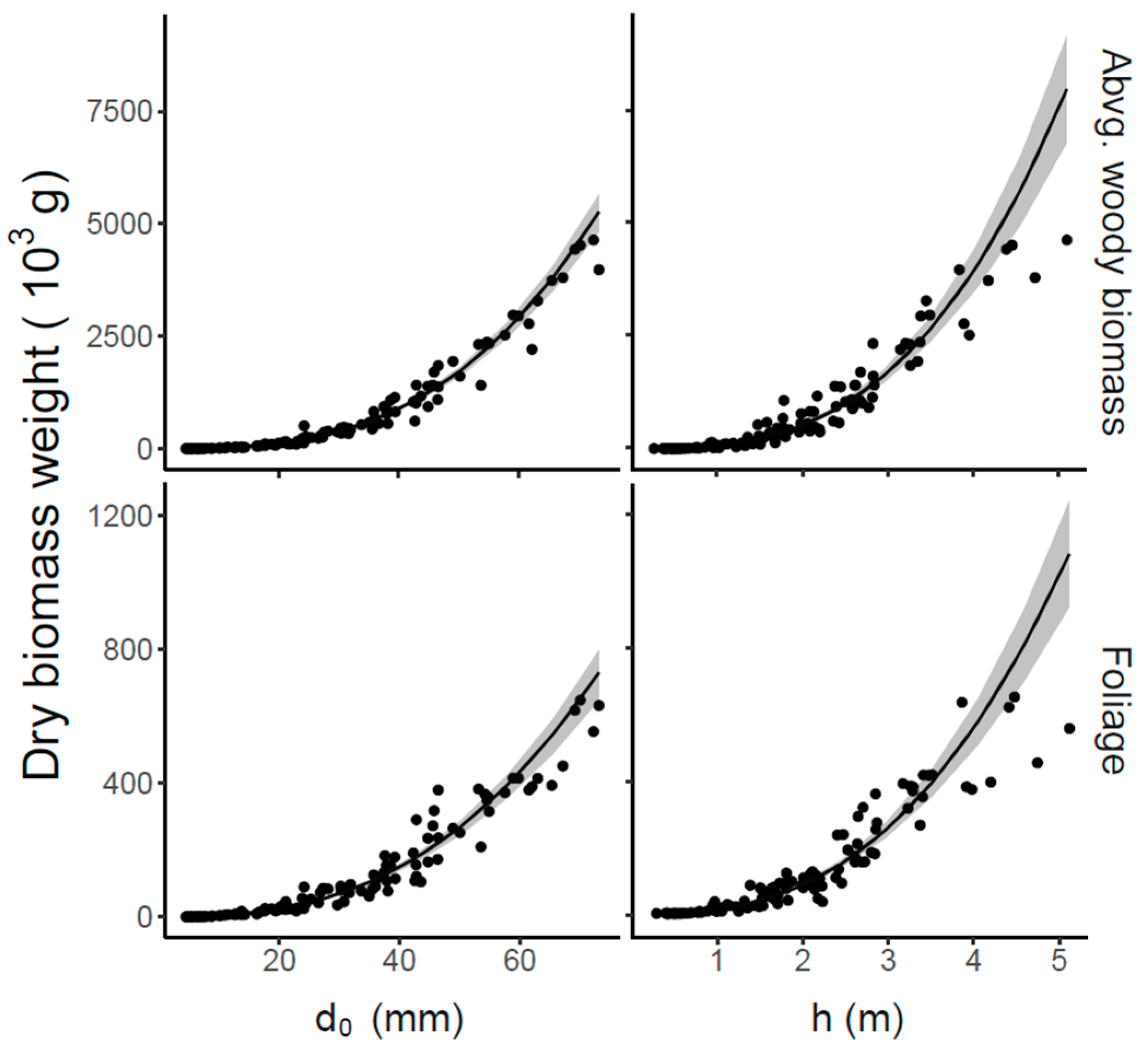
| Model | Variable | b0 (SE) pval | b1 (SE) pval | b2 (SE) pval | λ | X2 pval | AIC | RSE |
|---|---|---|---|---|---|---|---|---|
| f(d0) | foliage biomass | 0.00878 (0.00138) <0.001 | 2.63892 (0.04515) <0.001 | - | 1.821 | 0.82416 | 897.2186 | 0.44905 |
| f(h) | foliage biomass | 14.17258 (0.95707) <0.001 | 2.66097 (0.07205) <0.001 | - | 1.798 | 0.73579 | 997.9132 | 0.63101 |
| f(d0) | abvg. woody biomass | 0.01762 (0.0021) <0.001 | 2.93664 (0.03462) <0.001 | - | 1.877 | 0.58194 | 1211.257 | 0.34901 |
| f(h) | abvg. woody biomass | 68.26919 (5.10207) <0.001 | 2.92705 (0.07718) <0.001 | - | 1.764 | 0.86676 | 1387.4948 | 0.84839 |
| f(d0,h) | foliage biomass | 0.04424 (0.01768) 0.01381 | 2.03061 (0.14516) <0.001 | 0.73108 (0.15977) <0.001 | 1.983 | 0.55109 | 876.1298 | 0.30238 |
| f(d0,h) | abvg. woody biomass | 0.10546 (0.02987) <0.001 | 2.27041 (0.10274) <0.001 | 0.76727 (0.1126) <0.001 | 1.936 | 0.52545 | 1163.9754 | 0.24043 |
| Origin | Variable | b0 (S.E.) p | b1 (S.E.) p | R2 | MSE |
|---|---|---|---|---|---|
| Natural | foliage stock | 0.717 (0.167) <0.001 | 0.889 (0.084) <0.001 | 0.642 | 2.458 |
| woody parts stock | 0.802 (0.148) <0.001 | 1.844 (0.064) <0.001 | 0.946 | 250.0 | |
| aboveground stock | 1.031 (0.192) <0.001 | 1.777 (0.064) <0.001 | 0.940 | 287.5 | |
| woody parts NPP | 2.100 (0.938) 0.028 | 0.790 (0.161) <0.001 | 0.287 | 46.29 | |
| aboveground NPP | 2.700 (0.940) 0.005 | 0.833 (0.125) <0.001 | 0.423 | 57.43 | |
| Artificial | foliage stock | 0.00024 (0.00006) <0.001 | 3.763 (0.101) <0.001 | 0.890 | 0.155 |
| woody parts stock | 0.00084 (0.0002) <0.001 | 4.044 (0.109) <0.001 | 0.886 | 8.93 | |
| aboveground stock | 0.00104 (0.0002) <0.001 | 4.010 (0.108) <0.001 | 0.886 | 11.42 | |
| woody parts NPP | 0.00086 (0.00048) 0.072 | 3.622 (0.219) <0.001 | 0.673 | 4.53 | |
| aboveground NPP | 0.00124 (0.0005) 0.017 | 3.591 (0.165) <0.001 | 0.774 | 4.58 |
| Site Name | Code | Latitude (North) | Longitude (East) | Elevation (m a.s.l.) | Exposition | Slope (%) | Soil Type |
|---|---|---|---|---|---|---|---|
| Svaty Jur | 1 | 48.2728 | 17.1855 | 430 | NE | 20 | Dystric Cambisol |
| Myjava | 2 | 48.8365 | 17.6085 | 550 | W | 40 | Eutric Cambisol |
| Chocholna | 3 | 48.8833 | 17.9113 | 356 | NE | 40 | Rendzina |
| Poruba | 4 | 48.8527 | 18.5315 | 1005 | E | 30 | Dystric Cambisol |
| Fackov | 5 | 48.9752 | 18.5959 | 652 | SE | 65 | Orthic Rendzina |
| Turie | 6 | 49.1220 | 18.7869 | 660 | E | 65 | Eutric Cambisol |
| Husarik | 7 | 49.4131 | 18.7688 | 802 | NW | 25 | Dystric Cambisol |
| Geberanica | 8 | 48.5329 | 19.2292 | 520 | NE | 45 | Eutric Cambisol |
| Priechod | 9 | 48.7878 | 19.2094 | 600 | SE | 40 | Dystric Cambisol |
| Racibor | 10 | 49.2708 | 19.3197 | 674 | SW | 30 | Dystric Cambisol |
| Cierny Balog | 11 | 48.7648 | 19.6174 | 555 | - | 0 | Dystric Cambisol |
| Zdychava | 12 | 48.7446 | 20.1758 | 1130 | NW | 50 | Dystric Cambisol |
| Lopusna dolina | 13 | 49.0277 | 20.1591 | 902 | NW | 55 | Eutric Cambisol |
| Zdiar | 14 | 49.2621 | 20.2990 | 845 | NE | 60 | Dystric Cambisol |
| Bijacovce | 15 | 49.0498 | 20.8312 | 800 | NW | 20 | Dystric Cambisol |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konôpka, B.; Pajtík, J.; Marčiš, P.; Šebeň, V. Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians. Plants 2025, 14, 2992. https://doi.org/10.3390/plants14192992
Konôpka B, Pajtík J, Marčiš P, Šebeň V. Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians. Plants. 2025; 14(19):2992. https://doi.org/10.3390/plants14192992
Chicago/Turabian StyleKonôpka, Bohdan, Jozef Pajtík, Peter Marčiš, and Vladimír Šebeň. 2025. "Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians" Plants 14, no. 19: 2992. https://doi.org/10.3390/plants14192992
APA StyleKonôpka, B., Pajtík, J., Marčiš, P., & Šebeň, V. (2025). Aboveground Biomass Productivity Relates to Stand Age in Early-Stage European Beech Plantations, Western Carpathians. Plants, 14(19), 2992. https://doi.org/10.3390/plants14192992






