Near-Infrared Spectroscopy-Based Phenomics Data Can Improve Genomic Prediction of Agronomic and Grain Quality Traits Across Multi-Environment Sorghum Hybrid Trials
Abstract
1. Introduction
2. Results
2.1. Combined Analysis and Variance Components
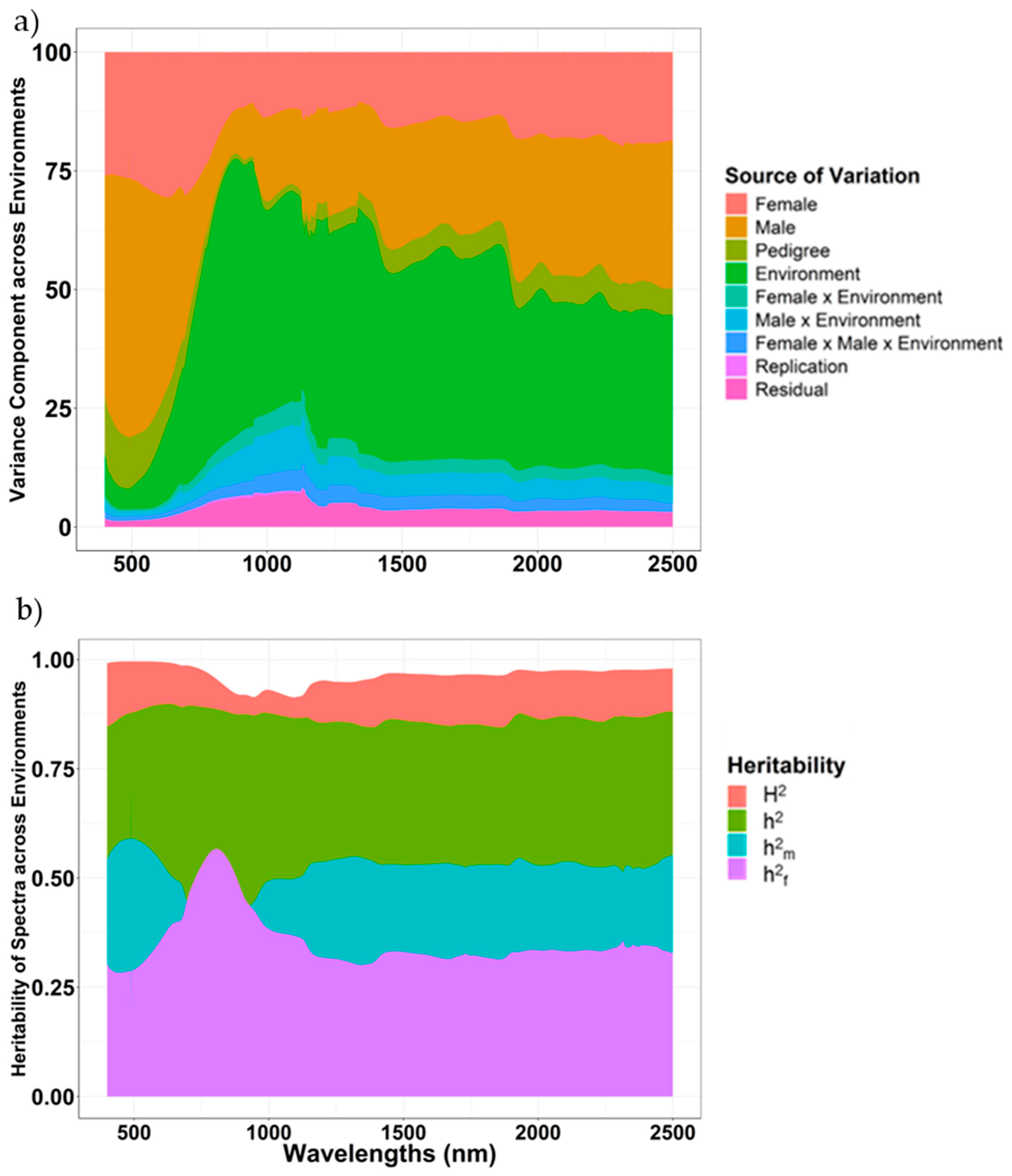
2.2. Variance Components and Heritability of NIR Spectra
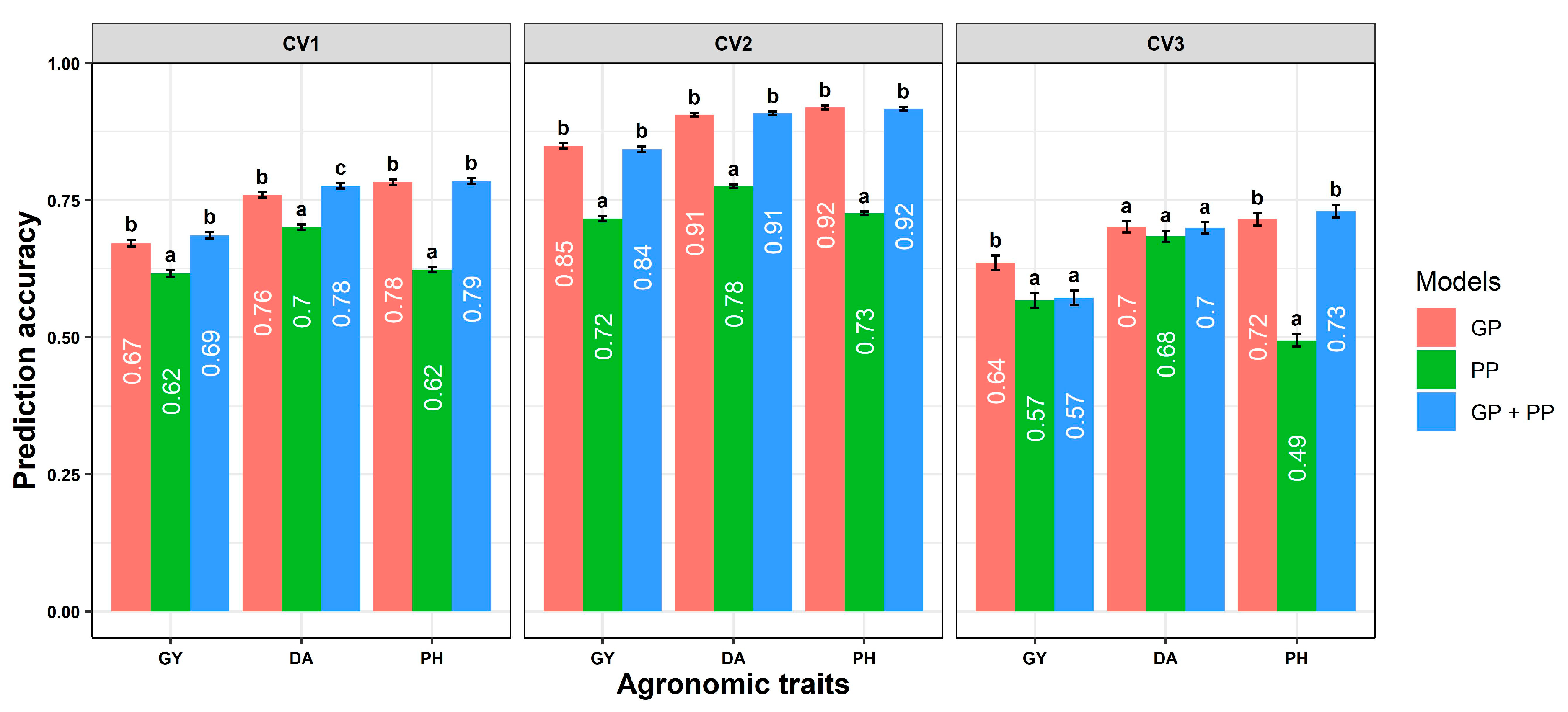
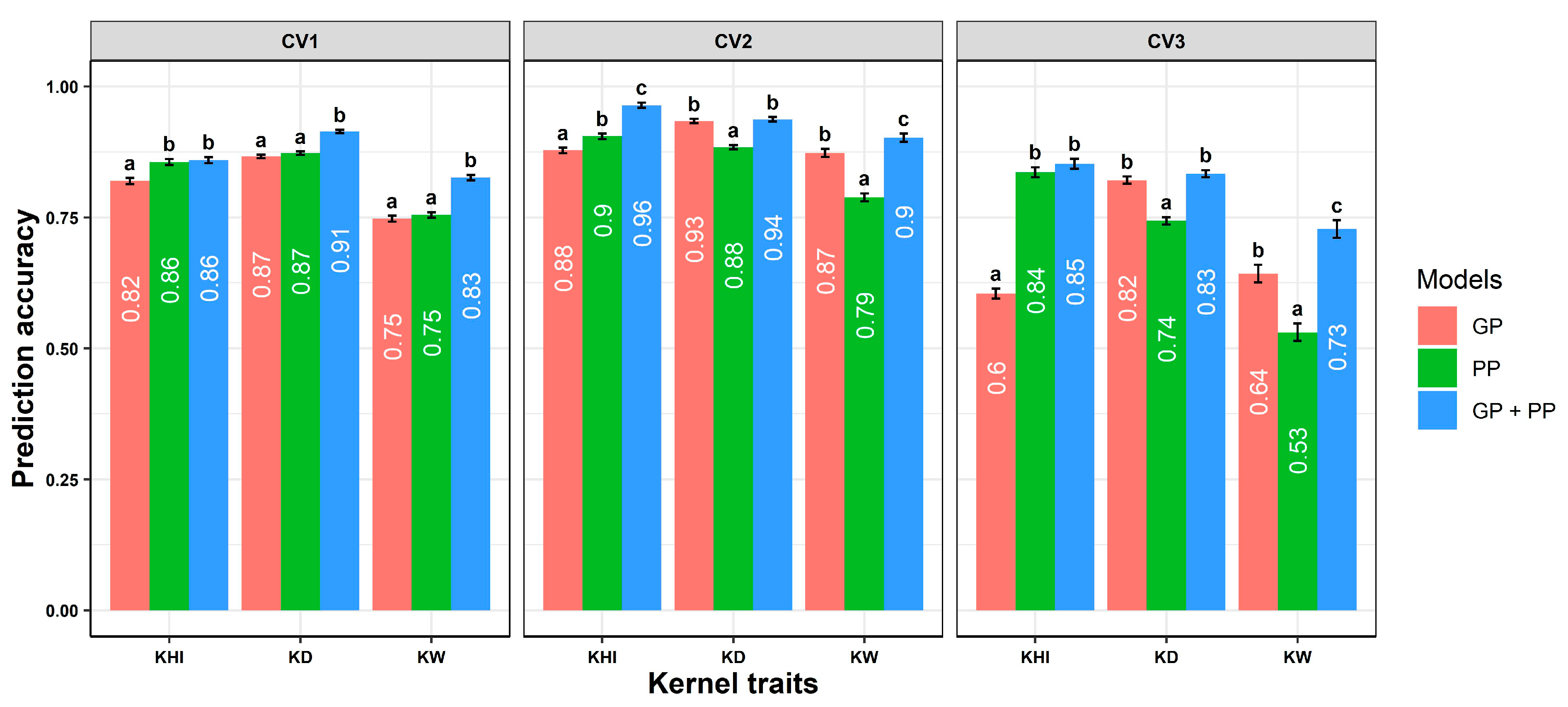
2.3. Predictive Abilities of Genomic or Phenomic Prediction Models
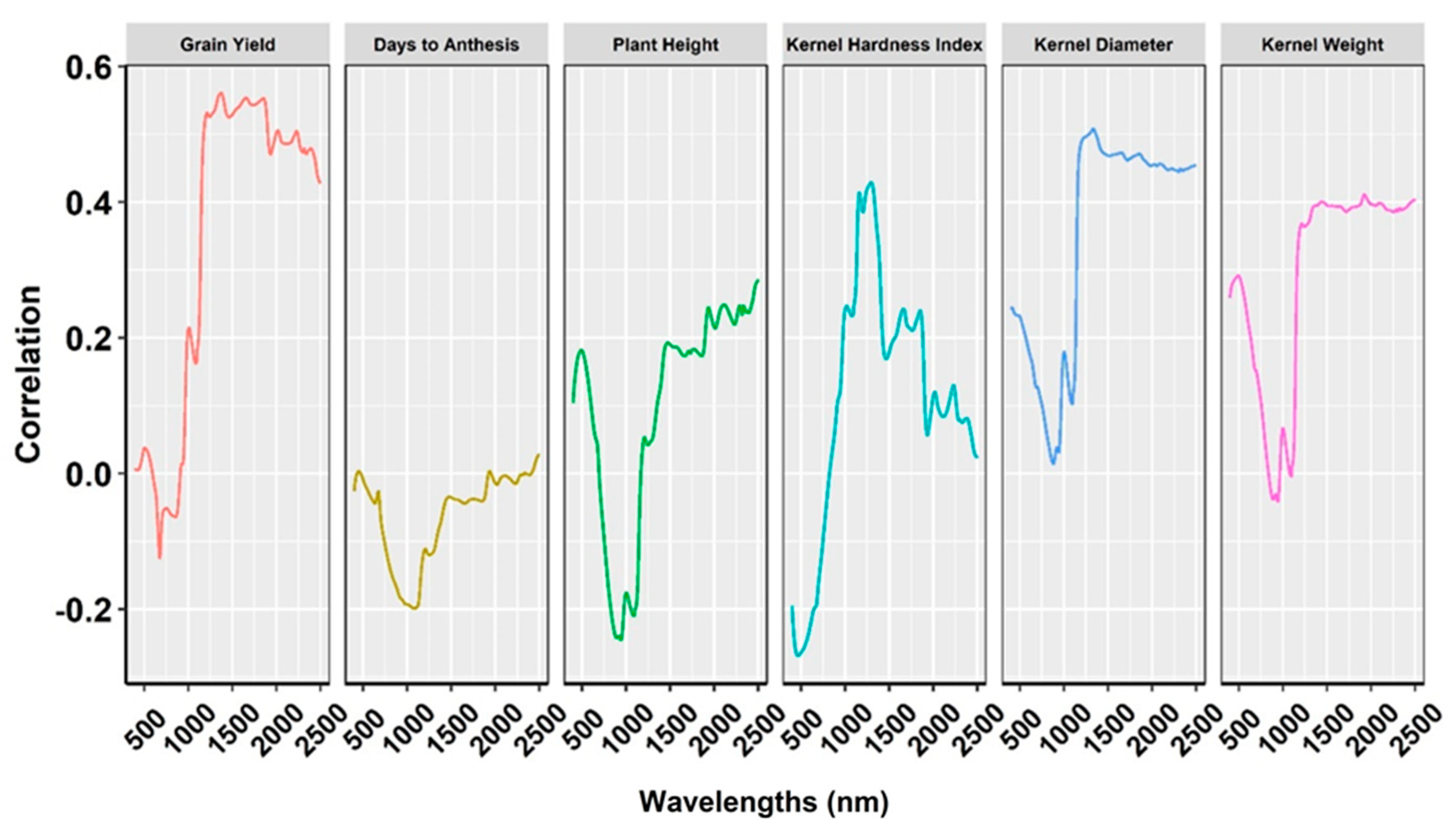
2.4. Relationship of NIRS Bands with Phenotypic Traits
3. Discussion
4. Conclusions
5. Materials and Methods
5.1. Experimental Design
5.2. Agronomic Evaluation and Traits
5.3. Grain Characterization
5.4. Phenomic Data
5.5. Genotypic Data
5.6. Variance Component Estimations
5.7. Genomic and Phenomic Prediction Models
5.7.1. Single-Environment Prediction Models
5.7.2. Combined Environment Prediction Models
5.7.3. Cross-Validation Performance Evaluation
5.8. Software
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GS | Genomic selection |
| NIRS | Near-infrared spectroscopy |
| PS | Phenomic selection |
| KHI | Kernel hardness index |
| GY | Grain yield |
| DA | Days to anthesis |
| PH | Plant height |
| KD | Kernel diameter |
| KW | Kernel weight |
| SKCS | Single-kernel characteristics system |
| BLUE | Best linear unbiased estimates |
| LRT | Likelihood ratio test |
| GCA | General combining ability |
| SCA | Specific combining ability |
| G × E | Genotype × environment |
| H2 | Broad sense heritability |
| h2 | Narrow sense heritability |
| GP | Genomic prediction |
| PP | Phenomic prediction |
References
- Crossa, J.; Fritsche-neto, R.; Montesinos-lopez, O.A.; Costa-neto, G.; Dreisigacker, S.; Montesinos-lopez, A. The modern plant breeding triangle: Optimizing the use of genomics, phenomics, and enviromics data. Front. Plant Sci. 2021, 12, 651480. [Google Scholar] [CrossRef]
- Herr, A.W.; Adak, A.; Carroll, M.E.; Elango, D.; Kar, S.; Li, C.; Jones, S.E.; Carter, A.H.; Murray, S.C.; Paterson, A.; et al. Unoccupied aerial systems imagery for phenotyping in cotton, maize, soybean, and wheat breeding. Crop Sci. 2023, 63, 1722–1749. [Google Scholar] [CrossRef]
- Hulse, J.H.; Laing, E.M.; Pearson, O.E. Sorghum and the Millets: Their Composition and Nutritive Value; Academic Press: Cambridge, MA, USA, 1980; p. 997. [Google Scholar]
- Rooney, L.W.; Awika, J.M. Overview of products and health benefits of specialty sorghums1. Cereals Foods World 2005, 50, 109. [Google Scholar]
- Taylor, J.R.; Schober, T.J.; Bean, S.R. Novel food and non-food uses for sorghum and millets. J. Cereal Sci. 2006, 44, 252–271. [Google Scholar] [CrossRef]
- Pfeiffer, B.K.; Pietsch, D.; Schnell, R.W.; Rooney, W.L. Long-term selection in hybrid sorghum breeding programs. Crop Sci. 2019, 59, 150–164. [Google Scholar] [CrossRef]
- Leon, F.; Harvey, L.; Rooney, W. Historical multi-environmental trials reveal trends in hybrid grain sorghum performance from 1970 to 2021 in Texas. Crop Sci. 2024, 64, 3014–3027. [Google Scholar] [CrossRef]
- Xin, Z.; Wang, M.; Cuevas, H.E.; Chen, J.; Harrison, M.; Pugh, N.A.; Morris, G. Sorghum genetic, genomic, and breeding resources. Planta 2021, 254, 114. [Google Scholar] [CrossRef]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef]
- Crossa, J.; Pérez-Rodríguez, P.; Cuevas, J.; Montesinos-López, O.; Jarquín, D.; de los Campos, G.; Burgueño, J.; González-Camacho, J.M.; Pérez-Elizalde, S.; Beyene, Y.; et al. Genomic selection in plant breeding: Methods, models, and perspectives. Trends Plant Sci. 2017, 22, 961–975. [Google Scholar] [CrossRef]
- Yang, W.; Feng, H.; Zhang, X.; Zhang, J.; Doonan, J.H.; Batchelor, W.D.; Xiong, L.; Yan, J. Crop phenomics and high-throughput phenotyping: Past decades, current challenges, and future perspectives. Mol. Plant 2020, 13, 187–214. [Google Scholar] [CrossRef]
- Pasquini, C. Near infrared spectroscopy: Fundamentals, practical aspects and analytical applications. J. Braz. Chem. Soc. 2003, 14, 198–219. [Google Scholar] [CrossRef]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M.C. Breaking with trends in pre-processing? TrAC-Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Rincent, R.; Charpentier, J.P.; Faivre-Rampant, P.; Paux, E.; Le Gouis, J.; Bastien, C.; Segura, V. Phenomic selection is a low-cost and high-throughput method based on indirect predictions: Proof of concept on wheat and poplar. G3 Genes Genomes Genet. 2018, 8, 3961–3972. [Google Scholar] [CrossRef] [PubMed]
- Barclay, V.J.; Bonner, R.F.; Hamilton, I.P. Application of wavelet transforms to experimental spectra: Smoothing, denoising, and data set compression. Anal. Chem. 1997, 69, 78–90. [Google Scholar] [CrossRef]
- Winn, Z.J.; Amsberry, A.L.; Haley, S.D.; DeWitt, N.D.; Mason, R.E. Phenomic versus genomic prediction—A comparison of prediction accuracies for grain yield in hard winter wheat lines. Plant Phenome J. 2023, 6, e20084. [Google Scholar] [CrossRef]
- Rutkoski, J.; Poland, J.; Mondal, S.; Autrique, E.; Pérez, L.G.; Crossa, J.; Reynolds, M.; Singh, R. Canopy temperature and vegetation indices from high-throughput phenotyping improve accuracy of pedigree and genomic selection for grain yield in wheat. G3 Genes Genomes Genet. 2016, 6, 2799–2808. [Google Scholar] [CrossRef]
- Sandhu, K.S.; Merrick, L.F.; Sankaran, S.; Zhang, Z.; Carter, A.H. Prospectus of genomic selection and phenomics in cereal, legume and oilseed breeding programs. Front. Genet. 2022, 6, 2799–2808. [Google Scholar] [CrossRef]
- Fonseca, J.M.O.; Klein, P.E.; Crossa, J.; Pacheco, A.; Perez-Rodriguez, P.; Ramasamy, P.; Klein, R.; Rooney, W.L. Assessing combining abilities, genomic data, and genotype × environment interactions to predict hybrid grain sorghum performance. Plant Genome 2021, 14, e20127. [Google Scholar] [CrossRef]
- Crozier, D.; Leon, F.; Fonseca, J.M.O.; Klein, P.E.; Klein, R.R.; Rooney, W.L. Inbred phenotypic data and non-additive effects can enhance genomic prediction models for hybrid grain sorghum. Crop Sci. 2023, 63, 1183–1196. [Google Scholar] [CrossRef]
- Kent, M.A.; Fonseca, J.M.O.; Klein, P.E.; Klein, R.R.; Hayes, C.M.; Rooney, W.L. Use of genomic prediction to screen sorghum B-lines in hybrid testcrosses. Plant Genome 2023, 16, e20369. [Google Scholar] [CrossRef]
- Winans, N.D.; Klein, R.R.; Fonseca, J.M.O.; Klein, P.E.; Rooney, W.L. Evaluating introgression sorghum germplasm selected at the population level while exploring genomic resources as a screening method. Plants 2023, 12, 444. [Google Scholar] [CrossRef]
- Are, A.K.; Srivastava, R.K.; Mahalingam, G.; Gorthy, S.; Gaddameedi, A.; Kunapareddy, A.; Kotla, A.; Jaganathan, J. Application of plant breeding and genomics for improved sorghum and pearl millet grain nutritional quality. In Sorghum and Millets; AACC International Press: Saint Paul, MN, USA, 2019; pp. 51–68. [Google Scholar]
- Jambunathan, R.; Kherdekar, M.S.; Stenhouse, J.W. Sorghum grain hardness and its relationship to mold susceptibility and mold resistance. J. Agric. Food Chem. 1992, 40, 1403–1408. [Google Scholar] [CrossRef]
- Menkir, A.; Ejeta, G.; Butler, L.; Melakeberhan, A. Physical and chemical kernel properties associated with resistance to grain mold in sorghum. Cereal Chem. 1996, 73, 613–617. [Google Scholar]
- Lee, W.J.; Pedersen, J.F.; Shelton, D.R. Relationship of sorghum kernel size to physiochemical, milling, pasting, and cooking properties. Food Res. Int. 2002, 35, 643–649. [Google Scholar] [CrossRef]
- Kent, M.A.; Crozier, D.S.; Rooney, W.L. Assessment of kernel characteristics to predict popping performance in grain sorghum. Crop Sci. 2022, 62, 1051–1059. [Google Scholar] [CrossRef]
- Galli, G.; Horne, D.W.; Collins, S.D.; Jung, J.; Chang, A.; Fritsche-Neto, R.; Rooney, W.L. Optimization of UAS-based high-throughput phenotyping to estimate plant health and grain yield in sorghum. Plant Phenome J. 2020, 3, e20010. [Google Scholar] [CrossRef]
- Cuevas, J.; Montesinos-López, O.; Juliana, P.; Guzmán, C.; Pérez-Rodríguez, P.; González-Bucio, J.; Burgueno, J.; Montesinos-Lopz, A.; Crossa, J. Deep kernel for genomic and near infrared predictions in multi-environment breeding trials. G3 Genes Genomes Genet. 2019, 9, 2913–2924. [Google Scholar] [CrossRef]
- DeSalvio, A.J.; Adak, A.; Murray, S.C.; Jarquín, D.; Winans, N.D.; Crozier, D.; Rooney, W.L. Near-infrared reflectance spectroscopy phenomic prediction can perform similarly to genomic prediction of maize agronomic traits across environments. Plant Genome 2024, 17, e20454. [Google Scholar] [CrossRef]
- Adunola, P.; Tavares Flores, E.; Riva-Souza, E.M.; Ferrão, M.A.G.; Senra, J.F.B.; Comério, M.; Espindula, M.C.; Verdin Filho, A.C.; Volpi, P.S.; Fonseca, A.F.A.d.; et al. A comparison of genomic and phenomic selection methods for yield prediction in Coffea canephora. Plant Phenome J. 2024, 7, e20109. [Google Scholar] [CrossRef]
- Alemu, A.; Åstrand, J.; Montesinos-López, O.A.; Isidro y Sánchez, J.; Fernández-Gónzalez, J.; Tadesse, W.; Vetukuri, R.R.; Carlsson, A.S.; Ceplitis, A.; Crossa, J.; et al. Genomic selection in plant breeding: Key factors shaping two decades of progress. Mol. Plant 2024, 17, 552–578. [Google Scholar] [CrossRef]
- Ye, S.; Li, J.; Zhang, Z. Multi-omics-data-assisted genomic feature markers preselection improves the accuracy of genomic prediction. J. Anim. Sci. Biotechnol. 2020, 11, 109. [Google Scholar] [CrossRef] [PubMed]
- Gullifa, G.; Barone, L.; Papa, E.; Giuffrida, A.; Materazzi, S.; Risoluti, R. Portable NIR spectroscopy: The route to green analytical chemistry. Front. Chem. 2023, 11, 1214825. [Google Scholar] [CrossRef]
- Robert, P.; Goudemand, E.; Auzanneau, J.; Oury, F.X.; Rolland, B.; Heumez, E.; Bouchet, S.; Caillebotte, A.; Mary-Huard, T.; Le Gouis, J.; et al. Phenomic selection in wheat breeding: Prediction of the genotype-by-environment interaction in multi-environment breeding trials. Theor. Appl. Genet. 2022, 135, 3337–3356. [Google Scholar] [CrossRef]
- Meyenberg, C.; Braun, V.; Friedrich, C.; Longin, H.; Thorwarth, P. Feature engineering and parameter tuning: Improving phenomic prediction ability in multi-environmental durum wheat breeding trials. Theor. Appl. Genet. 2024, 137, 188. [Google Scholar] [CrossRef]
- Krause, M.R.; González-Pérez, L.; Crossa, J.; Pérez-Rodríguez, P.; Montesinos-López, O.; Singh, R.P.; Dreisigacker, S.; Poland, J.; Rutkoski, J.; Sorrells, M.; et al. Hyperspectral reflectance-derived relationship matrices for genomic prediction of grain yield in wheat. G3 Genes Genomes Genet. 2019, 9, 1231–1247. [Google Scholar] [CrossRef]
- Osborne, B.G.; Anderssen, R.S. Single-kernel characterization principles and applications. Cereal Chem. 2003, 80, 613–622. [Google Scholar] [CrossRef]
- Maghirang, E.B.; Dowell, F.E. Hardness measurement of bulk wheat by single-kernel visible and near-infrared reflectance spectroscopy. Cereal Chem. 2003, 80, 316–322. [Google Scholar] [CrossRef]
- Cruickshank, R.H.; Munck, L. It’s barcoding Jim, but not as we know it. Zootaxa 2011, 2933, 55–56. [Google Scholar] [CrossRef]
- Brault, C.; Lazerges, J.; Doligez, A.; Thomas, M.; Ecarnot, M.; Roumet, P.; Bertrand, Y.; Berger, G.; Pons, T.; François, P.; et al. Interest of phenomic prediction as an alternative to genomic prediction in grapevine. Plant Methods 2022, 18, 108. [Google Scholar] [CrossRef]
- Zhu, X.; Leiser, W.L.; Hahn, V.; Würschum, T. Phenomic selection is competitive with genomic selection for breeding of complex traits. Plant Phenome J. 2021, 4, e20027. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Herr, A.W.; Crossa, J.; Montesinos-López, A.; Carter, A.H. Enhancing winter wheat prediction with genomics, phenomics and environmental data. BMC Genom. 2024, 25, 544. [Google Scholar] [CrossRef]
- Parmley, K.; Nagasubramanian, K.; Sarkar, S.; Ganapathysubramanian, B.; Singh, A.K. Development of optimized phenomic predictors for efficient plant breeding decisions using phenomic-assisted selection in soybean. Plant Phenomics 2019, 2019, 5809404. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Feldmann, M.J.; Runcie, D.E. Don’t benchmark phenomic prediction against genomic prediction accuracy. Plant Phenome J. 2025, 8, e70029. [Google Scholar] [CrossRef]
- Delwiche, S.R.; Graybosch, R.A.; Nelson, L.A.; Hruschka, W.R. Environmental effects on developing wheat as sensed by near-infrared reflectance of mature grains. Cereal Chem. 2002, 79, 885–891. [Google Scholar] [CrossRef]
- Robert, P.; Brault, C.; Rincent, R.; Vincent, S. Phenomic selection: A new and efficient alternative to genomic selection. In Genomic Prediction of Complex Traits: Methods and Protocols; Springer: Cham, Switzerland, 2022; pp. 397–420. [Google Scholar] [CrossRef]
- Sapkota, P.; Perumal, R.; Fonseca, J.; Klein, P.; Klein, R.R.; Awika, J.; Rooney, W.L. Heritability, combining ability and genomic selection for grain quality traits in sorghum hybrids across multi-environment trials. Crop Sci. 2025, submitted.
- Stevens, A.; Ramirez-Lopez, L. An Introduction to the Prospectr Package. 2014. Available online: https://CRAN.R-project.org/package=prospectr (accessed on 24 July 2025).
- Morishige, D.T.; Klein, P.E.; Hilley, J.L.; Sahraeian, S.M.E.; Sharma, A.; Mullet, J.E. Digital genotyping of sorghum—A diverse plant species with a large repeat-rich genome. BMC Genom. 2013, 14, 448. [Google Scholar] [CrossRef]
- Vanraden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Acosta-Pech, R.; Crossa, J.; de Los Campos, G.; Teyssèdre, S.; Claustres, B.; Pérez-Elizalde, S.; Pérez-Rodríguez, P. Genomic models with genotype × environment interaction for predicting hybrid performance: An application in maize hybrids. Theor. Appl. Genet. 2017, 130, 1431–1440. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing, R Foundation for Statistical Computing. 2023. Available online: https://www.r-project.org/ (accessed on 27 July 2025).
- Pérez, P.; de Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef] [PubMed]

| Variance Components a | Agronomic Traits | Kernel Traits | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grain Yield (GY) | Days to Anthesis (DA) | Plant Height (PH) | Kernel Hardness INDEX (KHI) | Kernel Diameter (KD) | Kernel Weight (KW) | |||||||
| Estimate | % | Estimate | % | Estimate | % | Estimate | % | Estimate | % | Estimate | % | |
| (Hybrid) | 0.39 | 14.5 | 6.23 | 11.8 | 94.6 | 48.1 | 76.6 | 56.7 | 0.023 | 54.1 | 4.76 | 41.5 |
| GCAf | 0.18 *** | 6.8 | 3.03 *** | 5.7 | 35.1 *** | 17.8 | 18.6 *** | 13.8 | 0.009 *** | 20.8 | 1.51 *** | 13.2 |
| GCAm | 0.18 *** | 6.6 | 2.93 *** | 5.5 | 51.0 *** | 25.9 | 42.8 *** | 31.7 | 0.013 *** | 29.3 | 2.34 *** | 20.5 |
| SCA | 0.03 ** | 1.2 | 0.28 *** | 0.5 | 8.5 *** | 4.3 | 15.2 *** | 11.2 | 0.001 *** | 4.05 | 0.90 *** | 7.85 |
| Env | 1.30 *** | 48.6 | 41.20 *** | 78.0 | 51.0 *** | 25.9 | 11.1 NS | 8.2 | 0.01 ** | 23.1 | 2.45 ** | 21.4 |
| (Hybrid × Env) | 0.32 | 12.1 | 2.58 | 4.9 | 15.2 | 7.7 | 58.2 | 19.4 | 0.003 | 10.8 | 1.76 | 15.4 |
| GCAf × Env | 0.16 *** | 6.0 | 1.41 *** | 2.7 | 4.1 *** | 2.1 | 9.3 *** | 6.9 | 0.001 *** | 3.65 | 0.57 *** | 4.94 |
| GCAm × Env | 0.09 *** | 3.5 | 1.03 *** | 1.9 | 8.5 *** | 4.3 | 10.8 *** | 8.0 | 0.001 *** | 3.21 | 0.50 *** | 4.39 |
| SCA × Env | 0.078 * | 2.6 | 0.14 NS | 0.3 | 2.7 * | 1.4 | 6.1 *** | 4.5 | 0.001 *** | 3.93 | 0.69 *** | 6.05 |
| Rep (Env) | 0.02 NS | 0.9 | 0.14 NS | 0.3 | 1.3 NS | 0.6 | 2.3 NS | 1.6 | 0 NS | 1.54 | 0.170 NS | 1.48 |
| Residual | 0.634 | 23.8 | 2.65 | 5.0 | 34.6 | 17.6 | 18.7 | 13.8 | 0.004 | 10.5 | 2.31 | 20.2 |
| H2 | 0.83 | 0.92 | 0.96 | 0.90 | 0.93 | 0.87 | ||||||
| h2 | 0.76 | 0.88 | 0.87 | 0.72 | 0.86 | 0.70 | ||||||
| h2f | 0.38 | 0.44 | 0.35 | 0.22 | 0.36 | 0.27 | ||||||
| h2m | 0.38 | 0.45 | 0.52 | 0.50 | 0.50 | 0.43 | ||||||
| CVe | 12.50 | 2.31 | 4.36 | 5.76 | 2.75 | 5.88 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapkota, P.; Fonseca, J.; Perumal, R.; Crossa, J.; Rooney, W.L. Near-Infrared Spectroscopy-Based Phenomics Data Can Improve Genomic Prediction of Agronomic and Grain Quality Traits Across Multi-Environment Sorghum Hybrid Trials. Plants 2025, 14, 2871. https://doi.org/10.3390/plants14182871
Sapkota P, Fonseca J, Perumal R, Crossa J, Rooney WL. Near-Infrared Spectroscopy-Based Phenomics Data Can Improve Genomic Prediction of Agronomic and Grain Quality Traits Across Multi-Environment Sorghum Hybrid Trials. Plants. 2025; 14(18):2871. https://doi.org/10.3390/plants14182871
Chicago/Turabian StyleSapkota, Pradip, Jales Fonseca, Ramasamy Perumal, José Crossa, and William L. Rooney. 2025. "Near-Infrared Spectroscopy-Based Phenomics Data Can Improve Genomic Prediction of Agronomic and Grain Quality Traits Across Multi-Environment Sorghum Hybrid Trials" Plants 14, no. 18: 2871. https://doi.org/10.3390/plants14182871
APA StyleSapkota, P., Fonseca, J., Perumal, R., Crossa, J., & Rooney, W. L. (2025). Near-Infrared Spectroscopy-Based Phenomics Data Can Improve Genomic Prediction of Agronomic and Grain Quality Traits Across Multi-Environment Sorghum Hybrid Trials. Plants, 14(18), 2871. https://doi.org/10.3390/plants14182871






