Research on Forest Carbon Sequestration and Its Economic Valuation: A Case Study of the Zixi Mountain Nature Reserve, Chuxiong Prefecture
Abstract
1. Introduction
2. Materials and Methods
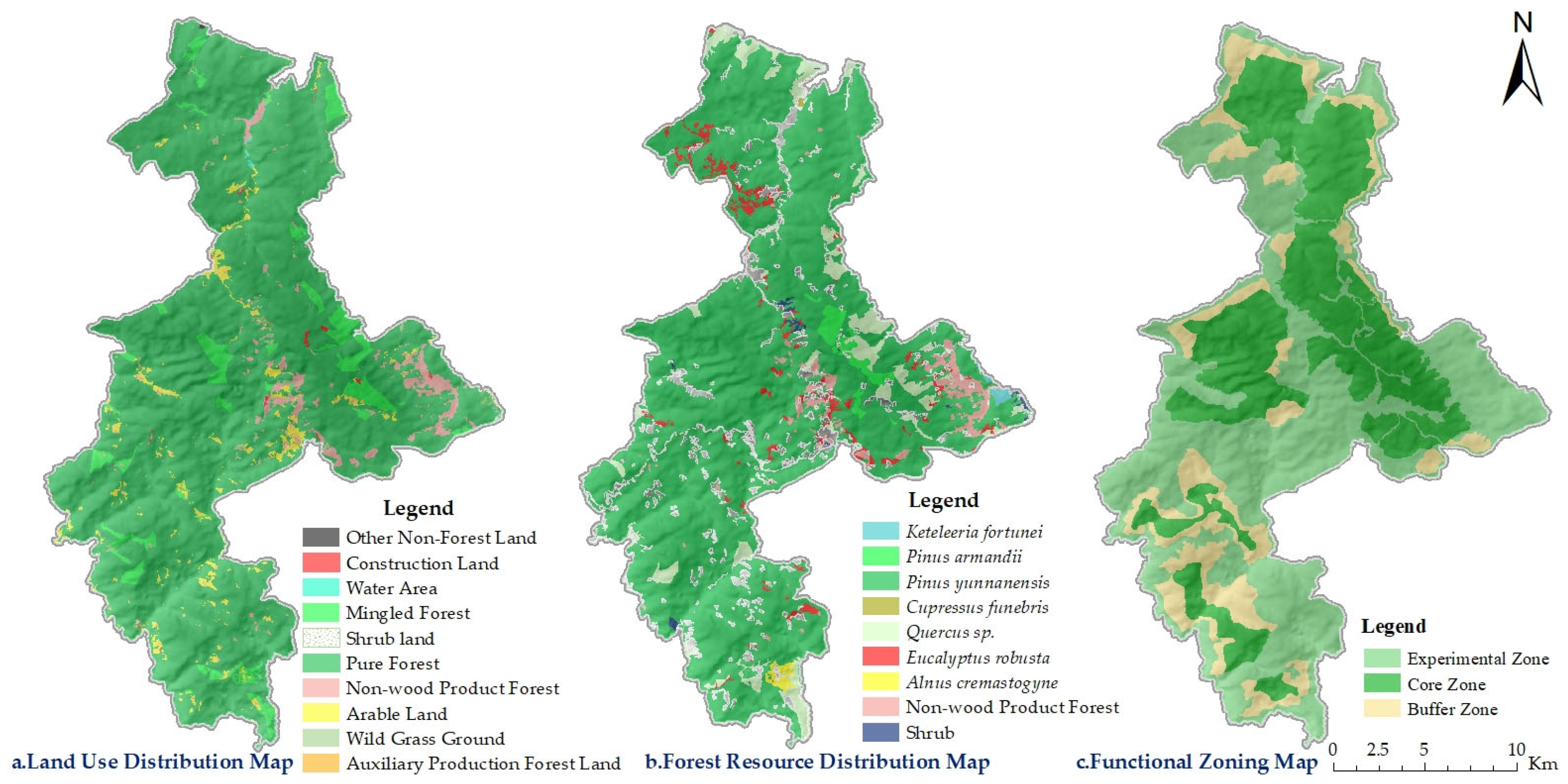
2.1. Study Area Overview
2.2. Data Source
2.3. Research Methods
2.3.1. Forest Carbon Stock Estimation
- (1)
- Estimation of arbor forest carbon stock
- (2)
- Estimation of carbon stock in economic forests
- (3)
- Estimation of carbon storage in shrub forests
2.3.2. Data Analysis
2.3.3. Valuation of Forest Carbon Sequestration
3. Results
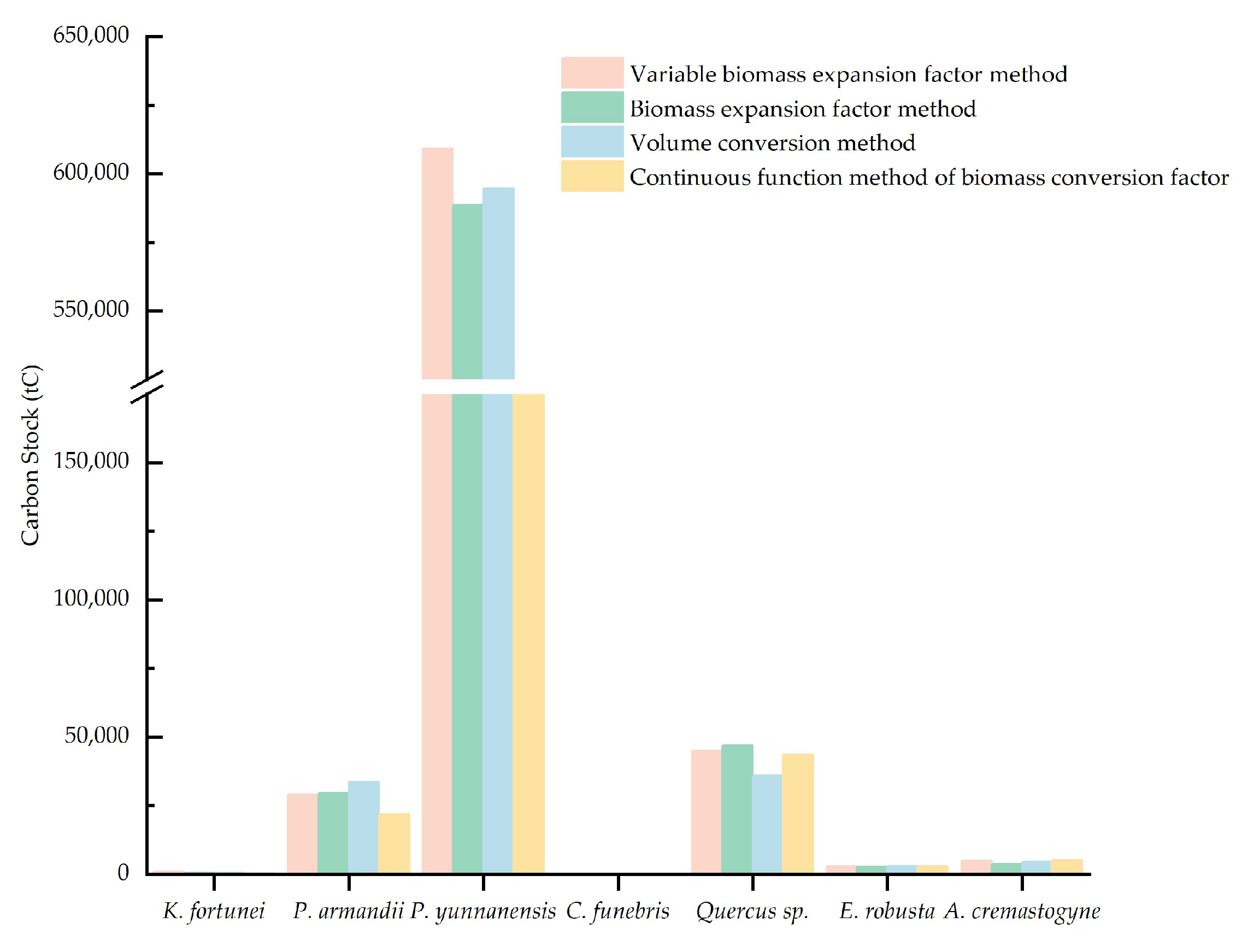
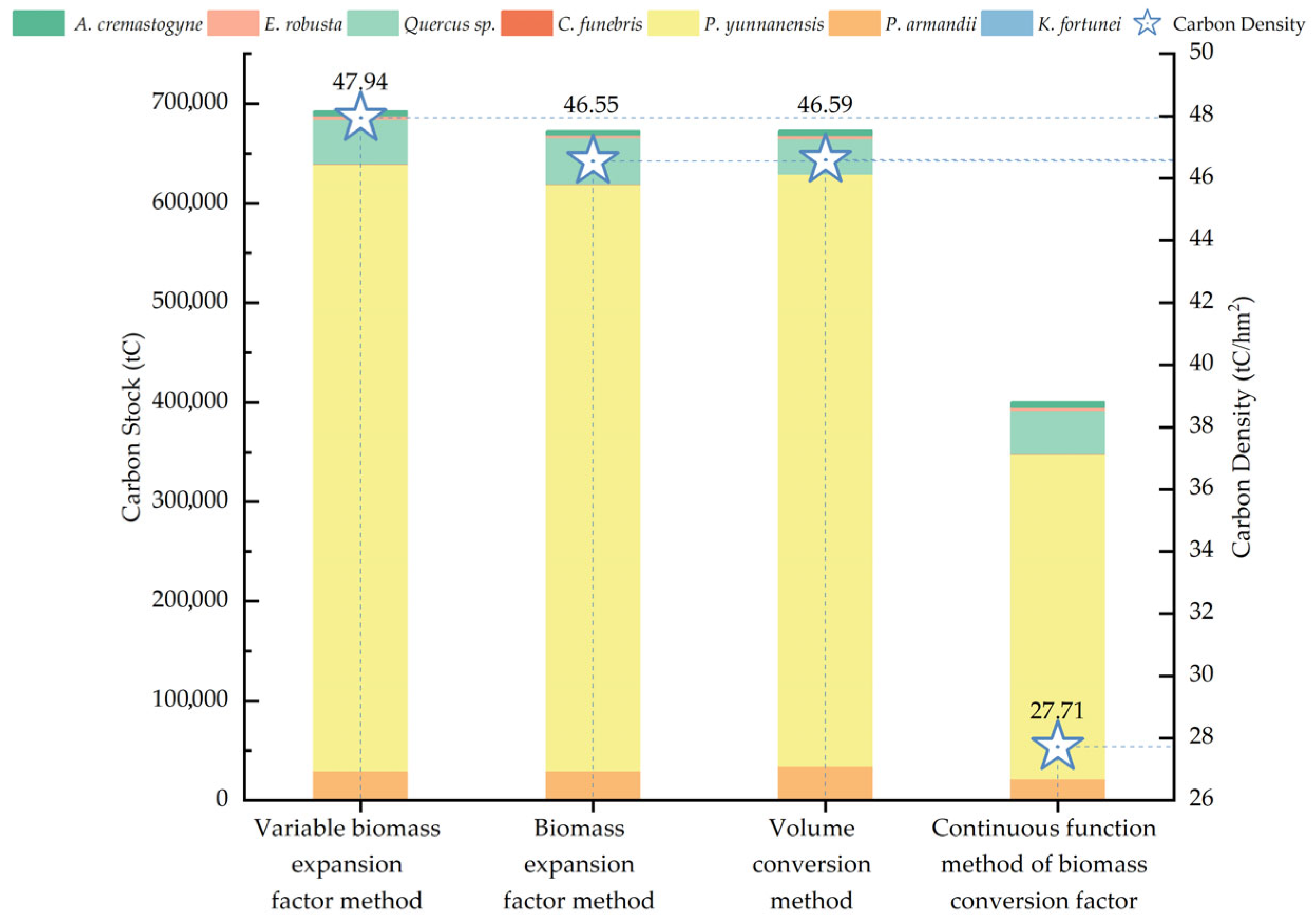
3.1. Analysis of Carbon Stock Estimates Derived from Different Methodologies
3.2. Current Status of Forest Resources and Carbon Stocks in the Nature Reserve
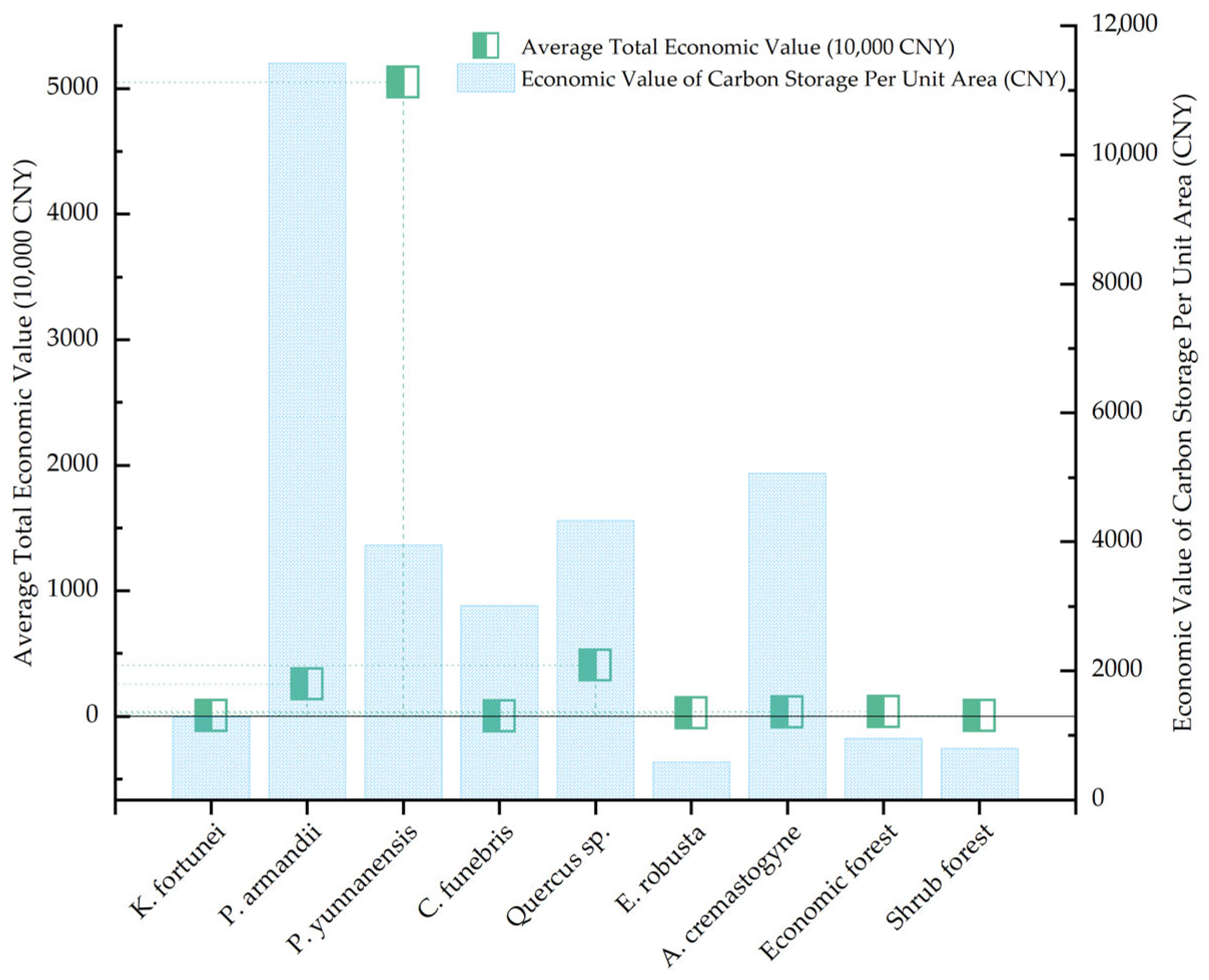
3.3. Analysis of Forest Carbon Sequestration Value
3.3.1. Economic Value of Carbon Sequestration Across Forest Vegetation Types
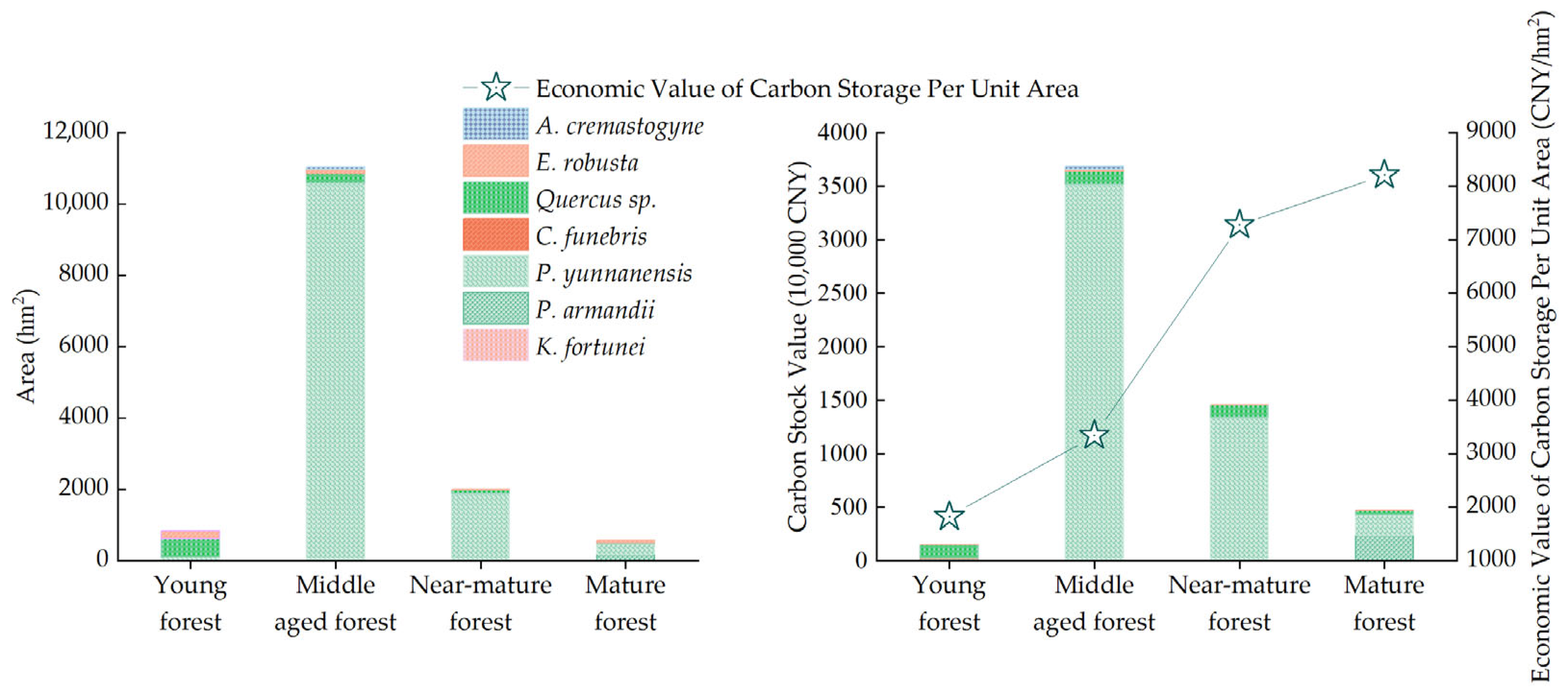
3.3.2. Carbon Sequestration Economic Value Across Age Groups of Arbor Forests
3.3.3. Carbon Sequestration Economic Value of Forest Vegetation Across Functional Zones
4. Discussion
4.1. Impact of Different Estimation Methods on Forest Carbon Stock Assessment
4.2. Influence of Different Estimation Methods on the Economic Value of Forest Carbon Sequestration
4.3. Comparative Analysis of Forest Carbon Sequestration Value by Forest Types, Age Classes, and Functional Zones
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson-Teixeira, K.J.; Wang, M.M.H.; McGarvey, J.C.; Herrmann, V.; Tepley, A.J.; Bond-Lamberty, B.; LeBauer, D.S. For C: A global database of forest carbon stocks and fluxes. Ecology 2018, 99, 1507. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhou, M.; Lv, J.; Chen, K. Trends in global research in forest carbon sequestration: A bibliometric analysis. J. Clean. Prod. 2020, 252, 119908. [Google Scholar] [CrossRef]
- Zhang, C.H.; Ju, W.M.; Wang, D.J.; Wang, X.Q.; Wang, X. Biomass carbon stocks and economic value dynamics of forests in Shandong Province from 2004 to 2013. Acta Ecol. Sin. 2018, 38, 1739–1749. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Shevliakova, E.; Stouffer, R.J.; Malyshev, S.; Krasting, J.P.; Hurtt, G.C.; Pacala, S.W. Historical warming reduced due to enhanced land carbon uptake. Proc. Natl. Acad. Sci. USA 2013, 110, 16730–16735. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.Y.; Guo, Z.D.; Hu, H.F.; Kato, T.; Muraoka, H.; Son, Y. Forest biomass carbon sinks in East Asia, with special reference to the relative contributions of forest expansion and forest growth. Glob. Change Biol. 2014, 20, 2019–2030. [Google Scholar] [CrossRef] [PubMed]
- vonHedemann, N.; Wurtzebach, Z.; Timberlake, T.J.; Sinkular, E.; Schultz, C.A. Forest policy and management approaches for carbon dioxide removal. Interface Focus 2020, 10, 20200001. [Google Scholar] [CrossRef] [PubMed]
- Katila, P.; Galloway, G.; Alfaro, R.I.; Kanninen, M.; Lobovikov, M.; Varjo, J. Forests and Society-Responding to Global Drivers of Change; IUFRO: Vienna, Austria, 2010. [Google Scholar]
- Guo, Z.D.; Hu, H.F.; Li, P.; Li, N.Y.; Fang, J.Y. Spatio-temporal changes in biomass carbon sinks in China’s forests from 1977 to 2008. Sci. China Life Sci. 2013, 56, 661–671. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.J.; Guo, Q.H.; Xue, B.L.; Hu, T.Y.; Alvarez, O.; Tao, S.L.; Fang, J.Y. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Fang, J.; Yu, G.; Liu, L.; Hu, H.; Chapin, F.S. Climate change, human impacts, and carbon sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [PubMed]
- Favero, A.; Daigneault, A.; Sohngen, B. Forests: Carbon sequestration, biomass energy, or both? Sci. Adv. 2020, 6, eaay6792. [Google Scholar] [CrossRef] [PubMed]
- Long, Y.; Zhu, Z.; Hong, Y.; Gong, Z.; Li, H.; Zhang, H. The effect of carbon taxes and subsidies on forest carbon sequestration in China. For. Policy Econ. 2024, 169, 103316. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Change Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef] [PubMed]
- Uttaruk, Y.; Laosuwan, T.; Sangpradid, S.; Butthep, C.; Rotjanakusol, T.; Sittiwong, W.; Nilrit, S. Thailand’s urban forestry programs are assisted by calculations of their ecological properties and economic values. Land 2024, 13, 1440. [Google Scholar] [CrossRef]
- Assmuth, A.; Autto, H.; Halonen, K.M.; Haltia, E.; Huttunen, S.; Lintunen, J.; Lonkila, A.; Nieminen, T.M.; Ojanen, P.; Peltoniemi, M. Forest carbon payments: A multidisciplinary review of policy options for promoting carbon storage in EU member states. Land Use Policy 2024, 147, 107341. [Google Scholar] [CrossRef]
- Yao, Q.; Zhang, J.; Song, H.; Yu, R.; Xiong, N.; Wang, J.; Cui, L. Estimation of Vegetation Carbon Sinks and Their Response to Land Use Intensity in the Example of the Beijing–Tianjin–Hebei Region. Forests 2024, 15, 2158. [Google Scholar] [CrossRef]
- Mu, Y.; Yu, Z.; Cheng, H.; Yang, H. Are There Spatial Spillover Effects of Carbon Emission Trading Policy on Forest Carbon Sink Growth in China? Forests 2025, 16, 386. [Google Scholar] [CrossRef]
- Gough, C.M.; Vogel, C.S.; Schmid, H.P.; Su, H.B.; Curtis, P.S. Multi-year convergence of biometric and meteorological estimates of forest carbon storage. Agric. For. Meteorol. 2008, 148, 158–170. [Google Scholar] [CrossRef]
- Potter, C.; Gross, P.; Klooster, S.; Fladeland, M.; Genovese, V. Storage of carbon in US forests predicted from satellite data, ecosystem modeling, and inventory summaries. Clim. Change 2008, 90, 269–282. [Google Scholar] [CrossRef]
- Wang, F.P.; Zhang, J.L.; Cao, J.; Yang, Z.D.; Xiao, Q.L.; Yang, K.; Yin, T.Y.; Cheng, T. Research on Estimation of Forest Carbon Stock by Integrating Landsat and GOSAT Satellite Data. J. Southwest For. Univ. 2025, 45, 151–158. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, X.; Zheng, J.; Liu, X.; Li, J.; Song, M. Estimation methods in predicting carbon stock of forest communities in the natural reserve of Baihua mountain. J. Northwest A&F Univ. Nat. Sci. Ed. 2012, 40, 139–146. (In Chinese) [Google Scholar] [CrossRef]
- Suárez-Fernández, G.E.; Martínez-Sánchez, J.; Arias, P. Enhancing carbon stock estimation in forests: Integrating multi-data predictors with random forest method. Ecol. Inform. 2025, 86, 102997. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and Evaluation of Three Methods for Estimating Forest above Ground Biomass Using TM and GLAS Data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Pasalodos-Tato, M.; Almazán Riballo, E.; Montero, G.; Diaz-Balteiro, L. Evaluation of tree biomass carbon stock changes in Andalusian forests: Comparison of two methodologies. Carbon Manag. 2017, 8, 125–134. [Google Scholar] [CrossRef]
- Domke, G.M.; Woodall, C.W.; Smith, J.E.; Westfall, J.A.; McRoberts, R.E. Consequences of alternative tree-level biomass estimation procedures on U.S. forest carbon stock estimates. For. Ecol. Manag. 2012, 270, 108–116. [Google Scholar] [CrossRef]
- Li, H.; Lei, Y. Estimation and Evaluation of Forest Biomass Carbon Storage in China; China Forestry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Li, C.; Dai, H. Forest Management Inventory in China: History, Current Status and Trend. World For. Res. 2021, 34, 72–80. (In Chinese) [Google Scholar] [CrossRef]
- Sun, W.; Liu, X. Review on carbon storage estimation of forest ecosystem and applications in China. For. Ecosyst. 2020, 7, 14. [Google Scholar] [CrossRef]
- Guo, Z.; Fang, J.; Pan, Y.; Birdsey, R. Inventory-based estimates of forest biomass carbon stocks in China: A comparison of three methods. For. Ecol. Manag. 2010, 259, 1225–1231. [Google Scholar] [CrossRef]
- Li, S.; Zhu, T.; Wei, C.; Ye, S.; Song, Y. Forest Carbon Storage Calculation and Carbon Sink Potential Prediction in Beijing. Environ. Sci. Manag. 2024, 49, 22–27. (In Chinese) [Google Scholar]
- Leley, N.C.; Langat, D.K.; Kisiwa, A.K.; Maina, G.M.; Muga, M.O. Total carbon stock and potential carbon sequestration economic value of mukogodo forest-landscape ecosystem in drylands of northern Kenya. Open J. For. 2022, 12, 19–40. [Google Scholar] [CrossRef]
- Zhang, C.; Ju, W.; Chen, J.M.; Zan, M.; Li, D.; Zhou, Y.; Wang, X. China’s forest biomass carbon sink based on seven inventories from 1973 to 2008. Clim. Change 2013, 118, 933–948. [Google Scholar] [CrossRef]
- Hu, J.X.; Huang, F.; Tie, L.H.; Liu, X.; Wei, S.Z.; Huang, C.D. Economic value dynamics of carbon sequestration in forest vegetation of Sichuan Province. Acta Ecol. Sin. 2019, 39, 158–163. [Google Scholar] [CrossRef]
- Pache, R.G.; Abrudan, I.V.; Niță, M.D. Economic valuation of carbon storage and sequestration in Retezat National Park, Romania. Forests 2020, 12, 43. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, Y.; Wang, Y.; Liu, Y.; Li, H. Spatiotemporal characteristics and factors influencing value of forest carbon sequestration in Henan Province. Bull. Soil Water Conserv. 2023, 43, 288–296. [Google Scholar] [CrossRef]
- Kazak, J.; Malczyk, J.; Castro, D.G.; Szewrański, S. Carbon sequestration in forest valuation. Real Estate Manag. Valuat. 2016, 24, 76–86. [Google Scholar] [CrossRef]
- Raihan, A.; Begum, R.A.; Said, M.N.M. A meta-analysis of the economic value of forest carbon stock. Geografia 2021, 17, 321–338. [Google Scholar] [CrossRef]
- Solberg, B. Forest biomass as carbon sink-economic value and forest management/policy implications. Crit. Rev. Environ. Sci. Technol. 1997, 27, 323–333. [Google Scholar] [CrossRef]
- Lin, B.; Ge, J. Valued forest carbon sinks: How much emissions abatement costs could be reduced in China. J. Clean. Prod. 2019, 224, 455–464. [Google Scholar] [CrossRef]
- Xu, G.; Schwarz, P.; Shi, X.; Duma, N. Scenario paths of developing forest carbon sinks for China to achieve carbon neutrality. Land 2023, 12, 1325. [Google Scholar] [CrossRef]
- Li, H.; Zhao, P.; Lei, Y.; Zeng, W. Comparison on Estimation of Wood Biomass Using Forest Inventory Data. Sci. Silvae Sin. 2012, 48, 44–52. (In Chinese) [Google Scholar] [CrossRef]
- Peng, S.; Wen, D.; He, N.; Yu, G.; Ma, A.; Wang, Q. Carbon storage in China’s forest ecosystems: Estimation by different integrative methods. Ecol. Evol. 2016, 6, 3129–3145. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Feng, Z.; Zhu, Y. Estimation of Forest Biomass and Carbon Storage in China Based on Forest Resources Inventory Data. Forests 2019, 10, 650. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q. Study on Economic Value Assessment of Forest Carbon Sequestration—Taking Fujian Province as an Example. J. Southwest Univ. Nat. Sci. Ed. 2021, 43, 121–128. (In Chinese) [Google Scholar] [CrossRef]
- Li, Q.; Xia, X.; Kou, X.; Niu, L.; Wan, F.; Zhu, J.; Xiao, W. Forest carbon storage and carbon sequestration potential in Shaanxi Province, China. Forests 2023, 14, 2021. [Google Scholar] [CrossRef]
- Department of Climate Change, National Development and Reform Commission. The People’s Republic of China National Greenhouse Gas Inventory 2008; China Planning Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Zhang, Y.; Chen, J.; Hu, M.; Offer, A. Valuation of forest carbon sinks in China within the framework of the system of national accounts. J. For. Res. 2016, 27, 1321–1328. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, X.; Qin, Q.; Chen, K. Value accounting of forest carbon sinks in China. J. Beijing For. Univ. 2013, 35, 124–131. (In Chinese) [Google Scholar]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Liu, G.; Xu, S. Biomass and Net Production of Forest Vegetation in China. Acta Ecol. Sin. 1996, 16, 497–508. (In Chinese) [Google Scholar]
- Ollikainen, M. Forest management, public goods, and optimal policies. Annu. Rev. Resour. Econ. 2016, 8, 207–226. [Google Scholar] [CrossRef]
- Li, M. Carbon stock and sink economic values of forest ecosystem in the forest industry region of Heilongjiang Province, China. J. For. Res. 2022, 33, 875–882. [Google Scholar] [CrossRef]
- Shi, T.M.; Wang, D.; Tang, Y.; Li, P.Y. Evaluation of Urban Composite Carbon Sink Value: A Case Study of Shenyang. Landsc. Archit. 2025, 32, 57–66. (In Chinese) [Google Scholar] [CrossRef]
- Qiao, D.; Zhang, Z.; Li, H. How Does Carbon Trading Impact China’s Forest Carbon Sequestration Potential and Carbon Leakage? Forests 2024, 15, 497. [Google Scholar] [CrossRef]
- Tang, X.; Fehrmann, L.; Guan, F.; Forrester, D.I.; Guisasola, R.; Kleinn, C. Inventory-based estimation of forest biomass in Shitai County, China: A comparison of five methods. Ann. For. Res. 2016, 59, 269–280. [Google Scholar] [CrossRef]
- Liao, S.; Li, M.; Peng, Y. The Forest Carbon Storage and Its Dynamic Changes in the Bandong Provincial Nature Reserve of Liannan, Guangdong. South China Agric. 2023, 17, 89–94. (In Chinese) [Google Scholar] [CrossRef]
- Wu, M.; Dong, G.; Wang, Y.; Xiong, R.; Li, Y.; Cheng, W.; Fu, Z.; Fan, S. Estimation of forest aboveground carbon storage in Sichuan Miyaluo Nature Reserve based on remote sensing. Acta Ecol. Sin. 2020, 40, 621–628. (In Chinese) [Google Scholar] [CrossRef]
- Graham, V.; Geldmann, J.; Adams, V.M.; Negret, P.J.; Sinovas, P.; Chang, H.C. Southeast Asian protected areas are effective in conserving forest cover and forest carbon stocks compared to unprotected areas. Sci. Rep. 2021, 11, 23760. [Google Scholar] [CrossRef] [PubMed]
- Honkomp, T.; Schier, F. Scoping review of carbon pricing systems in forest sector models. Environ. Res. Lett. 2023, 19, 013001. [Google Scholar] [CrossRef]
- Ge, J.; Zhang, Z.J.; Lin, B. Towards carbon neutrality: How much do forest carbon sinks cost in China? Environ. Impact Assess. Rev. 2023, 98, 106949. [Google Scholar] [CrossRef]
- Baumbach, L.; Hickler, T.; Yousefpour, R.; Hanewinkel, M. High economic costs of reduced carbon sinks and declining biome stability in Central American forests. Nat. Commun. 2023, 14, 2043. [Google Scholar] [CrossRef] [PubMed]
- Roh, T.W.; Koo, J.C.; Cho, D.S.; Youn, Y.C. Contingent feasibility for forest carbon credit: Evidence from South Korean firms. J. Environ. Manag. 2014, 144, 297–303. [Google Scholar] [CrossRef] [PubMed]
- Döbbeling-Hildebrandt, N.; Miersch, K.; Khanna, T.M.; Bachelet, M.; Bruns, S.B.; Callaghan, M.; Edenhofer, O.; Flachsland, C.; Forster, P.M.; Kalkuhl, M. Systematic review and meta-analysis of ex-post evaluations on the effectiveness of carbon pricing. Nat. Commun. 2024, 15, 4147. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gong, X.; Zhang, Y.; Duan, C.; Gao, W. An assessment on forest ecosystem services value of carbon fixation and oxygen release in Dianchi Lake Basin. J. Yunnan Univ. Nat. Sci. Ed. 2019, 41, 9. (In Chinese) [Google Scholar] [CrossRef]
- Geng, Y.; Liu, X.; Wu, S. Assessment and Prediction of Carbon Sink Resource Potential in Arbor Forests: A Case Study of Mentougou District, Beijing, China. Forests 2025, 16, 926. [Google Scholar] [CrossRef]
- Shi, X.; Wang, T.; Lu, S.; Chen, K.; He, D.; Xu, Z. Evaluation of China’ s forest carbon sink service value. Environ. Sci. Pollut. Res. 2022, 29, 44668–44677. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Forest Carbon Sink Accounting and Marketization; China Environmental Science Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Plantinga, A.J.; Wu, J.J. Co-benefits from carbon sequestration in forests: Evaluating reductions in agricultural externalities from an afforestation policy in Wisconsin. Land Econ. 2003, 79, 74–85. [Google Scholar] [CrossRef]
- Gizachew, B.; Solberg, S.; Puliti, S. Forest Carbon Gain and Loss in Protected Areas of Uganda: Implications to Carbon Benefits of Conservation. Land 2018, 7, 138. [Google Scholar] [CrossRef]
- Wei, Y.; Yu, D.; Lewis, B.J.; Zhou, L.; Zhou, W.; Fang, X.; Zhao, W.; Wu, S.; Dai, L. Forest Carbon Storage and Tree Carbon Pool Dynamics under Natural Forest Protection Program in Northeastern China. Chin. Geogr. Sci. 2014, 24, 397–405. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, Y.; Wang, L.; Zheng, S.; Xu, W. Assessment of carbon density in natural mountain forest ecosystems at northwest China. Int. J. Environ. Res. Public Health 2021, 18, 2098. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Yue, Y.; Qin, F.; Hai, L.; Yi, L.; Zhao, P.; Hao, L.; Shu, Y.; Zheng, Y.; Li, L. Carbon storage and carbon pool characteristics of Larix gmelinii forest in Daxing’anling, Inner Mongolia, China. Front. For. Glob. Change 2024, 7, 1419023. [Google Scholar] [CrossRef]
- Liu, X.; Trogisch, S.; He, J.S.; Niklaus, P.A.; Bruelheide, H.; Tang, Z.; Erfmeier, A.; Scherer-Lorenzen, M.; Pietsch, P.A.; Yang, B. Tree species richness increases ecosystem carbon storage in subtropical forests. Proc. R. Soc. B 2018, 285, 20181240. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Arnell, A.; Lamo, X.D.; García-Rangel, S.; Lewis, M.; Mark, J.; Merow, C.; Miles, L.; Ondo, L.; Pironon, S. Areas of global importance for conserving terrestrial biodiversity, carbon and water. Nat. Ecol. Evol. 2021, 5, 1499–1509. [Google Scholar] [CrossRef] [PubMed]
- Duncanson, L.; Liang, M.; Leitold, V.; Armston, J.; Krishna Moorthy, S.M.; Dubayah, R.; Costedoat, S.; Enquist, B.J.; Fatoyinbo, L.; Goetz, S.J. The effectiveness of global protected areas for climate change mitigation. Nat. Commun. 2023, 14, 2908. [Google Scholar] [CrossRef] [PubMed]




| Dominant Tree Species | Age Groups | BEF | R | D (t/m3) | CF |
|---|---|---|---|---|---|
| K. fortunei | Young forest | 1.667 | 0.277 | 0.448 | 0.500 |
| Middle-aged forest | 2.300 | 0.302 | |||
| Near-mature forest | 1.382 | 0.274 | |||
| Mature forest | 1.459 | 0.238 | |||
| Total value | 1.347 | 0.195 | |||
| P. armandii | Young forest | 1.785 | 0.170 | 0.396 | 0.523 |
| Middle-aged forest | 1.808 | 0.162 | |||
| Near-mature forest | 1.83 | 0.182 | |||
| Mature forest | 1.679 | 0.171 | |||
| Total value | 1.717 | 0.174 | |||
| P. yunnanensis | Young forest | 1.619 | 0.146 | 0.483 | 0.511 |
| Middle-aged forest | 1.837 | 0.143 | |||
| Near-mature forest | 1.333 | 0.238 | |||
| Mature forest | 1.585 | 0.190 | |||
| Total value | 1.585 | 0.202 | |||
| C. funebris | Young forest | 1.732 | 0.220 | 0.478 | 0.510 |
| Middle-aged forest | 1.847 | 0.218 | |||
| Near-mature forest | 1.497 | 0.233 | |||
| Mature forest | 1.233 | 0.329 | |||
| Total value | 1.535 | 0.365 | |||
| Quercus sp. | Young forest | 1.355 | 0.292 | 0.676 | 0.500 |
| Middle-aged forest | 1.380 | 0.260 | |||
| Near-mature forest | 1.327 | 0.275 | |||
| Mature forest | 1.360 | 0.410 | |||
| Total value | 1.587 | 0.153 | |||
| E. robusta | Young forest | 1.263 | 0.221 | 0.578 | 0.525 |
| Middle-aged forest | 1.297 | 0.219 | |||
| Near-mature forest | 1.178 | 0.221 | |||
| Mature forest | 1.165 | 0.181 | |||
| Total value | 1.151 | 0.226 | |||
| A. cremastogyne | Young forest | 1.424 | 0.248 | 0.541 | 0.491 |
| Middle-aged forest | 1.526 | 0.229 | |||
| Near-mature forest | 1.395 | 0.279 | |||
| Mature forest | 1.252 | 0.235 | |||
| Total value | 1.180 | 0.212 |
| Number | Dominant Tree Species (Group) | Biomass Estimation Model |
|---|---|---|
| 1 | K. fortunei | B = 0.4158V + 41.3318 |
| 2 | P. armandii | B = 0.5856V + 18.7435 |
| 3 | P. yunnanensis | B = 0.5101V + 1.0451 |
| 4 | C. funebris | B = 0.6129V + 46.1451 |
| 5 | Quercus sp. | B = 1.1453V + 8.5473 |
| 6 | E. robusta | B = 0.8873V + 4.5539 |
| 7 | A. cremastogyne | B = 1.0687V + 10.2370 |
| Number | Comparison of Methods | p-Value |
|---|---|---|
| 1 | variable biomass expansion factor method vs. biomass expansion factor method | 0.499 |
| 2 | variable biomass expansion factor method vs. volume conversion method | 0.176 |
| 3 | variable biomass expansion factor method vs. continuous function method of biomass conversion factor | 0.063 |
| 4 | biomass expansion factor method vs. volume conversion method | 0.310 |
| 5 | biomass expansion factor method vs. continuous function method of biomass conversion factor | 0.237 |
| 6 | volume conversion method vs. continuous function method of biomass conversion factor | 0.398 |
| Method | Variable Biomass Expansion Factor Method | Biomass Expansion Factor Method | Volume Conversion Method | Continuous Function Method of Biomass Conversion Factor |
|---|---|---|---|---|
| variable biomass expansion factor method | 1.000 | |||
| biomass expansion factor method | 1.000 ** | 1.000 | ||
| volume conversion method | 1.000 ** | 1.000 ** | 1.000 | |
| continuous function method of biomass conversion factor | 1.000 ** | 1.000 ** | 1.000 ** | 1.000 |
| Method | Advantages | Disadvantages |
|---|---|---|
| Variable biomass expansion factor method | Incorporates age-class-specific expansion factors, providing a closer representation of actual forest conditions. | Requires high data accuracy and involves complex calculations. |
| Biomass expansion factor method | Widely applicable across various spatial scales; parameters are readily accessible. | Relatively high data accuracy requirements; assumes a constant biomass-to-volume ratio. |
| Volume conversion method | Straightforward and efficient; parameters are explicit and easily obtainable; relatively high accuracy. | Applies a uniform conversion coefficient across all forest types; does not account for stand factors such as age class, which may introduce error. |
| Continuous function method of biomass conversion factor | Integrates stand structure and age dynamics; suitable for various forest types. | Parameter estimation for some tree species lacks sufficient sample support. |
| Forest Land Types | Area (hm2) | Carbon Storage (tC) | Proportion of Carbon Stock (%) | Carbon Density (t/hm2) |
|---|---|---|---|---|
| arbor forest | 14,447.58 | 672,599.83 | 99.30 | 46.55 |
| economic forest | 376.33 | 4191.94 | 0.62 | 11.14 |
| shrub forest | 56.37 | 523.52 | 0.08 | 9.29 |
| total | 14,880.28 | 677,315.29 | 100.00 | 45.52 |
| Forest Types | Carbon Stock Value (CNY 10,000) | Average Total Economic Value (CNY 10,000) | Value Proportion (%) | ||
|---|---|---|---|---|---|
| Market Value Method (27.76 CNY/tCO2e) | Optimal Price (19.02 CNY/tCO2e) | ||||
| arbor forests | K. fortune forest | 5.64 | 3.86 | 4.74 | 0.08 |
| P. armandii forest | 301.92 | 206.86 | 254.39 | 4.38 | |
| P. yunnanensis forest | 5991.35 | 4105.02 | 5048.18 | 86.90 | |
| C. funebris forest | 2.40 | 1.65 | 2.03 | 0.03 | |
| Quercus sp. forest | 478.70 | 327.99 | 403.34 | 6.94 | |
| E. robusta forest | 27.75 | 19.01 | 23.38 | 0.40 | |
| A. cremastogyne forest | 38.41 | 26.32 | 32.37 | 0.56 | |
| subtotal | 6846.17 | 4690.71 | 5768.44 | 99.30 | |
| economic forests | 42.67 | 29.23 | 35.95 | 0.62 | |
| shrub forests | 5.33 | 3.65 | 4.49 | 0.08 | |
| total | 6894.17 | 4723.60 | 5808.88 | 100 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, M.; Yang, S.; Chen, A.; Deng, Z. Research on Forest Carbon Sequestration and Its Economic Valuation: A Case Study of the Zixi Mountain Nature Reserve, Chuxiong Prefecture. Plants 2025, 14, 2746. https://doi.org/10.3390/plants14172746
Pu M, Yang S, Chen A, Deng Z. Research on Forest Carbon Sequestration and Its Economic Valuation: A Case Study of the Zixi Mountain Nature Reserve, Chuxiong Prefecture. Plants. 2025; 14(17):2746. https://doi.org/10.3390/plants14172746
Chicago/Turabian StylePu, Mengxue, Shaohui Yang, Aimei Chen, and Zhihua Deng. 2025. "Research on Forest Carbon Sequestration and Its Economic Valuation: A Case Study of the Zixi Mountain Nature Reserve, Chuxiong Prefecture" Plants 14, no. 17: 2746. https://doi.org/10.3390/plants14172746
APA StylePu, M., Yang, S., Chen, A., & Deng, Z. (2025). Research on Forest Carbon Sequestration and Its Economic Valuation: A Case Study of the Zixi Mountain Nature Reserve, Chuxiong Prefecture. Plants, 14(17), 2746. https://doi.org/10.3390/plants14172746







