Predicting Heterosis and Selecting Superior Families and Individuals in Fraxinus spp. Based on Growth Traits and Genetic Distance Coupling
Abstract
1. Introduction
2. Results
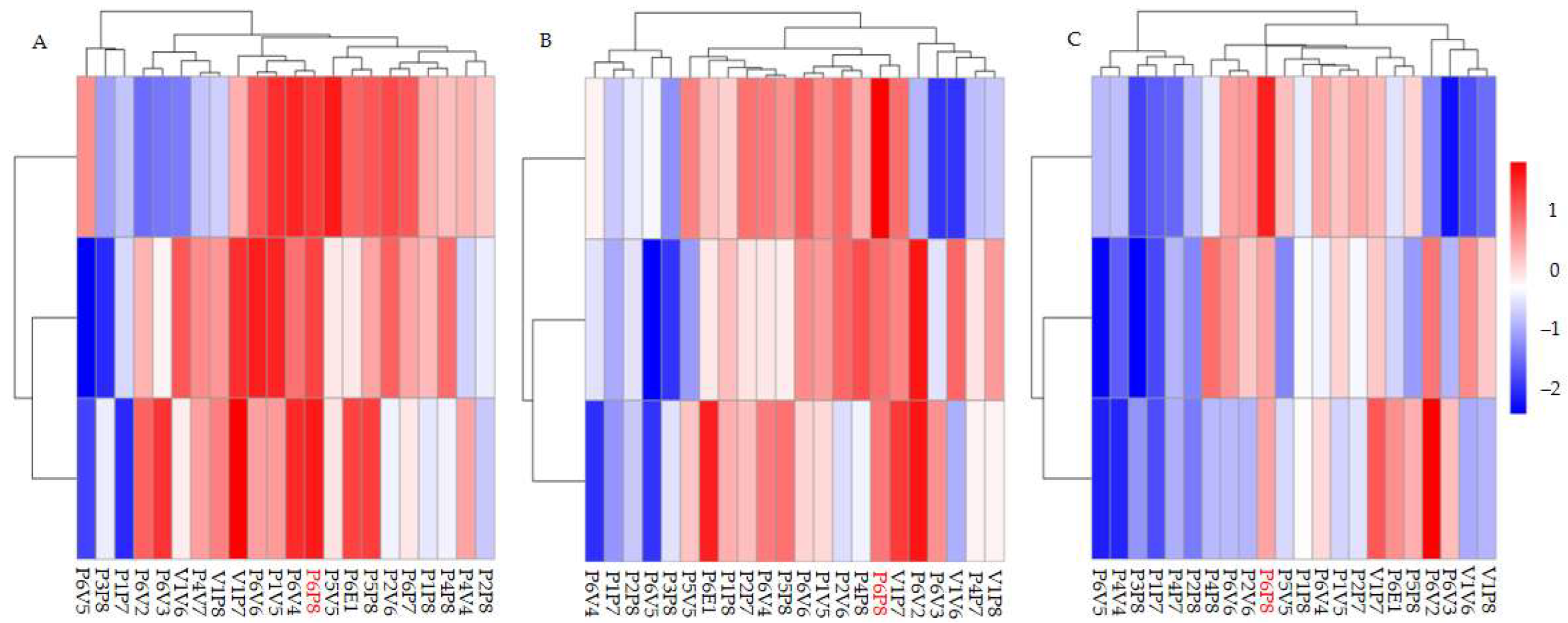
2.1. Genetic Variation in Growth Traits Among Full-Sib Fraxinus Families
2.2. Analysis of Genetic Correlation Among Fraxinus Parents
2.3. Analysis of Heterosis and Combining Ability for Growth Traits Among Fraxinus Families
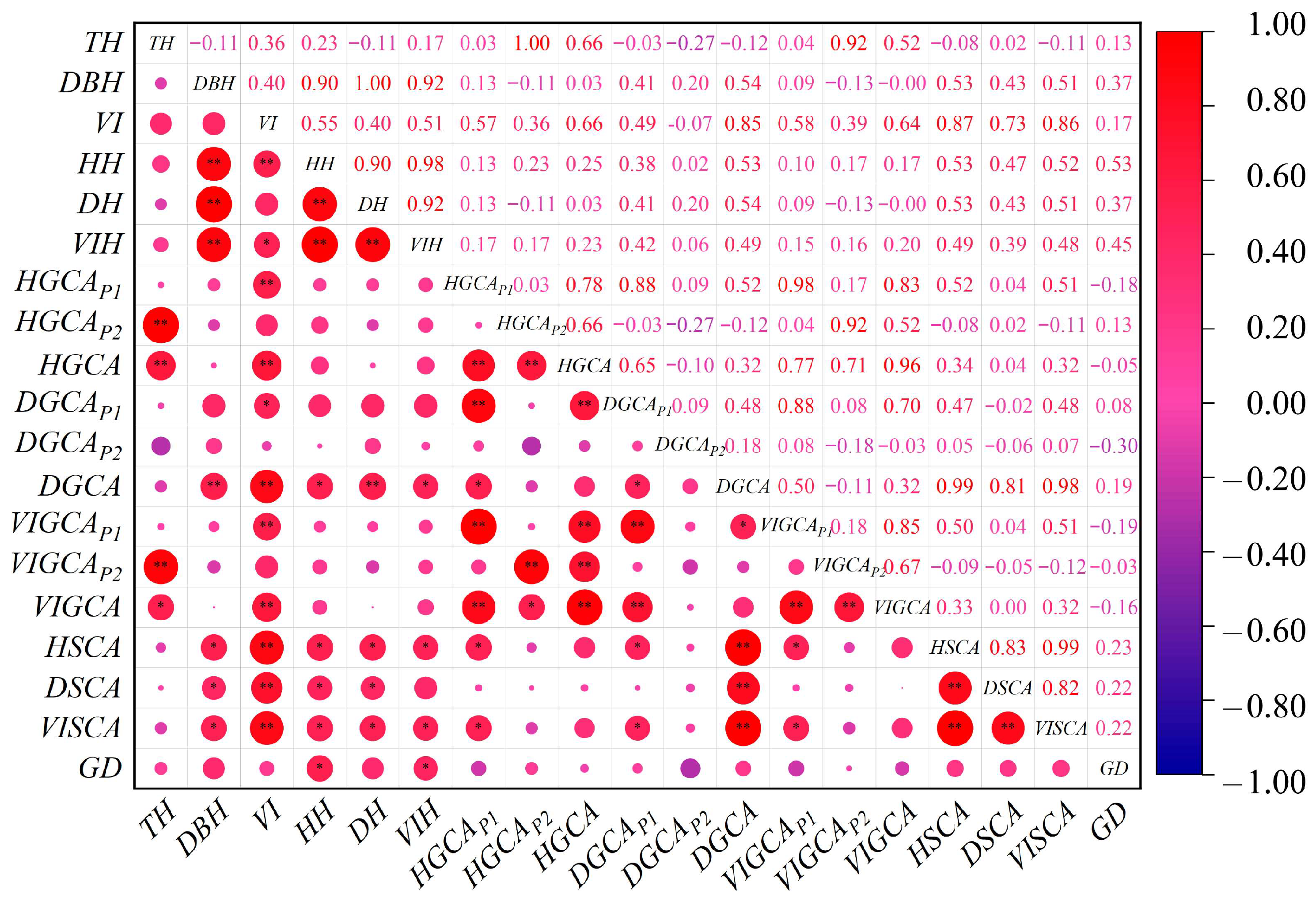
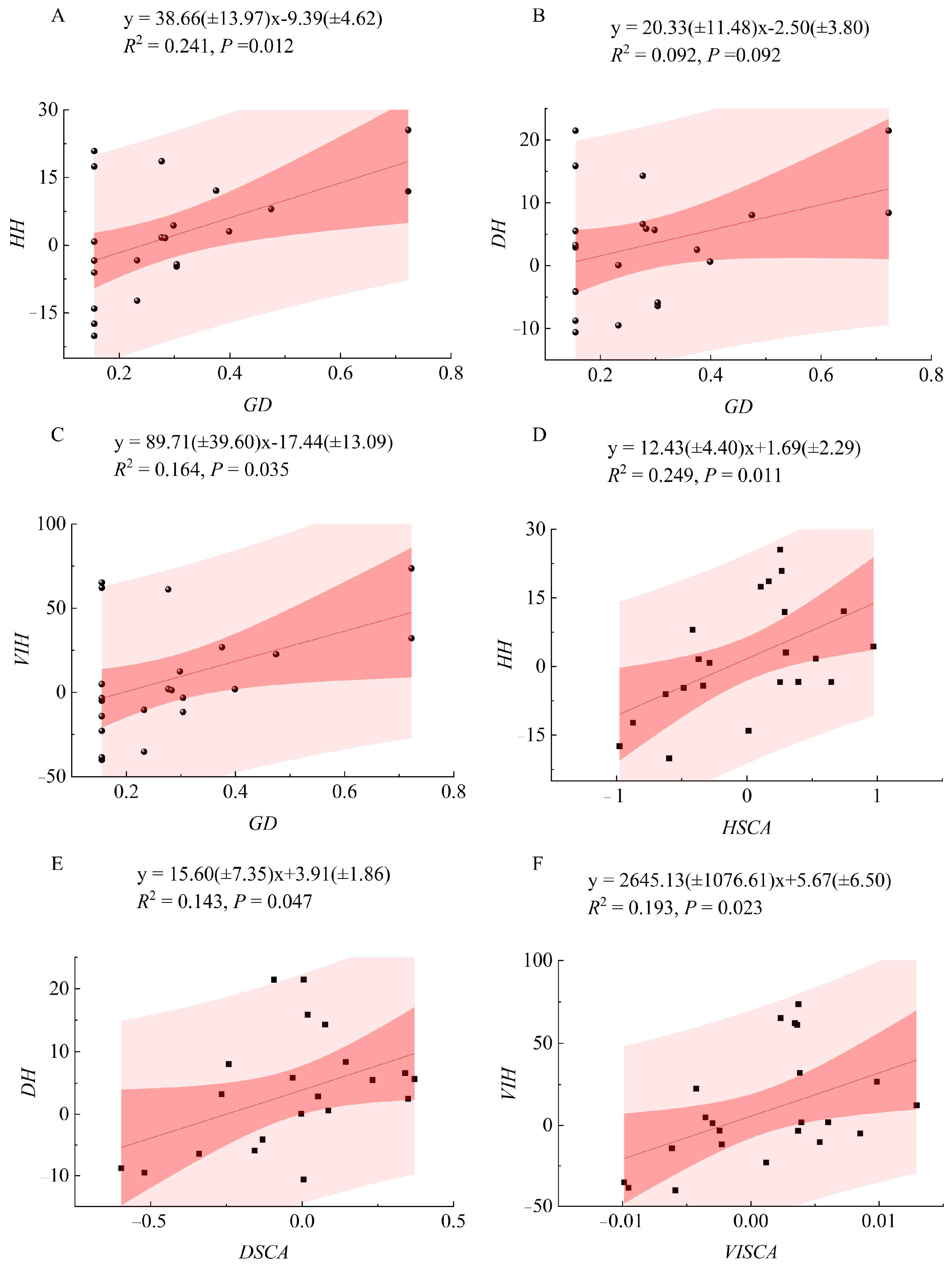
2.4. Correlation and Regression Analysis
2.5. Selection of Superior Families and Elite Individuals in Fraxinus
3. Discussion
4. Materials and Methods
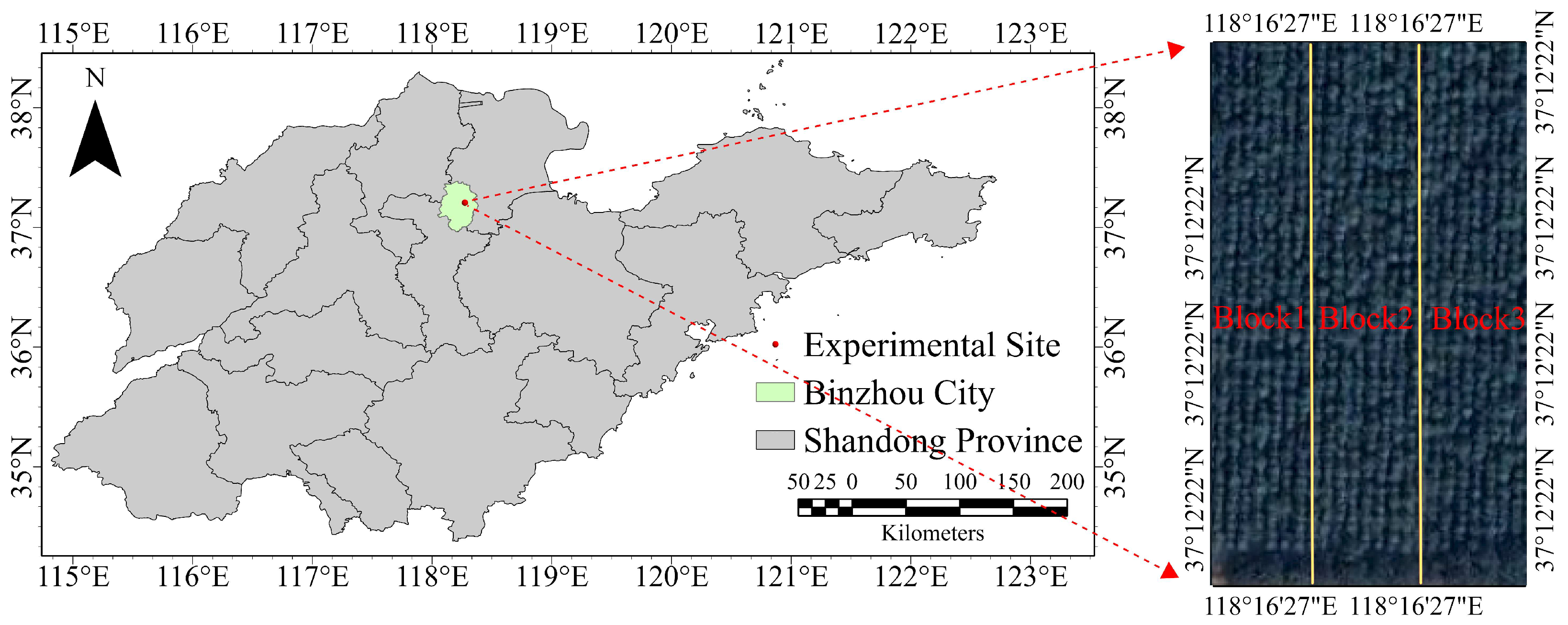
4.1. Test Materials
4.2. Growth Trait Measurements
4.3. DNA Extraction and SSR Analysis
4.4. Data Processing
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, E.; Wang, Y.; Liu, K.; Liu, Y.; Xu, C.; Dong, W.; Zhang, Z. Historical climate change and vicariance events contributed to the intercontinental disjunct distribution pattern of ash species (Fraxinus, Oleaceae). Commun. Biol. 2024, 7, 603. [Google Scholar] [CrossRef]
- Huff, M.; Seaman, J.; Wu, D.; Zhebentyayeva, T.; Kelly, L.J.; Faridi, N.; Nelson, C.D.; Cooper, E.; Best, T.; Steiner, K.; et al. A high-quality reference genome for Fraxinus pennsylvanica for ash species restoration and research. Mol. Ecol. Resour. 2022, 22, 1284–1302. [Google Scholar] [CrossRef] [PubMed]
- Wallander, E. Systematics and floral evolution in Fraxinus (Oleaceae). Belg. Dendrologie Belge 2012, 2012, 39–58. [Google Scholar]
- Sollars, E.S.; Harper, A.L.; Kelly, L.J.; Sambles, C.M.; Ramirez-Gonzalez, R.H.; Swarbreck, D.; Kaithakottil, G.; Cooper, E.D.; Uauy, C.; Havlickova, L.; et al. Genome sequence and genetic diversity of European ash trees. Nature 2017, 541, 212–216. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.N.; Yan, L.; Chai, Z.; Liang, Q.; Dong, Y.H.; Wang, C.X.; Li, X.C.; Li, C.Y.; Mu, Y.T.; Gong, A.D.; et al. Pan-genome analyses of 11 Fraxinus species provide insights into salt adaptation in ash trees. Plant Commun. 2024, 6, 101137. [Google Scholar] [CrossRef] [PubMed]
- Mao, P.; Tang, Q.; Cao, B.; Liu, J.; Shao, H.; Cao, Z.; Hao, M.; Zhu, Z. Eco-physiological adaptability in mixtures of Robinia pseudoacacia and Fraxinus velutina and coastal eco-engineering. Ecol. Eng. 2017, 106, 109–115. [Google Scholar] [CrossRef]
- Liu, H. Under siege: Ash management in the wake of the emerald ash borer. J. Integr. Pest Manag. 2018, 9, 5. [Google Scholar] [CrossRef]
- Abhainn, E.A.; Shirley, D.L.; Stanley, R.K.; Scarpato, T.; Koch, J.L.; Romero-Severson, J. Gene flow from Fraxinus cultivars into natural stands of Fraxinus pennsylvanica occurs range-wide, is regionally extensive, and is associated with a loss of allele richness. PLoS ONE 2024, 19, e0294829. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Wang, M.; Yang, Y.; Wang, Y.; Nie, Q.; Liang, F.; Qin, H.; Zhang, Z. The chromosome-level genome assembly of Fraxinus americana provides insights into the evolution of Oleaceae plants. Int. J. Biol. Macromol. 2023, 253, 127132. [Google Scholar] [CrossRef]
- Plumb, W.J.; Kelly, L.J.; Mullender, J.; Powell, R.F.; Csiba, L.; Nemesio-Gorriz, M.; Carey, D.; Mason, M.E.; Crowther, W.; Koch, J.; et al. Preliminary genetic barcodes for ash (Fraxinus) species and generation of new wide hybrids. Plants People Planet 2025, 1–14. [Google Scholar] [CrossRef]
- Zhu, Z.; Qi, F.H.; Yan, C.F.; Zhan, Y.G. Sexually different morphological, physiological and molecular responses of Fraxinus mandshurica flowers to floral development and chilling stress. Plant Physiol. Biochem. 2016, 99, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Xue, G.; Liu, F.Z.; Gong, X.L. Immunosuppressive effect of extracts from leaves of Fraxinus mandshurica Rupr. Bioengineered 2017, 8, 212–216. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.K.; Jin, J.M. China Plant Red Data Book—Rare and Endangered Plants, Volume 1; Science Press: Beijing, China, 1992. [Google Scholar]
- Diao, S.; Geng, Y.D. Efficiency evaluation and nonlinear multi-objective optimization of forestry industry transformation in the Heilongjiang state-owned forest region. Sci. Rep. 2023, 13, 21216. [Google Scholar] [CrossRef]
- Yang, W.; Min, Z.; Yang, M.X.; Yan, J. Exploration of the implementation of carbon neutralization in the field of natural resources under the background of sustainable development—An overview. Int. J. Environ. Res. Public Health 2022, 19, 14109. [Google Scholar] [CrossRef] [PubMed]
- Moll, R.H.; Lonnquist, J.H.; Fortuno, J.V.; Johnson, E.C. The Relationship of heterosis and genetic divergence in Maize. Genetics 1965, 52, 139–144. [Google Scholar] [CrossRef]
- Wang, B.B.; Hou, M.; Shi, J.P.; Ku, L.X.; Song, W.; Li, C.H.; Ning, Q.; Li, X.; Li, C.Y.; Zhao, B.B.; et al. De novo genome assembly and analyses of 12 founder inbred lines provide insights into maize heterosis. Nat. Genet. 2023, 55, 312–323. [Google Scholar] [CrossRef]
- Lu, H.; Chen, M.J.; Fu, M.; Yan, J.L.; Su, W.L.; Zhan, Y.G.; Zeng, F.S. Brassinosteroids affect wood development and properties of Fraxinus mandshurica. Front. Plant Sci. 2023, 14, 1167548. [Google Scholar] [CrossRef]
- Al-Ahmad, H. Biotechnology for bioenergy dedicated trees: Meeting future energy demands. Z. Naturforsch. C. J. Biosci. 2018, 73, 15–32. [Google Scholar] [CrossRef]
- Alix, K.; Gérard, P.R.; Schwarzacher, T.; Heslop-Harrison, J.S.P. Polyploidy and interspecific hybridization: Partners for adaptation, speciation and evolution in plants. Ann. Bot. 2017, 120, 183–194. [Google Scholar] [CrossRef]
- Zeng, F.S.; Li, L.L.; Liang, N.S.; Wang, X.; Li, X.; Zhan, Y.G. Salt tolerance and alterations in cytosine methylation in the interspecific hybrids of Fraxinus velutina and Fraxinus mandshurica. Euphytica 2015, 205, 721–737. [Google Scholar] [CrossRef]
- Zeng, F.S.; Zhou, S.; Zhan, Y.G.; Dong, J. Drought resistance and DNA methylation of interspecific hybrids between Fraxinus mandshurica and Fraxinus americana. Trees 2014, 28, 1679–1692. [Google Scholar] [CrossRef]
- He, Z.; Zhan, Y.; Zeng, F.; Zhao, X.T.; Wang, X. Drought physiology and gene expression characteristics of fraxinus interspecific hybrids. Plant Growth Regul. 2016, 78, 179–193. [Google Scholar] [CrossRef]
- Gu, Z.; Han, B. Unlocking the mystery of heterosis opens the era of intelligent rice breeding. Plant Physiol. 2024, 196, 735–744. [Google Scholar] [CrossRef]
- Guo, T.; Guo, M.; Li, C.; Wang, Z.; Zheng, W.; Xu, J.; Zhao, X.; Wang, X. Combination scale, variety selection probability and parental selection of soybean crossbreeding. Heilongjiang Agric. Sci. 2024, 4, 1–10. (In Chinese) [Google Scholar]
- Reddy, B.V.S.; Ramesh, S.; Reddy, P.S.; Ramaiah, B. Combining ability and heterosis as influenced by male-sterility inducing cytoplasms in sorghum [Sorghum bicolor(L.) Moench]. Euphytica 2007, 154, 153–164. [Google Scholar] [CrossRef]
- Rodríguez-Llanes, Y.; Pérez-Brito, D.; Guzmán-Antonio, A.; Mijangos-Cortés, J.O.; Iglesias-Andreu, L.G.; Canto- Flick, A.; Avilés-Viñas, S.A.; Pijeira-Fernández, G.; Santana-Buzzy, N. Combining ability, heterosis, and heterobeltiosis to select highly productive F1 hybrids of habanero pepper (Capsicum chinense Jacq.). Plant Genet. Res. 2023, 21, 1–11. [Google Scholar] [CrossRef]
- Chen, J.X.; Zhou, H.; Xie, W.B.; Xia, D.; Gao, G.J.; Zhang, Q.L.; Wang, G.W.; Lian, X.M.; Xiao, J.H.; He, Y.Q. Genome-wide association analyses reveal the genetic basis of combining ability in rice. Plant Biotechnol. J. 2019, 17, 2211–2222. [Google Scholar] [CrossRef]
- Muneera Parveen, A.B.; Muthupandi, M.; Kumar, N.; Chauhan, S.S.; Vellaichamy, P.; Senthamilselvam, S.; Rajasugunasekar, D.; Nagarajan, B.; Mayavel, A.; Bachpai, V.K.W.; et al. Quantitative genetic analysis of wood property traits in bipa rental population of Eucalyptus camaldulensis × E. tereticornis. J. Genet. 2021, 100, 46. [Google Scholar] [CrossRef]
- Vázquez-González, C.; López-Goldar, X.; Alía, R.; Bustingorri, G.; José, L.F.; Lema, M.; Mata, R.; Sampedro, L.; Touza, R.; Zas, R. Genetic variation in resin yield and covariation with tree growth in maritime pine. For. Ecol. Manag. 2021, 482, 118843. [Google Scholar] [CrossRef]
- Yousaf, M.F.; Tomar, V.; Romé, H.; Bagge, M.; Timmermann, M.; Chu, T.T.; Jensen, J. Rate of double reduction and genetic variability in yield, quality, and senescence related traits in tetraploid potato (Solanum tuberosum L.). Front. Plant Sci. 2025, 16, 1560123. [Google Scholar] [CrossRef]
- Gedil, M.; Menkir, A. An integrated molecular and conventional breeding scheme for enhancing genetic gain in maize in Africa. Front. Plant Sci. 2019, 10, 1430. [Google Scholar] [CrossRef]
- Charcosset, A.; Lefort-Buson, M.; Gallais, A. Relationship between heterosis and heterozygosity at marker loci: A theoretical computation. Theor. Appl. Genet. 1991, 81, 571–575. [Google Scholar] [CrossRef]
- Sun, X.P.; Jiao, C.; Schwaninger, H.D.; Chao, C.T.; Ma, Y.M.; Duan, N.B.; Khan, A.; Ban, S.; Xu, K.N.; Cheng, L.L.; et al. Phased diploid genome assemblies and pan-genomes provide insights into the genetic history of apple domestication. Nat. Genet. 2020, 52, 1423–1432. [Google Scholar] [CrossRef]
- Li, M.; Shi, J.S.; Gan, S.M.; He, Z.X.; Li, L.; Yi, N.J. Correlation between RAPD-based parental genetic distance and filial performance of Chinese fir. For. Res. 2001, 14, 35–40. (In Chinese) [Google Scholar]
- Kopp, R.F.; Smart, L.B.; Maynard, C.A.; Tuskan, G.A.; Abrahamson, L.P. Predicting within family variability in juvenile height growth of Salix based upon similarity among parental AFLP fingerprints. Theor. Appl. Genet. 2002, 105, 106–112. [Google Scholar] [CrossRef]
- Legarra, A.; Gonzalez-Dieguez, D.O.; Charcosset, A.; Vitezica, Z.G. Impact of interpopulation distance on dominance variance and average heterosis in hybrid populations within species. Genetics 2023, 224, iyad059. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.; Liu, H.; Wang, H.; Lu, Z.; Wang, Y.; Mullan, D.; Hamblin, J.; Liu, C. Accelerated generation of selfed pure line plants for gene identification and crop breeding. Front. Plant Sci. 2017, 8, 1786. [Google Scholar] [CrossRef]
- Keller, B.; Soto, J.; Steier, A.; Portilla-Benavides, A.E.; Raatz, B.; Studer, B.; Walter, A.; Muller, O.; Urban, M.O. Linking photosynthesis and yield reveals a strategy to improve light use efficiency in a climbing bean breeding population. J. Exp. Bot. 2024, 75, 901–916. [Google Scholar] [CrossRef] [PubMed]
- Watson, A.; Ghosh, S.; Williams, M.J.; Cuddy, W.S.; Simmonds, J.; Rey, M.D.; Asyraf Md Hatta, M.; Hinchliffe, A.; Steed, A.; Reynolds, D.; et al. Speed breeding is a powerful tool to accelerate crop research and breeding. Nat. Plants 2018, 4, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Zhao, Y.; Zhang, Y.; Wang, R.; Li, X.; Liu, Z.; Wang, W.; Zhu, S.; Fan, Y.; Xu, L.; et al. Insights into the genomic divergence of maize heterotic groups in China. J. Integr. Plant Biol. 2025, 67, 1467–1486. [Google Scholar] [CrossRef]
- Zhu, Z.D. Forest Tree Genetics Foundation; Forestry Publishing House: Beijing, China, 1989; pp. 190–191. [Google Scholar]
- Kang, X.Y. On conventional and unconventional tree breeding and their relationships. J. Beijing For. Univ. 2023, 48, 1–7. (In Chinese) [Google Scholar]
- Delpierre, N.; Guillemot, J.; Dufrêne, E.; Cecchini, S.; Nicolas, M. Tree phenological ranks repeat from year to year and correlate with growth in temperate deciduous forests. Agric. For. Meteorol. 2017, 234, 1–10. [Google Scholar] [CrossRef]
- Rizvi, R.H.; Gupta, V.K.; Gurunathan, N.; Datta, A. Age-age correlation models for early selection of Azadirachta indica provenances planted in semi-arid region. Indian J. Agrofor. 2012, 14, 1–5. [Google Scholar]
- Mwase, W.F.; Savill, P.S.; Hemery, G. Genetic parameter estimates for growth and form traits in common ash (Fraxinus excelsior L.) in a breeding seedling orchard at Little Wittenham in England. New For. 2008, 36, 225–238. [Google Scholar] [CrossRef]
- Fu, M.; Liang, R.; Wang, P.; Feng, Q.; Li, C.; Xin, Y.; Zhan, Y.; Zeng, F. Evaluation and selection of superior Fraxinus mandshurica families for genetic improvement using growth traits, morphological characteristics, and wood properties. Euphytica 2025, 221, 86. [Google Scholar] [CrossRef]
- Wei, X.; Chen, M.J.; Zhang, Q.; Gong, J.Y.; Liu, J.; Yong, K.C.; Wang, Q.; Fan, J.J.; Chen, S.H.; Hua, H.; et al. Genomic investigation of 18,421 lines reveals the genetic architecture of rice. Science 2024, 385, eadm8762. [Google Scholar] [CrossRef]
- Weng, Y.; Ford, R.; Tong, Z.; Krasowski, M. Genetic parameters for bole straightness and branch angle in jack pine estimated using linear and generalized linear mixed models. For. Sci. 2017, 63, 111–117. [Google Scholar] [CrossRef]
- Hochholdinger, F.; Yu, P. Molecular concepts to explain heterosis in crops. Trends Plant Sci. 2025, 30, 95–104. [Google Scholar] [CrossRef]
- Ene, C.O.; Ogbonna, P.E.; Agbo, C.U.; Chuakwudi, U.P. Heterosis and combining ability in cucumber (Cucumis sativus L.). Inf. Process. Agric. 2019, 6, 150–157. [Google Scholar] [CrossRef]
- Rahimi, M.; Rabiei, B.; Samizadeh, H.; Ghasemi, A.K. Combining ability and heterosis in rice (Oryza sativa L.) cultivars. J. Agric. Sci. Technol. 2010, 12, 223–231. [Google Scholar]
- Han, Y.Y.; Wang, K.Y.; Liu, Z.Q.; Pan, S.H.; Zhao, X.Y.; Zhang, Q.; Wang, S.F. Research on hybrid crop breeding information management system based on combining ability analysis. Sustainability 2020, 12, 4938. [Google Scholar] [CrossRef]
- Yu, K.C.; Wang, H.; Liu, X.G.; Xu, C.; Li, Z.W.; Xu, X.J.; Liu, J.C.; Wang, Z.H.; Xu, Y.B. Large-scale analysis of combining ability and heterosis for development of hybrid maize breeding strategies using diverse germplasm resources. Front. Plant Sci. 2020, 11, 660. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.Y.; Wang, K.L.; Xie, Y.H.; Wang, A.N.; Zhong, H.Q.; Yao, X.H.; Lin, P. Combining ability from complete diallel design of Camellia oleifera: Implications for the utility of GCA and SCA in oil-related traits breeding. Ind. Crops Prod. 2023, 205, 117434. [Google Scholar] [CrossRef]
- Bai, F.Y.; Kang, N.; Zhang, P.D.; Kang, X.Y. Selection of female parents with high fertility and high combining abilities for cross-breeding Populus tomentosa. J. For. Res. 2019, 30, 445–450. [Google Scholar] [CrossRef]
- Josue, A.D.L.; Brewbaker, J.L. Diallel analysis of grain filling rate and grain filling period in tropical maize (Zea mays L.). Euphytica 2018, 214, 39. [Google Scholar] [CrossRef]
- Ulmakanth, A.V.; Datil, I.V.; Rani, C.; Gadalch, C.R.; Kumar, C.C.; Ran, C.C.; Kotarthana, T.V. Comhininn ahility and hataro-cir ouar anuironmante for ctalk and cunar ralatad traite in cua et sorghum (Sorghum bicolor (L) Moench). Sugar Technol. 2012, 14, 237–246. [Google Scholar]
- Chai, J.Y.; Wang, K.L.; Yao, X.H.; Teng, J.H.; Lin, P. Genetic analysis of the fruit and oil related traits on hybrid offspring of nested mating of camellia oleifera. For. Res. 2023, 36, 1–10. (In Chinese) [Google Scholar]
- Zhang, Q.; Gao, Y.J.; Yang, S.H.; Ragab, R.A.; Maroof, M.A.; Li, Z.B. A diallel analysis of heterosis in elite hybrid rice based on RFLP and microsatellite. Theor. Appl. Genet. 1994, 89, 185–192. [Google Scholar] [CrossRef]
- Li, S.W.; Zhang, Z.Y.; Yu, Z.S.; He, C.Z.; An, X.M.; Li, B.L. Correlation between molecular genetic distances among parents and growth traits of progenies in Populus. For. Res. 2008, 44, 150–154. (In Chinese) [Google Scholar]
- Zhang, Y.; Yang, Q.; Zhou, Z.C.; Jin, G.Q. Divergence among masson pine parents revealed by geographical origins and SSR markers and their relationships with progeny performance. New For. 2013, 44, 341–355. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhao, F.C.; Wu, H.S.; Zhang, Y.Z.; Li, F.M.; Zhong, S.Y.; Li, X.Z.; Cai, J. Relationship between growth traits heterosis and genetic distance among parents of Pinus elliottii × P. caribaea based on SSR molecular markers. For. Res. 2012, 25, 138–143. (In Chinese) [Google Scholar]
- Akaogu, I.C.; Badu-Apraku, B.; Adetimirin, V.O.; Vroh-Bi, I.; Oyekunle, M.; Akinwale, R.O. Genetic diversity assessment of extra-early maturing yellow maize inbreds and hybrid performance in Striga-infested and Striga-free environments. J. Agric. Sci. 2013, 151, 519–537. [Google Scholar] [CrossRef]
- Nyaligwa, L.; Hussein, S.; Amelework, B.; Ghebrehiwot, H. Genetic diversity analysis of elite maize inbred lines of diverse sources using SSR markers. Maydica 2015, 60, M29. [Google Scholar]
- Sserumaga, J.P.; Ji, H.; Njoroge, K.; Muthomi, J.; Chemining’wa, G.; Si-myung, L.; Kim, H.; Asea, G.; Makumbi, D. Molecular characterization of tropical maize inbred lines using microsatellite DNA markers. Maydica 2014, 59, 267–274. [Google Scholar]
- Moriguchi, Y.; Yamazaki, Y.; Taira, H.; Tsumura, Y. Mating patterns in an indoor miniature Cryptomeria japonica seed orchard as revealed by microsatellite markers. New For. 2010, 39, 261–273. [Google Scholar] [CrossRef]
- Arcade, A.; Faivre-rampant, P.; Le Guerroue, B.; Pâques, L.E.; Prat, D. Heterozygosity and hybrid performance in larch. Theor. Appl. Genet. 1996, 93, 1274–1281. [Google Scholar] [CrossRef] [PubMed]
- He, J.W.; Jiang, H.; Yang, H.; Su, D.; Liu, Y.X. Relationship between SSR genetic distance and heterosis in hot pepper. Agric. Sci. Technol. 2013, 14, 1224–1227. [Google Scholar]
- Singh, S.; Gupta, S.K. Formation of heterotic pools and understanding relationship between molecular divergence and heterosis in pearl millet [Pennisetum glaucum (L.) R. Br.]. PLoS ONE 2019, 14, e0207463. [Google Scholar] [CrossRef]
- Napolitano, M.; Terzaroli, N.; Kashyap, S.; Russi, L.; Jones-Evans, E.; Albertini, E. Exploring Heterosis in Melon (Cucumis melo L.). Plants 2020, 9, 282. [Google Scholar] [CrossRef]
- Gupta, S.K.; Nepolean, T.; Shaikh, C.G.; Rai, K.; Hash, C.T.; Das, R.R.; Rathore, A. Phenotypic and molecular diversity-based prediction of heterosis in pearl millet (Pennisetum glaucum L. (R.) Br.). The Crop J. 2018, 6, 271–281. [Google Scholar] [CrossRef]
- Tian, H.Y.; Channa, S.A.; Hu, S.W. Relationships between genetic distance, combining ability and heterosis in rapeseed (Brassica napus L.). Euphytica 2016, 213, 1. [Google Scholar] [CrossRef]
- Snehi, S.; Prakash, N.R.; Pant, U.; Singh, P.K.; Kumar, S.; Jeena, A.S.; Bhajan, R. Prediction of heterotic combinations using correlation between genetic distance, heterosis and combining ability in yellow sarson (Brassica rapa var. yellow sarson Prain). Vegetos 2024, 37, 1552–1564. [Google Scholar] [CrossRef]
- Ali, M.; Copeland, L.O.; Elias, S.G.; Kelly, J.D. Relationship between genetic distance and heterosis for yield and morphological traits in winter canola (Brassica napus L.). Theor. Appl. Genet. 1995, 91, 118–121. [Google Scholar] [CrossRef]
- Wang, S.H. Effects of Different Amendments on Salt Removal and Organic Matter Enhancement of Saline-Alkali Soil in the Yellow River Delta. Master’s Thesis, Nanjing Agricultural University, Nanjing, China, 2021. (In Chinese). [Google Scholar]
- Ding, H.; Zheng, T.; Liang, D.; Qu, G. A simple and efficient method of DNA extraction from different plant samples. Bull. Bot. Res. 2015, 35, 457–461. (In Chinese) [Google Scholar]
- Yan, L.P.; Wu, D.J.; Mao, X.H.; Yao, J.X.; Ren, F.; Li, S.W.; Wang, K.F.; Wang, Y.H.; Liu, C.L. Construction of core collection of Fraxinus based on SSR molecular markers. J. Cent. South Univ. For. Technol. 2019, 39, 1–9. (In Chinese) [Google Scholar]
- Dong, H.Y.; Liu, Q.H.; Zhou, Z.C.; Jin, G.Q.; Shen, D.Y.; Song, X.H. Correlation between heterosis in the growth of progeny and combining ability and genetic distance of the parents for Pinus massoniana. For. Res. 2017, 53, 65–75. (In Chinese) [Google Scholar]
- Xu, J.R. Trees Quantitative Genetics; Higher Education Press: Beijing, China, 2006; pp. 42–43. [Google Scholar]
- Mohamed, L.M.; Mimoun, M.; Peter, J.M.; Eric, N.J.; Ouafae, B. Morphological variability, heritability and correlation studies within an argan tree population (Argania spinosa (L.) Skeels) preserved in situ. Int. J. Agric. For. 2017, 7, 42–51. [Google Scholar]
- Liu, Z.B.; Jiang, J.B.; Ren, A.; Xu, X.Y.; Zhang, H.; Zhao, T.T.; Jiang, X.M.; Sun, Y.G.; Li, J.F.; Yang, H.H. Heterosis and combining ability analysis of fruit yield, early maturity, and quality in tomato. Agronomy 2021, 11, 807. [Google Scholar] [CrossRef]
- Wang, M.X. Forest Tree Genetic Breeding; China Forestry Publishing House: Beijing, China, 2001. [Google Scholar]
| Traits | σF2 (%) | σBF2 (%) | σE2 (%) | PCV (%) | GCV (%) | FH | SH |
|---|---|---|---|---|---|---|---|
| TH | 6.49 ** | 3.71 | 81.36 | 4.34 | 5.10 | 0.724 | 0.284 |
| DBH | 21.70 ** | 2.38 | 320.87 | 6.62 | 7.43 | 0.793 | 0.252 |
| VI | 0.00279 ** | 0.00022 | 0.03603 | 16.04 | 17.73 | 0.818 | 0.286 |
| Family | TH (m) | DBH (cm) | VI (m3) | Family | TH (m) | DBH (cm) | VI (m3) |
|---|---|---|---|---|---|---|---|
| P1P7 | 5.29 ± 0.82 | 6.24 ± 1.26 | 0.02240 ± 0.01 | P5V5 | 5.98 ± 0.83 | 6.96 ± 1.91 | 0.03249 ± 0.02 |
| P1P8 | 5.78 ± 1.15 | 7.17 ± 1.97 | 0.03409 ± 0.02 | P6E1 | 5.89 ± 0.94 | 7.12 ± 1.74 | 0.03325 ± 0.02 |
| P1V5 | 6.26 ± 0.69 | 7.30 ± 1.52 | 0.03571 ± 0.02 | P6P8 | 6.35 ± 0.70 | 8.00 ± 1.91 | 0.04419 ± 0.02 |
| P2P7 | 5.96 ± 1.00 | 7.26 ± 1.92 | 0.03557 ± 0.02 | P6V2 | 5.63 ± 1.08 | 7.53 ± 2.63 | 0.03888 ± 0.03 |
| P2P8 | 5.62 ± 0.91 | 6.54 ± 1.73 | 0.02717 ± 0.02 | P6V3 | 5.64 ± 1.30 | 6.47 ± 1.98 | 0.02833 ± 0.02 |
| P2V6 | 6.03 ± 0.85 | 7.34 ± 1.84 | 0.03617 ± 0.02 | P6V4 | 6.30 ± 0.86 | 7.38 ± 1.57 | 0.03715 ± 0.02 |
| P3P8 | 5.25 ± 0.87 | 6.06 ± 1.57 | 0.02191 ± 0.01 | P6V5 | 5.31 ± 1.16 | 5.86 ± 1.86 | 0.02206 ± 0.02 |
| P4P7 | 5.79 ± 0.73 | 6.71 ± 1.10 | 0.02732 ± 0.01 | P6V6 | 6.22 ± 0.96 | 7.47 ± 1.89 | 0.03859 ± 0.02 |
| P4P8 | 5.84 ± 1.06 | 7.26 ± 1.89 | 0.03505 ± 0.02 | V1P7 | 6.26 ± 0.85 | 7.81 ± 1.86 | 0.04178 ± 0.02 |
| P4V4 | 5.85 ± 0.88 | 6.64 ± 1.46 | 0.02778 ± 0.01 | V1P8 | 5.84 ± 0.81 | 6.91 ± 1.78 | 0.03122 ± 0.02 |
| P5P8 | 6.16 ± 0.60 | 7.58 ± 2.15 | 0.03850 ± 0.03 | V1V6 | 5.64 ± 1.31 | 6.43 ± 2.45 | 0.03000 ± 0.03 |
| Average of 22 families | 5.87 ± 0.97 | 7.04 ± 1.86 | 0.03293 ± 0.02 | ||||
| Marker | Number of Alleles (Na) | Effective Number of Alleles (Ne) | Polymorphic Information Content (PIC) | Observed Heterozygosity (Ho) | Expected Heterozygosity (He) | Nei’s Gene Diversity Index (h) | Shannon’s Information Index (I) |
|---|---|---|---|---|---|---|---|
| SSR 82 | 2.000 | 1.276 | 0.325 | 0.214 | 0.178 | 0.357 | 0.326 |
| SSR 93 | 2.667 | 2.118 | 0.535 | 0.548 | 0.410 | 0.580 | 0.716 |
| SSR 95 | 2.333 | 2.051 | 0.507 | 0.381 | 0.433 | 0.549 | 0.683 |
| SSR 112 | 2.000 | 1.518 | 0.294 | 0.437 | 0.317 | 0.331 | 0.485 |
| SSR 120 | 2.667 | 2.190 | 0.512 | 0.667 | 0.407 | 0.592 | 0.704 |
| SSR 144 | 2.333 | 2.222 | 0.421 | 1.000 | 0.542 | 0.531 | 0.809 |
| SSR 147 | 2.000 | 1.756 | 0.260 | 0.333 | 0.333 | 0.287 | 0.534 |
| SSR 167 | 1.667 | 1.649 | 0.342 | 0.167 | 0.329 | 0.380 | 0.457 |
| SSR 186 | 2.667 | 2.200 | 0.549 | 0.833 | 0.514 | 0.611 | 0.833 |
| SSR 187 | 2.667 | 2.200 | 0.549 | 0.833 | 0.514 | 0.611 | 0.833 |
| SSR 202 | 3.333 | 2.493 | 0.670 | 0.833 | 0.553 | 0.718 | 0.962 |
| SSR 203 | 3.333 | 2.517 | 0.646 | 0.944 | 0.585 | 0.696 | 0.981 |
| SSR 208 | 2.000 | 1.616 | 0.232 | 0.222 | 0.259 | 0.242 | 0.442 |
| SSR 213 | 2.333 | 1.871 | 0.330 | 0.389 | 0.370 | 0.347 | 0.621 |
| Mean | 2.429 | 1.977 | 0.441 | 0.557 | 0.410 | 0.488 | 0.670 |
| Serial Number | Family | GD | Serial Number | Family | GD |
|---|---|---|---|---|---|
| 1 | P6V5 | 0.155 | 12 | P1P7 | 0.277 |
| 2 | P5V5 | 0.155 | 13 | P2P7 | 0.277 |
| 3 | P3P8 | 0.155 | 14 | P6V3 | 0.283 |
| 4 | P1V5 | 0.155 | 15 | V1V6 | 0.298 |
| 5 | P6P8 | 0.155 | 16 | P6V6 | 0.304 |
| 6 | P1P8 | 0.155 | 17 | P2V6 | 0.304 |
| 7 | P2P8 | 0.155 | 18 | V1P8 | 0.375 |
| 8 | P4P8 | 0.155 | 19 | P6V2 | 0.399 |
| 9 | P5P8 | 0.155 | 20 | V1P7 | 0.475 |
| 10 | P6V4 | 0.233 | 21 | P6E1 | 0.723 |
| 11 | P4V4 | 0.233 | 22 | P4P7 | 0.723 |
| Average of 22 families | 0.286 | ||||
| Family | Heterosis Degree (HH) (%) | Heterosis Degree (DH) (%) | Heterosis Degree (VIH) (%) | Family | Heterosis Degree (HH) (%) | Heterosis Degree (DH) (%) | Heterosis Degree (VIH) (%) |
|---|---|---|---|---|---|---|---|
| P1P7 | −12.32 | −9.51 | −35.21 | P5V5 | 17.46 | 21.45 | 62.15 |
| P1P8 | 3.04 | 0.62 | 1.96 | P6E1 | −3.38 | 0.08 | −10.40 |
| P1V5 | 1.71 | 6.60 | 1.99 | P6P8 | 4.36 | 5.66 | 12.39 |
| P2P7 | 18.62 | 14.3 | 61.13 | P6V2 | 0.78 | −4.09 | 4.87 |
| P2P8 | 8.02 | 8.04 | 22.60 | P6V3 | −14.07 | −4.17 | −22.88 |
| P2V6 | 20.87 | 15.87 | 65.21 | P6V4 | −3.40 | 5.52 | −4.99 |
| P3P8 | −17.41 | −10.61 | −38.61 | P6V5 | −20.10 | −8.77 | −40.11 |
| P4P7 | 1.60 | 5.87 | 1.30 | P6V6 | −3.44 | 2.88 | −3.32 |
| P4P8 | 11.91 | 8.37 | 32.12 | V1P7 | 12.09 | 2.51 | 26.81 |
| P4V4 | −6.07 | 3.26 | −14.20 | V1P8 | −4.20 | −5.88 | −11.66 |
| P5P8 | 25.53 | 21.46 | 73.67 | V1V6 | −4.70 | −6.41 | −3.24 |
| Average of 22 families | 1.68 | 3.32 | 8.25 | ||||
| Family | TH | DBH | VI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GCAP1 | GCAP2 | GCA | SCA | GCAP1 | GCAP2 | GCA | SCA | GCAP1 | GCAP2 | GCA | SCA | |
| P1P7 | −0.01 | 0.17 | 0.16 | −0.87 | −0.04 | 0.01 | −0.87 | −0.52 | −0.0012 | 0.0012 | 0.0000 | −0.0099 |
| P1P8 | −0.01 | 0.10 | 0.09 | 0.30 | −0.04 | −0.01 | 0.29 | 0.09 | −0.0012 | 0.0004 | −0.0008 | 0.0039 |
| P1V5 | −0.01 | −0.22 | −0.24 | 0.53 | −0.04 | 0.09 | 0.62 | 0.34 | −0.0012 | −0.0017 | −0.0029 | 0.0060 |
| P2P7 | 0.16 | 0.17 | 0.33 | 0.17 | 0.05 | 0.01 | 0.17 | 0.08 | 0.0010 | 0.0012 | 0.0022 | 0.0036 |
| P2P8 | −0.25 | 0.10 | −0.15 | −0.42 | 0.05 | −0.01 | −0.42 | −0.24 | −0.0039 | 0.0004 | −0.0035 | −0.0043 |
| P2V6 | 0.16 | 0.21 | 0.37 | 0.27 | 0.05 | 0.15 | 0.41 | 0.02 | 0.0010 | 0.0034 | 0.0044 | 0.0023 |
| P3P8 | −0.89 | 0.10 | −0.79 | −0.98 | −0.60 | −0.01 | −0.98 | 0.01 | −0.0103 | 0.0004 | −0.0099 | −0.0095 |
| P4P7 | −0.25 | 0.08 | −0.17 | −0.37 | −0.10 | 0.03 | −0.34 | −0.03 | −0.0039 | −0.0011 | −0.005 | −0.0030 |
| P4P8 | −0.25 | 0.10 | −0.15 | 0.29 | −0.10 | −0.01 | 0.28 | 0.14 | −0.0039 | 0.0004 | −0.0035 | 0.0038 |
| P4V4 | −0.25 | −0.18 | −0.42 | −0.62 | −0.10 | 0.13 | −0.50 | −0.27 | −0.0039 | −0.0021 | −0.006 | −0.0062 |
| P5P8 | 0.11 | 0.10 | 0.21 | 0.26 | 0.26 | −0.01 | 0.25 | 0.01 | 0.0017 | 0.0004 | 0.0021 | 0.0037 |
| P5V5 | 0.11 | −0.22 | −0.12 | 0.11 | 0.26 | 0.09 | 0.20 | −0.09 | 0.0017 | −0.0017 | 0.0001 | 0.0034 |
| P6E1 | 0.29 | 0.08 | 0.37 | 0.39 | 0.13 | 0.03 | 0.43 | 0.00 | 0.0035 | −0.0011 | 0.0024 | 0.0054 |
| P6P8 | 0.29 | 0.10 | 0.39 | 0.97 | 0.13 | −0.01 | 0.97 | 0.37 | 0.0035 | 0.0004 | 0.0039 | 0.0129 |
| P6V2 | 0.29 | 0.78 | 1.07 | −0.29 | 0.13 | −0.09 | −0.38 | −0.13 | 0.0035 | 0.0091 | 0.0127 | −0.0035 |
| P6V3 | 0.29 | −0.37 | −0.08 | 0.01 | 0.13 | −0.10 | −0.08 | −0.13 | 0.0035 | −0.0019 | 0.0016 | 0.0012 |
| P6V4 | 0.29 | −0.18 | 0.11 | 0.65 | 0.13 | 0.13 | 0.77 | 0.23 | 0.0035 | −0.0021 | 0.0014 | 0.0085 |
| P6V5 | 0.29 | −0.22 | 0.06 | −0.60 | 0.13 | 0.09 | −0.50 | −0.60 | 0.0035 | −0.0017 | 0.0019 | −0.0059 |
| P6V6 | 0.29 | 0.21 | 0.5 | 0.25 | 0.13 | 0.15 | 0.40 | 0.05 | 0.0035 | 0.0034 | 0.0069 | 0.0037 |
| V1P7 | 0.12 | 0.17 | 0.29 | 0.74 | 0.09 | 0.01 | 0.75 | 0.35 | 0.0022 | 0.0012 | 0.0034 | 0.0098 |
| V1P8 | 0.12 | 0.10 | 0.22 | −0.34 | 0.09 | −0.01 | −0.34 | −0.16 | 0.0022 | 0.0004 | 0.0026 | −0.0023 |
| V1V6 | 0.12 | 0.21 | 0.34 | −0.48 | 0.09 | 0.15 | −0.34 | −0.34 | 0.0022 | 0.0034 | 0.0056 | −0.0024 |
| Mean | 0.05 | 0.06 | 0.11 | 0.00 | 0.04 | 0.04 | 0.04 | −0.04 | 0.0003 | 0.0006 | 0.0009 | 0.0010 |
| Serial Number | Family | Qi | ΔGH-TH (%) | ΔGH-DBH (%) | ΔGH-VI (%) |
|---|---|---|---|---|---|
| 1 | P6P8 | 1.732 | 1.81 | 2.22 | 6.98 |
| 2 | V1P7 | 1.706 | 1.32 | −1.24 | 0.29 |
| 3 | P5P8 | 1.670 | 4.15 | 9.84 | 24.57 |
| 4 | P6V6 | 1.670 | 1.85 | 2.38 | 8.00 |
| 5 | P6V4 | 1.660 | 1.83 | 2.40 | 8.31 |
| 6 | P1V5 | 1.646 | −5.02 | −7.43 | −19.81 |
| 7 | P6V2 | 1.645 | 2.05 | 2.36 | 7.94 |
| 8 | P2V6 | 1.639 | 2.57 | 6.20 | 17.31 |
| 9 | P2P7 | 1.629 | 2.60 | 6.27 | 17.60 |
| 10 | P4P8 | 1.619 | −8.50 | −10.90 | −27.84 |
| 11 | P1P8 | 1.606 | −5.44 | −7.57 | −20.76 |
| 12 | P6E1 | 1.604 | 1.95 | 2.49 | 9.28 |
| 13 | P5V5 | 1.596 | 4.27 | 10.71 | 29.11 |
| 14 | V1P8 | 1.578 | 1.42 | −1.41 | 0.39 |
| 15 | P4V4 | 1.543 | −8.49 | −11.92 | −35.12 |
| 16 | V1V6 | 1.540 | 1.47 | −1.51 | 0.40 |
| 17 | P4P7 | 1.539 | −8.58 | −11.80 | −35.71 |
| 18 | P6V3 | 1.529 | 2.04 | 2.74 | 10.89 |
| 19 | P2P8 | 1.523 | 2.76 | 6.96 | 23.04 |
| 20 | P1P7 | 1.457 | −5.94 | −8.70 | −31.59 |
| 21 | P3P8 | 1.442 | −5.66 | −6.77 | −15.59 |
| 22 | P6V5 | 1.438 | 2.17 | 3.03 | 13.99 |
| Serial Number | Block | Family | Qi | ΔGh-TH (%) | ΔGh-DBH (%) | ΔGh-VI (%) |
|---|---|---|---|---|---|---|
| 1 | 3 | P5P8 | 1.704 | 4.48 | 4.73 | 6.69 |
| 2 | 2 | P6P8 | 1.634 | 1.56 | 1.49 | 2.94 |
| 3 | 2 | V1P8 | 1.633 | 1.09 | −0.84 | 0.12 |
| 4 | 1 | P2V6 | 1.612 | 1.94 | 4.25 | 6.83 |
| 5 | 1 | P6P8 | 1.608 | 1.64 | 1.48 | 3.06 |
| 6 | 3 | V1P7 | 1.601 | 1.15 | −0.84 | 0.13 |
| 7 | 2 | P6V6 | 1.594 | 1.44 | 1.71 | 3.57 |
| 8 | 2 | P5V5 | 1.593 | 3.60 | 6.42 | 9.90 |
| 9 | 2 | V1V6 | 1.577 | 1.16 | −0.86 | 0.13 |
| 10 | 1 | P6V4 | 1.574 | 1.53 | 1.66 | 3.59 |
| 11 | 1 | P2P7 | 1.571 | 2.18 | 4.06 | 7.03 |
| Family | Female Parent | Male Parent | Family | Female Parent | Male Parent |
|---|---|---|---|---|---|
| P1P7 | F. pennsylvanica ‘Hong 1’ | F. pennsylvanica ‘Jinguan’ | P5V5 | F. pennsylvanica ‘Hong 5’ | F. velutina ‘J30’ |
| P1P8 | F. pennsylvanica ‘Hong 1’ | F. pennsylvanica ‘Lula 5’ | P6E1 | F. pennsylvanica ‘Lula 6’ | F. excelsior ‘Jinzhi’ |
| P1V5 | F. pennsylvanica ‘Hong 1’ | F. velutina ‘J30’ | P6P8 | F. pennsylvanica ‘Lula 6’ | F. pennsylvanica ‘Lula 5’ |
| P2P7 | F. pennsylvanica ‘Hong 2’ | F. pennsylvanica ‘Jinguan’ | P6V2 | F. pennsylvanica ‘Lula 6’ | F. velutina ‘J16’ |
| P2P8 | F. pennsylvanica ‘Hong 2’ | F. pennsylvanica ‘Lula 5’ | P6V3 | F. pennsylvanica ‘Lula 6’ | F. velutina ‘J19’ |
| P2V6 | F. pennsylvanica ‘Hong 2’ | F. velutina ‘J31’ | P6V4 | F. pennsylvanica ‘Lula 6’ | F. velutina ‘J29’ |
| P3P8 | F. pennsylvanica ‘Hong 3’ | F. pennsylvanica ‘Lula 5’ | P6V5 | F. pennsylvanica ‘Lula 6’ | F. velutina ‘J30’ |
| P4P7 | F. pennsylvanica ‘Hong 4’ | F. pennsylvanica ‘Jinguan’ | P6V6 | F. pennsylvanica ‘Lula 6’ | F. velutina ‘J31’ |
| P4P8 | F. pennsylvanica ‘Hong 4’ | F. pennsylvanica ‘Lula 5’ | V1P7 | F. velutina ‘Qingbi’ | F. pennsylvanica ‘Jinguan’ |
| P4V4 | F. pennsylvanica ‘Hong 4’ | F. velutina ‘J29’ | V1P8 | F. velutina ‘Qingbi’ | F. pennsylvanica ‘Lula 5’ |
| P5P8 | F. pennsylvanica ‘Hong 5’ | F. pennsylvanica ‘Lula 5’ | V1V6 | F. velutina ‘Qingbi’ | F. velutina ‘J31’ |
| Family | Number of Trees | Survival Rate (%) | Family | Number of Trees | Survival Rate (%) |
|---|---|---|---|---|---|
| P1P7 | 57 | 95.00 | P5V5 | 57 | 95.00 |
| P1P8 | 59 | 98.33 | P6E1 | 59 | 98.33 |
| P1V5 | 58 | 96.67 | P6P8 | 58 | 96.67 |
| P2P7 | 59 | 98.33 | P6V2 | 59 | 98.33 |
| P2P8 | 56 | 93.33 | P6V3 | 56 | 93.33 |
| P2V6 | 58 | 96.67 | P6V4 | 58 | 96.67 |
| P3P8 | 55 | 91.67 | P6V5 | 55 | 91.67 |
| P4P7 | 60 | 100.00 | P6V6 | 60 | 100.00 |
| P4P8 | 56 | 93.33 | V1P7 | 56 | 93.33 |
| P4V4 | 60 | 100.00 | V1P8 | 60 | 100.00 |
| P5P8 | 54 | 90.00 | V1V6 | 54 | 90.00 |
| Number | Parameter/Model | Formula |
|---|---|---|
| 1 | Volume index [79] | VI = TH × DBH2 |
| 2 | Linear model [80] | Xijk = μ + Fi + Bj + FBij + eijk |
| 3 | Coefficient of variation [81] | |
| 4 | ||
| 5 | Heritability [82] | H2 = σF2/(σF2 + σFB2/B + σe2/NB) |
| 6 | h2 = 4σF2/(σF2 + σFB2 + σe2) | |
| 7 | Genetic gain [42] | ΔGH = H2S/X |
| 8 | ΔGh = h2S/X | |
| 9 | Heterosis [82] | H = (Fi − )/ × 100% |
| 10 | Combining ability [83] | GCAP1i = P1i − |
| 11 | GCAP2j = P2j − | |
| 12 | GCAij = GCAP1i + GCAP2j | |
| 13 | SCAij = ij − − GCAi − GCAj | |
| 14 | Comprehensive evaluation [83] | ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Gao, C.; Liu, C.; Wang, Y.; Liu, N.; Zhang, X.; Liu, F. Predicting Heterosis and Selecting Superior Families and Individuals in Fraxinus spp. Based on Growth Traits and Genetic Distance Coupling. Plants 2025, 14, 2601. https://doi.org/10.3390/plants14162601
Yan L, Gao C, Liu C, Wang Y, Liu N, Zhang X, Liu F. Predicting Heterosis and Selecting Superior Families and Individuals in Fraxinus spp. Based on Growth Traits and Genetic Distance Coupling. Plants. 2025; 14(16):2601. https://doi.org/10.3390/plants14162601
Chicago/Turabian StyleYan, Liping, Chengcheng Gao, Chenggong Liu, Yinhua Wang, Ning Liu, Xueli Zhang, and Fenfen Liu. 2025. "Predicting Heterosis and Selecting Superior Families and Individuals in Fraxinus spp. Based on Growth Traits and Genetic Distance Coupling" Plants 14, no. 16: 2601. https://doi.org/10.3390/plants14162601
APA StyleYan, L., Gao, C., Liu, C., Wang, Y., Liu, N., Zhang, X., & Liu, F. (2025). Predicting Heterosis and Selecting Superior Families and Individuals in Fraxinus spp. Based on Growth Traits and Genetic Distance Coupling. Plants, 14(16), 2601. https://doi.org/10.3390/plants14162601






