Prediction Model of Powdery Mildew Disease Index in Rubber Trees Based on Machine Learning
Abstract
1. Introduction
2. Results
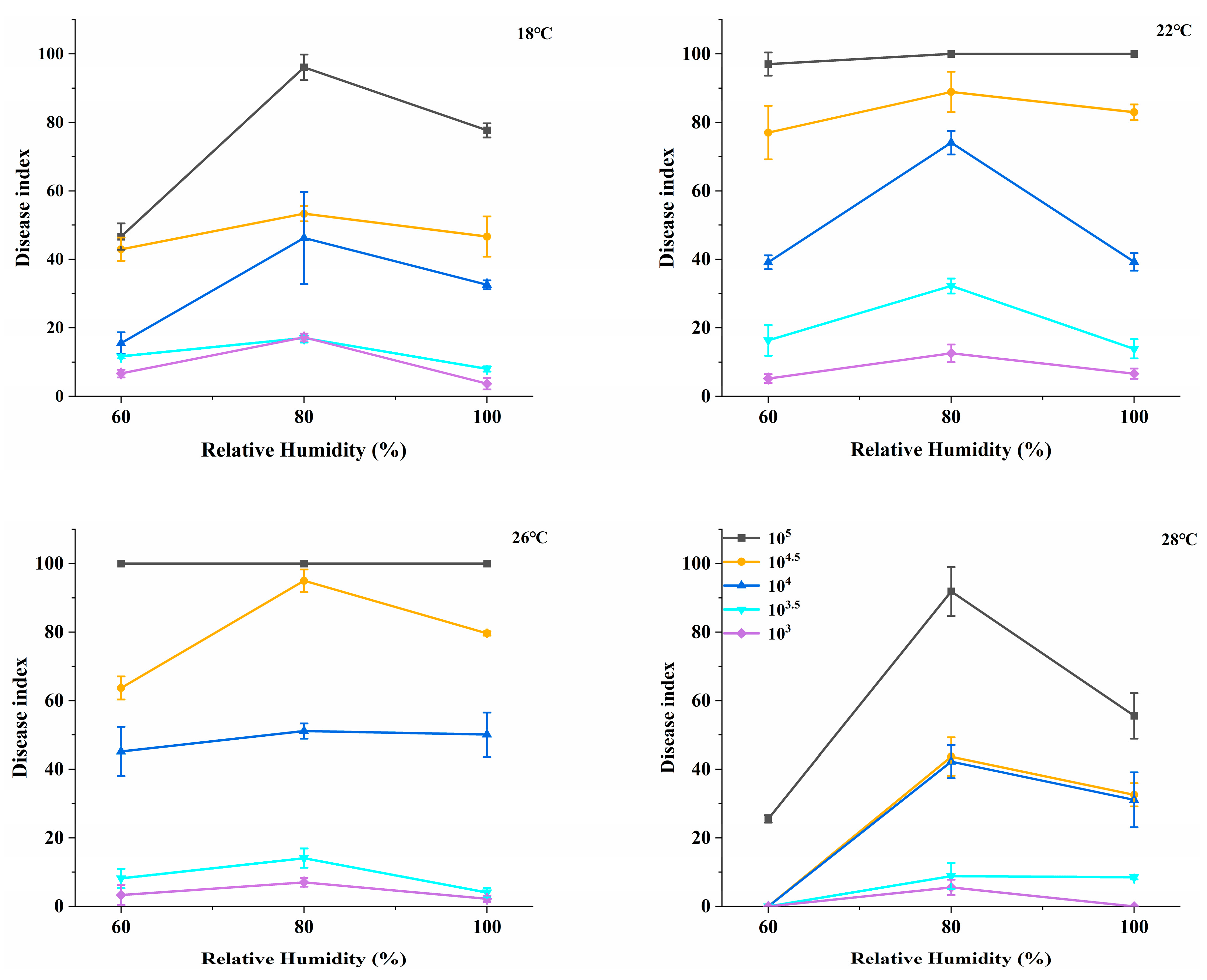
2.1. The Impact of Humidity on the Disease Index
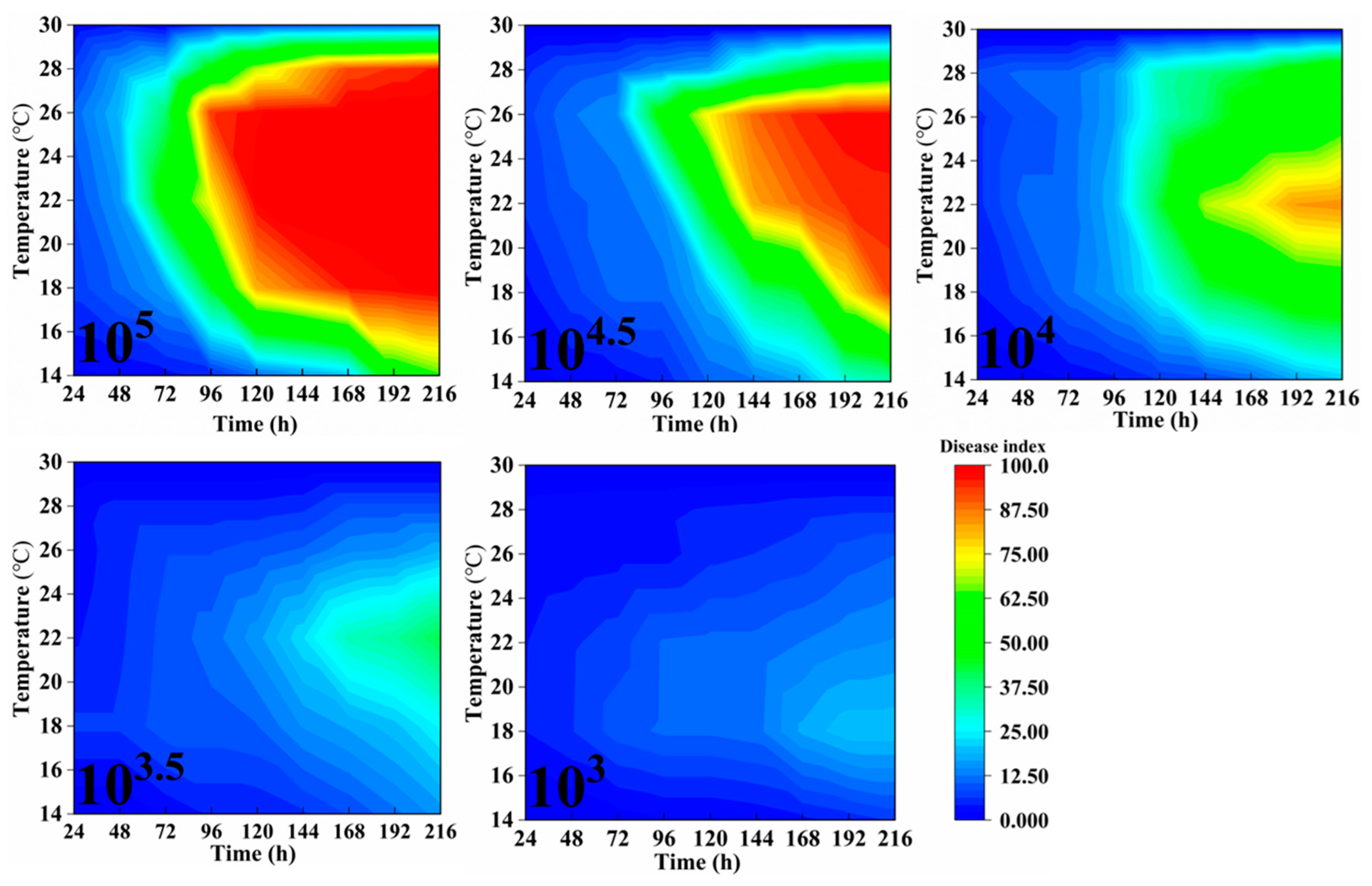
2.2. The Influence of Spore Concentration, Temperature, Humidity, and Inoculation Timing on the Disease Index of Powdery Mildew in Rubber Trees
2.3. The Correlations Between Spore Concentration, Temperature and Humidity, Infection Time and Disease Index
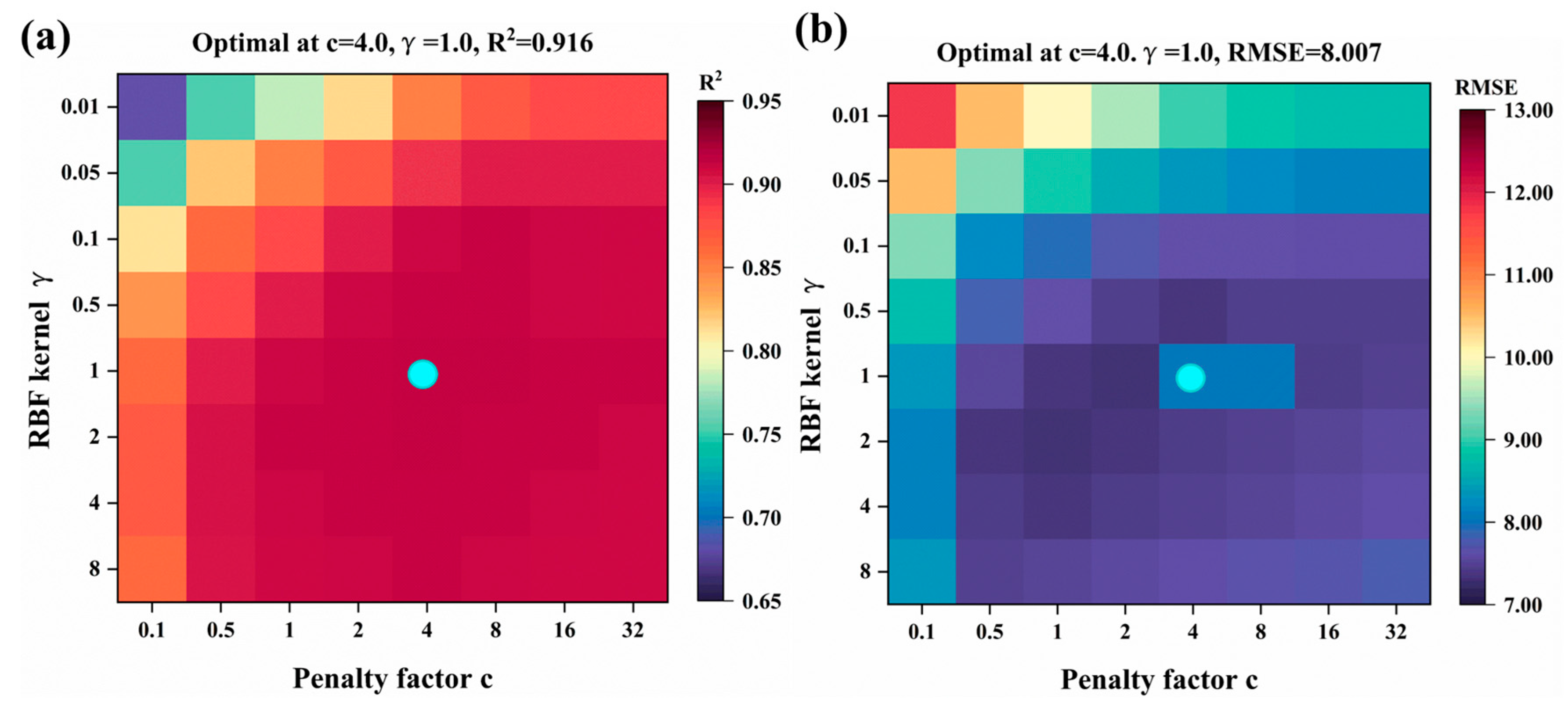
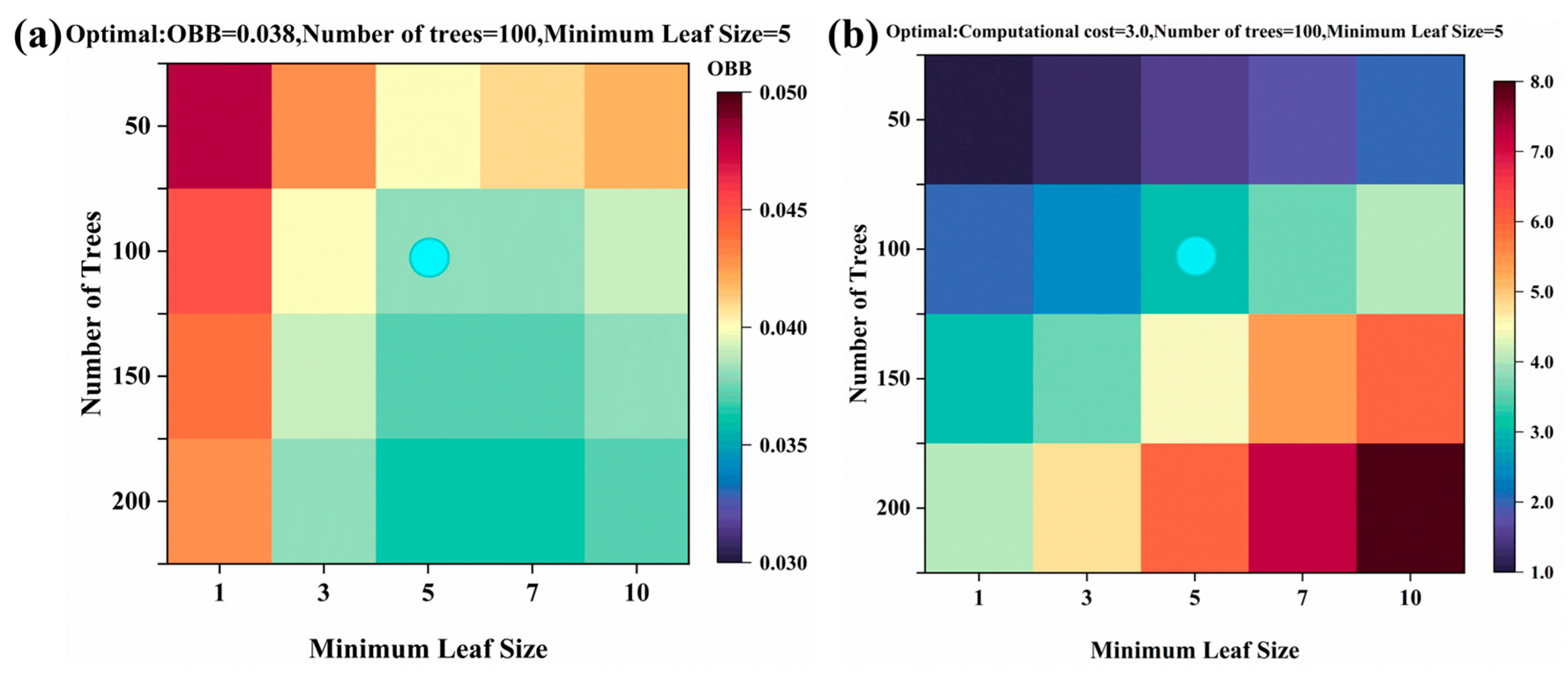
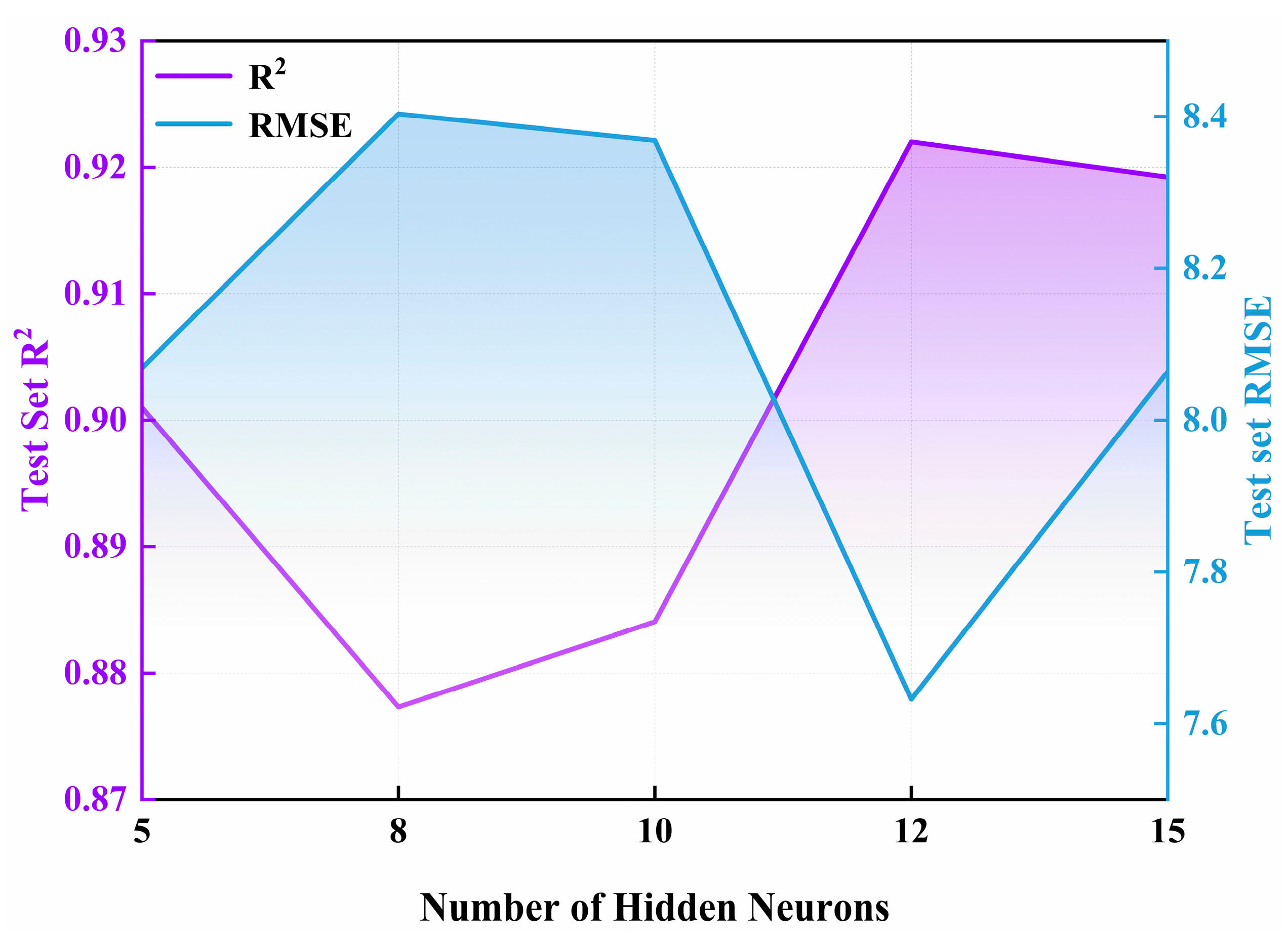
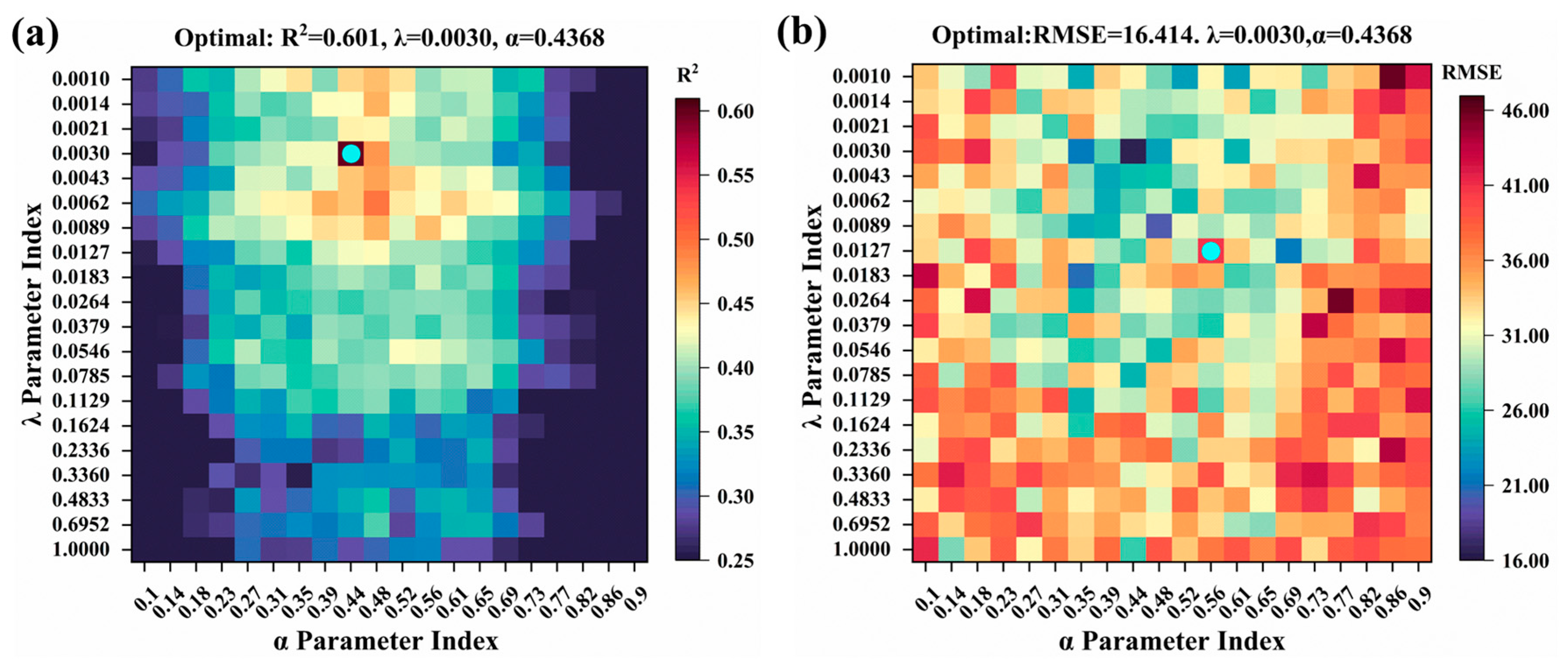
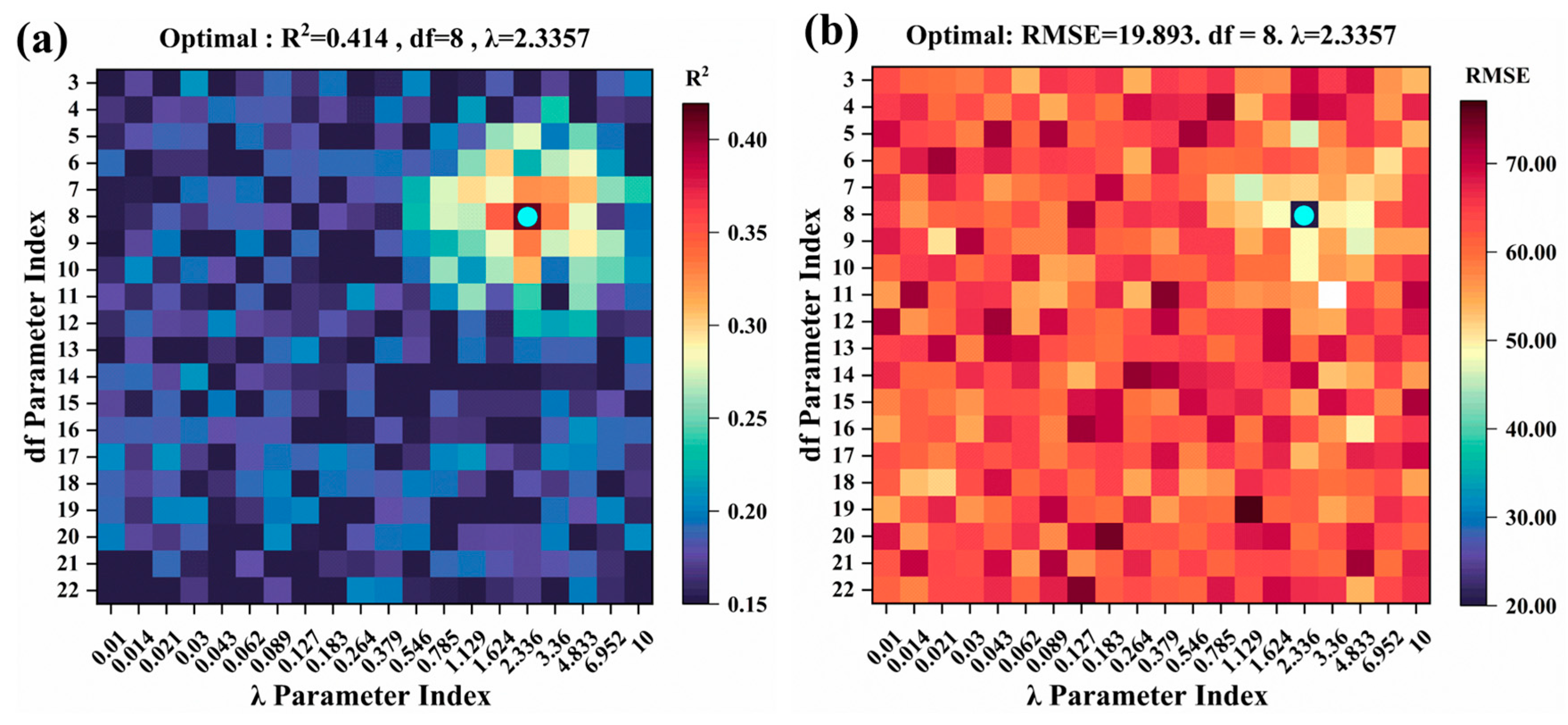
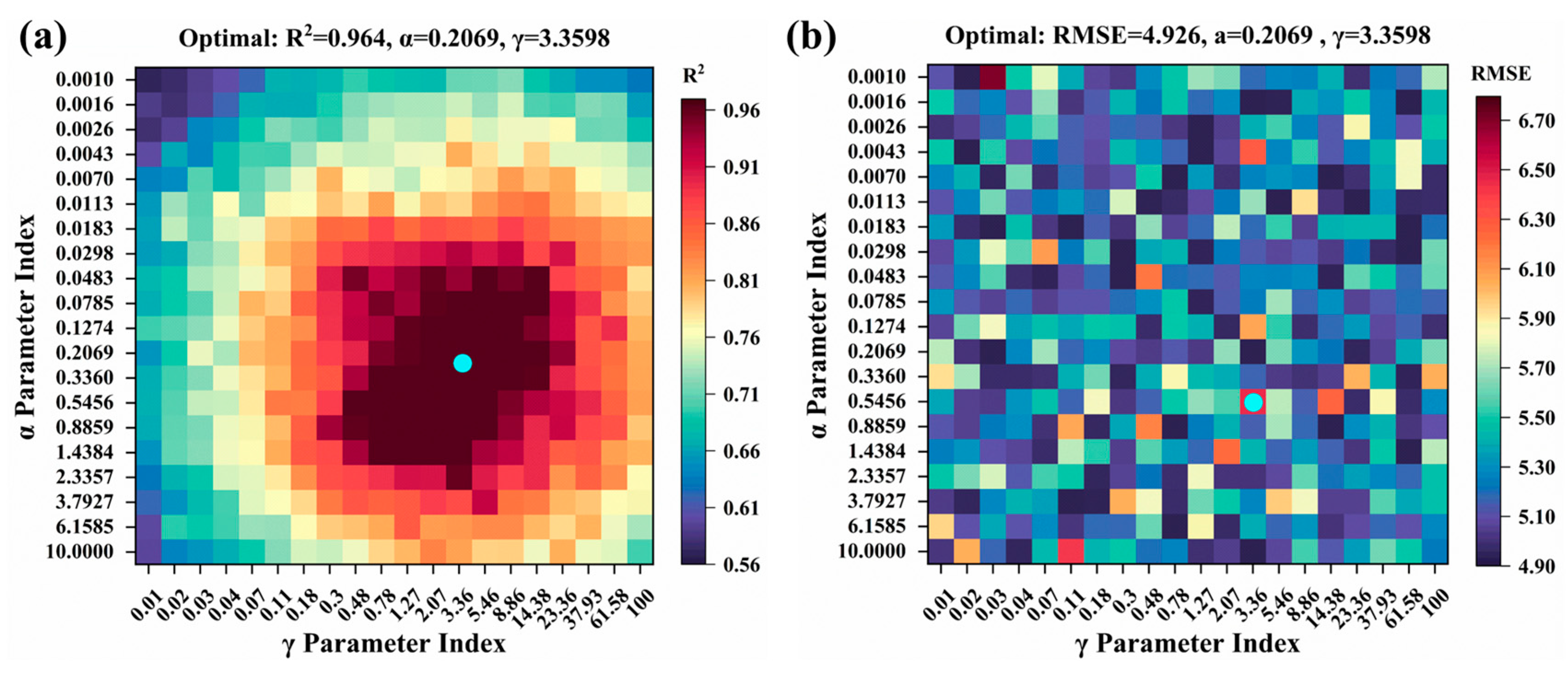
2.4. Model Hyperparameter Tuning
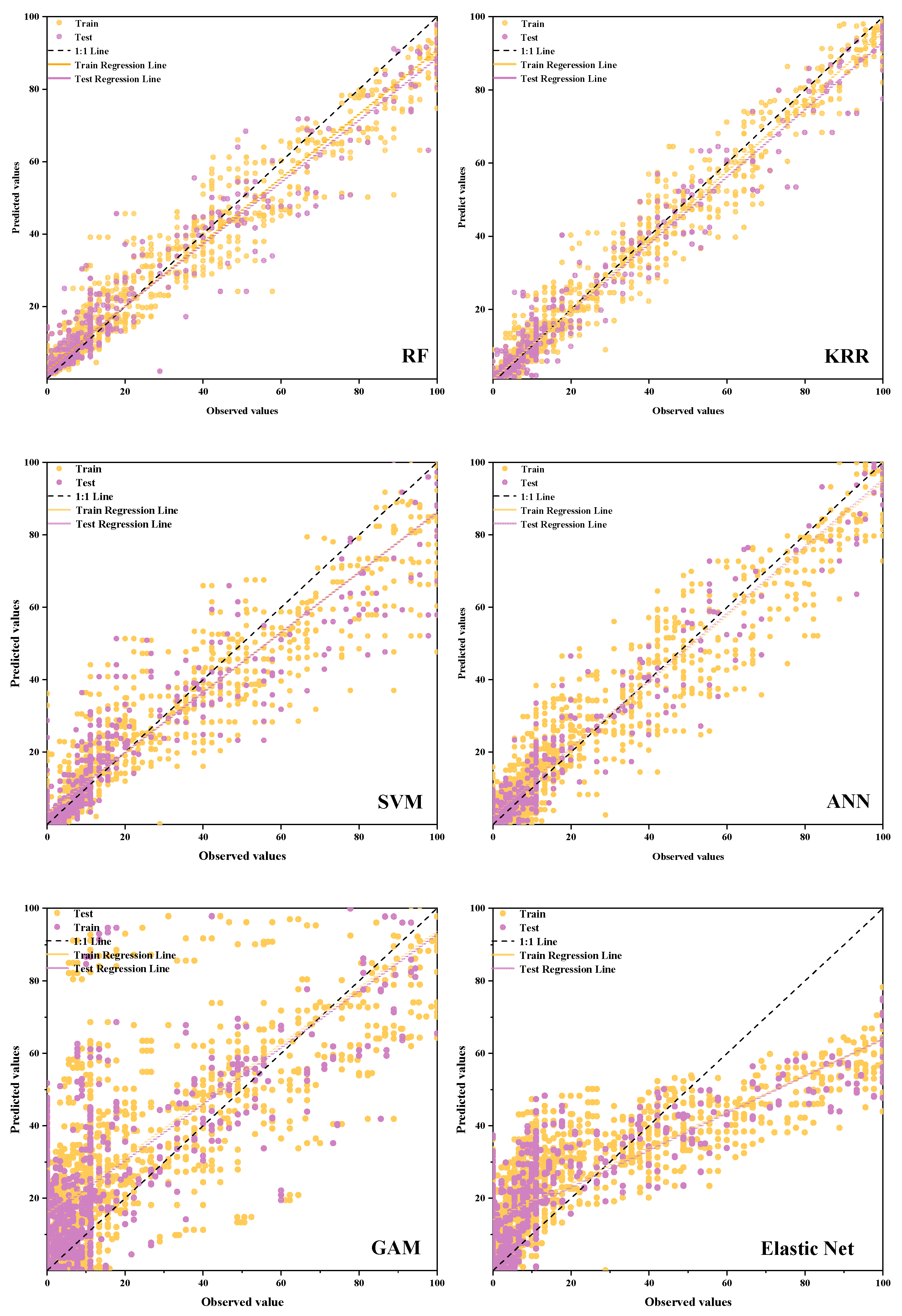
2.5. Comparative Analysis of Different Prediction Models for Rubber-Tree Powdery Mildew Disease Index
3. Discussion
4. Materials and Methods
4.1. Materials
4.2. Experiment on the Effects of Environmental Factors and Spore Concentration on the Disease Progression of Powdery Mildew in Rubber Trees
4.3. Grading Standards and Calculation Methods of Disease Index for Rubber-Tree Powdery Mildew Leaves
4.4. Prediction Model Construction and Model Hyperparameter Tuning
- (1)
- The KRR model maps input features into a high-dimensional feature space using the RBF kernel function with γ = 3.3598, while incorporating a regularization hyperparameter α = 0.2069 to balance model fitting and generalization performance.
- (2)
- The SVM model selected the RBF kernel function with hyperparameters (C = 4.0, γ = 1.0).
- (3)
- For the RF model, the number of decision trees was set to 100, and the minimum leaf size was set to 5.
- (4)
- The ANN model adopted a single-hidden-layer structure containing 12 neurons, with this configuration determined by balancing performance between the training and test sets.
- (5)
- The Elastic Net model determined the optimal hyperparameters by setting α = 0.4368 (representing the L1/L2 regularization weight ratio) and λ = 0.003.
- (6)
- The GAM captured nonlinear trends in individual features using spline functions (with a smoothing hyperparameter λ = 2.3357, df = 8) and integrated these into the interaction terms.
4.5. Prediction Model Performance Evaluation
4.6. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, R.; Wang, J.; Li, N. Climate change increases the suitable area and suitability degree of rubber tree powdery mildew in China. Ind. Crops Prod. 2022, 189, 115888. [Google Scholar] [CrossRef]
- Wu, H.; Pan, Y.; Di, R.; He, Q.; Rajaofera, M.J.N.; Liu, W.; Zheng, F.; Miao, W. Molecular identification of the powdery mildew fungus infecting rubber trees in China. For. Pathol. 2019, 49, e12519. [Google Scholar] [CrossRef]
- Cao, X.; Han, Q.; West, J.S. Spray-induced gene silencing as a potential tool to control rubber tree powdery mildew disease. Physiol. Mol. Plant Pathol. 2024, 129, 102182. [Google Scholar] [CrossRef]
- Liyanage, K.K.; Sehroon, K.; Siraprapa, B.; Mortimer, P.E.; Karunarathna, S.C.; Xu, J.; Hyde, K.D. Morpho-Molecular Characterization of Two Ampelomyces spp. (Pleosporales) Strains Mycoparasites of Powdery Mildew of Hevea brasiliensis. Front. Microbiol. 2018, 9, 12. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Zheng, F.; Zhang, Y. Molecular cloning and characterization of a Mlo gene in rubber tree (Hevea brasiliensis). J. Plant Physiol. 2015, 175, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Xiao, Y.; Han, Q.; West, J.S.; Luo, D. Temporal population structure of rubber tree powdery mildew pathogen Erysiphe quercicola in Hainan, China. Plant Pathol. 2023, 72, 1218–1225. [Google Scholar] [CrossRef]
- Zhai, D.-L.; Wang, J.; Thaler, P.; Luo, Y.; Xu, J. Contrasted effects of temperature during defoliation vs. refoliation periods on the infection of rubber powdery mildew (Oidium heveae) in Xishuangbanna, China. Int. J. Biometeorol. 2020, 64, 1835–1845. [Google Scholar] [CrossRef]
- Zhai, D.-L.; Thaler, P.; Luo, Y.; Xu, J. The powdery mildew disease of rubber (Oidium heveae) is jointly controlled by the winter temperature and host phenology. Int. J. Biometeorol. 2021, 65, 1707–1718. [Google Scholar] [CrossRef] [PubMed]
- Liyanage, K.K.; Khan, S.; Mortimer, P.E.; Hyde, K.D.; Xu, J.; Brooks, S.; Ming, Z. Powdery mildew disease of rubber tree. For. Pathol. 2016, 46, 90–103. [Google Scholar] [CrossRef]
- Liyanage, K.K.; Khan, S.; Brooks, S.; Mortimer, P.E.; Karunarathna, S.C.; Xu, J.; Hyde, K.D. Taxonomic revision and phylogenetic analyses of rubber powdery mildew fungi. Microb. Pathog. 2017, 105, 185–195. [Google Scholar] [CrossRef]
- Cao, X.; Xu, X.; Che, H.; West, J.; Luo, D. Effects of temperature and leaf age on conidial germination and disease development of powdery mildew on rubber tree. Plant Pathol. 2021, 70, 484–491. [Google Scholar] [CrossRef]
- Cheng, X.; Huang, M.; Guo, A.; Huang, W.; Cai, Z.; Dong, Y.; Guo, J.; Hao, Z.; Huang, Y.; Ren, K.; et al. Early Detection of Rubber Tree Powdery Mildew by Combining Spectral and Physicochemical Parameter Features. Remote Sens. 2024, 16, 1634. [Google Scholar] [CrossRef]
- Zeng, T.; Fang, J.; Yin, C.; Li, Y.; Fu, W.; Zhang, H.; Wang, J.; Zhang, X. Recognition of Rubber Tree Powdery Mildew Based on UAV Remote Sensing with Different Spatial Resolutions. Drones 2023, 7, 533. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Hamer, W.B.; Birr, T.; Verreet, J.-A.; Duttmann, R.; Klink, H. Spatio-Temporal Prediction of the Epidemic Spread of Dangerous Pathogens Using Machine Learning Methods. ISPRS Int. J. Geo Inf. 2020, 9, 44. [Google Scholar] [CrossRef]
- Patil, R.R.; Kumar, S. Predicting rice diseases across diverse agro-meteorological conditions using an artificial intelligence approach. PeerJ Comput. Sci. 2021, 7, e687. [Google Scholar] [CrossRef]
- Mishra, G.; Sulieman, M.M.; Kaya, F.; Francaviglia, R.; Keshavarzi, A.; Bakhshandeh, E.; Loum, M.; Jangir, A.; Ahmed, I.; Elmobarak, A.; et al. Machine learning for cation exchange capacity prediction in different land uses. CATENA 2022, 216, 106404. [Google Scholar] [CrossRef]
- Saidi, S.; Ayoubi, S.; Shirvani, M.; Azizi, K.; Zeraatpisheh, M. Comparison of Different Machine Learning Methods for Predicting Cation Exchange Capacity Using Environmental and Remote Sensing Data. Sensors 2022, 22, 6890. [Google Scholar] [CrossRef]
- Ren, H.-L.; Zhang, W.; Lian, T.; Xie, R.; Hayashi, M. Editorial: ENSO Nonlinearity and Complexity: Features, Mechanisms, Impacts and Prediction. Front. Earth Sci. 2022, 10, 967362. [Google Scholar] [CrossRef]
- Hickey, S.M.; Radford, B.; Callow, J.N.; Phinn, S.R.; Duarte, C.M.; Lovelock, C.E. ENSO feedback drives variations in dieback at a marginal mangrove site. Sci. Rep. 2021, 11, 8130. [Google Scholar] [CrossRef]
- Kriss, A.B.; Paul, P.A.; Madden, L.V. Variability in fusarium head blight epidemics in relation to global climate fluctuations as represented by the El Niño-Southern Oscillation and other atmospheric patterns. Phytopathology 2012, 102, 55–64. [Google Scholar] [CrossRef]
- Whipps, J.M.; Budge, S.P. Effect of Humidity on Development of Tomato Powdery Mildew (Oidium lycopersici) in the Glasshouse. Eur. J. Plant Pathol. 2000, 106, 395–397. [Google Scholar] [CrossRef]
- Van der Heyden, H.; Carisse, O.; Brodeur, L. Comparison of monitoring based indicators for initiating fungicide spray programs to control Botrytis leaf blight of onion. Crop Prot. 2012, 33, 21–28. [Google Scholar] [CrossRef]
- Martínez-Bracero, M.; González-Fernández, E.; Wójcik, M.; Alcázar, P.; Fernández-González, M.; Kasprzyk, I.; Rodríguez-Rajo, F.J.; Galán, C. Airborne fungal phytopathological spore assessment in three European vineyards from different bioclimatic areas. Aerobiologia 2020, 36, 715–729. [Google Scholar] [CrossRef]
- Kong, J.; Wu, L.; Cao, J.; Cui, W.; Nie, T.; An, Y.; Sun, Z. Meteorological Impacts on Rubber Tree Powdery Mildew and Projections of Its Future Spatiotemporal Pattern. Agriculture 2024, 14, 619. [Google Scholar] [CrossRef]
- Singh, M.; Savary, S.; Setiya, P.; Tewari, A.K.; Nain, A.S. Multivariate analysis of the effects of weather variables on white rust epidemics and yield reduction of mustard over multiple growing seasons. Plant Pathol. 2024, 73, 791–809. [Google Scholar] [CrossRef]
- Meng, L.; Xu, X.; Huang, X.; Li, X.; Chang, X.; Xu, D. High-resolution estimation of PM2.5 concentrations across China using multiple machine learning approaches and model fusion. Atmos. Pollut. Res. 2024, 15, 102110. [Google Scholar] [CrossRef]
- Chen, S.; Han, H.; Yu, J.; Sun, T.; Zhou, J. Response of diatoms to environmental changes in the Porphyra cultivation system in Haizhou Bay using GBT model and GAM. Mar. Pollut. Bull. 2025, 215, 117846. [Google Scholar] [CrossRef]
- Tay, J.K.; Aghaeepour, N.; Hastie, T.; Tibshirani, R. Feature-Weighted Elastic Net: Using “Features of Features” for Better Prediction. Stat. Sin. 2023, 33, 259–279. [Google Scholar] [CrossRef] [PubMed]
- Hafermann, L.; Becher, H.; Herrmann, C.; Klein, N.; Heinze, G.; Rauch, G. Statistical model building: Background “knowledge” based on inappropriate preselection causes misspecification. BMC Med. Res. Methodol. 2021, 21, 196. [Google Scholar] [CrossRef]
- Liang, Z.; Pandey, P.; Stoerger, V.; Xu, Y.; Qiu, Y.; Ge, Y.; Schnable, J.C. Conventional and hyperspectral time-series imaging of maize lines widely used in field trials. GigaScience 2017, 77, 1–11. [Google Scholar] [CrossRef]
- Sheikh, M.; Iqra, F.; Ambreen, H.; Pravin, K.A.; Ikra, M.; Chung, Y.S. Integrating artificial intelligence and high-throughput phenotyping for crop improvement. J. Integr. Agric. 2024, 23, 1787–1802. [Google Scholar] [CrossRef]
- Matsumoto, T.; Yamada, Y. Comprehensive and Comparative Analysis of GAM-Based PV Power Forecasting Models Using Multidimensional Tensor Product Splines against Machine Learning Techniques. Energies 2021, 14, 7146. [Google Scholar] [CrossRef]
- Guo, Q.; Wu, F.; Pang, S.; Zhao, X.; Chen, L.; Liu, J.; Xue, B.; Xu, G.; Li, L.; Jing, H.; et al. Crop 3D—A LiDAR based platform for 3D high-throughput crop phenotyping. Sci. China Life Sci. 2018, 61, 328–339. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P.K. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Yan, C.; Li, Y.; Liu, W.; Li, M.; Chen, J.; Wang, L. An artificial bee colony-based kernel ridge regression for automobile insurance fraud identification. Neurocomputing 2020, 393, 115–125. [Google Scholar] [CrossRef]
- de Queiróz Lamas, W. Algae’s potential as a bio-mass source for bio-fuel production: MLR vs. ANN models analyses. Fuel 2025, 395, 134853. [Google Scholar]
- Wei, X.; Xu, Y.; Li, X.; Fan, G.; Cheng, X.; Yu, T.; Jiang, B. Study on prediction model of nitrogen oxide concentration in reprocessing plant based on random forest. Int. J. Adv. Nucl. React. Des. Technol. 2025, 7, 63–69. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Tang, X.; Lv, J.; Zhang, R. Research on computer multi feature fusion SVM model based on remote sensing image recognition and low energy system. Results Eng. 2025, 26, 104861. [Google Scholar] [CrossRef]
- Shahoveisi, F.; Riahi Manesh, M.; Del Río Mendoza, L.E. Modeling risk of Sclerotinia sclerotiorum-induced disease development on canola and dry bean using machine learning algorithms. Sci. Rep. 2022, 12, 864. [Google Scholar] [CrossRef] [PubMed]
- Shivling, V.D.; Ghanshyam, C.; Kumar, R.; Kumar, S.; Sharma, R.; Kumar, D.; Sharma, A.; Sharma, S.K. Prediction Model for Predicting Powdery Mildew using ANN for Medicinal Plant—Picrorhiza kurrooa. J. Inst. Eng. India Ser. B 2017, 98, 77–81. [Google Scholar] [CrossRef]
- Bai, R.; Wang, J.; Li, N.; Chen, R. Short- and long-term prediction models of rubber tree powdery mildew disease index based on meteorological variables and climate system indices. Agric. For. Meteorol. 2024, 354, 110082. [Google Scholar] [CrossRef]
- Ruan, C.; Dong, Y.; Huang, W.; Huang, L.; Ye, H.; Ma, H.; Guo, A.; Sun, R. Integrating Remote Sensing and Meteorological Data to Predict Wheat Stripe Rust. Remote Sens. 2022, 14, 1221. [Google Scholar] [CrossRef]
- Yang, L.; Li, L.; Dong, Z.; Zhu, J.; Guo, W.; Song, Y.; Cui, H.; Lv, S.; Sindhu, L.; Men, X. EIRP model driven by machine learning for predicting the occurrence risk of southern corn rust (Puccinia polysora Underw. ) in northern China. Agric. For. Meteorol. 2024, 356, 110149. [Google Scholar] [CrossRef]
- Kurmi, Y.; Gangwar, S.; Agrawal, D.; Kumar, S.; Srivastava, H.S. Leaf image analysis-based crop diseases classification. Signal Image Video Process. 2021, 15, 589–597. [Google Scholar] [CrossRef]
- Kurmi, Y.; Gangwar, S. A leaf image localization based algorithm for different crops disease classification. Inf. Process. Agric. 2022, 9, 456–474. [Google Scholar] [CrossRef]
- Li, L.; Dong, Y.; Xiao, Y.; Liu, L.; Zhao, X.; Huang, W. Combining Disease Mechanism and Machine Learning to Predict Wheat Fusarium Head Blight. Remote Sens. 2022, 14, 2732. [Google Scholar] [CrossRef]
- Apangu, G.P.; Adams-Groom, B.; Satchwell, J.; Pashley, C.H.; Werner, M.; Kryza, M.; Szymanowski, M.; Malkiewicz, M.; Bruffaerts, N.; Hoebeke, L.; et al. Sentinel-2 satellite and HYSPLIT model suggest that local cereal harvesting substantially contribute to peak Alternaria spore concentrations. Agric. For. Meteorol. 2022, 326, 109156. [Google Scholar] [CrossRef]
- Wang, H.; Yang, X.B.; Ma, Z. Long-Distance Spore Transport of Wheat Stripe Rust Pathogen from Sichuan, Yunnan, and Guizhou in Southwestern China. Plant Dis. 2010, 94, 873–880. [Google Scholar] [CrossRef]
- NY/T 1089-2015; Technical Procedure for Forecasting the Powdery Mildew of Rubber Tree. Ministry of Agriculture and Rural affairs of the People’s Republic of China: Beijing, China, 2015.
- Wu, X.H.; Lu, Y.Y.; Zhao, P.W. Multi-task learning on nuclear masses and separation energies with the kernel ridge regression. Phys. Lett. B 2022, 834, 137394. [Google Scholar] [CrossRef]
- Qi, Y.; Xue, K.; Wang, W.; Cui, X.; Liang, R. Prediction Model of Borehole Spontaneous Combustion Based on Machine Learning and Its Application. Fire 2023, 6, 357. [Google Scholar] [CrossRef]
- M’hamdi, O.; Takács, S.; Palotás, G.; Ilahy, R.; Helyes, L.; Pék, Z. A Comparative Analysis of XGBoost and Neural Network Models for Predicting Some Tomato Fruit Quality Traits from Environmental and Meteorological Data. Plants 2024, 13, 746. [Google Scholar] [CrossRef] [PubMed]
- Noori, R.; Karbassi, A.R.; Moghaddamnia, A.; Han, D.; Zokaei-Ashtiani, M.H.; Farokhnia, A.; Gousheh, M.G. Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction. J. Hydrol. 2011, 401, 177–189. [Google Scholar] [CrossRef]
- Wang, W.; Liang, J.; Liu, R.; Song, Y.; Zhang, M. A Robust Variable Selection Method for Sparse Online Regression via the Elastic Net Penalty. Mathematics 2022, 10, 2985. [Google Scholar] [CrossRef]
- Comber, A.; Harris, P.; Murakami, D.; Nakaya, T.; Tsutsumida, N.; Yoshida, T.; Brunsdon, C. Encapsulating Spatially Varying Relationships with a Generalized Additive Model. ISPRS Int. J. Geo Inf. 2024, 13, 459. [Google Scholar] [CrossRef]




| Variable | Diseased Index, Mean ± SD | Statistic | p |
|---|---|---|---|
| Total | 18.77 ± 27.31 | ||
| Spore concentration (lg (Spores/mL)) | F = 194.51 | <0.001 | |
| 3 | 3.36 ± 4.36 | ||
| 3.5 | 6.57 ± 7.97 | ||
| 4 | 18.96 ± 20.60 | ||
| 4.5 | 25.72 ± 30.67 | ||
| 5 | 40.26 ± 38.18 | ||
| Humidity (%) | F = 27.39 | <0.001 | |
| 60 | 14.21 ± 24.02 | ||
| 80 | 23.76 ± 30.12 | ||
| 100 | 18.26 ± 26.53 | ||
| Temperature (°C) | F = 112.53 | <0.001 | |
| 14 | 6.51 ± 10.31 | ||
| 18 | 22.20 ± 24.85 | ||
| 22 | 32.34 ± 33.69 | ||
| 26 | 31.42 ± 34.31 | ||
| 28 | 14.98 ± 21.77 | ||
| 30 | 1.41 ± 3.21 | ||
| Time (h) | F = 66.77 | <0.001 | |
| 24 | 3.23 ± 3.02 | ||
| 48 | 5.04 ± 4.81 | ||
| 72 | 7.79 ± 10.19 | ||
| 96 | 12.66 ± 18.93 | ||
| 120 | 19.44 ± 26.40 | ||
| 144 | 25.12 ± 30.78 | ||
| 168 | 28.82 ± 32.39 | ||
| 192 | 32.65 ± 34.03 | ||
| 216 | 34.66 ± 35.08 |
| Non-standardized Coefficients | Standardized Coefficients | t | p | Collinearity Diagnosis | |||
|---|---|---|---|---|---|---|---|
| B | Standard Error | Beta | VIF | Tolerance | |||
| Constant | −80.757 | 3.687 | - | −21.904 | 0.000 *** | - | - |
| Spore concentration | 18.566 | 0.601 | 0.475 | 30.909 | 0.000 *** | 1.000 | 1.000 |
| Temperature | −0.181 | 0.077 | −0.036 | −2.363 | 0.018 * | 1.001 | 0.999 |
| Humidity | 0.098 | 0.026 | 0.058 | 3.759 | 0.000 *** | 1.001 | 0.999 |
| Infection time | 0.182 | 0.007 | 0.413 | 26.869 | 0.000 *** | 1.000 | 1.000 |
| R2 | 0.402 | ||||||
| Adjust R2 | 0.401 | ||||||
| F | 425.259 *** | ||||||
| Two-Factor Interaction | Significance (Two-Tailed) | Multiple Factors Interact | Significance (Two-Tailed) |
|---|---|---|---|
| Spore concentration (log) × Temperature | <0.001 | Spore concentration (log) × Temperature × RH | <0.001 |
| Spore concentration (log) × RH | <0.001 | Spore concentration (log) × Temperature × Infection time | <0.001 |
| Spore concentration (log) × Infection time | <0.001 | Spore concentration (log) × RH × Infection time | <0.001 |
| Temperature × humidity | <0.001 | Temperature × RH × Infection time | <0.001 |
| RH × Infection time | <0.001 | Spore concentration (log) × Temperature × RH × Infection time | <0.001 |
| Temperature × Infection time | <0.001 |
| Model | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | MBE | R2 | RMSE | MAE | MBE | |
| KRR | 0.978 | 4.037 | 2.389 | 0.272 | 0.964 | 4.926 | 2.880 | 0.336 |
| RF | 0.957 | 5.508 | 3.345 | 0.048 | 0.963 | 5.744 | 3.659 | 0.013 |
| ANN | 0.919 | 7.736 | 5.334 | 0.899 | 0.922 | 7.652 | 5.440 | 0.883 |
| SVM | 0.897 | 8.702 | 4.941 | 0.051 | 0.916 | 8.007 | 4.757 | 0.027 |
| Elastic Net | 0.612 | 17.113 | 13.364 | −4.240 | 0.601 | 16.414 | 12.417 | −4.381 |
| GAM | 0.412 | 21.075 | 15.612 | −11.440 | 0.414 | 19.893 | 14.301 | −10.849 |
| Disease Grade | Percentage of Spot Area to Leaf Area (x) |
|---|---|
| Level 0 | no powdery mildew spots on the leaf |
| Level 1 | 0 < x < 1/20 |
| Level 3 | 1/20 ≤ x< 1/16 |
| Level 5 | 1/16 ≤ x < 1/8 |
| Level 7 | 1/8 ≤ x <1/4 |
| Level 9 | x ≥ 1/4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Huang, X.; Liang, X.; Wang, M.; Zhang, Y. Prediction Model of Powdery Mildew Disease Index in Rubber Trees Based on Machine Learning. Plants 2025, 14, 2402. https://doi.org/10.3390/plants14152402
Zhu J, Huang X, Liang X, Wang M, Zhang Y. Prediction Model of Powdery Mildew Disease Index in Rubber Trees Based on Machine Learning. Plants. 2025; 14(15):2402. https://doi.org/10.3390/plants14152402
Chicago/Turabian StyleZhu, Jiazheng, Xize Huang, Xiaoyu Liang, Meng Wang, and Yu Zhang. 2025. "Prediction Model of Powdery Mildew Disease Index in Rubber Trees Based on Machine Learning" Plants 14, no. 15: 2402. https://doi.org/10.3390/plants14152402
APA StyleZhu, J., Huang, X., Liang, X., Wang, M., & Zhang, Y. (2025). Prediction Model of Powdery Mildew Disease Index in Rubber Trees Based on Machine Learning. Plants, 14(15), 2402. https://doi.org/10.3390/plants14152402






