Effects of Temperature Fluctuations on Cabernet Sauvignon Branches and Wine Grape Appellation Yields: An Analysis Based on the Standardized Temperature Adaptation Index
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Sources
2.2.1. Temperature Data During the Growing Season
2.2.2. Wine Grape Yield and Planting Area in the Production Area
2.2.3. Experiment on the Low-Temperature Fluctuations During the Wintering Period
2.3. Construction of the STAI
- (1)
- A retrospective time series of temperature variations was obtained and fitted to a probability distribution.
- (2)
- The estimated cumulative probability of current or retrospective temperature variations was derived from this probability distribution.
- (3)
- The resulting cumulative probability was then transformed into a standard normal deviation with a mean of zero and a unit variance.
- (i)
- Standardized index
- (ii)
- Here, p is the average temperature per unit of time (such as 1 month), n is the number of years, Ej(p) is the average temperature per unit of time (5 months) in the j-th year, and varj(p) is the temperature variance per unit of time (5 months) in the j-th year.
2.4. Analysis of Temperature Fluctuation Trends and Amplitude Sequences in Production Regions
2.5. Calculation of Comprehensive Stress Index
2.6. Statistical Analysis
3. Results and Analysis
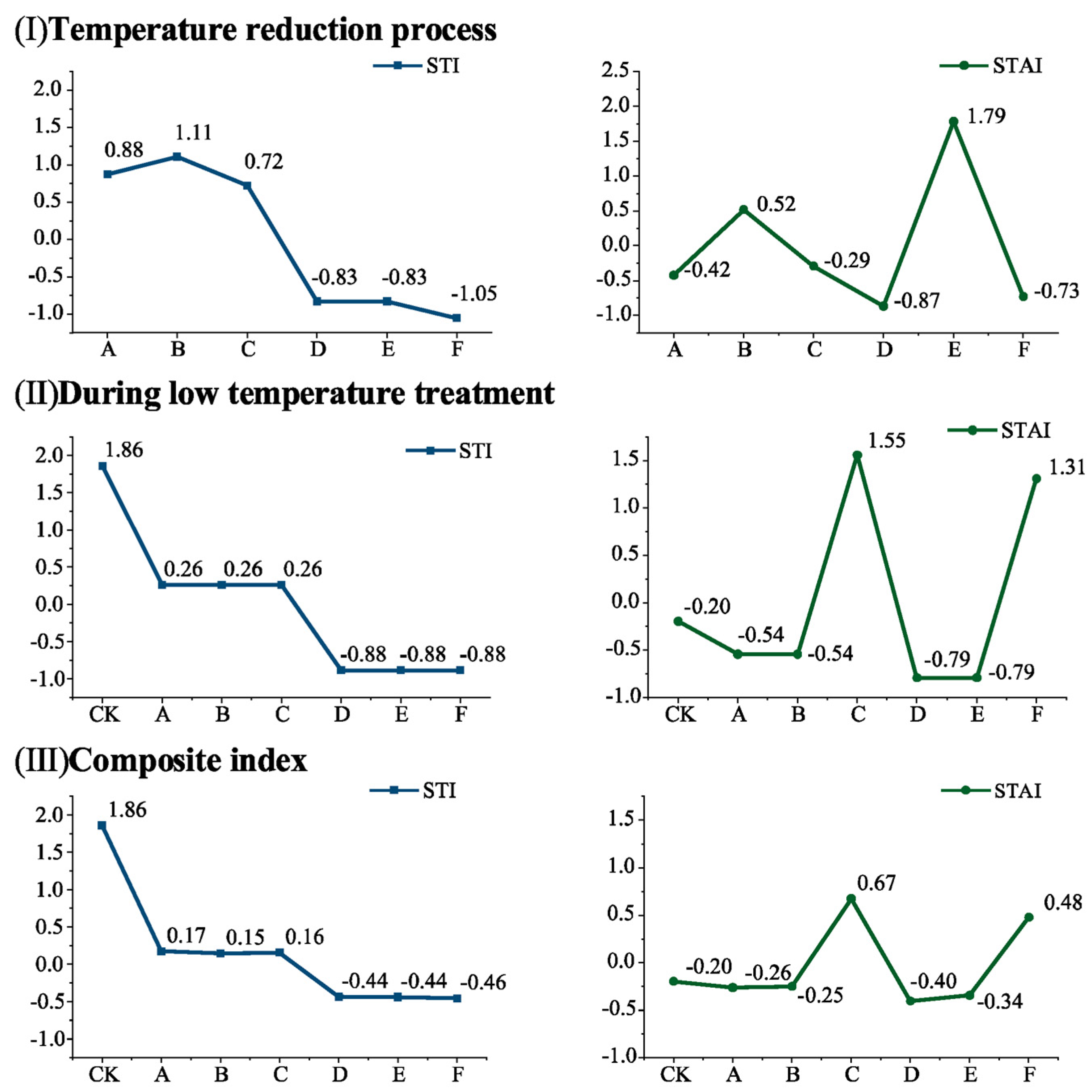
3.1. Analysis of Low-Temperature Fluctuations in Cabernet Sauvignon Branches During Winter Dormancy Period
3.1.1. Computation of the STI and STAI Under Varied Low-Temperature Fluctuation Treatment Conditions
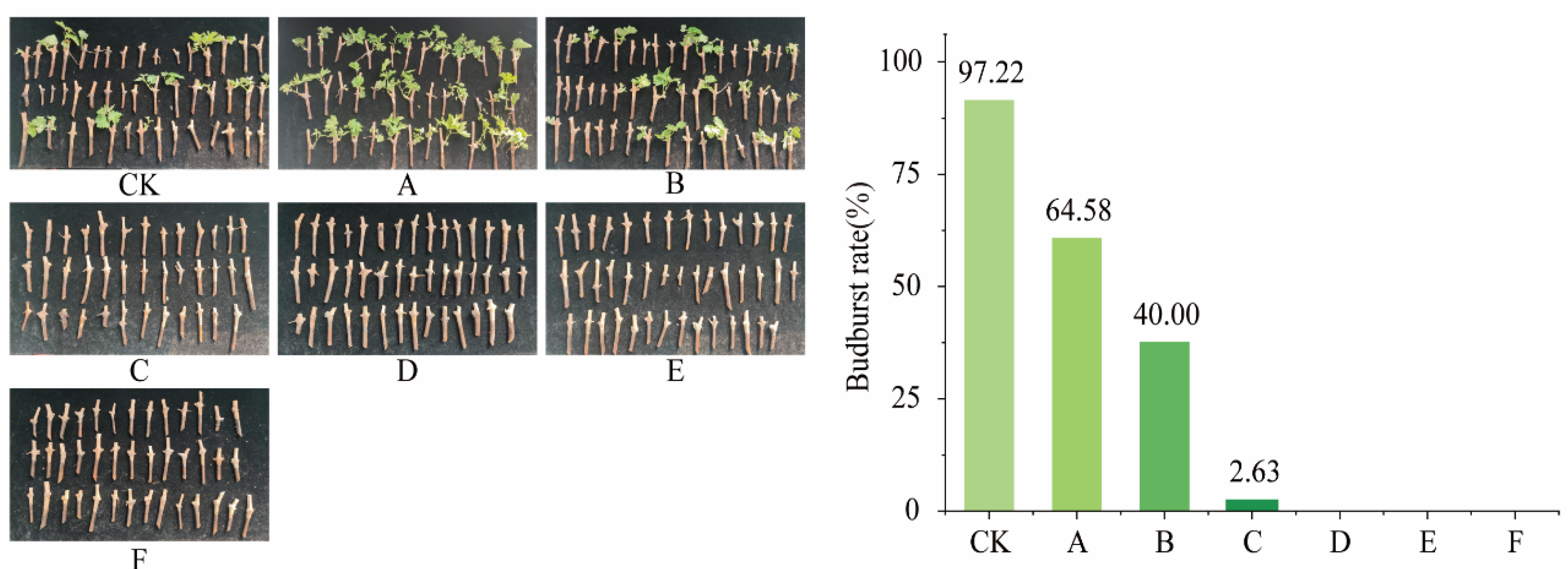
3.1.2. Recovery Growth of Cabernet Sauvignon Shoots Under the Influence of Low-Temperature Fluctuations
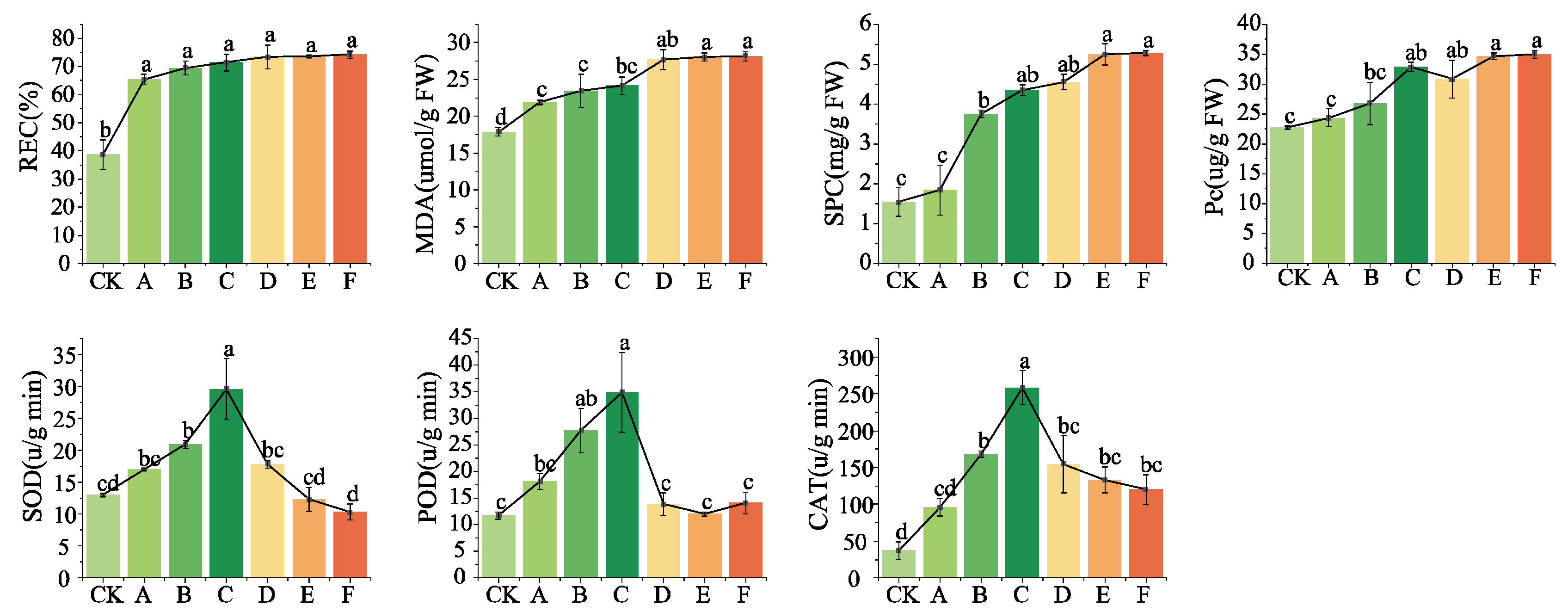
3.1.3. Repercussions of Low-Temperature Fluctuations on the Physiological Parameters of Cabernet Sauvignon Vines
3.1.4. Comprehensive Analysis of Low-Temperature Fluctuations’ Impact on Adversity Stress in Cabernet Sauvignon Branches
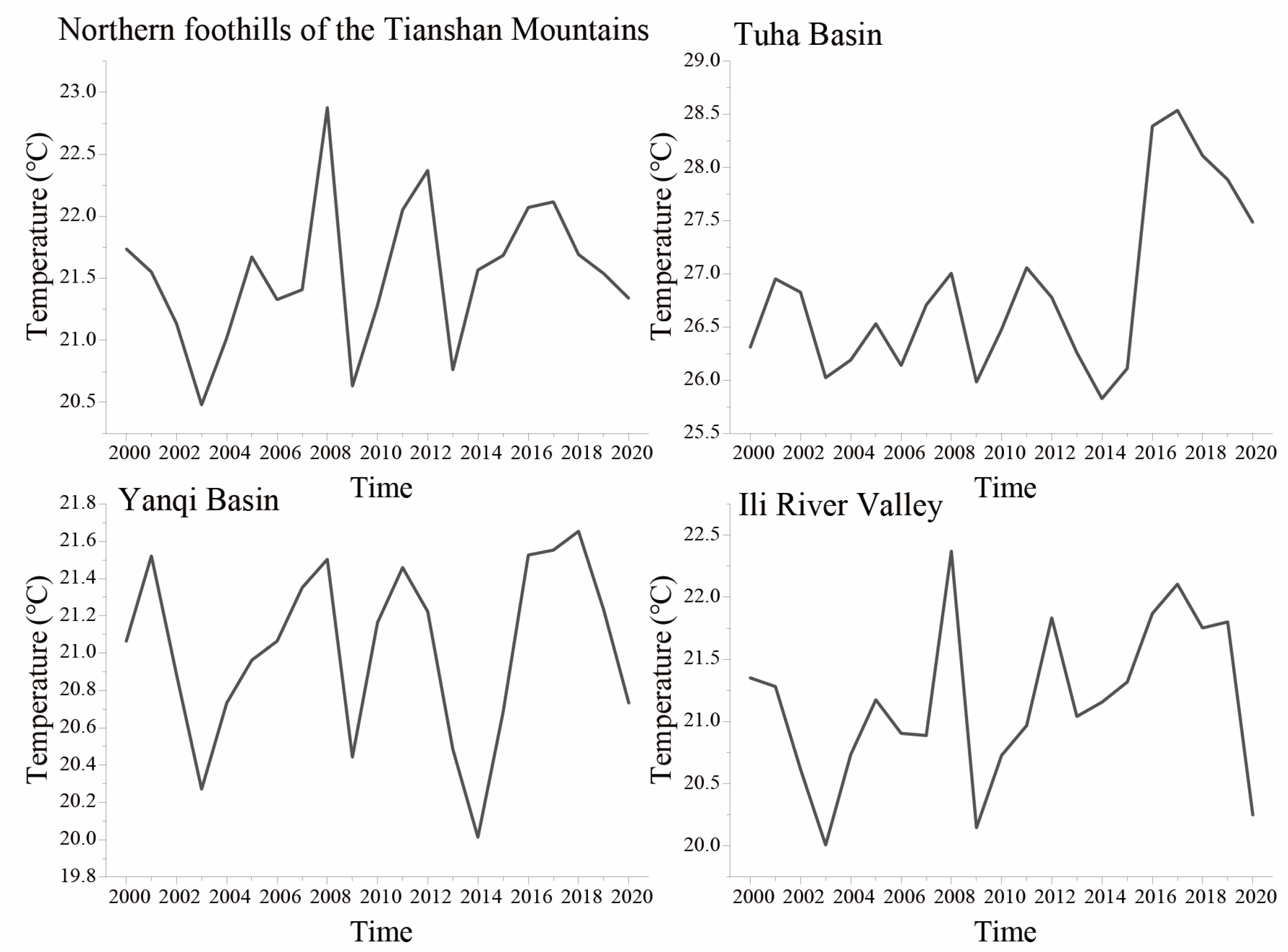
3.2. Investigation of Temperature Fluctuations in Wine Grape Production Regions of Xinjiang
3.2.1. Analysis of STAI Trends and Amplitude Sequences in Wine Grape Production Regions of Xinjiang
3.2.2. Relationship Between Wine Grape Yield and STAI in Xinjiang Production Regions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kim, S.; Kryjov, V.N.; Ahn, J. The roles of global warming and Arctic Oscillation in the winter 2020 extremes in East Asia. Environ. Res. Lett. 2022, 17, 65010. [Google Scholar] [CrossRef]
- Wang, X.; Lang, X.; Jiang, D. Linkage of future regional climate extremes to global warming intensity. Clim. Res. 2020, 81, 43–54. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, D.; Su, Y.; Hao, R. Quantifying the effect of trend, fluctuation, and extreme event of climate change on ecosystem productivity. Environ. Monit. Assess. 2014, 186, 8473–8486. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S.; Coumou, D. Increase of extreme events in a warming world. Proc. Natl. Acad. Sci. USA 2011, 108, 17905–17909. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Shi, P.; Zhang, Z.; Meng, Y.; Luan, Y.; Wang, J. Separating out the influence of climatic trend, fluctuations, and extreme events on crop yield: A case study in Hunan Province, China. Clim. Dyn. 2018, 51, 4469–4487. [Google Scholar] [CrossRef]
- Ray, D.K.; Gerber, J.S.; MacDonald, G.K.; West, P.C. Climate variation explains a third of global crop yield variability. Nat. Commun. 2015, 6, 5989. [Google Scholar] [CrossRef]
- Wheeler, T.R.; Craufurd, P.Q.; Ellis, R.H.; Porter, J.R.; Prasad, P.V.V. Temperature variability and the yield of annual crops. Agric. Ecosyst. Environ. 2000, 82, 159–167. [Google Scholar] [CrossRef]
- Alston, J.M.; Sambucci, O. Grapes in the World Economy. In The Grape Genome; Cantu, D., Walker, M.A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–24. ISBN 978-3-030-18601-2. [Google Scholar]
- Wang, H.; Yao, X.; Liu, M.; Xu, X.; Wang, Y.; Kong, J.; Chen, W.; Xu, Z.; Kuang, Y.; Fan, P.; et al. Climate, soil, and viticultural factors differentially affect the sub-regional variations in biochemical compositions of grape berries. Sci. Hortic. 2025, 339, 113858. [Google Scholar] [CrossRef]
- Ollat, N.; Leeuwen, C.V.; Cortazar-Atauri, I.G.D.; Touzard, J.-M. The challenging issue of climate change for sustainable grape and wine production. OENO One 2017, 51, 59–60. [Google Scholar] [CrossRef]
- Van Leeuwen, C.; Darriet, P. The Impact of Climate Change on Viticulture and Wine Quality. J. Wine Econ. 2016, 11, 150–167. [Google Scholar] [CrossRef]
- Hall, A.; Mathews, A.J.; Holzapfel, B.P. Potential effect of atmospheric warming on grapevine phenology and post-harvest heat accumulation across a range of climates. Int. J. Biometeorol. 2016, 60, 1405–1422. [Google Scholar] [CrossRef]
- Orduna, R.M.D. Climate change associated effects on grape and wine quality and production. Food Res. Int. 2010, 43, 1844–1855. [Google Scholar] [CrossRef]
- Leeuwen, C.V.; Friant, P.; Choné, X.; Tregoat, O.; Koundouras, S.; Dubourdieu, D. Influence of climate, soil, and cultivar on terroir. Am. J. Enol. Vitic. 2004, 553, 207–217. [Google Scholar] [CrossRef]
- Mozell, M.R.; Thach, L. The impact of climate change on the global wine industry: Challenges & solutions. Wine Econ. Policy 2014, 3, 81–89. [Google Scholar] [CrossRef]
- Tate, A.B. Global Warming’s Impact on Wine. J. Wine Res. 2001, 12, 95–109. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, J.; Yin, H.; Wang, J.; Wang, X.; Yang, Y.; Xi, Z. Microclimate diversity drives grape quality difference at high-altitude: Observation using PCA analysis and structural equation modeling (SEM). Food Res. Int. 2024, 191, 114644. [Google Scholar] [CrossRef]
- Castillo, N.; Cavazos, T.; Pavia, E.G. Impact of climate change in Mexican winegrape regions. Int. J. Climatol. 2023, 43, 6621–6642. [Google Scholar] [CrossRef]
- Hannah, L.; Roehrdanz, P.R.; Ikegami, M.; Shepard, A.V.; Shaw, M.R.; Tabor, G.; Zhi, L.; Marquet, P.A.; Hijmans, R.J. Climate change, wine, and conservation. Proc. Natl. Acad. Sci. USA 2013, 110, 6907–6912. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, S. Surviving and thriving: How plants perceive and respond to temperature stress. Dev. Cell 2022, 57, 947–958. [Google Scholar] [CrossRef]
- Aslam, M.A.; Ahmed, M.; Hassan, F.-U.; Afzal, O.; Mehmood, M.Z.; Qadir, G.; Asif, M.; Komal, S.; Hussain, T. Impact of Temperature Fluctuations on Plant Morphological and Physiological Traits. In Building Climate Resilience in Agriculture: Theory, Practice and Future Perspective; Jatoi, W.N., Mubeen, M., Ahmad, A., Cheema, M.A., Lin, Z., Hashmi, M.Z., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 25–52. ISBN 978-3-030-79408-8. [Google Scholar]
- Chiang, C.; Bånkestad, D.; Hoch, G. Effect of Asynchronous Light and Temperature Fluctuations on Plant Traits in Indoor Growth Facilities. Agronomy 2021, 11, 755. [Google Scholar] [CrossRef]
- Zepeda, A.C.; Heuvelink, E.; Marcelis, L. Non-structural carbohydrate dynamics and growth in tomato plants grown at fluctuating light and temperature. Front. Plant Sci. 2022, 13, 968881. [Google Scholar] [CrossRef] [PubMed]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Kamruzzaman, M.; Almazroui, M.; Salam, M.A.; Mondol, A.H.; Rahman, M.; Deb, L.; Kundu, P.K.; Zaman, A.U.; Islam, A.R.M.T. Spatiotemporal drought analysis in Bangladesh using the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI). Sci. Rep. 2022, 12, 20694. [Google Scholar] [CrossRef]
- Şen, Z.; Şişman, E. Probabilistic standardization index adjustment for standardized precipitation index (SPI). Theor. Appl. Climatol. 2024, 155, 2747–2756. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K.; Li, B.; Jiang, Z. Spatiotemporal analysis of meteorological drought across China based on the high-spatial-resolution multiscale SPI generated by machine learning. Weather. Clim. Extrem. 2023, 40, 100567. [Google Scholar] [CrossRef]
- Laimighofer, J.; Laaha, G. How standard are standardized drought indices? Uncertainty components for the SPI & SPEI case. J. Hydrol. 2022, 613, 128385. [Google Scholar] [CrossRef]
- Zscheischler, J.; Michalak, A.M.; Schwalm, C.; Mahecha, M.D.; Huntzinger, D.N.; Reichstein, M.; Berthier, G.; Ciais, P.; Cook, R.B.; El-Masri, B.; et al. Impact of large-scale climate extremes on biospheric carbon fluxes: An intercomparison based on MsTMIP data. Glob. Biogeochem. Cycles 2014, 28, 585–600. [Google Scholar] [CrossRef]
- Karbi, I.; Chemke, R. A shift towards broader and less persistent Southern Hemisphere temperature anomalies. NPJ Clim. Atmos. Sci. 2023, 6, 200. [Google Scholar] [CrossRef]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.J.; Shepherd, T.G. Changes in Northern Hemisphere temperature variability shaped by regional warming patterns. Nat. Geosci. 2020, 13, 414. [Google Scholar] [CrossRef]
- Kurnaz, M.L. Application of detrended fluctuation analysis to monthly average of the maximum daily temperatures to resolve different climates. Fractals 2004, 12, 365–373. [Google Scholar] [CrossRef]
- Zhang, M.; Guan, Y.; Qin, B.L.; Wang, X. Responses of phytoplankton species to diel temperature fluctuation patterns. Phycol. Res. 2019, 67, 184–191. [Google Scholar] [CrossRef]
- Mori, K.; Sugaya, S.; Gemma, H. Decreased anthocyanin biosynthesis in grape berries grown under elevated night temperature condition. Sci. Hortic. 2005, 105, 319–330. [Google Scholar] [CrossRef]
- Wu, J.; Liu, L.; Xu, G.; Jiang, J.; Lian, W.; Zhou, H.; Nan, L.; Ren, H. Grape planting situation and regional spatial analysis in Xinjiang, China. IOP Conf. Ser. Earth Environ. Sci. 2021, 705, 12028. [Google Scholar] [CrossRef]
- Xiao, L. Xinjiang Grape Wine Production Accounts for 24.5% of the National Total. Liquor-Making Sci. Technol. 2023, 129. (In Chinese) [Google Scholar]
- Tu, H.Y.; Mijiti, S. Analysis of Advantages and Disadvantages of Wine Grape Planting Regions in Xinjiang. In Proceedings of the Xinjiang Standardization 2024, Urumqi, China, 12 September 2024; China Institute of Standardization: Beijing, China; pp. 133–135. [Google Scholar] [CrossRef]
- Zhang, Q.; Tu, Y.H. The Impact of Climate Change on Wine Grape Production in China. J. Chin. Brew. 2021, 40, 1–6. (In Chinese) [Google Scholar]
- Zhang, Q.; Liu, Y.; Yu, Q.; Ma, Y.; Gu, W.; Yang, D. Physiological changes associated with enhanced cold resistance during maize (Zea mays) germination and seedling growth in response to exogenous calcium. Crop. Pasture Sci. 2020, 71, 529–538. [Google Scholar] [CrossRef]
- Bates, L.S.; Waldren, R.P.; Teare, I.D. Rapid determination of free proline for water-stress studies. Plant Soil. 1973, 39, 205–207. [Google Scholar] [CrossRef]
- Heath, R.L.; Packer, L. Photoperoxidation in isolated chloroplasts: I. Kinetics and stoichiometry of fatty acid peroxidation. Arch. Biochem. Biophys. 1968, 125, 189–198. [Google Scholar] [CrossRef]
- Giannopolitis, C.N.; Ries, S.K. Superoxide dismutases: I. Occurrence in higher plants. Plant Physiol. 1977, 59, 309–314. [Google Scholar] [CrossRef]
- Sohn, Y.G.; Lee, B.H.; Kang, K.Y.; Lee, J.J. Effects of NaCl stress on germination, antioxidant responses, and proline content in two rice cultivars. J. Plant Biol. 2005, 48, 201–208. [Google Scholar] [CrossRef]
- Kang, H.; Saltveit, M.E. Activity of enzymatic antioxidant defense systems in chilled and heat shocked cucumber seedling radicles. Physiol. Plant. 2001, 113, 548–556. [Google Scholar] [CrossRef]
- Kendall, M.G.; Gibbons, J.D. Rank Correlation Methods, 5th ed.; Oxford University Press: New York, NY, USA, 1990; pp. 154–196. [Google Scholar]
- Jones, G.V. Winegrape Phenology. In Phenology: An Integrative Environmental Science; Schwartz, M.D., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 523–539. ISBN 978-94-007-0632-3. [Google Scholar]
- Gray, D.J.; Li, Z.T.; Dhekney, S.A. Precision breeding of grapevine (Vitis vinifera L.) for improved traits. Plant Sci. 2014, 228, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Massano, L.; Fosser, G.; Gaetani, M.; Bois, B. Assessment of climate impact on grape productivity: A new application for bioclimatic indices in Italy. Sci. Total Environ. 2023, 905, 167134. [Google Scholar] [CrossRef]
- Yamori, N.; Levine, C.P.; Mattson, N.S.; Yamori, W. Optimum root zone temperature of photosynthesis and plant growth depends on air temperature in lettuce plants. Plant Mol. Biol. 2022, 110, 385–395. [Google Scholar] [CrossRef] [PubMed]
- Camut, L.; Regnault, T.; Sirlin-Josserand, M.; Sakvarelidze-Achard, L.; Carrera, E.; Zumsteg, J.; Heintz, D.; Leonhardt, N.; Lange, M.J.P.; Lange, T.; et al. Root-derived GA12 contributes to temperature-induced shoot growth in Arabidopsis. Nat. Plants 2019, 5, 1216–1221. [Google Scholar] [CrossRef] [PubMed]
- Martins, S.; Montiel-Jorda, A.; Cayrel, A.; Huguet, S.; Roux, C.P.-L.; Ljung, K.; Vert, G. Brassinosteroid signaling-dependent root responses to prolonged elevated ambient temperature. Nat. Commun. 2017, 8, 309. [Google Scholar] [CrossRef]
- Sidaway-Lee, K.; Josse, E.-M.; Brown, A.; Gan, Y.; Halliday, K.J.; Graham, I.A.; Penfield, S. SPATULA Links Daytime Temperature and Plant Growth Rate. Curr. Biol. 2010, 20, 1493–1497. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef]
- Cacoullos, T. Expectation. Variance. Moments. In Exercises in Probability; Cacoullos, T., Ed.; Springer: New York, NY, USA, 1989; pp. 24–29. ISBN 978-1-4612-4526-1. [Google Scholar]
- Jun, S.H.; Yu, D.J.; Hur, Y.Y.; Lee, H.J. Identifying reliable methods for evaluating cold hardiness in grapevine buds and canes. Hortic. Environ. Biotechnol. 2021, 62, 871–878. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Zhang, Y.L.; Shao, H.; Lu, J. Differential Physio-Biochemical Responses to Cold Stress of Cold-Tolerant and Non-Tolerant Grapes (Vitis L.) from China. J. Agron. Crop. Sci. 2010, 196, 212–219. [Google Scholar] [CrossRef]
- Kishor, P.; Hong, Z.; Miao, G.H.; Hu, C.; Verma, D. Overexpression of Delta-Pyrroline-5-Carboxylate Synthetase Increases Proline Production and Confers Osmotolerance in Transgenic Plants. Plant Physiol. 1995, 108, 1387–1394. [Google Scholar] [CrossRef]
- Tahmasebi, A.; Pakniyat, H. Comparative analysis of some biochemical responses of winter and spring wheat cultivars under low temperature. Int. J. Agron. Agric. Res. (IJAAR) 2015, 6, 1–13. [Google Scholar]
- Mittler, R. Oxidative stress, antioxidants and stress tolerance. Trends Plant Sci. 2002, 7, 405–410. [Google Scholar] [CrossRef] [PubMed]
- Poorter, H.; Larcher, W. Physiological Plant Ecology, 4th ed.; Ann Bot: London, UK, 2004; Volume 93, pp. 751–760. [Google Scholar] [CrossRef]
- Knight, M.R.; Knight, H. Low-temperature perception leading to gene expression and cold tolerance in higher plants. New Phytol. 2012, 195, 737–751. [Google Scholar] [CrossRef]
- Martinière, A.; Shvedunova, M.; Thomson, A.J.; Evans, N.H.; Penfield, S.; Runions, J.; McWatters, H.G. Homeostasis of plasma membrane viscosity in fluctuating temperatures. New Phytol. 2011, 192, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, F.; Kopka, J.; Sung, D.Y.; Zhao, W.; Popp, M.; Porat, R.; Guy, C.L. Transcript and metabolite profiling during cold acclimation of Arabidopsis reveals an intricate relationship of cold-regulated gene expression with modifications in metabolite content. Plant J. 2007, 50, 967–981. [Google Scholar] [CrossRef]
- Dong, C.-H.; Zolman, B.K.; Bartel, B.; Lee, B.-H.; Stevenson, B.; Agarwal, M.; Zhu, J.-K. Disruption of Arabidopsis CHY1 reveals an important role of metabolic status in plant cold stress signaling. Mol. Plant 2009, 2, 59–72. [Google Scholar] [CrossRef]
- Lee, B.-H.; Lee, H.; Xiong, L.; Zhu, J.-K. A mitochondrial complex I defect impairs cold-regulated nuclear gene expression. Plant Cell 2002, 14, 1235–1251. [Google Scholar] [CrossRef]
- Jiang, F.-Q.; Hu, R.-J.; Zhang, Y.-W.; Li, X.-M.; Tong, L. Variations and trends of onset, cessation and length of climatic growing season over Xinjiang, NW China. Theor. Appl. Climatol. 2011, 106, 449–458. [Google Scholar] [CrossRef]
- de Rességuier, L.; Mary, S.; Le Roux, R.; Petitjean, T.; Quénol, H.; van Leeuwen, C. Temperature Variability at Local Scale in the Bordeaux Area. Relations With Environmental Factors and Impact on Vine Phenology. Front. Plant Sci. 2020, 11, 515. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Prueger, J.H. Temperature extremes: Effect on plant growth and development. Weather. Clim. Extrem. 2015, 10, 4–10. [Google Scholar] [CrossRef]
- Ji, Y.; Zhou, G.; Wang, L.; Wang, S.; Li, Z. Identifying climate risk causing maize (Zea mays L.) yield fluctuation by time-series data. Nat. Hazards 2019, 96, 1213–1222. [Google Scholar] [CrossRef]
- Benitez-Alfonso, Y.; Soanes, B.K.; Zimba, S.; Sinanaj, B.; German, L.; Sharma, V.; Bohra, A.; Kolesnikova, A.; Dunn, J.A.; Martin, A.C.; et al. Enhancing climate change resilience in agricultural crops. Curr. Biol. 2023, 33, R1246–R1261. [Google Scholar] [CrossRef] [PubMed]

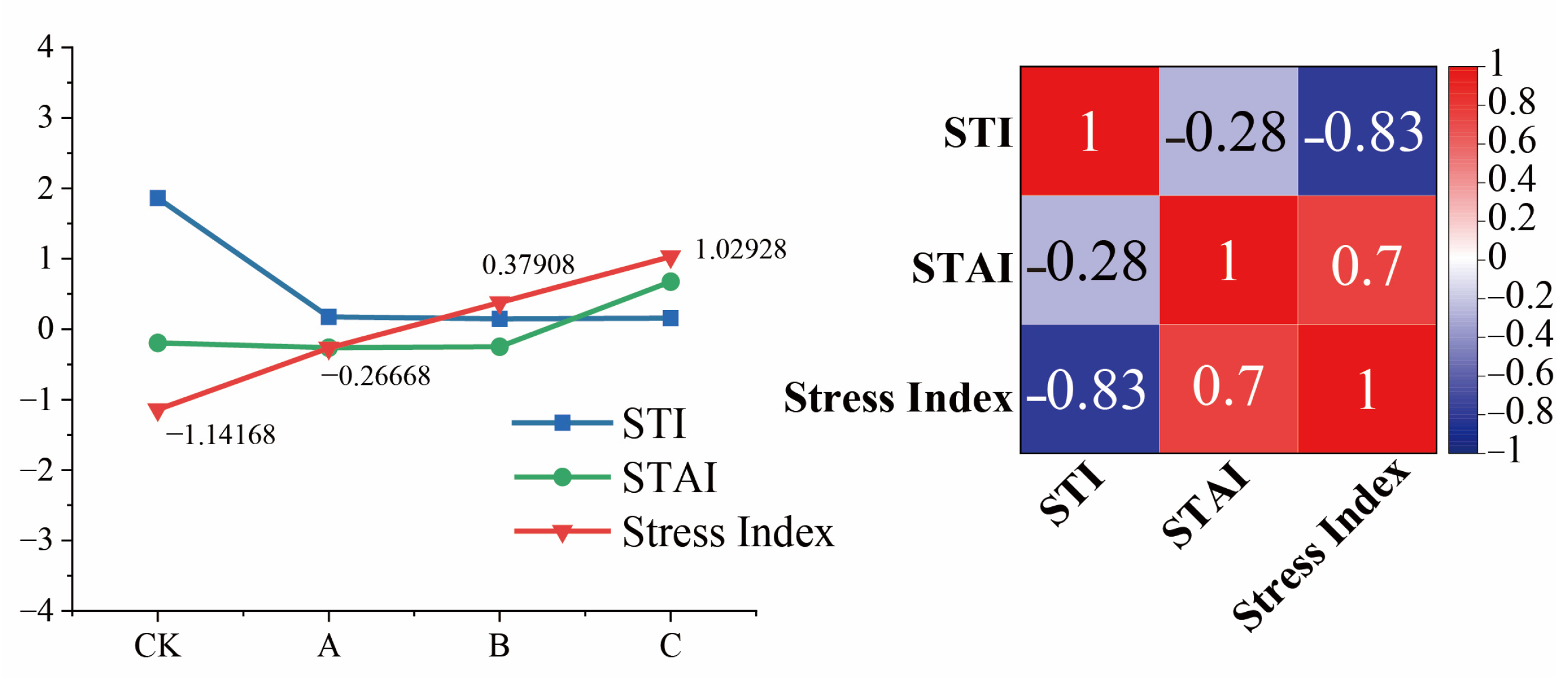

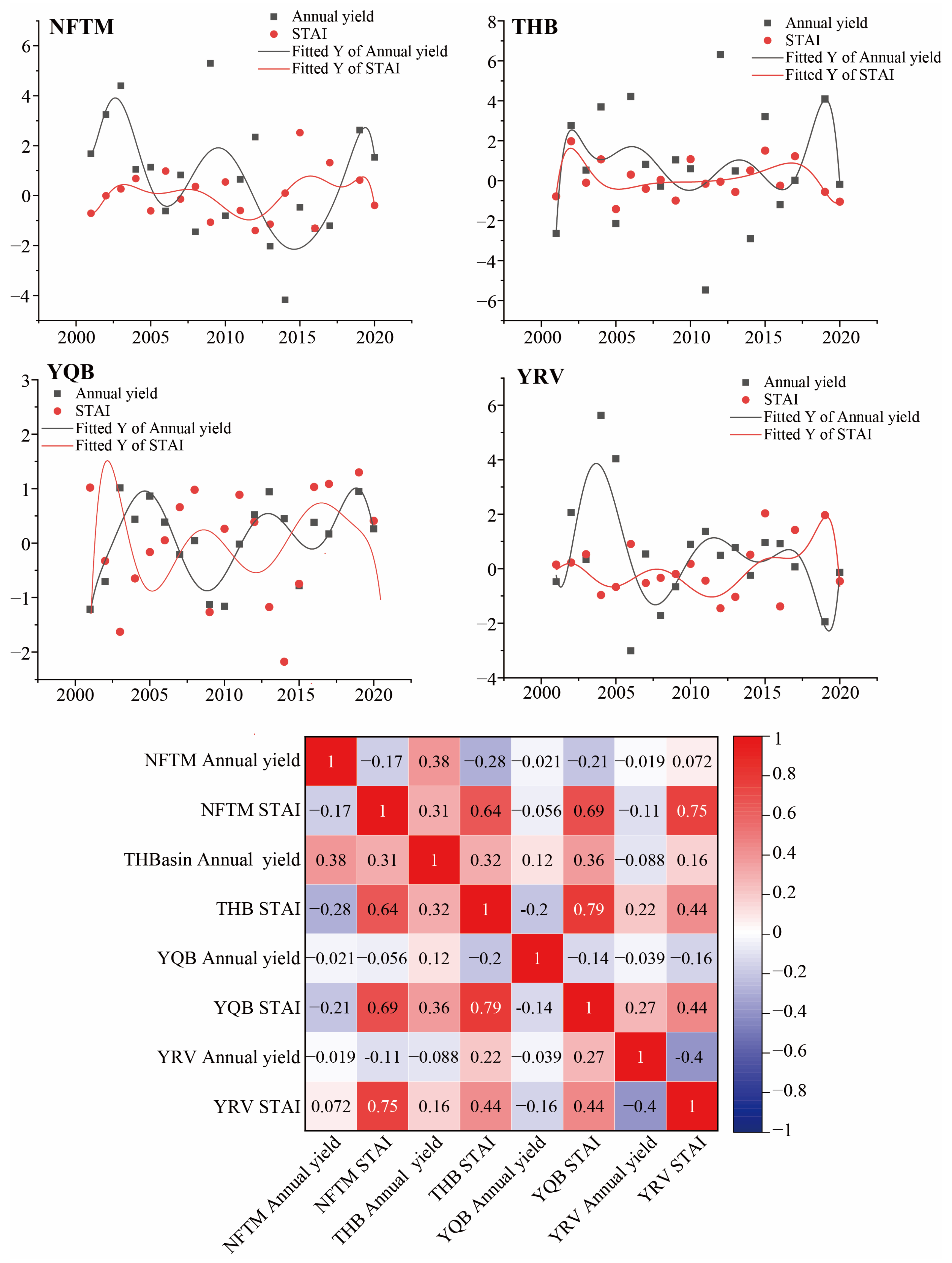
| Treatment Code | Treatment Details |
|---|---|
| CK | 4 °C for 24 h |
| A | Decreased at a rate of 4 °C/h to −10 °C, treated for 24 h |
| B | Decreased at a rate of 10 °C/s to −10 °C, treated for 24 h |
| C | Decreased at a rate of 4 °C/h to −5 °C, alternately treated between −5 °C and −15 °C for 24 h |
| D | Decreased at a rate of 4 °C/h to −20 °C, treated for 24 h |
| E | Decreased at a rate of 10 °C/s to −20 °C, treated for 24 h |
| F | Decreased at a rate of 4 °C/h to −15 °C, alternately treated between −15 °C and −25 °C for 24 h |
| Region. | Index | Max | Mini | Z | b | Linear Slope |
|---|---|---|---|---|---|---|
| NFTM | STAI | 2.52 | −1.39 | 0.16 | 0.01 | 0.02 |
| THB | STAI | 1.97 | −1.42 | 0.29 | 0.02 | 0.01 |
| YQB | STAI | 2.00 | −1.19 | 0.94 | 0.02 | 0.02 |
| YRV | STAI | 2.03 | −1.45 | 0.49 | 0.03 | 0.04 |
| NFTM | HSTAI | 3.92 | 0.62 | 4.55 | 0.18 | 0.19 |
| THB | HSTAI | 3.39 | 0.58 | −2.49 | −0.06 | −0.05 |
| YQB | HSTAI | 3.14 | 0.24 | −1.54 | 0 | 0.03 |
| YRV | HSTAI | 3.48 | 0.61 | 4.23 | 0.15 | 0.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Yang, J.; Wang, P.; Cheng, G.; Sun, Q. Effects of Temperature Fluctuations on Cabernet Sauvignon Branches and Wine Grape Appellation Yields: An Analysis Based on the Standardized Temperature Adaptation Index. Plants 2025, 14, 1886. https://doi.org/10.3390/plants14121886
Ma Y, Yang J, Wang P, Cheng G, Sun Q. Effects of Temperature Fluctuations on Cabernet Sauvignon Branches and Wine Grape Appellation Yields: An Analysis Based on the Standardized Temperature Adaptation Index. Plants. 2025; 14(12):1886. https://doi.org/10.3390/plants14121886
Chicago/Turabian StyleMa, Yunlong, Jinyue Yang, Ping Wang, Guoli Cheng, and Qinming Sun. 2025. "Effects of Temperature Fluctuations on Cabernet Sauvignon Branches and Wine Grape Appellation Yields: An Analysis Based on the Standardized Temperature Adaptation Index" Plants 14, no. 12: 1886. https://doi.org/10.3390/plants14121886
APA StyleMa, Y., Yang, J., Wang, P., Cheng, G., & Sun, Q. (2025). Effects of Temperature Fluctuations on Cabernet Sauvignon Branches and Wine Grape Appellation Yields: An Analysis Based on the Standardized Temperature Adaptation Index. Plants, 14(12), 1886. https://doi.org/10.3390/plants14121886







