Analysis of Electrome as a Tool for Plant Monitoring: Progress and Perspectives
Abstract
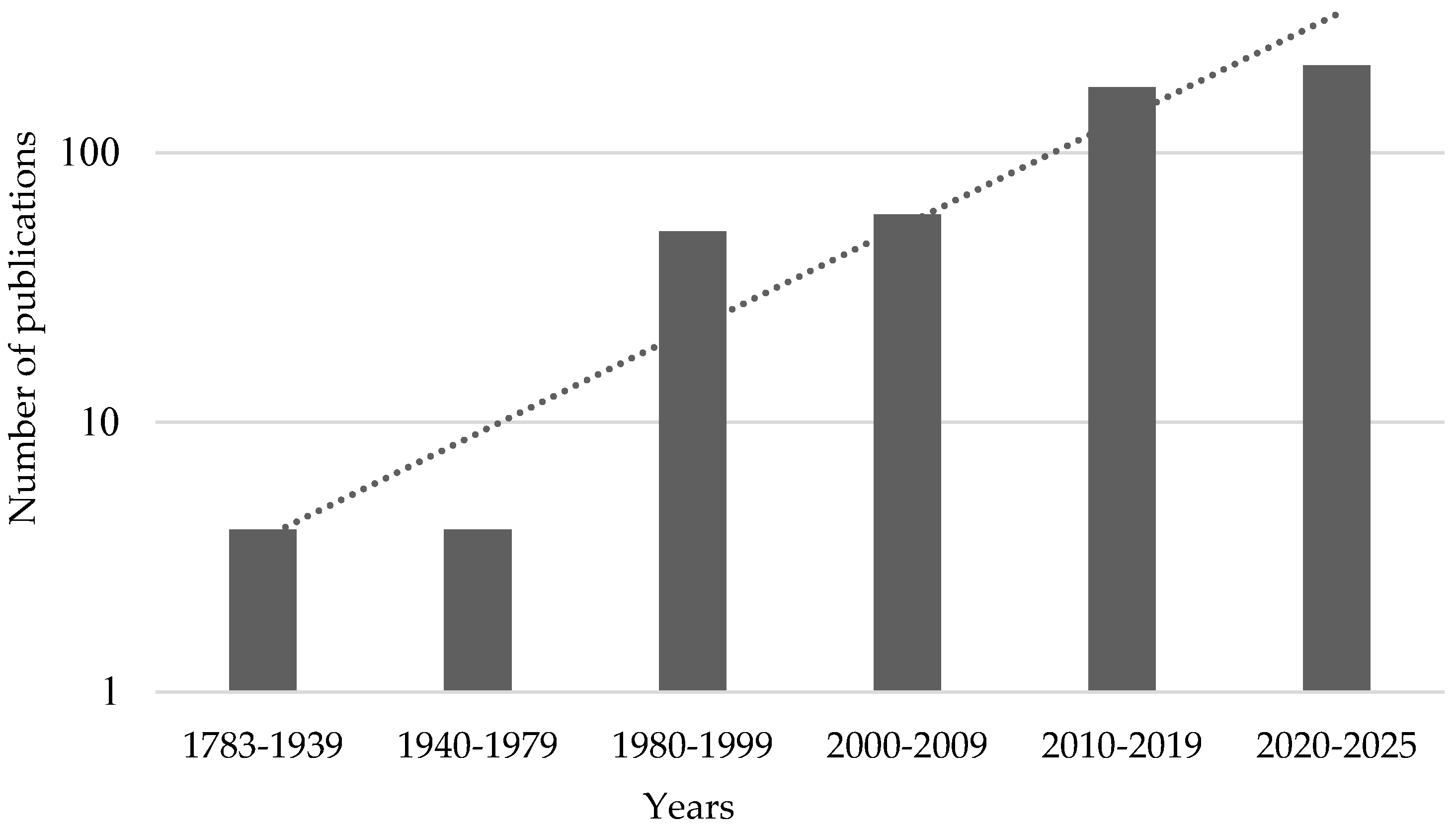
1. Introduction
2. Electrical Signals in Higher Plants: Brief Description
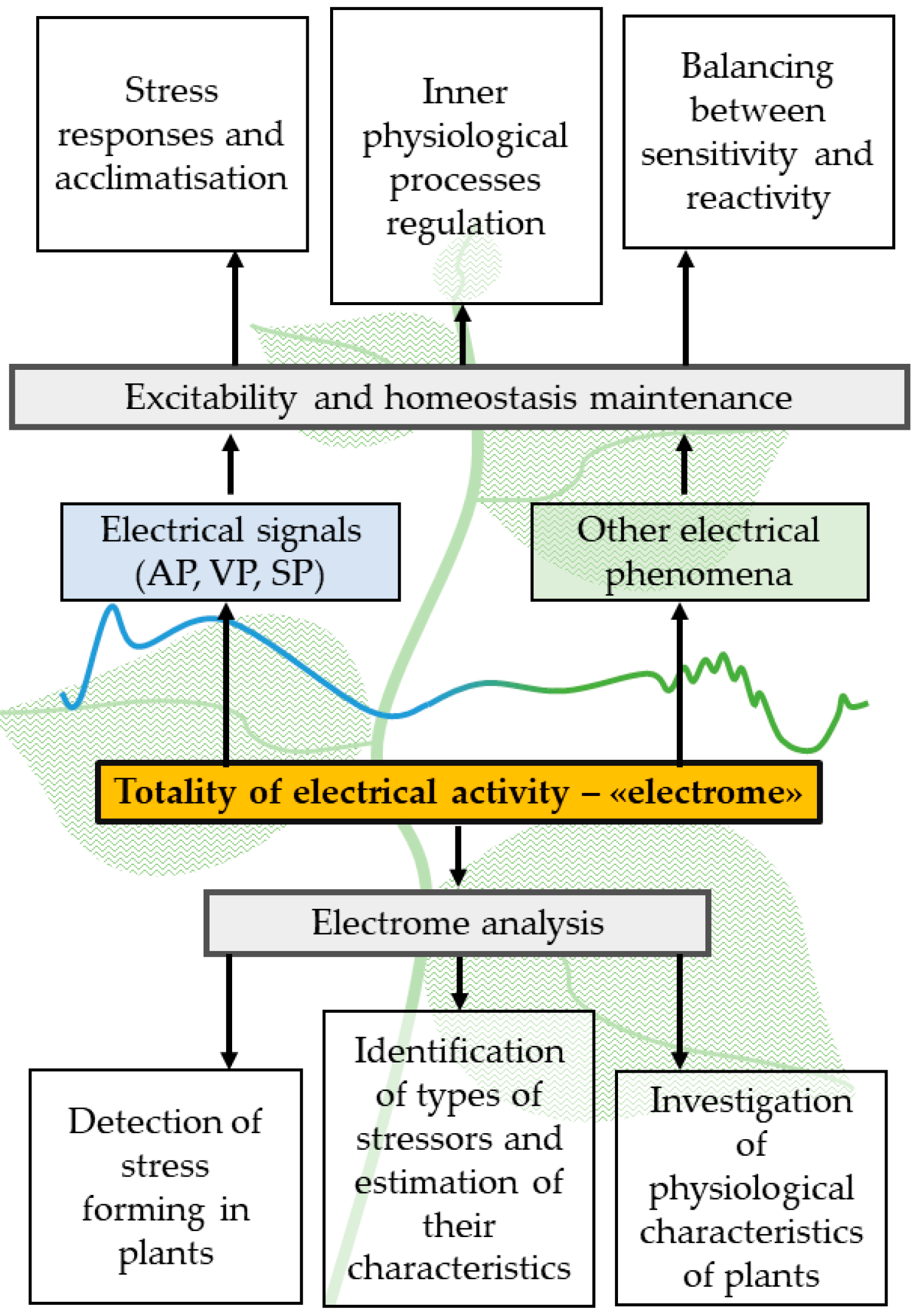
3. Limitations of Traditional Investigations of Electrical Signals and Plant ‘Electrome’ Concept
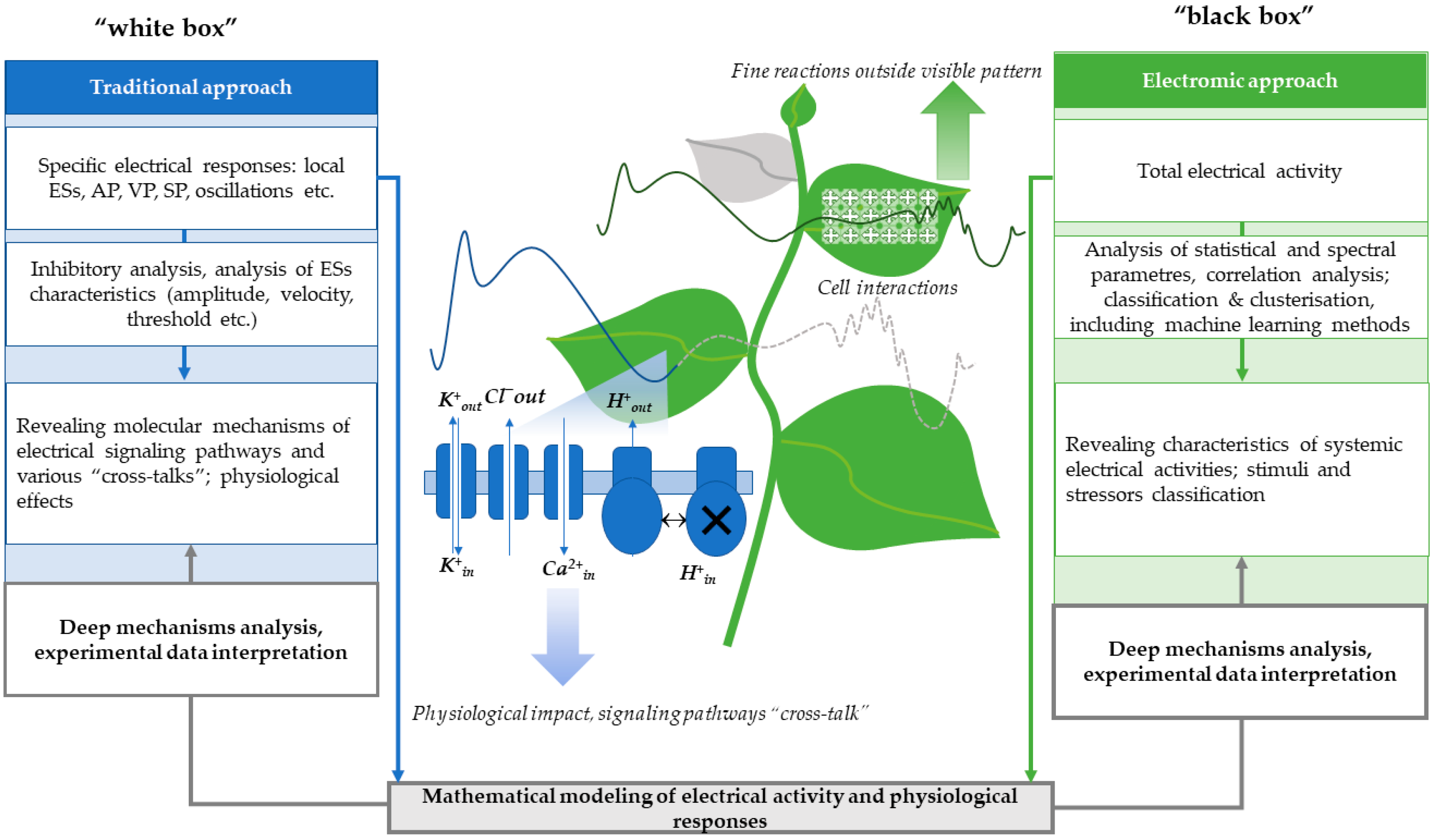
4. Methods of Measuring Electrical Activity and Approaches to Analyzing Electrome Parameters in Plants
5. Perspectives of Using Mathematical Models for Improving the Electrome Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AP | Action potential |
| EEG | Electroencephalography |
| EPG | Electrophytography |
| ESs | Electrical signals |
| ROS | Reactive oxygen species |
| SP | System potential |
| VP | Variation potential |
| WT | Wavelet transform |
References
- Shepherd, V.A. At the Roots of Plant Neurobiology. In Plant Electrophysiology; Volkov, A.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–43. [Google Scholar]
- Bertholon, P. De l’électricité Des Végétaux; Didot: Paris, France, 1783. [Google Scholar]
- Sanderson, J.B. Note on the Electrical Phenomena Which Accompany Irritation of the Leaf of Dionaea Muscipula. Proc. R. Soc. Lond. 1872, 21, 495–496. [Google Scholar]
- Darwin, C. Insectivorous Plants; John Murray: London, UK, 1875. [Google Scholar]
- Bose, J.C. The Nervous Mechanism of Plants. Nature 1926, 118, 654–655. [Google Scholar] [CrossRef]
- Chaparro-Cárdenas, S.L.; Ramirez Bautista, J.A.; Gamboa Contreras, W.; Moreno-Chacón, A.L.; Vargas-Tangua, F.C. Plant Electrophysiology: Bibliometric Analysis, Methods and Applications in the Monitoring of Plant-Environment Interactions. DYNA 2021, 88, 112–123. [Google Scholar] [CrossRef]
- Sukhov, V.; Sukhova, E.; Vodeneev, V. Long-Distance Electrical Signals as a Link between the Local Action of Stressors and the Systemic Physiological Responses in Higher Plants. Prog. Biophys. Mol. Biol. 2019, 146, 63–84. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhao, D.-J.; Wang, Z.-Y.; Wang, Z.-Y.; Tang, G.; Huang, L. Plant Electrical Signal Classification Based on Waveform Similarity. Algorithms 2016, 9, 70. [Google Scholar] [CrossRef]
- Souza, G.M.; Ferreira, A.S.; Saraiva, G.F.R.; Toledo, G.R.A. Plant “Electrome” Can Be Pushed toward a Self-Organized Critical State by External Cues: Evidences from a Study with Soybean Seedlings Subject to Different Environmental Conditions. Plant Signal. Behav. 2017, 12, e1290040. [Google Scholar] [CrossRef]
- De Toledo, G.R.A.; Parise, A.G.; Simmi, F.Z.; Costa, A.V.L.; Senko, L.G.S.; Debono, M.-W.; Souza, G.M. Plant Electrome: The Electrical Dimension of Plant Life. Theor. Exp. Plant Physiol. 2019, 31, 21–46. [Google Scholar] [CrossRef]
- Debono, M.-W.; Souza, G.M. Plants as Electromic Plastic Interfaces: A Mesological Approach. Prog. Biophys. Mol. Biol. 2019, 146, 123–133. [Google Scholar] [CrossRef]
- Chatterjee, S.K.; Ghosh, S.; Das, S.; Manzella, V.; Vitaletti, A.; Masi, E.; Santopolo, L.; Mancuso, S.; Maharatna, K. Forward and Inverse Modelling Approaches for Prediction of Light Stimulus from Electrophysiological Response in Plants. Measurement 2014, 53, 101–116. [Google Scholar] [CrossRef]
- Chatterjee, S.K.; Das, S.; Maharatna, K.; Masi, E.; Santopolo, L.; Mancuso, S.; Vitaletti, A. Exploring Strategies for Classification of External Stimuli Using Statistical Features of the Plant Electrical Response. J. R. Soc. Interface 2015, 12, 20141225. [Google Scholar] [CrossRef]
- Chatterjee, S.K.; Malik, O.; Gupta, S. Chemical Sensing Employing Plant Electrical Signal Response-Classification of Stimuli Using Curve Fitting Coefficients as Features. Biosensors 2018, 8, 83. [Google Scholar] [CrossRef] [PubMed]
- Saraiva, G.F.R.; Ferreira, A.S.; Souza, G.M. Osmotic Stress Decreases Complexity Underlying the Electrophysiological Dynamic in Soybean. Plant Biol. J. 2017, 19, 702–708. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.-H.; Wang, Z.-Y.; Yao, J.-P.; Zhou, Q.; Zhao, P.-F.; Wang, Z.-Y.; Huang, L. Using a One-Dimensional Convolutional Neural Network with a Conditional Generative Adversarial Network to Classify Plant Electrical Signals. Comput. Electron. Agric. 2020, 174, 105464. [Google Scholar] [CrossRef]
- Simmi, F.Z.; Dallagnol, L.J.; Ferreira, A.S.; Pereira, D.R.; Souza, G.M. Electrome Alterations in a Plant-Pathogen System: Toward Early Diagnosis. Bioelectrochemistry 2020, 133, 107493. [Google Scholar] [CrossRef]
- De Toledo, G.R.A.; Reissig, G.N.; Senko, L.G.S.; Pereira, D.R.; Da Silva, A.F.; Souza, G.M. Common Bean under Different Water Availability Reveals Classifiable Stimuli-Specific Signatures in Plant Electrome. Plant Signal. Behav. 2024, 19, 2333144. [Google Scholar] [CrossRef]
- Gilroy, S.; Białasek, M.; Suzuki, N.; Górecka, M.; Devireddy, A.R.; Karpiński, S.; Mittler, R. ROS, Calcium, and Electric Signals: Key Mediators of Rapid Systemic Signaling in Plants. Plant Physiol. 2016, 171, 1606–1615. [Google Scholar] [CrossRef]
- Szechyńska-Hebda, M.; Lewandowska, M.; Karpiński, S. Electrical Signaling, Photosynthesis and Systemic Acquired Acclimation. Front. Physiol. 2017, 8, 684. [Google Scholar] [CrossRef]
- García-Servín, M.Á.; Mendoza-Sánchez, M.; Contreras-Medina, L.M. Electrical Signals as an Option of Communication with Plants: A Review. Theor. Exp. Plant Physiol. 2021, 33, 125–139. [Google Scholar] [CrossRef]
- Li, J.-H.; Fan, L.-F.; Zhao, D.-J.; Zhou, Q.; Yao, J.-P.; Wang, Z.-Y.; Huang, L. Plant Electrical Signals: A Multidisciplinary Challenge. J. Plant Physiol. 2021, 261, 153418. [Google Scholar] [CrossRef]
- Stahlberg, R.; Cleland, R.E.; Van Volkenburgh, E. Slow Wave Potentials—A Propagating Electrical Signal Unique to Higher Plants. In Communication in Plants; Baluška, F., Mancuso, S., Volkmann, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 291–308. [Google Scholar] [CrossRef]
- Barlow, P.W. Reflections on ‘Plant Neurobiology’. Biosystems 2008, 92, 132–147. [Google Scholar] [CrossRef]
- Farmer, E.E.; Gao, Y.; Lenzoni, G.; Wolfender, J.; Wu, Q. Wound- and Mechanostimulated Electrical Signals Control Hormone Responses. New Phytol. 2020, 227, 1037–1050. [Google Scholar] [CrossRef] [PubMed]
- Staves, M.; Wayne, R. The Touch-Induced Action Potential in Chara: Inquiry into the Ionic Basis and the Mechanoreceptor. Funct. Plant Biol. 1993, 20, 471. [Google Scholar] [CrossRef]
- Yan, X.; Wang, Z.; Huang, L.; Wang, C.; Hou, R.; Xu, Z.; Qiao, X. Research Progress on Electrical Signals in Higher Plants. Prog. Nat. Sci. 2009, 19, 531–541. [Google Scholar] [CrossRef]
- Kupisz, K.; Dziubińska, H.; Trębacz, K. Generation of Action Potential-Type Changes in Response to Darkening and Illumination as Indication of the Plasma Membrane Proton Pump Status in Marchantia Polymorpha. Acta Physiol. Plant 2017, 39, 82. [Google Scholar] [CrossRef]
- Fromm, J.; Lautner, S. Electrical Signals and Their Physiological Significance in Plants. Plant Cell Environ. 2007, 30, 249–257. [Google Scholar] [CrossRef]
- Lautner, S.; Grams, T.E.E.; Matyssek, R.; Fromm, J. Characteristics of Electrical Signals in Poplar and Responses in Photosynthesis. Plant Physiol. 2005, 138, 2200–2209. [Google Scholar] [CrossRef]
- Baluška, F. (Ed.) Long-Distance Systemic Signaling and Communication in Plants; Signaling and Communication in Plants; Springer: Berlin/Heidelberg, Germany, 2013; Volume 19. [Google Scholar] [CrossRef]
- Klejchova, M.; Silva-Alvim, F.A.L.; Blatt, M.R.; Alvim, J.C. Membrane Voltage as a Dynamic Platform for Spatiotemporal Signaling, Physiological, and Developmental Regulation. Plant Physiol. 2021, 185, 1523–1541. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Maischak, H.; Mithöfer, A.; Boland, W.; Felle, H.H. System Potentials, a Novel Electrical Long-Distance Apoplastic Signal in Plants, Induced by Wounding. Plant Physiol. 2009, 149, 1593–1600. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Mithöfer, A.; Will, T.; Felle, H.H.; Furch, A.C.U. Herbivore-Triggered Electrophysiological Reactions: Candidates for Systemic Signals in Higher Plants and the Challenge of Their Identification. Plant Physiol. 2016, 170, 2407–2419. [Google Scholar] [CrossRef]
- Yudina, L.; Sukhova, E.; Popova, A.; Zolin, Y.; Abasheva, K.; Grebneva, K.; Sukhov, V. Local Action of Moderate Heating and Illumination Induces Propagation of Hyperpolarization Electrical Signals in Wheat Plants. Front. Sustain. Food Syst. 2023, 6, 1062449. [Google Scholar] [CrossRef]
- Yudina, L.; Popova, A.; Zolin, Y.; Sukhova, E.; Sukhov, V. Local Action of Increased Pressure Induces Hyperpolarization Electrical Signals and Influences Photosynthetic Light Reactions in Wheat Plants. Plants 2023, 12, 2570. [Google Scholar] [CrossRef] [PubMed]
- Yudina, L.; Sukhova, E.; Popova, A.; Zolin, Y.; Abasheva, K.; Grebneva, K.; Sukhov, V. Hyperpolarization Electrical Signals Induced by Local Action of Moderate Heating Influence Photosynthetic Light Reactions in Wheat Plants. Front. Plant Sci. 2023, 14, 1153731. [Google Scholar] [CrossRef] [PubMed]
- Yudina, L.; Popova, A.; Zolin, Y.; Grebneva, K.; Sukhova, E.; Sukhov, V. Local Action of Moderate Heating and Illumination Induces Electrical Signals, Suppresses Photosynthetic Light Reactions, and Increases Drought Tolerance in Wheat Plants. Plants 2024, 13, 1173. [Google Scholar] [CrossRef] [PubMed]
- Sukhova, E.M.; Yudina, L.M.; Sukhov, V.S. Changes in Activity of the Plasma Membrane H+-ATPase as a Link Between Formation of Electrical Signals and Induction of Photosynthetic Responses in Higher Plants. Biochemistry 2023, 88, 1488–1503. [Google Scholar] [CrossRef]
- Vodeneev, V.; Akinchits, E.; Sukhov, V. Variation Potential in Higher Plants: Mechanisms of Generation and Propagation. Plant Signal. Behav. 2015, 10, e1057365. [Google Scholar] [CrossRef]
- Malone, M. Wound-induced Hydraulic Signals and Stimulus Transmission in Mimosa pudica L. New Phytol. 1994, 128, 49–56. [Google Scholar] [CrossRef]
- Wildon, D.C.; Thain, J.F.; Minchin, P.E.H.; Gubb, I.R.; Reilly, A.J.; Skipper, Y.D.; Doherty, H.M.; O’Donnell, P.J.; Bowles, D.J. Electrical Signalling and Systemic Proteinase Inhibitor Induction in the Wounded Plant. Nature 1992, 360, 62–65. [Google Scholar] [CrossRef]
- Mousavi, S.A.R.; Chauvin, A.; Pascaud, F.; Kellenberger, S.; Farmer, E.E. GLUTAMATE RECEPTOR-LIKE Genes Mediate Leaf-to-Leaf Wound Signalling. Nature 2013, 500, 422–426. [Google Scholar] [CrossRef]
- Kumari, A.; Chételat, A.; Nguyen, C.T.; Farmer, E.E. Arabidopsis H+-ATPase AHA1 Controls Slow Wave Potential Duration and Wound-Response Jasmonate Pathway Activation. Proc. Natl. Acad. Sci. USA 2019, 116, 20226–20231. [Google Scholar] [CrossRef]
- Białasek, M.; Górecka, M.; Mittler, R.; Karpiński, S. Evidence for the Involvement of Electrical, Calcium and ROS Signaling in the Systemic Regulation of Non-Photochemical Quenching and Photosynthesis. Plant Cell Physiol. 2017, 58, 207–215. [Google Scholar] [CrossRef]
- Furch, A.C.U.; Zimmermann, M.R.; Will, T.; Hafke, J.B.; Van Bel, A.J.E. Remote-Controlled Stop of Phloem Mass Flow by Biphasic Occlusion in Cucurbita Maxima. J. Exp. Bot. 2010, 61, 3697–3708. [Google Scholar] [CrossRef] [PubMed]
- Van Bel, A.J.E.; Furch, A.C.U.; Will, T.; Buxa, S.V.; Musetti, R.; Hafke, J.B. Spread the News: Systemic Dissemination and Local Impact of Ca2+ Signals along the Phloem Pathway. J. Exp. Bot. 2014, 65, 1761–1787. [Google Scholar] [CrossRef] [PubMed]
- Lautner, S.; Stummer, M.; Matyssek, R.; Fromm, J.; Grams, T.E.E. Involvement of Respiratory Processes in the Transient Knockout of Net CO2 Uptake in Mimosa Pudica upon Heat Stimulation. Plant Cell Environ. 2014, 37, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Kaiser, H.; Grams, T.E.E. Rapid Hydropassive Opening and Subsequent Active Stomatal Closure Follow Heat-Induced Electrical Signals in Mimosa pudica*. J. Exp. Bot. 2006, 57, 2087–2092. [Google Scholar] [CrossRef]
- Retivin, V.G.; Opritov, V.A.; Fedulina, S.B. Generation of Action Potential Induces Preadaptation of Cucurbita pepo L. Stem Tissues to Freezing Injury. Russ. J. Plant Physiol. 1997, 44, 432–442. [Google Scholar]
- Retivin, V.G.; Opritov, V.A.; Lobov, S.A.; Tarakanov, S.A.; Khudyakov, V.A. Changes in the Resistance of Photosynthesizing Cotyledon Cells of Pumpkin Seedlings to Cooling and Heating, as Induced by the Stimulation of the Root System with KCl Solution. Russ. J. Plant Physiol. 1999, 46, 689–696. [Google Scholar]
- Szechyńska-Hebda, M.; Kruk, J.; Górecka, M.; Karpińska, B.; Karpiński, S. Evidence for Light Wavelength-Specific Photoelectrophysiological Signaling and Memory of Excess Light Episodes in Arabidopsis. Plant Cell 2010, 22, 2201–2218. [Google Scholar] [CrossRef]
- Sukhov, V.; Surova, L.; Sherstneva, O.; Bushueva, A.; Vodeneev, V. Variation Potential Induces Decreased PSI Damage and Increased PSII Damage under High External Temperatures in Pea. Funct. Plant Biol. 2015, 42, 727. [Google Scholar] [CrossRef]
- Zandalinas, S.I.; Fichman, Y.; Devireddy, A.R.; Sengupta, S.; Azad, R.K.; Mittler, R. Systemic Signaling during Abiotic Stress Combination in Plants. Proc. Natl. Acad. Sci. USA 2020, 117, 13810–13820. [Google Scholar] [CrossRef]
- Grinberg, M.A.; Gudkov, S.V.; Balalaeva, I.V.; Gromova, E.; Sinitsyna, Y.; Sukhov, V.; Vodeneev, V. Effect of Chronic β-Radiation on Long-Distance Electrical Signals in Wheat and Their Role in Adaptation to Heat Stress. Environ. Exp. Bot. 2021, 184, 104378. [Google Scholar] [CrossRef]
- Yudina, L.; Sherstneva, O.; Sukhova, E.; Grinberg, M.; Mysyagin, S.; Vodeneev, V.; Sukhov, V. Inactivation of H+-ATPase Participates in the Influence of Variation Potential on Photosynthesis and Respiration in Peas. Plants 2020, 9, 1585. [Google Scholar] [CrossRef] [PubMed]
- Grams, T.E.E.; Lautner, S.; Felle, H.H.; Matyssek, R.; Fromm, J. Heat-induced Electrical Signals Affect Cytoplasmic and Apoplastic pH as Well as Photosynthesis during Propagation through the Maize Leaf. Plant Cell Environ. 2009, 32, 319–326. [Google Scholar] [CrossRef]
- Mudrilov, M.; Ladeynova, M.; Grinberg, M.; Balalaeva, I.; Vodeneev, V. Electrical Signaling of Plants under Abiotic Stressors: Transmission of Stimulus-Specific Information. Int. J. Mol. Sci. 2021, 22, 10715. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.-J.; Wang, Z.-Y.; Li, J.; Wen, X.; Liu, A.; Huang, L.; Wang, X.-D.; Hou, R.-F.; Wang, C. Recording Extracellular Signals in Plants: A Modeling and Experimental Study. Math. Comput. Model. 2013, 58, 556–563. [Google Scholar] [CrossRef]
- Calvo, P.; Gagliano, M.; Souza, G.M.; Trewavas, A. Plants Are Intelligent, Here’s How. Ann. Bot. 2020, 125, 11–28. [Google Scholar] [CrossRef]
- González Juclà , D.I.; Najdenovska, E.; Dutoit, F.; Raileanu, L.E. Detecting Stress Caused by Nitrogen Deficit Using Deep Learning Techniques Applied on Plant Electrophysiological Data. Sci. Rep. 2023, 13, 9633. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Leng, Q.; Huang, L.; Zhao, L.-L.; Xu, Z.-L.; Hou, R.-F.; Wang, C. Monitoring System for Electrical Signals in Plants in the Greenhouse and Its Applications. Biosyst. Eng. 2009, 103, 1–11. [Google Scholar] [CrossRef]
- Oyarce, P.; Gurovich, L. Electrical Signals in Avocado Trees: Responses to Light and Water Availability Conditions. Plant Signal. Behav. 2010, 5, 34–41. [Google Scholar] [CrossRef]
- Vuralhan-Eckert, J.; Lautner, S.; Fromm, J. Effect of Simultaneously Induced Environmental Stimuli on Electrical Signalling and Gas Exchange in Maize Plants. J. Plant Physiol. 2018, 223, 32–36. [Google Scholar] [CrossRef]
- Cooper, R.L.; Thomas, M.A.; Vascassenno, R.M.; Brock, K.E.; McLetchie, D.N. Measuring Electrical Responses during Acute Exposure of Roots and Rhizoids of Plants to Compounds Using a Flow-Through System. Methods Protoc. 2022, 5, 62. [Google Scholar] [CrossRef]
- Buss, E.; Aust, T.; Wahby, M.; Rabbel, T.-L.; Kernbach, S.; Hamann, H. Stimulus Classification with Electrical Potential and Impedance of Living Plants: Comparing Discriminant Analysis and Deep-Learning Methods. Bioinspir. Biomim. 2023, 18, 025003. [Google Scholar] [CrossRef]
- Wang, G.; Hu, C.; Zhou, J.; Liu, Y.; Cai, J.; Pan, C.; Wang, Y.; Wu, X.; Shi, K.; Xia, X.; et al. Systemic Root-Shoot Signaling Drives Jasmonate-Based Root Defense against Nematodes. Curr. Biol. 2019, 29, 3430–3438.e4. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, M.R.; Felle, H.H. Dissection of Heat-Induced Systemic Signals: Superiority of Ion Fluxes to Voltage Changes in Substomatal Cavities. Planta 2009, 229, 539–547. [Google Scholar] [CrossRef] [PubMed]
- Hafke, J.B.; Furch, A.C.U.; Fricker, M.D.; Van Bel, A.J.E. Forisome Dispersion in Vicia faba Is Triggered by Ca2+ Hotspots Created by Concerted Action of Diverse Ca2+ Channels in Sieve Element. Plant Signal. Behav. 2009, 4, 968–972. [Google Scholar] [CrossRef] [PubMed]
- Saraiva, G.F.R.; Ferreira, A.S.; Souza, G.M. Beyond APs and VPs: Evidences of Chaos and Self-Organized Criticality in Electrical Signals in Plants. bioRxiv 2016. [Google Scholar] [CrossRef]
- Zhou, J.; Fan, P.; Zhou, S.; Pan, Y.; Ping, J. Machine Learning-Assisted Implantable Plant Electrophysiology Microneedle Sensor for Plant Stress Monitoring. Biosens. Bioelectron. 2025, 271, 117062. [Google Scholar] [CrossRef]
- Krol, E.; Dziubinska, H.; Stolarz, M.; Trebacz, K. Effects of Ion Channel Inhibitors on Cold- and Electrically-Induced Action Potentials in Dionaea muscipula. Biol. Plant. 2006, 50, 411–416. [Google Scholar] [CrossRef]
- Opritov, V.A.; Lobov, S.A.; Pyatygin, S.S.; Mysyagin, S.A. Analysis of Possible Involvement of Local Bioelectric Responses in Chilling Perception by Higher Plants Exemplified by Cucurbita pepo. Russ. J. Plant Physiol. 2005, 52, 801–808. [Google Scholar] [CrossRef]
- Pikulenko, M.M.; Bulychev, A.A. Light-Triggered Action Potentials and Changes in Quantum Efficiency of Photosystem II in Anthoceros Cells. Russ. J. Plant Physiol. 2005, 52, 584–590. [Google Scholar] [CrossRef]
- Nishizaki, Y. Rhythmic Changes in the Resting Potential of a Single Plant Cell. Plant Cell Physiol. 1968, 9, 613–616. [Google Scholar] [CrossRef]
- Pickard, B.G. Electrical Signals in Higher Plants. Naturwissenschaften 1974, 61, 60–64. [Google Scholar] [CrossRef]
- Fisahn, J.; Mcconnaughey, T.; Lucas, W.J. Oscillations in Extracellular Current, External pH and Membrane Potential and Conductance in the Alkaline Bands of Nitella and Chara. J. Exp. Bot. 1989, 40, 1185–1193. [Google Scholar] [CrossRef]
- Debono, M.-W. Dynamic Protoneural Networks in Plants: A New Approach of Spontaneous Extracellular Potential Variations. Plant Signal. Behav. 2013, 8, e24207. [Google Scholar] [CrossRef] [PubMed]
- Toko, K.; Souda, M.; Matsuno, T.; Yamafuji, K. Oscillations of Electrical Potential along a Root of a Higher Plant. Biophys. J. 1990, 57, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Shabala, S. Physiological Implications of Ultradian Oscillations in Plant Roots. In Roots: The Dynamic Interface Between Plants and the Earth; Abe, J., Ed.; Springer: Dordrecht, The Netherlands, 2003; pp. 217–226. [Google Scholar] [CrossRef]
- Damineli, D.S.C.; Portes, M.T.; Feijó, J.A. Electrifying Rhythms in Plant Cells. Curr. Opin. Cell Biol. 2022, 77, 102113. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Qin, X.-H.; Li, J.-H.; Fan, L.-F.; Zhou, Q.; Wang, Y.-Q.; Zhao, X.; Xie, C.-J.; Wang, Z.-Y.; Huang, L. Highly Reproducible Periodic Electrical Potential Changes Associated with Salt Tolerance in Wheat Plants. Environ. Exp. Bot. 2019, 160, 120–130. [Google Scholar] [CrossRef]
- Yao, J.; Ling, Y.; Hou, P.; Wang, Z.; Huang, L. A Graph Neural Network Model for Deciphering the Biological Mechanisms of Plant Electrical Signal Classification. Appl. Soft Comput. 2023, 137, 110153. [Google Scholar] [CrossRef]
- Novak, B.; Greppin, H. High-Frequency Oscillations and Circadian Rhythm of the Membrane Potential in Spinach Leaves. Planta 1979, 144, 235–240. [Google Scholar] [CrossRef]
- Kollist, H.; Zandalinas, S.I.; Sengupta, S.; Nuhkat, M.; Kangasjärvi, J.; Mittler, R. Rapid Responses to Abiotic Stress: Priming the Landscape for the Signal Transduction Network. Trends Plant Sci. 2019, 24, 25–37. [Google Scholar] [CrossRef]
- Debono, M.-W. The Cognitive Power of Plants: From Mesological Plasticity to Non-Explicit Cognitive Skills. Theor. Exp. Plant Physiol. 2024, 36, 477–490. [Google Scholar] [CrossRef]
- Costa, Á.V.L.; Oliveira, T.F.D.C.; Posso, D.A.; Reissig, G.N.; Parise, A.G.; Barros, W.S.; Souza, G.M. Systemic Signals Induced by Single and Combined Abiotic Stimuli in Common Bean Plants. Plants 2023, 12, 924. [Google Scholar] [CrossRef] [PubMed]
- Bhadra, N.; Chatterjee, S.K.; Das, S. Multiclass Classification of Environmental Chemical Stimuli from Unbalanced Plant Electrophysiological Data. PLoS ONE 2023, 18, e0285321. [Google Scholar] [CrossRef] [PubMed]
- Salvador-Recatalà, V.; Tjallingii, W.F. A New Application of the Electrical Penetration Graph (EPG) for Acquiring and Measuring Electrical Signals in Phloem Sieve Elements. JoVE 2015, 101, 52826. [Google Scholar] [CrossRef]
- Furch, A.C.U.; Zimmermann, M.R.; Will, T. Measurement of Electropotential Waves in Intact Sieve Elements Using Aphids as Bioelectrodes. In Phloem; Liesche, J., Ed.; Methods in Molecular Biology; Springer: New York, NY, USA, 2019; Volume 2014, pp. 449–457. [Google Scholar] [CrossRef]
- Cooper, R.L.; Thomas, M.A.; McLetchie, D.N. Impedance Measures for Detecting Electrical Responses during Acute Injury and Exposure of Compounds to Roots of Plants. Methods Protoc. 2022, 5, 56. [Google Scholar] [CrossRef]
- Miller, A.J.; Cookson, S.J.; Smith, S.J.; Wells, D.M. The Use of Microelectrodes to Investigate Compartmentation and the Transport of Metabolized Inorganic Ions in Plants. J. Exp. Bot. 2001, 52, 541–549. [Google Scholar] [CrossRef]
- Fromm, J.; Hajirezaei, M.-R.; Becker, V.K.; Lautner, S. Electrical Signaling along the Phloem and Its Physiological Responses in the Maize Leaf. Front. Plant Sci. 2013, 4, 239. [Google Scholar] [CrossRef]
- Zimmermann, M.R.; Hafke, J.B.; Paulmann, M.K.; Furch, A.C.U. Measurement of Electropotential Waves in Intact Phloem Sieve Elements Using Microelectrodes. In Phloem; Liesche, J., Ed.; Methods in Molecular Biology; Springer: New York, NY, USA, 2019; Volume 2014, pp. 439–447. [Google Scholar] [CrossRef]
- Najdenovska, E.; Dutoit, F.; Tran, D.; Plummer, C.; Wallbridge, N.; Camps, C.; Raileanu, L.E. Classification of Plant Electrophysiology Signals for Detection of Spider Mites Infestation in Tomatoes. Appl. Sci. 2021, 11, 1414. [Google Scholar] [CrossRef]
- Stanković, B.; Davies, E. Both Action Potentials and Variation Potentials Induce Proteinase Inhibitor Gene Expression in Tomato. FEBS Lett. 1996, 390, 275–279. [Google Scholar] [CrossRef]
- Cabral, E.F.; Pecora, P.C.; Arce, A.I.C.; Tech, A.R.B.; Costa, E.J.X. The Oscillatory Bioelectrical Signal from Plants Explained by a Simulated Electrical Model and Tested Using Lempel–Ziv Complexity. Comput. Electron. Agric. 2011, 76, 1–5. [Google Scholar] [CrossRef]
- Masi, E.; Azzarello, E.; Mancuso, S. Multielectrode Array: A New Approach to Plant Electrophysiology. In Plant Electrophysiology; Volkov, A.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 187–204. [Google Scholar] [CrossRef]
- Zhao, D.-J.; Wang, Z.-Y.; Huang, L.; Jia, Y.-P.; Leng, J.Q. Spatio-Temporal Mapping of Variation Potentials in Leaves of Helianthus annuus L. Seedlings in Situ Using Multi-Electrode Array. Sci. Rep. 2014, 4, 5435. [Google Scholar] [CrossRef]
- Armada-Moreira, A.; Dar, A.M.; Zhao, Z.; Cea, C.; Gelinas, J.; Berggren, M.; Costa, A.; Khodagholy, D.; Stavrinidou, E. Plant Electrophysiology with Conformable Organic Electronics: Deciphering the Propagation of Venus Flytrap Action Potentials. Sci. Adv. 2023, 9, eadh4443. [Google Scholar] [CrossRef] [PubMed]
- Favre, P.; Agosti, R.D. Voltage-dependent Action Potentials in Arabidopsis thaliana. Physiol. Plant. 2007, 131, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Favre, P.; Greppin, H.; Degli Agosti, R. Accession-Dependent Action Potentials in Arabidopsis. J. Plant Physiol. 2011, 168, 653–660. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Wang, L.; Li, H.; Li, D. Studies On the Weak Electric Wave Signals of Plants by the Wavelet Analysis. In Proceedings of the 2007 Chinese Control Conference, Zhangjiajie, China, 26–31 July 2007; IEEE: Piscataway, NJ, USA, 2006; pp. 104–107. [Google Scholar] [CrossRef]
- Das, S.; Ajiwibawa, B.J.; Chatterjee, S.K.; Ghosh, S.; Maharatna, K.; Dasmahapatra, S.; Vitaletti, A.; Masi, E.; Mancuso, S. Drift Removal in Plant Electrical Signals via IIR Filtering Using Wavelet Energy. Comput. Electron. Agric. 2015, 118, 15–23. [Google Scholar] [CrossRef]
- Addison, P.S. Wavelet Transforms and the ECG: A Review. Physiol. Meas. 2005, 26, R155–R199. [Google Scholar] [CrossRef]
- Quotb, A.; Bornat, Y.; Renaud, S. Wavelet Transform for Real-Time Detection of Action Potentials in Neural Signals. Front. Neuroeng. 2011, 4, 7. [Google Scholar] [CrossRef]
- Sai, K.; Sood, N.; Saini, I. Classification of Various Nutrient Deficiencies in Tomato Plants through Electrophysiological Signal Decomposition and Sample Space Reduction. Plant Physiol. Biochem. 2022, 186, 266–278. [Google Scholar] [CrossRef]
- Gardiner, J. Insights into Plant Consciousness from Neuroscience, Physics and Mathematics: A Role for Quasicrystals? Plant Signal. Behav. 2012, 7, 1049–1055. [Google Scholar] [CrossRef]
- Reissig, G.N.; Oliveira, T.F.D.C.; Oliveira, R.P.D.; Posso, D.A.; Parise, A.G.; Nava, D.E.; Souza, G.M. Fruit Herbivory Alters Plant Electrome: Evidence for Fruit-Shoot Long-Distance Electrical Signaling in Tomato Plants. Front. Sustain. Food Syst. 2021, 5, 657401. [Google Scholar] [CrossRef]
- Zaiosc Simmi, F.; José Dallagnol, L.; Oliveira Almeida, R.; Da Rosa Dorneles, K.; Maia Souza, G. Barley Systemic Bioelectrical Changes Detect Pathogenic Infection Days before the First Disease Symptoms. Comput. Electron. Agric. 2023, 209, 107832. [Google Scholar] [CrossRef]
- Parise, A.G.; Reissig, G.N.; Basso, L.F.; Senko, L.G.S.; Oliveira, T.F.D.C.; De Toledo, G.R.A.; Ferreira, A.S.; Souza, G.M. Detection of Different Hosts from a Distance Alters the Behaviour and Bioelectrical Activity of Cuscuta racemosa. Front. Plant Sci. 2021, 12, 594195. [Google Scholar] [CrossRef] [PubMed]
- Gensler, W. Bioelectric Potentials and Their Relation to Growth in Higher Plants. Ann. N. Y. Acad. Sci. 1974, 238, 280–299. [Google Scholar] [CrossRef]
- Reissig, G.N.; Oliveira, T.F.D.C.; Costa, Á.V.L.; Parise, A.G.; Pereira, D.R.; Souza, G.M. Machine Learning for Automatic Classification of Tomato Ripening Stages Using Electrophysiological Recordings. Front. Sustain. Food Syst. 2021, 5, 696829. [Google Scholar] [CrossRef]
- Nagarajan, R. Quantifying Physiological Data with Lempel-Ziv Complexity-Certain Issues. IEEE Trans. Biomed. Eng. 2002, 49, 1371–1373. [Google Scholar] [CrossRef] [PubMed]
- Tran, D.; Dutoit, F.; Najdenovska, E.; Wallbridge, N.; Plummer, C.; Mazza, M.; Raileanu, L.E.; Camps, C. Electrophysiological Assessment of Plant Status Outside a Faraday Cage Using Supervised Machine Learning. Sci Rep 2019, 9, 17073. [Google Scholar] [CrossRef]
- Shabala, S. Heterogeneity in Bean Leaf Mesophyll Tissue and Ion Flux Profiles: Leaf Electrophysiological Characteristics Correlate with the Anatomical Structure. Ann. Bot. 2002, 89, 221–226. [Google Scholar] [CrossRef]
- Sukhova, E.; Ratnitsyna, D.; Sukhov, V. Stochastic Spatial Heterogeneity in Activities of H+-ATP-Ases in Electrically Connected Plant Cells Decreases Threshold for Cooling-Induced Electrical Responses. Int. J. Mol. Sci. 2021, 22, 8254. [Google Scholar] [CrossRef]
- Sukhova, E.; Akinchits, E.; Sukhov, V. Mathematical Models of Electrical Activity in Plants. J. Membr. Biol. 2017, 250, 407–423. [Google Scholar] [CrossRef]
- Mummert, H.; Gradmann, D. Action Potentials in Acetabularia: Measurement and Simulation of Voltage-Gated Fluxes. J. Membr. Biol. 1991, 124, 265–273. [Google Scholar] [CrossRef]
- Sukhov, V.; Vodeneev, V. A Mathematical Model of Action Potential in Cells of Vascular Plants. J. Membr. Biol. 2009, 232, 59–67. [Google Scholar] [CrossRef]
- Jane Beilby, M.; Al Khazaaly, S. Re-Modeling Chara Action Potential: I. from Thiel Model of Ca2+ Transient to Action Potential Form. AIMS Biophys. 2016, 3, 431–449. [Google Scholar] [CrossRef]
- Jane Beilby, M.; Al Khazaaly, S. Re-Modeling Chara Action Potential: II. The Action Potential Form under Salinity Stress. AIMS Biophys. 2017, 4, 298–315. [Google Scholar] [CrossRef]
- Novikova, E.M.; Vodeneev, V.A.; Sukhov, V.S. Mathematical Model of Action Potential in Higher Plants with Account for the Involvement of Vacuole in the Electrical Signal Generation. Biochem. Moscow Suppl. Ser. A 2017, 11, 151–167. [Google Scholar] [CrossRef]
- Cuin, T.; Dreyer, I.; Michard, E. The Role of Potassium Channels in Arabidopsis Thaliana Long Distance Electrical Signalling: AKT2 Modulates Tissue Excitability While GORK Shapes Action Potentials. Int. J. Mol. Sci. 2018, 19, 926. [Google Scholar] [CrossRef]
- Sukhov, V.; Akinchits, E.; Katicheva, L.; Vodeneev, V. Simulation of Variation Potential in Higher Plant Cells. J. Membr. Biol. 2013, 246, 287–296. [Google Scholar] [CrossRef]
- Sukhov, V.S.; Sukhova, E.M.; Ratnitsyna, D.A.; Grinberg, M.A.; Yudina, L.M.; Vodeneev, V.A. Theoretical Analysis of the Influence of Fluctuations in the Activity of the Plasma Membrane H+-ATPase on Low-Temperature-Induced Electrical Responses in a Plant Cell. Biochem. Moscow Suppl. Ser. A 2020, 14, 298–309. [Google Scholar] [CrossRef]
- Gradmann, D.; Blatt, M.R.; Thiel, G. Electrocoupling of Ion Transporters in Plants. J. Membr. Biol. 1993, 136, 327–332. [Google Scholar] [CrossRef]
- Gradmann, D.; Hoffstadt, J. Electrocoupling of Ion Transporters in Plants: Interaction with Internal Ion Concentrations. J. Membr. Biol. 1998, 166, 51–59. [Google Scholar] [CrossRef]
- Gradmann, D. Impact of Apoplast Volume on Ionic Relations in Plant Cells. J. Membr. Biol. 2001, 184, 61–69. [Google Scholar] [CrossRef]
- Gradmann, D. Models for Oscillations in Plants. Funct. Plant Biol. 2001, 28, 577. [Google Scholar] [CrossRef]
- Shabala, S.; Shabala, L.; Gradmann, D.; Chen, Z.; Newman, I.; Mancuso, S. Oscillations in Plant Membrane Transport: Model Predictions, Experimental Validation, and Physiological Implications. J. Exp. Bot. 2006, 57, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Garkusha, I.V.; Petrov, V.A.; Vasiliev, V.A.; Romanovsky, Y.M. Propagating of Bioelectric Potentials in Green Plants’ Conducting System: Mathematical Modeling and Experiment. In Proceedings of the Saratov Fall Meeting 2001: Optical Technologies in Biophysics and Medicine III, Saratov, Russia, 2–5 October 2001; pp. 384–394. [Google Scholar] [CrossRef]
- Sukhov, V.; Nerush, V.; Orlova, L.; Vodeneev, V. Simulation of Action Potential Propagation in Plants. J. Theor. Biol. 2011, 291, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.J.; Morris, R.J. Chemical Agents Transported by Xylem Mass Flow Propagate Variation Potentials. Plant J. 2017, 91, 1029–1037. [Google Scholar] [CrossRef]
- Blyth, M.G.; Morris, R.J. Shear-Enhanced Dispersion of a Wound Substance as a Candidate Mechanism for Variation Potential Transmission. Front. Plant Sci. 2019, 10, 1393. [Google Scholar] [CrossRef] [PubMed]
- Sukhova, E.; Akinchits, E.; Gudkov, S.V.; Pishchalnikov, R.Y.; Vodeneev, V.; Sukhov, V. A Theoretical Analysis of Relations between Pressure Changes along Xylem Vessels and Propagation of Variation Potential in Higher Plants. Plants 2021, 10, 372. [Google Scholar] [CrossRef]
- Awan, H.; Adve, R.S.; Wallbridge, N.; Plummer, C.; Eckford, A.W. Communication and Information Theory of Single Action Potential Signals in Plants. IEEE Trans. Nanobiosci. 2019, 18, 61–73. [Google Scholar] [CrossRef]
- Awan, H.; Zeid, K.; Adve, R.S.; Wallbridge, N.; Plummer, C.; Eckford, A.W. Communication in Plants: Comparison of Multiple Action Potential and Mechanosensitive Signals With Experiments. IEEE Trans. Nanobiosci. 2020, 19, 213–223. [Google Scholar] [CrossRef]
- Awan, H.; Adve, R.S.; Wallbridge, N.; Plummer, C.; Eckford, A.W. Information Theoretic Based Comparative Analysis of Different Communication Signals in Plants. IEEE Access 2019, 7, 117075–117087. [Google Scholar] [CrossRef]
- Sukhova, E.; Ratnitsyna, D.; Sukhov, V. Simulated Analysis of Influence of Changes in H+-ATPase Activity and Membrane CO2 Conductance on Parameters of Photosynthetic Assimilation in Leaves. Plants 2022, 11, 3435. [Google Scholar] [CrossRef]
- Chen, Z.-H.; Hills, A.; Bätz, U.; Amtmann, A.; Lew, V.L.; Blatt, M.R. Systems Dynamic Modeling of the Stomatal Guard Cell Predicts Emergent Behaviors in Transport, Signaling, and Volume Control. Plant Physiol. 2012, 159, 1235–1251. [Google Scholar] [CrossRef]
- Hills, A.; Chen, Z.-H.; Amtmann, A.; Blatt, M.R.; Lew, V.L. OnGuard, a Computational Platform for Quantitative Kinetic Modeling of Guard Cell Physiology. Plant Physiol. 2012, 159, 1026–1042. [Google Scholar] [CrossRef]
- Minguet-Parramona, C.; Wang, Y.; Hills, A.; Vialet-Chabrand, S.; Griffiths, H.; Rogers, S.; Lawson, T.; Lew, V.L.; Blatt, M.R. An Optimal Frequency in Ca2+ Oscillations for Stomatal Closure Is an Emergent Property of Ion Transport in Guard Cells. Plant Physiol. 2016, 170, 33–42. [Google Scholar] [CrossRef] [PubMed]
- Gan, X.; Albert, R. Analysis of a Dynamic Model of Guard Cell Signaling Reveals the Stability of Signal Propagation. BMC Syst. Biol. 2016, 10, 78. [Google Scholar] [CrossRef] [PubMed]
- Parise, A.G.; De Toledo, G.R.A.; Oliveira, T.F.D.C.; Souza, G.M.; Castiello, U.; Gagliano, M.; Marder, M. Do Plants Pay Attention? A Possible Phenomenological-Empirical Approach. Prog. Biophys. Mol. Biol. 2022, 173, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Leng, Y.-N.; Zhu, F.-Y.; Li, S.-E.; Song, T.; Zhang, J. Water-Saving Techniques: Physiological Responses and Regulatory Mechanisms of Crops. Adv. Biotechnol. 2023, 1, 3. [Google Scholar] [CrossRef]
- Sha, S.; Cai, G.; Liu, S.; Ahmed, M.A. Roots to the Rescue: How Plants Harness Hydraulic Redistribution to Survive Drought across Contrasting Soil Textures. Adv. Biotechnol. 2024, 2, 43. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlova, E.; Yudina, L.; Sukhova, E.; Sukhov, V. Analysis of Electrome as a Tool for Plant Monitoring: Progress and Perspectives. Plants 2025, 14, 1500. https://doi.org/10.3390/plants14101500
Kozlova E, Yudina L, Sukhova E, Sukhov V. Analysis of Electrome as a Tool for Plant Monitoring: Progress and Perspectives. Plants. 2025; 14(10):1500. https://doi.org/10.3390/plants14101500
Chicago/Turabian StyleKozlova, Elizaveta, Lyubov Yudina, Ekaterina Sukhova, and Vladimir Sukhov. 2025. "Analysis of Electrome as a Tool for Plant Monitoring: Progress and Perspectives" Plants 14, no. 10: 1500. https://doi.org/10.3390/plants14101500
APA StyleKozlova, E., Yudina, L., Sukhova, E., & Sukhov, V. (2025). Analysis of Electrome as a Tool for Plant Monitoring: Progress and Perspectives. Plants, 14(10), 1500. https://doi.org/10.3390/plants14101500







