Can Grapevine Leaf Water Potential Be Modelled from Physiological and Meteorological Variables? A Machine Learning Approach
Abstract
:1. Introduction
2. Results
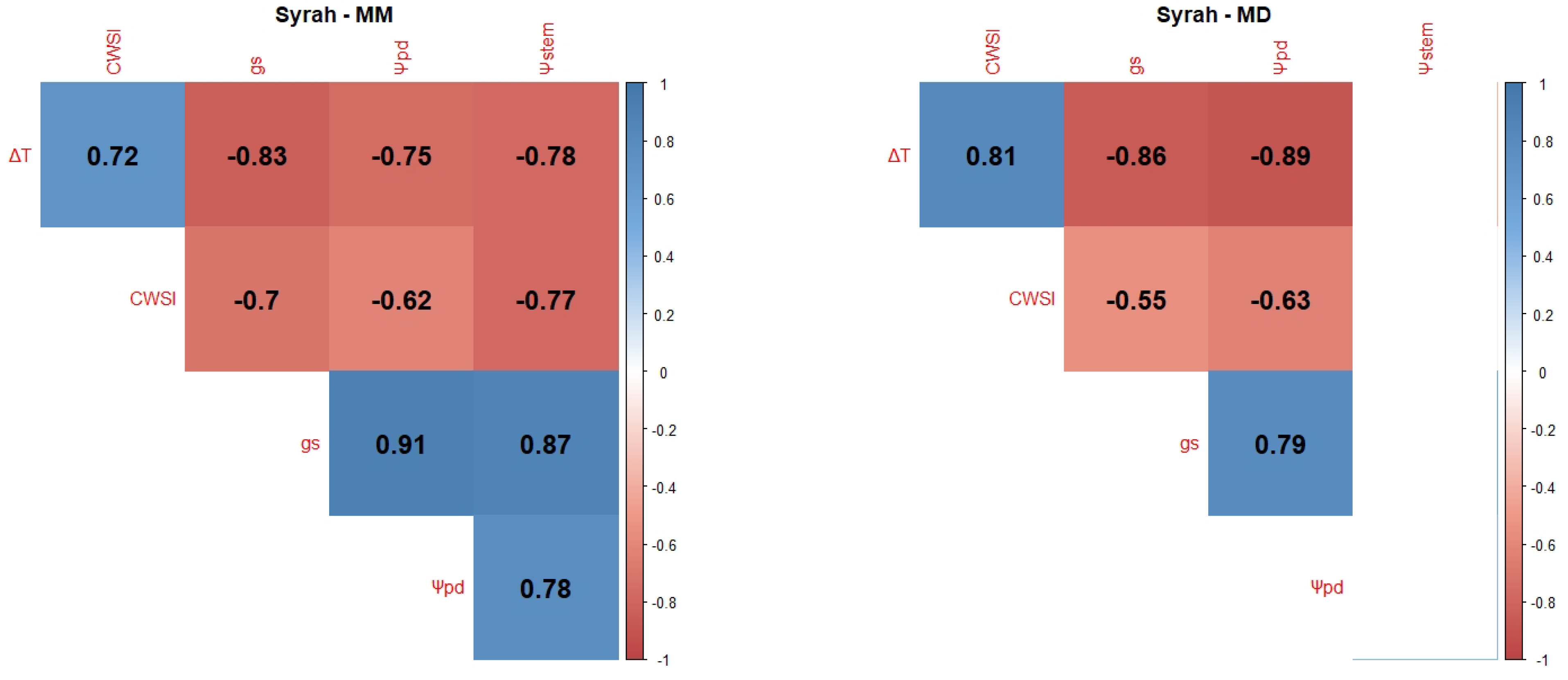
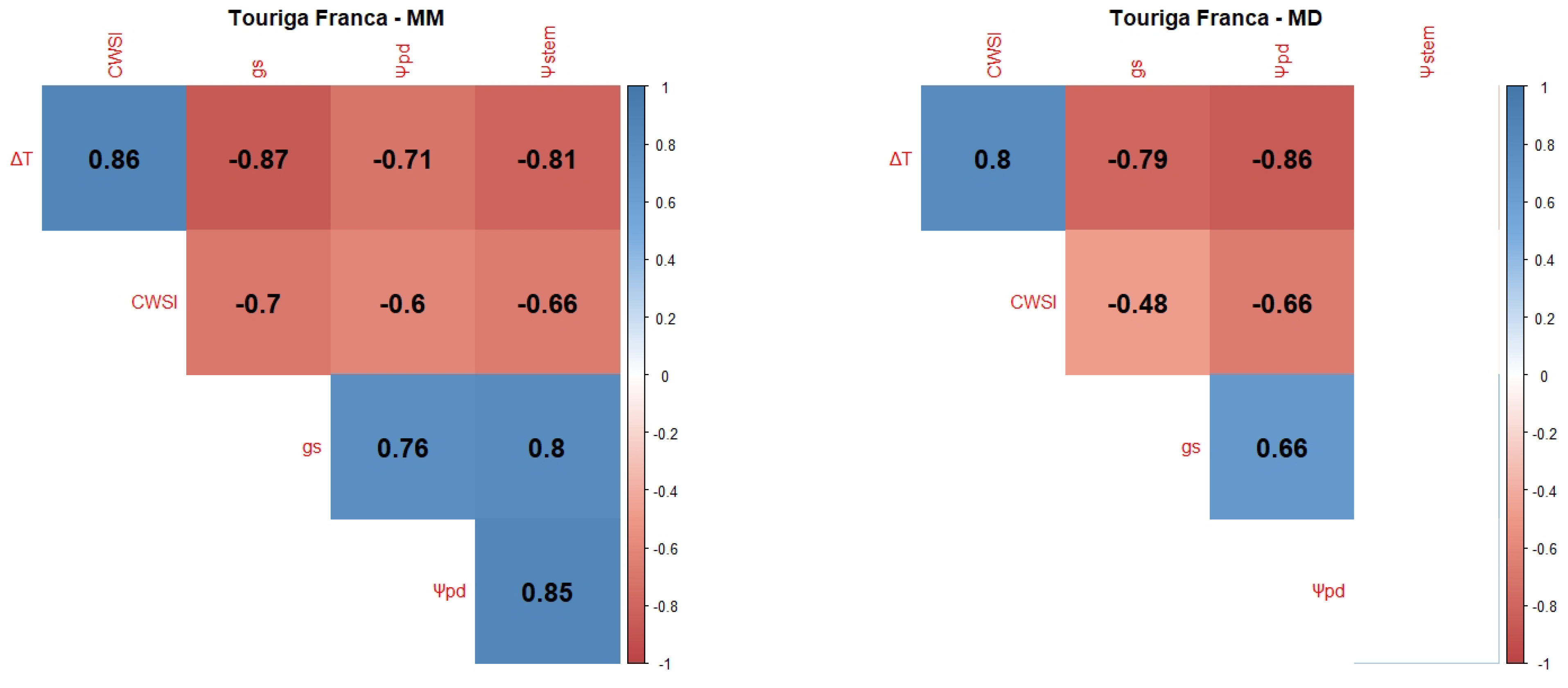
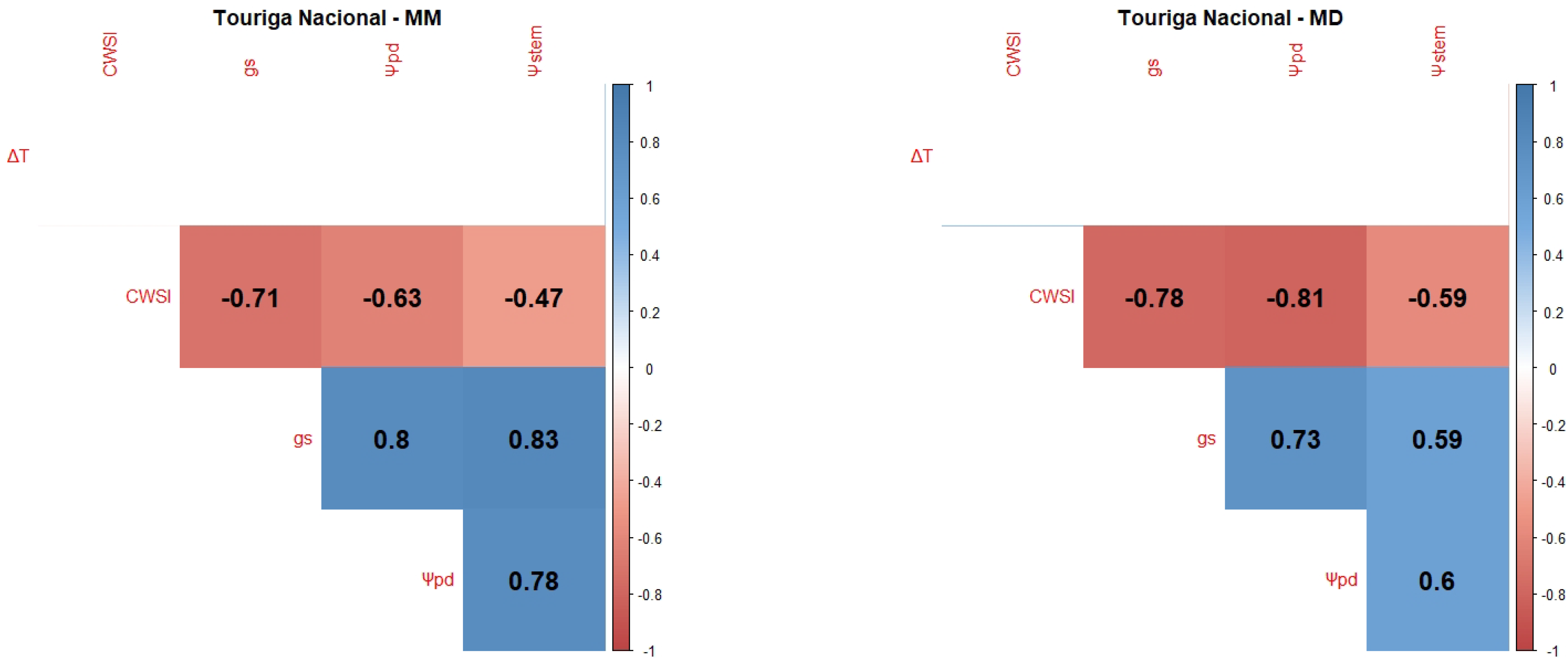
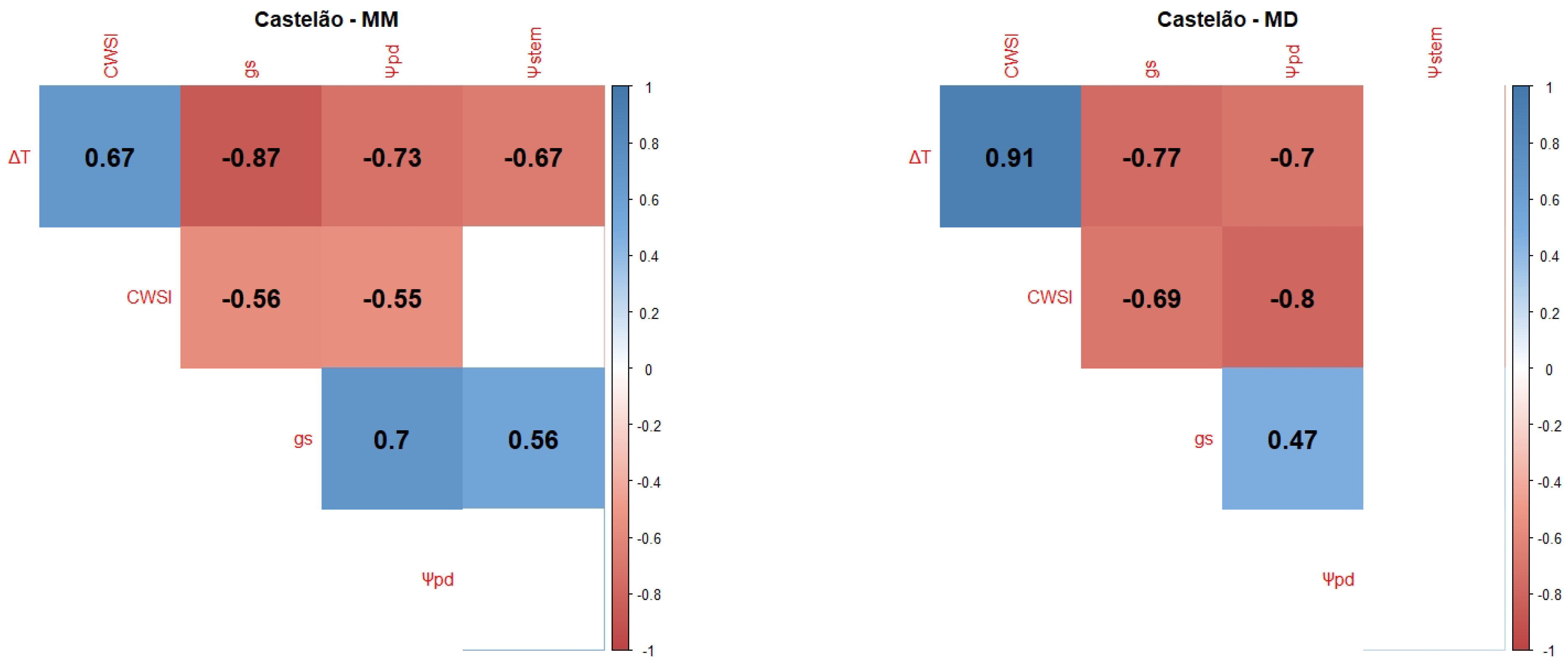
2.1. Correlations between WSI
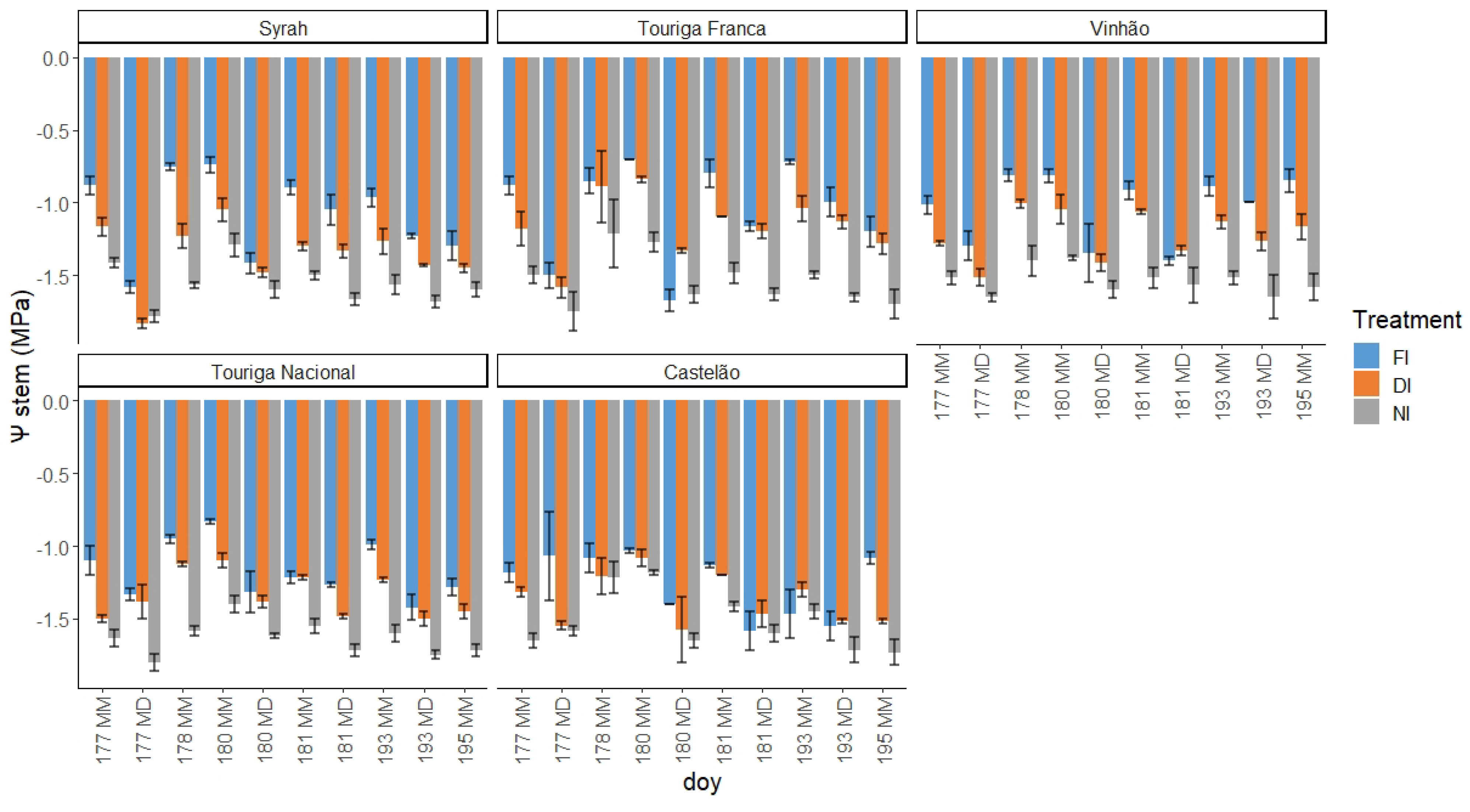
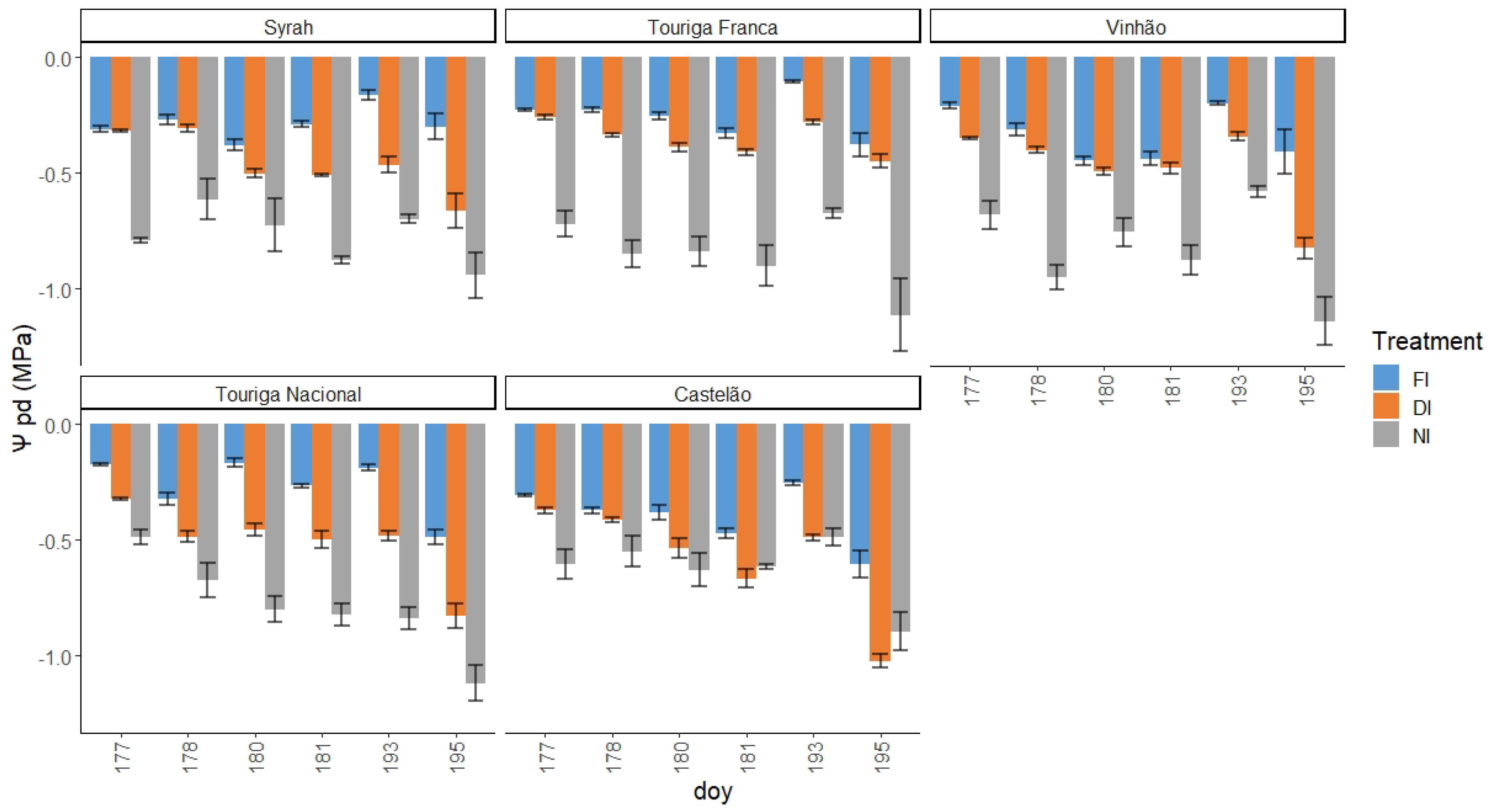
2.2. Water Potential
2.3. Indicators of Crop Water Status Based on Canopy Temperature
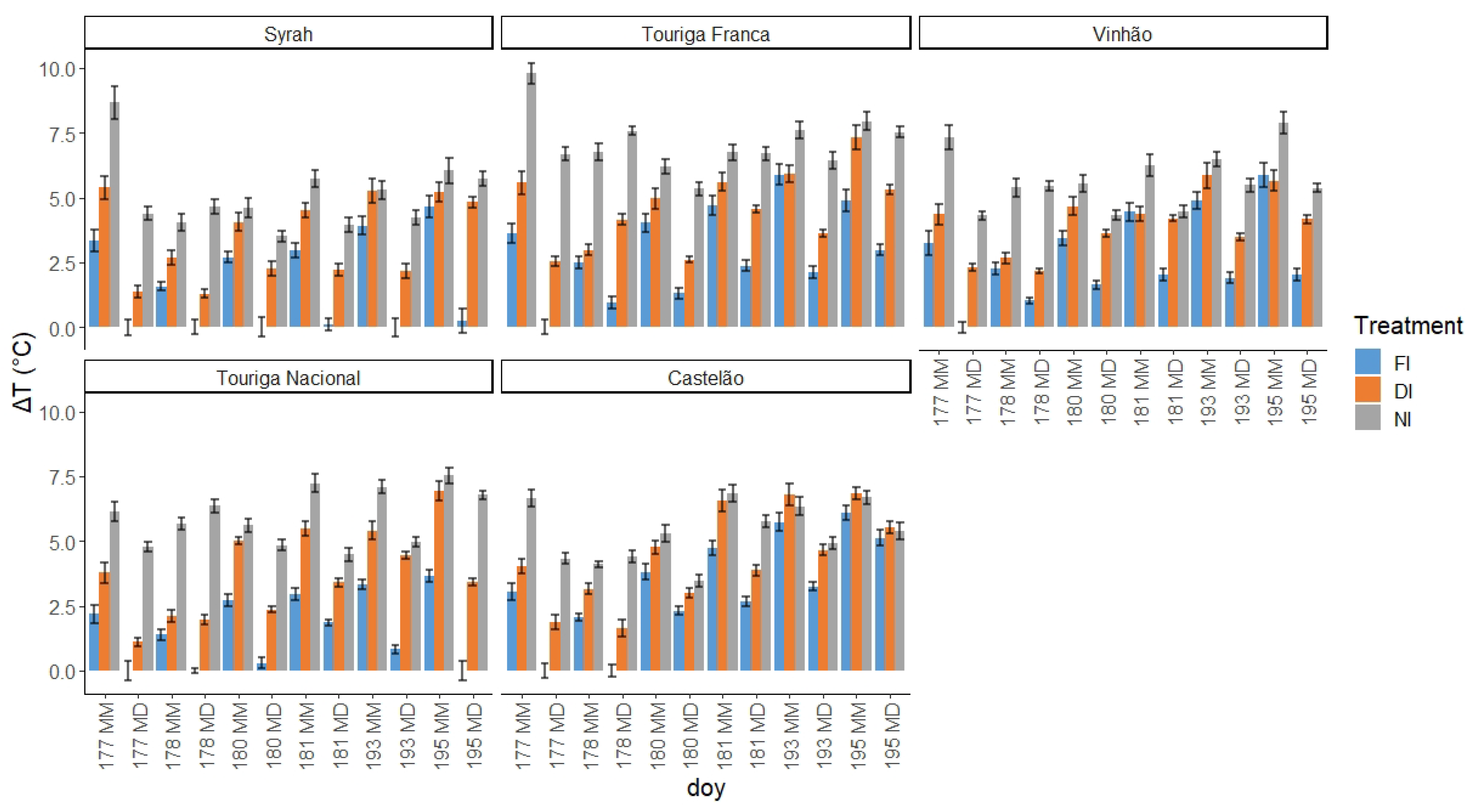
2.3.1. Normalised Canopy or Leaf Temperature with Reference to Air Temperature
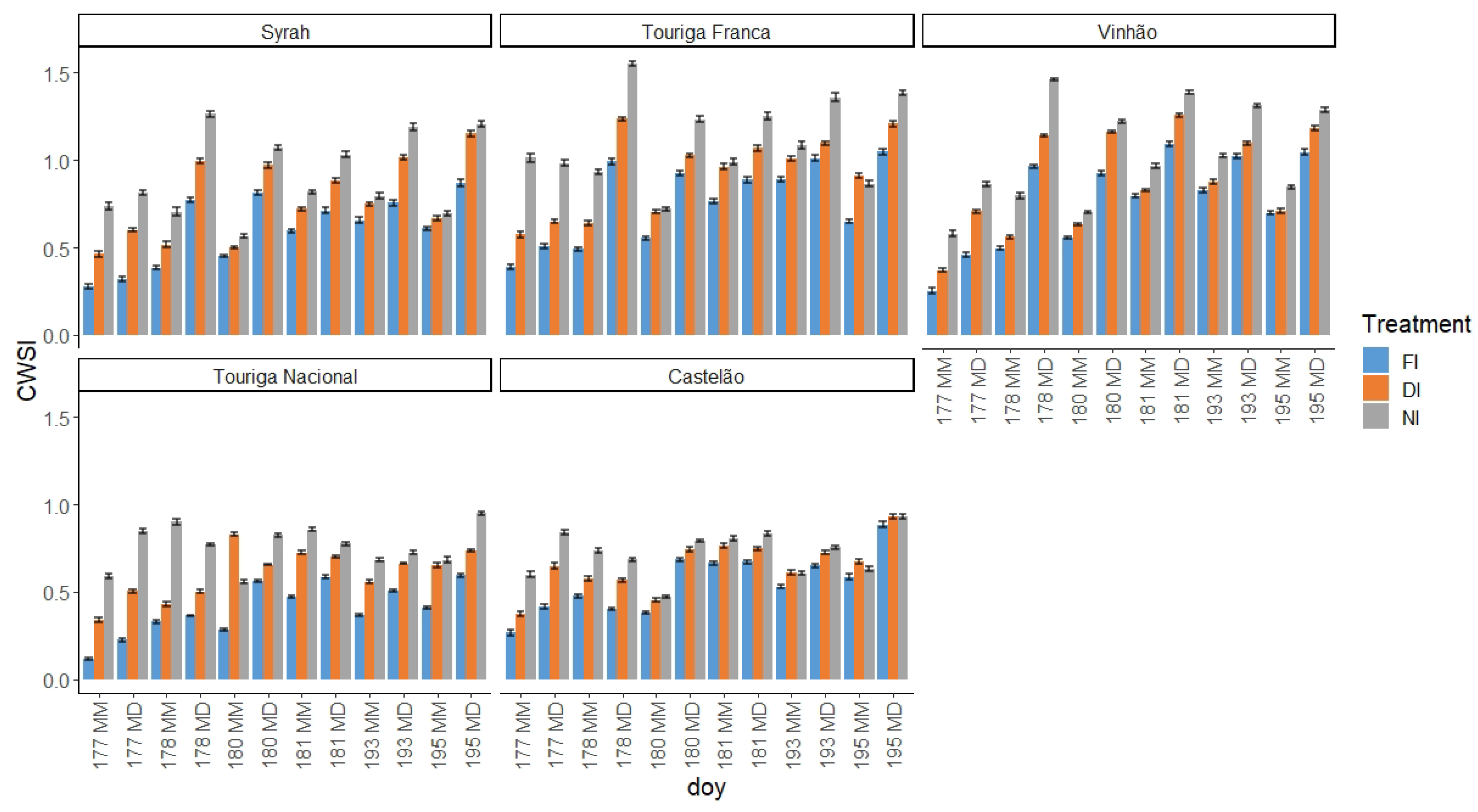
2.3.2. Crop Water Stress Index (CWSI)
2.4. Stomatal Conductance
2.5. Models
3. Discussion
4. Materials and Methods
4.1. Plant Material and Experimental Site
4.2. Meteorological Monitoring and Assessment
4.3. Grapevine Water Status
4.4. Stomatal Conductance
4.5. In Situ Thermal Imagery
4.6. Statistical Analysis
4.7. Machine Learning Methodology
4.7.1. Dataset Creation
- Plant description (grape variety, irrigation treatment);
- Meteorological information (relative humidity, air temperature);
- Thermal images;
- records;
- records.
4.7.2. Models
The idea of ensemble learning is to build a prediction model by combining the strengths of a collection of simpler base models. (…) Ensemble learning can be broken down into two tasks: developing a population of base learners from the training data and then combining them to form the composite predictor.
4.7.3. Evaluation Methodology
- 1.
- Model ranking;
- 2.
- Hyperparameter optimisation;
- 3.
- Final model evaluation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Hyperparameter | Search Space | Optimal Value |
|---|---|---|
| n_estimators | [50, …, 1000] | 585 |
| min_samples_split | [2, …, 133] | 6 |
| min_samples_leaf | [1, …, 133] | 6 |
| loss | [squared_error, absolute_error, quantile] | squared_error |
| learning_rate | [1 × 10−5, …, 100] | 0.020596 |
| subsample | [0.2, …, 1] | 0.4 |
| max_depth | [1, …, 1000] | 75 |
| Hyperparameter | Search Space | Optimal Value |
|---|---|---|
| n_estimators | [50, …, 1000] | 528 |
| min_samples_split | [2, …, 133] | 2 |
| min_samples_leaf | [1, …, 133] | 1 |
| bootstrap | [False, True] | False |
| criterion | [squared_error, friedman_mse] | squared_error |
| Hyperparameter | Search Space | Optimal Value |
|---|---|---|
| n_estimators | [50, …, 1000] | 806 |
| min_samples_split | [2, …, 133] | 2 |
| min_samples_leaf | [1, …, 133] | 1 |
| bootstrap | [False, True] | True |
| criterion | [squared_error, friedman_mse] | squared_error |
References
- Biasi, R.; Botti, F.; Barbera, G.; Cullotta, S. The role of mediterranean fruit tree orchards and vineyards in maintaining the traditional agricultural landscape. Acta Hortic. 2012, 940, 79–88. [Google Scholar] [CrossRef]
- OIV World Wine Production Outlook, OIV First Estimates, 31.10.2022. Available online: https://www.oiv.int/sites/default/files/documents/EN_OIV_2022_World_Wine_Production_Outlook.pdf (accessed on 30 September 2023).
- IPCC. Summary for Policymakers. In Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Report; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Cramer, W.; Guiot, J.; Marini, K.; Azzopardi, B.; Balzan, M.V.; Cherif, S.; Doblas-Miranda, E.; dos Santos, M.; Drobinski, P.; Fader, M.; et al. MedECC 2020 Summary for Policymakers. Climate and Environmental Change in the Mediterranean Basin—Current Situation and Risks for the Future. First Mediterranean Assessment Report; MedECC: Marseille, France, 2022. [Google Scholar] [CrossRef]
- Fraga, H.; de Cortázar Atauri, I.G.; Malheiro, A.C.; Moutinho-Pereira, J.; Santos, J.A. Viticulture in Portugal: A review of recent trends and climate change projections. OENO ONE 2017, 51, 61–69. [Google Scholar] [CrossRef]
- Pinto, C.; Henriques, M.; Figueiredo, J.; David, J.; Abreu, F.; Pereira, J.; Correia, I.; David, T. Phenology and growth dynamics in Mediterranean evergreen oaks: Effects of environmental conditions and water relations. For. Ecol. Manag. 2011, 262, 500–508. [Google Scholar] [CrossRef]
- Lovisolo, C.; Hartung, W.; Schubert, A. Whole-plant hydraulic conductance and root-to-shoot flow of abscisic acid are independently affected by water stress in grapevines. Funct. Plant Biol. 2002, 29, 1349. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, D.; Franck, N.; Pastenes, C.; Wallberg, B.; Garrido, M.; Silva, H. Improved physiological performance in grapevine (Vitis vinifera L.) cv. Cabernet Sauvignon facing recurrent drought stress. Aust. J. Grape Wine Res. 2021, 27, 258–268. [Google Scholar] [CrossRef]
- Williams, L.; Matthews, M. Grapevine. In Irrigation of Agricultural Crops; Agronomy Monographs No. 30; Technical Report; Stewart, B.J., Nielsen, D.R., Eds.; ASA-CSSA-SSSA: Madison, WI, USA, 1990; pp. 1019–1055. [Google Scholar]
- Schultz, H.R. Climate Change and Viticulture: Research Needs for Facing the Future. J. Wine Res. 2010, 21, 113–116. [Google Scholar] [CrossRef]
- Costa, J.; Vaz, M.; Escalona, J.; Egipto, R.; Lopes, C.; Medrano, H.; Chaves, M. Modern viticulture in southern Europe: Vulnerabilities and strategies for adaptation to water scarcity. Agric. Water Manag. 2016, 164, 5–18. [Google Scholar] [CrossRef]
- Tezara, W.; Mitchell, V.J.; Driscoll, S.D.; Lawlor, D.W. Water stress inhibits plant photosynthesis by decreasing coupling factor and ATP. Nature 1999, 401, 914–917. [Google Scholar] [CrossRef]
- Flexas, J.; Medrano, H. Drought-inhibition of Photosynthesis in C3 Plants: Stomatal and Non-stomatal Limitations Revisited. Ann. Bot. 2002, 89, 183–189. [Google Scholar] [CrossRef]
- Chaves, M.M.; Zarrouk, O.; Francisco, R.; Costa, J.M.; Santos, T.; Regalado, A.P.; Rodrigues, M.L.; Lopes, C.M. Grapevine under deficit irrigation: Hints from physiological and molecular data. Ann. Bot. 2010, 105, 661–676. [Google Scholar] [CrossRef]
- Costa, J.M.; Ortuño, M.F.; Chaves, M.M. Deficit Irrigation as a Strategy to Save Water: Physiology and Potential Application to Horticulture. J. Integr. Plant Biol. 2007, 49, 1421–1434. [Google Scholar] [CrossRef]
- Zarrouk, O.; Costa, M.; Francisco, R.; Lopes, C.; Chaves, M. Drought and water management in Mediterranean vineyards. In Grapevine in a Changing Environment: A Molecular and Ecophysiological Perspective; Wiley-Blackwell: Hoboken, NJ, USA, 2015; p. 400. [Google Scholar] [CrossRef]
- Galindo, A.; Collado-González, J.; Griñán, I.; Corell, M.; Centeno, A.; Martín-Palomo, M.; Girón, I.; Rodríguez, P.; Cruz, Z.; Memmi, H.; et al. Deficit irrigation and emerging fruit crops as a strategy to save water in Mediterranean semiarid agrosystems. Agric. Water Manag. 2018, 202, 311–324. [Google Scholar] [CrossRef]
- Leeuwen, C.V.; Trégoat, O.; Choné, X.; Bois, B.; Pernet, D.; Gaudillère, J.P. Vine water status is a key factor in grape ripening and vintage quality for red Bordeaux wine. How can it be assessed for vineyard management purposes? OENO ONE 2009, 43, 121. [Google Scholar] [CrossRef]
- Reynard, J.S.; Zufferey, V.; Nicol, G.C.; Murisier, F. Vine water status as a parameter of the « terroir » effect under the non-irrigated conditions of the Vaud viticultural area (Switzerland). OENO ONE 2011, 45, 139. [Google Scholar] [CrossRef]
- Zufferey, V.; Verdenal, T.; Dienes, A.; Belcher, S.; Lorenzini, F.; Koestel, C.; Gindro, K.; Spangenberg, J.E.; Viret, O.; Spring, J.L. The impact of plant water status on the gas exchange, berry composition and wine quality of Chasselas grapes in Switzerland. OENO ONE 2018, 52. [Google Scholar] [CrossRef]
- Serra, I.; Strever, A.; Myburgh, P.; Deloire, A. Review: The interaction between rootstocks and cultivars (Vitis Vinifera L.) Enhanc. Drought Toler. Grapevine: Rootstocks Enhanc. Drought Toler. Grapevine. Aust. J. Grape Wine Res. 2014, 20, 1–14. [Google Scholar] [CrossRef]
- van Leeuwen, C.; Destrac-Irvine, A.; Dubernet, M.; Duchêne, E.; Gowdy, M.; Marguerit, E.; Pieri, P.; Parker, A.; de Rességuier, L.; Ollat, N. An Update on the Impact of Climate Change in Viticulture and Potential Adaptations. Agronomy 2019, 9, 514. [Google Scholar] [CrossRef]
- Santos, J.A.; Fraga, H.; Malheiro, A.C.; Moutinho-Pereira, J.; Dinis, L.T.; Correia, C.; Moriondo, M.; Leolini, L.; Dibari, C.; Costafreda-Aumedes, S.; et al. A Review of the Potential Climate Change Impacts and Adaptation Options for European Viticulture. Appl. Sci. 2020, 10, 3092. [Google Scholar] [CrossRef]
- Holzapfel, B.P.; Smith, J.P.; Mandel, R.M.; Keller, M. Manipulating the Postharvest Period and Its Impact on Vine Productivity of Semillon Grapevines. Am. J. Enol. Vitic. 2006, 57, 148–157. [Google Scholar] [CrossRef]
- Lloyd, J.; Farquhar, G.D. The CO2 Dependence of Photosynthesis, Plant Growth Responses to Elevated Atmospheric CO2 Concentrations and Their Interaction with Soil Nutrient Status. I. General Principles and Forest Ecosystems. Funct. Ecol. 1996, 10, 4. [Google Scholar] [CrossRef]
- Tausz, M.; Tausz-Posch, S.; Norton, R.M.; Fitzgerald, G.J.; Nicolas, M.E.; Seneweera, S. Understanding crop physiology to select breeding targets and improve crop management under increasing atmospheric CO2 concentrations. Environ. Exp. Bot. 2013, 88, 71–80. [Google Scholar] [CrossRef]
- Jacinto, J.; Jesus, J.; Damásio, M.; Silvestre, J.; Máguas, C.; Antunes, C. Phloem carbon isotopic signature as a valuable tool to assess physiological adjustments among European grapevine varieties under a Mediterranean climate. Agric. Water Manag. 2023, 286, 108396. [Google Scholar] [CrossRef]
- McAdam, S.A.; Brodribb, T.J. The Evolution of Mechanisms Driving the Stomatal Response to Vapor Pressure Deficit. Plant Physiol. 2015, 167, 833–843. [Google Scholar] [CrossRef] [PubMed]
- Jalakas, P.; Takahashi, Y.; Waadt, R.; Schroeder, J.I.; Merilo, E. Molecular mechanisms of stomatal closure in response to rising vapour pressure deficit. New Phytol. 2021, 232, 468–475. [Google Scholar] [CrossRef] [PubMed]
- Sperry, J.S. Hydraulic constraints on plant gas exchange. Agric. For. Meteorol. 2000, 104, 13–23. [Google Scholar] [CrossRef]
- Trifiló, P.; Raimondo, F.; Savi, T.; Gullo, M.A.L.; Nardini, A. The contribution of vascular and extra-vascular water pathways to drought-induced decline of leaf hydraulic conductance. J. Exp. Bot. 2016, 67, 5029–5039. [Google Scholar] [CrossRef]
- Chaves, M.; Costa, J.; Zarrouk, O.; Pinheiro, C.; Lopes, C.; Pereira, J. Controlling stomatal aperture in semi-arid regions—The dilemma of saving water or being cool? Plant Sci. 2016, 251, 54–64. [Google Scholar] [CrossRef]
- de Souza, C.R.; Maroco, J.P.; dos Santos, T.P.; Rodrigues, M.L.; Lopes, C.M.; Pereira, J.S.; Chaves, M.M. Partial rootzone drying: Regulation of stomatal aperture and carbon assimilation in field-grown grapevines (Vitis vinifera cv. Moscatel). Funct. Plant Biol. 2003, 30, 653. [Google Scholar] [CrossRef]
- Singh, M.; Karada, M.S.; Rai, R.K.; Pratap, D.; Agnihotri, D.; Singh, A.K.; Singh, B.K. A Review on Remote Sensing as a Tool for Irrigation Monitoring and Management. Int. J. Environ. Clim. Change 2023, 13, 203–211. [Google Scholar] [CrossRef]
- Bausch, W.C.; Neale, C.M.U. Crop Coefficients Derived from Reflected Canopy Radiation: A Concept. Trans. ASAE 1987, 30, 0703–0709. [Google Scholar] [CrossRef]
- Choudhury, B.; Ahmed, N.; Idso, S.; Reginato, R.; Daughtry, C. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Pinter, P.J.; Kimball, B.A. Wheat basal crop coefficients determined by normalized difference vegetation index. Irrig. Sci. 2005, 24, 1–14. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI Assisted Monitoring of Vegetable Crop Evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- de Souza Siqueira Campos, P.R.; da Silva, J.F.C.; Vásquez, H.M.; Vittori, A.; de Almeida e Silva, M. Fractions of carbohydrates and of nitrogenous compounds of tropical grasses at different cutting ages. Rev. Bras. Zootec. 2010, 39, 1538–1547. [Google Scholar] [CrossRef]
- Mateos, L.; González-Dugo, M.; Testi, L.; Villalobos, F. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. I. Method validation. Agric. Water Manag. 2013, 125, 81–91. [Google Scholar] [CrossRef]
- Saadi, S.; Simonneaux, V.; Boulet, G.; Raimbault, B.; Mougenot, B.; Fanise, P.; Ayari, H.; Lili-Chabaane, Z. Monitoring Irrigation Consumption Using High Resolution NDVI Image Time Series: Calibration and Validation in the Kairouan Plain (Tunisia). Remote Sens. 2015, 7, 13005–13028. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- Siegfried, J.; Longchamps, L.; Khosla, R. Multispectral satellite imagery to quantify in-field soil moisture variability. J. Soil Water Conserv. 2019, 74, 33–40. [Google Scholar] [CrossRef]
- Ballester, C.; Zarco-Tejada, P.J.; Nicolás, E.; Alarcón, J.J.; Fereres, E.; Intrigliolo, D.S.; Gonzalez-Dugo, V. Evaluating the performance of xanthophyll, chlorophyll and structure-sensitive spectral indices to detect water stress in five fruit tree species. Precis. Agric. 2018, 19, 178–193. [Google Scholar] [CrossRef]
- Marino, S.; Cocozza, C.; Tognetti, R.; Alvino, A. Use of proximal sensing and vegetation indexes to detect the inefficient spatial allocation of drip irrigation in a spot area of tomato field crop. Precis. Agric. 2015, 16, 613–629. [Google Scholar] [CrossRef]
- Klem, K.; Záhora, J.; Zemek, F.; Trunda, P.; Tůma, I.; Novotná, K.; Hodaňová, P.; Rapantová, B.; Hanuš, J.; Vavříková, J.; et al. Interactive effects of water deficit and nitrogen nutrition on winter wheat. Remote sensing methods for their detection. Agric. Water Manag. 2018, 210, 171–184. [Google Scholar] [CrossRef]
- DeJonge, K.C.; Taghvaeian, S.; Trout, T.J.; Comas, L.H. Comparison of canopy temperature-based water stress indices for maize. Agric. Water Manag. 2015, 156, 51–62. [Google Scholar] [CrossRef]
- Kullberg, E.G.; DeJonge, K.C.; Chávez, J.L. Evaluation of thermal remote sensing indices to estimate crop evapotranspiration coefficients. Agric. Water Manag. 2017, 179, 64–73. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I. Derivation of a shortwave infrared water stress index from MODIS near- and shortwave infrared data in a semiarid environment. Remote Sens. Environ. 2003, 87, 111–121. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Hochberg, U.; Rockwell, F.E.; Holbrook, N.M.; Cochard, H. Iso/anisohydry: A plant–environment interaction rather than a simple hydraulic trait. Trends Plant Sci. 2018, 23, 112–120. [Google Scholar] [CrossRef]
- Schultz, H.R. Differences in hydraulic architecture account for near-isohydric and anisohydric behaviour of two field-grown Vitis vinifera L. cultivars during drought. Plant Cell Environ. 2003, 26, 1393–1405. [Google Scholar] [CrossRef]
- Shelden, M.C.; Vandeleur, R.; Kaiser, B.N.; Tyerman, S.D. A comparison of petiole hydraulics and aquaporin expression in an anisohydric and isohydric cultivar of grapevine in response to water-stress induced cavitation. Front. Plant Sci. 2017, 8, 1893. [Google Scholar] [CrossRef]
- Pou, A.; Medrano, H.; Tomàs, M.; Martorell, S.; Ribas-Carbó, M.; Flexas, J. Anisohydric behaviour in grapevines results in better performance under moderate water stress and recovery than isohydric behaviour. Plant Soil 2012, 359, 335–349. [Google Scholar] [CrossRef]
- Jones, H.G. Physiological Aspects of the Control of Water Status in Horticultural Crops. HortScience 1990, 25, 19–25. [Google Scholar] [CrossRef]
- Williams, L.; Araujo, F. Correlations among Predawn Leaf, Midday Leaf, and Midday Stem Water Potential and their Correlations with other Measures of Soil and Plant Water Status in Vitis vinifera. J. Am. Soc. Hortic. Sci. 2002, 127, 448–454. [Google Scholar] [CrossRef]
- Correia, M.J.; Pereira, J.S.; Chaves, M.M.; Rodrigues, M.L.; Pacheco, C.A. ABA xylem concentrations determine maximum daily leaf conductance of field-grown Vitis vinifera L. plants. Plant Cell Environ. 1995, 18, 511–521. [Google Scholar] [CrossRef]
- McCutchan, H.; Shackel, K. Stem-water Potential as a Sensitive Indicator of Water Stress in Prune Trees (Prunus domestica L. cv. French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar] [CrossRef]
- Améglio, T. Significance and Limits in the Use of Predawn Leaf Water Potential for Tree Irrigation. Plant Soil 1998, 207, 155–167. [Google Scholar] [CrossRef]
- Rogiers, S.Y.; Greer, D.H.; Hutton, R.J.; Landsberg, J.J. Does night-time transpiration contribute to anisohydric behaviour in a Vitis vinifera cultivar? J. Exp. Bot. 2009, 60, 3751–3763. [Google Scholar] [CrossRef]
- Yi, K.; Dragoni, D.; Phillips, R.P.; Roman, D.T.; Novick, K.A. Dynamics of stem water uptake among isohydric and anisohydric species experiencing a severe drought. Tree Physiol. 2017, 37, 1379–1392. [Google Scholar] [CrossRef]
- Benyahia, F.; Campos, F.B.; Abdelkader, A.B.; Basile, B.; Tagliavini, M.; Andreotti, C.; Zanotelli, D. Assessing Grapevine Water Status by Integrating Vine Transpiration, Leaf Gas Exchanges, Chlorophyll Fluorescence and Sap Flow Measurements. Agronomy 2023, 13, 464. [Google Scholar] [CrossRef]
- Juillion, P.; Gelly, M.; Chopard, J.; Tarsitano, D.; Chalayer, L.; Guaus, A.; Hublart, P.; Lopez, G.; Fumey, D. Using stomatal conductance as a water status indicator in grapevine: Implementation into a decision support system for irrigation management. Acta Hortic. 2021, 1314, 1–8. [Google Scholar] [CrossRef]
- Cifre, J.; Bota, J.; Escalona, J.; Medrano, H.; Flexas, J. Physiological tools for irrigation scheduling in grapevine (Vitis vinifera L.). Agric. Ecosyst. Environ. 2005, 106, 159–170. [Google Scholar] [CrossRef]
- Idso, S.; Reginato, R.; Jackson, R.; Pinter, P. Foliage and air temperatures: Evidence for a dynamic “equivalence point”. Agric. Meteorol. 1981, 24, 223–226. [Google Scholar] [CrossRef]
- Fuentes, S.; Bei, R.D.; Pech, J.; Tyerman, S. Computational water stress indices obtained from thermal image analysis of grapevine canopies. Irrig. Sci. 2012, 30, 523–536. [Google Scholar] [CrossRef]
- Pou, A.; Diago, M.P.; Medrano, H.; Baluja, J.; Tardaguila, J. Validation of thermal indices for water status identification in grapevine. Agric. Water Manag. 2014, 134, 60–72. [Google Scholar] [CrossRef]
- Belfiore, N.; Vinti, R.; Lovat, L.; Chitarra, W.; Tomasi, D.; de Bei, R.; Meggio, F.; Gaiotti, F. Infrared Thermography to Estimate Vine Water Status: Optimizing Canopy Measurements and Thermal Indices for the Varieties Merlot and Moscato in Northern Italy. Agronomy 2019, 9, 821. [Google Scholar] [CrossRef]
- Ishimwe, R.; Abutaleb, K.; Ahmed, F. Applications of Thermal Imaging in Agriculture—A Review. Adv. Remote Sens. 2014, 3, 128–140. [Google Scholar] [CrossRef]
- La Fata, A. Thermography to Assess Grapevine Status and Traits Opportunities and Limitations in Crop Monitoring and Phenotyping—A Review. Master’s Thesis, Universidade de Lisboa, Lisboa, Portugal, 2021. [Google Scholar]
- van Dijk, A.D.J.; Kootstra, G.; Kruijer, W.; de Ridder, D. Machine learning in plant science and plant breeding. iScience 2021, 24, 101890. [Google Scholar] [CrossRef]
- Hesami, M.; Jones, A.M.P. Application of artificial intelligence models and optimization algorithms in plant cell and tissue culture. Appl. Microbiol. Biotechnol. 2020, 104, 9449–9485. [Google Scholar] [CrossRef]
- Gill, T.; Gill, S.K.; Saini, D.K.; Chopra, Y.; de Koff, J.P.; Sandhu, K.S. A Comprehensive Review of High Throughput Phenotyping and Machine Learning for Plant Stress Phenotyping. Phenomics 2022, 2, 156–183. [Google Scholar] [CrossRef]
- Jafari, M.; Shahsavar, A. The application of artificial neural networks in modeling and predicting the effects of melatonin on morphological responses of citrus to drought stress. PLoS ONE 2020, 15, e0240427. [Google Scholar] [CrossRef]
- Hesami, M.; Alizadeh, M.; Jones, A.M.P.; Torkamaneh, D. Machine learning: Its challenges and opportunities in plant system biology. Appl. Microbiol. Biotechnol. 2022, 106, 3507–3530. [Google Scholar] [CrossRef] [PubMed]
- Grinblat, G.L.; Uzal, L.C.; Larese, M.G.; Granitto, P.M. Deep learning for plant identification using vein morphological patterns. Comput. Electron. Agric. 2016, 127, 418–424. [Google Scholar] [CrossRef]
- Hesami, M.; Alizadeh, M.; Naderi, R.; Tohidfar, M. Forecasting and optimizing Agrobacterium-mediated genetic transformation via ensemble model-fruit fly optimization algorithm: A data mining approach using chrysanthemum databases. PLoS ONE 2020, 15, e0239901. [Google Scholar] [CrossRef] [PubMed]
- Mishra, B.; Kumar, N.; Mukhtar, M.S. Systems Biology and Machine Learning in Plant–Pathogen Interactions. Mol. Plant-Microbe Interact. 2019, 32, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Benos, L.; Tagarakis, A.C.; Dolias, G.; Berruto, R.; Kateris, D.; Bochtis, D. Machine Learning in Agriculture: A Comprehensive Updated Review. Sensors 2021, 21, 3758. [Google Scholar] [CrossRef] [PubMed]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguila, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.; González-Dugo, V.; Williams, L.; Suárez, L.; Berni, J.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Poblete, T.; Ortega-Farías, S.; Moreno, M.; Bardeen, M. Artificial Neural Network to Predict Vine Water Status Spatial Variability Using Multispectral Information Obtained from an Unmanned Aerial Vehicle (UAV). Sensors 2017, 17, 2488. [Google Scholar] [CrossRef]
- Borgogno-Mondino, E.; Novello, V.; Lessio, A.; de Palma, L. Describing the spatio-temporal variability of vines and soil by satellite-based spectral indices: A case study in Apulia (South Italy). Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 42–50. [Google Scholar] [CrossRef]
- Helman, D.; Bahat, I.; Netzer, Y.; Ben-Gal, A.; Alchanatis, V.; Peeters, A.; Cohen, Y. Using Time Series of High-Resolution Planet Satellite Images to Monitor Grapevine Stem Water Potential in Commercial Vineyards. Remote Sens. 2018, 10, 1615. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Fernández-Novales, J.; Saiz-Rubio, V.; Barrio, I.; Rovira-Más, F.; Cuenca-Cuenca, A.; Alves, F.S.; Valente, J.; Tardaguila, J.; Diago, M.P. Monitoring and Mapping Vineyard Water Status Using Non-Invasive Technologies by a Ground Robot. Remote Sens. 2021, 13, 2830. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, J.R.; Riaño, D.; Carlisle, E.; Ustin, S.; Smart, D.R. Evaluation of Hyperspectral Reflectance Indexes to Detect Grapevine Water Status in Vineyards. Am. J. Enol. Vitic. 2007, 58, 302–317. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M. Data Mining and NIR Spectroscopy in Viticulture: Applications for Plant Phenotyping under Field Conditions. Sensors 2016, 16, 236. [Google Scholar] [CrossRef]
- Pôças, I.; Gonçalves, J.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Hyperspectral-based predictive modelling of grapevine water status in the Portuguese Douro wine region. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 177–190. [Google Scholar] [CrossRef]
- Diago, M.P.; Fernández-Novales, J.; Gutiérrez, S.; Marañón, M.; Tardaguila, J. Development and Validation of a New Methodology to Assess the Vineyard Water Status by On-the-Go Near Infrared Spectroscopy. Front. Plant Sci. 2018, 9, 59. [Google Scholar] [CrossRef]
- Pôças, I.; Tosin, R.; Gonçalves, I.; Cunha, M. Toward a generalized predictive model of grapevine water status in Douro region from hyperspectral data. Agric. For. Meteorol. 2020, 280, 107793. [Google Scholar] [CrossRef]
- Tosin, R.; Pôças, I.; Gonçalves, I.; Cunha, M. Estimation of grapevine predawn leaf water potential based on hyperspectral reflectance data in Douro wine region. VITIS J. Grapevine Res. 2020, 59, 9–18. [Google Scholar] [CrossRef]
- Laroche-Pinel, E.; Albughdadi, M.; Duthoit, S.; Chéret, V.; Rousseau, J.; Clenet, H. Understanding Vine Hyperspectral Signature through Different Irrigation Plans: A First Step to Monitor Vineyard Water Status. Remote Sens. 2021, 13, 536. [Google Scholar] [CrossRef]
- Tosin, R.; Martins, R.; Pôças, I.; Cunha, M. Canopy VIS-NIR spectroscopy and self-learning artificial intelligence for a generalised model of predawn leaf water potential in Vitis vinifera. Biosyst. Eng. 2022, 219, 235–258. [Google Scholar] [CrossRef]
- Bellvert, J.; Zarco-Tejada, P.J.; Girona, J.; Fereres, E. Mapping crop water stress index in a ‘Pinot-noir’ vineyard: Comparing ground measurements with thermal remote sensing imagery from an unmanned aerial vehicle. Precis. Agric. 2014, 15, 361–376. [Google Scholar] [CrossRef]
- Bellvert, J.; Zarco-Tejada, P.; Marsal, J.; Girona, J.; González-Dugo, V.; Fereres, E. Vineyard irrigation scheduling based on airborne thermal imagery and water potential thresholds. Aust. J. Grape Wine Res. 2016, 22, 307–315. [Google Scholar] [CrossRef]
- Acevedo-Opazo, C.; Valdés-Gómez, H.; Taylor, J.; Avalo, A.; Verdugo-Vásquez, N.; Araya, M.; Jara-Rojas, F.; Tisseyre, B. Assessment of an empirical spatial prediction model of vine water status for irrigation management in a grapevine field. Agric. Water Manag. 2013, 124, 58–68. [Google Scholar] [CrossRef]
- Faria, A. Nuvem de Fumo dos incêNdios do Canadá Chegou a Portugal. Available online: https://www.publico.pt/2023/06/27/a-zul/noticia/nuvem-fumo-incendios-canada-chega-portugal-so-ate-quintafeira-2054782 (accessed on 29 September 2023).
- Deloire, A.; Pellegrino, A.; Rogiers, S. A few words on grapevine leaf water potential. Ives Tech. Rev. Vine Wine 2020. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Maimon, O.Z.; Rokach, L. Data Mining with Decision Trees: Theory and Applications; World Scientific: Singapore, 2014; Volume 81. [Google Scholar]
- Damásio, M.; Pinto, C.; Soares-David, T.; Carvalho, L.; Silvestre, J.; Zarrouk, O. Managing precision irrigation in vineyards: Hydraulic and molecular signaling in eight grapevine varieties. In Proceedings of the IVES Conference Series, GiESCO, Ithaca, NY, USA, 17–21 July 2023. [Google Scholar]
- IPMA—Clima Normais. Available online: https://www.ipma.pt/pt/oclima/normais.clima/ (accessed on 29 September 2023).
- Suter, B.; Triolo, R.; Pernet, D.; Dai, Z.; Leeuwen, C.V. Modeling Stem Water Potential by Separating the Effects of Soil Water Availability and Climatic Conditions on Water Status in Grapevine (Vitis vinifera L.). Front. Plant Sci. 2019, 10, 1485. [Google Scholar] [CrossRef] [PubMed]
- Bahat, I.; Netzer, Y.; Grünzweig, J.M.; Alchanatis, V.; Peeters, A.; Goldshtein, E.; Ohana-Levi, N.; Ben-Gal, A.; Cohen, Y. In-Season Interactions between Vine Vigor, Water Status and Wine Quality in Terrain-Based Management-Zones in a ‘Cabernet Sauvignon’ Vineyard. Remote Sens. 2021, 13, 1636. [Google Scholar] [CrossRef]
- Mirás-Avalos, J.; Araujo, E. Optimization of Vineyard Water Management: Challenges, Strategies, and Perspectives. Water 2021, 13, 746. [Google Scholar] [CrossRef]
- Cole, J.; Pagay, V. Usefulness of early morning stem water potential as a sensitive indicator of water status of deficit-irrigated grapevines (Vitis vinifera L.). Sci. Hortic. 2015, 191, 10–14. [Google Scholar] [CrossRef]
- Santesteban, L.; Miranda, C.; Marín, D.; Sesma, B.; Intrigliolo, D.; Mirás-Avalos, J.; Escalona, J.; Montoro, A.; de Herralde, F.; Baeza, P.; et al. Discrimination ability of leaf and stem water potential at different times of the day through a meta-analysis in grapevine (Vitis vinifera L.). Agric. Water Manag. 2019, 221, 202–210. [Google Scholar] [CrossRef]
- Rodrigues, P.; Pedroso, V.; Gouveia, J.P.; Martins, S.; Lopes, C.; Alves, I. Influence of soil water content and atmospheric conditions on leaf water potential in cv. “Touriga Nacional” deep-rooted vineyards. Irrig. Sci. 2012, 30, 407–417. [Google Scholar] [CrossRef]
- Idso, S.; Jackson, R.; Pinter, P.; Reginato, R.; Hatfield, J. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J. Remote-Sensing of Crop Yields. Science 1977, 196, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Matese, A.; Baraldi, R.; Berton, A.; Cesaraccio, C.; Gennaro, S.D.; Duce, P.; Facini, O.; Mameli, M.; Piga, A.; Zaldei, A. Estimation of Water Stress in Grapevines Using Proximal and Remote Sensing Methods. Remote Sens. 2018, 10, 114. [Google Scholar] [CrossRef]
- Blanco-Ward, D.; Monteiro, A.; Lopes, M.; Borrego, C.; Silveira, C.; Viceto, C.; Rocha, A.; Ribeiro, A.; Andrade, J.; Feliciano, M.; et al. Analysis of climate change indices in relation to wine production: A case study in the Douro region (Portugal). BIO Web Conf. 2017, 9, 01011. [Google Scholar] [CrossRef]
- Lovisolo, C.; Perrone, I.; Carra, A.; Ferrandino, A.; Flexas, J.; Medrano, H.; Schubert, A. Drought-induced changes in development and function of grapevine (Vitis spp.) organs and in their hydraulic and non-hydraulic interactions at the whole-plant level: A physiological and molecular update. Funct. Plant Biol. 2010, 37, 98. [Google Scholar] [CrossRef]
- Costa, J.M.; Ortuño, M.F.; Lopes, C.M.; Chaves, M.M. Grapevine varieties exhibiting differences in stomatal response to water deficit. Funct. Plant Biol. 2012, 39, 179. [Google Scholar] [CrossRef]
- García-Tejero, I.; Costa, J.; Egipto, R.; Durán-Zuazo, V.; Lima, R.; Lopes, C.; Chaves, M. Thermal data to monitor crop-water status in irrigated Mediterranean viticulture. Agric. Water Manag. 2016, 176, 80–90. [Google Scholar] [CrossRef]
- Patakas, A.; Noitsakis, B.; Chouzouri, A. Optimization of irrigation water use in grapevines using the relationship between transpiration and plant water status. Agric. Ecosyst. Environ. 2005, 106, 253–259. [Google Scholar] [CrossRef]
- Pineda, M.; Barón, M.; Pérez-Bueno, M.L. Thermal Imaging for Plant Stress Detection and Phenotyping. Remote Sens. 2020, 13, 68. [Google Scholar] [CrossRef]
- Williams, L.E.; Baeza, P.; Vaughn, P. Midday measurements of leaf water potential and stomatal conductance are highly correlated with daily water use of Thompson Seedless grapevines. Irrig. Sci. 2012, 30, 201–212. [Google Scholar] [CrossRef]
- Pagay, V.; Kidman, C.M. Evaluating Remotely-Sensed Grapevine (Vitis vinifera L.) Water Stress Responses Across a Viticultural Region. Agronomy 2019, 9, 682. [Google Scholar] [CrossRef]
- Jackson, M.; Marvin, G.; Chakrabarty, A. Robust Ensemble Machine Learning for Precision Agriculture. In Proceedings of the 2022 International Conference on Innovations in Science, Engineering and Technology (ICISET), Chittagong, Bangladesh, 26–27 February 2022. [Google Scholar] [CrossRef]
- Shahhosseini, M.M. Optimized Ensemble Learning and Its Application in Agriculture. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2021. [Google Scholar]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Hochberg, U.; Degu, A.; Fait, A.; Rachmilevitch, S. Near isohydric grapevine cultivar displays higher photosynthetic efficiency and photorespiration rates under drought stress as compared with near anisohydric grapevine cultivar. Physiol. Plant. 2013, 147, 443–452. [Google Scholar] [CrossRef]
- Barreales, D.; Capitão, S.d.A.; Monteiro, Â.M.A.; Andrade, J.V.; Ribeiro, A. Influence of pruning system and deficit irrigation on grapevine physiology, yield and grape quality of cv. Sousão (Vitis vinifera L.) growing under Mediterranean conditions. In Proceedings of the 7th International Congress of Mountain and Steep Slopes Viticulture, Vila Real, Portugal, 12–14 May 2022; pp. 348–352. [Google Scholar]
- Santos, T.P.D.; Lopes, C.M.; Rodrigues, M.L.; Souza, C.R.D.; Maroco, J.P.; Pereira, J.S.; Silva, J.R.; Chaves, M.M. Partial rootzone drying: Effects on growth and fruit quality of field-grown grapevines (Vitis vinifera). Funct. Plant Biol. 2003, 30, 663. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 56. [Google Scholar]
- Romero, P.; García García, J.; Fernández-Fernández, J.I.; Muñoz, R.G.; del Amor Saavedra, F.; Martínez-Cutillas, A. Improving berry and wine quality attributes and vineyard economic efficiency by long-term deficit irrigation practices under semiarid conditions. Sci. Hortic. 2016, 203, 69–85. [Google Scholar] [CrossRef]
- Jones, H.G. Use of infrared thermography for monitoring stomatal closure in the field: Application to grapevine. J. Exp. Bot. 2002, 53, 2249–2260. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. An Introduction to Statistical Learning: With Applications in Python; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. Ensemble Learning. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 605–624. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Tong, H. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2009; pp. 532–538. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]


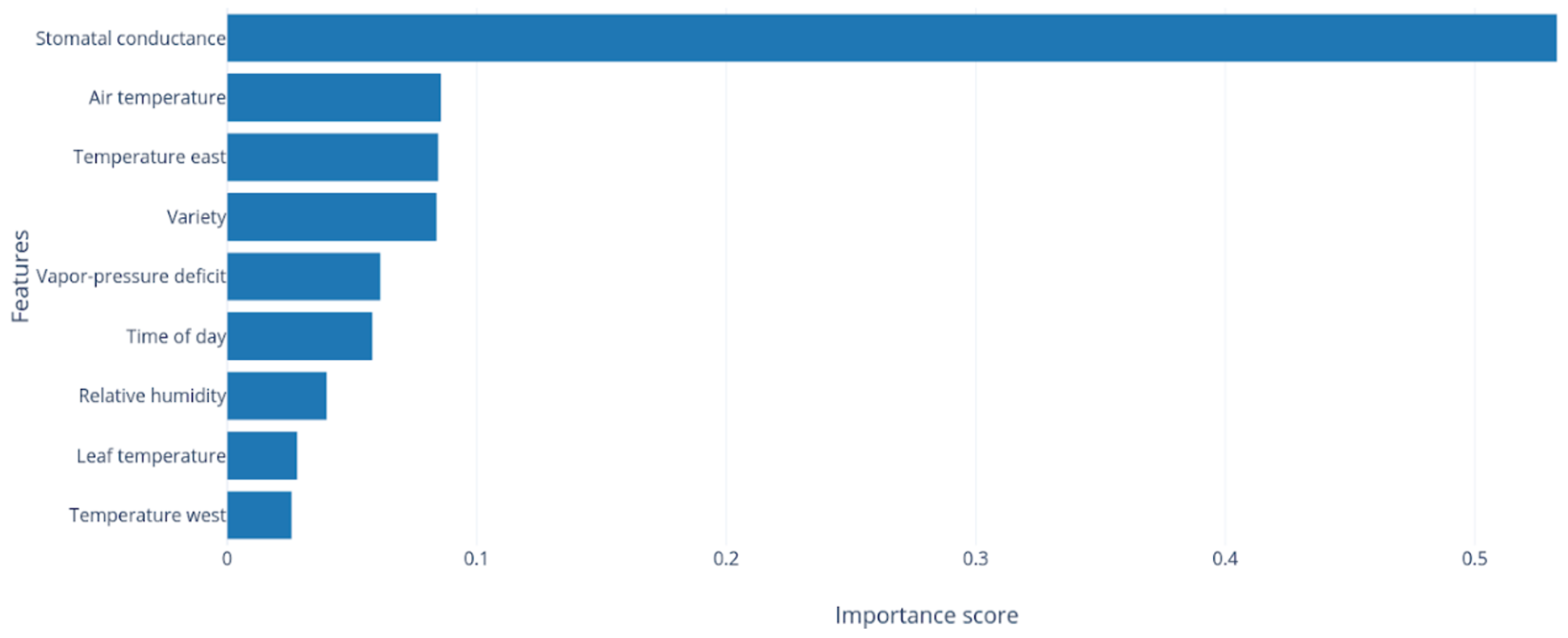
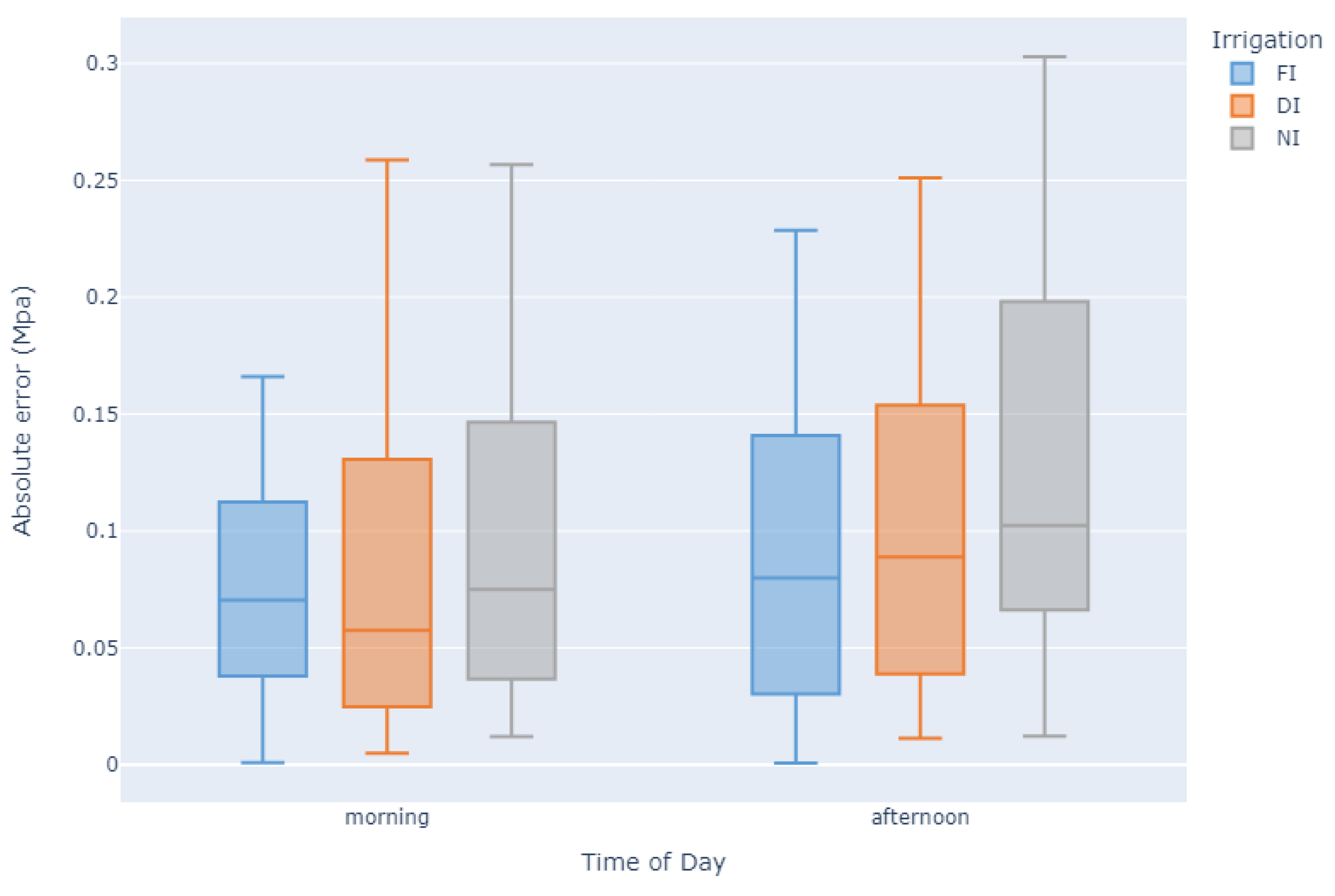

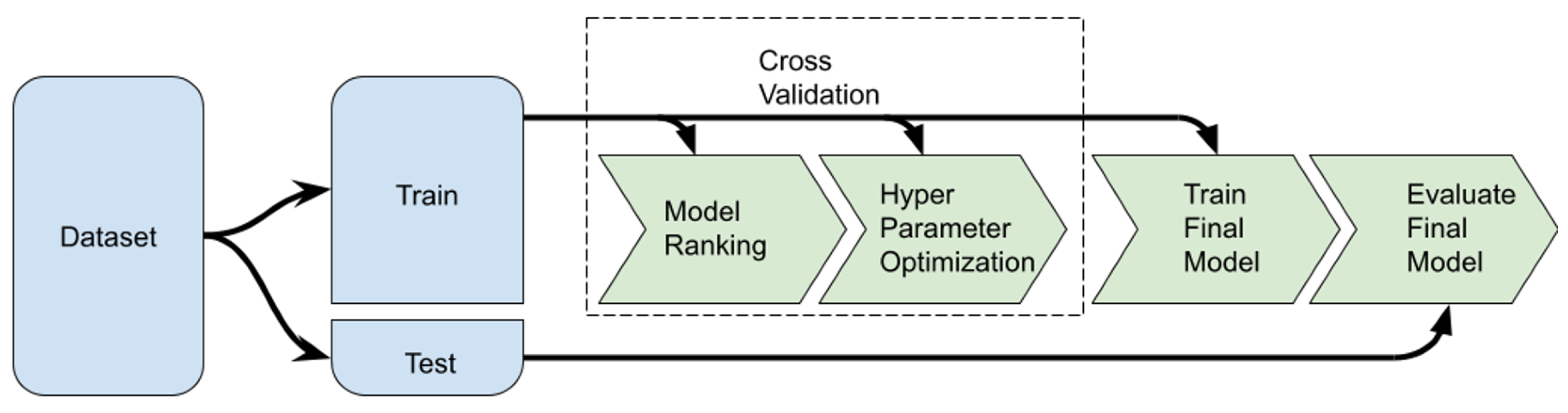
| Rank | Model | Module | MAE (MPa) | |
|---|---|---|---|---|
| 1 | GradientBoostingRegressor | Ensemble | 0.761 | 0.097 |
| 2 | ExtraTreesRegressor | Ensemble | 0.756 | 0.101 |
| 3 | RandomForestRegressor | Ensemble | 0.709 | 0.107 |
| 6 | SVR | SVM | 0.687 | 0.113 |
| 7 | NuSVR | SVM | 0.676 | 0.118 |
| 9 | LassoLarsIC | Linear | 0.599 | 0.132 |
| 10 | LinearRegression | Linear | 0.596 | 0.132 |
| 25 | DecisionTreeRegressor | Tree | 0.548 | 0.130 |
| 29 | MLPRegressor | Neural Network | 0.490 | 0.140 |
| 31 | KNeighborsRegressor | Neighbors | 0.445 | 0.155 |
| 36 | GaussianProcessRegressor | Gaussian Process | 0.218 | 0.146 |
| 42 | RadiusNeighborsRegressor | Neighbors | −0.029 | 0.213 |
| Model | Validation | Test | ||
|---|---|---|---|---|
| MAE (MPa) | MAE (MPa) | |||
| GradientBoostingRegressor | 0.786 | 0.093 | 0.830 | 0.073 |
| ExtraTreesRegressor | 0.759 | 0.100 | 0.833 | 0.072 |
| RandomForestRegressor | 0.710 | 0.107 | 0.798 | 0.079 |
| Reference | No. of Varieties | Target | Predictors | Model | Platform | |
|---|---|---|---|---|---|---|
| Our approach | 5 | Thermal imaging, gs, meteorology | ExtraTrees | Handheld | 0.83 | |
| [96] | 2 | Hyperspectral bands | Algorithm based on the search for covariance | Handheld | 0.97 | |
| [84] | 1 | (MD) | Hyperspectral bands | Artificial Neural Network | UAV | 0.87 |
| [90] | 6 | (MD) | NIR spectrometer | Rotation Forest, M5 trees | Handheld | 0.84 |
| [97] | 1 | (MD) | CWSI | Linear Regression | UAV, Field sensors | 0.83 |
| [92] | 1 | (MD) | NIR spectrometer | Partial Least Squares | ATV | 0.69 |
| [98] | 1 | (MD) | CWSI | Linear Regression | UAV | 0.51 |
| [123] | 2 | Thermal indices | Two-way Analysis of Variance (ANOVA) | UAV, Handheld | 0.50 |
| Source | Variable |
|---|---|
| Porometer | Leaf temperature |
| Thermal Camera | Temperature canopy east Temperature canopy west |
| Manually Recorded | Time of day (MM/MD) Variety |
| Meteorological Station | VPD Relative humidity Air temperature |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damásio, M.; Barbosa, M.; Deus, J.; Fernandes, E.; Leitão, A.; Albino, L.; Fonseca, F.; Silvestre, J. Can Grapevine Leaf Water Potential Be Modelled from Physiological and Meteorological Variables? A Machine Learning Approach. Plants 2023, 12, 4142. https://doi.org/10.3390/plants12244142
Damásio M, Barbosa M, Deus J, Fernandes E, Leitão A, Albino L, Fonseca F, Silvestre J. Can Grapevine Leaf Water Potential Be Modelled from Physiological and Meteorological Variables? A Machine Learning Approach. Plants. 2023; 12(24):4142. https://doi.org/10.3390/plants12244142
Chicago/Turabian StyleDamásio, Miguel, Miguel Barbosa, João Deus, Eduardo Fernandes, André Leitão, Luís Albino, Filipe Fonseca, and José Silvestre. 2023. "Can Grapevine Leaf Water Potential Be Modelled from Physiological and Meteorological Variables? A Machine Learning Approach" Plants 12, no. 24: 4142. https://doi.org/10.3390/plants12244142
APA StyleDamásio, M., Barbosa, M., Deus, J., Fernandes, E., Leitão, A., Albino, L., Fonseca, F., & Silvestre, J. (2023). Can Grapevine Leaf Water Potential Be Modelled from Physiological and Meteorological Variables? A Machine Learning Approach. Plants, 12(24), 4142. https://doi.org/10.3390/plants12244142





