Modeling of Flowering Time in Vigna radiata with Artificial Image Objects, Convolutional Neural Network and Random Forest
Abstract
1. Introduction
- -
- The methodology is proposed that combines AIOs and modern ML algorithms,
- -
- Using random forest and three feature importance measures, SNPs are selected that influence the time to flowering in the available Vigna dataset,
- -
- A model based on AIOs and CNNs is developed for prediction of time to flowering in the available Vigna dataset using selected SNPs and climatic factors for only 5 days before and 20 days after planting,
- -
- The impacts of genotypic and climatic factors and their combinations to the model solution are evaluated using two visual explanation methods.
2. Related Work
3. Materials and Methods
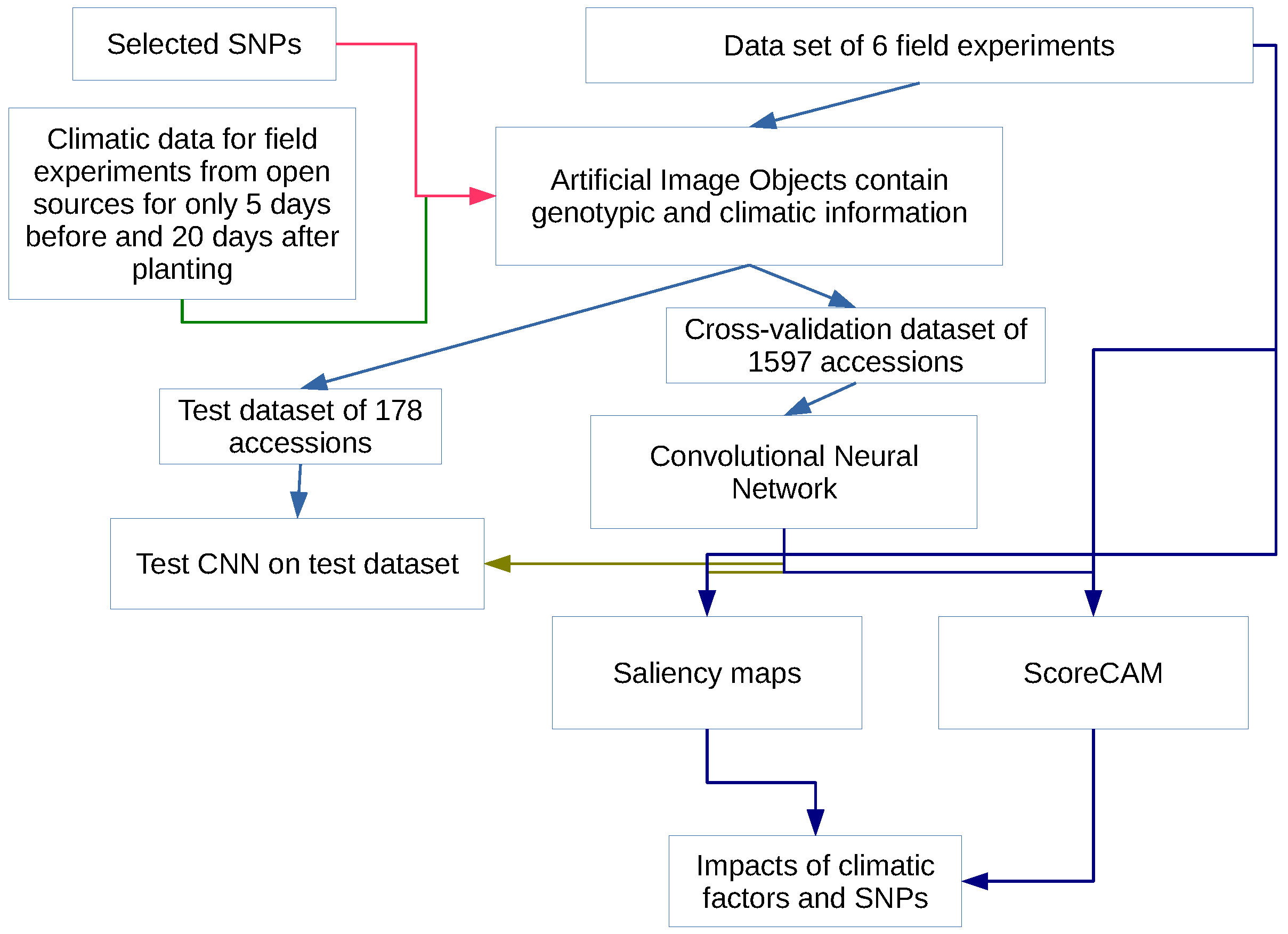
3.1. The Overview
- 1.
- Identification of SNP with maximal influence on flowering time using three feature importance metrics for random forest models,
- 2.
- Construction of artificial images for each accession encoding information on the SNP values and climatic factors for a limited period of time,
- 3.
- Building a convolutional neural network for prediction of flowering time,
- 4.
- Investigation of the impacts of different factors on the model using two class activation mapping techniques.
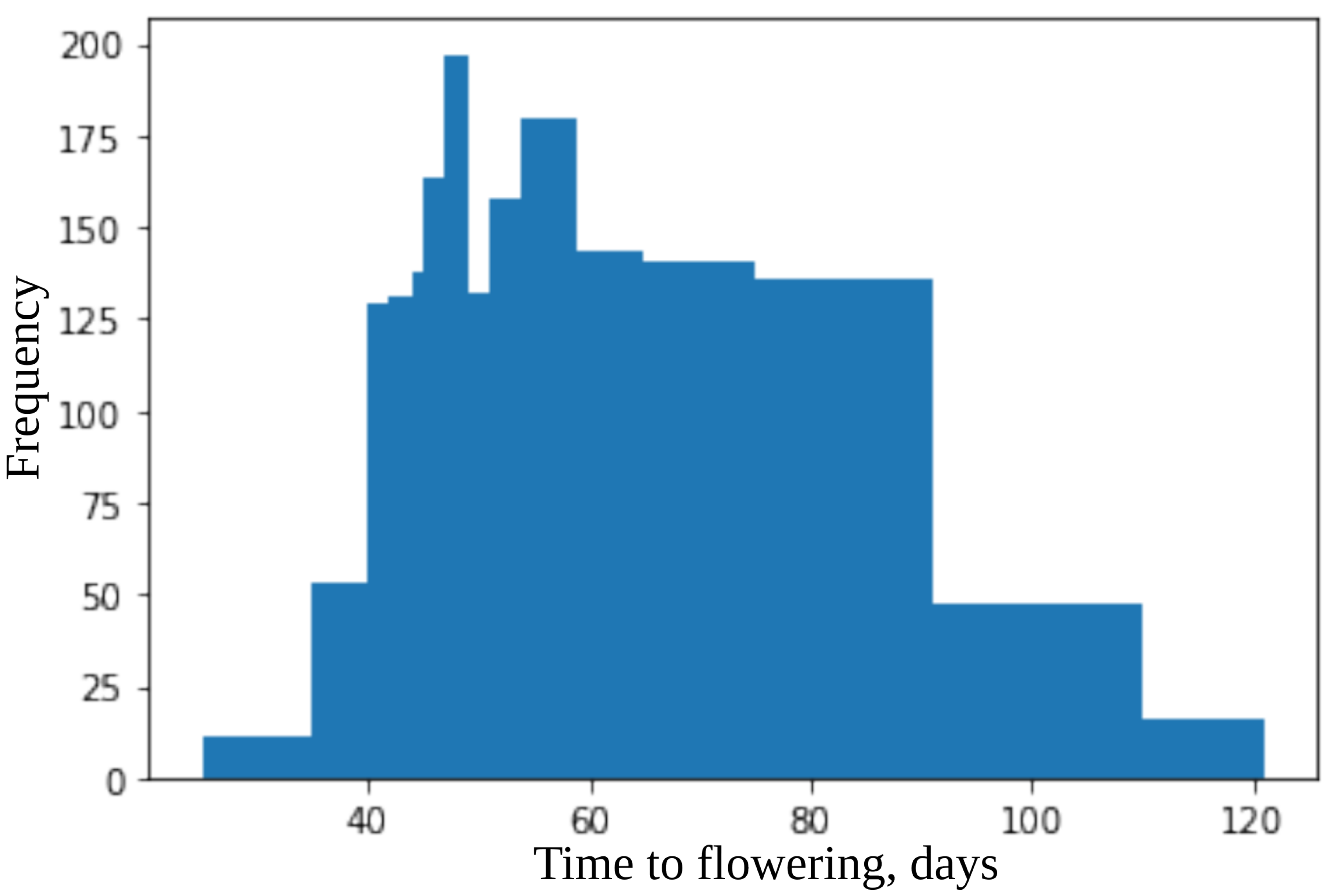
3.2. Plant Material
- -
- 1984: sown on 28/08/1984; harvested on 24/10/1984, geographical coordinates: N 23650 E 1201755;
- -
- 1985: sown on 17/09/1985; harvested on 03/10/1985, geographical coordinates: N 23650 E 1201755;
- -
- 2016: sown on 16/06/2016, harvested from 22/08 to mid-September, geographical coordinates: N 173028 E 781610;
- -
- 2018: sown 21/09/2018 and harvested from 24–28 December 2018, geographical coordinates: N 23650 E 1201755;
- -
- 2018: sown 03/05/2018 and harvested from mid-July, geographical coordinates: N 4518 E 4052;
- -
- 2019: sown 12/05/2018 and harvested from mid-July, geographical coordinates: N 4614 E 4801.
3.3. SNP Selection
3.3.1. Accounting for Population Structure
3.3.2. Random Forest
3.3.3. Gini Index
3.3.4. Boruta Algorithm
3.3.5. SHAP Values
3.4. Climate Data
- A day length D,
- A minimal temperature ,
- A maximal temperature ,
- A precipitation R,
- A relative humidity H,
- A solar radiation S,
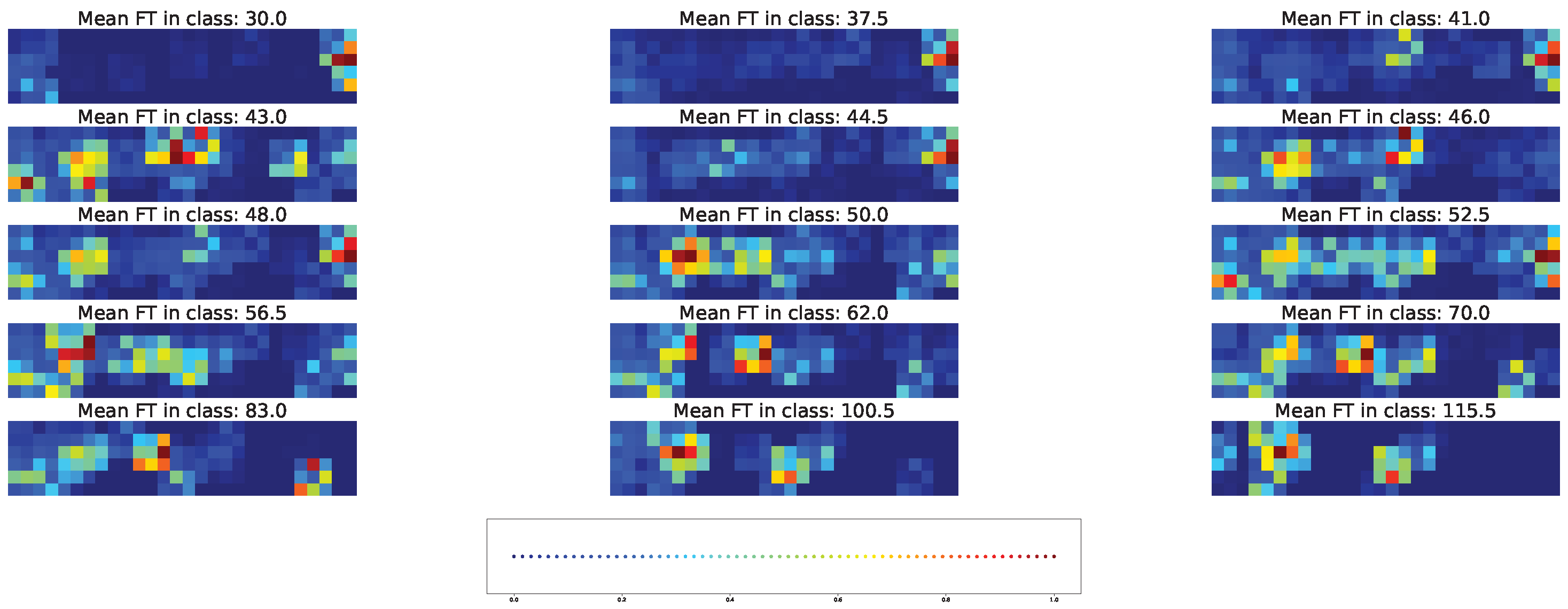
3.5. Artificial Image Objects
3.6. Convolutional Neural Network
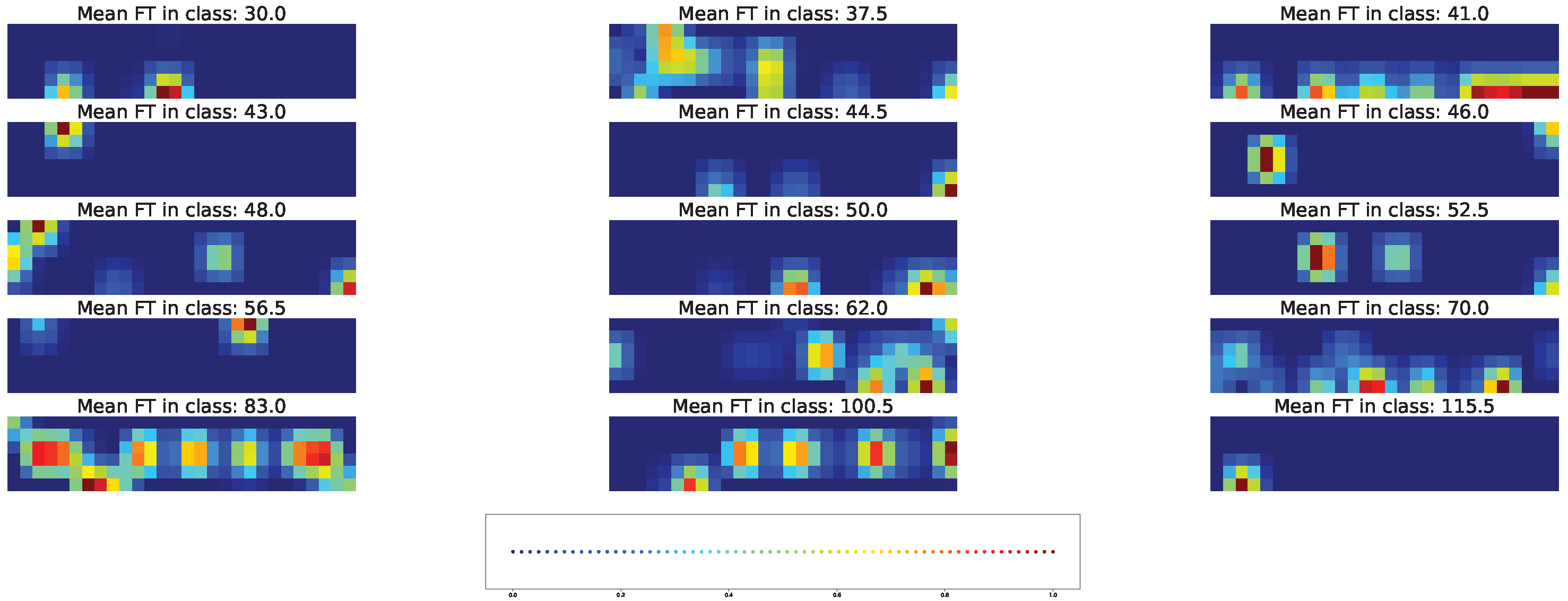
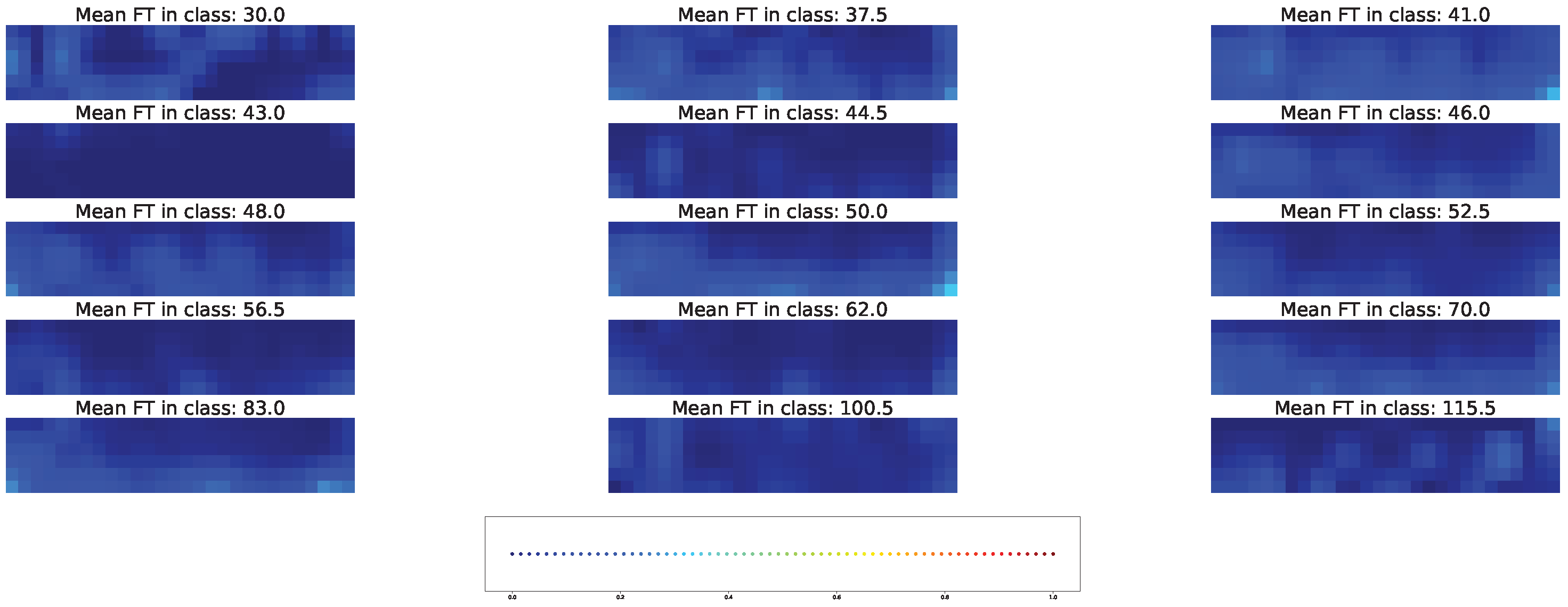
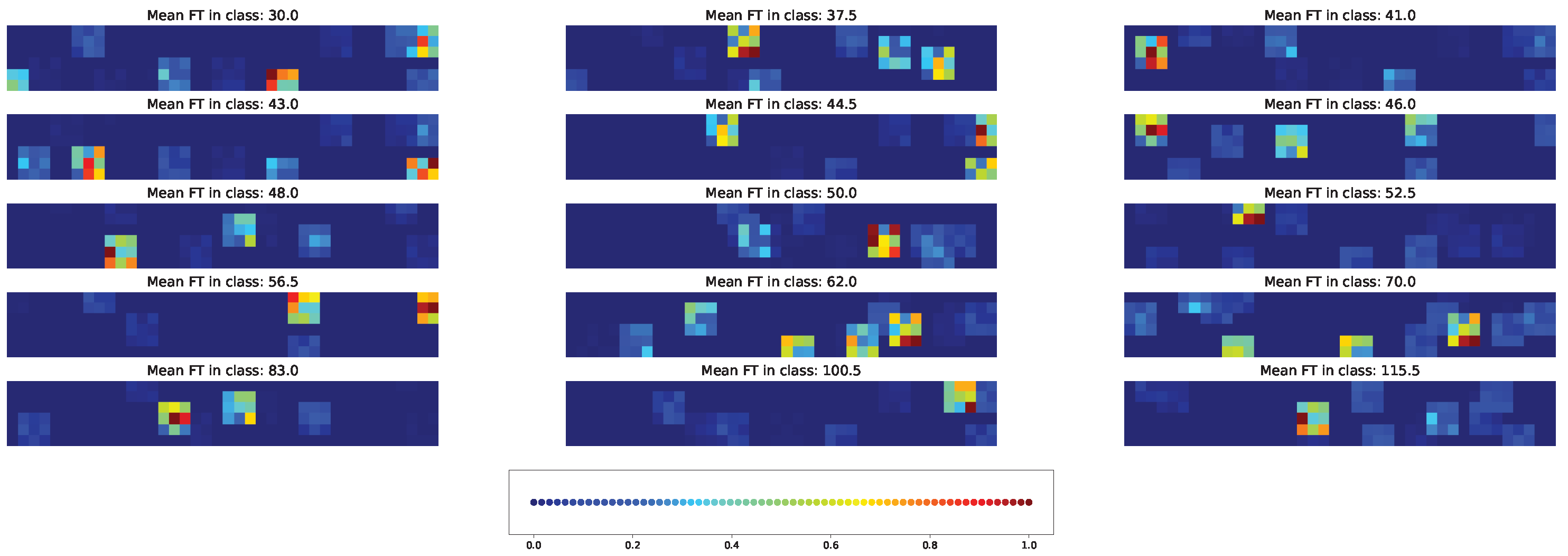
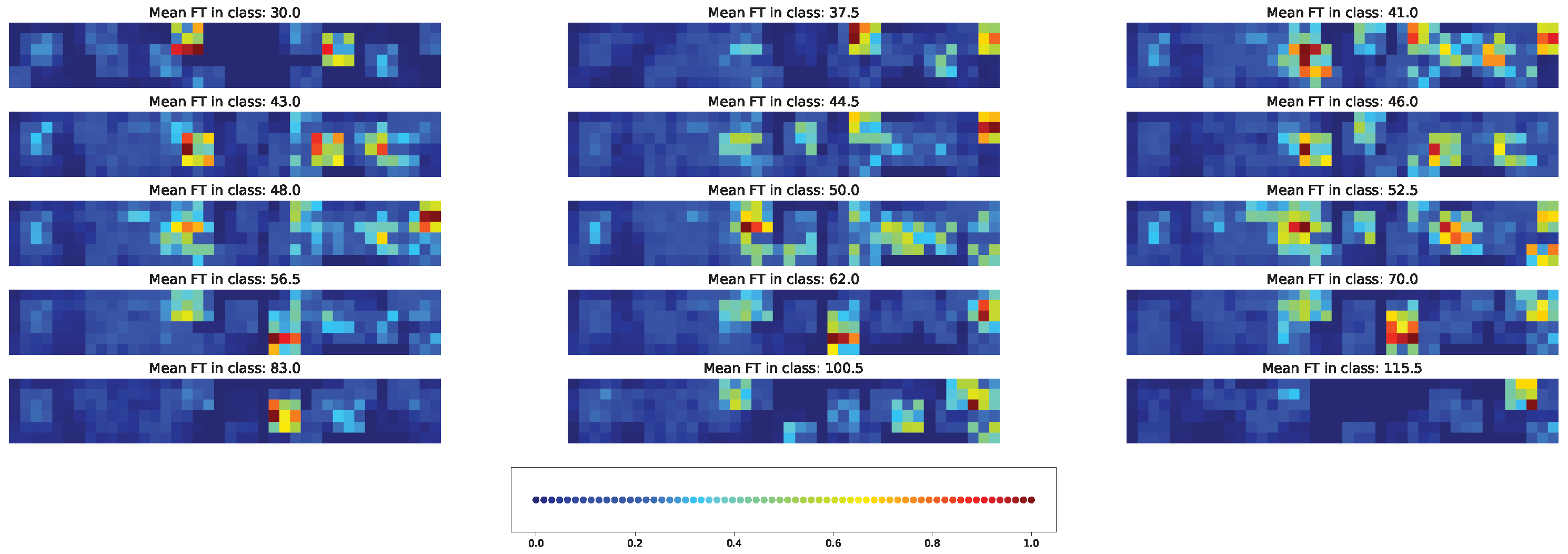
3.7. Impacts of Different Factors to the Model Solution
4. Results
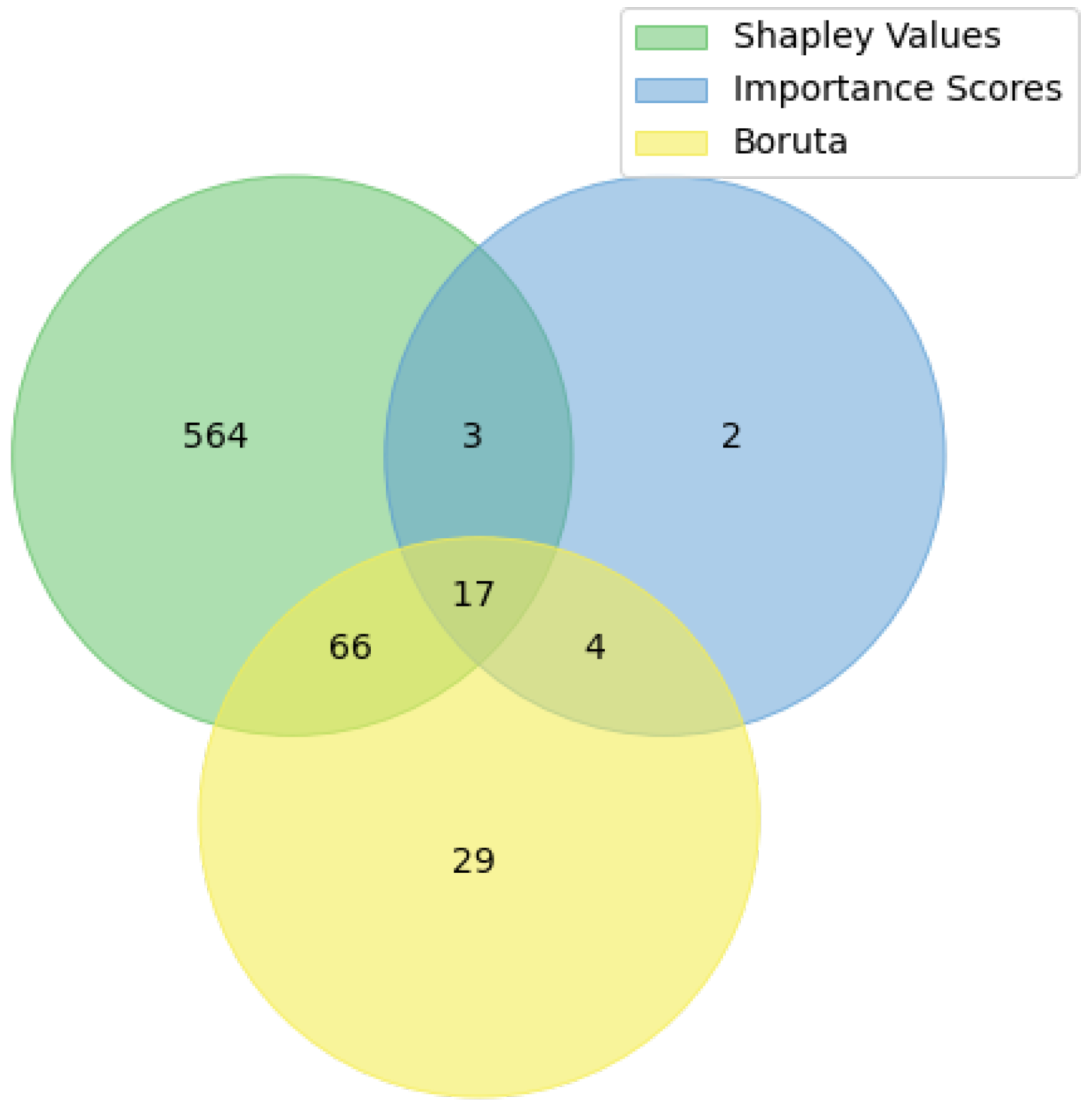
4.1. Selected SNPs
- -
- The cross-SNP set includes 17 SNPs from the intersection of all three results (see Table 1),
- -
- The union SNP set includes 90 SNPs from pair-wise intersections of three results (see Zenodo link in Data Availability Statement).
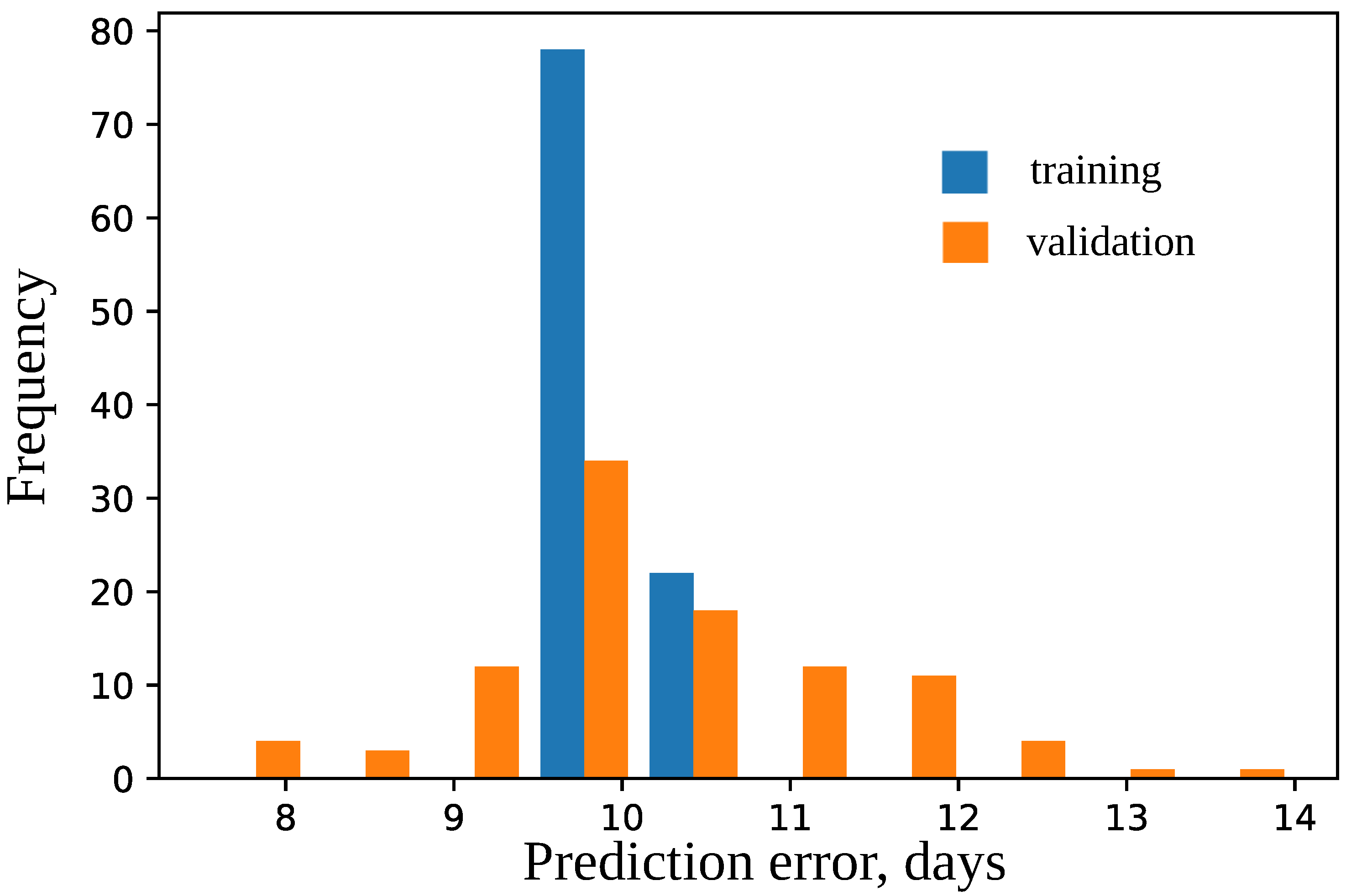
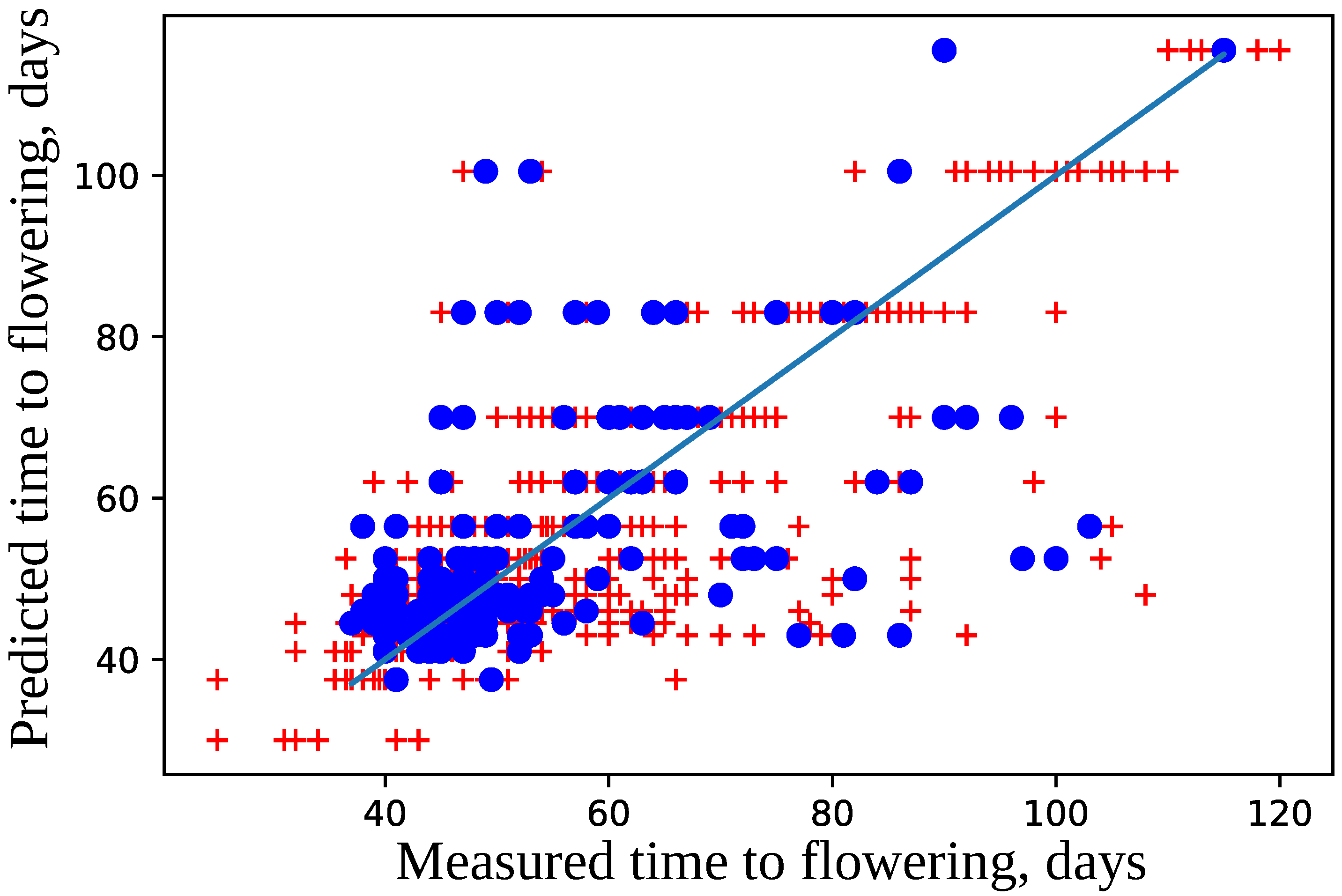
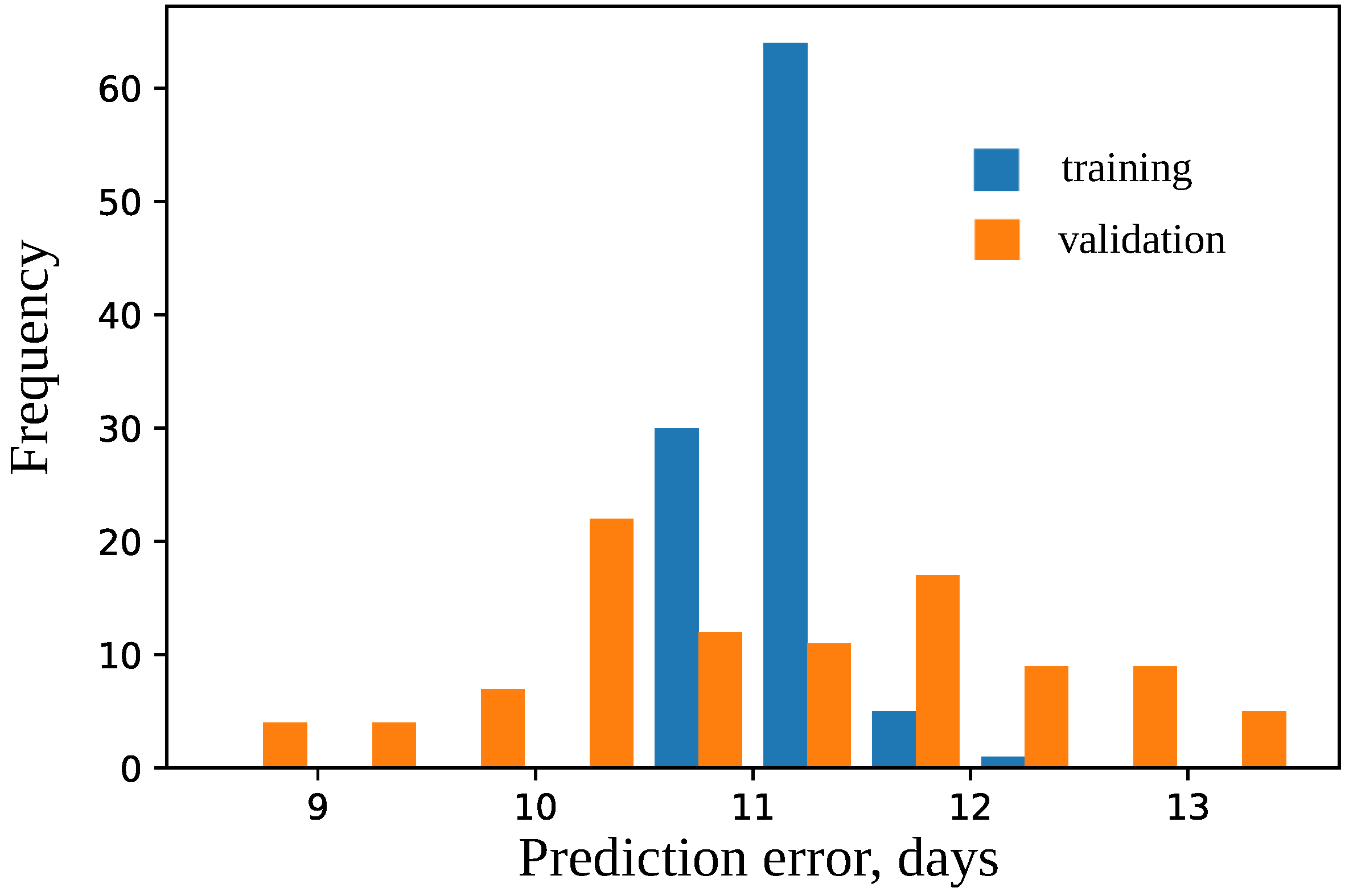
4.2. Model for Time to Flowering
4.3. Important Features for Models Based on the Cross-SNP Set
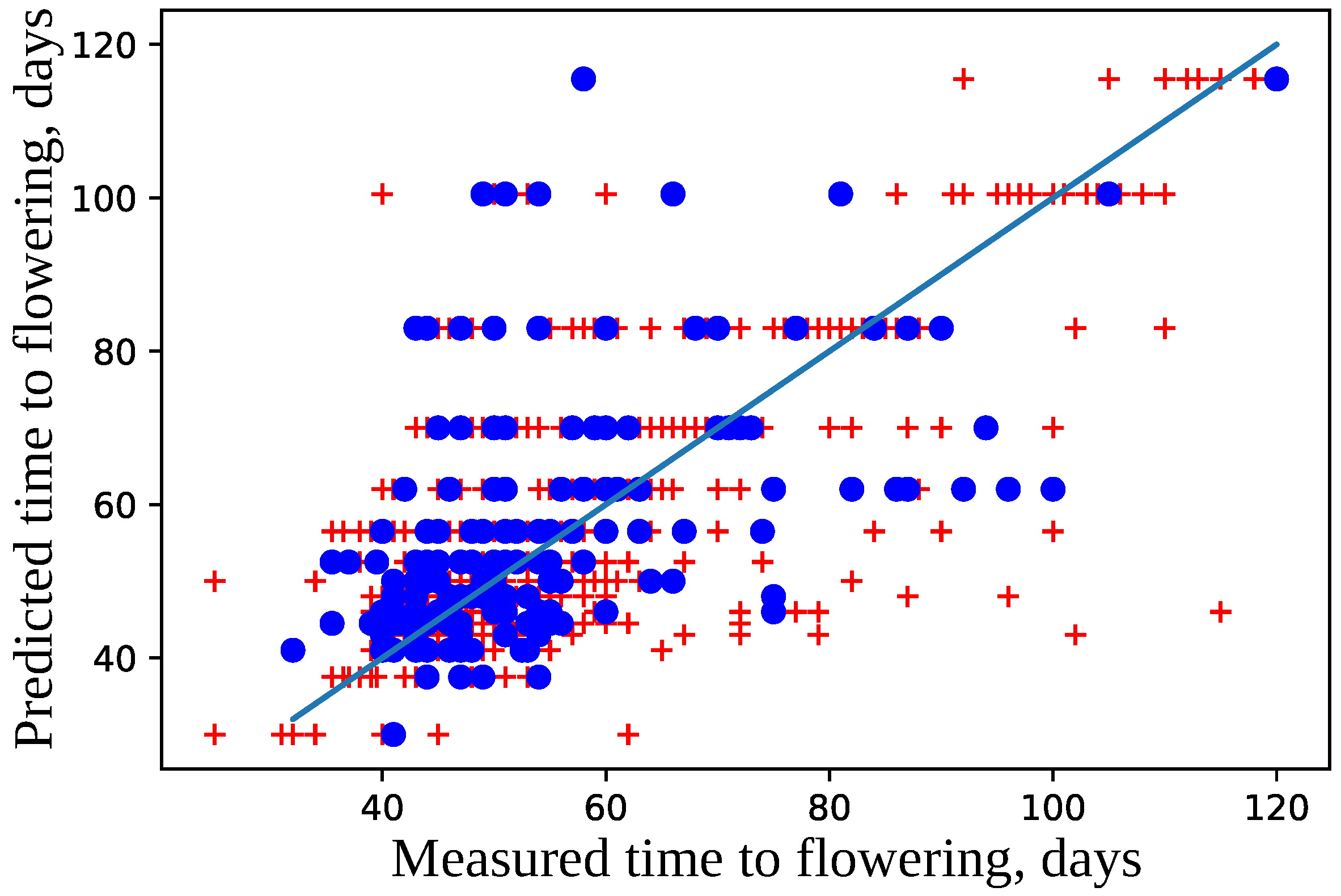
4.4. Important Features for Models Based on the Union SNP Set
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chivenge, P.; Mabhaudhi, T.; Modi, A.; Mafongoya, P. The Potential Role of Neglected and Underutilised Crop Species as Future Crops under Water Scarce Conditions in Sub-Saharan Africa. Int. J. Environ. Res. Public Health 2015, 12, 5685–5711. [Google Scholar] [CrossRef] [PubMed]
- Vara-Ubol, S.; Chambers, E.; Chambers, D.H. Sensory characteristics of chemical compounds potentially associated with beany aroma in foods. J. Sens. Stud. 2004, 19, 15–26. [Google Scholar] [CrossRef]
- Vishnyakova, M.A.; Burlyaeva, M.O.; Samsonova, M.G. Green gram and black gram: Prospects of cultivation and breeding in Russian Federation. Vavilov J. Genet. Breed. 2018, 22, 957–966. [Google Scholar] [CrossRef]
- Burlyaeva, M.; Vishnyakova, M.; Gurkina, M.; Kozlov, K.; Lee, C.R.; Ting, C.T.; Schafleitner, R.; Nuzhdin, S.; Samsonova, M.; von Wettberg, E. Collections of Mungbean [Vigna radiata (L.) R. Wilczek] and urdbean [V. mungo (L.) Hepper] in Vavilov Institute (VIR): Traits diversity and trends in the breeding process over the last 100 years. Genet. Resour. Crop. Evol. 2019, 66, 767–781. [Google Scholar] [CrossRef]
- Schafleitner, R.; Nair, R.M.; Rathore, A.; Wang, Y.W.; Lin, C.Y.; Chu, S.H.; Lin, P.Y.; Chang, J.C.; Ebert, A.W. The AVRDC—The World Vegetable Center mung bean (Vigna radiata) core and mini core collections. BMC Genom. 2015, 16, 344. [Google Scholar] [CrossRef]
- Singh, V.; Yadav, N.R.; Singh, J. Role of Genomic tools for Mungbean [Vigna radiata (L.) Wilczek] improvement. Legume Res. Int. J. 2017, 40, 601–608. [Google Scholar] [CrossRef][Green Version]
- Kang, Y.J.; Kim, S.K.; Kim, M.Y.; Lestari, P.; Kim, K.H.; Ha, B.K.; Jun, T.H.; Hwang, W.J.; Lee, T.; Lee, J.; et al. Genome sequence of mung bean and insights into evolution within Vigna species. Nat. Commun. 2014, 5, 5443. [Google Scholar] [CrossRef]
- Kim, S.K.; Nair, R.M.; Lee, J.; Lee, S.H. Genomic resources in mung bean for future breeding programs. Front. Plant Sci. 2015, 6. [Google Scholar] [CrossRef]
- Swindell, R.; Poehlman, J.M. Inheritance of photoperiod response (Vigna radiata [L.] wilczek). Euphytica 1978, 27, 325–333. [Google Scholar] [CrossRef]
- Ellis, R.H.; Lawn, R.J.; Summerfield, R.J.; Qi, A.; Roberts, E.H.; Chay, P.M.; Brouwer, J.B.; Rose, J.L.; Yeates, S.J.; Sandover, S. Towards the Reliable Prediction of Time to Flowering in Six Annual Crops. IV. Cultivated and Wild Mung Bean. Exp. Agric. 1994, 30, 31–43. [Google Scholar] [CrossRef]
- Imrie, B.C.; Drake, D.W.; Delacy, I.H.; Byth, D.E. Analysis of genotypic and environmental variation in international mung bean trials. Euphytica 1981, 30, 301–311. [Google Scholar] [CrossRef]
- Nath, D.; Dasgupta, T. Genotype × Environment Interaction and Stability Analysis in Mungbean. IOSR J. Agric. Vet. Sci. 2013, 5, 62–70. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sun, Y.V. Multigenic Modeling of Complex Disease by Random Forests. In Advances in Genetics; Elsevier: Amsterdam, The Netherlands, 2010; Volume 72, pp. 73–99. [Google Scholar] [CrossRef]
- Shapley, L.S.; Roth, A.E. (Eds.) The Shapley Value: Essays in Honor of Lloyd S. Shapley; Cambridge University Press: Cambridge, NY, USA, 1988. [Google Scholar]
- Ramzan, F.; Klees, S.; Schmitt, A.O.; Cavero, D.; Gültas, M. Identification of Age-Specific and Common Key Regulatory Mechanisms Governing Eggshell Strength in Chicken Using Random Forests. Genes 2020, 11, 464. [Google Scholar] [CrossRef] [PubMed]
- Piekutowska, M.; Niedbała, G.; Piskier, T.; Lenartowicz, T.; Pilarski, K.; Wojciechowski, T.; Pilarska, A.A.; Czechowska-Kosacka, A. The Application of Multiple Linear Regression and Artificial Neural Network Models for Yield Prediction of Very Early Potato Cultivars before Harvest. Agronomy 2021, 11, 885. [Google Scholar] [CrossRef]
- Chen, X.; Chen, D.G.; Zhao, Z.; Zhan, J.; Ji, C.; Chen, J. Artificial image objects for classification of schizophrenia with GWAS-selected SNVs and convolutional neural network. Patterns 2021, 2, 100303. [Google Scholar] [CrossRef]
- Chen, X.; Chen, D.G.; Zhao, Z.; Balko, J.M.; Chen, J. Artificial image objects for classification of breast cancer biomarkers with transcriptome sequencing data and convolutional neural network algorithms. Breast Cancer Res. 2021, 23, 96. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Du, M.; Yang, F.; Zhang, Z.; Ding, S.; Mardziel, P.; Hu, X. Score-CAM: Score-Weighted Visual Explanations for Convolutional Neural Networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Seattle, WA, USA, 14–19 June 2020; pp. 111–119. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, J. Measuring Feature Importance of Convolutional Neural Networks. IEEE Access 2020, 8, 196062–196074. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2014, arXiv:1312.6034. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
- Ageev, A.; Aydogan, A.; Bishop-von Wettberg, E.; Nuzhdin, S.V.; Samsonova, M.; Kozlov, K. Simulation Model for Time to Flowering with Climatic and Genetic Inputs for Wild Chickpea. Agronomy 2021, 11, 1389. [Google Scholar] [CrossRef]
- Ageev, A.Y.; Bishop-von Wettberg, E.J.; Nuzhdin, S.V.; Samsonova, M.G.; Kozlov, K.N. Forecasting the Timing of Floral Initiation in Wild Chickpeas under Climate Change. Biophysics 2021, 66, 107–116. [Google Scholar] [CrossRef]
- Kozlov, K.; Singh, A.; Berger, J.; Wettberg, E.B.V.; Kahraman, A.; Aydogan, A.; Cook, D.; Nuzhdin, S.; Samsonova, M. Non-linear regression models for time to flowering in wild chickpea combine genetic and climatic factors. BMC Plant Biol. 2019, 19, 94. [Google Scholar] [CrossRef] [PubMed]
- Ageev, A.; Lee, C.R.; Ting, C.T.; Schafleitner, R.; Bishop-von Wettberg, E.; Nuzhdin, S.V.; Samsonova, M.; Kozlov, K. Modeling of Flowering Time in Vigna radiata with Approximate Bayesian Computation. Agronomy 2021, 11, 2317. [Google Scholar] [CrossRef]
- Kozlov, K.; Sokolkova, A.; Lee, C.R.; Ting, C.T.; Schafleitner, R.; Bishop-von Wettberg, E.; Nuzhdin, S.; Samsonova, M. Dynamical climatic model for time to flowering in Vigna radiata. BMC Plant Biol. 2020, 20, 202. [Google Scholar] [CrossRef]
- Boote, K.J.; Jones, J.; Pickering, N. Potential Uses and Limitations of Crop Models. Agron. J. 1996, 88, 704–716. [Google Scholar] [CrossRef]
- Jones, J.; Hoogenboom, G.; Porter, C.; Boote, K.; Batchelor, W.; Hunt, L.; Wilkens, P.; Singh, U.; Gijsman, A.; Ritchie, J. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Mabhaudhi, T.; Chibarabada, T.P.; Chimonyo, V.G.P.; Modi, A.T. Modelling climate change impact: A case of bambara groundnut (Vigna subterranea). Phys. Chem. Earth Parts A/B/C 2018, 105, 25–31. [Google Scholar] [CrossRef]
- Chapman, S.C.; Cooper, M.; Hammer, G.L.; Butler, D.G. Genotype by environment interactions affecting grain sorghum. II. Frequencies of different seasonal patterns of drought stress are related to location effects on hybrid yields. Aust. J. Agric. Res. 2000, 51, 209. [Google Scholar] [CrossRef]
- Soltani, A.; Khooie, F.; Ghassemi-Golezani, K.; Moghaddam, M. A simulation study of chickpea crop response to limited irrigation in a semiarid environment. Agric. Water Manag. 2001, 49, 225–237. [Google Scholar] [CrossRef]
- Chauhan, Y.S.; Douglas, C.; Rachaputi, R.C.N.; Agius, P.; Martin, W.; Skerman, A. Physiology of mung bean and development of the mung bean crop model. In Proceedings of the 1st Australian Summer Grains Conference, Gold Coast, Australia, 21–24 June 2010; p. 11. [Google Scholar]
- Mieth, B.; Kloft, M.; Rodríguez, J.A.; Sonnenburg, S.; Vobruba, R.; Morcillo-Suárez, C.; Farré, X.; Marigorta, U.M.; Fehr, E.; Dickhaus, T.; et al. Combining Multiple Hypothesis Testing with Machine Learning Increases the Statistical Power of Genome-wide Association Studies. Sci. Rep. 2016, 6, 36671. [Google Scholar] [CrossRef] [PubMed]
- Paré, G.; Mao, S.; Deng, W.Q. A machine-learning heuristic to improve gene score prediction of polygenic traits. Sci. Rep. 2017, 7, 12665. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, H.L.; John, C.R.; Watson, D.S.; Munroe, P.B.; Barnes, M.R.; Cabrera, C.P. Reaching the End-Game for GWAS: Machine Learning Approaches for the Prioritization of Complex Disease Loci. Front. Genet. 2020, 11, 350. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Huang, J.Z.; Wu, Q.; Nguyen, T.T.; Li, M.J. Genome-wide association data classification and SNPs selection using two-stage quality-based Random Forests. BMC Genom. 2015, 16, S5. [Google Scholar] [CrossRef] [PubMed]
- Szymczak, S.; Holzinger, E.; Dasgupta, A.; Malley, J.D.; Molloy, A.M.; Mills, J.L.; Brody, L.C.; Stambolian, D.; Bailey-Wilson, J.E. r2VIM: A new variable selection method for random forests in genome-wide association studies. BioData Min. 2016, 9, 7. [Google Scholar] [CrossRef] [PubMed]
- Stephan, J.; Stegle, O.; Beyer, A. A random forest approach to capture genetic effects in the presence of population structure. Nat. Commun. 2015, 6, 7432. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 839–847. [Google Scholar] [CrossRef]
- Jiang, P.T.; Zhang, C.B.; Hou, Q.; Cheng, M.M.; Wei, Y. LayerCAM: Exploring Hierarchical Class Activation Maps for Localization. IEEE Trans. Image Process. 2021, 30, 5875–5888. [Google Scholar] [CrossRef] [PubMed]
- Sokolkova, A.; Burlyaeva, M.; Valiannikova, T.; Vishnyakova, M.; Schafleitner, R.; Lee, C.R.; Ting, C.T.; Nair, R.M.; Nuzhdin, S.; Samsonova, M.; et al. Genome-wide association study in accessions of the mini-core collection of mung bean (Vigna radiata) from the World Vegetable Gene Bank (Taiwan). BMC Plant Biol. 2020, 20, 363. [Google Scholar] [CrossRef]
- Ong, P.W.; Lin, Y.P.; Chen, H.W.; Lo, C.Y.; Burlyaeva, M.; Noble, T.; Nair, R.; Schafleitner, R.; Vishnyakova, M.; Bishop-von Wettberg, E.; et al. The climatic constrains of the historical global spread of mung bean. bioRxiv 2022. [Google Scholar] [CrossRef]
- Christopoulos, D.T. On the Efficient Identification of an Inflection Point. Int. J. Math. Sci. Comput. 2016, 6, 9. [Google Scholar]
- Bhardwaj, A.; Bag, S.K. PLANET-SNP pipeline: PLants based ANnotation and Establishment of True SNP pipeline. Genomics 2019, 111, 1066–1077. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Yu, K. Improved correction for population stratification in genome-wide association studies by identifying hidden population structures. Genet. Epidemiol. 2008, 32, 215–226. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley Series in Probability and Mathematical Statistics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zhao, Y.; Chen, F.; Zhai, R.; Lin, X.; Wang, Z.; Su, L.; Christiani, D.C. Correction for population stratification in random forest analysis. Int. J. Epidemiol. 2012, 41, 1798–1806. [Google Scholar] [CrossRef] [PubMed]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 13. [Google Scholar] [CrossRef]
- Strumbelj, E.; Kononenko, I. An Efficient Explanation of Individual Classifications using Game Theory. J. Mach. Learn. Researc 2010, 11, 18. [Google Scholar]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable; OCLC: Munich, Germany, 2022; p. 1306621094. [Google Scholar]
- Bayer, P.E.; Petereit, J.; Danilevicz, M.F.; Anderson, R.; Batley, J.; Edwards, D. The application of pangenomics and machine learning in genomic selection in plants. Plant Genome 2021, 14, e20112. [Google Scholar] [CrossRef] [PubMed]
- Stackhouse, P.W.; Perez, R.; Sengupta, M.; Knapp, K.; Mikovitz, J.C.; Schlemmer, J.; Scarino, B.; Zhang, T.; Cox, S.J. An Assessment of New Satellite Data Products for the Development of a Long-term Global Solar Resource At 10–100 km. In Proceedings of the Solar 2016 Conference; International Solar Energy Society: San Francisco, CA, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Dell’Acqua, M.; Zuccolo, A.; Tuna, M.; Gianfranceschi, L.; Pè, M. Targeting environmental adaptation in the monocot model Brachypodium distachyon: A multi-faceted approach. BMC Genom. 2014, 15, 801. [Google Scholar] [CrossRef]
- Westengen, O.T.; Berg, P.R.; Kent, M.P.; Brysting, A.K. Spatial Structure and Climatic Adaptation in African Maize Revealed by Surveying SNP Diversity in Relation to Global Breeding and Landrace Panels. PLoS ONE 2012, 7, e47832. [Google Scholar] [CrossRef]
- Vadez, V.; Berger, J.D.; Warkentin, T.; Asseng, S.; Ratnakumar, P.; Rao, K.P.C.; Gaur, P.M.; Munier-Jolain, N.; Larmure, A.; Voisin, A.S.; et al. Adaptation of grain legumes to climate change: A review. Agron. Sustain. Dev. 2012, 32, 31–44. [Google Scholar] [CrossRef]
- Van Bel, M.; Silvestri, F.; Weitz, E.M.; Kreft, L.; Botzki, A.; Coppens, F.; Vandepoele, K. PLAZA 5.0: Extending the scope and power of comparative and functional genomics in plants. Nucleic Acids Res. 2022, 50, D1468–D1474. [Google Scholar] [CrossRef]



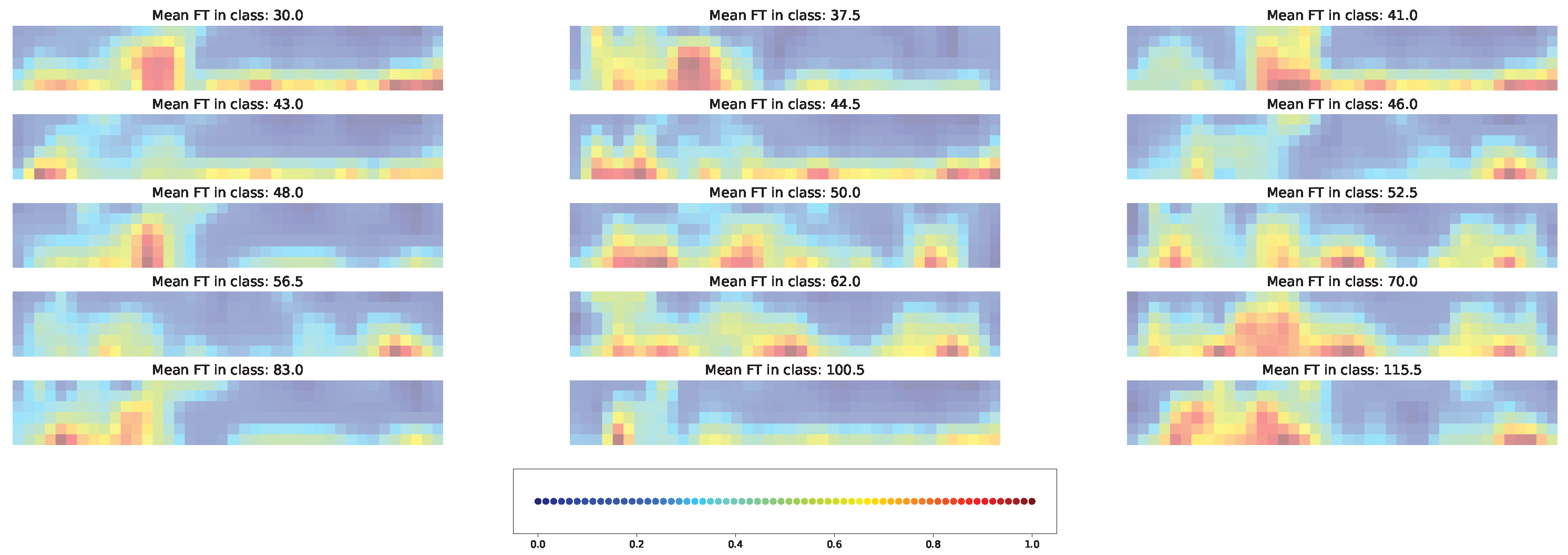
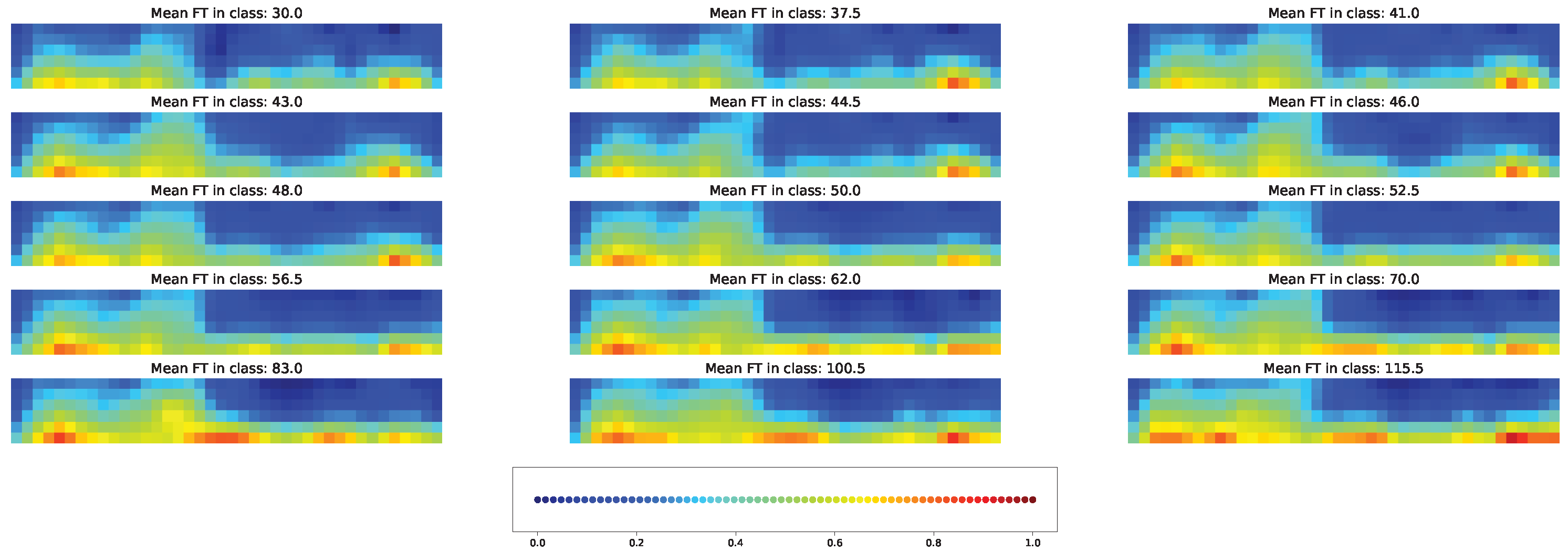
| Num | Chr | Pos | Major | Minor |
|---|---|---|---|---|
| 0 | 1 | 5205070 | G | A |
| 1 | 8 | 41054773 | A | G |
| 2 | 1 | 35363026 | C | T |
| 3 | 11 | 13512065 | T | C |
| 4 | 8 | 14888418 | C | T |
| 5 | 1 | 33528594 | A | T |
| 6 | scaffold 375 | 174056 | T | G |
| 7 | 7 | 50907346 | G | A |
| 8 | scaffold 209 | 359166 | G | A |
| 9 | 9 | 1712557 | A | G |
| 10 | 6 | 15592645 | T | C |
| 11 | scaffold 261 | 18461 | A | G |
| 12 | 3 | 2134396 | A | G |
| 13 | 8 | 41054763 | A | G |
| 14 | scaffold 343 | 148518 | A | G |
| 15 | scaffold 207 | 213949 | A | G |
| 16 | 8 | 1049804 | A | G |
| Layer (Type) | Output Shape | Param Number |
|---|---|---|
| conv2d (Conv2D) | (6, 40, 10) | 280 |
| max_pooling2d (MaxPooling2D) | (3, 20, 10) | 0 |
| conv2d_1 (Conv2D) | (3, 20, 50) | 4550 |
| max_pooling2d_1 (MaxPooling2D) | (1, 10, 50) | 0 |
| flatten (Flatten) | (500) | 0 |
| dense (Dense) | (45) | 22,545 |
| dense_1 (Dense) | (15) | 690 |
| Layer (Type) | Output Shape | Param Number |
|---|---|---|
| conv2d (Conv2D) | (6, 28, 7) | 196 |
| max_pooling2d (MaxPooling2D) | (3, 14, 7) | 0 |
| conv2d_1 (Conv2D) | (3, 14, 42) | 2688 |
| max_pooling2d_1 (MaxPooling2D) | (1, 7, 42) | 0 |
| flatten (Flatten) | (294) | 0 |
| dense (Dense) | (45) | 13,275 |
| dense_1 (Dense) | (15) | 690 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bavykina, M.; Kostina, N.; Lee, C.-R.; Schafleitner, R.; Bishop-von Wettberg, E.; Nuzhdin, S.V.; Samsonova, M.; Gursky, V.; Kozlov, K. Modeling of Flowering Time in Vigna radiata with Artificial Image Objects, Convolutional Neural Network and Random Forest. Plants 2022, 11, 3327. https://doi.org/10.3390/plants11233327
Bavykina M, Kostina N, Lee C-R, Schafleitner R, Bishop-von Wettberg E, Nuzhdin SV, Samsonova M, Gursky V, Kozlov K. Modeling of Flowering Time in Vigna radiata with Artificial Image Objects, Convolutional Neural Network and Random Forest. Plants. 2022; 11(23):3327. https://doi.org/10.3390/plants11233327
Chicago/Turabian StyleBavykina, Maria, Nadezhda Kostina, Cheng-Ruei Lee, Roland Schafleitner, Eric Bishop-von Wettberg, Sergey V. Nuzhdin, Maria Samsonova, Vitaly Gursky, and Konstantin Kozlov. 2022. "Modeling of Flowering Time in Vigna radiata with Artificial Image Objects, Convolutional Neural Network and Random Forest" Plants 11, no. 23: 3327. https://doi.org/10.3390/plants11233327
APA StyleBavykina, M., Kostina, N., Lee, C.-R., Schafleitner, R., Bishop-von Wettberg, E., Nuzhdin, S. V., Samsonova, M., Gursky, V., & Kozlov, K. (2022). Modeling of Flowering Time in Vigna radiata with Artificial Image Objects, Convolutional Neural Network and Random Forest. Plants, 11(23), 3327. https://doi.org/10.3390/plants11233327







