Performance of the Improved Priestley-Taylor Model for Simulating Evapotranspiration of Greenhouse Tomato at Different Growth Stages
Abstract
1. Introduction
2. Results
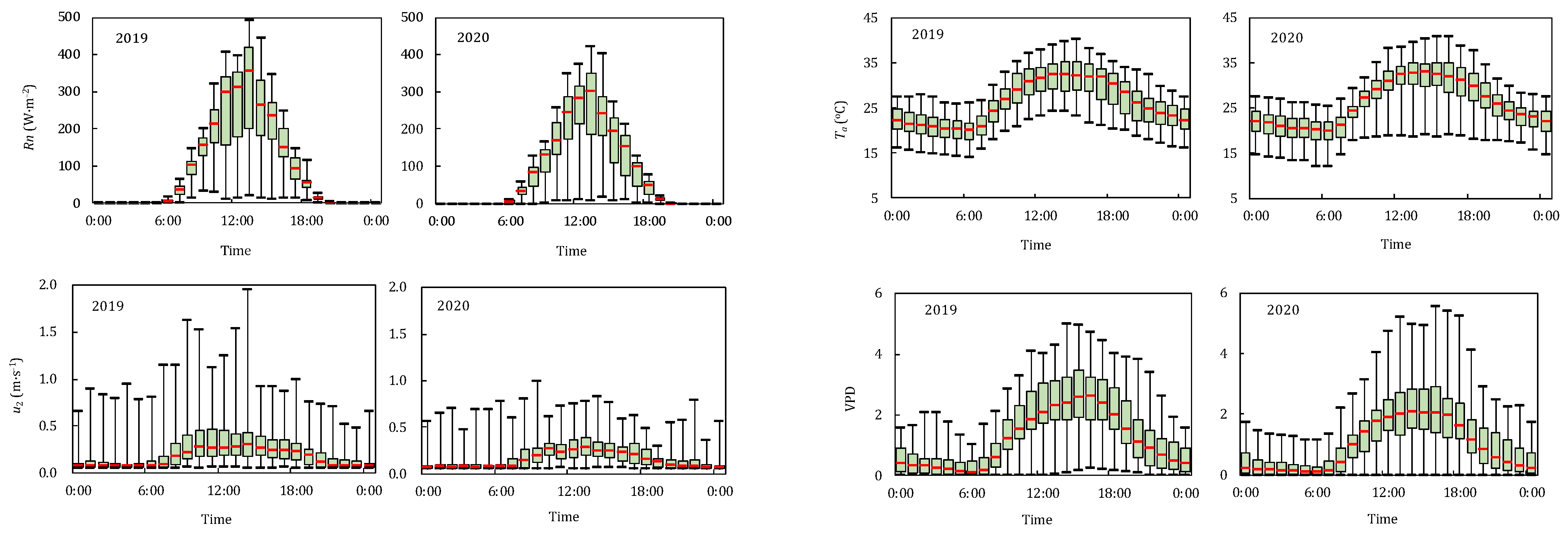
2.1. Meteorological Conditions
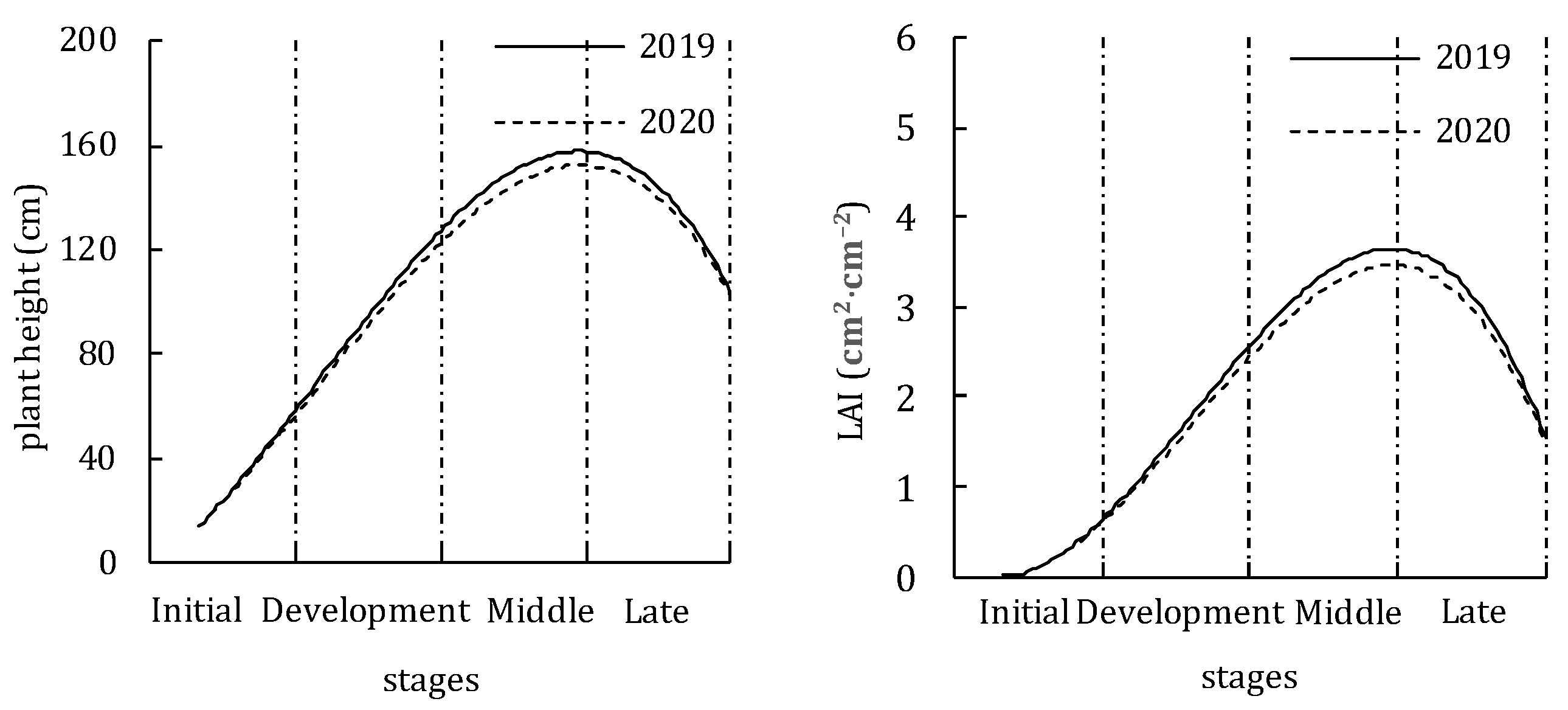
2.2. Variations of Plant Height and LAI
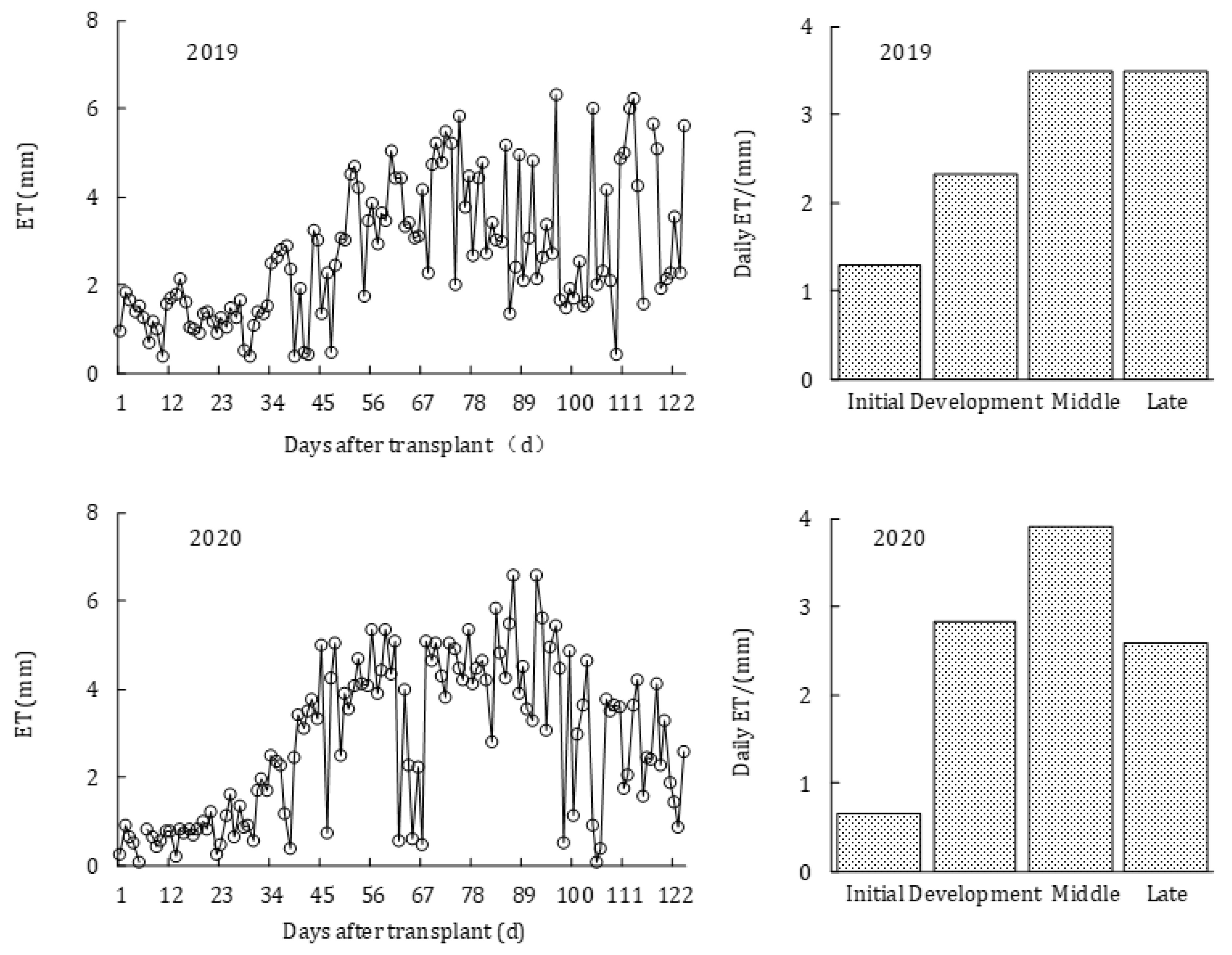
2.3. Variations of ET
2.4. Main Meteorological Factors Affecting ET
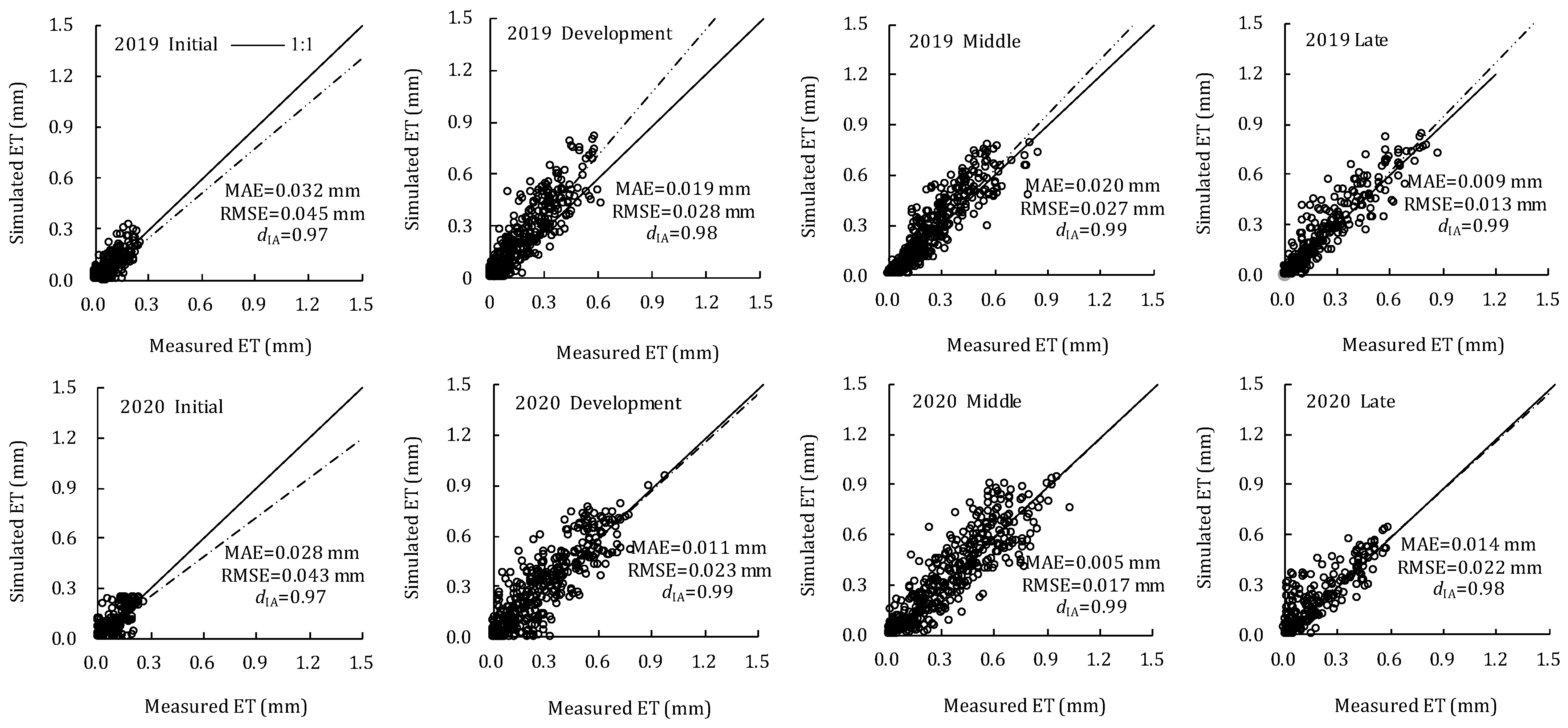
2.5. Performance of the Improved PT Model
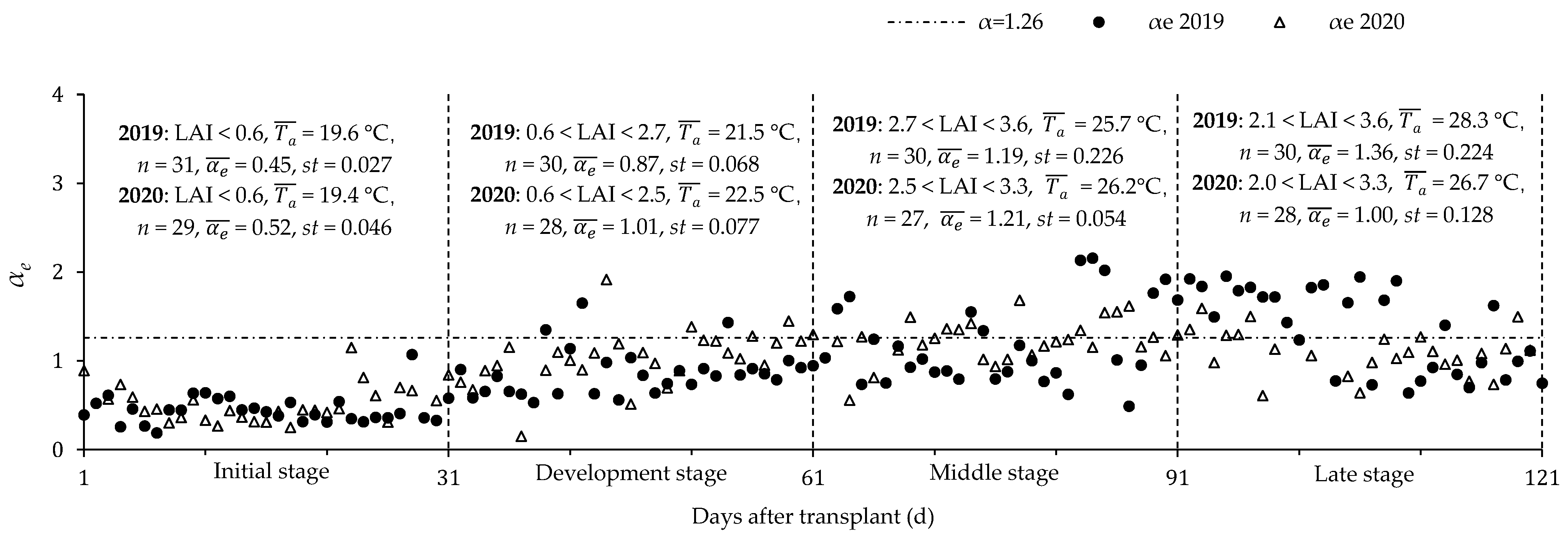
2.6. Variation of Improved PT Coefficient and Its Influencing Factors
3. Materials and Methods
3.1. Experimental Site
3.2. Experimental Design
3.3. Measurements
3.4. Improved Priestley-Taylor Model
3.5. Model Evaluation
4. Discussion
4.1. Variation of ET and Its Influencing Factors
4.2. Evaluation of Improved Priestley-Taylor Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katsoulas, N.; Stanghellini, C. Modelling crop transpiration in greenhouses: Different models for different applications. Agronomy 2019, 392, 392. [Google Scholar] [CrossRef]
- Qiu, R.J.; Kang, S.Z.; Li, F.S.; Du, T.S.; Ling, T.; Wang, F.; Chen, R.Q.; Liu, J.Q.; Li, S.E. Energy partitioning and evapotranspiration of hot pepper grown in greenhouse with furrow and drip irrigation methods. Sci. Hortic. 2011, 191, 790–797. [Google Scholar] [CrossRef]
- Li, B.; Shi, B.; Yao, Z.; Kumar Shukla, M.; Du, T. Energy partitioning and microclimate of solar greenhouse under drip and furrow irrigation systems. Agric. Water Manag. 2020, 234, 106096. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Sun, J.S.; Ge, J.K.; Li, Y.B.; Wang, S.S. Evapotranspiration and crop coefficient of tomato grown in a solar greenhouse under full and deficit irrigation. Agric. Water Manag. 2020, 235, 106154. [Google Scholar] [CrossRef]
- Zhang, B.Z.; Xu, D.; Liu, Y.; Li, F.S. Multi-scale evapotranspiration of summer maize and the controlling meteorological factors in north China. Agric. For. Meteorol. 2016, 216, 1–12. [Google Scholar] [CrossRef]
- Chen, J.L.; Kang, S.Z.; Du, T.S.; Qiu, R.J.; Guo, P.; Chen, R.Q. Quantitative response of greenhouse tomato yield and quality to water deficit at different growth stages. Agric. Water Manag. 2013, 129, 152–162. [Google Scholar] [CrossRef]
- Gong, X.W.; Liu, H.; Sun, J.S.; Gao, Y.; Zhang, X.X.; Jha, S.K.; Zhang, H.; Ma, X.J.; Wang, W.N. A proposed surface resistance model for the Penman-Monteith formula to estimate evapotranspiration in a solar greenhouse. J. Arid Land. 2017, 9, 530–546. [Google Scholar] [CrossRef]
- Yan, H.; Acquah, S.J.; Zhang, C.; Wang, G.; Huang, S.; Zhang, H.; Zhao, B.; Wu, H. Energy partitioning of greenhouse cucumber based on the application of Penman-Monteith and Bulk Transfer models. Agric. Water Manag. 2019, 217, 201–211. [Google Scholar] [CrossRef]
- Morille, B.; Migeon, C.; Bournet, P.E. Is the Penman–Monteith model adapted to predict crop transpiration under greenhouse conditions? Application to a New Guinea Impatiens crop. Sci. Hortic. 2013, 152, 80–91. [Google Scholar] [CrossRef]
- Qiu, R.J.; Song, J.J.; Du, T.S.; Kang, S.Z.; Tong, L.; Chen, R.Q.; Wu, L.S. Response of evapotranspiration and yield to planting density of solar greenhouse grown tomato in northwest China. Agric. Water Manag. 2013, 130, 44–51. [Google Scholar] [CrossRef]
- Li, Y.; Guo, W.; Wu, J.; Duan, M.; Yang, Y.; Liu, S. Estimation of Greenhouse-Grown Eggplant Evapotranspiration Based on a Crop Coefficient Model. Water 2022, 14, 2959. [Google Scholar] [CrossRef]
- PolizelLibardi, L.G.; Faria, R.T.; Alexandre, B.; Glaucode, S.R.; Luiz, F.; Anderson, P.; Izabela, P. Evapotranspiration and crop coefficient (Kc) of pre-sprouted sugarcane plantlets for greenhouse irrigation management. Agric. Water Manag. 2019, 212, 306–316. [Google Scholar] [CrossRef]
- Ding, R.S.; Kang, S.Z.; Li, F.S.; Zhang, Y.Q.; Tong, L. Evapotranspiration measurement and estimation using modified Priestley-Taylor model in an irrigated maize field with mulching. Agric. For. Meteorol. 2013, 168, 140–148. [Google Scholar] [CrossRef]
- Ai, Z.P.; Yang, Y.H. Modification and validation of Priestley-Taylor model for estimating cotton evapotranspiration under plastic mulch condition. J. Hydrometeorol. 2016, 17, 1281–1293. [Google Scholar] [CrossRef]
- Qiu, R.J.; Liu, C.W.; Cui, N.B.; Wu, Y.J.; Wang, Z.C.; Li, G. Evapotranspiration estimation using a modified Priestley-Taylor model in a rice-wheat rotation system. Agric. Water Manag. 2019, 224, 105755. [Google Scholar] [CrossRef]
- Pereira, A.R. The Priestley-Taylor parameter and the decoupling factor for estimating reference evapotranspiration. Agric. For. Meteorol. 2004, 3, 305–313. [Google Scholar] [CrossRef]
- Utset, A.; Farré, I.; Martınez-Cob, A.; Cavero, J. Comparing Penman–Monteith and Priestley-Taylor approaches as reference evapotranspiration inputs for modeling maize water-use under Mediterranean conditions. Agric. For. Meteorol. 2004, 66, 205–219. [Google Scholar] [CrossRef]
- Jiao, L.J.; Ding, R.S.; Kang, S.Z.; Du, T.S.; Tong, L.; Li, S.E. A comparison of energy partitioning and evapotranspiration over closed maize and sparse grapevine canopies in northwest China. Agric. Water Manag. 2018, 203, 251–260. [Google Scholar] [CrossRef]
- Shao, M.X.; Liu, H.J.; Yang, L. Estimating Tomato Transpiration Cultivated in a Sunken Solar Greenhouse with the Penman-Monteith, Shuttleworth-Wallaceand Priestley-Taylor Models in the North China Plain. Agronomy 2022, 12, 2382. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Zhang, B.Z.; Wang, S.S.; Ge, J.K.; Gao, S.K.; Yang, Z.Q. Energy budget for tomato plants grown in a greenhouse in northern China. Agric. Water Manag. 2021, 255, 107039. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Ge, J.K.; Bo, G.K.; Ping, Y.L.; Xin, Q.S.; Wang, S.S. Evapotranspiration partitioning of greenhouse grown tomato using a modified Priestley-Taylor model. Agric. Water Manag. 2021, 247, 106709. [Google Scholar] [CrossRef]
- Liu, H.; Duan, A.W.; Li, F.S.; Sun, J.S.; Wang, Y.C.; Sun, C.T. Drip irrigation scheduling for tomato grown in solar greenhouse based on pan evaporation in North China plain. J. Integr. Agr. 2013, 12, 520–531. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Deardorff, J.W. A parameterization of ground-surface moisture content for use in atmospheric prediction models. J. Appl. Meteorol. 1977, 16, 1182–1185. [Google Scholar] [CrossRef]
- Tanner, C.B.; Jury, W.A. Estimating evaporation and transpiration from a row crop during incomplete cover. Agron. J. 1976, 68, 239–243. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.; Evans, J.; Chaney, N.; Wood, E. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Morgan, C.; Norman, J.; Lowery, B. Estimating plant-available water across a field with an inverse yield model. Soil Sci. Soc. Am. J. 2003, 67, 620–629. [Google Scholar] [CrossRef]
- Rodriguez-Ortega, W.; Martinez, V.; Rivero, R.; Camara-Zapata, J.; Mestre, T.; Garcia-Sanchez, F. Use of a smart irrigation system to study the effects of irrigation management on the agronomic and physiological responses of tomato plants grown under different temperatures regimes. Agric. Water Manag. 2017, 183, 158–168. [Google Scholar] [CrossRef]
- Ge, J.K.; Xin, Q.C.; Gong, X.W.; Ping, Y.L.; Bo, G.K.; Li, Y.B. Effects of greenhouse ventilation and water control conditions on water consumption characteristics and yield of tomato. Trans. Chin. Soc. Agric. Eng. 2021, 37, 204–213. [Google Scholar] [CrossRef]
- Demrati, H.; Boulard, T.; Fatnassi, H.; Bekkaoui, A.; Majdoubi, H.; Elattir, H.; Bouirden, L. Microclimate and transpiration of a greenhouse banana crop. Biosyst. Eng. 2007, 98, 66–78. [Google Scholar] [CrossRef]
- Granier, A.; Huc, R.; Barigah, S. Transpiration of natural rain forest and its dependence on climatic factors. Agric. For. Meteorol. 1996, 78, 19–29. [Google Scholar] [CrossRef]
- Hayat, M.; Iqbal, S.; Zha, T.; Jia, X.; Qian, D.; Bourque, C.; Khan, A.; Tian, Y.; Bai, Y.; Liu, P. Biophysical control on nighttime sap flow in Salix psammophila in a semiarid shrubland ecosystem. Agric. For. Meteorol. 2021, 300, 108329. [Google Scholar] [CrossRef]
- Gong, X.W.; Li, X.M.; Qiu, R.J.; Bo, G.K.; Ping, Y.L.; Xin, Q.S.; Ge, J.K. Ventilation and irrigation management strategy for tomato cultivated in greenhouses. Agric. Water Manag. 2022, 273, 107908. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Smith, M.; Raes, D.; Wright, J. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain Eng. 2005, 131, 1–13. [Google Scholar] [CrossRef]
- Valdés-Gómez, H.; Ortega-Farías, S.; Argote, M. Evaluation of water requirements for a greenhouse tomato crop using the Priestley-Taylor method. Chil. J. Agr. Res. 2009, 69, 3–11. [Google Scholar]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]

| Year | Factors | Correlation Coefficient | Direct Path Coefficient | Indirect Path Coefficient | Decision Coefficient | ||||
|---|---|---|---|---|---|---|---|---|---|
| Total Indirect Path Coefficient | Rn | Ta | VPD | u2 | |||||
| 2019 | Rn | 0.952 | 0.744 | 0.208 | −0.082 | 0.257 | 0.033 | 0.863 | |
| Ta | 0.811 | −0.108 | 0.919 | 0.564 | 0.320 | 0.035 | −0.187 | ||
| VPD | 0.833 | 0.353 | 0.481 | 0.541 | −0.098 | 0.038 | 0.463 | ||
| u2 | 0.672 | 0.056 | 0.416 | 0.445 | −0.067 | 0.038 | 0.072 | ||
| 2020 | Rn | 0.888 | 0.775 | 0.256 | −0.020 | 0.218 | 0.058 | 0.776 | |
| Ta | 0.731 | −0.026 | 0.933 | 0.605 | 0.265 | 0.064 | −0.039 | ||
| VPD | 0.751 | 0.291 | 0.630 | 0.581 | −0.024 | 0.073 | 0.352 | ||
| u2 | 0.615 | 0.112 | 0.461 | 0.403 | −0.015 | 0.073 | 0.125 | ||
| Year | Growth Stages | Rn | Ta | VPD | u2 |
|---|---|---|---|---|---|
| 2019 | Initial | 114.81 | 19.19 | 1.031 | 0.118 |
| Development | 125.65 | 21.26 | 0.716 | 0.120 | |
| Middle | 149.92 | 26.39 | 1.419 | 0.102 | |
| Late | 148.44 | 28.23 | 1.296 | 0.089 | |
| Whole growth stage | 135.80 | 23.92 | 1.106 | 0.101 | |
| 2020 | Initial | 103.32 | 18.88 | 0.791 | 0.114 |
| Development | 131.53 | 20.82 | 0.700 | 0.112 | |
| Middle | 142.53 | 25.48 | 1.172 | 0.145 | |
| Late | 154.09 | 27.03 | 0.710 | 0.138 | |
| Whole growth stage | 138.11 | 23.07 | 0.877 | 0.128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Bo, G.; Liu, H.; Ge, J.; Li, X.; Gao, S. Performance of the Improved Priestley-Taylor Model for Simulating Evapotranspiration of Greenhouse Tomato at Different Growth Stages. Plants 2022, 11, 2956. https://doi.org/10.3390/plants11212956
Gong X, Bo G, Liu H, Ge J, Li X, Gao S. Performance of the Improved Priestley-Taylor Model for Simulating Evapotranspiration of Greenhouse Tomato at Different Growth Stages. Plants. 2022; 11(21):2956. https://doi.org/10.3390/plants11212956
Chicago/Turabian StyleGong, Xuewen, Guokui Bo, Hao Liu, Jiankun Ge, Xiaoming Li, and Shikai Gao. 2022. "Performance of the Improved Priestley-Taylor Model for Simulating Evapotranspiration of Greenhouse Tomato at Different Growth Stages" Plants 11, no. 21: 2956. https://doi.org/10.3390/plants11212956
APA StyleGong, X., Bo, G., Liu, H., Ge, J., Li, X., & Gao, S. (2022). Performance of the Improved Priestley-Taylor Model for Simulating Evapotranspiration of Greenhouse Tomato at Different Growth Stages. Plants, 11(21), 2956. https://doi.org/10.3390/plants11212956








