1. Introduction
Wild rocket (
Diplotaxis tenuifolia (L.) DC) is a cruciferous perennial herb, spontaneous in the Mediterranean Basin. In the last 25 years, Italy has become one of the major European producers of wild rocket using the species in intensified cultivation systems devoted to harvesting fresh-cut baby-leaf for the high convenience salad chain. It is sown with precision seed drills on 1.8–2.2 m width beds under polytunnels, fertigated with sprinklers and mechanically cut at complete foliar development. The harvested product quickly enters the cold chain, is minimally processed by washing, wiping, and bagging, and distributed through retail nets across several countries as ready-to-eat preparations. Packaged wild rocket meets the consumer preferences for the characteristic pungent–aromatic flavor associated with glucosinolates [
1] and a few other nutraceutical properties (i.e., vitamins, antioxidants, fibers, and low calories) [
2].
This makes the market very sensitive to the sustainability levels of the production process from field to shelf, conceived with a considerable reduction in the applied synthetic fungicides [
3,
4]. Nevertheless, this vegetable crop as well as all the other baby leaf species is susceptible to a plethora of both specific and non-specific pathogens that significantly reduce yields and impair their quality. As a consequence, the deployment of non-traditional effective control measures that include biological strategies is necessary [
5].
Biologically-based disease resistance inducers may be biomimetic compounds or substances sourced from plants or microbes, or non-pathogenic microorganisms capable of eliciting the plant’s own defense mechanism(s) through microbe/pathogen-associated molecular patterns and/or the recognition of host-derived damage-associated molecular patterns to enhance their innate defense response against upcoming broad-spectrum diseases to varying degrees [
6,
7,
8]. Therefore, innovative resistance activators can then be used as biopesticides in plant protection protocols as a safer alternative to synthetic chemicals to reduce the environmental disease management footprint and stimulate plant performances [
9]. However, they still need to improve their efficacy under field conditions [
10].
Non-invasive technologies may be helpful to optimize the field applications of these plant-targeted protectants [
11]. Plants react to exogenous application of plant resistance inducers by possibly activating many metabolic pathways involved in biochemical and mechanical defense responses including shifts of cytosolic ion content, oxidative burst, synthesis of enzymes, proteins, and other secondary metabolites related to the defense, in addition to the activation of resistance-related hormones [
12]. Changes in leaf composition and plant health may be detected in the reflected electromagnetic radiation once it is captured by optoelectronic sensors such as hyperspectral ones.
In optics, reflectance measures the ability of a given surface or material to send back part of the incident light on it. In particular, a hyperspectral sensor can record the part of the electromagnetic radiation of a natural (sun) or artificial light source that is reflected by a leaf at a very fine spectral resolution in the range of wavelengths between 350–2500 nm. The spectrum is divided into three regions called, in sequence: Visible (VIS), between 350 and 750 nm; Near Infrared (NIR) until 1400 nm; and the Short-Wave Infrared (SWIR) region until 2500 nm. Each region has been associated with many parameters describing the plant status [
13]. Hyperspectral data analysis represents a very effective and sustainable tool for evaluating changes induced in the plant by abiotic and biotic stresses. Recently, hyperspectral data have been adopted on a large scale in the detection of biotic stresses on plants as in the case of the sudden spread of Xylella infection on entire olive cultivations in the Mediterranean area [
14,
15,
16]. Some vegetation indices based on reflectance data in the VIS range have been used to assess changes occurring in the plant health status through the related effect on pigments such as carotenoids, anthocyanins, and chlorophyll. However, these variations might be due to either specific or non-specific infections [
17,
18,
19,
20,
21], hence further laboratory phytopathogenic analysis on the leaves remains necessary.
The transition from low reflectance values in the red to high values in the infrared spectral range is very rapid: this portion of the spectrum, called Red Edge, is more indicative of the chlorophyll content than that of water [
22,
23,
24,
25]. Moreover, it is influenced by the cell structures of leaves that poorly absorb in the NIR because of the multiple scattering of radiation by the mesophyll. As for SWIR, the overlap between information on water content and organic compounds makes data interpretation more difficult. Statistical processing [
26], mathematical regressions [
16], and radiative transfer models [
27,
28,
29] have been used for this purpose.
This leads to hyperspectral data being used as indicators of possible stress in the plant, although a direct relationship between the alteration observed in the spectra and its cause has not been discovered yet.
The analysis and interpretation of spectral data are further complicated by the way in which agronomic trials are generally conducted. The purpose of the agronomic experiments is to test whether the compared treatments (in this case the use of different plant resistance inducers) have any effect on the supposed response variable. If one treatment is taken as a control (e.g., zero treatment), the experiment will consist of testing whether every other treatment has an effect compared to the control treatment. The biggest challenge in an agronomic trial is to be able to separate the intrinsic variation of the response variable from that induced by the experimental treatments. In traditional agronomic trials, this is achieved by replicating each treatment according to a well-defined experimental design. Traditional statistical methods based on the design then allow for the determination of the probability that any measured difference between treatments is due to chance (null hypothesis).
Many times, when the experiment is conducted in a confined space such as a greenhouse, or on-farm, for purely practical reasons, there is a tendency to follow a more systematic pattern, with one treatment, for example, assigned to a particular part of the field. In addition, there may be too few plots per treatment (repetitions) to assess the underlying variability, and furthermore, such variability may be correlated [
30].
These experiments very often fail to meet the fundamental assumptions required by classical statistical methods. It is therefore necessary to use more complex statistical methods [
31,
32] that are based on a model-based statistical approach [
33]. This consists in describing both the variation and the correlations between the observations of the response variable using a statistical model. In this regard, the theory of linear mixed effects models (LMM) [
34,
35,
36] allows for the total variance to be broken down into that which is attributable to fixed effects, corresponding to the treatments, and that which is attributable to random effects. The latter are linked to the intrinsic spatial variability of the agronomic system, which cannot be described by fixed effects and can be estimated by the covariance/correlation function of residuals.
Therefore, with a view to increasing sustainability in greenhouse cultivations of wild rocket, the use of naturally derived products can be proposed, but their actual interaction with the plants must be continuously monitored. For this purpose, among micro- and macroorganisms, certain active components described as plant defense promoters can be found and formulated in some successful experimental and commercial products to induce resistance in the plants. These may differ in the level of purity of the active ingredients, ranging from microorganisms to a single molecule, in the hormonal signaling pathways involved in the elicited plant reactions (i.e., oxidative burst, cell-wall fortification, etc.) and in the ranges of efficacy. Furthermore, proper organic soil management with compost amendments that promote plant growth and development by improving soil chemical, physical, and microbiological quality and fertility can synergize with inputs to the aerial part, leading to greater beneficial effects.
The specific objective of the work is to characterize the hyperspectral response of greenhouse-grown wild rocket to the application of three immunity-stimulating active ingredients (resistance inducers), split over plots amended and non-amended with green compost, using the mixed effect model theory to account for the actual experimental conditions.
3. Discussion
The statistical results obtained are consistent with a biological interpretation, which reinforces the idea that the spectral response of the plant can be used as an effective and reliable indicator of its health. PC1 summarizes information about N content and other biochemical compounds, which to date, has come from several studies regarding the SWIR region on potato and other mapped vegetation [
49,
50]. As far as PC2 is concerned, the main loadings fell in the ranges more related to the LAI as confirmed by recent studies on rice and maize in both proximal and remote sensing [
51,
52], and to the water absorption peaks that are used to calculate new vegetation indices associated with water content in different plant species [
53]. Finally, PC3 can explain the ratio Car/Chla as an indicator of plant stress [
54].
It is generally recognized that the incorporation of compost into the soil increases the water available to plants [
55], delaying the possible wilting associated with drought [
56] and thus protecting and/or enhancing photosynthetic activity [
57]. On the other hand, the lack of statistical significance of the COMPOST effect for rPC2, which was associated with plant vigor, can be explained on the basis of the reduced nutrient supply capacity shown by green composts in the presence of a large fraction of non-labile carbon, whose degradation implies the net immobilization of N [
58]. In addition, compost in combination with LAM and TRI had a positive effect on the water content (PC1) and in combination with LAM and CHE on the general health of the plant (PC3). In contrast, compost in combination with CER did not produce any positive effects in terms of either water content or LAI.
However, the resistance inducers used in this study, on the basis of their specific characteristics, might be implicated in the physiological processes underlying the interpretation of the PCs. Antagonistic fungi belonging to the genus
Trichoderma have been reported to induce a resistance response into plants through multiple hormonal signaling pathways that modulate jasmonic acid, ethylene, and salicylic acid levels toward a wide-spectrum of pathogens [
59]. Their biocontrol efficacy might result in the modulation of plant growth and yield improvement [
60]. Kumar and Kumar [
61] reported that root colonization of
Trichoderma sp. can induce the production of stress enzymes such as peroxidase and glutathione reductase, which may be responsible for decreasing disease incidence in
Brassica juncea. In a different way in cabbage,
Trichoderma treatments increased the transcript levels of genes related to photosynthesis and sucrose transport, PR proteins, chitinases, and oxidases [
62]. Yeast cell-wall extract, which carries polysaccharidic and peptidic polymers and oligomers of highly variable molecular mass, acts as MAMPs in inducing defense-related events through SA signaling [
40,
41,
42,
63]. However, there is no evidence in the literature that it has an impact on the reflectance of plants. On the other hand, concerning laminarin, which is a water-soluble glucan storage polysaccharide extracted from brown algae (i.e.,
Laminaria digitata Hudson, Lamouroux), it has been shown that it can elicit defense reactions in several plant species [
64] via salicylic acid and reactive oxygen species pathways [
65]. This is most likely due to the association with bound β-1,3–1,6 glucosyl residues [
39]. It is also worth pointing out that in this study, the LAM effect on TRI was significantly higher in all pairwise COMPOST × TREATMENT interactions relative to PC3 associated with indicating stress occurrence. Consistently, laminarin has been reported as an unconventional elicitor of plant secondary metabolites [
66]. In
Arabidopsis, this molecule increased chloroplast stability by activating the antioxidant system under stress conditions [
67]. Consequently, with regard to PC3, the current hyperspectral study indicated that LAM treatment associated with the compost effect is linked to the improved plant health status.
4. Materials and Methods
4.1. Experimental Design
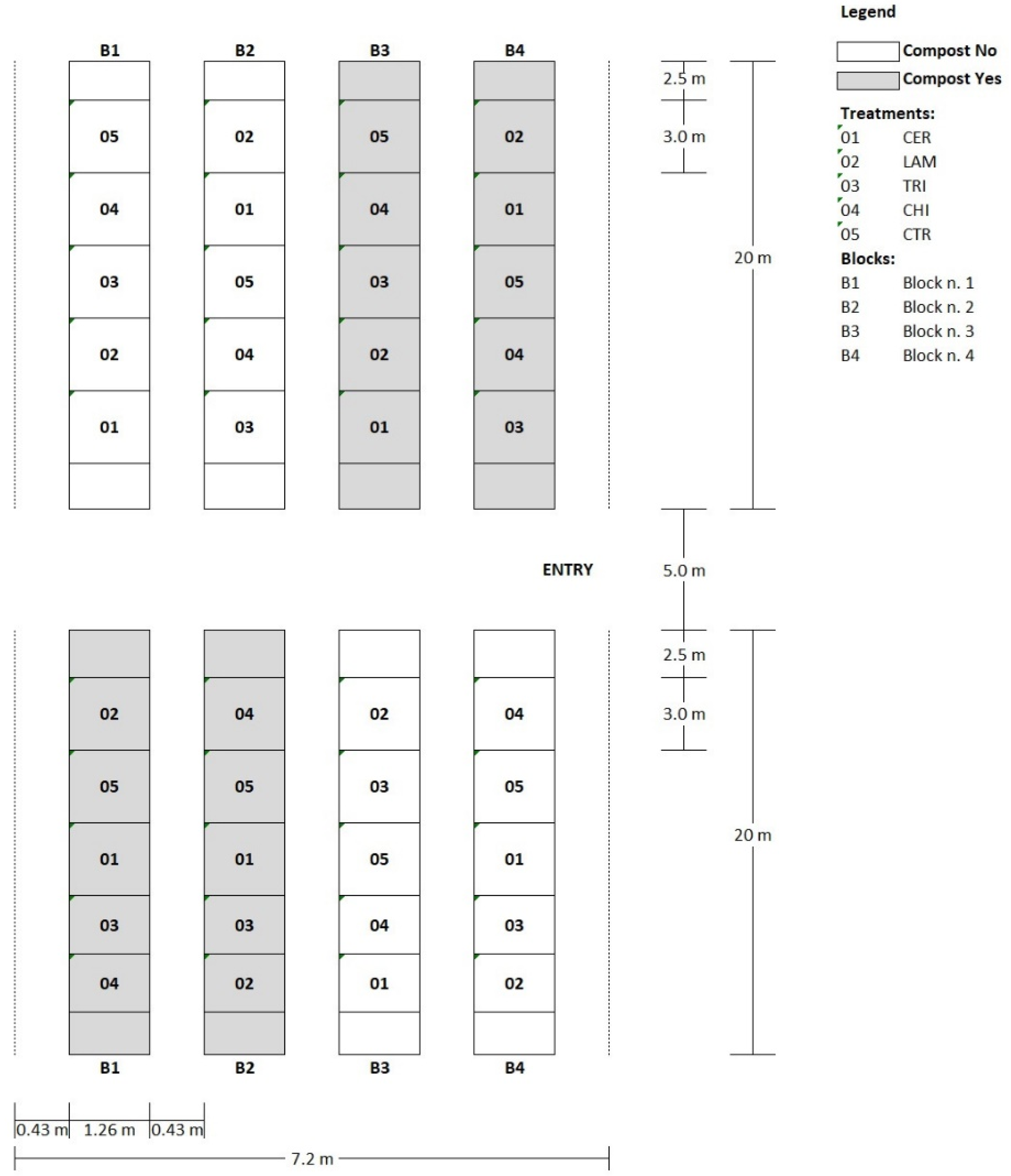
The trial was conducted under a multi-tunnel greenhouse located at the CREA-Research Center for Vegetable and Ornamental Crops (Pontecagnano Faiano, Italy, 40°38′54.0″ N 14°53′21.4″ E). Wild rocket cv Yeti (Maraldi Sementi, Italy), suitable for the winter–spring cropping cycle, was precision sown on 19 November 2019 (2500 seeds m−2) and grown on 1.3 m wide beds under two polyethylene tunnels (20 × 7.2 m) with four beds each equally spaced by 0.5 m.
The experimental design was a two-way split-plot with the external effect (COMPOST) represented by the application or not of green compost as an amendant (two levels: Yes/No). The internal effect (TREATMENT) was represented by the application of inducers including five treatments: (1) two applications (at seeding and pre-emergence) of
Trichoderma atroviride strain TA35 from CREA Collection [
68] at a dose of 1000 L ha
−1 (10
5 cells mL
−1) (TRI); (2) four weekly spray applications of commercial laminarin-based product (Vacciplant
®, Arysta Lifescience s.a.s., France) at dose of 1 L ha
−1 (LAM); (3) four weekly spray applications of
Saccharomyces cerevisiae strain LAS117 cell wall extract-based commercial product (Romeo
®, Agrauxine, France) at a dose of 750 g ha
−1 (CER); (4) local standard approach including one spray with Cyprodinil, Fludioxonil, Mandipropamide, and Metalaxil-M (CHE); and (5) no treatment (CTR) used as reference control. Main plots were not-amended or amended with green compost (10 t ha
−1 dry matter) (COMPOST). The experimental design consisted of four blocks (each one including a single bed but split into two tunnels North/South); each block was split longitudinally into two halves randomly assigned to one level of COMPOST; each half of the block was randomly split into the five levels of the internal effect. The trial then consisted of 40 experimental units (plots) with a size of 3.0 × 1.3 m (
Figure 2 and
Figure 3).
4.2. Hyperspectral Reflectance Measurements
Leaf spectral measurements were performed in the spectral range 350–2500 nm, using a portable non-imaging spectroradiometer (FieldSpec® 4 Hi-Res, ASD Inc., Boulder, CO, USA) through a fiber-optic contact probe (ASD Plant Probe; ASD Inc., USA) with a spectral resolution of 3 nm in VIS-NIR and 8 nm in SWIR, a 10 mm field of view, and an integrated halogen reflector lamp. The instrument was warmed up for 90 min before measurements to increase the quality and homogeneity of acquired data. Calibration was obtained with the pre-calibrated white 99% spectral reference panel. Each sample scan represents a mean of 10 reflectance spectra.
Within each plot, 12 spots spaced 50 cm apart were selected based on the orientation of the leaves in sunlight, with preference given to the top and most exposed leaves; the reflectance measurement for each spot was obtained as an average of three replicates. The reflectance data were then averaged over 10-nm intervals, thus reducing the number of wavelengths from 2151 to 215, smoothing the spectra and keeping the risk of over-fitting low [
69]. Pre-processing methods were applied to reduce the impact of multiplicative and additive effects of possible backscattering within the instrument [
70]. The pre-processing first involved the splice correction, in order to minimize the inconsistency recorded at the spectral intervals among the three detectors of the spectroradiometer: the VIS-NIR range 350–1000 nm, which is characterized by a sampling interval of 1.4 nm and the two ranges in the NIR-SWIR, 1000–1800 nm and 1800–2500 nm, with a sampling interval of 2 nm. After that, two pretreatments were performed on the reflectance spectra: (1) multiple scattering correction (MSC); and (2) smoothing/denoising with Savitzky–Golay polynomials [
71]. Multiple scattering correction (MSC) works mainly when the scattering effect is the dominant source of variability and removes additive and multiplicative components [
72].
The first order Savitzky–Golay (SG) polynomial algorithm reduces the random noise of the measurements. The algorithm is based on a moving polynomial fit of any order and the filter size consists of (2n + 1) points, where n is the half-width of the smoothing window (w). The polynomial fit interpolates the points between the 2n’s. A window size (w) of 11 (w = 2n + 1) and the second polynomial order were applied here [
73].
Splice correction was achieved using ViewSpecPro software (Analytical Spectral Devices Inc., Boulder, CO, USA). The other preprocessing methods were performed using ParLeS software [
74].
4.3. Principal Component Analysis
Principal component analysis is a widely used dimensionality reduction technique that allows for the extraction of principal components (PCs), expressed as a linear combination of variables [
75,
76]. The PCs found in this way do not represent directly observable variables and must therefore be interpreted from a scientific-rational perspective. Mathematically, PCA works on the correlation matrix and extracts a few PCs equal to the number of measured variables, but only a part of them is useful.
The number of PCs was fixed by selecting the PCs with eigenvalues greater than or equal to 1 (Kaiser’s criterion) [
77]. The eigenvalues refer to the share of variability “explained” by the PC and take on descending values as the first PC moves toward the last one. The result can then be subjected to rotation by various methods. Methods using orthogonal rotations preserve the independence of the PCs. The VARIMAX procedure was used in this study.
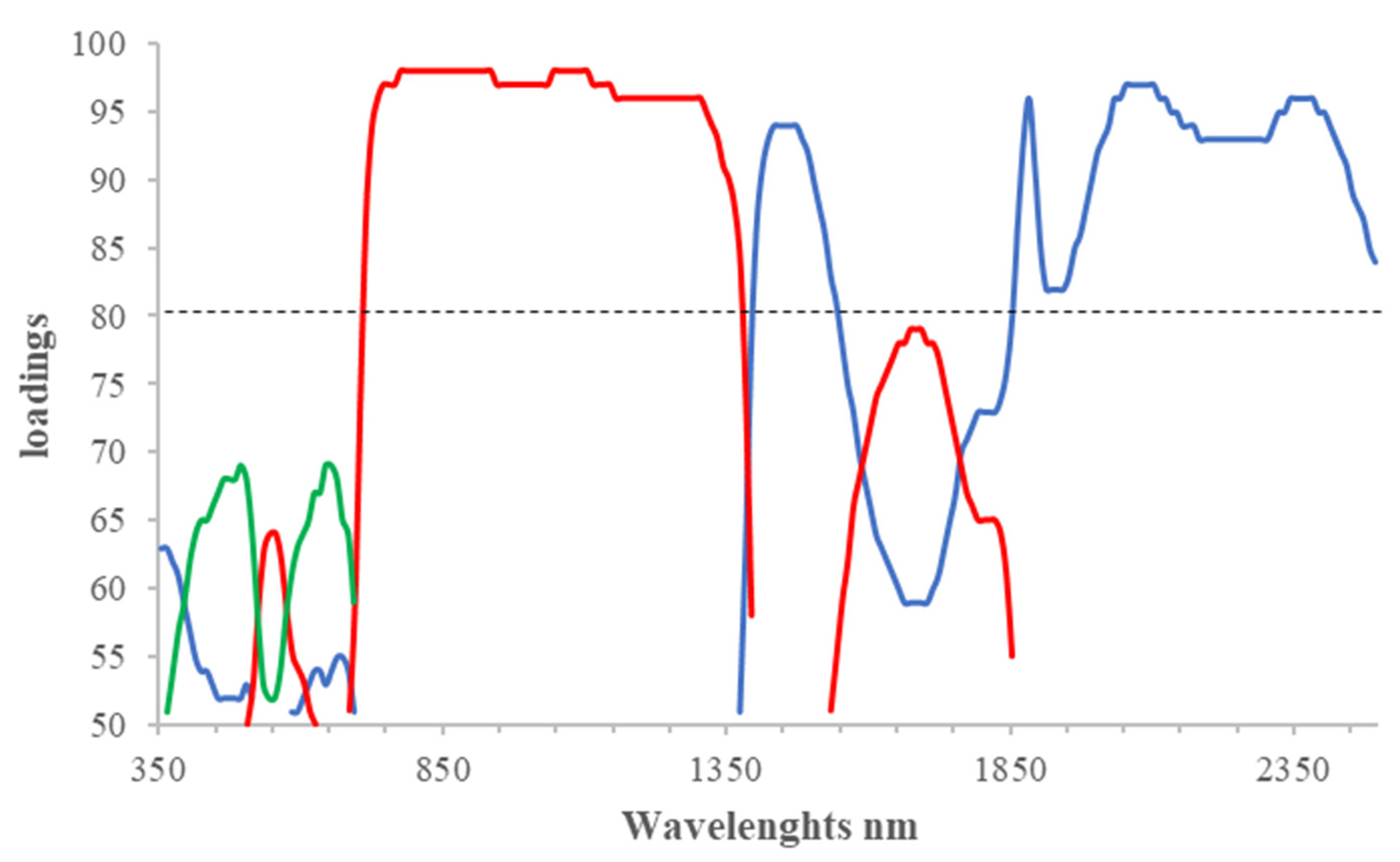
The most important parameters to evaluate were:
The amount of variance “explained” by both the set of the retained PCs (cumulative) and by each PC individually;
PC loadings, which describe the strength of the relationship between the PC and the variable being measured.
PCA was performed with the SAS/FACTOR procedure of the statistical software package SAS/STAT (release 9.4 SAS ANALYTICS U software).
For each PC, the loading values were multiplied by 100. The value of 80 was chosen as a limit above which to select the most relevant wavelengths.
The raw spectral data were preferred over the pretreated ones because with the same number of PCs, they explained a greater proportion of variance, probably due to the specific measurement modalities of the plant probe that reduced the random error.
4.4. Statistical Analysis
The assumption of univariate normality for each PC was checked with three non-parametric tests (Kolmogorov–Smirnov, Cramer-von Mises, and Anderson–Darling) [
78].
If the variable showed large departures from normal distribution, to improve the linearization of the mixed effect model, PC was transformed to normal scores (
yi) using Blom’s formula [
79]:
where Φ
−1 is the inverse cumulative normal (PROBIT) function;
ri is the rank of the
ith observation; and
n is the number of observations that have non-missing values for the ranking variable.
The spatial association of the residuals from the OLS models, obtained assuming independence of the residuals, was verified in two ways:
(1) By calculating the spatial autocorrelation statistics of Moran (1950) [
80] and Geary [
81] and comparing them to the null hypothesis statistics of completely random spatial model; and
(2) By fitting an authorized mathematical model to the experimental variogram of the OLS residuals, according to the least squares estimation (LSE) technique and testing the statistical significance of its parameters.
4.5. Linear Mixed Effect Model (LMM)
A LMM can be written in the form:
where
z is a vector of length n corresponding to the measurements of the response variable; and
M is the fixed effects design matrix of size n × t, where t is the total number of different experimental treatment levels. In the case under study, there are two levels for the COMPOST effect, five for the TREATMENT, and 10 for the interaction effect.
β is the vector of length t of the coefficients of the fixed effects and ε the vector of length n of the random effects. The product
Mβ represents the fixed effects. All entries of the matrix
M (M
ij) can assume the values 0 or 1. The entries of the first column (M
1j) are all equal to 1 while the other Mij entries are 1 if observation i corresponds to the treatment level j, otherwise they are 0. Therefore, β
1 corresponds to the overall mean and the other β
j correspond to the adjustment of this mean concerning each treatment level j. The elements of the vector
ε (e
i), also known as residuals, are assumed to follow a normal distribution with mean 0 and covariance matrix Cov[e
i, e
j]. This matrix may differ from the identity matrix, and the random effects may also be spatially correlated.
Usually, the covariance is assumed to be a function of the distance between the locations x
i and x
j. If by
h we denote the distance between x
i and x
j, the covariance model takes the general form:
where σ is known as the partial sill and with the symbol f, one of the authorized mathematical functions used to represent a covariance function, is indicated. The models, for which f(
h) is the same for all pairs of observations equally distant in a given direction, are called stationary models (of the second order if the average, assumed constant, is known). If f(
h) does not depend on direction, then the covariance structure is said to be isotropic. Many isotropic covariance models exist, however, in this study, we used the spherical model:
This model has three parameters that must be determined from the data: the nugget variance (σ 0), the partial sill (σ)m and the range ρ. These spatial models are drawn from geostatistics and refer to one of the numerous manuals [
82,
83,
84] for an interpretation of these parameters. It is commonly preferred to use the variogram instead of the covariance function given by the formula:
Furthermore, complexity in determining the covariance model may arise from the heteroscedasticity of the variance relative to the individual PCs tested, as this may result in heterogeneity in the covariance function. The homogeneity of the variance was tested with Levene’s test [
85].
The method of fitting the spherical model to the values of mean covariance for each class of distance,
h, is based on an iterative procedure, aimed at maximizing the log likelihood of the residuals using the restricted maximum likelihood method (REML) [
86]. Once the spatial covariance function is estimated, the fixed effects coefficients are obtained as generalized least squares estimates [
86]. For comparison, traditional models (OLS), which assume residuals are normally distributed with zero mean but not correlated spatially, were also determined.
All statistical analyses were performed using statistical software package SAS/STAT (release 9.4 SAS ANALYTICS U software) and in particular, LMMs were estimated using the procedure MIXEDe.