A Hierarchical Matching Method for Vectorial Road Networks Using Delaunay Triangulation
Abstract
:1. Introduction
- (1)
- This paper highlights the importance of the hierarchical semantics of urban road networks and develops a hierarchical matching framework for road networks. The framework fuses the probability relaxation method and the spatial adjacency relationship among hierarchical structures to achieve matching in the hierarchical context by using a layer-by-layer control strategy;
- (2)
- This paper proposes a novel algorithm based on a “node-area” structure instead of a “node-arc” structure to suppress the rotation offset in the matching of the nonskeletal network level. The road network of the nonskeletal level is converted into triangular meshes constrained by natural nodes and segments. The minimum matching unit (MMU) in the triangular meshes is used as the basic calculation unit. Depending on the characteristic of rotation invariance of a triangle, the similarity among MMUs drives the nonskeletal road network matching to overcome the rotation angle problem. The matching relationship among the vertices of triangle meshes is identified using the global probability relaxation method. This study provides a new way to minimize the effect of rotation offset in road network matching due to nontrivial angular deflection.
2. Method
2.1. Methodological Framework
2.2. Hierarchical Generation of Road Network
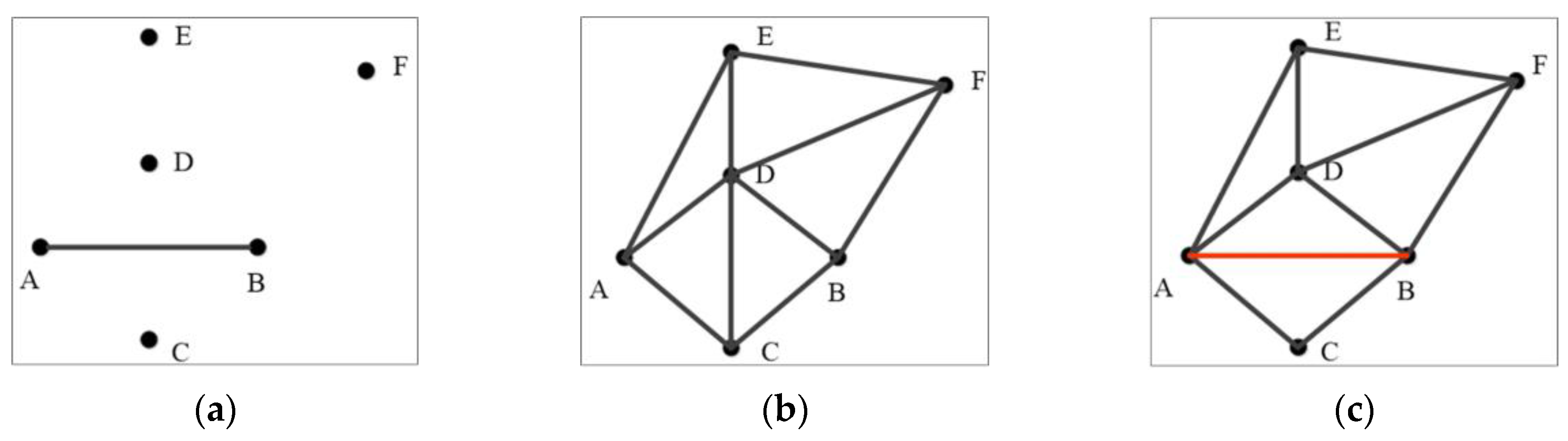
2.3. Delaunay Triangulation Construction Constrained by Road Nodes and Segments
- (1)
- The convex hull (M) of all nodes in the frame roads of the source and target datasets is calculated.
- (2)
- The convex hull M is extended using a given distance threshold to obtain a new convex hull N that is parallel to M.
- (3)
- The nodes of all line segments on the convex hull N and the nodes and segments of the frame roads in the road network dataset are triangulated together.
2.4. Similarity Metrics Based on MMU
- (1)
- MMUP with P as the center node and TSMO with O as the center node are prepared.
- (2)
- MMUP centering on P is moved to O to obtain a new MMU, namely, MMUP′.
- (3)
- The distance between all nodes in MMUP′ and TSMO is calculated to form a distance matrix. We use the distance matrix to select the nodes in TSMO, in which the sum of the distance between all the nodes in MMUP′ and them is the smallest, which is called CPSO. The selected node cannot be repeated.
- (4)
- The MMU is reconstructed with O as the center node and CPSO as the surrounding nodes, which is called MMUO′.
- (5)
- The similarity between all triangles in MMUP′ and MMUO′ is calculated to obtain a triangle similarity matrix. In this triangle similarity matrix, a diagonal line of the matrix with the largest sum of similarity values is chosen. The similarity between MMUP and MMUO, namely SimOP, is represented by the sum of the similarity values divided by the number of triangles. The correspondence between the nodes of the two MMUs is also obtained.
- (1)
- The similarity of all triangle pairs in the two MMUs is calculated to obtain a similarity matrix M.
- (2)
- The two largest similarity values on each diagonal of the similarity matrix, ,
- (3)
- , are selected, and the sum of the two values, which is denoted as , is calculated.
- (4)
- The largest similarity values , which indicate the similarity values on the i-th diagonal, are selected as the best indicator for characterizing the matching relationships between the triangles in the two MMUs.
- (5)
- The maximum similarity value on the i-th diagonal is chosen, and the deflection angle δ of the two triangles is calculated in accordance with the correspondence between the triangle pair <i,j>. Then, the MMU centered at P is rotated using the angle δ to generate a new MMU, as shown in Figure 11. Lastly, the similarities between the two MMUs are calculated.
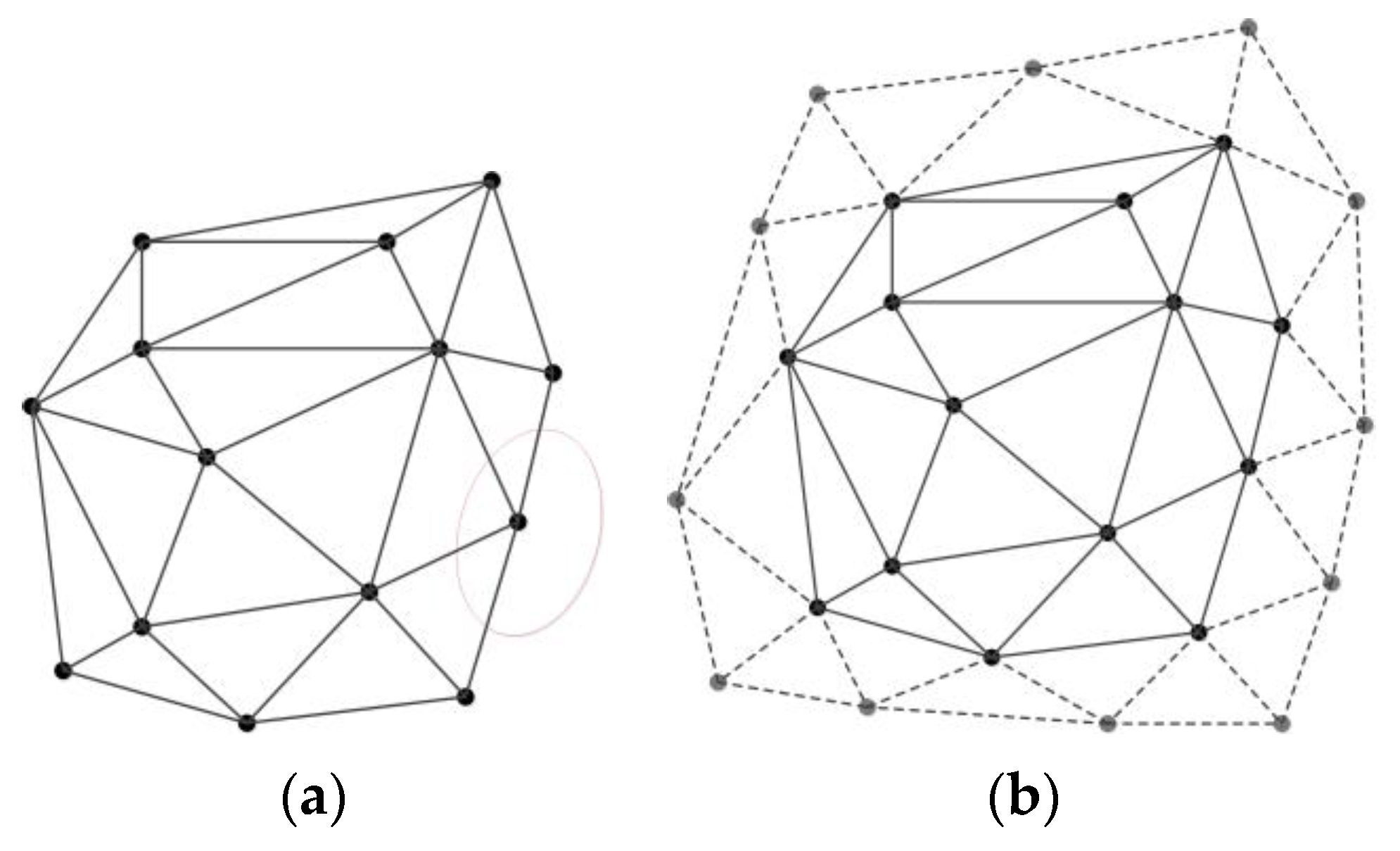
2.5. Identification of the Matching Relationship by Using the Hierarchical Matching Strategy
- (1)
- The convex hull M of all nodes in Va and Vb is calculated and extended using a certain distance (here, the distance value is set to 90 m) to obtain a new convex hull N parallel to M.
- (2)
- The nodes on the edge of the convex hull N, all the nodes in Va and Vb, and all the road segments are used as constraints to generate two triangulations, expressed as Sa and Sb.
- (3)
- A circular buffer with point ai as the center and a certain radius is set, and all the nodes in the buffer area of Vb are regarded as candidate matching nodes of ai and recorded as Mi.
- (4)
- The method mentioned in Section 2.4 is used to calculate the MMU similarity of all nodes with nodes ai and Mi sequentially, and the probability relaxation method is used to obtain a globally optimal similarity result.
- (5)
- Steps 3 and 4 are performed for all nodes in Va to determine all matches in L2.
- (1)
- Each Li has two endpoints, Vi1 and Vi2. The connected road in L3 is denoted as CLi with two endpoints CVi1, CVi2, and CVi1 is on Li. Similarly, each Lj has two endpoints, Vj1 and Vj2.
- (2)
- In accordance with the matching results of L2, if the matching pairs of (Vi1, Vj1) and (Vi2, Vj2) are obtained, then the matching relationship between (Li, Lj) can be determined. The road connected to Lj is denoted as CLj (j = 1,2, 3,...,k). CVj1, CVj2 are the two endpoints of Lj, and CVj1 is on Lj.
- (3)
- If CLi and CLj meet the following two conditions: 1) CLi and CLj are on the same side of Li and Lj, respectively; 2) The relative position of CVi1 in Li is closest to the relative position of CVj1 in Lj, and the difference should not be greater than 20%, then CVi1 matches CVj1.
- (4)
- If CVi2 and CVj2 are not connected to other roads, then CVi2 matches CVj2, and the matched nodes are placed into the same road layer.
- (5)
- Steps 1–4 are repeated until no new matches exist.
3. Implementation and Experiments
3.1. Experimental Area and Data
3.2. Model Evaluation Indices
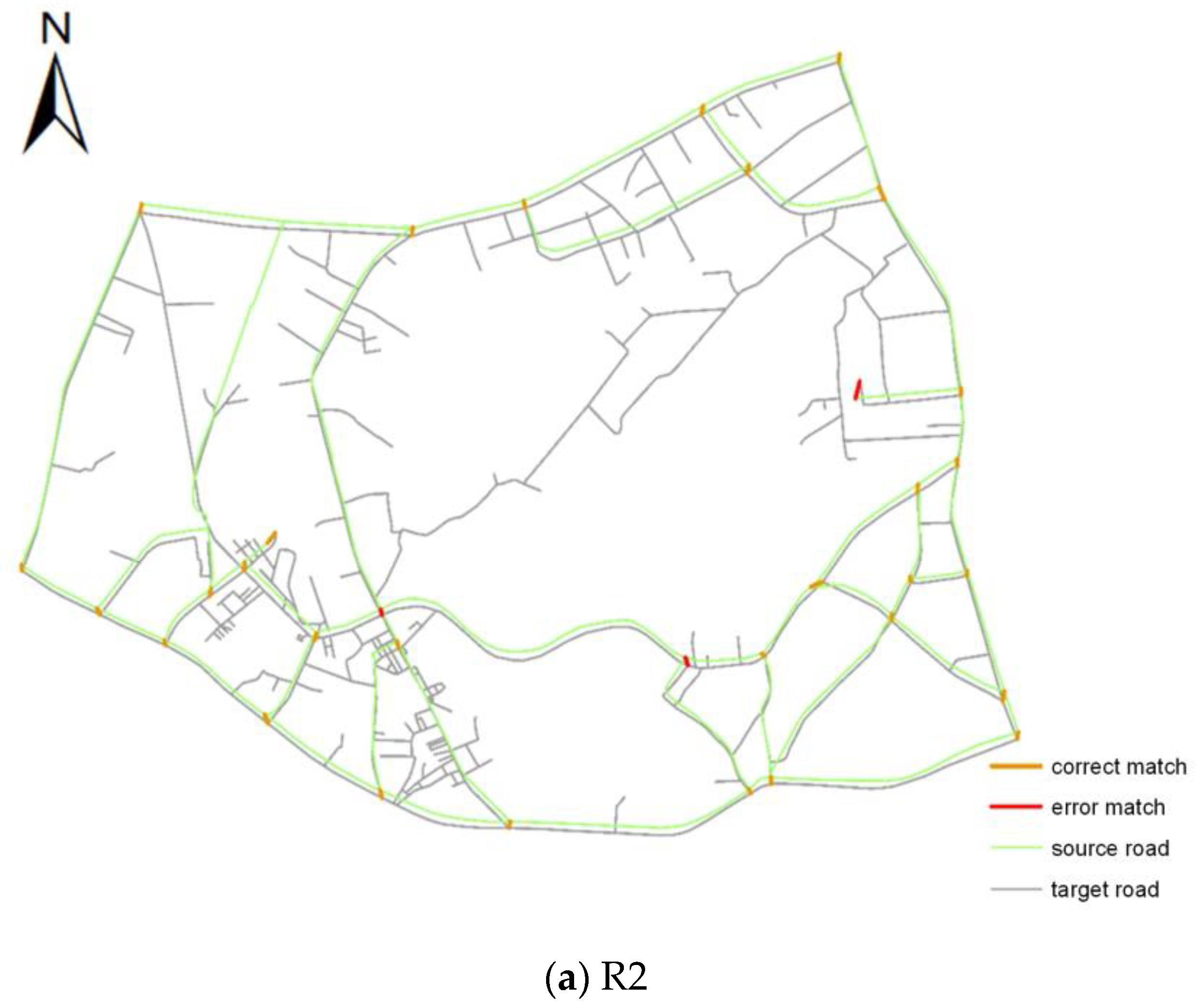
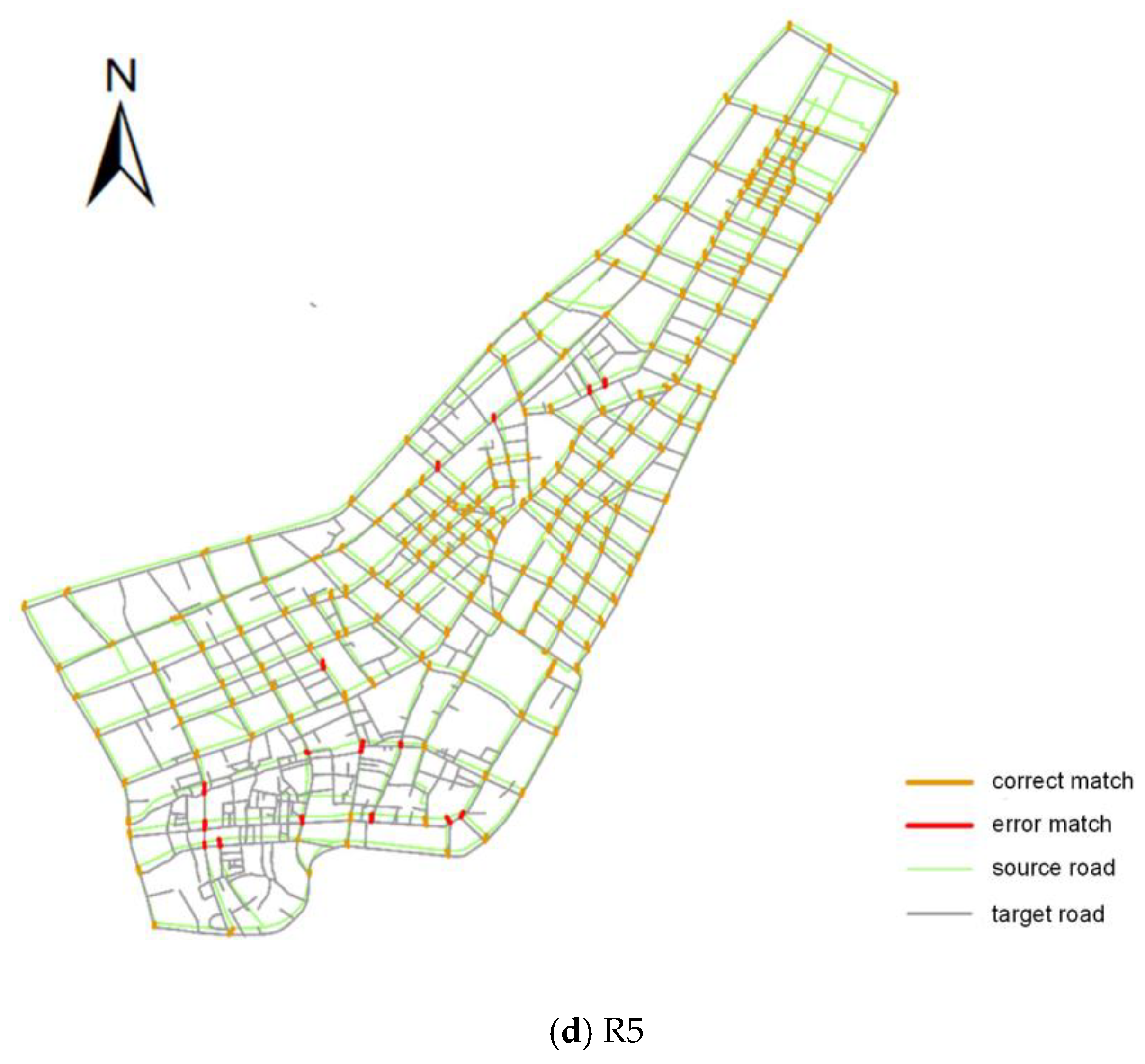
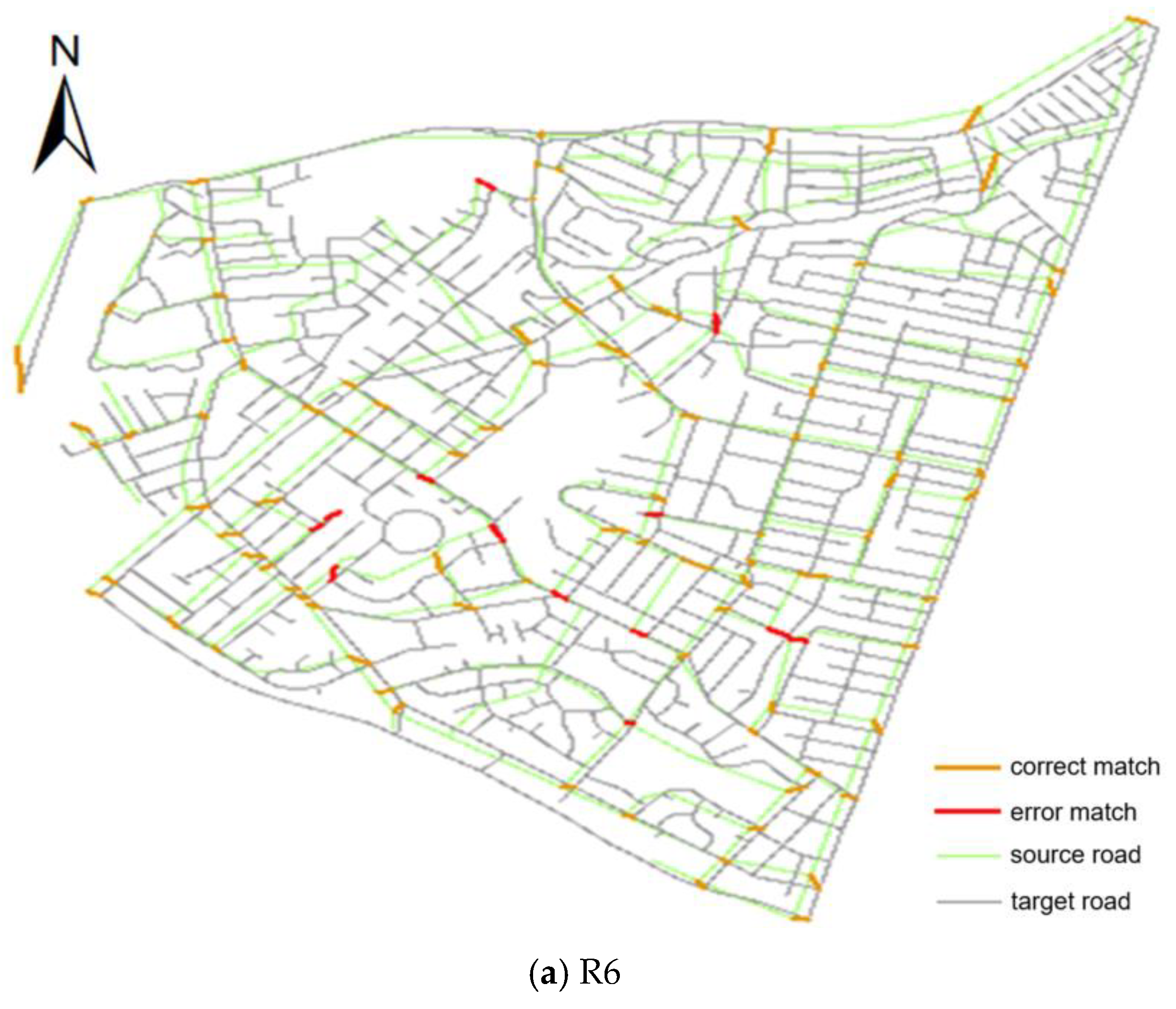
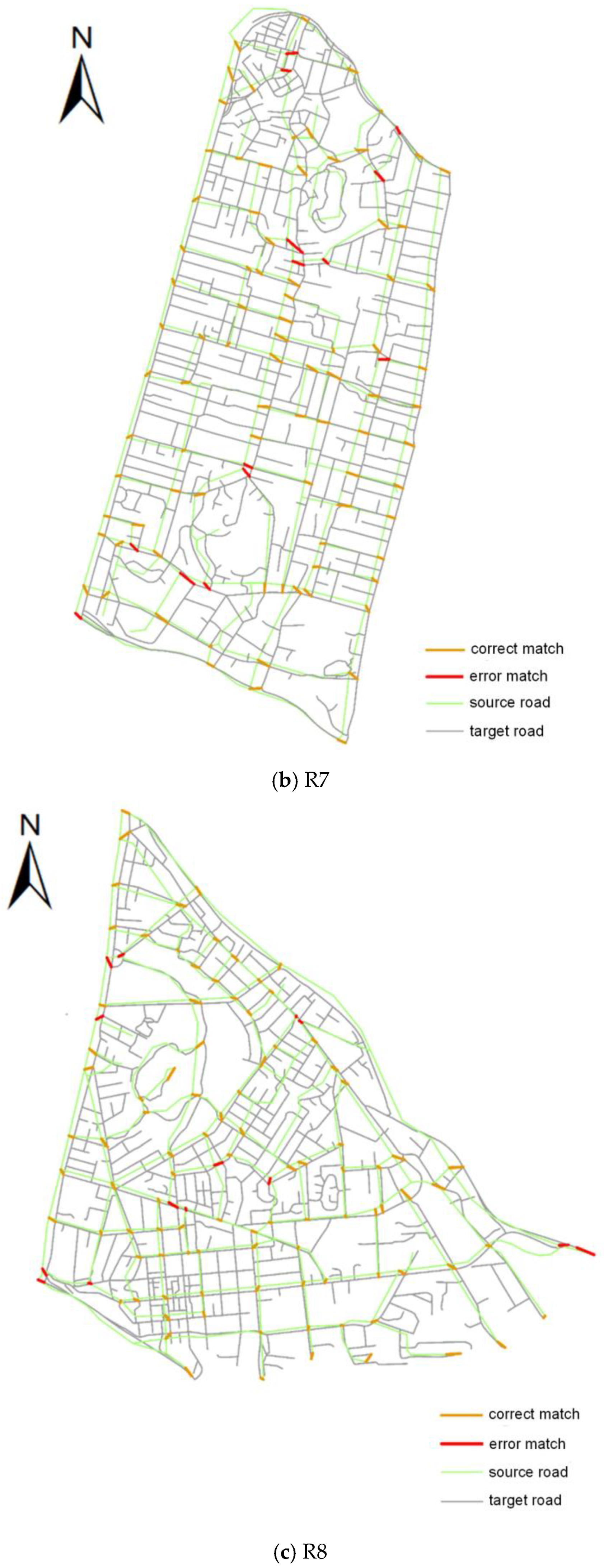
3.3. Evaluation of Algorithm Performance
3.4. Rotation Test on MMU
3.5. Rotation Test on the Road Network
3.6. Sensitivity Analysis of the Buffer Threshold
3.7. Impact of the Hierarchical Classification Threshold
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data and Codes Availability Statement
Appendix A


References
- Lei, T.L. Geospatial data conflation: A formal approach based on optimization and relational databases. Int. J. Geogr. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Luan, X. A probabilistic relaxation approach for matching road networks. Int. J. Geogr. Inf. Sci. 2013, 27, 319–338. [Google Scholar] [CrossRef]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data Fusion 2011, 2, 309–328. [Google Scholar] [CrossRef]
- Walter, V.; Fritsch, D. Matching spatial data sets: A statistical approach. Int. J. Geogr. Inf. Sci. 1999, 13, 445–473. [Google Scholar] [CrossRef]
- Yang, B.; Luan, X.; Zhang, Y. A pattern-based approach for matching nodes in heterogeneous urban road networks. Trans. GIS 2014, 18, 718–739. [Google Scholar] [CrossRef]
- Beeri, C.; Kanza, Y.; Safra, E.; Sagiv, Y. Object fusion in geographic information systems. In Proceedings of the Thirtieth International Conference on Very Large Data Bases-Volume 30; Morgan Kaufmann: Toronto, ON, Canada, 2004; pp. 816–827. [Google Scholar]
- Song, W.; Keller, J.M.; Haithcoat, T.L.; Davis, C.H. Relaxation-based point feature matching for vector map conflation. Trans. GIS 2011, 15, 43–60. [Google Scholar] [CrossRef]
- Safra, E.; Kanza, Y.; Sagiv, Y.; Doytsher, Y. Ad hoc matching of vectorial road networks. Int. J. Geogr. Inf. Sci. 2013, 27, 114–153. [Google Scholar] [CrossRef]
- Min, D.; Zhilin, L.; Xiaoyong, C. Extended hausdorff distance for spatial objects in gis. Int. J. Geogr. Inf. Sci. 2007, 21, 459–475. [Google Scholar] [CrossRef]
- Tong, X.; Liang, D.; Jin, Y. A linear road object matching method for conflation based on optimization and logistic regression. Int. J. Geogr. Inf. Sci. 2014, 28, 824–846. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, L. Delimited stroke oriented algorithm-working principle and implementation for the matching of road networks. Geogr. Inf. Sci. 2008, 14, 44–53. [Google Scholar] [CrossRef]
- Yang, L.; Wan, B.; Wang, R.; Zuo, Z.; An, X. Matching road network based on the structural relationship constraint of hierarchical strokes. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1661–1668. [Google Scholar]
- Zhao, D.; Sheng, Y. Research on automatic matching of vector road networks based on global optimization. Acta Geod. Cartogr. Sin. 2010, 39, 416–421. [Google Scholar]
- Zhang, J.; Wang, Y.; Zhao, W. An improved probabilistic relaxation method for matching multi-scale road networks. Int. J. Digit. Earth 2018, 11, 1–21. [Google Scholar] [CrossRef]
- Sébastien, M.; Devogele, T. Matching Networks with Different Levels of Detail. Geoinformatica 2008, 12, 435–453. [Google Scholar]
- Volz, S. An Iterative Approach for Matching Multiple Representations of Street Data. In Proceedings of the JOINT ISPRS Workshop on Multiple Representations and Interoperability of Spatial Data; University of Stuttgart: Stuttgart, Germany, 2006; Volume XXXVI Part 2/W40, pp. 101–110. [Google Scholar]
- Siriba, D.N.; Dalyot, S. Automatic georeferencing of non-geospatially referenced provisional cadastral maps. Surv. Rev. 2012, 44, 142–152. [Google Scholar] [CrossRef]
- Saalfeld, A. Conflation Automated map compilation. Int. J. Geogr. Inf. Syst. 1988, 2, 217–228. [Google Scholar] [CrossRef]
- Chen, C.C.; Knoblock, C.; Kolahdouzan, M. Automatically and Efficiently Matching Road Networks with Spatial Attributes in Unknown Geometry Systems. In Proceedings of the 3rd Workshop on STDBM, Seoul, Korea, 11 September 2006. [Google Scholar]
- Luan, X. A structure-based approach for matching road junctions with different coordinate systems. In Proceedings of the Twenty-Second ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 41–46. [Google Scholar]
- Müslüm, H.; Türkay, G. A New, Score-Based Multi-Stage Matching Approach for Road Network Conflation in Different Road Patterns. Int. J. Geo Inf. 2019, 8, 81. [Google Scholar]
- Jiang, B. Street hierarchies: A minority of streets account for a majority of traffic flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Thomson, R.C. The ‘stroke’ concept in geographic network generalization and analysis. In Proceedings of the 12th International Symposium on Spatial Data Handling, Vienna, Austria, 12–14 July 2006. [Google Scholar]
- Serge, S. Cities and Forms on Sustainable Urbanism; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Zhen, W.; Yang, L.; Kwan, M.; Zuo, Z.; Wan, B.; Zhou, S.; Li, S.; Ye, Y.; Qian, H.; Pan, X. Capturing what human eyes perceive: A visual hierarchy generation approach to emulating saliency-based visual attention for grid-like urban street networks. Comput. Environ. Urban Syst. 2020, 80, 101454. [Google Scholar] [CrossRef]
- Finch, A.M.; Wilson, R.C.; Hancock, E.R. Matching Delaunay Triangulations by Probabilistic Relaxation; Springer: Berlin/Heidelberg, Germany, 1995; pp. 350–358. [Google Scholar]
- Yang, T.R. Understanding commuting patterns and changes: Counterfactual analysis in a planning support framework. Environ. Plan. B Urban Anal. City Sci. 2020. [Google Scholar] [CrossRef]
- Lim, L.; Yang, T.; Vialard, A.; Chen, F.; Peponis, J. Urban morphology and syntactic structure: A discussion of the relationship of block size to street integration in some settlements in the Provence. J. Space Syntax 2015, 6, 142–169. [Google Scholar]
- Jiang, B.; Claramunt, C. Topological analysis of urban street networks. Environ. Plan. B Plan. Design. 2004, 31, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Marshall, S.; Gil, J.; Kropf, K.; Tomko, M.; Figueiredo, L. Street Network Studies: From Networks to Models and their Representations. Netw. Spat. Econ. 2018, 18, 735–749. [Google Scholar] [CrossRef] [Green Version]



























| Similarity | z | y | x | w | v |
|---|---|---|---|---|---|
| a | 0.61 | 0.78 | 0.83 | 0.72 | 0.92 |
| b | 0.76 | 0.84 | 0.80 | 0.47 | 0.63 |
| c | 0.78 | 0.86 | 0.79 | 0.83 | 0.76 |
| d | 0.71 | 0.45 | 0.81 | 0.43 | 0.79 |
| e | 0.91 | 0.62 | 0.75 | 0.78 | 0.22 |
| No. | Number of Road Segments | Number of Nodes | Number of Strokes |
|---|---|---|---|
| Area1_Src | 107 | 68 | 31 |
| Area1_Des | 109 | 69 | 32 |
| Area2_Src | 715 | 431 | 148 |
| Area2_Des | 2083 | 1486 | 463 |
| Area3_Src | 608 | 386 | 134 |
| Area3_Des | 2805 | 1574 | 764 |
| No | DTRM | PRM | ||||
|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | |
| R1 | 98.68% | 98.68% | 98.68% | 97.33% | 97.33% | 97.33% |
| No | DTRM | PRM | ||||
|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | |
| R2 | 85.71% | 90.91% | 88.23% | 82.86% | 87.88% | 85.30% |
| R3 | 91.67% | 94.83% | 93.22% | 90.00% | 93.13% | 91.54% |
| R4 | 92.55% | 94.56% | 93.54% | 91.49% | 93.48% | 92.47% |
| R5 | 92.25% | 95.20% | 93.70% | 93.02% | 96.00% | 94.49% |
| No | DTRM | PRM | ||||
|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | |
| R6 | 86.09% | 88.39% | 87.22% | 84.35% | 86.61% | 85.47% |
| R7 | 84.4% | 87.62% | 85.98% | 86.24% | 89.52% | 87.85% |
| R8 | 85.71% | 88.07% | 86.87% | 80.36% | 85.74% | 82.96% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Z.; Yang, L.; An, X.; Zhen, W.; Qian, H.; Dai, S. A Hierarchical Matching Method for Vectorial Road Networks Using Delaunay Triangulation. ISPRS Int. J. Geo-Inf. 2020, 9, 509. https://doi.org/10.3390/ijgi9090509
Zuo Z, Yang L, An X, Zhen W, Qian H, Dai S. A Hierarchical Matching Method for Vectorial Road Networks Using Delaunay Triangulation. ISPRS International Journal of Geo-Information. 2020; 9(9):509. https://doi.org/10.3390/ijgi9090509
Chicago/Turabian StyleZuo, Zejun, Lin Yang, Xiaoya An, Wenjie Zhen, Haoyue Qian, and Songling Dai. 2020. "A Hierarchical Matching Method for Vectorial Road Networks Using Delaunay Triangulation" ISPRS International Journal of Geo-Information 9, no. 9: 509. https://doi.org/10.3390/ijgi9090509
APA StyleZuo, Z., Yang, L., An, X., Zhen, W., Qian, H., & Dai, S. (2020). A Hierarchical Matching Method for Vectorial Road Networks Using Delaunay Triangulation. ISPRS International Journal of Geo-Information, 9(9), 509. https://doi.org/10.3390/ijgi9090509




