Accounting for Local Geological Variability in Sequential Simulations—Concept and Application
Abstract
1. Introduction
2. Theoretical Background
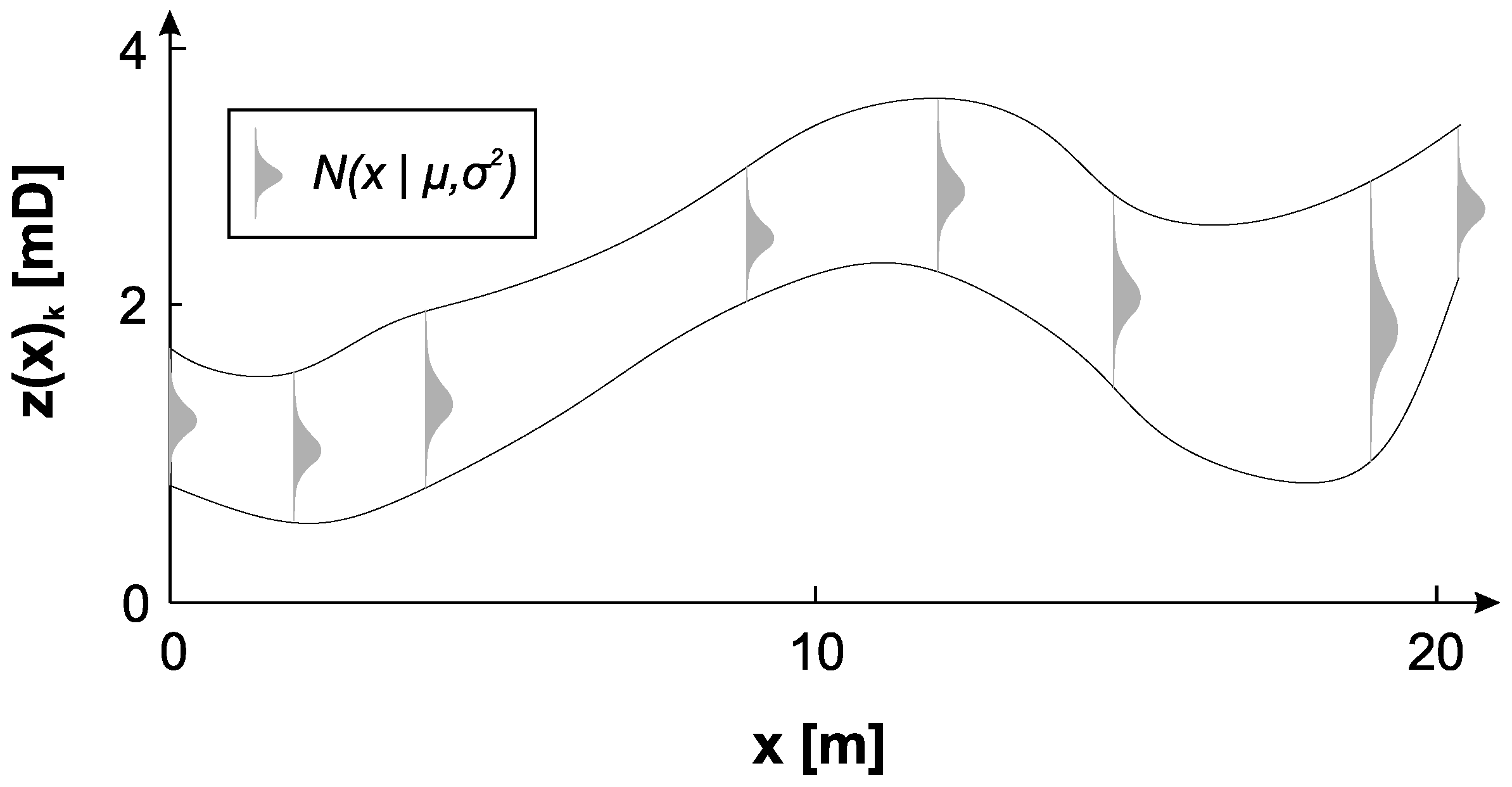
2.1. Spatial Variability
2.2. Geostatistical Interpolation
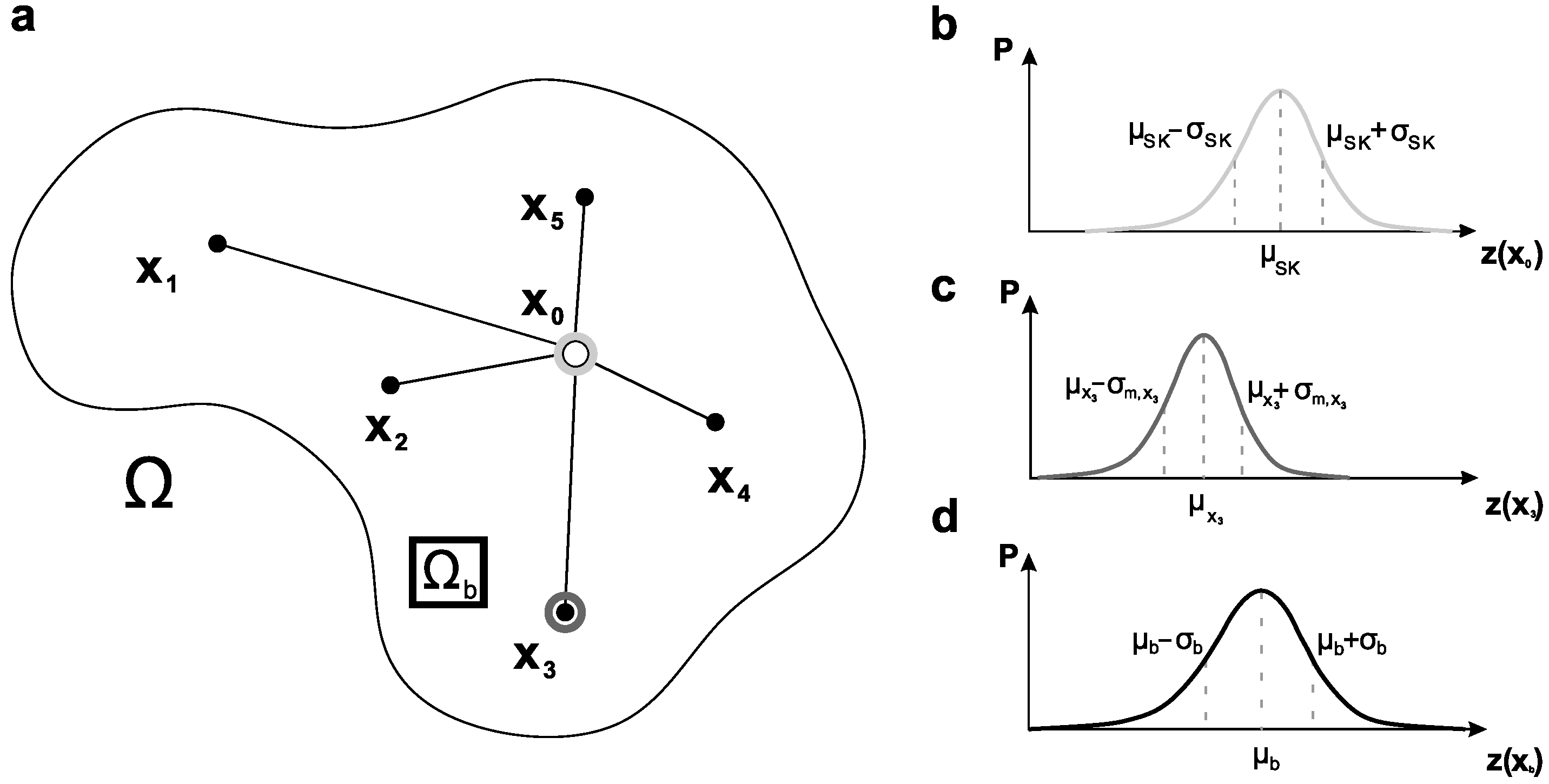
2.2.1. Spatial Neighborhood
2.2.2. Variography
2.2.3. Simple Kriging
2.2.4. Consideration of Measurement Error Variance
2.3. Sequential Simulation
2.4. Model Validation
2.4.1. Cross-Validation
2.4.2. Ergodic Fluctuations
3. Sequential Simulation using a Local Variance Model
| Algorithm 1 LVM-SGS and LVM-DSS |
|
3.1. Case Study
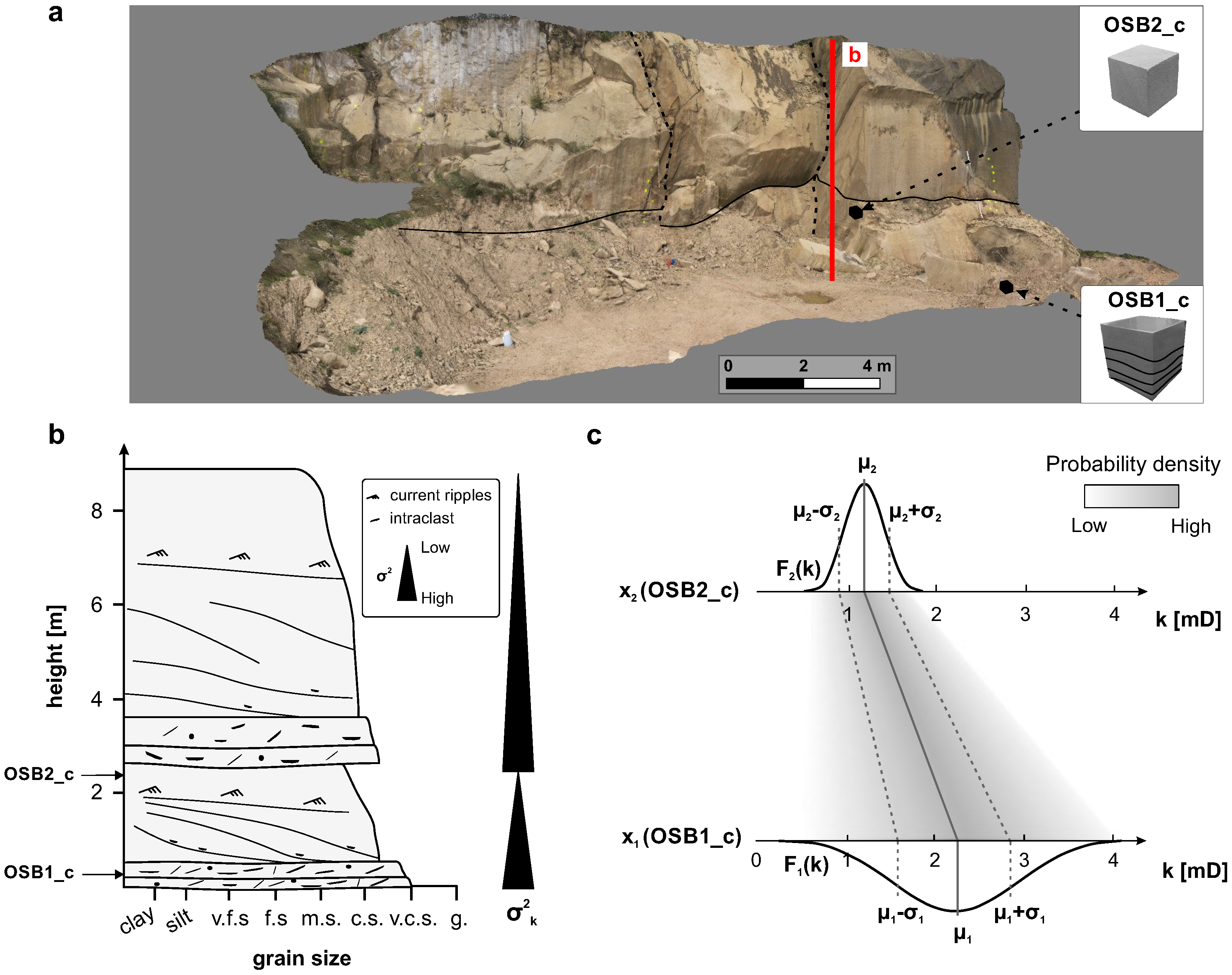
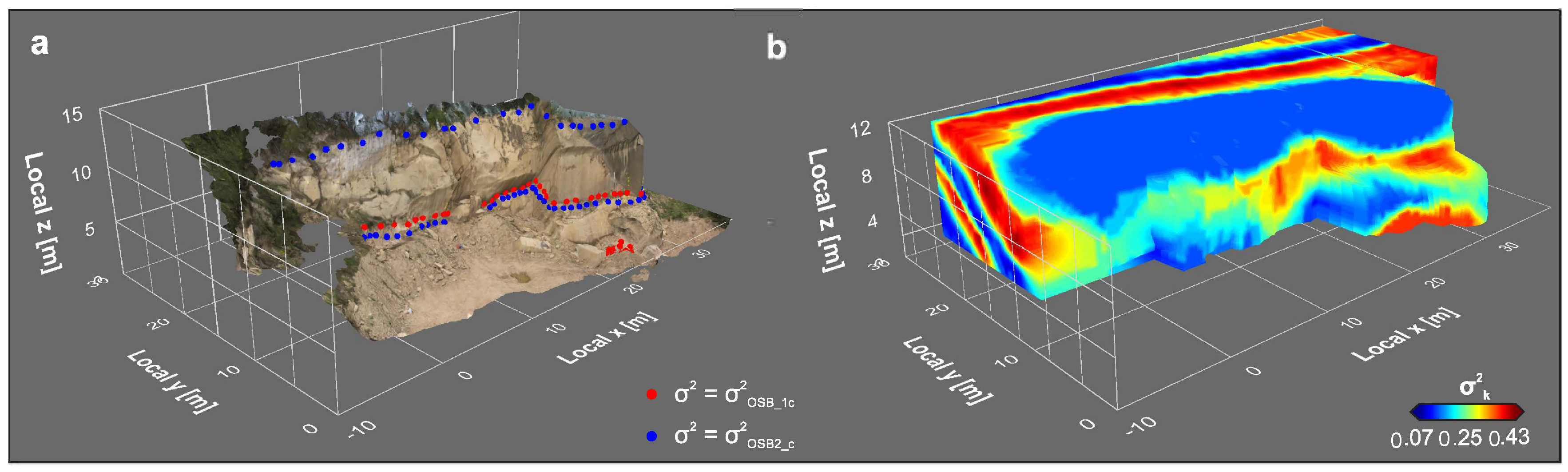
3.1.1. Object of Investigation
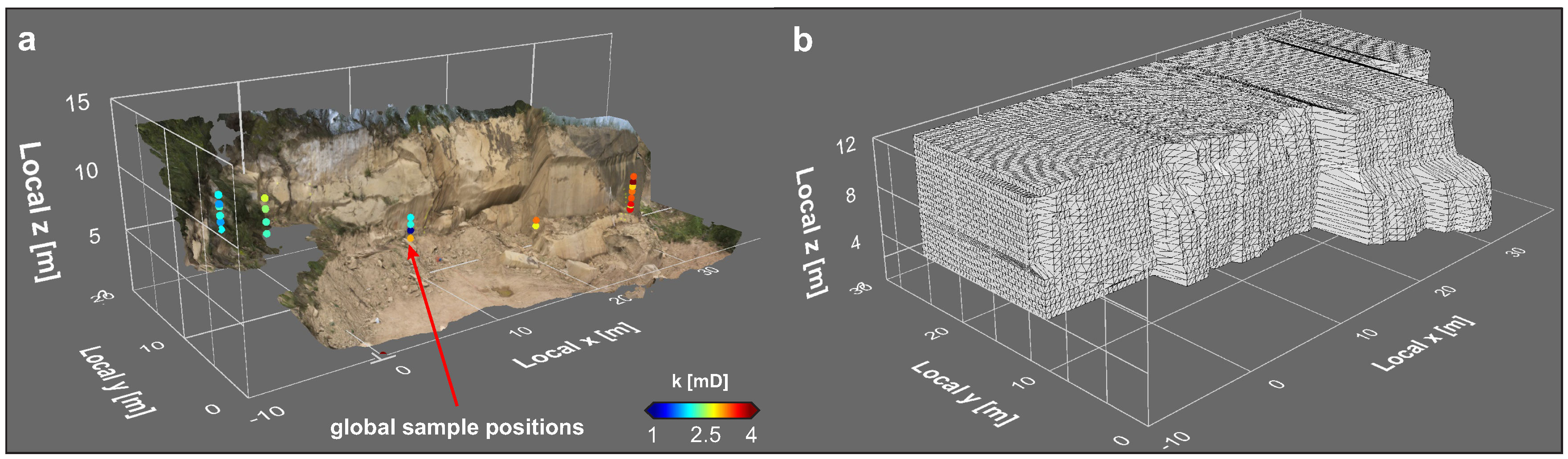
3.1.2. Sampling Strategy
3.1.3. Laboratory Measurements
3.1.4. Mesh Generation
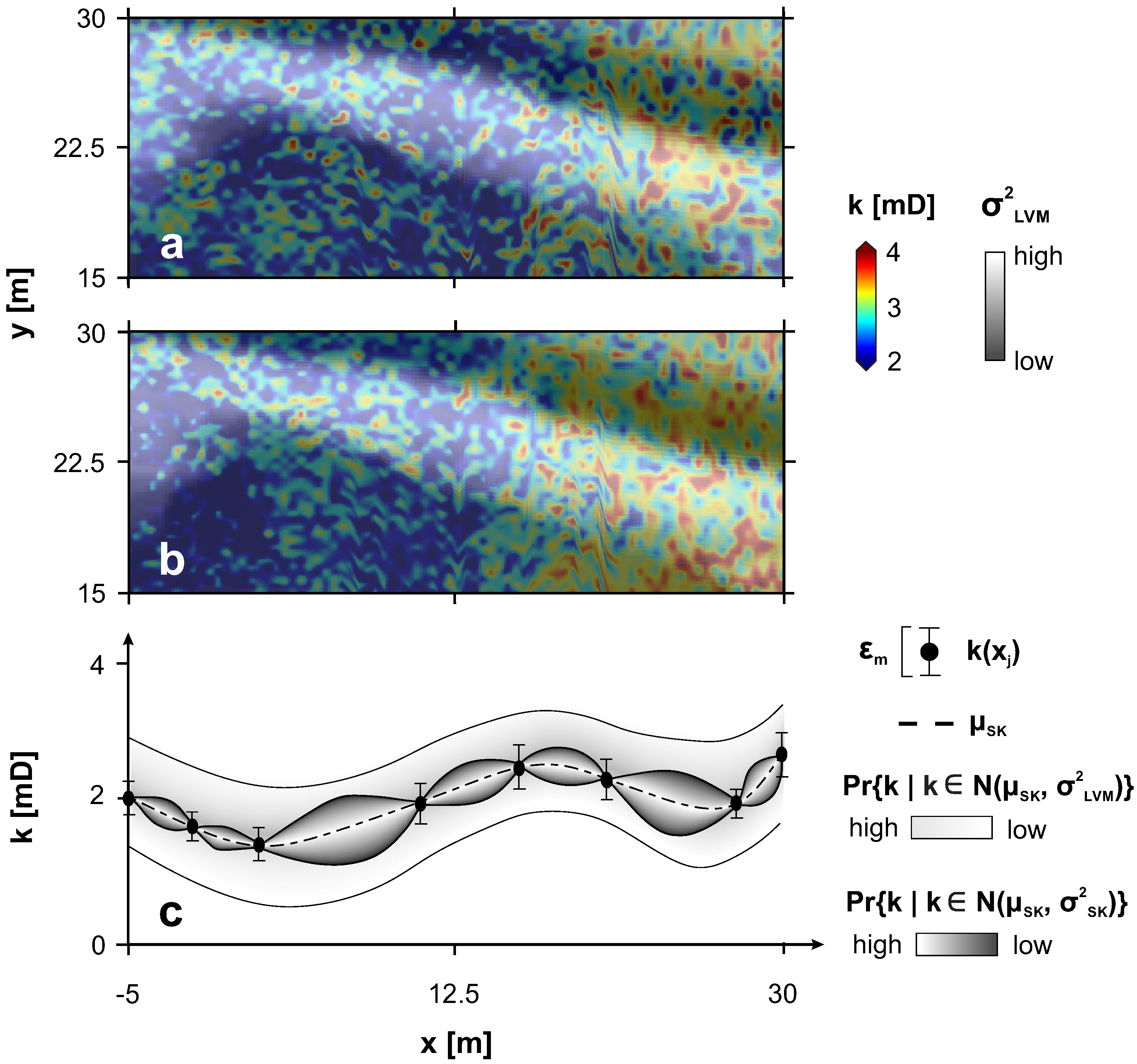
4. Results
4.1. Spatial Variability
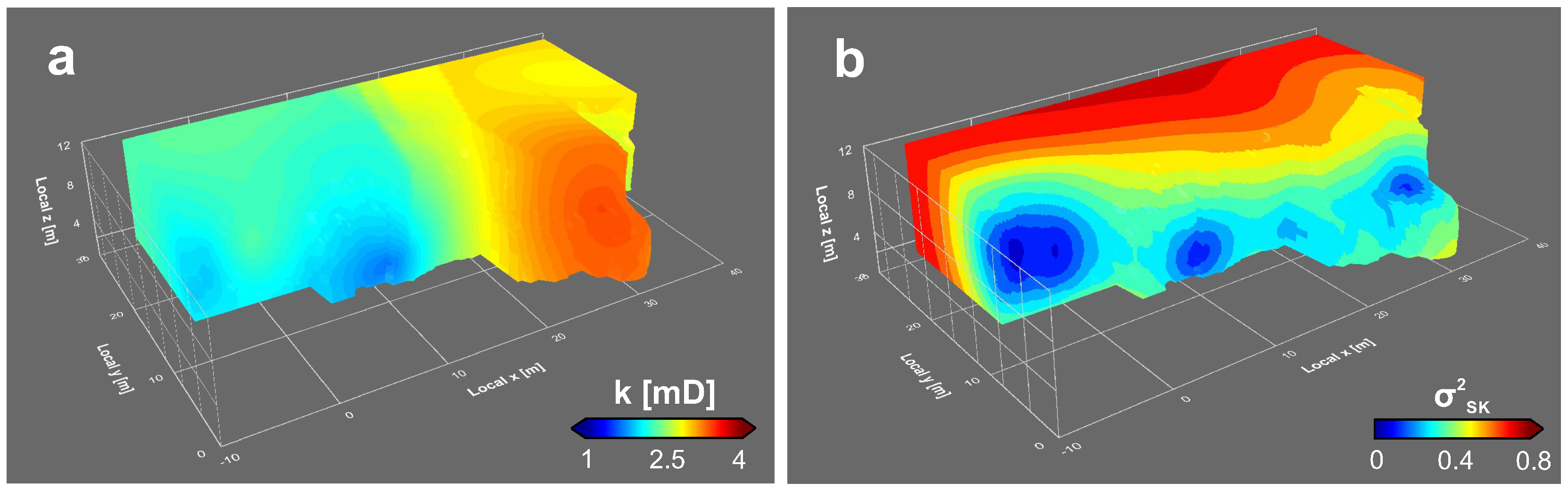
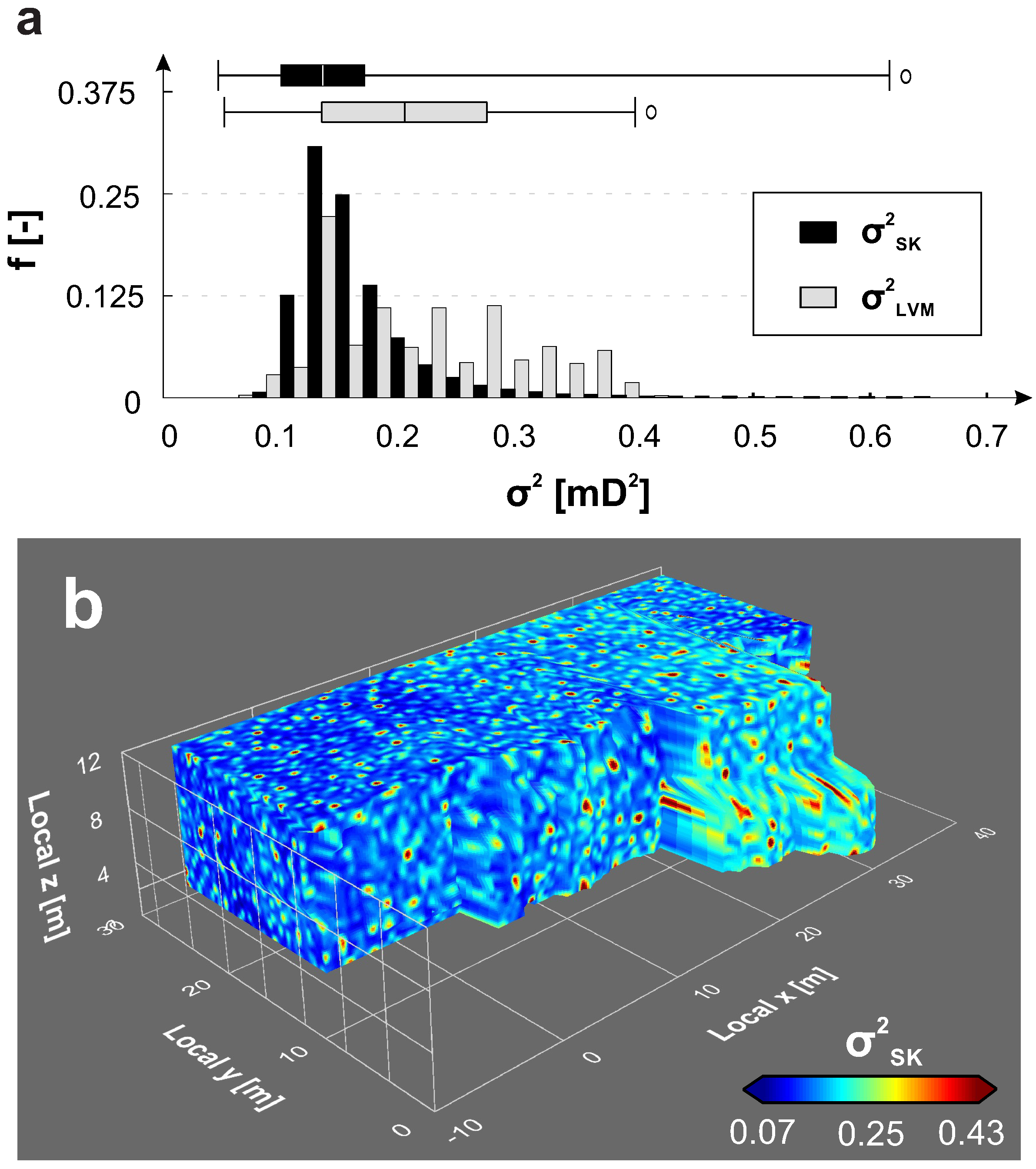
4.2. Constructing the LVM
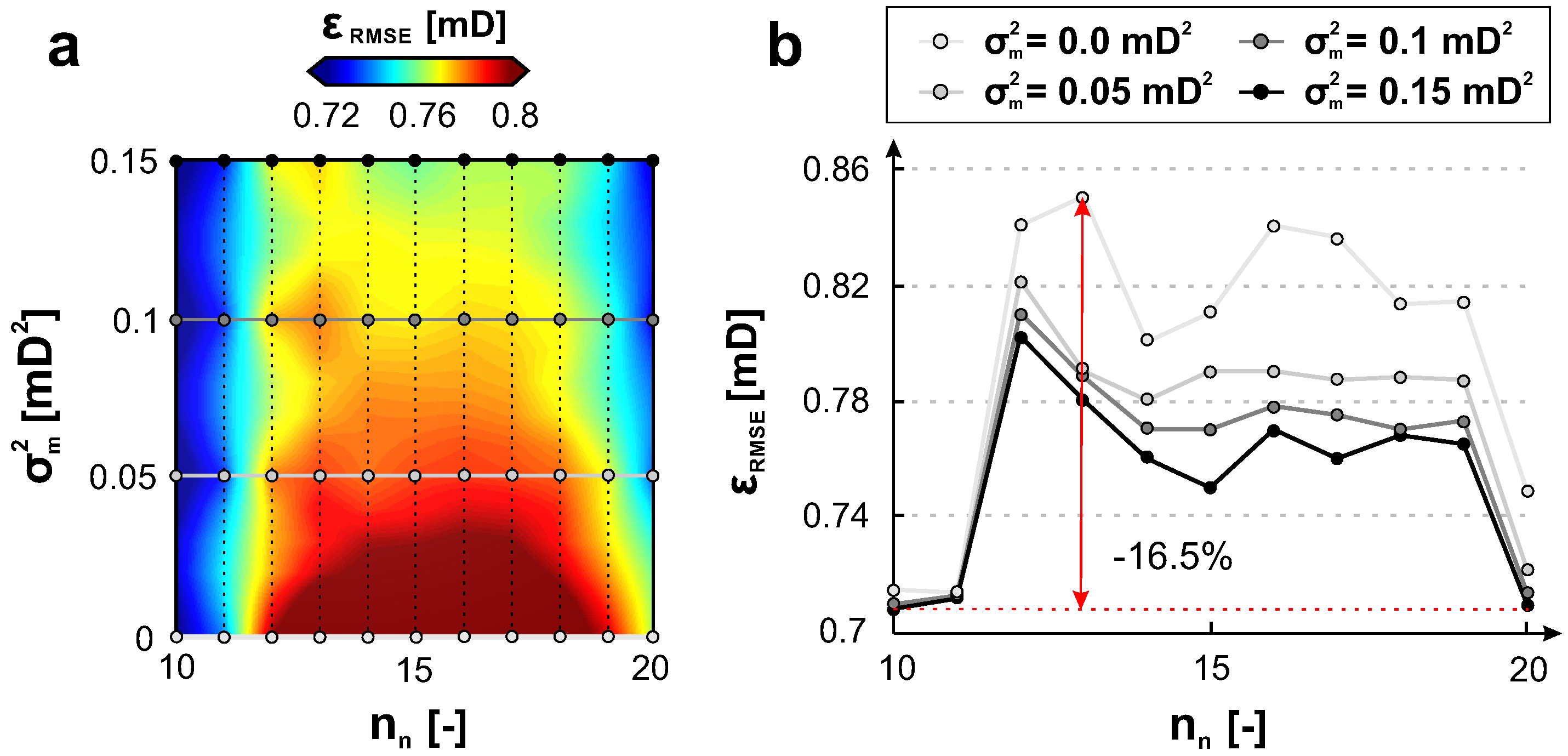
4.3. Optimizing the BLUE for Sequential Simulation
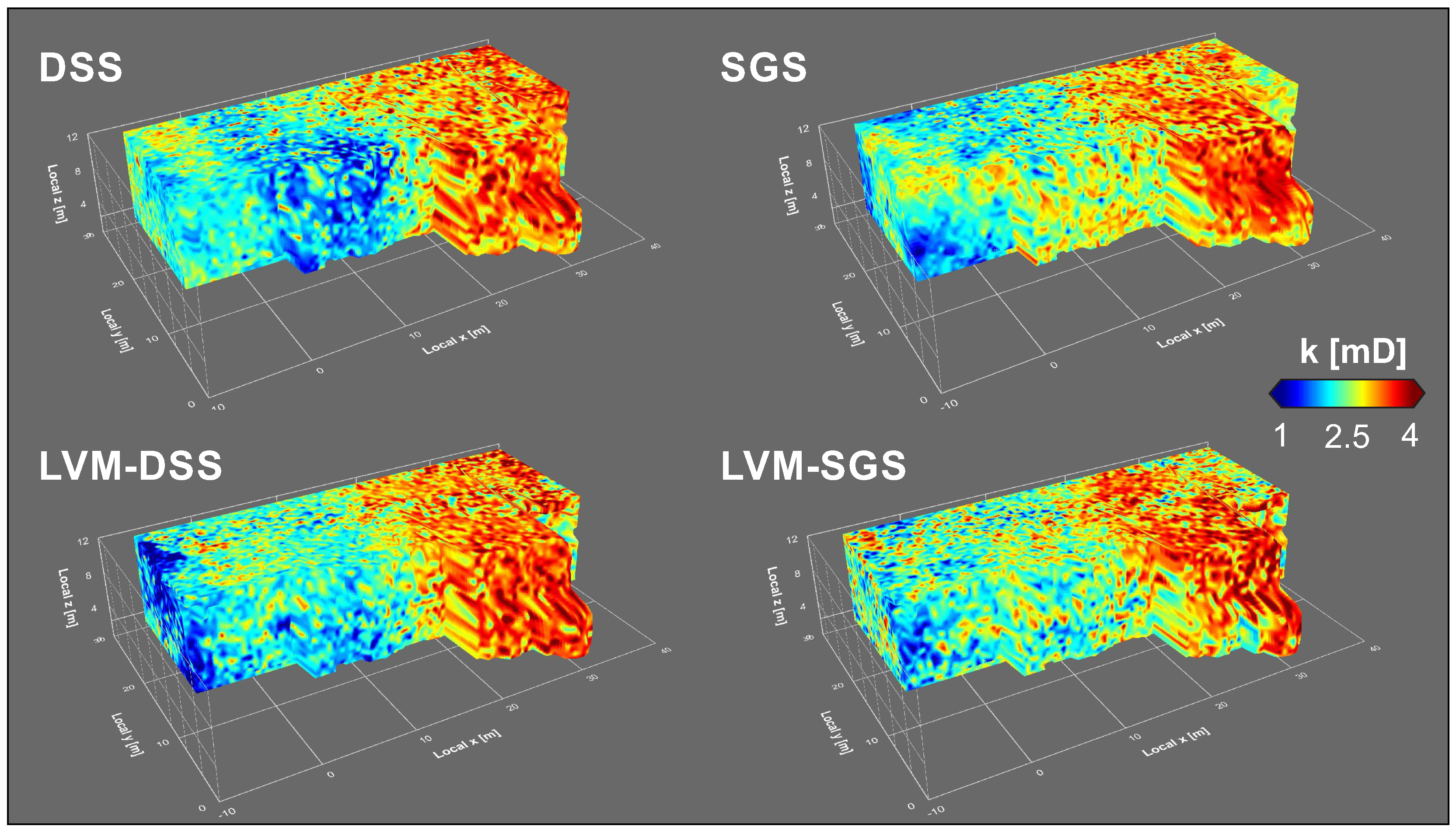
4.4. versus
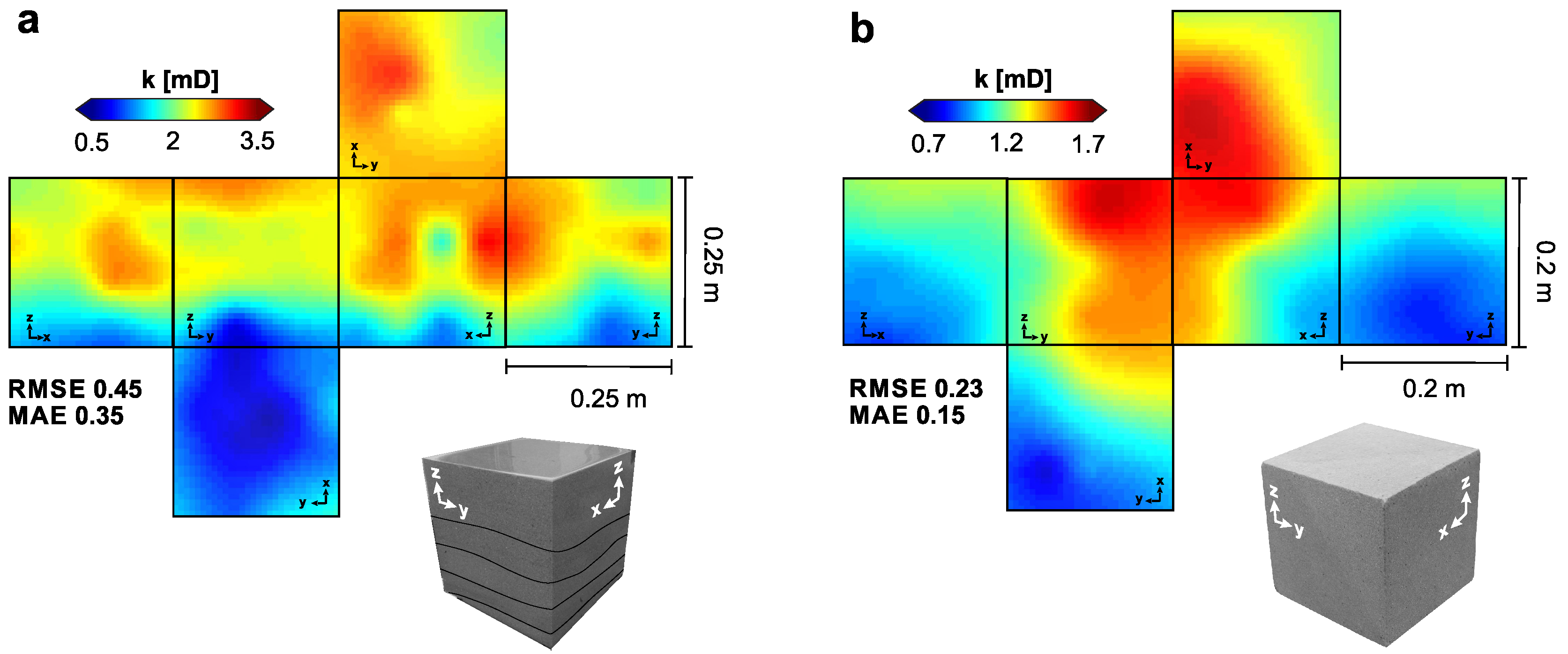
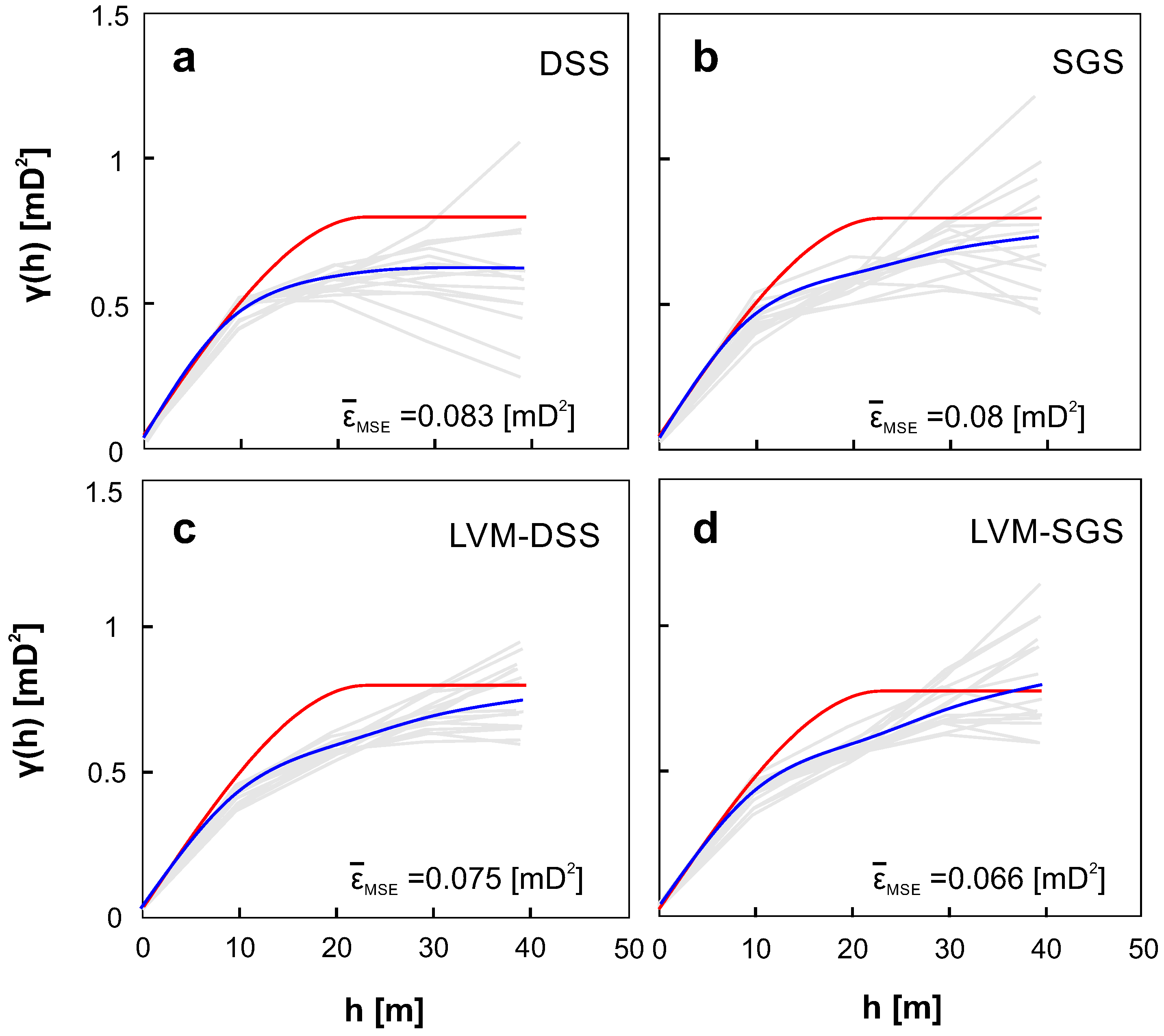
4.5. Model Validation
Visual Outputs
5. Discussion
5.1. Construction of the LVM
5.2. Comparison of the Spatial Distribution of the Local Variance
6. Conclusions
- The distance metrics RMSE and MAE in spatial interpolations can be optimized with regard to the measurement error variance and the optimal neighborhood.
- Geological samples always represent a small subset of the local variability, which should be accounted for by high-resolution sampling at a random basis at the least.
- The simple kriging variance does not necessarily account for the magnitude of local variability in geological media and definitely does not account for its spatial distribution.
- The fact that the local simple kriging variance does not reflect a geological trend might lead to unforeseen problems when using sequential simulation-derived models as a basis for subsurface utilization processes because the full geological heterogeneity might not have been taken into account properly.
- By introducing a measurement-constrained, geology-driven local variance model, the spatial distribution of the variance that is expected in the investigated quarry can be integrated into sequential simulations. This allows to simulate the geological variability, which might be greater than the simulated variability in conventional sequential simulation algorithms.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDF | Cumulative distribution function |
| DSS | Direct sequential simulation |
| LVM | Local variance model |
| LpO CV | Leave-p-out cross-validation |
| MAE | Mean-absolute-error |
| MSE | Mean-square error |
| probability density function | |
| REV | Representative elementary volume |
| RMSE | Root-mean-square error |
| RF | Random function |
| RV | Random variable |
| SGS | Sequential Gaussian simulation |
| SK | Simple kriging |
Appendix A. Code and Data Availability
References
- Li, H.; Reynolds, J. On Definition and Quantification of Heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Crooijmans, R.A.; Willems, C.J.L.; Nick, H.M.; Bruhn, D.F. The influence of facies heterogeneity on the doublet performance in low-enthalpy geothermal sedimentary reservoirs. Geothermics 2016, 64, 209–219. [Google Scholar] [CrossRef]
- Rodrigo-Ilarri, J.; Reisinger, M.; Gómez-Hernández, J.J. Influence of Heterogeneity on Heat Transport Simulations in Shallow Geothermal Systems. In Geostatistics Valencia 2016; Springer: Berlin, Germany, 2017; pp. 849–862. [Google Scholar] [CrossRef]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 1968 ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar] [CrossRef]
- Webster, R.; Margaret, A.O. Geostatistics for Environmental Scientists, 2nd ed.; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; p. 330. [Google Scholar]
- Deutsch, C.V.; Journel, A. GSLIB: Geostatistical Software Library and User’s Guide; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Tran, T.T. Improving variogram reproduction on dense simulation grids. Comput. Geosci. 1994, 20, 1161–1168. [Google Scholar] [CrossRef]
- Leuangthong, O.; McLennan, J.A.; Deutsch, C.V. Minimum Acceptance Criteria for Geostatistical Realizations. Nat. Resour. Res. 2004, 13, 131–141. [Google Scholar] [CrossRef]
- Soares, A. Direct Sequential Simulation and Cosimulation. Math. Geol. 2001, 33, 911–926. [Google Scholar] [CrossRef]
- Robertson, R.K.; Mueller, U.A.; Bloom, L.M. Direct sequential simulation with histogram reproduction: A comparison of algorithms. Comput. Geosci. 2006, 32, 382–395. [Google Scholar] [CrossRef]
- Journel, A.; Alabert, F. Non-Gaussian data expansion in the Earth Sciences. Terra Nova 1989, 1, 123–134. [Google Scholar] [CrossRef]
- Verly, G. Sequential Gaussian Simulation: A Monte Carlo Method for Generating Models of Porosity and Permeability. In Generation, Accumulation and Production of Europe’s Hydrocarbons III; Spencer, A.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 345–356. [Google Scholar]
- Ersoy, A.; Yünsel, T.Y. Geostatistical Conditional Simulation for the Assessment of the Quality Characteristics of Cayırhan Lignite Deposits. Energy Explor. Exploit. 2006, 24, 391–416. [Google Scholar] [CrossRef]
- Delbari, M.; Afrasiab, P.; Loiskandl, W. Using sequential Gaussian simulation to assess the field-scale spatial uncertainty of soil water content. CATENA 2009, 79, 163–169. [Google Scholar] [CrossRef]
- Pinheiro, M.; Emery, X.; Miranda, T.; Lamas, L.; Espada, M. Modelling Geotechnical Heterogeneities Using Geostatistical Simulation and Finite Differences Analysis. Minerals 2018, 8, 52. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A Note on the Generation of Random Normal Deviates. Ann. Math. Statist. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Matheron, G. Principles of Geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Anyiam, O.A.; Andrew, P.J.; Okwara, I.C. Assessment of the heterogeneity and petrophysical evaluation of reservoirs in the “Akbar Field”, Niger Delta, Nigeria. J. Pet. Explor. Prod. Technol. 2017, 7, 1035–1050. [Google Scholar] [CrossRef]
- Michie, E.A.H.; Haines, T.J. Variability and heterogeneity of the petrophysical properties of extensional carbonate fault rocks, Malta. Pet. Geosci. 2016, 22, 136–152. [Google Scholar] [CrossRef]
- Mukerji, T.; Mavko, G.; Rio, P. Scales of Reservoir Heterogeneities and Impact of Seismic Resolution on Geostatistical Integration. Math. Geol. 1997, 29, 933–950. [Google Scholar] [CrossRef]
- De Ros, L.F.; Scherer, C.M.S. Stratigraphic Controls on the Distribution of Diagenetic Processes, Quality and Heterogeneity of Fluvial-Aeolian Reservoirs from the Recôncavo Basin, Brazil. In Linking Diagenesis to Sequence Stratigraphy; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 105–132. [Google Scholar] [CrossRef]
- Oxford English Dictionary. Heterogeneity; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Fitch, P.J.R.; Lovell, M.A.; Davies, S.J.; Pritchard, T.; Harvey, P.K. An integrated and quantitative approach to petrophysical heterogeneity. Mar. Pet. Geol. 2015, 63, 82–96. [Google Scholar] [CrossRef]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2003; p. 388. [Google Scholar] [CrossRef]
- Armstrong, M. Experimental Variograms. In Basic Linear Geostatistics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 47–58. [Google Scholar] [CrossRef]
- Ringrose, P.; Bentley, M. Reservoir Model Design, 1st ed.; Springer: Dordrecht, The Netherlands, 2015; p. 249. [Google Scholar] [CrossRef]
- Gu, Y.; Rühaak, W.; Bär, K.; Sass, I. Using seismic data to estimate the spatial distribution of rock thermal conductivity at reservoir scale. Geothermics 2017, 66, 61–72. [Google Scholar] [CrossRef]
- Rühaak, W.; Guadagnini, A.; Geiger, S.; Bär, K.; Gu, Y.; Aretz, A.; Homuth, S.; Sass, I. Upscaling thermal conductivities of sedimentary formations for geothermal exploration. Geothermics 2015, 58, 49–61. [Google Scholar] [CrossRef]
- Rühaak, W. 3-D interpolation of subsurface temperature data with measurement error using kriging. Environ. Earth Sci. 2015, 73, 1893–1900. [Google Scholar] [CrossRef]
- Bailey, T.; Gatrell, A. Interactive Spatial Data Analysis; Longman Group Limited: Harlow, UK, 1995; p. 432. [Google Scholar]
- Journel, A.G. Nonparametric estimation of spatial distributions. J. Int. Assoc. Math. Geol. 1983, 15, 445–468. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Remy, N. Algorithmic and Software Methods for a Better Integration of the Geological Information into Numerical Models; Standford University: Stanford, CA, USA, 2004. [Google Scholar]
- Ökten, G.; Göncü, A. Generating low-discrepancy sequences from the normal distribution: Box—Muller or inverse transform? Math. Comput. Model. 2011, 53, 1268–1281. [Google Scholar] [CrossRef]
- Celisse, A. Optimal cross-validation in density estimation with the L2-loss. Ann. Stat. 2014, 42, 1879–1910. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K.; Robeson, S.M. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Environ. 2009, 43, 749–752. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Emery, X. Testing the correctness of the sequential algorithm for simulating Gaussian random fields. Stoch. Environ. Res. Risk Assess. 2004, 18, 401–413. [Google Scholar] [CrossRef]
- Linsel, A.; Wiesler, S.; Hornung, J.; Hinderer, M. High-Resolution Analysis of the Physicochemical Characteristics of Sandstone Media at the Lithofacies Scale. Solid Earth Discuss. 2020, 2020, 1–28. [Google Scholar] [CrossRef]
- Linsel, A. ApirsAL/GeoReVi: GeoReVi v1.0.0 Pre-Release. Available online: https://zenodo.org/record/3541136#.XvhBb3ERWUk (accessed on 20 December 2019).
- Becker, A.; Schwarz, M.; Schäfer, A. Lithostratigraphische Korrelation des Rotliegend im östlichen Saar-Nahe-Becken. Jahresberichte Und Mitteilungen Des Oberrheinischen Geologischen Vereins 2012, 94, 105–133. [Google Scholar] [CrossRef]
- Aretz, A.; Bär, K.; Götz, A.E.; Sass, I. Outcrop analogue study of Permocarboniferous geothermal sandstone reservoir formations (northern Upper Rhine Graben, Germany): Impact of mineral content, depositional environment and diagenesis on petrophysical properties. Int. J. Earth Sci. 2015, 105, 1431–1452. [Google Scholar] [CrossRef]
- Farkhutdinov, A.; Goblet, P.; de Fouquet, C.; Cherkasov, S. A case study of the modeling of a hydrothermal reservoir: Khankala deposit of geothermal waters. Geothermics 2016, 59, 56–66. [Google Scholar] [CrossRef]
- Nordahl, K.; Ringrose, P.S. Identifying the Representative Elementary Volume for Permeability in Heterolithic Deposits Using Numerical Rock Models. Math. Geosci. 2008, 40, 753. [Google Scholar] [CrossRef]
- Nordahl, K.; Messina, C.; Berland, H.; Rustad, A.B.; Rimstad, E.; Martinius, A.W.; Howell, J.A.; Good, T.R. Impact of multiscale modelling on predicted porosity and permeability distributions in the fluvial deposits of the Upper Lunde Member (Snorre Field, Norwegian Continental Shelf). In Sediment-Body Geometry and Heterogeneity: Analogue Studies for Modelling the Subsurface; Geological Society of London: London, UK, 2014; Volume 387, p. 25. [Google Scholar] [CrossRef]
- Middleton, G.V. Sediment Deposition from Turbidity Currents. Annu. Rev. Earth Planet. Sci. 1993, 21, 89–114. [Google Scholar] [CrossRef]
- Agemar, T.; Weber, J.; Schulz, R. Deep Geothermal Energy Production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Filomena, C.M.; Hornung, J.; Stollhofen, H. Assessing accuracy of gas-driven permeability measurements: A comparative study of diverse Hassler-cell and probe permeameter devices. Solid Earth 2014, 5, 1–11. [Google Scholar] [CrossRef]
- Bär, K. Untersuchung der tieFengeothermischen Potenziale von Hessen; Technische Universität Darmstadt: Darmstadt, Germany, 2012; p. 297. [Google Scholar]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Simard, R.; Ecuyer, P. Computing the Two-Sided Kolmogorov-Smirnov Distribution. J. Stat. Softw. 2011, 1. [Google Scholar] [CrossRef]
- Tukey, J. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977; p. 712. [Google Scholar]
- Corbett, P.; Jensen, J.L. Estimating the mean permeability: How many measurements do you need? First Break 1992, 10, 5. [Google Scholar] [CrossRef]
- Catmull, E. A Subdivision Algorithm for Computer Display of Curved Surfaces; University of Utah: Salt Lake City, Utah, 1974. [Google Scholar]
- Journel, A.G. Geostatistics: Models and tools for the earth sciences. Math. Geol. 1986, 18, 119–140. [Google Scholar] [CrossRef]
- Matheron, G. The intrinsic random functions and their applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef]
- Mantoglou, A.; Wilson, J.L. The Turning Bands Method for simulation of random fields using line generation by a spectral method. Water Resour. Res. 1982, 18, 1379–1394. [Google Scholar] [CrossRef]
- Emery, X.; Lantuéjoul, C. TBSIM: A computer program for conditional simulation of three-dimensional Gaussian random fields via the turning bands method. Comput. Geosci. 2006, 32, 1615–1628. [Google Scholar] [CrossRef]
- Paravarzar, S.; Emery, X.; Madani, N. Comparing sequential Gaussian and turning bands algorithms for cosimulating grades in multi-element deposits. Comptes Rendus Geosci. 2015, 347, 84–93. [Google Scholar] [CrossRef]
Sample Availability: The investigated rock samples are available at the Institute of Applied Geosciences
Darmstadt and can be requested under linsel@geo.tu-darmstadt.de. Moreover, the samples are registered in the
System for Earth Sample Registration (SESAR, www.geosamples.org). |
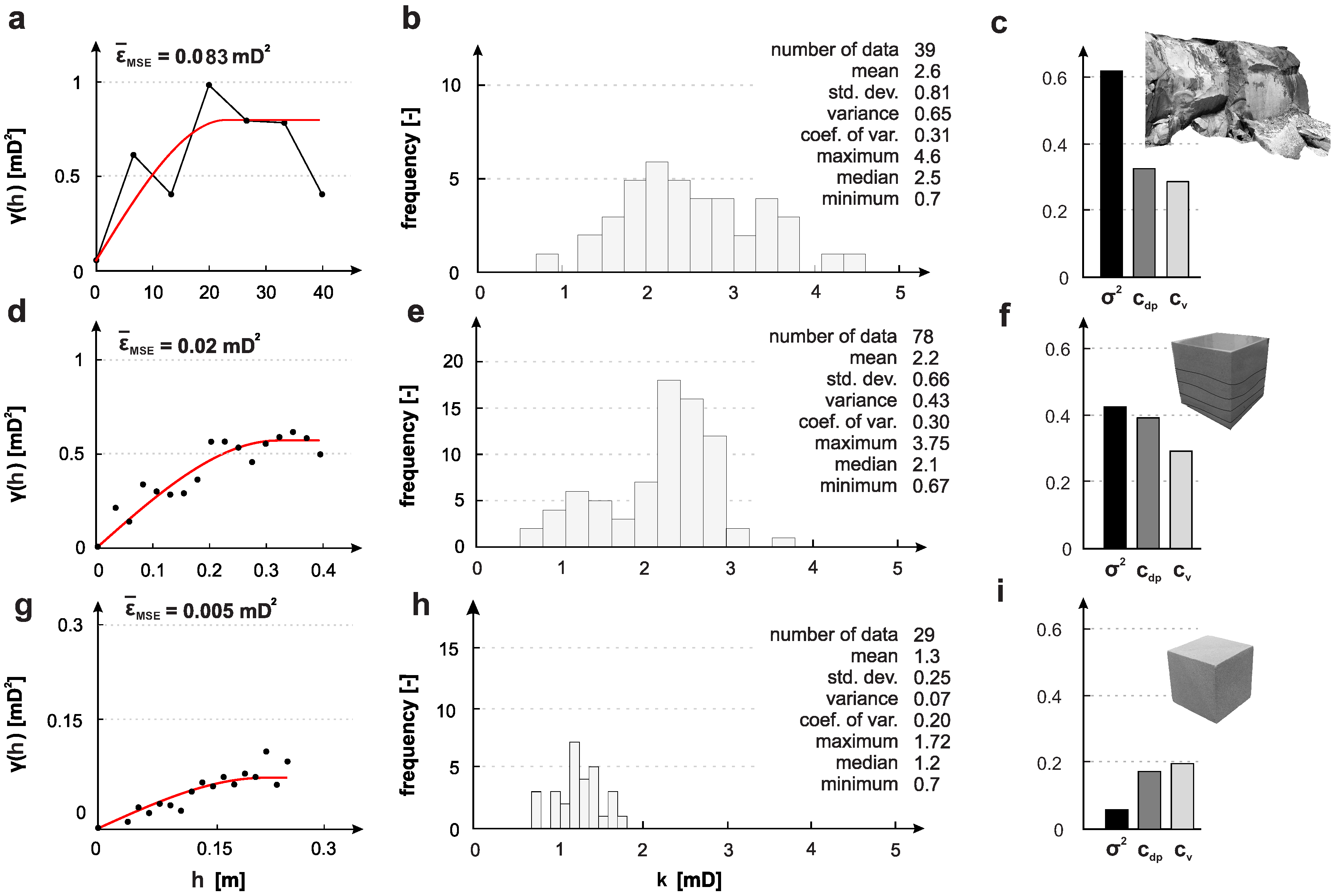
| Object | [-] | [-] | V [m] | [m] |
|---|---|---|---|---|
| Outcrop () | 82,000 | 75,240 | 9000 | 0.12 |
| OSB1_c () | 68,921 | 64,000 | 0.0156 | 6.19 |
| OSB2_c () | 31,500 | 25,230 | 0.008 | 1.25 |
| Variable | SGS & LVM-SGS | DSS & LVM-DSS |
|---|---|---|
| BLUE | SK | SK |
| Normal score transform | yes | no |
| Quantile-quantile back transform | yes | yes |
| Range x | 50 m | 50 m |
| Range y | 50 m | 50 m |
| Range z | 15 m | 15 m |
| Nugget | 0.05 | 0 |
| Sill | 0.75 mD | 1 mD |
| Range | 23 m | 23 m |
| Max. number of neighbors | 20 | 20 |
| Azimuth | 0 | 0 |
| Dip | 0 | 0 |
| Plunge | 10 | 10 |
| Measurement error variance | 0.15 mD | 0.15 mD |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linsel, A.; Wiesler, S.; Haas, J.; Bär, K.; Hinderer, M. Accounting for Local Geological Variability in Sequential Simulations—Concept and Application. ISPRS Int. J. Geo-Inf. 2020, 9, 409. https://doi.org/10.3390/ijgi9060409
Linsel A, Wiesler S, Haas J, Bär K, Hinderer M. Accounting for Local Geological Variability in Sequential Simulations—Concept and Application. ISPRS International Journal of Geo-Information. 2020; 9(6):409. https://doi.org/10.3390/ijgi9060409
Chicago/Turabian StyleLinsel, Adrian, Sebastian Wiesler, Joshua Haas, Kristian Bär, and Matthias Hinderer. 2020. "Accounting for Local Geological Variability in Sequential Simulations—Concept and Application" ISPRS International Journal of Geo-Information 9, no. 6: 409. https://doi.org/10.3390/ijgi9060409
APA StyleLinsel, A., Wiesler, S., Haas, J., Bär, K., & Hinderer, M. (2020). Accounting for Local Geological Variability in Sequential Simulations—Concept and Application. ISPRS International Journal of Geo-Information, 9(6), 409. https://doi.org/10.3390/ijgi9060409





