A Vector Line Simplification Algorithm Based on the Douglas–Peucker Algorithm, Monotonic Chains and Dichotomy
Abstract
1. Introduction
2. Methodology
2.1. Basic Theory of the Douglas–Peucker (D–P) Algorithm
2.2. Monotonic Chains and Dichotomy
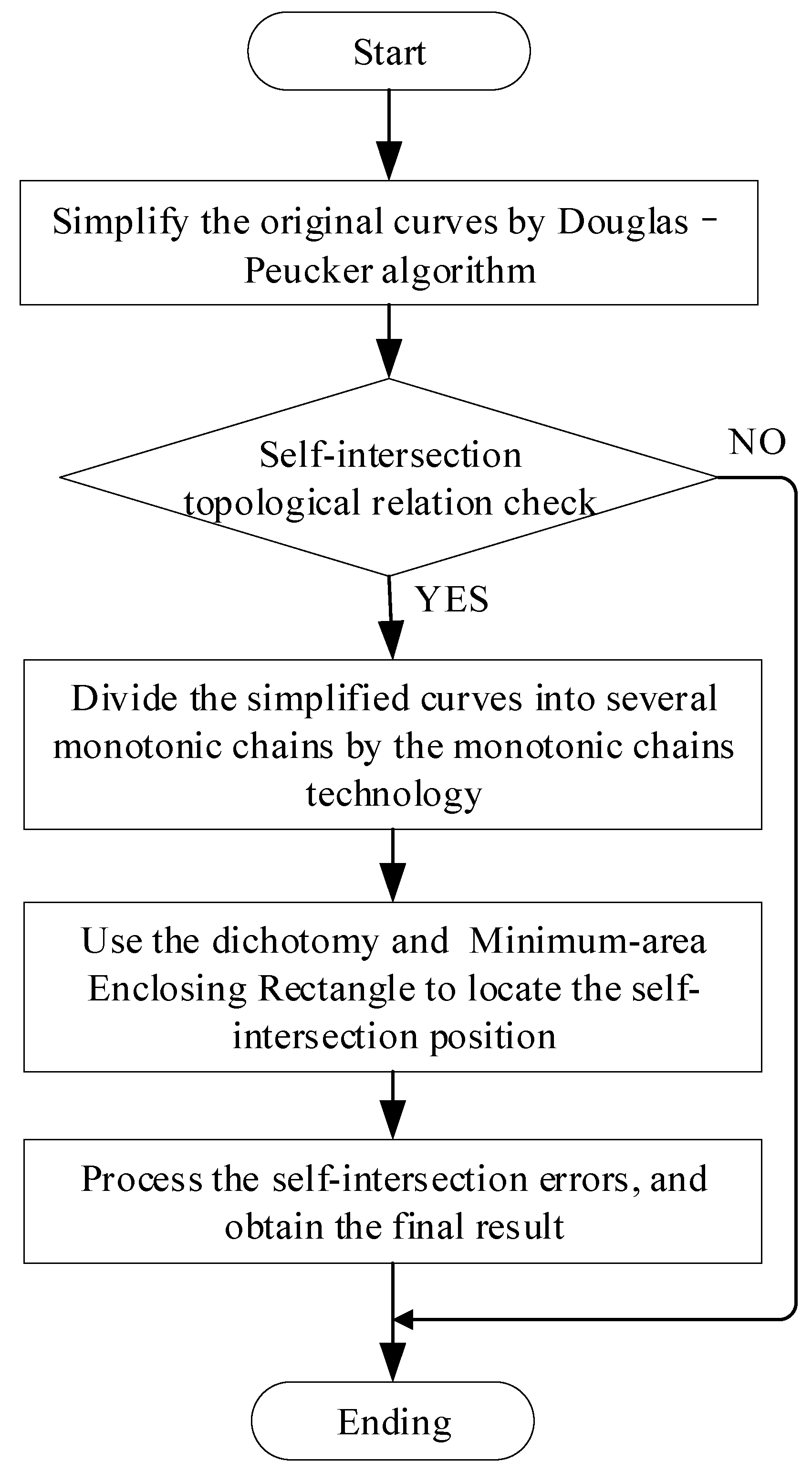
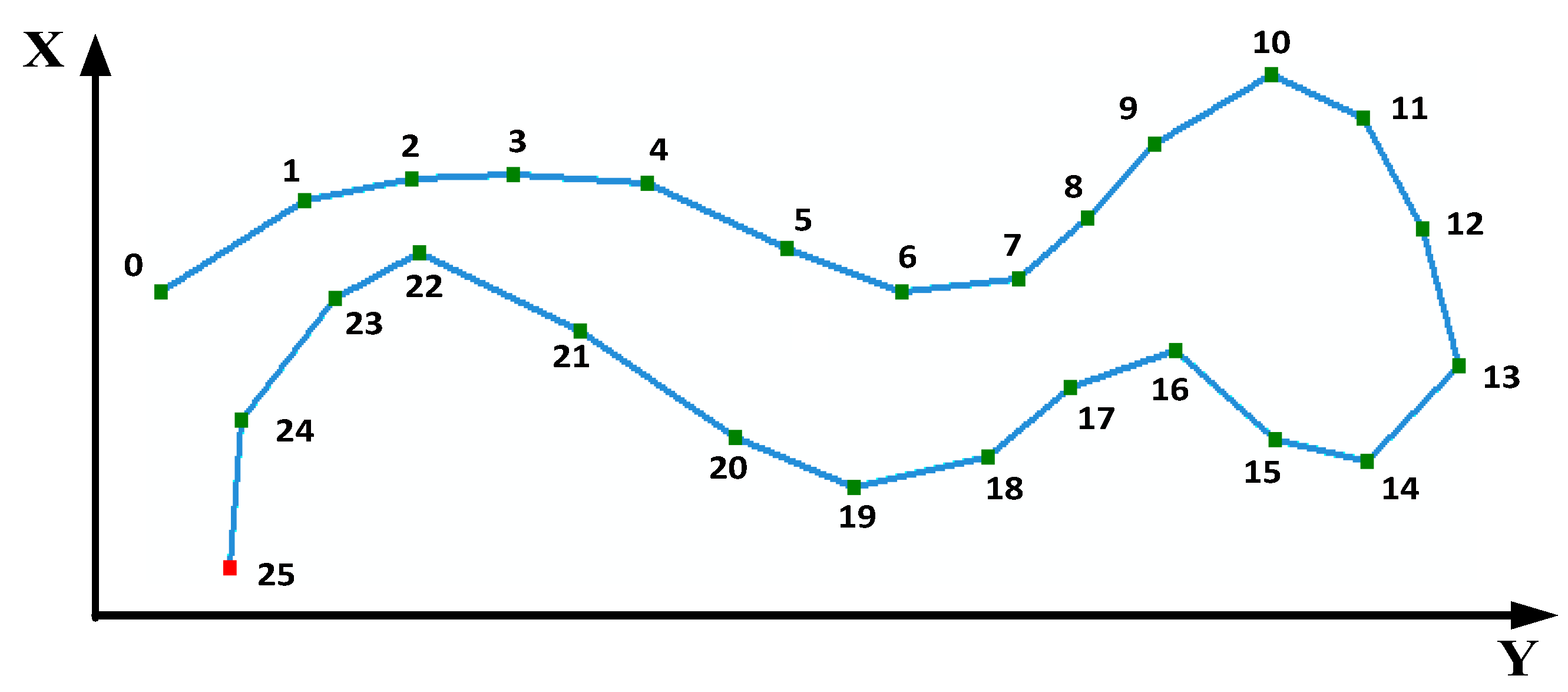
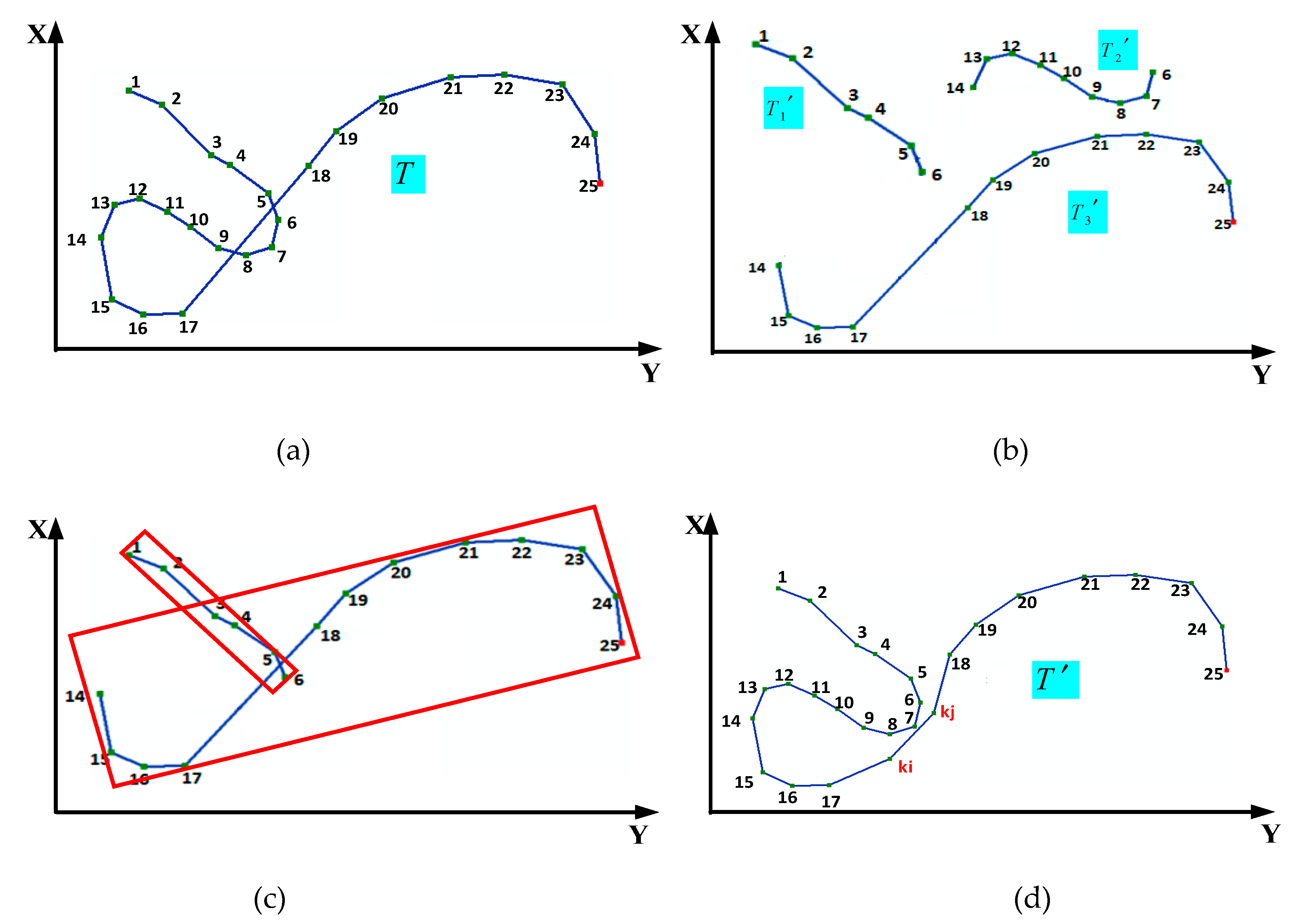
2.3. The New Vector Line Simplification Algorithm based on the D–P Algorithm, Monotonic Chains and Dichotomy
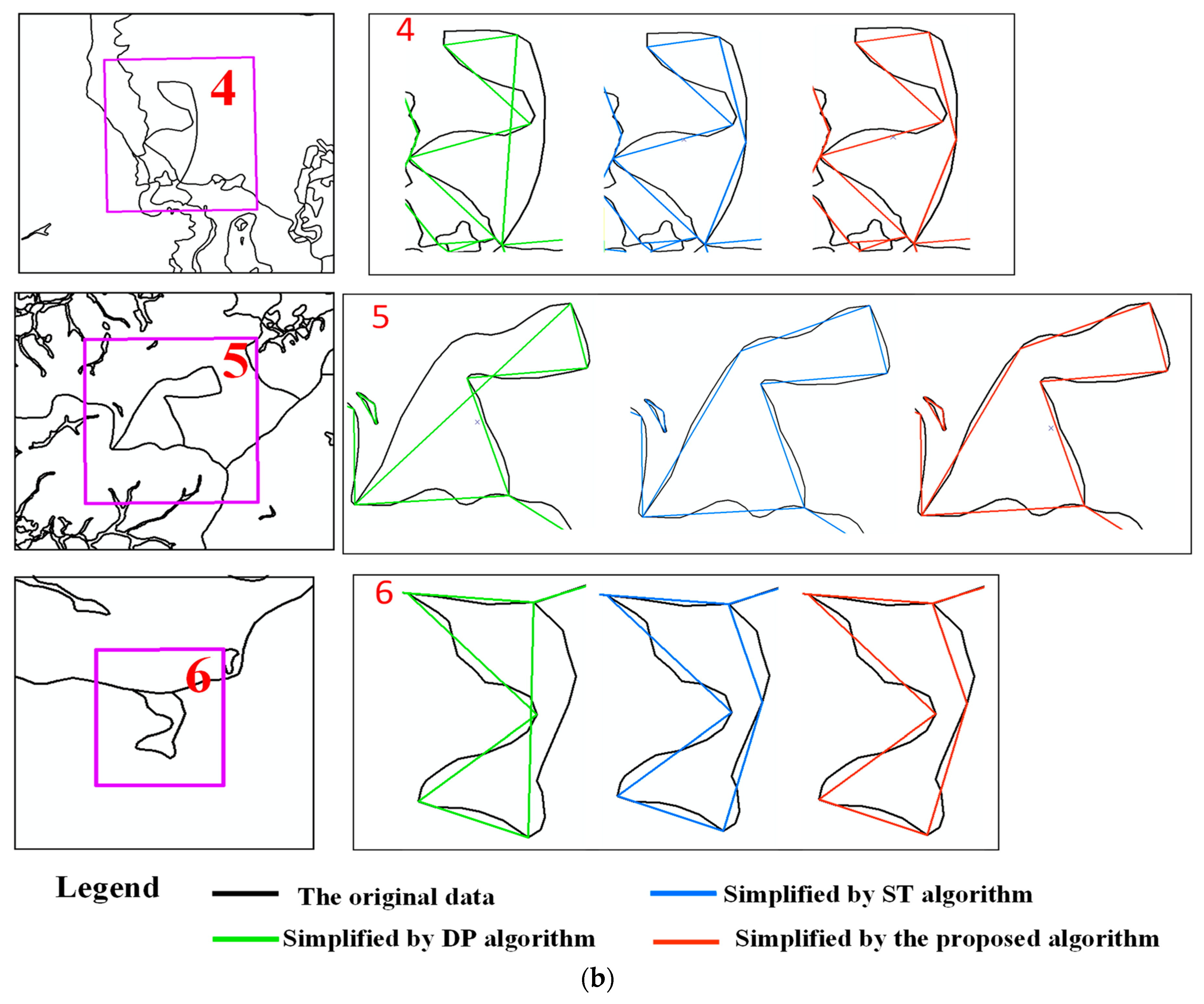
3. Experiments and Analysis
3.1. Assessment
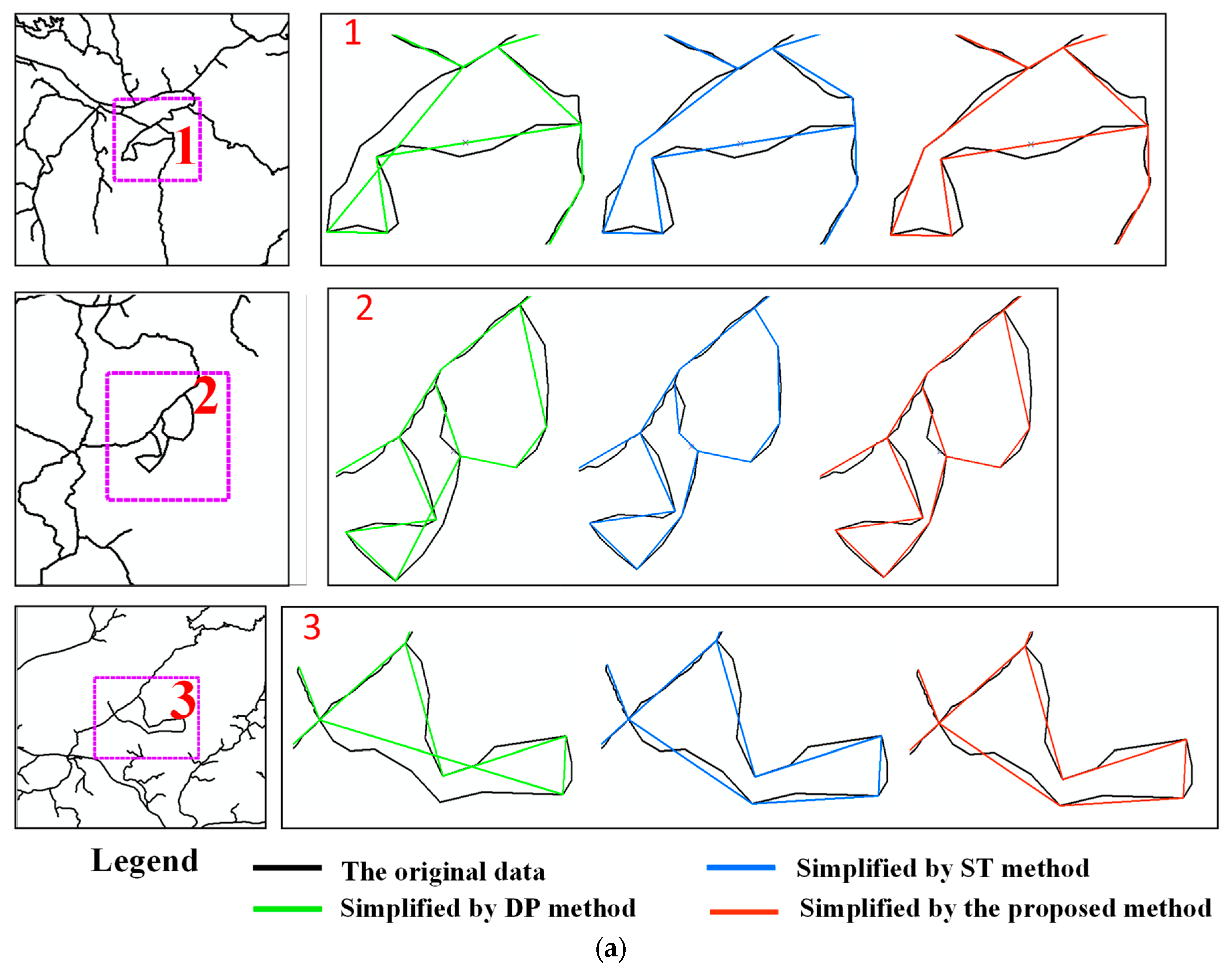
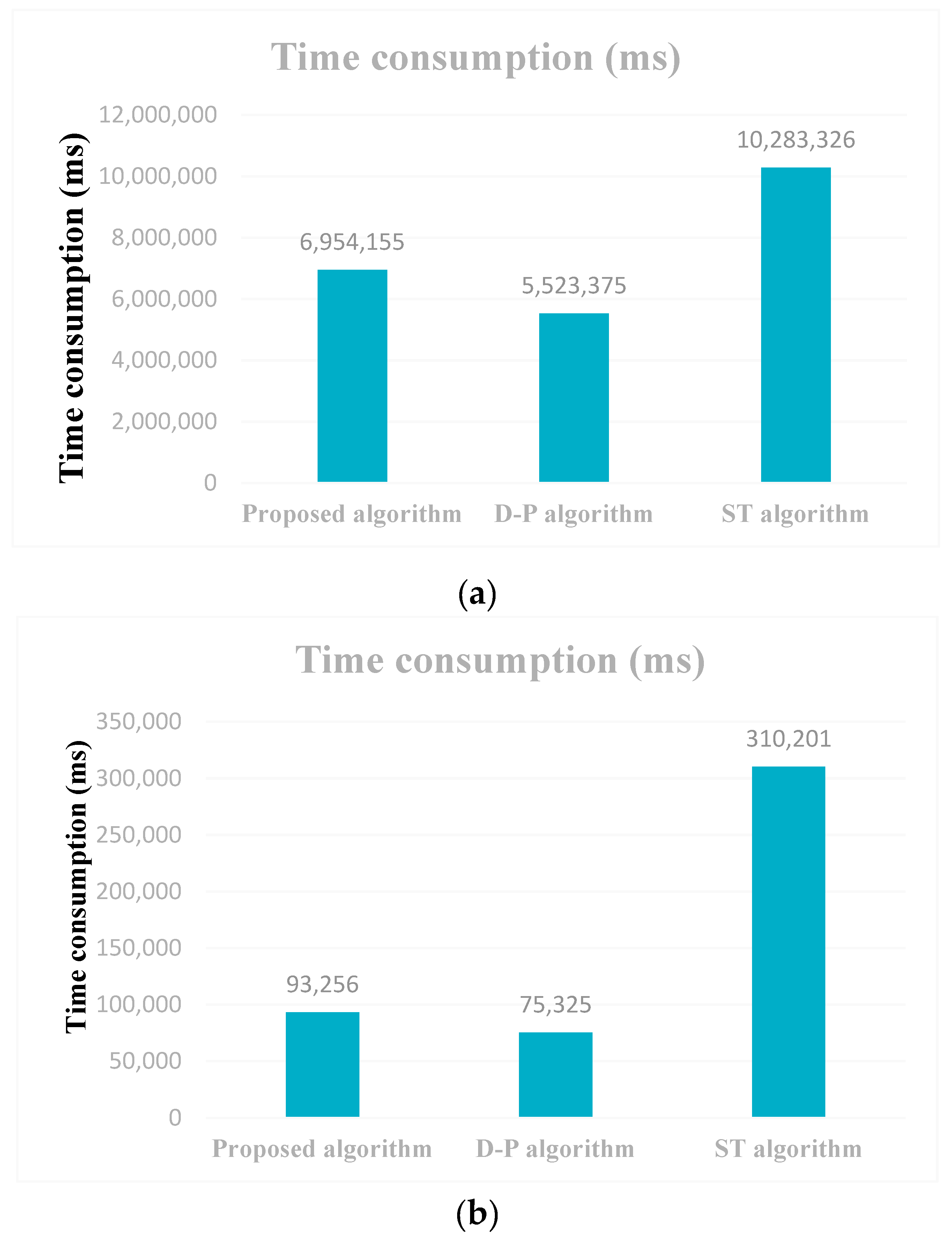
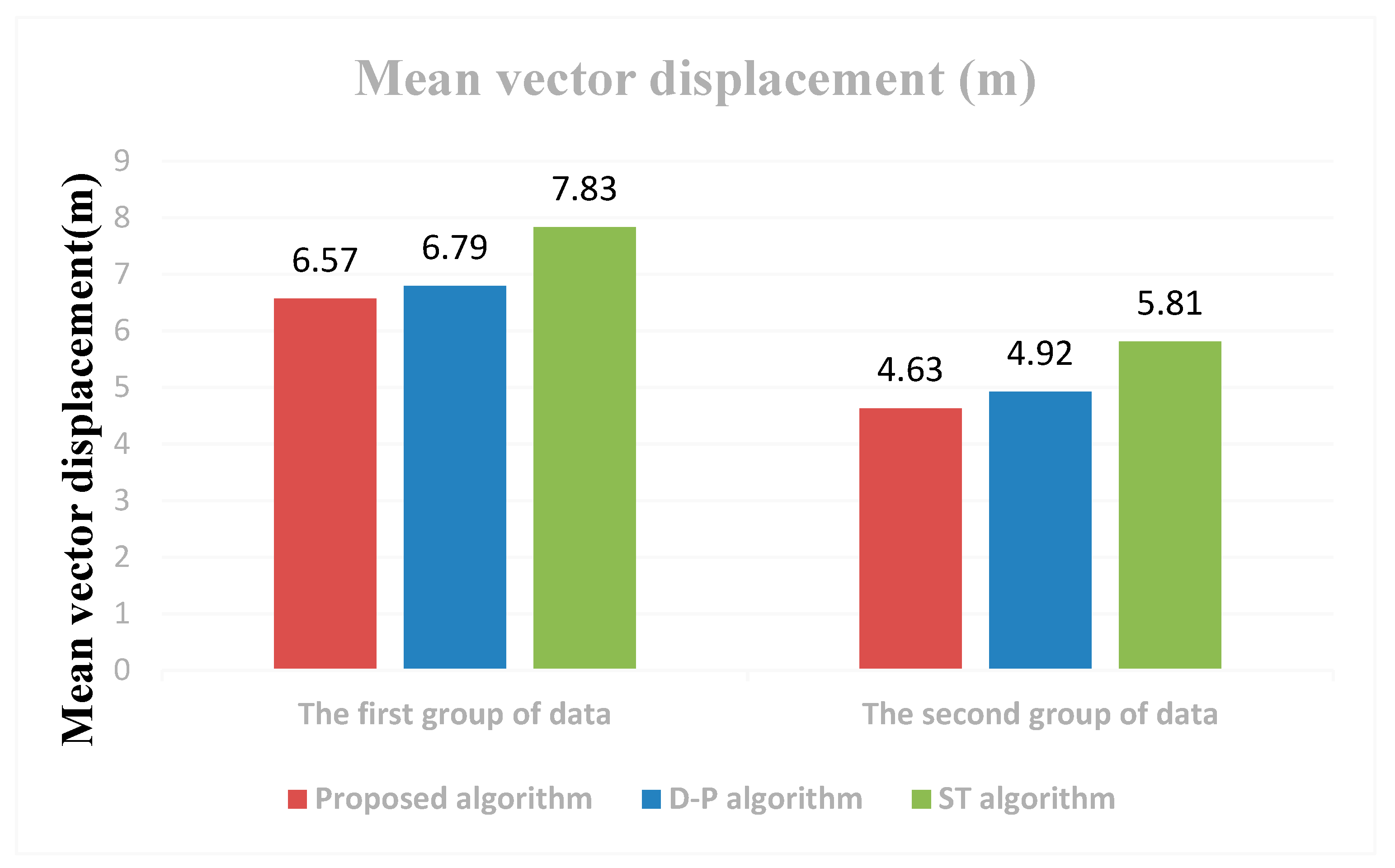
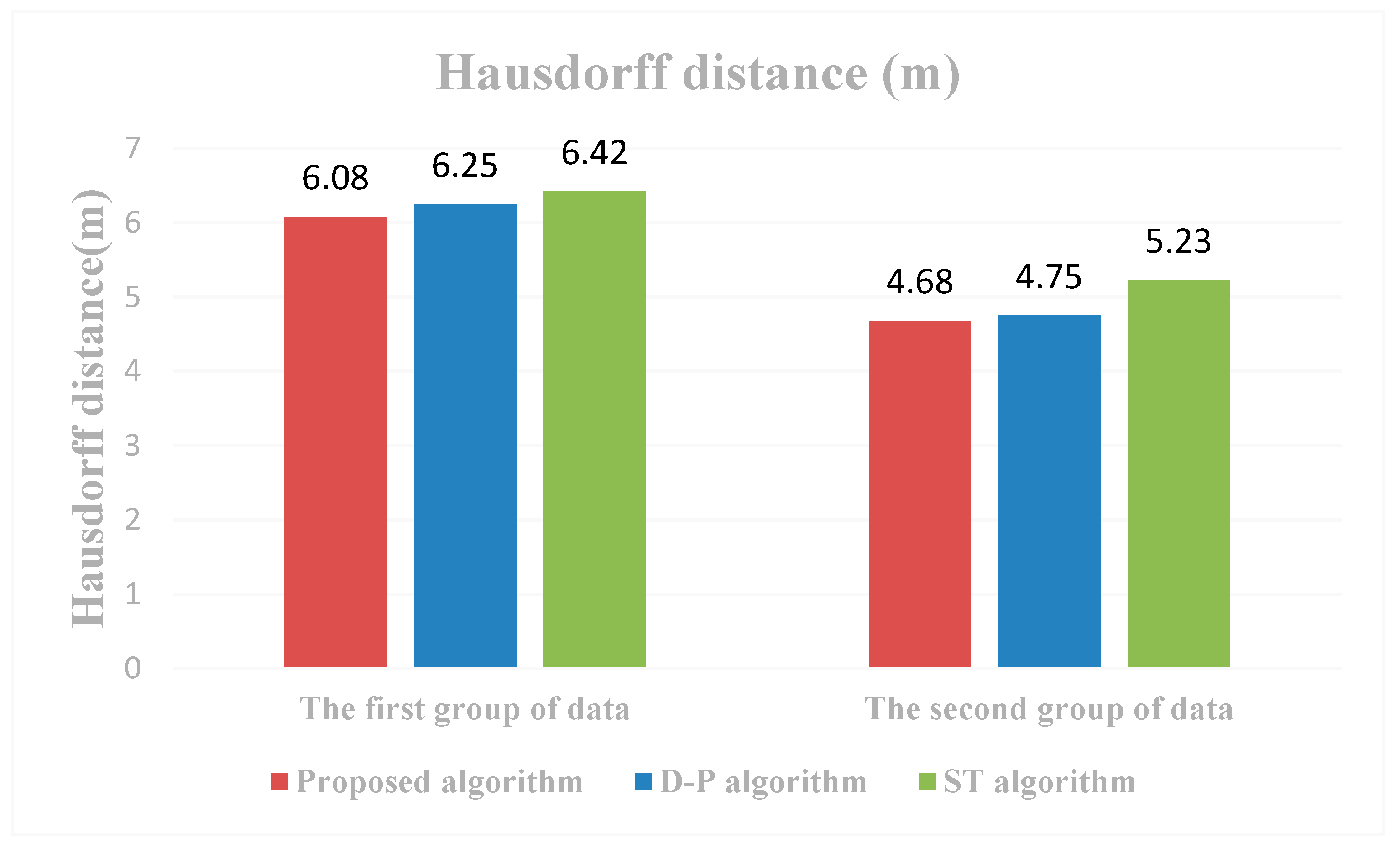
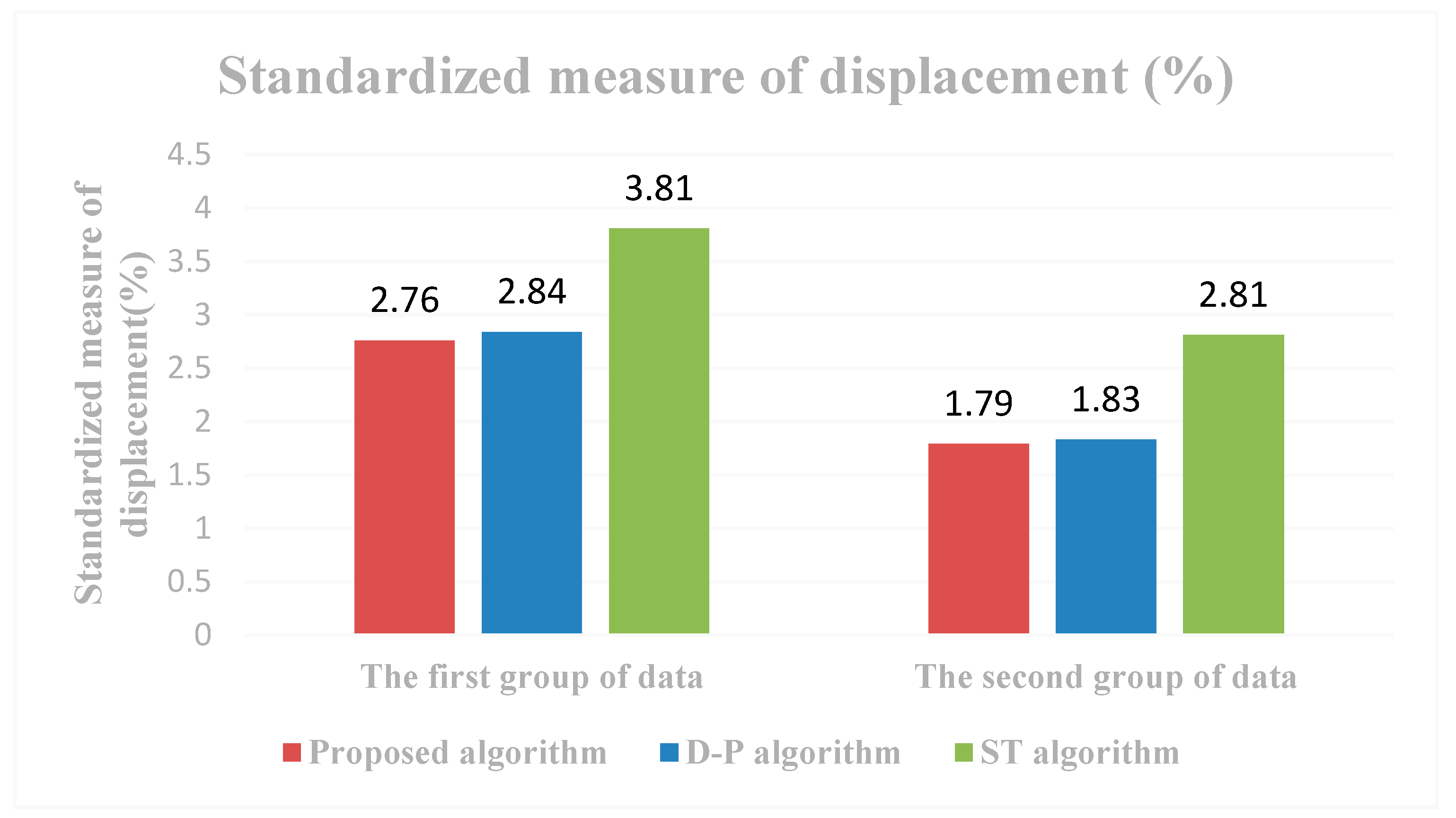
3.2. Results
3.3. Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Ramer, U. An iterative procedure for the polygonal approximation of plane curves. Comput. Graph. Image Process. 1972, 1, 244–256. [Google Scholar] [CrossRef]
- Lang, T. Rules for robot draughtsmen. Geogr. Mag. 1969, 42, 50–51. [Google Scholar]
- McMaster, R.B. The integration of simplification and smoothing algorithms in line generalization. Can. Cartogr. 1989, 26, 101–121. [Google Scholar] [CrossRef]
- Li, Z.L. An Algorithm for Compressing Digital Contour Data. Cartogr. J. 1988, 25, 143–146. [Google Scholar] [CrossRef]
- Visvalingam, M.; Whyatt, J. Line generalisation by repeated elimination of the smallest area. Technical Report, Discussion Paper 10, Cartographic Information Systems Research Group (CISRG); The University of Hull: Hull, UK, 1992. [Google Scholar]
- Ratschek, H.; Rokne, J.; Leriger, M. Robustness in GIS algorithm implementation with application to line simplification. Int. J. Geogr. Inf. Sci. 2001, 15, 707–720. [Google Scholar] [CrossRef]
- Wang, Z.S.; Muller, J.-C. Line Generalization Based on Analysis of Shape Characteristics. Cartogr. Geogr. Inf. Syst. 1998, 25, 3–15. [Google Scholar] [CrossRef]
- Zhao, Z.; Saalfeld, A. Linear-Time Sleeve-Fitting Polyline simplification algorithms. In Proceedings of the AutoCarto 13, Seattle, WA, USA, 7–10 April 1997; Published by American Congress on Surveying and Mapping & American Society for Photogrammetry and Remote Sensing, Maryland. pp. 214–223, ISBN -1-57083-043-6. [Google Scholar]
- Gary, R.H.; Wilson, A.D.; Archuleta, C.M.; Thompson, F.E.; Vrabel, J. Production of a National 1:1000000-Scale Hydrography Dataset for the United States: Feature selection, Simplification, and Refinement; U.S. Geological Survey Scientific Investigations Report 2009–5202. Revised May 2010; U.S. Geological Survey: Reston, VA, USA, 2010; 22p. [CrossRef]
- Li, Z.L.; Openshaw, S. Algorithms for automated line generalization based on a natural principle of objective generalization. Int. J. Geogr. Inf. Sci. 1992, 6, 373–389. [Google Scholar] [CrossRef]
- Samsonov Timofey, E.; Yakimova, O.P. Shape adaptive geometric simplification of heterogeneous line datasets. Int. J. Geogr. Inf. Sci. 2017, 31, 1485–1520. [Google Scholar] [CrossRef]
- de Berg, M.; van Kreveld, M.; Overmars, M.; Overmars, M.; Schwarzkopf, O. Computational Geometry: Algorithms and Applications, 2nd ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Cromley, R.G. Principal axis line simplification. Comput. Geosci. 1992, 18, 1003–1011. [Google Scholar] [CrossRef]
- Raposo, P. Scale-specific automated line simplification by vertex clustering on a hexagonal tessellation. Cartogr. Geogr. Inf. Syst. 2013, 40, 427–443. [Google Scholar] [CrossRef]
- Kronenfeld, B.J.; Stanislawski, L.V.; Buttenfield, B.P.; Tyler, B. Simplification of polylines by segment collapse: Minimizing areal displacement while preserving area. Int. J. Cartogr. 2020, 6, 22–46. [Google Scholar] [CrossRef]
- Shi, W.Z.; Cheung, C.K. Performance Evaluation of Line Simplification Algorithms for Vector Generalization. Cartogr. J. 2006, 43, 27–44. [Google Scholar] [CrossRef]
- Mi, X.J.; Sheng, G.M.; Zhang, J.; Bai, H.X.; Hou, W. A new algorithm of vector date compression based on the tolerance of area error in GIS. Sci. Geogr. Sin. 2012, 32, 1236–1240. [Google Scholar]
- Saalfeld, A. Topologically consistent line simplification with the Douglas-Peucker algorithm. Cartogr. Geogr. Inf. Sci. 1999, 26, 7–18. [Google Scholar] [CrossRef]
- Ho, P.S.; Kim, M.H. A hierarchical scheme for representing curves without self-intersections. In Proceedings of the 2001 IEEE Computer Society Conference (CVPR 2001), Kauai, HI, USA, 8–14 December 2001. [Google Scholar] [CrossRef]
- Mantler, A.; Snoeyink, J. Safe sets for line simplification. In 10th Annual Fall workshop on Computational Geometry; Stony Brok University: New York, NY, USA, 2000; Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi.10.1.1.32.402 (accessed on 29 March 2020).
- Avelar, S.; Müller, M. Generating topologically correct schematic maps. In Proceedings of the 9th International Symposium on Spatial Data Handling; Technical Report; Swiss Federal Institute of Technolog Zurich: Zurich, Switzerland, 2000; pp. 4–28. [Google Scholar] [CrossRef]
- Wu, S.T.; Marquez, M.R.G. A non-self-intersection Douglas-Peucker algorithm. In Proceedings of the 16th Brazilian Symosium on Computer Graphics and Image Processing (SIBGRAPI), Sao Carlos, Brazil, 12–15 October 2003. [Google Scholar] [CrossRef]
- Ebisch, K. Short note: A correction to the Douglas-Peucker line generalization. Comput. Geosci. 2002, 28, 995–997. [Google Scholar] [CrossRef]
- Yan, H.W.; Wang, M.X.; Wang, Z.H. Computational Geometry: Spatial Data Processing Algorithm; Science Press: Beijing, China, 2012. [Google Scholar]
- White, E.R. Assessment of line-generalization algorithms using characteristic points. Cartogr. Geogr. Inf. Sci. 1985, 12, 17–28. [Google Scholar] [CrossRef]
- Hangouët, J.F. Computation of the Hausdorff distance between plane vector polylines. In Auto-Carto XII: Proceedings of the International Symposium on Computer-Assisted Cartography, Charlotte, North Carolina; American Congress on Surveying and Mapping & American Society for Photogrammetry and Remote Sensing: Gaithersburg, MD, USA, 1995; Volume 4, pp. 1–10. ISBN -1-57083-019-3. [Google Scholar]
- Joao, E.M. Gauses and Consequences of Map Generalization; Taylor and Francis: London, UK, 1998. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Liu, X.; Li, D.; Shi, Y.; Fernandez, G.; Wang, Y. A Vector Line Simplification Algorithm Based on the Douglas–Peucker Algorithm, Monotonic Chains and Dichotomy. ISPRS Int. J. Geo-Inf. 2020, 9, 251. https://doi.org/10.3390/ijgi9040251
Liu B, Liu X, Li D, Shi Y, Fernandez G, Wang Y. A Vector Line Simplification Algorithm Based on the Douglas–Peucker Algorithm, Monotonic Chains and Dichotomy. ISPRS International Journal of Geo-Information. 2020; 9(4):251. https://doi.org/10.3390/ijgi9040251
Chicago/Turabian StyleLiu, Bo, Xuechao Liu, Dajun Li, Yu Shi, Gabriela Fernandez, and Yandong Wang. 2020. "A Vector Line Simplification Algorithm Based on the Douglas–Peucker Algorithm, Monotonic Chains and Dichotomy" ISPRS International Journal of Geo-Information 9, no. 4: 251. https://doi.org/10.3390/ijgi9040251
APA StyleLiu, B., Liu, X., Li, D., Shi, Y., Fernandez, G., & Wang, Y. (2020). A Vector Line Simplification Algorithm Based on the Douglas–Peucker Algorithm, Monotonic Chains and Dichotomy. ISPRS International Journal of Geo-Information, 9(4), 251. https://doi.org/10.3390/ijgi9040251




